Fault diagnosis methods for imbalanced samples of hydraulic pumps based on DA-DCGAN

Abstract

Status monitoring and fault diagnosis of mechanical equipment are vital for ensuring operational safety. However, real-world diagnostic scenarios often suffer from limited and imbalanced fault data, affecting model accuracy and reliability. This study addresses these challenges by focusing on bearings and hydraulic pumps as research objects. A dual attention-deep convolutional generative adversarial network (DA-DCGAN) is proposed to generate fault signals and enhance diagnosis under imbalanced conditions.Initially, fault vibration signals are converted into time-frequency maps using continuous wavelet transform (CWT) to highlight key features. These maps are used to train the DA-DCGAN, which generates additional fault samples to augment the imbalanced dataset. The expanded dataset is then used to train two classifiers, CNN and DA-CNN, to evaluate their ability to capture minority class fault features. Experimental evaluations on bearing and hydraulic pump datasets reveal that the proposed approach significantly improves classification performance across varying imbalance ratios.The results demonstrate that DA-DCGAN effectively enhances diagnostic accuracy and model generalization under imbalanced sample conditions, offering a robust solution for fault diagnosis in mechanical systems.

Introduction

The piston pump is the power element of a hydraulic system, offering the advantages of high-rated pressure, compact design, and high volumetric efficiency, and is widely used in heavy machinery, national defense equipment, and other fields. Typically, piston pumps operate under high-speed and high-pressure conditions. Identifying equipment failures and making accurate decisions promptly helps improve system operation efficiency, reduce maintenance costs, and even lower the risk of major catastrophic accidents. Therefore, researching fault diagnosis methods for piston pumps is essential. In recent years, some researchers have proposed novel adaptive multi-level feature learning frameworks that dynamically integrate online monitoring data with deep representation techniques, providing more efficient and intelligent solutions for the intelligent health management of pump equipment^{1– 2}.

The vibration, temperature, and sound data of mechanical equipment contain valuable information about its operational status³. Traditional fault diagnosis techniques typically rely on complex noise reduction, filtering, and feature extraction methods to process the collected equipment data, followed by approaches such as expert knowledge or machine learning to achieve fault classification. With the advancements in big data technology, deep learning empowers computers with the ability to learn, enabling them to analyze data, identify patterns, and derive insights, thus providing robust technical support for equipment fault diagnosis in the big data era. When encountering new equipment condition monitoring data, deep learning technology leverages the empirical knowledge gained from past experiences to make accurate judgments about equipment status⁴. Hence the fault diagnosis of mechanical equipment in the context of big data can be viewed as a way to accurately recognize the operating state of equipment based on the acquisition of the operating state of the equipment by sensors, and the accumulation of experience by deep learning, to realize the operating state of the equipment. These features not only contain familiar equipment information but also contain potential information that can help identify and locate faults. Therefore, more and more researchers are attracted to applying deep learning methods in the field of fault diagnosis⁵. However, deep learning techniques are based on the assumptions that the distribution of samples across categories is roughly balanced and that the misclassification cost is the same for all categories. In most real-world scenarios, these assumptions often do not hold⁶such as in cases of sporadic mechanical failures. Typically, in fault detection, the amount of normal condition data far exceeds the amount of fault data. Therefore, applying classification algorithms to fault detection and diagnosis with imbalanced data often leads to higher recognition rates for the majority class (normal conditions) and lower recognition rates for the minority class (fault conditions). However, in practical engineering applications, the recognition rates for the minority class are usually of greater importance. Paper^{7– 8} highlights that when traditional classification methods such as Decision Trees and Naive Bayes are applied to classify a breast cancer image dataset (comprising 10,923 healthy samples and 260 diseased samples) in medical and healthcare diagnostics, the accuracy for healthy samples reaches 100%, but for diseased samples, it drops to just 0–10%, This implies that at least 234 patients are misdiagnosed. Papers^{9– 10} further explore the relationship between the distribution of the training dataset and classifier performance, revealing that a relatively balanced class distribution typically produces better results. However, the sample size and sample dispersion also influence classification performance, making it challenging to qualitatively determine the extent to which class imbalance degrades classification performance. Efficiently addressing the issue of imbalanced data classification has thus become a critical bottleneck for successfully applying classification techniques to real-world problems. Papers^11,12,13,14 have significantly improved fault diagnosis performance for rotating machinery by integrating advanced signal processing techniques with machine learning. These approaches have shown promising progress in handling imbalanced datasets and monitoring single-component faults. Although system-level diagnosis is also developing, further research is needed in areas such as real-time algorithm deployment, multi-sensor information fusion, and adaptation to extreme operating conditions.

With the advancement of deep learning and the growing awareness of its heavy reliance on large datasets, generative models have started to gain attention from researchers. Generative models compute joint probability distributions, enabling them to capture the overall structure of the data. Early generative models, such as Gaussian Mixture Models and Hidden Markov Models, demonstrated good performance in addressing small-scale problems or scenarios with many constraints. However, as the complexity of the problems increased, shallow models could no longer meet the requirements, leading to the gradual evolution of generative models into deep generative models.

By Goodfellow et al.¹⁵Generative Adversarial Networks were proposed, offering a novel approach to addressing the data imbalance problem. GANs can generate artificial data that closely resembles real data, making them well-suited for handling imbalanced datasets.

GANs exhibited several notable shortcomings in their early stages of development¹⁶Such as: (1) Difficulty in achieving convergence during the training process. GAN training alternates between the generator and the discriminator, where for each update of the discriminator’s parameters, the generator’s parameters are updated multiple times. This imbalance makes it challenging to achieve stable training. (2) Mode collapse, especially when the number of real samples is small. This issue causes the generator to produce repetitive data, preventing GANs from learning the true distribution of the real data. To address these issues, both domestic and international scholars have proposed numerous derivative models. Common optimization approaches include modifications to network structures and improvements to loss functions, aiming to balance the modeling capabilities of the generator and the discriminator.

The Deep convolutional generative adversarial network (DCGAN)¹⁷ is a notable improvement in GAN models. DCGAN combines supervised learning CNN with unsupervised learning GAN by modifying the network structure. In DCGAN, the fully connected and pooling layers are replaced with convolutional layers in the generator’s architecture. Additionally, the introduction of batch normalization (BN) in both the generator and discriminator alleviates the problem of model instability and significantly enhances the model’s convergence performance.

Although fault diagnosis based on deep learning has shown promising results, it still faces significant limitations, which are reflected in the following aspects: (1) The performance of deep learning heavily depends on large-scale datasets. In real-world production conditions, although sensors can collect a substantial amount of mechanical operational data, the majority of it corresponds to the normal operating state, while fault state data is limited. This data imbalance hinders the neural network from learning effectively, thereby reducing the fault diagnosis accuracy of the model; (2) An imbalanced training set causes the model to become biased toward learning and memorizing the majority class (normal state) during training while neglecting the minority class (fault state). This leads to a high rate of false alarms and missed detections, compromising the model’s reliability¹⁸.

To address the above challenges, this paper combines the generative adversarial network (GAN) with the attention mechanism and incorporates the two-timescale updating rule (TTUR)¹⁹A novel fault sample generation method is proposed, integrating TTUR into the network’s training process, which achieves a more stable generation process and ensures higher similarity between the generated and real samples. The generated fault samples are subsequently utilized to expand the unbalanced dataset and are applied to the fault diagnosis of hydraulic pumps and bearings.

In this paper, a hydraulic pump fault diagnosis method based on data generation is proposed to address the issue of limited fault information caused by the scarcity of actual fault state data. First, one-dimensional fault signals are converted into two-dimensional image signals using continuous wavelet transform (CWT)²⁰ to fully leverage the advantages of DA-DCGAN in image processing. Next, to generate high-quality fault data, improvements are made to both the generator and discriminator, enabling fault sample generation. Channel and spatial features are captured using channel attention and spatial attention, resulting in the generation of high-quality feature images. Finally, the generated samples are incrementally added to the unbalanced dataset to create datasets with varying proportions of class imbalance. Two general classifiers are trained on these constructed datasets, and the method’s effectiveness and superiority in fault diagnosis under imbalanced sample conditions are validated using two device datasets.

The remainder of the paper is organized as follows: Section II provides a brief overview of the theories related to CWT, DCGAN, and attention mechanisms. Section III presents the proposed DA-DCGAN method in detail, including the overall framework, network training approach, and the construction of unbalanced datasets. Section IV describes the constant pressure variable pump fault simulation test. Finally, Section V concludes the paper.

Theoretical basis

Continuous wavelet transform (CWT)

The Fourier Transform (FT) converts complex signals from the time domain to the frequency domain for analysis. However, it fails to capture the signal’s information in the time dimension. For non-stationary signals, such as mechanical vibrations, the frequency domain characteristics vary over time. Therefore, understanding the frequency domain characteristics of vibration signals at any given moment is crucial, as time and frequency domains are inherently intertwined and cannot be analyzed in isolation. The Short-Time Fourier Transform (STFT) enhances the ability to perform local signal analysis by introducing a time window. However, the size and shape of this window remain fixed, making it incapable of adapting to the signal’s frequency, thereby limiting its ability to adjust time-frequency resolution dynamically. In contrast, the Continuous Wavelet Transform (CWT) builds upon the local analysis concept of STFT. By applying scaling and translation operations to the wavelet mother function, CWT achieves multi-scale signal refinement. This allows for time subdivision at high frequencies and frequency subdivision at low frequencies, effectively capturing the detailed characteristics of the signal. The mother wavelet function²¹ can be expressed by Eq. (1):

$${\psi _{a,b}}(t)=\frac{1}{{\sqrt {|a|} }}\psi \left( {\frac{{t - b}}{a}} \right)$$

(1)

.

The a is called the scale parameter, which is used to scale the basic wavelet transform, b is the translation parameter, which moves the wavelet function along the time axis. The continuous wavelet transform of the signal$f(t)$ can be expressed by Eq. (2):

$${W_f}(a,b)=\langle f(t),{\psi _{a,b}}(t)\rangle =\frac{1}{{\sqrt {|a|} }}\int_{R} f (t)\overline {{\psi \left( {\frac{{t - b}}{a}} \right)}} dt$$

(2)

.

$\overline {{\psi \left( {\frac{{t - b}}{a}} \right)}}$ is the complex conjugation of the function$\psi \left( {\frac{{t - b}}{a}} \right)$.

Generative adversarial network (GAN)

GAN is a generative network model whose core idea is to create new samples that share the same distribution as the original data by learning the distribution of real data or predicting its probability density function²²A generative adversarial network consists of two parts: the generator and the discriminator, which engage in an adversarial process during training. The generator takes an n-dimensional random noise input and produces new samples by learning the distribution of real data, aiming to generate samples indistinguishable from the real ones. Meanwhile, the discriminator, a binary classification network, evaluates whether the input data is real or generated. If the input is a real sample, the discriminator outputs 1; otherwise, it outputs 0.

During the training process of a Generative Adversarial Network (GAN), the generator and discriminator train in opposition to each other. The generator’s objective is to produce samples with probability distributions increasingly close to the real data, while the discriminator’s goal is to enhance its ability to distinguish between real and generated samples. Through gradient backpropagation, the two networks iteratively optimize their performance until achieving a Nash equilibrium, where neither can improve without altering the other’s outcome. The loss functions for the generator and discriminator networks²³ are expressed as follows:

$${L_G}={E_{z\sim {p_z}}}\log \left( {1 - D(G(z))} \right)$$

(3)

$${L_D}={E_{x\sim {p_{\text{d}\text{a}\text{t}\text{a}}}(x)}}[\log D(x)]+{E_{z\sim {p_z}}}[\log (1 - D(G(z)))]$$

(4)

.

where $x\sim {p_{\text{d}\text{a}\text{t}\text{a}}}(x)$ denotes the statistical distribution that the true data x conforms to ${p_{\text{d}\text{a}\text{t}\text{a}}}(x)$, $z\sim {p_z}$ denotes the statistical distribution that the generated data z conforms to ${p_z}$. $D(x)$ denotes the probability that the original sample X is judged to be true, and $D(G(z))$ denotes the probability that the generated sample is identified as true by the discriminator D.

Attention mechanism

Attention mechanisms have emerged as crucial tools in natural language processing and computer vision^{24– 25}. The introduction of attention mechanisms enables networks to focus on important regions of an image, enhancing the model’s ability to learn relevant features. This focus not only accelerates network training but also improves the quality of image generation by allowing the network to prioritize key information. Paper²⁶ firstly presents the attention mechanism for Neural Machine Translation (NMT). This mechanism allows the model to dynamically select relevant parts of the source sentence during translation, thus improving the translation quality. Vision Transformer (ViT) was proposed in the paper²⁷and the application of the Transformer to image categorization tasks demonstrated that the attention mechanism also has a strong potential in the field of computer vision. Subsequently, OpenAI proposed a series of Generative Pre-trained Transformer (GPT) based on the Transformer architecture, which performed well in the task of generating text, demonstrating the important role of the attention mechanism in capturing the temporal relationship between pre and post-text. The Convolutional Block Attention Mechanism (CBAM) proposed in this paper²⁸ is a simple and effective attention module that infers an attention map along the order of the channel and spatial dimensions of the feature map and then performs adaptive feature refinement of the attention map with the feature map. Its advantage lies in the fact that it can be integrated into any neural network and can significantly improve the feature extraction capability of the network to the extent that it introduces little computational effort. In recent years, the self-attention mechanism and multi-head attention mechanism have also been applied in the diagnostic field after combining with convolutional neural networks and recurrent neural networks, which have significantly improved the anti-interference ability of the models^29,30,31. Attentional mechanisms introduced into GAN for vibration data generation tasks²²The time-attention and channel-attention mechanisms can focus on the signal distance dependence and no longer focus on a region independently, and experimental results show that they can significantly improve the quality of synthetic vibration data.

Two time-scale update rule (TTUR)

The dual time scale update rule is a simpler and more effective update strategy: using a smaller learning rate to update the generator and a larger learning rate to update the discriminator, allowing the discriminator to converge more quickly¹⁹. In the training process, set the discriminator parameter to be$\omega :D(.;\omega )$, and the generator parameter to be $\theta :G(.;\theta )$ The stochastic gradient of the discriminator is $\tilde {d}(\theta ,\omega )$, and the stochastic gradient of the generator is $\tilde {g}(\theta ,\omega )$. The random variables ${M^{(\omega )}}$ and ${M^{(\theta )}}$ are defined as follows:

$$\left\{ \begin{gathered} \tilde {g}(\theta ,\omega )=g(\theta ,\omega )+{M^{(\omega )}} \hfill \\ \tilde {d}(\theta ,\omega )=d(\theta ,\omega )+{M^{(\theta )}} \hfill \\ \end{gathered} \right.$$

(5)

.

in which $d(\theta ,\omega )={\nabla _\omega }{L_D},g(\theta ,\omega )={\nabla _\theta }{L_G}$ are the gradients of the real and generated samples, respectively. Set the learning rate of the discriminator D to be $b(n)$, and the learning rate of the generator G to be $a(n)$:

$$\left\{ \begin{gathered} {\omega _{{\text{n}}+1}}={\omega _n}+b(n)\tilde {g}(\theta ,\omega ) \\ {\theta _{{\text{n}}+1}}={\theta _n}+a(n)\tilde {d}(\theta ,\omega ) \\ \end{gathered} \right.$$

(6)

.

Fault sample generation method based on DA-DCGAN

In this section, the general framework of the proposed dual-attention generative adversarial network is first introduced, followed by two attentional mechanisms for capturing long-range feature information in spatial and channel dimensions in DCGAN, and finally, a methodology for fault diagnosis of hydraulic pumps based on dual-attention deep convolutional generative adversarial network (DA-DCGAN) under data imbalance conditions is presented.

General architecture of the methodology

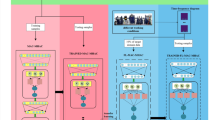
Hydraulic pumps operate in a healthy state for the vast majority of the time, and engineering fault data is more difficult to obtain compared to health data. The purpose of the fault diagnosis method proposed in this paper is to solve the data imbalance problem due to small samples. To this end, a DA-DCGAN incorporating spatial attention mechanism and channel attention mechanism is proposed as a way to improve the sample generation capability of DCGAN. Subsequently, a sufficient number of fault samples are generated by DA-DCGAN, and finally, fault diagnosis is performed on the balanced dataset. The overall flow of the proposed method is shown in Fig. 1 and the main steps are summarized as follows:

• (1) The vibration signal is divided into multiple segments according to the experimental speed setting, and then the time series is converted into 2D time-frequency images by CWT.

• (2) Input the time-frequency image into DA-DCGAN to learn the characteristics of fault data and generate corresponding fault samples.

• (3) Subsequently, the generated fault samples are gradually expanded into the original unbalanced fault sample set to form multiple proportional unbalanced sample sets.

• (4) Use the unbalanced sample sets formed in step 3) to train the classification models separately, and then use the same test set to test the classification models trained by different unbalanced sample sets, output the diagnostic results, and use the diagnostic accuracy and clustering effect to evaluate the fault diagnosis capability of the classification models.

Fig. 1

Overall framework of the proposed method.

Dual attention (DA)

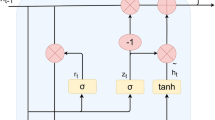
• (1) Channel attention mechanism (CAM): each channel map of a high-dimensional feature can be regarded as a response of a specific class and different feature responses are correlated with each other, by capturing the correlation between the channels, the feature representation of a specific fault can be effectively obtained³²This improves the feature representation of specific faults, enabling the GAN to generate higher quality fault samples. Therefore CAM is introduced in GAN to extract the channel feature information. The structure of CAM is shown in Fig. 2, and the computation of CAM³³ is shown in the Eq. (7):

$$\left\{ \begin{gathered} {x_{ji}}=\frac{{\exp ({{\varvec{A}}_i} \cdot {{\varvec{A}}_j})}}{{\Sigma _{{i=1}}^{C}\exp ({{\varvec{A}}_i} \cdot {{\varvec{A}}_j})}} \hfill \\ {{\varvec{E}}_j}=\beta \Sigma _{{i=1}}^{C}({x_{ji}}{{\varvec{A}}_i})+{{\varvec{A}}_j} \hfill \\ \end{gathered} \right.$$

(7)

where ${x_{ji}}$ denotes the effect of the ith channel on the jth channel in the feature map A, $\beta$is the scaling factor, and E is the output of the CAM.

• (2) Spatial attention mechanism (SAM): the spatial attention mechanism is concerned with the positional feature information in the time-frequency image. To compute the spatial attention, the average pooling and maximum pooling operations are first performed on the feature map along the channel axis, and then the feature map is spliced in the third dimension, and the spatial attention map is generated using a convolutional layer (convolutional kernel size $7 \times 7$), which will adaptively learn the important features and assign different degrees of weight to the features at different locations.

The structure of SAM is shown in Fig. 2, and the spatial attention is calculated in the following Eq. 2⁰:

$${{\mathbf{M}}_{\mathbf{s}}}({\varvec{F}})=\sigma ({f^{7 \times 7}}([AvgPool({\varvec{F}});MaxPool({\varvec{F}})]))$$

(8)

.

where $\sigma$ denotes the sigmoid function, ${f^{7 \times 7}}$ denotes the convolution operation, and F denotes the input features.

Fig. 2

Structure of the dual-Attention Network.

Taking advantage of the attention mechanism of the dual attention network, while focusing on the frequency features in the time-frequency diagram of the vibration signal, the dependence between the sample channels can also be captured effectively, realizing the efficient capture of the fault features in both channels and space.

DA-DCGAN

The activation mappings from each channel can be thought of as fault-specific responses, and these mappings are related to each other¹⁴. Existing GANs’ generators and discriminators treat all channel features equally and cannot adaptively determine the importance of different channels, which hampers the generative power of GANs. By exploiting the complex dependencies between channels, the network can efficiently capture cross-channel interaction information and improve the feature representation of specific faults to generate high-quality fault samples for DA-DCGAN. Therefore, in this paper, we construct a channel attention module to recalibrate cross-channel feature responses, and spatial attention to capture fault feature responses in image space. The overall framework of the DA-DCGAN is shown in Fig. 1. The overall network is based on a DCGAN as a skeleton for generating time-frequency images of fault data.

For the generator, the fully connected layer is removed and random noise of dimension is used as input, the samples are up-sampled by transposition convolution to expand them to dimension $4 \times 4 \times 256$, and the features are gradually output to the dual attention (DA) layer by transposition convolution completion. The DA layer extracts the features by sequentially and adaptively refining them in both spatial and channel directions, which are subsequently fed into the transposition convolution layer. In the generator, the original random noise features are gradually expanded to 64. the generator finally generates data of dimension$64 \times 64 \times 3$, which is taken as the final generated data of the generator. The structure of the generator is shown in Fig. 3.

Fig. 3

Structure of generator.

Fig. 4

Structure of the discriminator.

For the discriminator, its inputs are real fault time-frequency maps and generator-generated fault type time-frequency maps, the discriminator corresponds to the authenticity labeling of the two types of images and outputs 1 if it is judged to be true, and 0 if it is judged to be false. The real image is first transformed into tensor data through data preprocessing and the data dimension is converted to $64 \times 64 \times 3$and then passed through the DA layer, which can selectively locate the feature positions in the original image and selectively learn the important features. Subsequently, the data features are fed into the convolutional layer to further extract the important features reduce the feature dimensions, and further extract the information differences between the real and generated samples. The discriminator is structurally similar to the generator. The output layer directly uses a convolutional layer, which helps to reduce network complexity, reduce computational burden, and improve model generalization. The 4th convolutional layer employs a larger size convolutional kernel to convert the received features into a single scalar which represents the probability that the input sequence is from real data. The structure of the discriminator is shown in Fig. 4.

ReLU is used as the activation function for the convolutional layer of the generator, and Tanh is used for the activation function of the output layer, which mitigates the gradient vanishing problem and accelerates the convergence of the network as compared to the sigmoid function. In this paper, both the generator and the discriminator use the binary cross entropy loss function, for the generator, its loss is calculated as the Eq. (9), for the discriminator, its loss contains the sum of the loss of judgmental generated samples and the loss of judgmental real samples, the specific calculation is as the Eq. (10).

$${L_G}=\sum\limits_{{i=1}}^{N} {\left[ {{x_i}\log (D(G({z_i})))+(1 - {x_i})\log (1 - D(G({z_i})))} \right]}$$

(9)

$$\begin{gathered} {L_D}\ominus =\sum\limits_{{i=1}}^{N} {\left[ {\log (D({x_i}))+\log (1 - D(G({z_i})))} \right]} \\ ={L_{{\text{real}}}}+{L_{{\text{fake}}}} \\ \end{gathered}$$

(10)

.

in which ${x_i}$ is the ith sample label, true is 1, and false is 0.$D({x_i})$ is the output probability of the discriminator D on the true sample, and $D{\text{(}}G{\text{(}}{z_i}{\text{))}}$ s the output probability of the discriminator D on the generated sample (the probability that the discriminator considers this image to be true).

Method of DA-DCGAN training based on TTUR

The training process of DA-DCGAN is shown in Table 1. During each iteration, the generator (D) needs to be trained first, and the discriminator (G) is trained after D has some classification ability. Adam is chosen as the optimizer, and weight decay is used to reduce the complexity of the model and suppress the overfitting of the model.

In Fig. 5(a), when the learning rates of G and D are trained with the same rate update, the training process cannot converge, and the convergence rate of D is always higher than that of the generator, which leads to the pattern collapse phenomenon (the generated samples no longer change within a very small distribution) throughout the whole training process that means the generated samples are the same. The reason that G and D weaken each other during the training process, and the reason for the instability of the training is that G and D’s ability between the imbalance can be adjusted by observing the loss between G and D and the quality of the generated images during the training process to adjust the training times ratio of G and D. By updating at different rates can be effective in balancing the ability between G and D.

However, updating at different rates leads to an increase in the training time of the model and the difficulty in the choice of the training times ratio of G and D. Therefore, it is hoped that G and D will improve the convergence of the model while the number of training times is 1:1 to generate higher quality samples. In Fig. 5(b), TTUR is added during the training process, and the G and D learning rates are set to $2 \times 1{0^{ - 4}}$ and $1 \times 1{0^{ - 4}}$. After the addition of TTUR training, the quality of the generated samples of DA-DCGAN is significantly improved after 4000 iterations, and at the same time, the loss in the late stage of the network training is stable, with an increase in the generator loss, a decrease in the discriminator loss, and the existence of a slightly oscillating state, which indicates that the TTUR on the training of DA-DCGAN is effectiveness. The training process of DA-DCGAN is shown in Table 1.

Fig. 5

Training Loss Curve of DA-DCGAN (a) No TTUR (b) With TTUR.

Table 1 Algorithm of the training processes of DA-DCGAN.

Structure of the classification model

To verify that the proposed DA-DCGAN method can effectively improve the fault diagnosis of equipment under unbalanced samples, the classification accuracy and clustering effect are used as indicators, and diagnostic experiments are carried out by using dual-attention convolutional neural network (DA-CNN) and CNN, and the detailed structure of the DA-CNN classification model is shown in Fig. 6, which the structure of the DA layer is shown in Fig. 2, and the parameters of the convolutional layer and the number of convolutional layers are set as the same as the CNN model. The parameters of the CNN classification model are shown in Table 2.

Fig. 6

Fault diagnosis with DA-CNN.

Table 2 The parameter of CNN.

Tests and data sets

Fault simulation of constant pressure variable pump

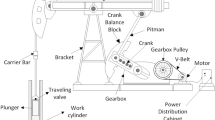
Fault simulation experiments are carried out according to the causes and mechanisms of wear failure of variable pumps under actual working conditions. For the swash plate axial piston pump used in this paper, its main friction vice includes: 1, the slipper ball nest and plunger ball head; 2, the slipper and swash plate; 3, the plunger and cylinder plunger hole. The above friction vice in the process of pump use will inevitably lead to wear and tear, resulting in different degrees of failure. Therefore, this paper is based on theoretical analysis and production experience to summarize the setting of the following types of failure: Wear of Slipper (WS), Loose Shoe (LS), and Wear of Plunger (WP), as shown in Fig. 7. The WS and WP faults were introduced by manually grinding the contact surfaces of the slipper and plunger using high-grit sandpaper, simulating the wear process that occurs during prolonged operation. The degree of wear was controlled by measuring the component’s weight loss to match a predefined mass reduction. For the LS (loose shoe) condition, a fault component with a clearance between the slipper sleeve and the plunger ball head was assembled to simulate a loose shoe fault caused by poor assembly or in-service loosening. This method allows for a realistic reproduction of the structural characteristics and vibration responses associated with this type of fault. The above faults were experimented with by replacing the normal parts in the pump with the faulty parts and the corresponding data were collected. Constant pressure variable pump fault simulation test bench to variable piston pump as the core of the design, the use of proportional relief valve as a system safety valve, through the adjustment of the variable pump in the pressure adjustment screw to control the pump operating pressure, adjust the adjustable throttle valve opening size to control the output flow rate, and at the same time, select the temperature sensors, pressure sensors, acceleration sensors to form a complete system. The hydraulic principle of the test bench is shown in Fig. 8.

Fig. 7

Photographs of faulty parts for hydraulic pump tests.

Fig. 8

Hydraulic system schematic diagram of constant pressure variable pump failure simulation test bench. 1. Suction Filter, 2. Constant Pressure Variable Displacement Piston Pump, 3. Motor, 4. Proportional Relief Valves, 5. Flowmeter, 6. Check Valve, 7. Pressure Sensor, 8. Pressure Gauge, 9, 14. Temperature Sensor, 10. Adjustable Throttle, 11. Air Cooler, 12. Level Gauge, 13. Air Filter, 15. Oil Tank.

During the test, the type of pump fault is simulated by replacing normal parts with faulty parts. To avoid changing the viscosity of the oil due to temperature changes, which in turn causes differences in the experimental data, the air-cooler is controlled to keep the temperature of the oil at 35–40℃. The installation position of the test bench sensor is shown in Fig. 9, and the main components and their performance parameters are shown in Table 3. In this experiment, the vibration sensor is fixed in the three mutually perpendicular directions of the pump under test, and it is stipulated that the direction perpendicular to the ground is the x-direction, the plunger movement direction is the z-direction and the direction perpendicular to the xz-plane is the y-direction.

Table 3 Main components of the test bench and their information.

Fig. 9

Photograph of test bench.

Fig. 10

LabVIEW data acquisition program front panel.

Each sensor passes the signals to the data acquisition card, which is used to collect the data and display and store the data in real-time graphically through the LabVIEW program written for this purpose. The front panel of the acquisition program is shown in Fig. 10.

Test datasets

In this paper, the following data acquisition conditions are chosen: sampling frequency of 20 kHz, system pressure of 10 MPa, and flow rate of 6 L/min. This condition represents a typical medium-load working scenario, which ensures the long-term stable operation of the test system and maintains a high level of safety. The sampling frequency was selected based on the Nyquist sampling theorem and by considering the common fault frequency distribution in rotating machinery, aiming to capture complete fault information as much as possible, avoid aliasing distortion, and strike a balance between data acquisition efficiency and storage capacity. The data contain the z-axis vibration acceleration signals of the hydraulic pump in the normal operating condition (N) and in three types of fault conditions (Wear of Slipper WS, loose shoe LS, and plunger wear WP), and the fault degree of WS, LS, and WP is also divided into three levels of light, medium, and heavy, and the details of fault degree will be presented in Experimental Section. Figure 11 shows the time-domain and power spectra of the z-axis acceleration data of the constant pressure variable pump under the normal state and the severe fault degree of the three fault types, WS, LS, and WP, for a given operating condition of the hydraulic pump.

Figure 11 Time and frequency domain plots of vibration signals of a hydraulic pump under given conditions can not be observed as obvious differences, although there are amplitude differences between the categories, but its numerical size can not be used as the main basis for fault classification. In the power spectra plots, the various types of signals are mainly distributed in the low-frequency band, although they have their differences, but can not be distinguished from the corresponding fault category and degree of fault.

Fig. 11

Time and frequency domain plots of vibration signals of a hydraulic pump under given conditions.

Experimental analysis

The effectiveness of the proposed method is tested on two datasets. The datasets are from the Western Reserve University bearing dataset and the hydraulic pump fault dataset collected from the experiments in “Conclusions” (three of the fault types are selected for this paper). The detailed treatment of the corresponding datasets will be described in detail in the subsequent subsections. The experimental configuration is AMD Ryzen 4800 H @2.9 GHz, RAM 16G, NVIDIA RTX 2060 GPU, 6GB, PyTorch 1.12.1 used to build the experimental model for this paper.

Case 1: fault diagnosis of CWRU bearing dataset

Bearing data preprocessing

Selected drive end sampling frequency of 12 kHz, 0HP load, 1797r/min operating conditions fault diameter of 0.007 inches, 0.014 inches, 0.021 inches, respectively, the outer ring, the inner ring, rolling body faults, as well as the normal condition of a total of 10 types of data used to form the dataset, the detailed types of faults and labels as shown in Table 4.

The experimental samples should contain at least one week’s information on the equipment operation, and In the experimental process, each sample is selected from the original vibration signal with 1024 sampling points, and at the same time, 512 points are set to overlap. Finally, the vibration acceleration signals are converted into time-frequency diagrams by CWT, and a total of 1500 experimental samples (150 × 10) are obtained, and the time-frequency diagrams of normal state samples and various types of fault samples are shown in Fig. 12.

Table 4 Classification and degree of failure simulation test data.

Fig. 12

CWT time-frequency images of different faults. (a)-(j) corresponds to the fault representing labels 0–9, respectively.

Fault sample generation

The proposed DA-DCGAN is trained using 50 real samples with a training epoch of 5000. During the training process, the model parameters are saved for every 100 batches of training completed. The hyperparameters and training parameters of the DA-DCGAN network are shown in Table 5.

Table 5 The hyperparameters of DA-DCGAN.

Generate fault samples for evaluation

To further qualitatively assess the quality of the generated samples, the bearing outer ring 0.014 inches fault(Label 5 in Table 4) is taken as an example. Their time-frequency images were quantitatively investigated by three image correlation metrics, including structural similarity index (SSIM), peak signal-to-noise ratio (PSNR), and Pearson correlation coefficient (PCC). The defining equations of the three metrics are as follows:

$$SSIM(x,y)=\frac{{(2{\mu _x}{\mu _y}+{c_1})(2{\sigma _{xy}}+{c_2})}}{{(\mu _{x}^{2}+\mu _{y}^{2}+{c_1})(\sigma _{x}^{2}+\sigma _{y}^{2}+{c_2})}}$$

(11)

$$PSNR=10 \cdot {\log _{10}}\left( {\frac{{MAX_{I}^{2}}}{{MSE}}} \right)=20 \cdot {\log _{10}}\left( {\frac{{MA{X_I}}}{{\sqrt {MSE} }}} \right)$$

(12)

$${\rho _{xy}}=\frac{{\operatorname{cov} (x,y)}}{{{\sigma _x}{\sigma _y}}}$$

(13)

.

Here, ${\mu _x}$ denotes the mean of x, $\sigma _{x}^{{}}$ denotes the variance of x, ${\sigma _{xy}}$ denotes the covariance between$x,{\text{y}}$,${c_1},{c_2}$are constants, $MAX_{I}^{{}}$denotes the maximum pixel value of the color of the image point, and $MSE$ denotes the mean square error.

For SSIM and PSNR, a larger value indicates a stronger similarity between the two variables, and a higher PCC value means that the two variables have a stronger linear relationship. Fifty generation samples are selected from the samples generated by DA-DCGAN, in addition, 50 real samples are selected as references and quantitatively analyzed with the same real samples for the above three indicators. Compare the differences between the generated samples and the real samples. We calculated the average, maximum, and minimum values of the three metrics, and the results are shown in Table 6. The data show that the values of the metrics of the generated samples are as close to the real samples, indicating that DA-DCGAN can generate high-quality fault samples, which can provide sufficient training samples to support fault diagnosis under unbalanced conditions.

Table 6 Three indicators of the original and generated sample.

Fault diagnosis of unbalanced datasets

The core purpose of DA-DCGAN is to generate more high-quality training samples by augmenting a small number of class samples in the original unbalanced dataset, to improve the classification accuracy of the classification model in the task. In the experiments, five training sets (A ~ E) with five number ratios (10:1, 5:1, 3:1, 2:1, 3:2) (i.e., the number of normal samples is 150, and the number of fault samples in each subclass is 15, 30, 50, 75, and 100, respectively) are constructed by gradually adding the generated fault samples into the training set of the classification models for training the two kinds of classification models (CNN, DA-CNN), and the specific settings of the number of samples for datasets A- E are shown in Table 7. The hyperparameters for model training are set as shown in Table 8 In addition, to serve as a benchmark for comparison, a dataset (F) consisting entirely of real samples is used as a reference. To ensure the reliability of the experimental results, each experiment was repeated 10 times and the average diagnostic accuracy was used as the final diagnostic performance metric.

Table 7 Imbalance dataset of the experiment.

Table 8 The hyperparameters of DA-CNN.

Figure 13 shows the change in accuracy of both classifiers on the test set during the training process. From the figure, it can be seen that with the gradual addition of the generated samples (dataset A to dataset E), the accuracy of both classifiers on the test set is gradually increasing, and the training accuracy of both classifiers tends to stabilize after 10 Epochs of training.

As seen in Fig. 13(a), the diagnostic accuracy of DA-CNN gradually increases from 89.47% (dataset A) to 98.09% (dataset E) after 10 batches of training, while the validation set accuracy of dataset F, which consists of all real data, is 98.66%, from Fig. 13(b), the diagnostic accuracy of CNN gradually increases from 78.94% (dataset A) to 87.30% (dataset E) after 10 generations of training. Gradually increases from 78.94% (dataset A) to 87.30% (dataset E), while the validation set accuracy of the balanced dataset F, which is composed of all real data, is 86.77%. This indicates that the proposed method can generate high-quality fault samples, and the expanded dataset can help the classifier learn better and significantly improve the accuracy of the classifier for fault diagnosis on unbalanced datasets. In addition, the introduction of DA significantly enhances the ability of CNN in image channel and spatial feature extraction, which can significantly improve the classifier classification accuracy with a small increase in computational effort (on dataset E, DA-CNN takes 27.93s and CNN takes 25.34s to train 10 generations).

Fig. 13

Fault diagnosis accuracies of two classification models under different imbalance ratios during training. (a) DA-CNN. (b) CNN.

DA-CNN and CNN were trained separately using the training set, and the classifiers’ classification ability was subsequently tested using the test set, with each experiment repeated five times, using the average of the accuracies as the evaluation metrics. Figure 14 shows that the accuracies of both classification methods increase significantly as the imbalance ratio decreases, and their diagnostic accuracies are the same as that of the balanced dataset is equal to that of the balanced dataset. The reason lies in the relatively balanced distribution of samples among different classes in these two datasets, which facilitates the effective extraction of key features by the model. In addition, the training sample sizes of datasets E and F are relatively large, with good representativeness and diversity, providing sufficient conditions for CNN to learn and generalize effectively. Compared with CNN, DA-CNN maintains a diagnostic accuracy of 89.47% under a higher imbalance ratio (10:1), reflecting that dual-attention networks can better capture the internal features of the data when dealing with the imbalanced dataset and improve the accuracy of fault diagnosis. Meanwhile, for datasets with severe class imbalance, the classification performance of the basic CNN model is significantly limited, highlighting its shortcomings in handling complex imbalanced fault data. This, in turn, validates the effectiveness of the proposed DA-DCGAN method in enhancing sample diversity and improving classification accuracy.

Fig. 14

Result under different methods.

In addition, it shows the clustering effect of the diagnostic method more clearly. The feature extraction effect of the feature extraction layer is demonstrated on the test set using t-distributed stochastic neighborhood embedding (t-SNE). As shown in Fig. 15, when the imbalance ratio is at 10:1, even though the accuracy rate reaches 89%, the categories are intertwined with each other and the fault sample categories cannot be accurately discriminated as seen in Fig. 15(a). As the imbalance ratio of the dataset decreases, the model after training, as shown in Fig. 15(e), the sample categories are more tightly aggregated, and the intraclass aggregation and interclass separability are significantly improved compared with before expansion. This also confirms that the model feature extraction ability of the classification model is further improved after training with the expanded dataset. Meanwhile, the clustering between categories reflects the high similarity of features between the generated samples and the real samples, and the generative network generates high-quality samples.

Fig. 15

Visualization by t-SNE of the DA-CNN under different imbalance ratios. (a)-(f) represent imbalance datasets(A)-(F).

Case 2: fault diagnosis of axial piston pump

This section utilizes the hydraulic pump dataset collected from the experiments in Sect. 4. The fault data sample generation is realized by DA-DCGAN and unbalanced datasets are created (the proportion of unbalanced datasets is the same as that in case 1), finally, two types of general classifiers (DA-CNN and CNN) are trained on the unbalanced dataset, and the classification accuracy is used as an index to verify that the proposed method can achieve high accuracy hydraulic pump fault diagnosis under the condition of data unbalance。.

Hydraulic pump datasets preprocessing

The dataset used contains a total of 10 categories of fault types and normal conditions, and the fault details and labels are shown in Table 9, where the WS fault uses sandpaper to sand down the upper-end face of the sliding shoe to reduce its mass by 0.2 g, 0.4 g, 0.6 g, respectively, the LS fault selects the loose shoe gap as 0.24 mm, 0.36 mm, 0.48 mm, respectively, and the WP fault uses sandpaper to sand down the longitudinal direction of the plunger to reduce its mass by 0.15 g, 0.3 g, 0.45 g.

In the experimental process, 2048 sampling points are selected from the original vibration signal for each sample, and 50% overlap degree is set at the same time. Finally, the vibration acceleration signals were converted into time-frequency diagrams by CWT, and a total of 1500 experimental samples (150 × 10) were obtained for 10 states, and the time-frequency diagrams of normal and fault state samples are shown in Fig. 16. When using DA-DCGAN to augment the few types of fault samples, the same number of samples and the same network structure are used as in case 1, and the generator generates the corresponding types of fault samples after the training is completed, which are used for the construction of the subsequent unbalanced dataset.

Table 9 Classification and degree of failure simulation test data.

Fig. 16

CWT time-frequency images of different faults. (a)-(j) correspond to the faults representing labels 0–9, respectively.

Axial piston pump unbalance dataset fault diagnosis results

As shown in Fig. 17, The visual analysis of the feature extraction layer of DA-CNN through t-SNE found that the imbalance of the dataset samples is significantly improved after the imbalance dataset is expanded by generating samples, and the classifier can learn the sample features more deeply, and the feature extraction ability is further enhanced. At the same time, it is found that although the generated samples produce an obvious clustering phenomenon with the real samples, the clustering situation cannot be compared with the real samples, which is caused by the difference between the quality of the generated samples and the quality of the real samples. Figure 17(e) and Fig. 17(f) show that the intra-class aggregation and inter-class separability of the expanded dataset are significantly improved compared to the pre-expansion one, which indicates that DA-CNN has a strong feature extraction capability when dealing with highly unbalanced datasets, and the feature extraction capability of the classifier can be further enhanced by the sample expansion of DA-DCGAN to improve the accuracy of fault diagnosis.

Fig. 17

Visualization by t-SNE of DA-CNN under different imbalance ratios. (a)-(f) represent datasets (A)-(F).

During the experiment, to reduce the influence of randomness on the experimental results, each experiment was repeated five times, using the average of the accuracy rate as an evaluation index, and the diagnostic accuracy rate is shown in Fig. 18. From the experimental diagnostic accuracy, it can be seen that DA-CNN achieves a diagnostic accuracy of 85.96% when the dataset is highly unbalanced (10:1), and its diagnostic result is also significantly better than that of CNN (70.18%). With the increase of adding the number of generated samples, the imbalance ratio gradually decreases and the model diagnostic accuracy gradually increases, when the imbalance ratio of various categories within the dataset is reduced to 3:2, the diagnostic accuracies of both DA-CNN and CNN converge to the same level, and the diagnostic accuracies differ from those of the balanced dataset (F) by 1% and 24%, respectively. In the case of balanced data, the diagnostic accuracies of the two diagnostic methods are similar.

Fig. 18

Result under different methods.

Fig. 19

The confusion matrix of DA-CNN in the testing set, (a)-(b) corresponds to the datasets (E)-(F).

Figure 19 shows the confusion matrix of fault diagnosis results of DA-CNN tested based on the same test set after training using dataset E and dataset F separately. The results show that the classifier trained using dataset E is close to the classifier trained using dataset F in terms of accuracy (98.8%, and 99.28% respectively). By Observation. Both datasets achieve 100% accuracy on normal classes, except on labeled 4 categories where the precision is 88.2% and 90.9% respectively. From the recall rate, it is seen that the lowest recall rate is on category 5, with 90% and 93.33% for the two datasets respectively, which indicates that the few categories of data samples are expanded, and their effect on classification model training is similar to that of the classification model trained on real data samples in terms of feature capture ability, reflecting the fact that the classification model better learns the features of the samples after the data expansion, which improves the classification accuracy rate. The results further validate the effectiveness of the generated samples and demonstrate that the learning and prediction ability of the classifier can be effectively improved by sample expansion.

Conclusions

In this paper, a fault sample generation method based on DA-DCGAN is proposed for generating minority class fault samples in fault diagnosis problems, which effectively solves the problem of uneven training samples of intelligent diagnosis models and thus low diagnosis accuracy of minority class by generating high-quality fault samples. Through the training process loss and diagnosis results, the main conclusions are drawn as follows:

(1) By combining the dual-attention mechanism and DCGAN, the DA-DCGAN fault sample generation method is proposed, which can generate a large number of high-quality fault samples through a small number of fault samples by capturing the channel and spatial dependence of the images, providing sufficient learning samples for the subsequent fault diagnosis network.

(2) Introduce TTUR training stabilization technique to make DA-DCGAN training stable. The TTUR is introduced in the training process, the network with the introduction of TTUR training rule can converge more quickly, the quality of samples generated by the network is evaluated using PSNR, SSIM, and PCC quantitative metrics, and the results show that there is a high degree of similarity between the generated data and the real data.

(3) Based on the dual-attention mechanism and CNN, the DA-CNN classification model is proposed, which can better capture the features of minority class samples in the unbalanced dataset compared with the traditional neural network, and can effectively improve the fault diagnosis accuracy and classification precision under unbalanced samples.

The method proposed in this paper addresses the problem of insufficient data volume in the field of fault diagnosis by generating high-quality samples. However, the training process of generating adversarial networks and the reliance on high computing power are still a great challenge. Therefore, how to reduce the training difficulty with lightweight adversarial networks and attention mechanisms or better training methods will be an important research direction.