Novel machine learning approach for enhanced smart grid power use and price prediction using advanced shark Smell-Tuned flexible support vector machine

Abstract

Energy management has enhanced sustainability, dependability, and efficiency in smart grids. Urbanisation, technology, and consumer behaviour have boosted need for innovative power use and price control systems. The paper intends to construct ML for smart grid power use and price prediction. This work used an advanced shark smell-tuned flexible support vector machine (ASS-FSVM) to forecast smart grid price and power use. Weather stations, smart meters, and market price databases document power use and pricing. The quality and consistency of data are enhanced via the processes of cleaning and normalizing inputs. PCA reduces dimensionality by extracting pre-processed data characteristics. Optimized and tested FSVM models can anticipate smart grid power use and pricing. ASS may identify the most important dataset properties. The research evaluates electricity consumption forecasting using accuracy (98.05%), recall (98.93%), precision (97.10%), and F1-score (98.04%), and electricity price predicting using MAPE (4.32%), RMSE (5.80%), MSE (8.50%), and MAE (2.95%). The recommended strategy greatly increases forecast accuracy, helping utilities improve grid stability, demand responsiveness, and customer pricing.

Introduction

Smart grids are updated electrical networks that optimize energy transmission between utilities and customers in real-time by using digital technologies. In contrast to conventional networks, smart grids facilitate mutual communication, facilitate the combination of renewable energy sources, and improve efficiency and dependability. Automated metering, sophisticated analytics, and resilience enhancements are important components that promote an energy system that is responsive and sustainable¹.

Electrical consumption prediction is potential energy demand based on chronological data, seasonal patterns, socio-economic factors, and real-time variables like weather. Accurate prediction is necessary for competent energy organizations in power grids, helping to balance supply and demand, reduce operational costs, and prevent outages. Advanced techniques, including machine learning, enhance accuracy, enabling better resource planning and sustainable energy use².

Smart grids are essential for anticipating power consumption since they offer real-time information on demand trends, energy use, and grid status. Smart grids provide more precise and timely forecasting models using sophisticated sensors, automated metering, and two-way communication. For effective grid management, this data-driven strategy aids in supply-demand dynamics balancing, energy distribution optimization, and consumption trend prediction³. Figure 1 shows the prediction process of electricity consumption in smart grids.

Fig. 1

Prediction process of the electricity consumption.

Smart grids provide real-time data. They enable precise demand-response management, less stress from peak loads, and better forecasting of electricity usage. They lower costs and environmental impact by optimizing energy distribution, improving prediction accuracy, and supporting renewable energy sources⁴.

Forecasting electricity usage is hampered by smart grids due to issues with data security and privacy, expensive installation costs, and the difficulty of handling large amounts of data. Accurate forecasting is made more difficult by interoperability problems, legal restrictions, consumer behavior variability, integration hurdles with renewable energy, a lack of historical data, and a lack of technical skill⁵.

The forecasting of electricity usage using traditional techniques has drawbacks, such as linear assumptions that miss intricate, nonlinear interactions. They are prone to overfitting, have trouble integrating varied features, and are not flexible enough to adjust to shifting trends. Efficiency is further hampered by the fact that these models frequently rely on batch processing, ignore temporal dependencies, and necessitate intensive human feature engineering.

A more robust, effective, and sustainable energy infrastructure is promoted by smart grids’ proactive modifications, which also reduce the likelihood of outages⁶. The study objective is to generate an advanced shark smell-tuned flexible support vector machine (ASS-FSVM) model to enhance the prediction accuracy of electricity consumption and pricing within smart grids. The goal of the study is to show how this innovative approach could improve grid stability, optimize demand response, and give customers more sophisticated pricing options.

The primary research question of the study is how to enhance the accuracy of electricity pricing and consumption prediction in smart grids using an Advanced Shark Smell-Tuned Flexible Support Vector Machine (ASS-FSVM) model.

This study has applied the ASS-FSVM approach to smart grid systems, which are advanced electric grids with the objective of optimizing energy exchange between consumers and utilities in real-time using digital technologies. Two-way communication is facilitated, and renewable energy is integrated, as well as improved efficiency and reliability through features like automated metering, advanced analytics, and making the system resilient. The study seeks to forecast electricity demand and prices in such smart grids based on the utilization of past data from various sources such as weather stations, smart meters, and market price databases. It seeks to improve grid stability, optimize demand response measures, and provide consumers with more sophisticated pricing options, ultimately supporting sustainable and efficient energy management based on modern urban and technological needs.

• The goal of the research is to establish a robust ML technique that accurately predicts electricity consumption and pricing in smart grids.

• The study gathers historical data on energy use, weather conditions and market prices, and then preprocessing using data cleaning and normalization techniques.

• It introduces a PCA for dimensionality reduction and an ASS-FSVM model for optimized feature selection. The ASS-FSVM model significantly improves prediction accuracy, enabling better management of grid stability and a customer-centric pricing model.

• This demonstrates that ASS-FSVM enhances energy management in smart grids, supporting sustainable and efficient operations aligned with modern urban and technological demands.

The remaining of the study is separated into sections. Section “Related work” summarizes the related works. Section “Methodology” provides the methodology. Section “Dataset description” presents the results of the study. Sections “Data preprocessing” and “Feature extraction ” give the discussion and conclusion.

Related work

Several methods were provided in the field of electricity consumption and pricing prediction. For example,

Aurangzeb et al. presented an FPS that separates LEC from HEC by anticipating electricity loads using an ELM⁷. FPS ensured equity and steady utility revenue by lowering LEC prices by up to 11% and charging HECs more during peak hours.

Bashir et al. used a number of sophisticated ML methods, including SVM, LR, KNN, NN, NB, and DT, to forecast SG stability using a UCI dataset. DT outperformed other algorithms, according to the superior accuracy results⁸.

Xia et al. presented an improved GRU-RNN model for forecasting electricity load and RE generation in both univariate and multivariate scenarios⁹. Select variables are accurately mapped to energy outputs using a layered; AdaGrad optimized GRU-RNN using correlation analysis. Tests verify that it outperformed current techniques in terms of smart grid forecast efficiency and accuracy.

Hafeez et al. offered a framework for effective domestic energy management that balances electricity prices with user comfort, manages peak demands, and lowers expenditures¹⁰. When paired with a modified differential evolution algorithm DA-GmEDE for scheduling and an ANN-based forecast engine, it achieved 33.3% more energy efficiency than conventional techniques.

Jahangir et al. analyzed the Ontario dataset to anticipate wind speed, load demand, and power prices and compared the findings to benchmarks¹¹. The suggested approach, which has been improved by MC techniques and Bi-LSTM networks, showed increased forecasting accuracy and robustness and is particularly successful in capturing spike spots.

Ibrahim et al. investigated STLF, which forecasts power consumption up to twenty-four hours in advance¹². The results of experiments using a Panama case study and different ML techniques showed that DL performs best, with an R² of 0.93 and MAPE (2.9%), while AdaBoost performs nastiest, with an R² (0.75) and MAPE (5.7%).

Hafeez et al. presented a cross-method for short-term electric stipulate protection that combined a GWDO module, an MMI approach, an FCRBM-based forecasting module, along with data pre-processing and feature extraction¹³. The model has been tested on PJM market data and sought to improve prediction accuracy by optimizing parameter tweaking.

Aslam et al. presented an energy management technique that maximized user comfort while lowering peak-to-average ratios and electricity expenses¹⁴. It scheduled EVs and smart appliances optimally using MILP, and it integrated energy forecasts for increased efficiency with energy generation from solar, wind, and storage systems.

Mostafa et al. examined large data analytics in renewable energy and suggested a five-step approach for forecasting the constancy of smart grids using a variety of ML models. In a dataset with 60,000 instances, the accuracy of the PLR was 96% that of the random forest was 84%, that of the DR was 78%, and that of the CNN and gradient-boosted models was 87%¹⁵.

Ahmad et al. evaluated the use of data-driven probabilistic ML methods in elegant energy systems. It emphasized ML’s significance in important energy technologies, like new materials and efficiency, in addition to its use in energy distribution utilities for pricing strategies and consumption forecasts¹⁶.

Ahmed et al. integrated GPR and ML with EMM. For GR, PEC, and PES, it developed an optimization model¹⁷. The competence of the model was established by comparing it with conventional optimization techniques and accounting for seasonal variations.

Hong et al. presented a DL based temporary residential load prediction framework to examine the spatiotemporal correlations in appliance load data¹⁸. To increase forecasting accuracy, it used an iterative DNN based on ResBlock and numerous time series. Using real-world data, experiments showed better performance than current approaches.

Hafeez et al. suggested FA-HELF architecture integrated feature engineering, data pre-processing, and a customized improved disparity evolutionary optimizer with an SVM-based forecaster¹⁹. When compared to benchmarks, it exhibited better accuracy and faster convergence on ISO-NE organization data by using a hybrid feature selection technique with radial basis kernel PCA for dimensionality reduction.

Syed et al. presented a cross clustering-based DL approach for distribution transformer STLF²⁰. A k-Medoids system was used to cluster transformers according to energy consumption profiles, improving scalability and cutting down on training time, resulting in fewer models and more accurate projections.

Hafeez et al. introduced a new mixture electrical energy consumption prediction technique based on an FCRBM method²¹. Tested using actual power grid data from the USA, it combined a ReLU activation function and multivariate autoregressive approaches, showing better performance across several measures than previous models.

Zulfiqar et al. introduced a hybrid load forecasting approach that combined adaptive grasshopper optimization, feature engineering, and LWSVR²². Using methods like Relief-F and RFE, it optimized feature selection to lessen dimensionality and overfitting. Tested using load data from California and Australia, the method performed improved accuracy and stability than current standards.

Mounir et al. introduced a BI-LSTM and EMD method for electricity forecasting²³. Before being predicted by BI-LSTM, EMD preprocessed the initial time series into stationary components. The model outperformed previous research with accuracy near 1 and a minimal MAPE of 0.28%.

Bourhnaneet al. investigated ML models, particularly those utilizing Genetic Algorithms and ANN, implemented in a real-world SB testbed with CompactRIO²⁴. Even though the model’s prediction accuracy was restricted by the available data, it nonetheless provided a framework for future research on scheduling and energy consumption prediction.

Syed et al. proposed a technique that incorporates phases for data cleaning and system construction to anticipate energy usage in smart buildings²⁵. On test datasets, the model outperformed current hybrid models by combining fully connected layers with unidirectional and bi-directional LSTM networks, improving accuracy and performance.

Sarker et al. proposed an attention-based 1D-CNN-GRU system that makes use of preprocessing methods and PSO for hyper-parameter optimization to anticipate load on four datasets²⁶. Low MAE values were obtained by the model, which also used federated learning for cooperative, privacy-preserving training and SHAP for interpretability.

Methodology

The study uses historical data from several sources, like weather stations and smart meters, and then pre-process the data using methods including Z-score normalization and data cleaning. Feature extraction is done using PCA to minimize dimensionality. The authors use Principal Component Analysis (PCA) for dimensionality reduction via feature extraction to retain the most vital information in the data set and thus enhance computational efficiency and prevent issues like multicollinearity among features. By mapping the original correlated variables onto a lower number of uncorrelated principal components, PCA simplifies the model without such significant loss of vital information.

This dimensionality reduction not only saves computation overhead, but also minimizes noise, leading to more accurate forecasts. Compared to other feature extraction techniques, PCA is computationally efficient due to the fact that it operates in terms of linear algebra operations like eigendecomposition or singular value decomposition (SVD), which in practice are extremely well optimized.

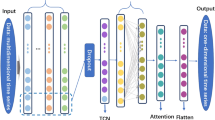
Compared to methods such as Recursive Feature Elimination (RFE) or domain-specific feature engineering, PCA provides an objective technique that maximizes the amount of variance retained in the data and is therefore particularly well adapted to high-dimensional datasets common in smart grid scenarios. PCA is both efficient and generalizable, certainly, but may sometimes overlook details of local interest captured more robustly by specialized techniques at the expense of some interpretability. The ASS-FSVM is used for precise forecasting of electricity usage and price in smart grids. Figure 2 illustrates the methodological flow.

Fig. 2

Methodological Flow.

Dataset description

This study leveraged datasets from multiple sources, including weather stations, smart meters, and market pricing databases, to gather historical records of electricity consumption, pricing, temperature, wind speed, humidity, and other relevant variables. The datasets comprised electricity consumption data from smart meters, weather data such as temperature, wind speed, and humidity from weather stations, and market pricing data to reflect concurrent electricity pricing. By combining these datasets, the authors created a comprehensive foundation for analysis that captured variations over time and across diverse weather conditions, ultimately enabling the development and validation of their ASS-FSVM model for predicting electricity consumption and pricing in smart grids.

Data preprocessing

The electricity consumption and pricing data is pre-processed using data cleaning and normalization. Data cleaning ensures high quality and prevent errors during normalization. Handling missing values to recognize and tackle missing values using imputation or by removing records with significant gaps. Calculate the mean using Eq. (1).

$$\:\mu\:=\frac{1}{N}\sum\:_{j=1}^{N}{y}_{j}$$

(1)

.

where, $\:\mu\:\:$represents the mean of a set of values. $\:N$ denotes the sum of observations. $\:{y}_{j}$ represents the individual data point and $\:\sum\:_{j=1}^{N}{y}_{j}$ indicates that the individual is summing up a series of values. Calculate standard deviation using Eq. (2).

$$\:\sigma\:=\sqrt{\frac{1}{N}}\sum\:_{j=1}^{N}{({y}_{j}-\mu\:)}^{2}$$

(2)

.

where, $\:\sigma\:$ denotes the standard deviation of a set of values, $\:{({y}_{j}-\mu\:)}^{2}$ is to calculate the deviation of each data point $\:{y}_{j}$ from the mean $\:\mu\:$. Cleaned data is normalized using Z-score normalization. It is a method of scaling data to have a mean of $\:0$ and a deviation of $\:1$. This transforms the sensitive data to the scale of the input data. The Z-score $\:\left({Z}_{j}\right)$ is computed using the following Eq. (3).

$$\:{Z}_{j}=\frac{{y}_{j}-\mu\:}{\sigma\:}$$

(3)

.

where, $\:{y}_{j}$ is the original value of the data point, $\:\mu\:$ is a mean of the attribute$\:\:y$ and $\:\sigma\:$ is a deviation of the attribute$\:\:y$. This method ensures that every attribute contributes evenly to the method, preventing features with better scales from disproportionately influencing the results. Data cleaning and Z-score normalization methods are essential for enhancing data quality and model performance.

Feature extraction

The normalized data features are extracted using PCA. PCA is a statistical method that makes use of an independent modification. A set of connected variables is transformed into a collection of distinct variables using PCA. PCA is employed in exploratory data analysis. A group of variables’ associations can also be examined using PCA. Thus, it can be functional in the reduction of dimensionality.

The data with $\:m$ dimension inputs is $\:{y}^{\left(1\right)},\:{y}^{\left(2\right)},\dots\:,\:{y}^{\left(n\right)}$. PCA is required to convert $\:m$-dimension data to $\:k$-dimension $\:(k\:\sim\:m).$ The raw data should be standardized by having a zero mean and unit variance using Eq. (4).

$$\:{y}_{i}^{j}=\frac{{y}_{i}^{j}-{y}_{i}}{{\sigma\:}_{i}},\:{\forall\:}_{i}$$

(4)

.

where, $\:{y}_{i}^{j}$ denotes the $\:{j}^{th}$ observation of the$\:{\:i\:}^{th}$ feature, $\:{y}_{i}$ represents the mean value and $\:{\sigma\:}_{i}$ denotes the standard deviation. Use the following Eq. (5) to determine the raw data’s covariance matrix:

$$\:\sum\:=\frac{1}{n}\sum\:_{j}^{n}({y}_{j}){\left({y}_{j}\right)}^{S},\:\sum\:\in\:{Q}^{m*m}$$

(5)

.

where, $\:\sum\:$ denotes a summation operation, $\:n$ represents the number of elements, $\:S$ is often used as a power, $\:{Q}^{m*m}$ denotes a space $\:m*m$ matrics with elements the set of rational numbers $\:Q$. Determine the co-variance matrix’s eigenvector and eigenvalue using Eq. (6).

$$\:{w}^{S}\sum\:\lambda\:\mu\:W=\left[{w}_{1,\:}{w}_{2,\:}\dots\:..{w}_{m,\:}\right],{w}_{j\:}\in\:{Q}^{m}$$

(6)

.

where, $\:W$is a vector composed of m components, $\:{w}_{j\:}$is an individual element, $\:m$ is the number of components or dimensions, $\:\lambda\:$ represents a coefficient and $\:\mu\:$ represents another coefficient. It is essential to develop fresh data onto a $\:k$-dimensional subspace: The Hessian Matrix top $\:k$ eigenvectors are selected. These provide the original data foundation. Equation (7) offers the corresponding vector computation.

$$\:{y}_{j}^{new}=\left[\begin{array}{c}{w}_{1}^{S}{y}^{j}\\\:{w}_{2}^{S}{y}^{j}\\\:\dots\:\dots\:\\\:\dots\:\dots\:\\\:{w}_{k}^{S}{y}^{j}\end{array}\right]\:\in\:{Q}^{k}$$

(7)

.

where, $\:{y}_{j}^{new}$ represents the transformed or updated version of $\:{y}^{j}$ and $\:{Q}^{k}$ indicates that the resulting vector. If the fresh data is with $\:n$ dimensionality, it decreases to a new $\:k$-dimensional illustration of the data. This method significantly enhances the study by reducing dimensionality, improving model performance, and eliminating noise. PCA facilitates better interpretability and visualization while addressing multicollinearity among features, ultimately leading to more accurate predictions of electricity consumption and pricing in smart grids.

Model prediction using advanced shark smell-tuned flexible support vector machine (ASS-FSVM)

This section provides a process for forecasting electricity consumption and pricing in smart grids using ASS-FSVM. FSVM introduces flexibility in handling non-linear relationships within the data and ASS optimization to fine-tune its parameters.

Flexible support vector machine (FSVM)

Dimension-reduced data is classified using FSVM. An expansion of the conventional SVM model, the FSVM model is intended to manage non-linear interactions and enhance classification accuracy by adding greater flexibility to the decision boundary. The FSVM approach is formulated to solve classification problems involving $\:m\:$ pairs of samples and labels represented as $\:T=\left({w}_{j},{z}_{j}\right),\left(\:j=\text{1,2},\dots\:.,m\right)$. Here, $\:{w}_{j}$ belongs to the set of real numbers $\:Q$, while $\:{z}_{j}$ denotes class labels $\:{z}_{j}\in\:\left\{-1,+1\right\}.$ Hyperplane is defined by Eq. (8).

$$\:{\omega\:}^{S}w+a=0$$

(8)

.

where, $\:w$ is the matrix of hyperplane parameters and $\:a$ is a bias component. To find the optimal hyperplane, an optimization problem is set up as follows in Eq. (9). To ensure that the hyperplane maximizes the edge among the two classes.

$$\:{min}_{\omega\:,a}\frac{1}{2}\left|\right|{\omega\:\left|\right|\:}^{2}$$

(9)

.

where, $\:\omega\:$is represents a vector of parameters, $\:a$ represents additional parameters, $\:\left|\right|{\omega\:\left|\right|\:}^{2}$ represents the objective function being minimized. Where data points cannot be perfectly separated, a soft margin approach is employed to avoid overfitting as given in Eq. (10).

$$\:{min}_{\omega\:,a,t}\frac{1}{2}{\left|\left|\omega\:\right|\right|}^{2}+D\sum\:_{j=1}^{m}{\epsilon\:}_{j}$$

(10)

.

where, Here$\:t$ indicates that finds the minimum value of the function,$\:{\epsilon\:}_{j}$ is a slack variable that allows for some misclassification and $\:D$ is a penalty parameter. In practical applications, data often exhibits non-linear separability. To address this, FSVM employs a non-linear transformation $\:{\Phi\:}\left({w}_{j}\right)$ to project the original data into a higher-dimensional gap where linear division is possible. The corresponding optimization trouble in the double form is given by Eq. (11).

$$\:\underset{\alpha\:}{\text{min}}\sum\:_{j}^{m}{\alpha\:}_{j}-\frac{1}{2}\sum\:_{j}^{m}\sum\:_{i}^{m}{\alpha\:}_{j}{\alpha\:}_{i}{z}_{j}{z}_{i}{\langle{\Phi\:}\left({w}_{j}\right),{\Phi\:}\left({w}_{i}\right)\rangle}_{E}$$

(11)

.

where, $\:\alpha\:$represents the Lagrange multipliers in the context of SVM. The last categorization is resolute by the decision mechanism given in Eq. (12). It utilizes the Lagrange multipliers $\:{\alpha\:}_{j}$ to weight the contributions of support vectors.

$$\:class\left(w\right)=sign\left(\sum\:_{j}^{m}{\propto\:}_{j}{z}_{j}{\langle{\Phi\:}\left({w}_{j}\right),{\Phi\:}\left(\text{w}\right)\rangle}_{E}+a\:\right)$$

(12)

.

where, $\:sign$ is to determine the class label based on the weighted sum calculated inside the parentheses, $\:{and\:z}_{j}$ denotes the actual class label of the $\:{j}^{th}$ support vector. The kernel function is integral to the FSVM framework, as defined in Eq. (13).

$$\:L\left(w,z\right)={\langle{\Phi\:}\left(\text{w}\right),{\Phi\:}\left(\text{z}\right)\rangle}_{E}$$

(13)

.

where, $\:L\left(w,z\right)$is the function that measures the relationship, $\:{\Phi\:}$ is a mapping function and $\:E$ denotes the inner product in the reproducing kernel Hilbert space. This function quantifies the similarity between new data points and support vectors. Commonly used kernels include polynomial, radial basis function, and custom-defined kernels tailored to specific data. FSVM model provides greater flexibility and robustness in classification tasks; its ability to handle non-linear data, incorporate feature selection, and effectively manage noise makes it a valuable tool in various applications.

Advanced shark smell (ASS) optimization

The classified data is optimized using ASS optimization for improving prediction capability. The traditional SSO technique has been enhanced using the ASS algorithm. With the use of sharks’ sensory abilities and predatory habits, ASS seeks to increase search efficiency in challenging optimization tasks. Sharks are renowned for their notable capability to sense prey utilizing their fabulous physical traits, as well as their admirable trial and sense of smell. The search space is split into smaller sub-regions via the ASS approach. The best answers are found in these areas using both local and global search tactics. Tracking prey and searching for prey are the two primary stages of the search process.

• (A) Prey tracking.

Sharks move freely through their surroundings, continuously adjusting their locations in response to the sensory characteristics of possible prey. Their amazing sensory system, which can pick up on even the smallest changes in their environment, is essential for tracking prey.$\:\:R$is a matrix representing the position of all sharks across $\:n$ dimensions is represented by Eq. (14).

$$\:R=\left[\begin{array}{c}{R}_{1}^{1}{\dots\:..R}_{1}^{n}\\\:\dots\:\dots\:\dots\:\\\:\dots\:\dots\:\dots\:\\\:\dots\:\dots\:\dots\:\\\:{R}_{n}^{1}\dots\:\dots\:{R}_{n}^{n}\end{array}\right]$$

(14)

.

• (B) Prey searching.

Sharks use their special senses to investigate their surroundings and find prey. This involves identifying the electromagnetic fields and vibrations produced by the prey’s motions, which enables them to efficiently focus on possible targets. Velocity detection is given in Eq. (15).

$$\:\upsilon=w\times\:{w}_{e}$$

(15)

.

where, $\:\upsilon\:$represents the velocity of the waves, $\:w$ denotes the distance between consecutive points, and $\:{w}_{e}$ represent the frequency of the waves. Position update based on movement is given in Eq. (16).

$$\:\rho\:={\rho\:}_{j}+\left({\upsilon}_{j}\times\:\varDelta\:S\right)+0.5\times\:Acc\times\:\varDelta\:{S}^{2}$$

(16)

.

where, $\:\rho\:$ represents the new position of the shark, $\:{\rho\:}_{j}$ denotes the previous position of the shark, and $\:\varDelta\:S$ represents the time interval. Each decision variable’s upper and lower boundaries are assigned at random to the search space, enabling the sharks to investigate different locations within the specified dimensions. The initialization is calculated using Eq. (17).

$$\:{R}_{y}^{x}={LB}_{x}+rand\times\:({LB}_{y}-{UB}_{x})$$

(17)

.

where, $\:{R}_{y}^{x}$ represents the randomly generated value, $\:{LB}_{x}$ indicates the lower bound, $\:{UB}_{x}$ represents the upper bound, and $\:rand$ randomly generated number. Sharks change their locations and speeds to follow prey when they spot them. To mimic efficient movement methods toward ideal solutions, this behavior is mathematically described. Equation (18) mentions the movement of the shark.

$$\:{\upsilon}_{b}^{t+1}={\upsilon}_{b}^{t}+({T}_{1}\times\:\left({R}_{hat}-{Rb}^{t}\right)\times\:{rand\:}_{1}+({T}_{2}\times\:({R}_{\upsilon\:a}{T}^{a}-{Rb}^{t})\times\:{rand}_{2})$$

(18)

.

where, $\:{\upsilon}_{b}^{t+1}$denotes the update velocity, $\:{\upsilon}_{b}^{t}$ is the current velocity, $\:{T}_{1}$ is a scaling factor, $\:{R}_{hat}$ represents the estimated, $\:{and\:Rb}^{t}$ is the current position of the $\:{b\:}^{th}$ agent. Sharks move to new locations when the target is not close by, adjusting their positions in response to external stimuli and the scent of prey. Equation (19) is to update the position of the shark.

$$\:{Rb}^{T+1}=\left\{\begin{array}{c}{Rb}^{T}\pm\:{R}_{p}+UB.h+LB.g\:if\:rand<nE\\\:{Rb}^{T}+{\upsilon}_{b}^{T}{x}_{e}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:rand\:\ge\:nE\end{array}\right.$$

(19)

.

where, $\:h$represents a directional and $\:g$ is another directional factor. To sustain equilibrium between inclusive search exposure and targeted optimization attempts, the ASS algorithm includes parameters that dynamically adjust exploration and exploitation actions. The sharks’ capacity to regulate to their environment and the effectiveness of their search strategy are both reflected in Eq. (20).

$$\:Recall=1-{f}^{-r\times\:\frac{t}{T}}$$

(20)

.

where, $\:r$ is a positive invariable, $\:t$ represents the present iteration and $\:S\:$is the maximum of iterations. The ASS optimization algorithm leverages the predatory instincts of sharks to improve feature selection and optimization procedures. Through complicated tracking, searching, and position regulation strategies, ASS optimization offers an effectual framework for solving multifaceted optimization troubles in related fields. Its capacity to adaptively explore and exploit search spaces makes it a powerful tool for improving prediction accuracy and operational efficiency in different applications.

The ASS-FSVM uses a feature selection technique modeled after sharks’ capacity to locate prey to evaluate smart grid pricing and electricity consumption estimates. This technique uses FSVM’s capacity to detain complex, non-linear correlations while extracting the most relevant features from historical data. When compared to conventional techniques, the model’s exacting optimization and validation procedures greatly increase prediction accuracy; utilities enhance grid stability and pricing tactics. Algorithm 1 provides an ASS-FSVM algorithm.

Algorithm 1: Advanced Shark Smell-Tuned Flexible Support Vector Machine (ASS-FSVM)

Results and discussions

Python 3.10 is employed to implement the ASS-FSVM model for predicting the power consumption and power price at smart grids. This model is trained with the latest machine learning algorithms to improve the precision and validity of its predictions. The performance of the ASS-FSVM model is comprehensively evaluated using important metrics: F1-score, Accuracy, Recall, Precision, MAPE, MAE, RMSE, and MSE^27,28,29. These indicators provide a thorough evaluation of the model’s efficacy in forecasting power usage and price^{30,31,32,33,34,35}. The efficacy of the ASS-FSVM model is meticulously contrasted with other existing methodologies, such as GRU-RNN⁹, FCRBM²¹, XGBoost³⁶, CNN-GRU-EWA³⁷ and CNN-CHIO³⁸, to illustrate its superiority and resilience in managing smart grid data. This comparative study emphasizes the advantages and capabilities of the ASS-FSVM model in enhancing smart grid management and decision-making processes. The employed measures are formulated below.

$$\:Accuracy=\frac{TP+TN}{TP+TN+FP+FN}\times\:100$$

(21)

$$\:Sensitivity=\frac{TP}{TP+FN}\times\:100$$

(22)

$$\:Precision=\frac{TP}{TP+FP}\times\:100$$

(23)

$$\:F1=2\times\:\frac{Precision\times\:Sensitivity}{Precision+Sensitivity}\times\:100$$

(24)

In the following, a brief description about the utilized measures have been presented.

• Accuracy: This measure shows the percentage of true outcomes of both TP and TN between all the instances. It gives a broad indication of the method’s performance.

• Precision: It demonstrates the percentage of TP cases that were expected. Extreme precision is necessary when FP costs are large. It is computed by separating the sum of FP by the number of TP.

• Recall: It is the fraction of TP to the sum of TP and FN. It illustrates how well the method can establish all pertinent cases. High recall is necessary when recording as many happy occurrences as possible is essential.

• F1-score: This offers a single value that balances precision and recall by attracting the harmonic mean. When there is inequity in the circulation of a program, it is extremely helpful.

Comparative analysis

Figure 3 shows the comparative analysis of different models as a 3-D column diagram.

Fig. 3

Comparative Analysis of Different Models.

The higher-order results based on various evaluation metrics suggest that the ASS-FSVM model clearly outperforms the higher-order models. The lowest invalid classification is still the OAK1 at 10.15%, meaning that there are 10.15% errors when the model identifies positive cases per thousands, which is the best recall value from the other models.

ASS-FSVM is the robust and reliable 98.05% accurate power usage prediction. This, our model achieved an F1-score of 98.04%, reflective of a perfect balance between the precision and recall metrics, demonstrating the model was not only successful but also resistant to more sophisticated patterns within the data. The Major improvements in various dimensions at present reflect the superior ASS-FSVM algorithm that grasp the highly complex, non-linear association and assess and compute vast dataflows, Resulting in Best predictive evaluation. This makes the ASS − FSVM model a continuation of a series of prediction modelling with applications to smart grid confirming stability of grid, demand response mechanisms and more advanced customer-centric pricing methods.

In addition to this investigation, error analysis has been used for more clarification. In the following, a brief description about the employed measures have been presented.

• Root Mean Squared Error (RMSE): The standard squared disparity among the predictable and genuine principles is measured by the RMSE. It conveys the degree of concentration of the data around the row of greatest fit.

• Mean Squared Error (MSE): MSE computes the average squared distinction between estimated and actual values.

• Mean Absolute Error (MAE): By averaging the absolute values of the errors, MAE calculates the mean degree of the errors in a series of predictions without attractive into reporting their course.

Figure 4 illustrates the comparative analysis of different models based on errors as a 3-D column diagram.

Fig. 4

Comparative errors analysis of different models based on 3-D column diagram.

As can be observed, in all of these three metrics, the improvement of the ASS-FSVM is evident. In terms of the minimum MSE of 8.50, the minimum RMSE of 5.80 and the minimum MAE of 2.95, the ASS-FSVM model outperforms the other models’ properties and demonstrate the ASS-FSVM model have better predicting ability to minimize the prediction error.

The results of these metrics thus prove that ASS-FSVM is a superior model in predicting electricity consumption and pricing with more precision and reliability which eventually results in obtaining more precise and closer results as compared to the actual values. This improved precision is essential for refining energy management in smart grids, which leads to better grid reliability, demand response techniques, and customer-driven pricing structures.

The model based on ASS-FSVM not only achieved the lowest error rates, but also demonstrated strong robustness and proficiency in capturing the information of the complicated and nonlinear relationships in the data, markedly distinguishing itself from the other models.

Analysis of an additional dataset

To further verify the generalizability and robustness of the Advanced Shark Smell-Tuned Flexible Support Vector Machine (ASS-FSVM) model, we tested it using another dataset obtained from a different geographic region with distinct energy consumption patterns and market conditions. The dataset had hourly electricity consumption records, weather conditions such as temperature, humidity, and wind speed, and real-time market prices for two years. This dataset was included to check how well the model would continue evolving with shifting environmental and economic states during preserving prediction accuracy. Data preprocessing in the form of Z-score normalization and dimensionality reduction via Principal Component Analysis (PCA) allowed consistency of processing a variety of data sets. The ASS-FSVM model was then utilized to forecast electricity demand and prices, allowing us to directly compare its performance metrics with those attained from the original dataset.

Table 1 Analysis of an additional dataset.

The analysis of the additional dataset reiterates again the improved performance of the ASS-FSVM model across several measures, indicating its superior predictability across all situations. The ASS-FSVM model performed better consistently in precision, recall, accuracy, and F1-score measures with values at 97.8%, 97.5%, 97.9%, and 97.8%, respectively, over the other models including GRU-RNN, FCRBM, XGBoost, CNN-GRU-EWA, and CNN-CHIO. Moreover, the measures of error (MSE, RMSE, and MAE) were significantly lower in the ASS-FSVM model case at 8.2, 5.6, and 2.85 respectively, which is a reflection of its ability to minimize prediction errors. The findings show the stability and reliability of the model in different environments, thus qualifying it for use in different smart grid environments. The multiple dataset performance success not only supports the model’s generalizability but also strengthens the use rationale towards enhanced grid stability, demand response optimization, and customer-centric price regimes. Cross-domain generalizability places the ASS-FSVM in the forefront of state-of-the-art solutions to cutting-edge smart grid operations, competent at solving advanced, nonlinear profiles inherent in most energy systems.

Discussion

The development of the ASS-FSVM model for smart grid pricing and consumption prediction was the main goal of this work. Existing techniques like CNN-GRU-EWA³⁷, CNN-CHIO³⁸, and XGBoost³⁶ show varied degrees of efficacy, but they also have serious drawbacks. Even with its strong performance, XGBoost³⁶ has trouble with the intricacies of time-series data and is prone to overfitting. The CNN-GRU-EWA³⁷ method encounters problems with hyper-parameter tuning and computational effectiveness despite combining CNN with GRU. Additionally, CNN-CHIO’s³⁸ ability for simplification can be limited by its incapacity to handle outliers in energy consumption data. The suggested ASS-FSVM model improves its capability to assess time-series data by integrating sophisticated feature selection technique with a flexible optimization framework. Through the use of shark smell-tuning methods for efficient feature selection, the model enhances computational effectiveness and forecasting accuracy. Furthermore, ASS-FSVM adapts to the active nature of smart grids by outstanding a cooperation between interpretability and difficulty. A significant improvement in the field, the ASS-FSVM model not only performs better than conservative techniques but also gives utilities useful insights for attractive pricing models and demand response strategy optimization.

Conclusion

Accurate price forecasting and demand forecasting of electricity in smart grids is necessary to achieve the optimum demand response measures, utilize the resources to the maximum extent, enhance the reliability of the system, particularly owing to growing urbanization and technological advancements on the consumers’ behavior. This study created an Advanced Shark Smell-Tuned Flexible Support Vector Machine (ASS-FSVM) model based on historical data from smart meters, weather stations, and market price data bases to predict accurate electric power consumption and prices. The findings showed the improved performance of the ASS-FSVM model compared to traditional forecasting methods, with very high accuracy rates: precision (97.10%), accuracy (98.05%), recall (98.93%), F1-score (98.04%), and lowest error rates (MAPE: 4.32%, RMSE: 5.80, MSE: 8.50, MAE: 2.95). The results emphasize the model’s ability to identify complex, nonlinear relationships in smart grid data, which benefits utilities by allowing them to identify key insights for best-pricing models and demand response measures. While such success is quoted, the study does point out that there are some limitations. Its reliance on historical data which could never reflect sudden changes in market forces, and that it needs to be validated across different demographic and geographic contexts. Future research has to concentrate on the use of real-time data streams, the analysis of hybrid models, and the inclusion of other parameters such as socioeconomic factors and renewable energy sources to further enhance predictive power. These developments will allow the flexibility and credibility of the model in various smart grid systems over a period of time, eventually giving rise to more sustainable and efficient energy management systems.