Introduction

Random sampling is an often overlooked, yet pervasive, component of many computing workloads. In machine learning, random sampling is used in initialization of network parameters1,2, regularization of learning3,4, and stimulating generative models5,6. In stochastic computing, streams of random bits are sampled with different probabilities of 1 and combined through digital operations to produce a stream with a probability that is a function of the input probabilities7. In biology8, finance9, and physics10, random sampling is used to approximate solutions using Monte Carlo methods. Generating large amounts of random numbers for sampling more complex applications can be a computationally intensive process. For example, in scientific computing when simulating high-energy particle collisions, generating uniform random numbers can consume between \(30{-}50\%\) of CPU-time11. Due to the pressing need for efficient random number generators, we look towards systems of single-device true random number generators (TRNGs), called coinflip devices, to generate random bits efficiently, quickly, and in parallel11.

Coinflip devices use physical noise or stochastic quantum behavior to switch between two states, such as high and low resistances or voltages. Ideal coinflip devices are compact, consume little energy per bit, switch at high speeds, and are unpredictable but with a weight that can be tuned to different probabilities of 1. Notable examples of potential coinflip devices include magnetic tunnel junctions (MTJs)12,13, diffusive memristors14, single photon avalanche diodes15,16,17,18, and tunnel diodes19,20,21. MTJs, for example, can generate random bits for as little at 0.1pJ per sample12 by switching between high and low resistive states. Devices are usually either physically stimulated by some current or electric field to randomly adopt one of two states before being evaluated (e.g. tunnel diodes19) or the state of the device flips occasionally over time and is sampled intermittently (e.g. MTJs13). These sequences of analog values are interpreted as digital states, i.e. 1’s and 0’s (heads and tails). Bitstreams can then be partitioned into multi-bit slices to form integers by taking N sequential bits from a bitstream for an N-bit integer or used directly in probabilistic computing. These integers are expected to be uniformly distributed for a fair coin with a probability p of heads (also written as P(H)) of \(p=0.5\)22. We call this probability the “weight” of a coin or coinflip device. From a uniform distribution, algorithms such as rejection sampling can be used to generate more complicated distributions such as a Gaussian distribution23.

Whereas here we focus on the TRNGs for use in otherwise conventional computations, coinflip devices have much in common with p-bits and probabilistic computing. Many p-bits are built from coinflip devices24,25,26,27, which can be processed through analog or digital means for probabilistic computing28,29 or can even augment low quality PRNGs to generate high quality samples30.

However, while they generate digital outputs, coinflip devices are analog by nature and subject to nonidealities and variation. For example, the stochastic behaviors of diffusive memristors (random delay time) and tunnel diodes (random high or low voltage) can vary with temperature14,19. Sampling bits from devices with a fair weight despite variation requires compensation or control electronics. Furthermore, it is important to understand the practical implications of integrating multiple coinflip devices into a single system. If the behavior of one device can deterministically affect other devices, this can have deleterious effects on the ability of the system to generate high quality random samples with high throughput. In this work, we examine the random bit generation capabilities of multiple coinflip devices integrated into a single system, using a tunnel diode (TD) as our representative coinflip device. We use a control loop to adapt to variation with temperature that causes deterministic behavior and maintain a fair coin, which can be generalized to adapt to other forms of variation. Furthermore, we examine dependencies of the probability of 1 on previous results and other devices, finding that sampling devices out-of-phase and combining results from multiple devices with an XOR operation (similarly to previous works31,32,33,34) can substantially improve sampling quality. Finally, using experimentally collected bits from our system of coinflip devices, we demonstrate performance in a probabilistic computing application with a Monte Carlo approximation of \(\pi\). While it is vital for TRNGs used in cryptography to maintain certain strict standards such as those outlined in the NIST Statistical Test Suite35, the requirements for probabilistic computing may differ significantly. For example, certain PRNGs that fail these NIST statistical tests may still produce statistically identical results to TRNGs that pass all tests36. It is for this reason that we examine the ability of our coinflip devices to generate uniform distributions and perform accurate Monte Carlo simulations. Results for the NIST Statistical Test Suite and the NIST SP 800-90B IID track Most Common Value Estimate test for estimating entropy can be found in the supplementary materials for context. Our work demonstrates that multiple TRNGs can be controlled and processed to overcome both device-to-device variation and changes in operating conditions to produce high-quality random samples for a probabilistic computing application.

Results

Tunnel diodes are degenerately-doped PN junctions with a very narrow depletion region, allowing carriers to tunnel through at low forward biases37. Tunneling current increases with voltage initially, but peaks and begins decreasing as fewer and fewer states are available for the carriers to tunnel into, creating a region of negative differential resistance. The current then increases with voltage again as thermionic emission takes effect, demonstrating standard diode behavior38. Driving a current through the device near the peak tunneling current (PTC) will cause the voltage across the device to either remain low or stochastically flip to a higher bias, representing tunneling current and thermionic emission current, respectively19. A low voltage is interpreted as a logical 0 or “tails” and a high voltage as a logical 1 or “heads”. This stochastic behavior is attributed to trap filling in the band gap19. The probability of a high voltage increases for currents approaching the PTC and is 1 above the PTC. This behavior is seen in P(H) vs. current pulse magnitude in Fig. 1a.

Fig. 1
figure 1

(a) P(H) measured empirically over 10,000 flips vs. the amplitude of the current pulse through the TD at room temperature. Error bars here represent the standard deviation over 100 trials, which are notably wider near 0.5. (b) Peak tunnel current of a TD vs. the ambient temperature. (c) Our system for stimulating TDs and detecting stochastic results. \(V_{EN}\) enables the current mirror, which drives a \(I_{REF}\) through the load and reflects it through the tunnel diode. \(V_{TD}\) is compared to \(V_{TH}\) to digitize the result into a 1 or 0. (d) P(H) for a single TD while the control loop is on (green) and after it is turned off (magenta). P(H) begins to drift before maxing out at 1.

Full size image

We designed a system for generating random bitstreams with discrete, off-the-shelf TDs on a battery-powered printed circuit board (PCB). A diagram of the system is shown in Fig. 1c. Full details on circuit operation are outlined in the “Methods” section. This system pulses the TDs with current that has a magnitude corresponding to a P(H) of 0.5 in the middle of the sigmoidal curve in Fig. 1a. P(H) can be tuned by increasing or decreasing current magnitude along this curve.

However, despite calibrating the TD to a fair weight initially, current pulses of a constant magnitude very quickly lead to deterministic behavior, producing all 1’s or 0’s as shown in Fig. 1d. Change in temperature causes the PTC to vary over time, affecting P(H)19. The change in PTC over a range of temperatures for a TD is shown in Fig. 1b. PTC can vary by up to around \(200\,\textrm{nA}\) per degree K, and P(H) is very sensitive to current, with about \(500\,\textrm{nA}\) difference between \(P(H) = 1\) and \(P(H) = 0\). Therefore, a very small change in temperature can cause a radical shift in P(H) for the TD. Although a feedback mechanism is recommended in Bernardo-Gavito et al. (2017)19, it is not fully analyzed in the text. We compensate for the shifting PTC by implementing a digital control loop in the data collection system, adjusting the current magnitude based on calculated P(H) of the bitstream. We call the process of controlling the TD to be fair “retuning”. The details of this control loop are outlined in the “Methods” section.

Retuning single TDs can lead to deterministic behavior

We collect 32M bits with the PCB, sampling continuously. We calculate P(H) for retuning by averaging together bits in disjoint windows of 32 bits as they are generated, but we calculate P(H) from disjoint windows of 320 bits (or 10 retuning windows) when plotting. P(H) for a single, retuned TD is shown in Fig. 2a. Compared to an untuned TD, this bitstream’s P(H) is tightly distributed around 0.5 despite variations due to temperature or noise. This indicates that our bitstream produces an approximately even number of 1’s and 0’s over the span of several retuning windows. However, this is insufficient evidence of randomness, as predictable patterns can appear in bitstreams with even numbers of 1’s and 0’s, such as a simple square wave that flips each cycle. A fair and random coin should have a \(50\%\) chance of heads or tails at any time, regardless of previous results35.

Fig. 2
figure 2

A single TD with retuning: (a) P(H) over time is controlled to stay around 0.5. (b) The dependency, or P(H) for n bits given an initial result of heads. (c) Counted streaks of 1’s (magenta points), compared to the expected number of streaks of exactly length N (black dashed line). (d) A temporal XOR of a single TD, computed by taking the XOR of pairs of sequential bits as they are produced and creating a new bitstream of half the length. (e) P(H) over time given an initial result of heads. Results are shown for a single TD as well as the TD after one, two, and three temporal XOR operations.

Full size image

To determine how random our fair bitstream is, we start by checking for a dependency on previous bits. Compactly, if \(b_m=1\) is a bit in our stream, we want to know what the probability that a future bit is also heads, or \(P(b_{m+n}=1|b_m=1)\) for \(n\in \left\{ 1,\ldots ,N\right\}\). To calculate this for each n, we iterate through a section of our bitstream, and whenever we encounter a 1, we look n bits forward in the stream for \(n\in \left\{ 1,\ldots ,250\right\}\) (although 250 is an arbitrary choice and any value of N would work). If any of these bits are also 1, we increment the corresponding counter. Once we have gone through the bitstream, we divide the counters by the total number of 1’s encountered. More information on this computation can be found in the “Methods” section.

We calculate this probability, which we call the “dependency”, for a single TD with retuning and plot the results in Fig. 2b. P(H) is shown to be higher than 0.5 given an initial result of heads and decreases linearly with each subsequent flip until 32 bits after the initial result. P(H) is below 0.5 at this point and abruptly begins increasing again before eventually settling near 0.5. Note that this abrupt change in trajectory for P(H) happens a full retuning window of 32 bits after the initial heads. TD collection is retuned after a retuning window, which causes this change in slope. Further experiments (shown in the supplementary material) show that changing the retuning window length \(L_{\text {retune}}\) results in a corresponding change to the position of this point. These results indicate that our bitstream is not only more predictable than a random coin, but that the retuning algorithm plays a part in this dependency.

The dependency of our TD, which shows that a result of heads is more likely to be followed by another heads, is manifested in the length and number of streaks of 1’s and 0’s that appear in the bitstream. Intuitively, if a coin is more likely to produce the same result than it is to switch, we can expect longer streaks of both states. We count all streaks of 1’s exactly of length N for N from 1 to 40. A streak of 1’s exactly of length N is any section of the bitstream that is comprised of a 0, followed by N consecutive 1’s, and then another 0. An exception to this would be a streak that starts at the beginning or finishes at the end of the bitstream, which would not have a starting 0 or ending 0, respectively. We then compare these counts for each N to their expected values, which are dependent on the total length of the bitstream. Figure 2c shows the counted streaks for our bitstream, which are overwhelmingly higher than expected. Notably, a jump at 32, the value of \(L_{\text {retune}}\), suggests that many retuning windows are full of only 1’s. We speculate that this could be attributed to retuning steps that are too large, causing subsequent windows to be filled with all 1’s or all 0’s.

To combat dependencies and suppress “streaky” behavior, previous works32,33,39 have used XOR gates in TRNGs. For a bitstream with an unfair weight, XOR operations on sequential bits, also known as a temporal XOR, have been shown to reduce the error40. Unfortunately, while this works well for bitstreams with no dependencies and unfair weight, bitstreams with dependencies can result in larger error40, disqualifying this method for increasing the unpredictability of our bitstreams. Nevertheless, we compute the temporal XOR throughout the bitstream as in Fig. 2d and plot the dependency after one, two, and three operations in Fig. 2e. After the temporal XOR, the error is quite large, but the dependency is also eliminated. While subsequent temporal XOR operations gradually reduce the error, each one divides the length of the bitstream in half.

Multiple devices sampled simultaneously can be correlated

Instead of a temporal XOR, other works have used the XOR of parallel TRNGs, also known as a bit-wise XOR31,32,33,34. We again take 32M bits, but this time from each of three TDs, labelled TD0, TD1, and TD2, which are pulsed simultaneously. Rather than computing temporal XOR operations like we did with the individual TD bitstreams, we perform bit-wise XOR operations on bitstreams from multiple TDs as in Fig. 3d. Our expectation of the results would be that the individual TDs are producing bits independently, and their bit-wise XOR should remove the dependency as occurred in Fig. 2e without a substantial increase in error due to having no correlation.

Figure 3a and b show the distributions of P(H) for a single TD and the bitstream resulting from the XOR of two TDs, respectively. The distributions show that the average value of P(H) is significantly lower than 0.5 and closer to 0.3 instead, indicating that the individual TDs are correlated40, causing substantial error.

Fig. 3
figure 3

(a) P(H) distribution for a single TD. (b) P(H) distribution for the bit-wise XOR of two TDs, pulsed simultaneously. (c) Correlation versus overlap between individual pulses to two TDs. A negative value for overlap indicates a gap between the two pulses. The results indicate that a gap between pulses consistently results in lower correlation (magnitude) than pulsing TDs simultaneously. The insert demonstrates pulse 1 to TD0 (orange) and pulse 2 to TD1 (blue) with an overlap in time (gray). (d) A bit-wise XOR of multiple TDs, computed by taking the XOR of a single bit from multiple TDs in parallel to produce a new bitstream of the same length. (e) Dependency curves for each TD and bit-wise XOR operations on multiple TDs. (f) Counted streaks for each TD and bit-wise XOR operations on multiple TDs.

Full size image

To illustrate the cause of this correlation, we collect random bits from two TDs and incrementally delay the pulse to one TD (TD1) with respect to the other TD (TD0). Initially, both TD0 and TD1 are pulsed simultaneously for \(30 \; \upmu s\), and we collect 500k bits in this manner, computing the correlation between the two bitstreams at the end. We then add a \(5\; \upmu s\) delay to TD1’s pulse such that the two pulses overlap in time for \(25\; \upmu s\). Another 500k bits are collected, and the process is repeated, delaying TD1 by an additional \(5\; \upmu s\) such that the two pulses overlap in time for \(20\; \upmu s\) and computing the correlation between the bitstreams. We repeat an additional 10 times until TD1’s pulse starts a full \(30\; \upmu s\) after TD0’s pulse has ended and we have 12 correlations recorded.

The median of six trials are plotted in Fig. 3c, and the inset figure visually shows the overlap mentioned. When the rising or falling edges of the pulses occur approximately concurrently, such as when the pulses completely overlap or one pulse ends as the other begins, the correlation’s magnitude is higher. When the falling edge of the first pulse occurs in the middle of the second pulse, this causes a large negative correlation. These results could indicate that the correlation is as a result of cross-talk in the PCB causing one TD’s behavior to affect the other. Another possibility is that the overlap of the pulses in time increases the likelihood that shared noise in the PCB, such as in the power rail, might cause the TDs to exhibit similar behavior. Moreover, as the delay between the pulses increases such that they have “negative” overlap (a gap between the pulses), the correlation converges towards 0.

Cross-device XOR operations lead to high-quality TRNG behavior

We take 32M bits from each of the three TDs, now pulsed out-of-phase with a gap of \(15\; \upmu s\) between pulses to different TDs, and compute a bit-wise XOR between two TDs and all three TDs. We note that the data shown in Fig. 2 was from TD0 in this collection. The weight of TD0, TD1, and TD2 are all exactly 0.5 with a negligible error. Previously, temporal XOR operations on TD0 had weights of 0.4421, 0.4814, and 0.4934 for one, two, and three XOR operations, respectively. Comparatively, the weight of the bit-wise XOR of TD0 and TD1 when pulsed simultaneously was 0.311, which increased to 0.5086 after an additional bit-wise XOR with TD2. Now, with the TDs pulsed out-of-phase with a gap of \(15\; \upmu s\) between pulses to each TD, the weights from two and three combined TDs are 0.4902 and 04997, respectively. While the first two methods consumed three TD bits to generate one high quality random bit, the latter method achieves a comparable weight by consuming two bits to generate one high quality bit. Consuming an additional bit gives the resulting bitstream a lower error than the other two methods. Looking at the dependency curves in Fig. 3e, both bitstreams produced from the bit-wise XOR of multiple TDs have eliminated dependency on previous bits, with a P(H) given an initial heads that is relatively flat. Furthermore, the error is minimal in the case of the XOR of two TDs and nearly nonexistent in the case of the XOR of three TDs.

The counted streaks of exactly length N for each individual TD and the XOR of two and three TDs are plotted in Fig. 3f. The bit-wise XOR of two TDs is sufficient to significantly reduce the amount of overcounted streaks of 1’s. The additional XOR with TD2 reduces these further, conforming very closely to the line of expected values. As these data points are plotted with a logarithmic y-axis, the cluster of points at the bottom of the plot are off by just a few streaks, for example counting two streaks of 27 in a bitstream of millions of bits when much less than one are expected. While this method of pulsing individual TDs one at a time can be inefficient, decreasing the throughput of high quality bits by a factor of 3, we address this issue by recommending a pipelined pulsing method later in this work.

A system of TDs is suitable for Monte Carlo approximations

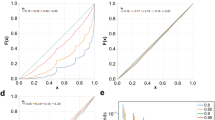
To see these bitstreams in action, we partition them into N-bit integers and generate distributions of 500k integers each. These distributions are expected to be uniform for an ideal coin22. We choose \(N=8\) and plot the distributions for three distributions: one from a single TD’s bitstream, one from a single TD’s bitstream after three temporal XOR sweeps, and one from the bit-wise XOR of three individual TDs. P(int) is the probability of sampling a given integer. These distributions are shown in Fig. 4a–c. The spikes at 0 and 255 for the single TD’s distribution can be attributed to its streaky behavior, as many 8-bit samples are all 0’s or all 1’s. However, the distributions for the TD after three temporal XOR operations and the bit-wise XOR of three TDs are both very uniform. The former has a slight bias to lower numbers, which reflects the bitstream’s slightly lower weight of 0.4904, indicating more 0’s. The latter, with a weight of 0.4997, is very flat, with almost equal probability at each number.

Fig. 4
figure 4

The distribution of 8-bit numbers generated from: (a) TD0. (b) TD0 after 3 temporal XOR operations. (c) the bit-wise XOR of TD0, TD1, and TD2. Distributions for TD1 and TD2 can be found in the supplementary materials. (d) Diagram of pipelined TDs. Each \(b_x\) represents a bit collected during cycle x, which are buffered until an XOR operation with bits collected by other TDs during other cycles. Results of pipelining bits from TDs pulsed simultaneously: (e) P(H) over time is distributed around 0.5. (f) P(H) for n bits after an initial heads. (g) Counted streaks of 1’s, compared to the expected number of streaks of exactly length N.

Full size image

For a more robust test of these distributions, we use them in a Monte Carlo approximation of \(\pi\). We sample pairs of numbers from a distribution, square and add them, and divide the number of pairs \(>255^2\) by the total number of pairs41,42. This should approximate \(\pi /4\), which we multiply by 4 to compare to \(\pi\).

500k 8-bit integers were sampled from each bitstream. These were split into groups of 2k integers. We then ran 250 trials with 1k pairs of 8-bit integers used to approximate \(\pi\). The mean and standard deviation of these results are recorded in Table 1.

Table 1 Approximations of \(\pi\).
Full size table

Based on the results in the table, the bit-wise XOR of three TDs has the closest approximation of \(\pi\) as well as the smallest standard deviation. The bit-wise XOR of two TDs also achieves a closer approximation than the three temporal XOR operations on a single TD. Moreover, this is accomplished by consuming only two TD bits for every output bit, compared to the temporal XOR operations which consume three TD bits for every output bit. This implies that combining bitstreams could be a more efficient method of generating high quality bitstreams than post-processing a bitstream from a single source.

Pipelining XOR reduces correlation without sacrificing throughput

A system where no two devices can be pulsed simultaneously to avoid correlation would be limited in throughput. Crucially, avoiding an XOR of bits collected simultaneously may significantly reduce correlation. If we were to pipeline bit collection with coinflip devices, we could consider the XOR of bits collected simultaneously a data hazard due to their correlation in the same way that we consider simultaneously executing dependent instructions in a CPU a data hazard. In Fig. 4d, we portray a pipeline of three TDs, each producing a bit at every cycle. This allows the system as a whole to continue generating a random bit every cycle rather than every three cycles.

Bits can be buffered in a shift-register after being measured from a TD. On cycle 2, three bits are available for an XOR operation: \(b_0\) from TD0, \(b_1\) from TD1, and \(b_2\) from TD2. In the next cycle, the XOR of \(b_1\) from TD0, \(b_2\) from TD1, and \(b_3\) from TD2 is computed. This continues each cycle, and a new bit is computed from the XOR of bits taken from three TDs on different cycles. Pipelining allows TDs to be pulsed simultaneously while computing an XOR on bits from different cycles to prevent correlation. Thus, we are able to both minimize correlation between devices and eliminate self-dependency of the bitstream through XOR operations.

Taking bits collected from three TDs simultaneously, we simulate this pipeline by circular-shifting one bitstream by one and another bitstream by two before computing a bit-wise XOR. The resulting bitstream’s P(H) over time, counted streaks, and dependency curve are shown in Fig. 4e–g. These show similar results to the XOR of three TDs pulsed out-of-phase. The correlation between TDs is not only reduced through pipelining, but the XOR of the three TDs mitigates the self-dependency as well, as shown in Fig. 4f. Furthermore, using the same uniform distribution sampling and \(\pi\) approximation technique with 250 trials of 1k integer pairs, this bitstream approximates \(\pi\) as 3.1499 with a standard deviation of 0.0541.

While some systems, including stream-based stochastic computing systems7, may desire coinflip devices tuned to other values of P(H), our work shows that control loops can introduce dependency and other pathologies. Furthermore, while XOR operations reduce bias from a fair coin, there is not an equivalent digital operation currently known for reducing bias from other values of P(H). One potential method of sampling a coin with a different value of P(H) is to sample from a uniform distribution, as we did in our Monte Carlo approximations, and compare the sample to the desired P(H), producing a 1 when the sample is \(< P(H)\). Sampling an N-bit integer from a uniform distribution and comparing to P(H) could be accomplished by sampling N fair coins in parallel to minimize any sacrifices to throughput. Therefore, although a coin cannot be tuned to an unfair weight and improved through a digital operation as a fair coin can, our efforts toward achieving a high quality fair coin can also benefit efforts to design systems of coins with unfair weights.

Discussion

In this work, we explored integration of stochastic devices into a high quality TRNG, using TDs as representative devices. We show that a control loop can compensate for non-idealities like thermal drift in PTC. This control loop is able to maintain a bias near that of a fair coinflip but introduces dependency into the bitstream that results in long streaks of 1’s and 0’s. Through bit-wise XOR operations of independent TDs, we are able to mitigate dependency without sacrificing desired weight of the bitstream. Furthermore, while potential nonidealities in our system introduce correlation between individual devices pulsed simultaneously, we found that pulsing TDs out-of-phase results in sufficient independence. We recommend pipelining so that devices can be sampled in parallel while performing XOR operations only on uncorrelated samples.

Some of these concepts, such as the use of a feedback mechanism for maintaining fair coinflips32,43 and performing bit-wise XOR operations on many lower quality TRNGs31,32,33,34 have been used in TRNG designs before. However, this work shows that an active control loop can even assist simple single-device TRNGs in producing high quality and fair bitstreams. We have also shown experimentally that bit-wise XOR operations can overcome second-order nonidealities in device statistics other than weight, such as dependency on previous results that cause long bitstreaks.

While other coinflip devices such as the MTJ are not as sensitive to temperature variations as TDs (depending on collection method13), control loops could potentially be utilized to adapt to other sources of variation such as device-to-device variation or unexpectedly noisy operating conditions. Alternatively, they can be used to compensate for relaxed fabrication or operating constraints, such as fabricating MTJs that are less robust to temperature or using stochastic reading instead of stochastic writing for lower power consumption13. Furthermore, systems experiencing a high degree of correlation between coinflip devices might consider pipelining to improve fairness without sacrificing throughput.

Ultimately, we built a true random number generator from nonideal, off-the-shelf components and found that these measures were sufficient to generate random samples suitable for a Monte Carlo approximation of \(\pi\). The use of control loops and digital operations between devices was shown to be capable of sampling from a uniform distribution, a vital step toward many powerful Monte Carlo simulation techniques. We look to the future and envision large arrays of integrated coinflip devices with control logic, buffers, and XOR gates that facilitate low power, high throughput generation of trillions of random bits per second for use in artificial intelligence, stochastic computing, scientific computing, and other vital applications.

Methods

Data collection system

Our data was collected with a custom PCB designed in KiCAD. We used MP1103 tunnel diodes from M-Pulse Microwave Inc. To sample a TD, a Microchip Technology ATmega328P microcontroller sends a pulse (\(V_{EN}\)) to a Texas Instruments CD74HC4050 buffer, which drives the pulse across a resistive load to generate a reference current (\(I_{REF}\)). This load consists of an Analog Devices AD5175 rheostat (or potentiometer) in parallel and series with SMD resistors. An Analog Devices ADL5315 current mirror reflects the reference current through the TD. The voltage across the TD (\(V_{TD}\)) is compared to an intermediate voltage between the high and low states (the threshold voltage, or \(V_{TH}\)) by a Analog Devices LT1116 comparator to determine the state of the TD. The microcontroller reads and then writes the result to an SD card on the PCB. The entire module is placed in a large metal box during collection to mitigate the influence of external noise sources. Our ability to collect data in noisier environments is limited by the dynamic range of our potentiometers and number of TDs integrated on the PCB, but a system with sufficient range should be able to comfortably adapt to sources of noise such as wireless signals and vibrations. For details regarding robustness of TRNGs to more intense noise like ionizing radiation, see Martín et al.44. Bits are collected continuously, and P(H) is determined by averaging together bits in disjoint windows of 32 as they are produced.

To compensate for the shifting PTC, the potentiometer’s resistance can be controlled by the microcontroller using a proportional control loop. If \(P(H) > 0.5\) or \(< 0.5\), the potentiometer can be set to higher or lower resistance, respectively. In the proportional controller, the process variable is P(H) for the TD and the control variable is the magnitude of the current pulses. The output bits of the TD are averaged over 32 flips to produce the empirical P(H), which is passed through the controller equations

$$\begin{aligned} & e = 0.5-P(H), \end{aligned}$$
(1)
$$\begin{aligned} & i = i+k_pe, \end{aligned}$$
(2)

where \(e\) is the error signal and \(i\) is the magnitude of the current for sampling the TD. The parameter \(k_p\) is the proportional feedback gain, set to \(8\times 10^{-9}\) in our controller. The length of the window over which the P(H) is estimated (\(L_{\text {retune}}\)), as well as the constant \(k_p\), were chosen through a sweep of the search-space.

Tuning the TD control loop

We searched \(L_{\text {retune}}\in \left\{ 16,32,64,128\right\}\) and \(k_p\in \left\{ 1\times 10^{-9}, 2\times 10^{-9}, 4\times 10^{-9}, 8\times 10^{-9}, 16\times 10^{-9}\right\}\) to find the optimal controller parameters. After collecting 500k bits with each configuration of \(L_{\text {retune}}\) and \(k_p\), we plotted P(H) and dependency curves for each TD. P(H) and dependency curves for TD0, TD1, and TD2 are shown in the supplementary materials. We identified a trade-off between fairness (weight near 0.5) and dependency (deviation of P(H) from 0.5 given an initial heads). While P(H) seems to improve with increased \(k_p\) and decreased \(L_{\text {retune}}\) for all TDs, it can increase dependence in some cases. Notably, TD2 demonstrates this the most for \(k_p=16\times 10^{-9}\) and \(L_{\text {retune}}=16\), where P(H) is tightly distributed around 0.5, but the dependency curve oscillates significantly around 0.5. We chose \(L_{\text {retune}}=32\) and \(k_p=8\times 10^{-9}\) as these values resulted in an acceptable trade-off between fairness and dependency.

Data selection and analysis

When pulsing multiple TDs simultaneously, the current required for a fair weight decreased compared to that of the TDs pulsed sequentially. Consequently the resistance required to maintain a fair coin went outside of the operating range of the potentiometers, causing P(H) to increase to 1. Eventually, the control variable returned again to the potentiometer’s operating range, and P(H) returned to its narrow margin around 0.5 (refer to the potentiometer value and P(H) over time shown in the supplementary materials). Our analysis used the 32M bits collected after the control variable returned to the potentiometer’s operating range. To ensure fair comparison between this data and data collected from sequentially pulsed TDs, we used the same slice of 32M bits from the sequentially pulsed bitstream. Data was read from the SD card and analyzed by a MATLAB script.

Calculation of expected streaks of 1 and dependency of a bitstream

Assume we have a bitstream of M bits and want to find the number of streaks of 1’s of exactly length N. This value, which we will call Y, is calculated by

$$\begin{aligned} Y_N = \delta _1 + \delta _M + \sum _{i=2}^{M-N-1} \delta (b_i, \ldots , b_{i+N}), \end{aligned}$$
(3)

where \(\delta\) is 1 if the given window of bits is all 1’s with a 0 on either side, written as \(b_{i-1} = 0\), \(b_{i+N+1} = 0\), and \(b_i = \ldots = b_{i+N} = 1\), but is 0 otherwise. The term \(\delta _1\) represents the corner case of the first N bits, which have no preceding bit, and it is 1 if \(b_1 = \ldots = b_N = 1\) and \(b_{N+1} = 0\), but is 0 otherwise. The term \(\delta _M\) represents the corner case of the last N bits, which have no succeeding bit, and it is 1 if \(b_{M-N} = \ldots = b_{M} = 1\) and \(b_{M-N-1} = 0\), but is 0 otherwise. Assuming independence of the \(b_i\)’s, the expected value of each term in the summation is equal to the probability that the term is 1. Therefore, the expected value of \(Y_N\) is

$$\begin{aligned} {\mathbb {E}}(Y_N) = 2(1-p)p^N + (M-N-2)(1-p)^2p^N. \end{aligned}$$
(4)

The first term represents the two corner cases, and the second term represents the summation. We can calculate the expected value of \(Y_N\) for all N from 1 to the length of the bitstream, M, but this value quickly decreases to be much lower than 1, even for a very large M. For 32M bits, the expected value for streaks of exactly length 23 is slightly less than 1 and continues to decrease to approximately 0 for streaks of 30 or longer.

To calculate the dependency of a bitstream, we examined windows of length n after every 1 appearing in a bitstream. The bit-wise average of all such windows produces the effective probability of encountering a 1 within n bits of an initial 1. For the sake of a manageable data array size, we took a slice of 100K bits from the bitstream and chose \(n = 250\) for our analysis.