Introduction

The increase in car ownership has exacerbated the imbalance between road traffic demand and supply, contributing to worsening congestion. As a result, substantial scholarly attention has focused on understanding vehicle interaction dynamics under congested conditions, uncovering the underlying mechanisms of traffic flow, and developing effective strategies to improve traffic stability and reduce congestion. With the advancement of autonomous driving and vehicle communication technologies, connected and autonomous vehicles (CAVs) are gradually becoming more widespread. Owing to their capabilities in real-time communication, precise decision-making, and control, CAVs offer effective solutions for alleviating traffic congestion. Therefore, studying and modeling CAV car-following behavior is highly important for addressing traffic congestion and enhancing traffic stability.

To investigate the evolution of traffic flow and the mechanisms underlying congestion, researchers have developed microscopic car-following models that utilize mathematical theories to depict vehicle movements and interactions on the road. Among these models, the optimal velocity (OV) model proposed by Bando et al.1 in 1995 stands out as a simple yet widely employed car-following model that effectively simulates stop-and-go phenomena and congestion phase transitions in real traffic. To address the unrealistic acceleration and deceleration processes inherent in the OV model, Jiang et al.2 introduced the full velocity difference (FVD) model. Zhao et al.3 and Yu et al.4 examined the influence of the preceding vehicle’s acceleration, leading to an extension of the FVD model, now referred to as the full velocity difference and acceleration (FVDA) model. Peng et al.5 introduced a memory term for the optimal velocity to enhance the FVD model, resulting in the optimal velocity changes with memory (OVCM) model. Sun et al.6 proposed an extended backward looking effect velocity difference (BLVD) model and demonstrated that the BLVD model outperforms the FVD model in terms of traffic stability. Building upon the OV model and its extensions, Wang et al.7, Xie et al.8, and Li et al.9 integrated headway and velocity difference information from multiple preceding vehicles, further expanding the OV car-following model field.

Previous studies have focused primarily on human-driven vehicles (HVs). In contrast, CAVs can achieve real-time communication and interaction through vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) systems. CAVs can obtain status information from multiple surrounding vehicles, allowing for real-time, precise decision-making and control. As a result, CAVs are expected to substantially enhance the traffic flow operating environment. In the field of OV car-following models, Wu et al.10 and Wang et al.11 incorporated state information from multiple surrounding vehicles, such as the optimal velocity, its memory term, and velocity difference values into car-following models. Zhu et al.12 and Kuang et al.13 extended car-following models to consider the mean expected velocity of the leading vehicle group, effectively describing the car-following behavior of CAVs. Yadav S et al.14,15 and Sunita et al.16 incorporated driving predictions of headway and velocity, the driver’s advanced reaction time, and the concept of psychological headway in the V2V communication environment to develop a series of enhanced car-following models. Stability and instability analyses demonstrated that, compared with the FVD model, these models exhibit superior stability. Siwach et al.17 proposed an improved car-following model for vehicles equipped with advanced driving assistance system (ADAS), which was designed to increase driver attentiveness and overtaking efficiency. Mehta et al.18 introduced a two-lane lattice hydrodynamic model that integrates self-anticipation and the optimal current difference in lane-changing behavior, leading to improved traffic stability. Yadav D et al.19 further developed a car-following model within a V2X communication framework, considering factors such as visibility and driver attentiveness under adverse weather conditions. These findings highlight the critical role of these factors in enhancing traffic stability and safety. Li et al.20 utilized the nearest electronic throttle angle information of a vehicle to propose a CAV car-following model based on the FVD framework, which enhances the stability of traffic flow to some extent.

With respect to other car-following models, Milanés et al.21 introduced a car-following model equipped with adaptive cruise control (ACC) and cooperative adaptive cruise control (CACC), utilizing parameters such as the error between actual and desired distances, velocity differences, and the differential term of the distance error. Xie et al.22 proposed a general car-following framework based on the intelligent driver model (IDM), deriving its linear stability conditions. The development and adoption of CAVs is an incremental process, and roads will, for some time, exhibit mixed traffic flow environments comprising both CAVs and HVs. To address these conditions, Hou et al.23 proposed a multiple vehicle state information fusion model using exponential smoothing. This model comprehensively considers factors such as the rearview mirror effect, state information from multiple preceding vehicles, and headway perception errors. Peng et al.24,25,26 analyzed the stability and instability of mixed traffic flows by accounting for communication delays and the transmission characteristics of HVs and CAVs, and proposed a macroscopic continuous traffic model to account for adverse weather conditions such as rain and snow.

In summary, significant progress has been made in modeling CAV car-following behavior. Although existing studies have considered factors such as multi-leader headway, velocity differences, acceleration, predicted state information, rear vehicle influence, weather conditions, and vehicle throttle angles, few models comprehensively incorporate state information from multiple preceding and following vehicles. Moreover, some studies have focused solely on linear stability analysis without addressing the nonlinear stability characteristics of the models. This study improves the car-following model by integrating the optimal velocity, velocity differences, and acceleration information from multiple leading vehicles and a single following vehicle, and proposes the multi-leading and single-following vehicles state information car-following (MLSFICF) model. To validate the model’s effectiveness, linear stability analysis is first conducted to determine the critical stability conditions of the proposed model. Subsequently, nonlinear analysis is employed to derive the mKdV equation, which describes the evolution of traffic congestion stability near critical points. Finally, numerical simulations are performed to verify the effectiveness of the MLSFICF model and assess the impact of CAVs on mixed traffic flow. The proposed model can be applied to CAV car-following behavior simulations and provides a theoretical foundation and modeling framework for improving traffic flow stability and developing traffic control strategies.

The structure of this paper is as follows: “The MLSFICF model” introduces the model. “Linear stability analysis” presents the linear stability analysis, followed by the nonlinear analysis in “Nonlinear analysis”. “Numerical simulation and results analysis” discusses the numerical simulations and analyzes the results in detail. Finally, “Conclusions” concludes the study.

The MLSFICF model

Bando et al.1 introduced the OV model, which adjusts vehicle acceleration based on the discrepancy between the current speed and the optimal velocity, ensuring a gradual convergence to the latter. The model is formulated as follows:

$$\frac{{d{v_n}\left( t \right)}}{{dt}}=\alpha \left[ {V\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right]$$
(1)

where α is the optimal velocity sensitivity coefficient, typically defined as the reciprocal of the driver’s response delay τ; Δxn(t) is the headway distance between vehicle n and the leading vehicle n + 1 at time t; and V(Δxn(t)) is the optimal velocity of vehicle n.

Building upon this foundational framework, researchers have introduced various enhancements by incorporating factors such as velocity differences, the acceleration of the preceding vehicle, the influence of following vehicles, and the state information of two or more leading vehicles. These advancements have further enriched car-following theory and improved the adaptability of the OV model to complex traffic conditions.

Leveraging the OV model and its extensions, this study integrates the V2V communication capabilities of CAVs to propose a refined car-following model that accounts for the state information of multiple leading vehicles as well as a single following vehicle. The model integrates parameters such as the optimal velocity, velocity difference, and acceleration and is termed the MLSFICF model. It is represented as follows:

$$\begin{gathered} \frac{{d{v_n}\left( t \right)}}{{dt}}=\alpha \left[ {\eta \sum\limits_{{l=1}}^{m} {{\xi _l}{V_F}\left( {\Delta {x_{n+l - 1}}\left( t \right)} \right)} +\left( {1 - \eta } \right){V_B}\left( {\Delta {x_{n - 1}}\left( t \right)} \right) - {v_n}\left( t \right)} \right] \hfill \\ +\lambda \left[ {\mu \sum\limits_{{l=1}}^{m} {{\zeta _l}\Delta {v_{n+l - 1}}\left( t \right)} +\left( {1 - \mu } \right)\Delta {v_{n - 1}}\left( t \right)} \right]+\gamma \left[ {\rho \sum\limits_{{l=1}}^{m} {{\varsigma _l}{a_{n+l}}\left( t \right)} +\left( {1 - \rho } \right){a_{n - 1}}\left( t \right)} \right] \hfill \\ \end{gathered}$$
(2)

where λ and γ are the sensitivity coefficient of the velocity difference and acceleration; m is the number of vehicles ahead of the observed vehicle n; Δvn(t) is the velocity difference between vehicle n and the leading vehicle n + 1 at time t; an(t) is the acceleration of vehicle n at time t; and η, µ, and ρ are the degrees of influence exerted by the leading vehicle on vehicle n regarding the optimal velocity, velocity difference, and acceleration, respectively. VF(Δxn(t)) is the optimized velocity observed in the forward direction, and VB(Δxn−1(t)) is the optimal velocity observed in the backward direction. The calculation formula is as follows:

$${V_F}\left( {\Delta {x_n}\left( t \right)} \right)=\alpha ^{\prime}\left\{ {{V_1}+{V_2}\tanh \left[ {{C_1}\left( {\Delta {x_n}\left( t \right) - {l_c}} \right) - {C_2}} \right]} \right\}$$
(3)
$${V_B}\left( {\Delta {x_{n - 1}}\left( t \right)} \right)=\alpha ^{\prime\prime}\left\{ {{V_1}+{V_2}\tanh \left[ {{C_1}\left( {\Delta {x_{n - 1}}\left( t \right) - {l_c}} \right) - {C_2}} \right]} \right\}$$
(4)

where lc is the length of the vehicle; and α′, α′′, V1, V2, C1, and C2 are parameters that require calibration and do not have inherent physical significance. The values are set as follows4,5,6: α′ = 1, α′′ = -1, V1 = 6.75 m/s, V2 = 7.91 m/s, C1 = 0.13 m− 1, C2 = 1.57 m− 1, lc = 5 m. Following the approach of Peng et al.26, the weight coefficients ξl, ζl, and ςl are defined as follows for q = 7:

$${\xi _l},{\zeta _l},{\varsigma _l}=\left\{ {\begin{array}{*{20}{l}} {{{\left( {q - 1} \right)} \mathord{\left/ {\vphantom {{\left( {q - 1} \right)} {{q^l}}}} \right. \kern-0pt} {{q^l}}}, l \ne m} \\ {{1 \mathord{\left/ {\vphantom {1 {{q^{l - 1}}}}} \right. \kern-0pt} {{q^{l - 1}}}}, l=m} \end{array}} \right.$$
(5)

When m = 1, µ = 1, and γ = 0, the MLSFICF model degenerates into the BLVD model; when m = 1, η = 1, µ = 1, and γ = 0, the MLSFICF model degenerates into the FVD model; and when m = 1, η = 1, µ = 1, and ρ = 1, the MLSFICF model degenerates into the FVDA model; therefore, the BLVD, FVD, and FVDA models can be considered special cases of the MLSFICF model. Additionally, the optimization velocity functions VF(Δxn(t)) and VB(Δxn−1(t)) can be chosen with different functional forms and parameters.

Linear stability analysis

The stability of traffic flow examines the impact of small disturbances on the state of traffic flow. When the traffic flow is unstable, small disturbances propagate upstream along the traffic flow, gradually causing it to evolve into congestion. However, when the traffic flow is stable, small disturbances gradually diminish and disappear during propagation, or ultimately become confined within a small range, thereby maintaining the smooth flow of traffic. Both the Lyapunov and the perturbation methods are employed for analysis to verify the stability of the model. Assuming that all vehicles maintain a constant headway ℎ and an optimal velocity V(ℎ) in steady-state traffic flow, the positions of the vehicles under these conditions are expressed as follows:

$${X_n}\left( t \right)=nh+V\left( h \right)t,h=L/N$$
(6)

where N is the number of vehicles, and L is the length of the road.

It is assumed that a small disturbance yn(t) is added under steady-state conditions, and the position of the vehicle after the disturbance is:

$${x_n}\left( t \right)={X_n}\left( t \right)+{y_n}\left( t \right)$$
(7)
$$\Lambda {x_n}\left( t \right)=h+\Lambda {y_n}\left( t \right)$$
(8)

The first-order and second-order derivatives of Eqs. (7) and (8) are substituted into Eq. (2) and linearized to yield:

$$\begin{gathered} \frac{{{d^2}{y_n}\left( t \right)}}{{d{t^2}}}=\alpha \left[ {\eta \sum\limits_{{l=1}}^{m} {{\xi _l}{{V^{\prime}}_F}\left( h \right)\Delta {y_{n+l - 1}}\left( t \right)} +\left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)\Delta {x_{y - 1}}\left( t \right) - \frac{{d{y_n}\left( t \right)}}{{dt}}} \right] \hfill \\ +\lambda \left[ {\mu \sum\limits_{{l=1}}^{m} {{\zeta _l}\frac{{d\Delta {y_{n+l - 1}}\left( t \right)}}{{dt}}} +\left( {1 - \mu } \right)\frac{{d\Delta {y_{n - 1}}\left( t \right)}}{{dt}}} \right]+\gamma \left[ {\rho \sum\limits_{{l=1}}^{m} {{\varsigma _l}\frac{{{d^2}{y_{n+l}}\left( t \right)}}{{d{t^2}}}} +\left( {1 - \rho } \right)\frac{{{d^2}{y_{n - 1}}\left( t \right)}}{{d{t^2}}}} \right] \hfill \\ \end{gathered}$$
(9)

where VF′(h) = dVF(Δxn)/dΔxn|Δxn = h, and VB′(h) = dVB(Δxn−1)/dΔxn−1|Δxn−1 = h.

Let yn(t) = e(ikn+zt) and expand by a Fourier series; then,

$$\frac{{d{y_n}\left( t \right)}}{{dt}}=z{e^{\left( {ikn+zt} \right)}},\frac{{{d^2}{y_n}\left( t \right)}}{{d{t^2}}}={z^2}{e^{\left( {ikn+zt} \right)}},\Delta {y_n}\left( t \right)={e^{\left( {ikn+zt} \right)}}\left( {{e^{ik}}-1} \right),\frac{{d\Delta {y_n}\left( t \right)}}{{dt}}=z{e^{\left( {ikn+zt} \right)}}\left( {{e^{ik}}-1} \right)$$
(10)

By substituting Eq. (10) into Eq. (9), we can obtain:

$$\begin{gathered} {z^2}=\alpha \left[ {\eta \sum\limits_{{l=1}}^{m} {{\xi _l}{{V^{\prime}}_F}\Delta {y_{n+l - 1}}\left( t \right){e^{ikl}}\left( {1-{e^{ - ik}}} \right)} +\left( {1 - \eta } \right){{V^{\prime}}_B}\Delta {y_{n - 1}}\left( t \right)\left( {1-{e^{ - ik}}} \right) - z} \right] \hfill \\ +\lambda z\left[ {\mu \sum\limits_{{l=1}}^{m} {{\zeta _l}{e^{ikl}}} +\left( {1 - \mu } \right)} \right]\left( {1-{e^{ - ik}}} \right)+\gamma {z^2}\left[ {\rho \sum\limits_{{l=1}}^{m} {{\varsigma _l}{e^{ikl}}} +\left( {1 - \rho } \right){e^{ - ik}}} \right] \hfill \\ \end{gathered}$$
(11)

Substituting z = z1(ik) + z2(ik)2 + ··· into Eq. (11), we can obtain:

$$\left\{ \begin{gathered} {z_1}=\eta \sum\limits_{{l=1}}^{m} {{\xi _l}} {{V^{\prime}}_F}\left( h \right)+\left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right) \hfill \\ {z_2}=\frac{1}{2}\left[ {\eta {{V^{\prime}}_F}\left( h \right)\sum\limits_{{l=1}}^{m} {{\xi _l}\left( {2l - 1} \right)} - \left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)} \right] - {{\left[ {\left( {1 - \gamma } \right){z_1}^{2} - \lambda {z_1}} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {1 - \gamma } \right){z_1}^{2} - \lambda {z_1}} \right]} \alpha }} \right. \kern-0pt} \alpha } \hfill \\ \end{gathered} \right.$$
(12)

If z2 < 0, the steady-state traffic flow becomes unstable under the influence of disturbance. When z2 > 0, the disturbed traffic flow gradually evolves into a steady-state traffic flow27. Therefore, the steady-state condition of traffic flow is as follow:

$$\alpha >\frac{{2\left\{ {\left( {1 - \gamma } \right)\left[ {\eta \sum\limits_{{l=1}}^{m} {{\xi _l}} {{V^{\prime}}_F}\left( h \right)+\left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)} \right] - \lambda } \right\}\left[ {\eta \sum\limits_{{l=1}}^{m} {{\xi _l}} {{V^{\prime}}_F}\left( h \right)+\left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)} \right]}}{{\eta {{V^{\prime}}_F}\left( h \right)\sum\limits_{{l=1}}^{m} {{\xi _l}\left( {2l - 1} \right) - \left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)} }}$$
(13)

When m = 1, µ = 1, and γ = 0, only the optimal velocity and velocity difference information of both the leading and following vehicles are considered, and the resulting stability condition is consistent with the BLVD model.

$$\alpha >\frac{{2\left\{ {\left[ {\eta {{V^{\prime}}_F}\left( h \right)+\left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)} \right] - \lambda } \right\}\left[ {\eta {{V^{\prime}}_F}\left( h \right)+\left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)} \right]}}{{\eta {{V^{\prime}}_F}\left( h \right) - \left( {1 - \eta } \right){{V^{\prime}}_B}\left( h \right)}}$$
(14)

When m = 1, η = 1, µ = 1, and γ = 0, only the optimal velocity and velocity difference information of the leading vehicle are considered, and the resulting stability condition is consistent with the FVD model.

$$\alpha >2\left( {{{V^{\prime}}_F}\left( h \right) - \lambda } \right)$$
(15)

When m = 1, η = 1, µ = 1, and ρ = 1, only the complete state information of the single lead vehicle is considered, and the resulting stability condition aligns with the FVDA model.

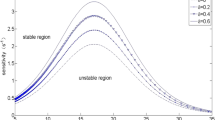
$$\alpha >2\left[ {\left( {1 - \gamma } \right){{V^{\prime}}_F}\left( h \right) - \lambda } \right]$$
(16)

Based on Eq. (13), the phase diagram illustrating the relationship between the headway and the sensitivity coefficient is presented in Fig. 1. The solid line represents the neutral stability curve of the model, and the dotted line represents the coexistence line derived from the modified mKdV equation (refer to Sect. 4). This diagram reveals that the phase space is divided into three distinct regions according to the neutral stability curve and the coexistence line: the stable region above the coexistence line, the unstable region below the neutral stability curve, and the metastable region between these two curves. Each curve contains a vertex, referred to as a critical point.

Fig. 1
figure 1

Neutral stability curves of the models.

Full size image

Based on the stability region area in Fig. 1(a), the stable region of the models can be determined as follows: OV < FVD < FVDA < MHVD < MHVDA < BLVD < MLSFICF (m = 1) < MLSFICF (m = 3). Compared with the BLVM model, the MLSFICF (m = 1) model reduces the unstable region by 10.04%. The incorporation of acceleration information from leading vehicles enhances traffic flow stability. Compared with the FVDA model, MLSFICF (m = 1) reduces the unstable region by 35.99%, demonstrating that the inclusion of following vehicle state information improves the stability of traffic flow. Additionally, MLSFICF (m = 3) reduces the unstable region by 22.74% compared with MLSFICF (m = 1), highlighting that incorporating multivehicle state information further enhances traffic flow stability, thereby validating the model’s stability. Compared with those of MHVD model and MHVDA model, the stability of the MLSFICF (m = 3) model is also verified. These findings indicate that the stable region of the MLSFICF model is significantly larger than that of the other models, demonstrating its superior ability to maintain traffic flow stability. Furthermore, the model coefficients η, λ, and γ positively influence stability, with increasing values of λ and γ or decreasing values of η improving the model’s stability.

Nonlinear analysis

When stable traffic flow encounters a random disturbance, the change in traffic flow near the critical point propagates upstream in the form of a density wave. To analyze the nonlinear characteristics of the MLSFICF model, we employ the reduced perturbation method27 to investigate the slow-varying behavior of the time and space variables near the critical stable point (hc, αc). For clarity, we rewrite the formula as follows:

$$\begin{gathered} \frac{{{d^2}\Delta {x_n}\left( t \right)}}{{d{t^2}}}=\alpha \left\{ {\eta \sum\limits_{{l=1}}^{m} {{\xi _l}\left[ {{V_F}\left( {\Delta {x_{n+l}}\left( t \right)} \right) - {V_F}\left( {\Delta {x_{n+l - 1}}\left( t \right)} \right)} \right]} +\left( {1 - \eta } \right)\left[ {{V_B}\left( {\Delta {x_n}\left( t \right)} \right) - {V_B}\left( {\Delta {x_{n - 1}}\left( t \right)} \right)} \right]} \right\} \hfill \\ - \alpha \frac{{d\Delta {x_n}\left( t \right)}}{{dt}}+\lambda \left[ {\mu \sum\limits_{{l=1}}^{m} {{\zeta _l}\left( {\frac{{d\Delta {x_{n+l}}\left( t \right)}}{{dt}} - \frac{{d\Delta {x_{n+l - 1}}\left( t \right)}}{{dt}}} \right)} +\left( {1 - \mu } \right)\left( {\frac{{d\Delta {x_n}\left( t \right)}}{{dt}} - \frac{{d\Delta {x_{n - 1}}\left( t \right)}}{{dt}}} \right)} \right] \hfill \\ +\gamma \left[ {\rho \sum\limits_{{l=1}}^{m} {{\varsigma _l}\frac{{{d^2}\Delta {x_{n+l}}\left( t \right)}}{{d{t^2}}}} +\left( {1 - \rho } \right)\frac{{{d^2}\Delta {x_{n - 1}}\left( t \right)}}{{d{t^2}}}} \right] \hfill \\ \end{gathered}$$
(17)

In the vicinity of the critical point αc = 1/τc, τ = (1 + ε2)τc, 0 < ε ≪ 1, and the slow variables X and T are defined as follows:

$$X=\varepsilon \left( {n+bt} \right)$$
(18)
$$T={\varepsilon ^3}t$$
(19)

where b is a parameter to be determined, and the headway is set as follows:

$$\Delta {x_n}\left( t \right)={h_c}+\varepsilon R\left( {X,T} \right)$$
(20)

By expanding the Taylor of Eq. (2) to the order of ε5, we obtain the following equation:

$$\begin{gathered} {\varepsilon ^2}\left( {b - {d_1}} \right){\partial _X}R+{\varepsilon ^3}\left[ {\left( {1 - \gamma } \right){b^2}\tau - \lambda b\tau - \frac{1}{2}{d_2}} \right]\partial _{X}^{2}R \hfill \\ +{\varepsilon ^4}\left\{ {{\partial _T}R - \left( {\frac{1}{6}{d_3}+\frac{1}{2}\lambda b\tau {c_1}+\gamma {b^2}\tau {c_2}} \right)\partial _{X}^{3}R - \frac{1}{6}{d_4}{\partial _X}{R^3}} \right\} \hfill \\ +{\varepsilon ^5}\left\{ {\left[ {2b\left( {1 - \gamma } \right) - \lambda } \right]\tau {\partial _X}{\partial _T}R - \left( {\frac{1}{{24}}{d_5}+\frac{1}{6}\lambda b\tau {c_3}+\frac{1}{2}\gamma {b^2}\tau {c_4}} \right)\partial _{X}^{4}R - \frac{1}{{12}}{d_6}\partial _{X}^{2}{R^3}} \right\}=0 \hfill \\ \end{gathered}$$
(21)

where \({V^{\prime\prime\prime}_F}\left( {{h_c}} \right)={{{{d^3}{V_F}\left( {\Delta {x_n}} \right)} \mathord{\left/ {\vphantom {{{d^3}{V_F}\left( {\Delta {x_n}} \right)} {d\Delta {x_n}^{3}|}}} \right. \kern-0pt} {d\Delta {x_n}^{3}|}}_{\Delta {x_n}={h_c}}}\), and \({V^{\prime\prime\prime}_B}\left( {{h_c}} \right)={{{{d^3}{V_B}\left( {\Delta {x_{n - 1}}} \right)} \mathord{\left/ {\vphantom {{{d^3}{V_B}\left( {\Delta {x_{n - 1}}} \right)} {d\Delta {x_{n - 1}}^{3}|}}} \right. \kern-0pt} {d\Delta {x_{n - 1}}^{3}|}}_{\Delta {x_{n - 1}}={h_c}}}\). The expressions of d1, d2, d3, d4, d5 and d6, c1, c2, c3, c4 and c5 are shown in Table 1.

Table 1 Coefficient di and ci.
Full size table
$${\partial _T}R - {g_1}\partial _{X}^{3}R+{g_2}{\partial _X}{R^3}+\varepsilon \left( {{g_3}\partial _{X}^{2}R+{g_4}\partial _{X}^{4}R+{g_5}\partial _{X}^{2}{R^3}} \right)=0$$
(22)

The expressions of g1, g2, g3, g4 and g5 are shown in Table 2.

Table 2 Coefficient gi.
Full size table
$$T^{\prime}={g_1}T,R=\sqrt {\frac{{{g_1}}}{{{g_2}}}} R^{\prime}$$
(23)

The mKdV equation with the O(ε) correction term is obtained:

$${\partial _T}R^\prime - \partial _{X}^{3}R^\prime +{\partial _X}{R^{\prime 3}}+\varepsilon M\left[ {R^\prime } \right]=0$$
(24)

Which

$$M\left[ {R^{\prime}} \right]=\sqrt {\frac{1}{{{g_1}}}} \left[ {{g_3}\partial _{X}^{2}R^{\prime}+\frac{{{g_1}{g_5}}}{{{g_2}}}\partial _{X}^{2}{{R^{\prime}}^3}+{g_4}\partial _{X}^{4}R^{\prime}} \right]$$
(25)

Ignoring the O(ε) term, Eq. (25) is precisely the mKdV equation. Thus, the kink–antikink wave solution is as follow:

$${R^{\prime}_0}\left( {X,T} \right)=\sqrt c \tanh \sqrt {\frac{c}{2}} \left( {X - cT^{\prime}} \right)$$
(26)

To obtain the propagation velocity c of Eq. (26), the solvability condition must be satisfied:

$$\left( {{{R^{\prime}}_0},M\left[ {{{R^{\prime}}_0}} \right]} \right)=\int_{{ - \propto }}^{{+ \propto }} {dX{{R^{\prime}}_0}\left( {X,T^{\prime}} \right)} M\left[ {{{R^{\prime}}_0}\left( {X,T^{\prime}} \right)} \right]=0$$
(27)

According to the literature28, the propagation velocity of the kink–antikink wave can be obtained via an integral:

$$c={{5{g_2}{g_3}} \mathord{\left/ {\vphantom {{5{g_2}{g_3}} {\left( {2{g_2}{g_4} - 3{g_1}{g_5}} \right)}}} \right. \kern-0pt} {\left( {2{g_2}{g_4} - 3{g_1}{g_5}} \right)}}$$
(28)

Therefore, the kink–antikink wave solution of the headway is as follow:

$$\Delta {x_n}\left( t \right)={h_c}+\sqrt {\frac{{{g_1}c}}{{{g_2}}}\left( {\frac{\tau }{{{\tau _c}}} - 1} \right)} \tanh \sqrt {\frac{c}{2}\left( {\frac{\tau }{{{\tau _c}}} - 1} \right)} \left[ {j+\left( {1 - c{g_1}\left( {\frac{\tau }{{{\tau _c}}} - 1} \right)} \right)t} \right]$$
(29)

Therefore, the amplitude A of the kink–antikink wave solution is:

$$A=\sqrt {\frac{{{g_1}c}}{{{g_2}}}\left( {\frac{\tau }{{{\tau _c}}} - 1} \right)}$$
(30)

The kink–antikink solution represents a coexisting phase that encompasses both the free-moving phase and the blocking phase at high density. This solution can be expressed as Δx(t) = hc + A and Δx(t) = hc – A (see the dotted line in Fig. 1). Through nonlinear analysis, we derive the propagation velocity c and the critical sensitivity coefficient αc for varying parameters λ, γ, η, μ and ρ while keeping other parameters constant, as presented in Fig. 2.

Fig. 2
figure 2

The propagation velocity c and critical sensitivity coefficient αc under different conditions.

Full size image

As shown in Fig. 2 the MLSFICF (m = 3) model results in the lowest values of propagation speed (c) and critical sensitivity coefficient (αc) compared with those of the other models, indicating its superior stability. Holding other parameters constant, increasing λ and γ leads to a gradual decrease in both c and αc, suggesting that these parameters enhance traffic flow stability. Similarly, reducing η also improves traffic flow stability. Additionally, the effects of µ and ρ on αc are negligible, and their influence on c is minimal. Therefore, the impact of the speed and acceleration differences of the following vehicle on traffic flow stability is minimal; thus, µ and ρ are set to 1.

Numerical simulation and results analysis

To assess the impact of the factors considered in the model on traffic flow stability intuitively, a numerical simulation test is conducted to verify the model’s validity. The simulations employ periodic boundary conditions, with initial parameters: road length = 1500, number of vehicles = 100, and vehicles evenly distributed along the road with equal headway spacing. Once the traffic flow reaches a stable state, a small disturbance is introduced to the leading vehicle, specifically:

$${x_1}\left( 0 \right)=L/N+1, \quad {x_n}\left( 0 \right)=\left( {n - 1} \right)L/N,n=2,3, \cdots ,N$$
(31)
$${v_n}\left( 0 \right)=V\left( {L/N} \right),n=1,2,3, \cdots ,N$$
(32)

Stability analysis of different models

Numerical simulations were performed for the MLSFICF model with = 1 and = 3, and the results were compared to those of the FVD, FVDA, BLVD, and MHVD models. Figure 3 shows the spatial and temporal evolution of the traffic flow headway for different car-following models after 3000 s of simulation: (a) the FVD model, (b) the FVDA model, (c) the BLVD model, (d) the MHVD model, (e) the MLSFICF model with = 1, and (f) the MLSFICF model with = 3. Following a minor disturbance, the traffic flow shifts from an initial steady state to an unsteady state, resulting in stop-and-go behavior and congestion. The results indicate that, compared with the FVD model, the range of headway fluctuations gradually decreases in the FVDA, BLVD, and MHVD models, leading to reduced traffic flow oscillation. This suggests that the acceleration of the leading vehicle, the influence of following vehicles, and the number of leading vehicles positively contribute to traffic flow stability. Moreover, the MLSFICF model developed in this study exhibits superior stability compared with the other models.

Fig. 3
figure 3

The headway distributions of different models.

Full size image
Fig. 4
figure 4

Headway distributions and headway-velocity trajectories of different models.

Full size image

Figure 4 (a) depicts the headway distributions across various models at a simulation time of 3000 s. The results clearly show that, in comparison with other models, the MLSFICF model’s headway spacing distribution forms a near-linear pattern, indicating greater traffic flow stability. Figure 4 (b) shows the headway-velocity trajectories of the different models. Over time, the traffic flow reaches a steady state, and the vehicle motion hysteresis loops become apparent. A comparison of the hysteresis loop sizes among the models reveals the following order: FVD > FVDA > MHVD > BLVM > MLSFICF (m = 1) > MLSFICF (m = 3). The FVD model results in the largest hysteresis loop, indicating the poorest traffic flow stability and a higher risk of severe congestion. Conversely, the hysteresis loop of the MLSFICF (m = 3) model decreases to a point, indicating that the traffic flow has reached a stable state.

The ACC/CACC car-following model, developed by the PATH Laboratory at the University of California, Berkeley21,28,29, is widely recognized in the field of CAV car-following models. Given its simplicity, the model has been validated through real-world applications. The ACC model’s formulation is as follows:

For the ACC model:

$$\left\{ {\begin{array}{*{20}{l}} {{e_n}\left( t \right)={x_{n+1}}\left( t \right) - {x_n}\left( t \right) - {v_n}\left( t \right){T_{{\text{ACC}}}}} \\ {{a_n}\left( t \right)={p_0}{e_n}\left( t \right)+{p_1}\left( {{v_{n+1}}\left( t \right) - {v_n}\left( t \right)} \right)} \end{array}} \right.$$
(33)

For the CACC model:

$$\left\{ {\begin{array}{*{20}{l}} {{e_n}\left( t \right)={x_{n+1}}\left( t \right) - {x_n}\left( t \right) - {v_n}\left( t \right){T_{{\text{CACC}}}}} \\ {{a_n}\left( t \right)={k_0}{a_{n+1}}\left( t \right)+{k_1}{e_n}\left( t \right)+{k_2}\left( {{v_{n+1}}\left( t \right) - {v_n}\left( t \right)} \right)} \end{array}} \right.$$
(34)

where en(t) is the error between the actual headway distance and the desired headway distance of vehicle n; T is the desired headway distance; and p0, p1, k0, k1, and k2 are model parameters, where p0 = 0.23, p1 = 0.07, k0 = 1.1, k1 = 0.23, k2 = 0.07, TACC = 1.1, and TCACC = 0.6.

Through simulation experiments, a comparative analysis was conducted on the headway, velocity, and acceleration characteristics of the ACC and CACC models, as well as the MLSFICF models with m = 1 and m = 3. The key results are presented in Table 3, and the headway distribution is illustrated in Fig. 5.

Table 3 indicates that the mean velocities for the MLSFICF models with m = 1 and m = 3 are 4.01 m/s and 4.01 m/s, respectively, whereas those for the ACC and CACC models are 11.53 m/s and 18.19 m/s, respectively. This suggests that vehicles operating under the ACC and CACC models travel at higher speeds than those under the MLSFICF models do. However, the peak-to-valley differences and standard deviations of headway, velocity, and acceleration in the MLSFICF (m = 1) and MLSFICF (m = 3) models are significantly lower than those observed in the ACC and CACC models. This implies that, relative to the ACC and CACC models, the MLSFICF framework effectively mitigates acceleration and velocity fluctuations, thereby demonstrating superior vehicular stability under perturbation conditions. This conclusion is further corroborated by Fig. 5. A comparative analysis of Figs. 2(e), 2(f), and Fig. 5 reveals that, following initial disturbances, the ACC and CACC models exhibit pronounced fluctuations in headway, indicating instability in traffic flow. In contrast, the MLSFICF models with m = 1 and m = 3 exhibit reduced headway fluctuation amplitudes, suggesting convergence toward a stable state. Consequently, the MLSFICF models with m = 1 and m = 3 present a clear advantage in enhancing traffic flow stability.

Table 3 Comparison of vehicle driving characteristic indices.
Full size table
Fig. 5
figure 5

Headway distribution under the PATH ACC/CACC model.

Full size image

Stability analysis under different CAV permeabilities

Before traffic flow transitions to being fully composed of CAVs, mixed traffic involving both CAVs and HVs will remain the norm on roads30. Therefore, analyzing the stability of mixed traffic flow under different CAV penetration rates is crucial for understanding its impact on traffic dynamics and management. In mixed traffic flow, HVs perceive information solely through the driver, so the type of preceding vehicle does not affect their car-following behavior. When a CAV follows an HV, it lacks V2V communication and must rely on onboard sensors to detect the motion state of the HV, essentially functioning as an autonomous vehicle (AV). In contrast, when a CAV follows multiple CAVs, it can utilize onboard sensors and V2V communication to perceive the motion state of several preceding vehicles. As a result, the mixed traffic flow analyzed in this study comprises three car-following models: HV, AV, and CAV, as illustrated in Fig. 6. This diversity in car-following types and the presence of different preceding vehicles leads to varying car-following behaviors, which are reflected in distinct car-following model expressions.

Fig. 6
figure 6

Car-following types in mixed traffic flow.

Full size image

(1) When the target vehicle is an HV, it is unable to discern the impact of the leading vehicle type and cannot access the acceleration information of that vehicle. Consequently, Eq. (2) reduces to the FVD model:

$$\frac{{d{v_n}\left( t \right)}}{{dt}}=\alpha \left[ {V\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right]+\lambda \Delta {v_n}\left( t \right)$$
(35)

(2) When the target vehicle is a CAV, its behavior is influenced by both the type of vehicle directly ahead and other CAVs in the platoon. Two scenarios can be identified:

When the target vehicle is a CAV, and the leading vehicle is an HV, the CAV cannot use V2V communication with the HV, causing a reduction in communication capability. In this situation, the CAV essentially functions as an AV, acquiring information about the velocity, acceleration, and other driving characteristics of the leading vehicle exclusively through its onboard sensors. Hence, m = 1 in Eq. (2), resulting in:

$$\frac{{d{v_n}\left( t \right)}}{{dt}}=\alpha \left[ {\eta {V_F}\left( {\Delta {x_n}\left( t \right)} \right)+\left( {1 - \eta } \right){V_B}\left( {\Delta {x_{n - 1}}\left( t \right)} \right) - {v_n}\left( t \right)} \right]+\lambda \Delta {v_n}\left( t \right)+\gamma {a_{n+1}}\left( t \right)$$
(36)

When the following vehicle is a CAV and the leading vehicle or multiple leading vehicles are also CAVs, the following model takes the complete form of Eq. (2), with the parameter m determined by the number of CAVs ahead.

The model parameters determined from relevant research7,8,9,10,11,12,13,24,25,26 are presented in Table 4.

Table 4 Parameter values of the model.
Full size table

To investigate the effects of different CAV penetration rates on the stability of mixed traffic flows, numerical simulations were performed with CAV penetration rates of 0.2, 0.4, 0.6, and 0.8. Figure 7 shows the temporal and spatial evolution of headway under these varying penetration rates. Figure 8(a) shows the distribution of headway spacing for each penetration rate at 3000 s of simulation time. Figure 8(b) shows the velocity‒headway trajectories corresponding to the different CAV penetration rates.

Fig. 7
figure 7

Headway distribution under different CAV penetration rates (P).

Full size image
Fig. 8
figure 8

Headway distribution and the headway‒velocity trajectory under different CAV penetration rates (P).

Full size image

Figure 3(a) shows a CAV penetration rate of 0.0, which represents the traffic flow of HVs, whereas Fig. 3(f) depicts a CAV penetration rate of 1.0, which represents the traffic flow of CAVs. A comparative analysis of Figs. 3(a) and 7 and 3(f) indicates that as the CAV penetration rate increases, the fluctuation range of the vehicle headway decreases, leading to a reduction in overall traffic flow oscillations. This trend suggests that a greater proportion of CAVs in mixed traffic flow improves traffic stability, as also demonstrated in Fig. 8.

Conclusions

This paper presents a car-following model for CAVs in V2V communication environments. The model integrates complete state information from multiple leading vehicles and a single following vehicle, building upon the FVD, FVDA, BLVD, MHVD, and MHVDA models. Linear stability analysis is employed to derive the model’s stability conditions, and perturbation theory is used to examine changes in traffic density waves, demonstrating that traffic congestion propagates as a density wave. Kink–antikink wave evolution characterizes the phase transition to a blocking state, as described by the modified mKdV equation. The results indicate that MLSFICF exhibits superior stability compared with the FVD, FVDA, BLVD, MHVD, and MHVDA models. Improving a vehicle’s ability to perceive state information, such as the optimal velocity, velocity difference, and acceleration, enhances traffic flow stability. In mixed traffic scenarios, increasing the penetration rate of CAVs further improves the overall stability. This research extends the theoretical framework of traffic flow and contributes to understanding traffic congestion mechanisms under CAV traffic conditions. Future work will focus on calibrating the MLSFICF model parameters using accurate vehicle test data to enhance its ability to simulate real-world traffic systems.