Introduction

HQ, a crucial chemical substance in the oil and gas sector, is extensively used to inject in-situ or preformed particle gel into oil reservoirs1,2. This substance can greatly influence sandstone formations’ physical and chemical characteristics3,4,5. Grasping the adsorption characteristics of HQ and various chemicals on petroleum reservoir rocks enables us to enhance industrial procedures and boost the effectiveness of oil and gas recovery, particularly in-situ gel activities6,7,8.

A key aspect of adsorption research is how crosslinkers influence fluid characteristics and flow dynamics in oil reservoirs. Crosslinkers, which are substances that can convert polymers into gels, may enhance reservoir management and flow within reservoirs9,10,11. These materials are exceptionally efficient in situations with high water cuts because they enhance the likelihood of oil extraction by decreasing water output from the reservoir12,13,14,15. In the gel in situ injection procedure, the crosslinker’s adsorption onto the rock surface might influence the operation and cause the dilution of the injected gel, rendering it a weak gel16,17,18. For this purpose, numerous studies have been carried out on the adsorption of crosslinkers in oil reservoirs. Hence, determining the reservoir’s adsorption strength and mineral composition is essential for effectively modeling the process. The prediction and identification of polymer and crosslinker adsorption on rock surfaces are not accurately achieved, resulting in subpar simulation outcomes19,20,21. Chemical adsorption is not only a critical factor during the in-situ gel injection process but also plays a vital role in other phases of reservoir engineering, including drilling and fracturing operations. Identifying and understanding chemical adsorption in these processes is essential for optimizing performance and ensuring operational efficiency22,23,24,25.

Utilizing various laboratory and analytical techniques is crucial for examining the adsorption characteristics of chemicals on reservoir rocks26,27,28. These techniques encompass adsorption tests in regulated environments, mathematical modeling, and thermodynamic evaluations. Adsorption experiments typically entail assessing the adsorption capacity through adsorption isotherms, which can offer significant insights into the relationships between the adsorbent and the surface of the adsorbent29,30,31. Among the typical models used to characterize adsorption processes, we can cite the Langmuir and Freundlich models32,33,34. The Langmuir model posits that adsorption occurs solely at the active sites of the adsorbent surface, with each site capable of adsorbing a single molecule only. This model is typically appropriate for surface adsorption systems and can effectively characterize the adsorption behavior under various conditions35,36,37.

Numerous studies have been conducted on the adsorption of substances onto oil reservoir rocks and the influence of temperature and pressure on these processes. For instance, research indicates that raising the temperature may lower the adsorption capacity of surfactants on oil-bearing rocks38,39,40. This study focuses on hydroquinone (HQ) adsorption on quartz and sandstone. It demonstrates that different chemical compounds exhibit varying adsorption and permeability effects on rocks, underlining the importance of selecting appropriate chemicals for flooding operations. By analyzing experimental data using adsorption isotherm models and thermodynamic evaluations, this research provides valuable insights into HQ’s adsorption capacity and the influence of temperature on its behavior in porous media41,42,43,44.

The findings of this study contribute to improving in-situ gel applications and optimizing HQ use as a crosslinking agent in oil reservoirs. They enhance understanding of the interactions between chemical agents and reservoir rocks, enabling more effective solutions for industrial applications while reducing operational costs. These results are particularly relevant for improving oil and gas extraction efficiency and addressing the challenges of chemical flooding in sandstone formations. Overall, this research serves as a foundation for future studies to advance chemical flooding strategies and enhance production processes in the oil and gas industry.

Materials and methodology

Materials

Adsorbate (quartz)

Quartz (SiO₂) was selected as the primary adsorbate in this study due to its prominence as the main constituent of sandstone reservoirs. This naturally occurring mineral typically appears in transparent or semi-transparent crystalline forms and exhibits high hardness (7 on the Mohs scale), ensuring its structural stability under the harsh conditions of reservoir environments. With a density of approximately 2.65 g/cm³, quartz disperses effectively across sandstone formations, enabling efficient interaction during adsorption. Its hexagonal crystalline structure, a key characteristic, influences its adsorption properties.

Chemically, quartz is highly stable, showcasing exceptional resistance to extreme temperatures and chemical agents, including acids and alkalis, except for fluorine and hot alkali solutions. The silicon-oxygen structure of quartz provides active adsorption sites that facilitate interactions with various molecules, making it particularly suitable for adsorbing hydroquinone (HQ). X-ray diffraction (XRD) analysis (Table 1) confirmed the high purity of the quartz sample used in this study, with a more than 96% quartz composition.

Table 1 XRD analysis results related to sand minerals used in this study.
Full size table

Scanning electron microscopy (SEM) images (Fig. 1) revealed quartz particle sizes ranging from 10 to 250 micrometers. This size distribution enhances the specific surface area and influences the adsorption efficiency of HQ, with the variety of particle sizes supporting the optimization of the adsorption process.

Fig. 1
figure 1

SEM images related to quartz minerals used in this work.

Full size image

Adsorbent (HQ)

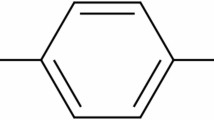
Hydroquinone (HQ), chemically known as benzene-1,4-diol, is an aromatic organic compound characterized by a benzene ring with two hydroxyl (–OH) groups at the para positions, as shown in Fig. 2. Its chemical structure highlights hydroxyl groups that can readily form interactions, such as hydrogen bonding and covalent linkage, with other molecules or surfaces, including quartz. These properties are critical for its application as an adsorbent in chemical processes.

Fig. 2
figure 2

Chemical structure of HQ.

Full size image

Merck supplied the HQ used in this study with a purity higher than 98%. The HQ used in this work was further characterized to confirm its identity and purity. HQ’s structural integrity and composition were assessed using Fourier Transform Infrared (FTIR) Spectroscopy. FTIR analysis provided confirmation of the hydroxyl functional groups through characteristic peaks observed at ~ 3350 cm–1 indicative of O–H stretching vibrations, and approximately 1600 cm⁻–1 corresponding to aromatic ring vibrations.

Hydroquinone typically appears as a white crystalline solid highly soluble in water and polar organic solvents. Its unique structure confers strong reducing properties, as the hydroxyl groups enable electron donation in various chemical reactions. These characteristics make HQ suitable for various applications, particularly in the cosmetic and photographic industries. In cosmetics, hydroquinone serves as a skin-lightening agent by inhibiting melanin production. In contrast, photography is utilized as a reducing agent during the development of photographic films.

Experimental procedure

Preparation of aqueous solution

In this study, a series of aqueous HQ solutions with concentrations ranging from 100 to 100,000 mg/L were prepared using distilled water to investigate the adsorption behavior of HQ on quartz particles. A magnetic stirrer operating at a consistent speed of 400 rpm was employed to ensure complete dissolution and uniform mixing of HQ in the solvent, achieving homogeneous solutions across all concentrations. The choice of this method was critical to prevent inconsistencies in solution preparation and guarantee precise experimental conditions.

The prepared solutions also served as calibration standards for the ultraviolet-visible spectrophotometer (UV-Vis), a key analytical tool to determine HQ concentrations in subsequent experiments. Calibration of the UV-Vis device, based on the prepared standard solutions, enabled the accurate quantification of unknown HQ concentrations during adsorption testing. This ensured high accuracy and precision in measuring HQ concentrations, which is critical for generating reliable and reproducible experimental data. The systematic preparation of these solutions provided a strong foundation for studying the interaction between HQ and quartz under varying conditions and contributed significantly to understanding HQ adsorption behavior. This stage underscores the necessity of meticulous solution preparation and proper calibration procedures to enable robust modeling and analysis of adsorption processes.

Adsorption test as a batch experiment

A systematic batch experiment was conducted to determine the adsorption capacity of HQ onto quartz particles, following the steps below.

Aqueous HQ solutions with concentrations ranging from 100 to 100,000 mg/L were prepared in distilled water. These solutions served as test media for the adsorption experiments. The uniformity of the solutions was ensured using magnetic stirring. Granulated quartz (20 g per test) was added to 100 mL of the HQ solution. The quartz-solution mixture was stirred continuously for 24 h using a magnetic stirrer at the desired test temperature. Adequate stirring ensured consistent mixing, enhanced the contact area between quartz and the HQ solution, and promoted uniform exposure for optimal adsorption.

After the stirring process, the quartz particles were separated from the solution using a centrifuge operating at 6000 rpm. This step removed the quartz particles from the remaining HQ solution, ensuring that only the solution would undergo subsequent concentration analysis. The remaining HQ concentration in the solution after quartz separation was quantified using a UV-Vis spectrophotometer (MAPADA V-100D). This device allowed accurate determination of the residual HQ concentration, which is critical for assessing the adsorption performance of quartz.

The adsorption of HQ onto quartz particles was calculated using the following equation:

$$\:{q}_{e}=1000\frac{({C}_{i}-{C}_{e}){V}_{s}}{{m}_{q}}$$
(1)

.

In Eq. (1), qe represents the adsorption of HQ on quartz (mg-HQ/g-Quartz), Ci signifies the initial HQ concentration (mg/L), Ce denotes the residual concentration of HQ post-adsorption (mg/L), Vs is the solution’s volume (L), and mq indicates the mass of quartz (g).

The quantity of HQ adsorption on quartz can be determined by plugging the values into the equation. This computation aids in assessing the extent of HQ adsorption by quartz and analyzing the influence of various factors on this mechanism. The acquired data can enhance the comprehension of HQ’s behavior in various systems and improve the adsorption parameters for industrial uses.

Measurement of adsorption in porous media

The adsorption of HQ in porous media was evaluated using a core flooding setup to simulate the conditions found in oil reservoirs and provide insights into the behavior of HQ under realistic subsurface conditions. The experimental procedure is as follows.

A sandstone core plug was carefully prepared and placed into the core holder of the Vinci core flooding apparatus. A confining pressure of 500 psi was applied to replicate reservoir-like conditions and ensure the sealing of the core within the holder. A Solutions of HQ, with concentrations100000 mg/L, were freshly prepared. These solutions served as the injection medium to study adsorption. The HQ solution was injected into the sandstone core at a controlled flow rate of 1 mL/min, ensuring uniform distribution through the porous medium.

The volume of HQ solution injected was equivalent to ten pore volumes (10 PV), ensuring complete contact between the HQ solution and the internal surface area of the sandstone core. After the injection process, the effluent (the liquid leaving the rock core) was collected, and the residual HQ concentration in the solution was determined using the UV-Vis spectrophotometer (MAPADA V-100D). This allowed for precise quantification of the remaining HQ concentration in the solution after interacting with the sandstone core. This experimental setup replicates oil reservoirs’ flow and adsorption conditions, providing valuable data on HQ adsorption behavior in porous media. The results offer critical insights into the adsorption efficiency of HQ under reservoir-like conditions and help refine injection parameters for optimized in-situ gel applications in industrial processes.

Modeling method and data analysis

Multiple isotherm models were utilized to examine HQ’s adsorption data on quartz. These models assist in illustrating the adsorption behavior and forecasting the adsorption capacity under various conditions. The models utilized comprised Langmuir Isotherm, Temkin, Freundlich, and the linear model.

Langmuir Isotherm model

The Langmuir model posits that adsorption occurs uniformly, with all adsorption sites being alike and independent. This model is well-suited for substances absorbed on a single layer’s surface. Equation 2 denotes the typical representation of the Langmuir model.

$$\:\frac{{q}_{e}}{{q}_{o}}=\frac{{K}_{L}{C}_{e}}{1+{K}_{L}{C}_{e}}\:\to\:\:\frac{1}{{q}_{e}}=\left(\frac{1}{{K}_{L}{q}_{o}}\right)\frac{1}{{C}_{e}}+\frac{1}{{q}_{o}}.$$
(2)

In this equation, qe indicates the adsorption rate at equilibrium (mg/g-rock), whereas qo denotes the maximum adsorption capacity. KL is the equilibrium constant (L/g), indicating the HQ’s inclination to adsorb onto the quartz surface. This model is commonly employed in adsorption research because of its simplicity and reliable predictability.

The adsorption capacity (qe) was calculated based on the mass balance of HQ in solution before and after adsorption. Using the equation qe = (Co − Ce)V / M, equilibrium adsorption capacities were determined for each experimental condition. In this equation, Co represents the initial HQ concentration, Ce is the equilibrium HQ concentration, V is the volume of the solution, and M is the mass of the adsorbent. This calculation method ensures consistency and reliability, as it directly relates the amount of HQ adsorbed to changes in solution concentration.

The linearized Langmuir equation was utilized for model fitting, enabling direct calculation of qo (maximum adsorption capacity) and KL (equilibrium constant). These parameters were obtained from the slope and intercept of the linearized Langmuir plot (1/qe vs. 1/Ce). This straightforward, widely accepted methodology guarantees precise estimation of adsorption parameters, which is essential for thermodynamic and kinetic modeling.

Temkin model

The Temkin model posits that the adsorption energy reduces linearly as the adsorption charge increases. This model relies on the nonlinear relationships between the adsorbed molecules and the adsorbent’s surface. Equation (3) signifies this model.

$$\:{q}_{e}=\frac{RT}{b}\text{ln}\left({K}_{T}\right)+\frac{RT}{b}\text{l}\text{n}\left({C}_{e}\right).$$
(3)

b denotes the Temkin constant, which is connected to the adsorption energy, while KT signifies Temkin’s equilibrium constant. This model is advantageous for multilayer adsorption and aids in comprehending adsorption behavior across varying temperatures.

Freundlich model

The Freundlich model is intended for nonlinear and multilayer adsorption and is primarily applied in systems where the adsorbent surface exhibits heterogeneity. Equation 4 represents the model.

$$\:\text{ln}\left({q}_{e}\right)=\text{ln}\left({K}_{f}\right)+\frac{1}{n}\text{ln}\left({C}_{e}\right).$$
(4)

In this equation, Kf represents the Freundlich constant, which relies on the adsorption capacity; n is an exponent that signifies the extent of deviation from the linear isotherm. This model is very effective, particularly in cases where adsorption takes place in a multilayered and nonlinear fashion, and it aids in clarifying the differences in adsorption behavior.

Linear model

A linear model is a simple approach to data analysis that can be expressed using Eq. (5).

$$q_{e}=KC_{e}+I$$
(5)

In this equation, qe indicates the adsorption value, Ce denotes the HQ concentration values at equilibrium, K represents the slope of the line, and I signifies the intercept of the line. This model is notably effective for modeling adsorption behavior in certain conditions and examining differences from other isotherms.

Error analysis and model accuracy

Various statistical metrics were employed to assess the precision of isotherm models in portraying the experimental data of HQ adsorption on quartz. These metrics consist of ARE (Absolute Relative Error), AAE (Average Absolute Error), ASE (Average Squared Error), and R2 (Coefficient of Determination). The equations listed below pertain to these statistical metrics.

$$\:ASE=\frac{1}{n}\sum\:_{i=1}^{n}{\left({q}_{e,cal-}{q}_{e,lab}\right)}_{i}^{2}$$
(6)
$$\:AAE=\frac{1}{n}\sum\:_{i=1}^{n}{\left|{q}_{e,cal-}{q}_{e,lab}\right|}_{i}$$
(7)
$$\:ARE=\frac{1}{n}\sum\:_{i=1}^{n}{\left|\frac{{q}_{e,cal-}{q}_{e,lab}}{{q}_{e,lab}}\right|}_{i}$$
(8)

ASE is among the most powerful techniques for analyzing errors. Nonetheless, it significantly relies on larger datasets; thus, the inaccuracies associated with solutions with a high quantity of HQ will be exaggerated. Nevertheless, AAE performs a superior error analysis at elevated concentrations. ARE aims to reduce functional mistakes across all ranges.

Thermodynamic modeling of the adsorption process

Thermodynamic modeling was employed to examine the influence of temperature on the adsorption of HQ onto quartz. This approach aids in examining the adsorption behavior and quantifying the energy variations in the adsorption processes. Thermodynamic parameters can be determined by utilizing experimental data on adsorption at various temperatures, including ΔH0, ΔS0, and ΔG0.

Calculation of Gibbs free energy changes (ΔG)

The change in Gibbs free energy for an adsorption process can be determined using Eq. (9)

$$\:{\varDelta\:G}^{0}=-RTln\left({K}_{D}\right).$$
(9)

In the Eq. (9), KD denotes the thermodynamic equilibrium constant (moles of water per mole of adsorbent). This parameter is established by computing the intersection of the qe/Ce versus qe graph. R symbolizes the universal gas constant. In this context, T denotes the temperature of the experiment measured in kelvin (K). According to the second law of thermodynamics, the value of ∆G0 is established by the Eq. 

$$\:{\varDelta\:G}^{0}={\varDelta\:H}^{0}-T{\varDelta\:S}^{0}.$$
(10)

In the equation above, ∆H0 represents the change in enthalpy of the system, while ∆S0 indicates the change in entropy. The negative value observed for ∆G suggests that the process occurs spontaneously. Otherwise, it is not spontaneous. By merging Eqs. (10) and (9), Eq. (11) will be produced.

$$\:\text{ln}\left({K}_{D}\right)=-\frac{{\varDelta\:H}^{0}}{RT}+\frac{{\varDelta\:S}^{0}}{R}-1.204.$$
(11)

1.204 converts the unit of KD from mole water/mole rock to grwater/rock. According to Eq. 11, by plotting ln(KD) vs. 1/T, H and ∆S will be determined:- slope×R and (intercept + 1.204)×R, respectively.

Results and discussion

Adsorption modeling at 25 °C and selection of descriptive model

In this section, the adsorption data of HQ on quartz were analyzed, and the relationship between adsorption capacity and equilibrium HQ concentration was visually represented. Figure 3 shows the experimental data points obtained from laboratory measurements and the fitted curves from various adsorption isotherm models. The discrete points indicate observed changes in HQ adsorption under the test conditions, while the fitted curves represent the theoretical predictions of the adsorption behavior, enabling a clear comparison between experimental results and model performance.

Fig. 3
figure 3

Lab data pertains to the adsorption of HQ on quartz particles at 25 °C and fitting via various models.

Full size image

By fitting the experimental data to multiple adsorption isotherm models (Langmuir, Freundlich, Temkin, and others), the corresponding parameters were calculated and are summarized in Table 2. Among the tested models, the Langmuir isotherm best represented the experimental data. Its statistical performance, including high R2 values and minimal prediction error, indicates excellent agreement with the observed adsorption behavior. This suggests that the adsorption of HQ on quartz is characterized by monolayer coverage on homogeneous surface sites, which is consistent with the assumptions of the Langmuir model.

The experimental data were compared against Langmuir, Freundlich, Temkin, and linear models using statistical performance metrics including R2, ARE, AAE, and ASE to determine the most descriptive adsorption isotherm model. The Langmuir model’s high R2 score (0.999) reflects its superior ability to describe the adsorption process compared to alternative models (Freundlich: R2 = 0.834). Additionally, the low error metrics for Langmuir (ARE = 0.01, AAE = 0.01, ASE = 0.02) confirm its predictive accuracy (Table 2).

The Langmuir model’s assumption of monolayer adsorption on homogeneous surface sites is consistent with the observed HQ adsorption behavior, as quartz particles lack significant surface heterogeneity. The maximum adsorption capacity (qo = 47.1 mg/g at 25 °C) derived from the Langmuir equation aligns with experimental observations, reinforcing the model’s validity. Figure 4 demonstrates the excellent fit between experimental data and theoretical predictions, confirming that Langmuir accurately describes the HQ adsorption process under the tested conditions.

Fig. 4
figure 4

FTIR spectroscopy results from analyzing HQ.

Full size image
Table 2 Tabulated results obtained from fitting lab data with various adsorption isotherm models.
Full size table

The maximum adsorption capacity (qo) derived from the Langmuir model was 47.1 mg/g at 25 °C. This indicates that quartz has a relatively high efficiency for HQ adsorption under these conditions, making it particularly useful for subsurface applications, such as in-situ gel processes for clay stabilization. The ability of quartz to adsorb HQ efficiently at standard conditions holds practical significance for optimizing HQ injection processes in oil reservoirs. These findings also highlight the potential of quartz in mitigating challenges posed by excess HQ in subsurface environments, maximizing the efficiency of chemical treatments.

By confirming the Langmuir model as the best fit for the adsorption data (Table 2), this research provides a robust framework for predicting and analyzing HQ behavior under different conditions. The model’s predictive power enables precise design and optimization of injection processes in subsequent research. It also facilitates the assessment of HQ performance in real-world situations, helping to bridge the gap between laboratory results and field applications in reservoir engineering. This approach lays the foundation for improved chemical flooding strategies and provides valuable insights for industrial processes.

Investigating the effect of temperature on adsorption behavior

To evaluate the influence of temperature on the adsorption behavior of HQ, experiments were conducted at various temperatures: 40, 55, 70, 85, and 95 °C. The results of these tests, presented in Fig. 5 and summarized in Table 3, provide critical insights into the variations in HQ adsorption capacity and the interactions between HQ molecules and the quartz surface under thermal effects. By analyzing the data, significant patterns emerge, revealing the thermodynamic and kinetic factors influencing the adsorption process with changing temperatures.

Fig. 5
figure 5

Lab data pertain to adsorption of HQ on quartz particles in different temperatures.

Full size image

The experimental results demonstrate a consistent decrease in the adsorption capacity of HQ as temperature increases. At 25 °C, the maximum adsorption capacity was measured as 47.1 mg/g-rock, but this value dropped significantly to 27.5 mg/g-rock at 80 °C. This reduction indicates that the adsorption process is highly temperature-sensitive. The decrease in adsorption capacity at elevated temperatures can be attributed to increased thermal energy, which enhances molecular motion and disrupts HQ’s interactions with the quartz surface. Faster-moving HQ molecules encounter more excellent kinetic resistance, reducing their ability to adsorb onto active sites on quartz.

Modeling the adsorption data using the Langmuir isotherm showed that the equilibrium constant decreases with increasing temperature, confirming the exothermic nature of the adsorption process. Thermodynamic analysis further supports this finding, as the decline in adsorption capacity is consistent with an increase in system entropy and a decrease in Gibbs free energy. Notably, the negative ΔG values across all temperatures indicate that the adsorption process remains spontaneous, albeit less favorable at higher temperatures. This behavior highlights the energy-dependent nature of HQ adsorption and the diminishing tendency of the system to adsorb HQ with increasing thermal energy.

Moreover, temperature may also alter the physical and chemical properties of the quartz surface, influencing its adsorption performance. At higher temperatures, structural changes might affect the availability or efficiency of active sites on the quartz surface. For instance, some adsorptive sites may become deactivated or rearranged, reducing their interaction potential with HQ molecules. These surface modifications, in combination with thermodynamic mechanisms, help explain the observed decrease in adsorption capacity at elevated temperatures.

Table 3 Tabulated results obtained from adsorption experiments in various temperatures.
Full size table

This comprehensive analysis of the effect of temperature on HQ adsorption onto quartz provides valuable insights for optimizing HQ injection into sandstone reservoirs. Understanding the temperature dependence of adsorption supports the design of effective chemical injection strategies, ensuring maximum efficiency in subsurface applications. The results of this study serve as a foundation for future research, particularly on the thermodynamic optimization of chemical flooding and adsorption processes in oil reservoir environments.

Thermodynamic modeling

A detailed thermodynamic analysis was conducted to gain deeper insight into the HQ adsorption process. The relationship between equilibrium adsorption capacity (qe​) and equilibrium concentration (Ce​) was examined by plotting qe​/Ce​ against qe​. The intercept from the resulting linear regression was used to determine the distribution coefficient (Kd​) at various temperatures, as shown in Fig. 6. The plot reveals a clear trend that Kd​ values increase with rising temperature, indicating that temperature significantly impacts the adsorption process.

Fig. 6
figure 6

The plot of qe/ce versus ce of lab data obtained in different temperatures.

Full size image

Thermodynamic parameters, including enthalpy (ΔH), entropy (ΔS), and Gibbs free energy (ΔG), were calculated based on the adsorption data. Table 4 summarizes the results derived from the Kd​ values at different temperatures.

Plotting ln(Kd​) versus T− 1 ​, the slope and intercept of the linear regression were used to calculate the enthalpy and entropy changes of the process. The enthalpy of adsorption was determined to be -8018 J/mol, indicating an endothermic reaction. This result highlights that the adsorption process relies on temperature increases to achieve higher molecular energy levels and improved adsorption efficiency. The entropy change (ΔS) was calculated as 6.12 J/mol·K, reflecting the increased randomness at the solid-liquid interface during HQ adsorption.

Table 4 Gibbs free energy change calculation for HQ adsorption process in different temperatures.
Full size table

The calculated Gibbs free energy (ΔG) for HQ adsorption at various temperatures is also shown in Table 4. The ΔG values were negative across all temperatures tested, confirming that the adsorption process is thermodynamically favorable and spontaneous under the given experimental conditions. A negative ΔG implies the system can proceed naturally without an external energy input. This phenomenon is critical in practical applications, as it supports the feasibility of HQ adsorption on quartz under reservoir-like conditions.

Moreover, the increased adsorption equilibrium constant (Kd) with rising temperature indicates enhanced adsorption at elevated temperatures. From a thermodynamic perspective, this behavior underscores that the adsorption process is spontaneous. The rise in adsorption efficiency can be attributed to the increased kinetic energy of HQ molecules, which enhances their diffusion and interaction with active sites on the quartz surface.

Examining the adsorption behavior in the porous medium

At this research stage, six sandstone cores, with characteristics summarized in Table 5, were subjected to flooding with an HQ solution at a concentration of 100,000 mg/L. Experiments were conducted at various temperatures (25, 40, 55, 70, 85, and 95 °C) to evaluate the adsorption behavior of HQ in porous media. The results revealed a significantly lower sandstone cores’ adsorption capacity than the previous quartz batch experiments. This is attributable to the porous sandstone media’s inherently heterogeneous structure and surface properties.

Several factors influence the reduction in adsorption capacity. First, the physical structure of sandstone cores, characterized by pores, voids, and constricted channels, affects the accessibility of active adsorption sites for HQ molecules. Variations in pore size and distribution within the cores can hinder HQ molecules from reaching the quartz surfaces effectively. These factors collectively explain the divergence in adsorption performance between the sandstone cores and the pure quartz examined in previous experiments.

Table 5 Core plug specifications and data obtained from the core adsorption experiment.
Full size table

Despite the differences in adsorption capacity, the experiments confirmed that HQ adsorption in the sandstone cores follows a temperature-dependent pattern similar to the pure quartz system. As shown in Table 5, the adsorption capacity decreased from 24 mg/g-rock at 25 °C to 14 mg/g-rock at 95 °C. This increase aligns with the expected thermodynamic response of adsorption processes. The increased thermal energy enhances molecular motion at higher temperatures, reducing adsorption onto the rock surface. Furthermore, higher temperatures can hinder the diffusion of HQ molecules into the porous structure of the sandstone cores, reducing the overall adsorption process.

Thermodynamically, the temperature-dependent reduction in adsorption capacity reflects the exothermic nature of the HQ adsorption process. The reduction in adsorption equilibrium constant with temperature indicates that the system inherently favors adsorption at elevated temperatures. This behavior is likely driven by an increase in system entropy and a corresponding decrease in Gibbs free energy (ΔG), which makes the process spontaneous.

Limitations of this study and recommendations for future work

While this study provides valuable insight into the thermodynamic adsorption behavior of HQ on sandstone rock surfaces, it is important to note that the adsorption of the polymer was not accounted for in this analysis. The presence of polymers in real-world applications can alter the adsorption equilibrium and influence the interaction of crosslinking agents with the rock surface. Future studies are recommended to investigate the combined adsorption behavior of polymers and crosslinking agents to simulate practical conditions better. Additionally, experimental investigations examining the dynamic interactions between polymers, crosslinking agents, and reservoir rock surfaces would provide a more comprehensive understanding, which could further optimize crosslinker selection for enhanced oil recovery applications.

Conclusion

This study provides a thorough analysis of the adsorption behavior of hydroquinone (HQ) on quartz, offering essential insights into adsorption modeling, temperature effects, and the behavior in porous media. Key findings include:

  1. 1.

    Adsorption Modeling at 25 °C: The Langmuir isotherm was identified as the most accurate model for describing HQ adsorption on quartz at 25 °C. This suggests monolayer adsorption on homogeneous surfaces, as demonstrated by the model’s excellent statistical fit (R2 = 0.999) and derived parameters. The predictive capability of the Langmuir model underscores its utility in designing and optimizing industrial applications involving HQ, particularly in subsurface environments like oil reservoirs.

  2. 2.

    Temperature Influence on Adsorption: It was observed that HQ adsorption capacity decreases with increasing temperature, indicating a temperature-sensitive and exothermic process. The decline in adsorption efficiency at higher temperatures can be attributed to enhanced molecular motion, which disrupts interactions with quartz surfaces. Despite reduced adsorption at elevated temperatures, the process remains spontaneous, as indicated by negative Gibbs free energy values across the tested range.

  3. 3.

    Thermodynamic Insights: Thermodynamic parameters revealed that the adsorption process is exothermic. The calculated enthalpy and entropy changes provide a framework for understanding the energy dynamics of HQ adsorption on quartz.

  4. 4.

    Adsorption in Porous Medium: Experiments with sandstone cores highlighted a distinct adsorption behavior compared to pure quartz, primarily due to the heterogeneous structure of the media, which limits active site accessibility. Despite lower adsorption capacities in sandstone, the temperature-dependent trend remains consistent, reinforcing the thermodynamic principles observed in quartz systems.

These findings form a robust basis for future research to optimize HQ injection strategies in subsurface engineering and other industrial processes. This study contributes to developing more efficient chemical flooding strategies and advancing reservoir engineering applications by enhancing the understanding of HQ adsorption behavior under varying conditions.