Introduction

Precise point positioning (PPP) has the advantages of single-station operation, flexibility, convenience, and high positioning accuracy. It is currently used in meteorology, global navigation satellite system (GNSS) seismology, precision timing, satellite positioning, precision agriculture, and other scientific research and civil applications1,2,3,4. However, traditional PPP float solutions take long time to converge to a better level. Fortunately, ambiguity resolution (AR) can improve the positioning accuracy and accelerate the convergence time5,6. Therefore, many scholars have proposed some methods to fix ambiguity such as clock error decoupling model, integer clock method, and method based on uncalibrated phase delay (UPD) estimation and so on5,6,7,8, among which the UPD estimation is simple and easy to use with good results. Wang et al. (2018) used reference network of different scales to calculate UPD products, and the results showed that the UPD products calculated by the smaller network had better accuracy9. Li et al. (2018) estimated the UPDs of global positioning system (GPS), global navigation satellite system (GLONASS), Galileo satellite navigation system (Galileo), and BeiDou navigation satellite system (BDS) and achieved multi-GNSS PPP-AR. The time to first fix (TTFF) was 9.21 min, which was substantially shorter than that of single- and dual-system positioning, and the positioning accuracy of 1.84 cm, 1.11 cm, and 1.53 cm in the east, north, and up directions was achieved within 10 min10. Zhao et al. (2021) estimated the UPDs using only data from observation stations and used estimated UPD products for partial AR of GNSS. The results showed that the positioning accuracy of static PPP fix solutions was improved by 24%, 21% and 18% in the east, north, and up components, respectively, compared with the float solutions11. Zeng et al. (2023) systematically investigated the influencing factors of wide- (WL) and narrow-lane (NL) UPDs of four satellite systems from the perspective of parameter estimation, and found that using regional networks can improve the temporal stability and residual distributions of UPDs of BDS12.

Multi-system positioning can increase the number of observable satellites and improve the positioning performance. Li et al. (2015) investigated a four-system positioning model to make full use of the available observation data of each system13. Pan et al. (2019) investigated the availability of four-constellation integration of GPS, Galileo, GLONASS, and BDS, and the results showed that multi-constellation integration can significantly improve the positioning accuracy14. In 2020, the Beidou-3 navigation satellite system (BDS-3) was officially launched, and the full constellation was in orbit and provided open services10,14,15,16. With the completion of BDS-3, many scholars have carried out a lot of research on the multi-system positioning of BDS-3, GPS, and Galileo. Chen et al. (2022) studied the multi-GNSS tight combination PPP, and experiments showed that the tight combination PPP can significantly improve the positioning accuracy, especially in harsh environments, and the positioning accuracy was improved by 98.8% and 31.3% compared with the loose combination in the case of static and dynamic PPP, respectively17. Yuan et al. (2023) investigated the tight combination PPP of GPS, Galileo, BDS-2, andBDS-3 considering inter-system bias (ISB), and the results showed that compared with the loose combination PPP, when there were only two observable satellites in each system, the positioning accuracy was improved by 60.6%, 56.6%, and 61.2% in the east, north, and up directions, respectively18.

In recent years, low-Earth orbit (LEO) satellites have developed rapidly. Since 2015, many commercial companies and enterprises, such as OneWeb (USA), SpaceX (USA), Samsung (South Korea), and China Aerospace Science and Technology Group (CASTG) have announced the launch of LEO satellites to establish a global LEO satellite constellation19,20,21. LEO satellites operate fast and thus provide rapid geometric change relation to the ground stations in a short period of time, which is expected to further solve the problem of long PPP convergence time. In order to verify the positioning performance of LEO satellites, many scholars have carried out a large number of LEO satellite enhanced high-precision positioning experiments using simulated LEO satellite observation data. Ge et al. (2018) enhanced GNSS with simulated LEO satellite observations, which shortened the PPP convergence time to 5 min22. Li et al. (2019) designed three LEO constellations consisting of 60, 192, and 288 satellites. By introducing the observation data of the three constellations, the TTFF of the combined GPS, GLONASS, Galileo, BDS fix solution was shortened from 7.1 min to 4.8, 1.1, and 0.7 min, respectively, and the positioning accuracy was also improved by 60%, 80%, and 90%, respectively23. Ge et al. (2020) statistically analyzed LEO constellations in terms of number of LEO orbital planes, number of LEO satellites, and orbital inclinations, and selected the LEO constellation with a total 240 LEO satellites of orbital inclinations at 90, 60, and 35 degrees, and one-minute convergence time for PPP was achieved on a global scale24. Liu et al. (2022) designed two LEO constellations consisting of 177 and 186 satellites to enhance BDS. The results showed that the positioning accuracy was improved from decimeter level to less than 5 cm in 10 min, and the convergence time was shortened to within 3.5 min and 3 min, respectively25. Hong et al. (2023) enhanced GNSS with simulated LEO observations, and the results showed that the convergence time of GPS, BDS, and combined GPS, GLONASS, Galileo, BDS was improved by 90.0%, 91.0%, and 90.7%, respectively26.

In this study, based on the given multi-system tight combination PPP model, we introduced the GPS, Galileo, BDS-3, LEO UPDs estimation method, and AR method, and evaluated the UPDs quality of the satellite-end of the four systems. Based on this, we performed multi-system tight combination PPP float and fix solutions, evaluated the positioning performances, and analyzed the performance of AR.

Methods

LEO constellation design and observations simulation

The Satellite Tool Kit (STK) software was used to design LEO constellation and simulate LEO observations27. We designed polar and inclined orbits with an altitude of 1000 km. 70 LEO satellites are distributed in 6 polar orbits with an inclination of 90º and 90 LEO satellites are distributed in 10 inclined orbits with an inclination of 60º.

The simulation of LEO satellites observations is actually the inverse process of LEO satellites positioning, the equations are as follows:

$$\left\{ \begin{gathered} p_{{r,i}}^{L}=\rho _{r}^{L}+cd{t_r} - cd{t^L}+I_{{r,i}}^{L}+T_{r}^{L}+{d_{r,i}} - d_{i}^{L}+e_{{r,i}}^{L} \hfill \\ \varphi _{{r,i}}^{L}=\rho _{r}^{L}+cd{t_r} - cd{t^L} - I_{{r,i}}^{L}+T_{r}^{L}+\lambda _{i}^{L}(\bar {N}_{{r,i}}^{L}+{b_{r,i}} - b_{i}^{L})+\varepsilon _{{r,i}}^{L} \hfill \\ \end{gathered} \right.$$
(1)

Where p and \(\varphi\) represent the pseudorange and carrier phase observations; r, i and L represent the identifiers of the receiver, frequency and LEO satellite system, respectively; \(\rho\) refers to the geometric distance between the receiver and satellite; c refers to the speed of light; \(d{t_r}\) and \(d{t^L}\) refer to the clock error of the receiver and LEO satellite, respectively; I indicates the ionospheric delay; T indicated the tropospheric delay; \({d_{r,i}}\) and \(d_{i}^{L}\) refer to the pseudorange hardware delays at the receiver- and satellite-ends, respectively; \(\lambda\) refers to the wavelength; \(\bar {N}\) refers to the integer ambiguity; \({b_{r,i}}\) and \(b_{i}^{L}\) refer to the phase hardware delays at the receiver- and satellite-ends, respectively; e and \(\varepsilon\) refer to the observation noise of pseudorange and carrier phase, respectively.

The receiver clock errors were set to 0.0. The STK software was used to obtain the orbit errors of LEO satellites. The GPS satellites were used to replace the LEO satellites randomly. The ionospheric delays were set to 0.0. The Saastamoinen model was used to simulate the dry and wet component of tropospheric delays. The multi-GNSS differential code bias (DCB) products were used to simulate the code bias of each frequency. The integer ambiguity and UPD at each frequency were assumed to be a constant integer and a small floating-point value, respectively. The measurement noise of code and phase was simulated to Gaussian white noise with standard deviations (STDs) of 0.5 m and 0.003 m, respectively. The phase center variation (PCV) and phase center offset (PCO) were both set to 0.0. Phase windup, general relativistic effects, Earth solid tides, ocean tides and Sagnac effects can be accurately calculated from existing models. We assumed all LEO satellites transmit same signals on two frequencies, L1 at 1575.42 MHz, L2 at 1227.6 MHz, which are consistent with L1 and L2 frequencies of GPS signals.

Multi-system tight combination PPP model

In this study, GPS, Galileo, and BDS-3 (denoted by G, E, and C below, respectively) observations and simulated LEO observations were used to perform experiments. The observation model for the tight combination PPP of G, E, C, and LEO is as follows:

$$\left\{ {\begin{array}{*{20}{l}} {p_{{r,i}}^{Q}=\rho _{r}^{Q}+cd{t_r} - cd{t^Q}+k \cdot ISB+m_{r}^{Q} \cdot zwd_{r}^{Q}+I_{{r,i}}^{Q}+{d_{r,i}} - d_{i}^{Q}+e_{{r,i}}^{Q}} \\ {p_{{r,i}}^{L}=\rho _{r}^{L}+cd{t_r} - cd{t^L}+k \cdot ISB+m_{r}^{L} \cdot zwd_{r}^{L}+I_{{r,i}}^{L}+{d_{r,i}} - d_{i}^{L}+e_{{r,i}}^{L}} \\ {\varphi _{{r,i}}^{Q}=\rho _{r}^{Q}+cd{t_r} - cd{t^Q}+k \cdot ISB+m_{r}^{Q} \cdot zwd_{r}^{Q} - I_{{r,i}}^{Q}+\lambda _{i}^{Q}\left( {\bar {N}_{{r,i}}^{Q}+{b_{r,i}} - b_{i}^{Q}} \right)+\varepsilon _{{r,i}}^{Q}} \\ {\varphi _{{r,i}}^{L}=\rho _{r}^{L}+cd{t_r} - cd{t^L}+k \cdot ISB+m_{r}^{L} \cdot zwd_{r}^{L} - I_{{r,i}}^{L}+\lambda _{i}^{L}\left( {\bar {N}_{{r,i}}^{L}+{b_{r,i}} - b_{i}^{L}} \right)+\varepsilon _{{r,i}}^{L}} \end{array}} \right.$$
(2)

Where r and i denote the identifier of the receiver and frequency, respectively; Q denotes G, E, C satellite system identifier; L denotes LEO satellite system identifier; c refers to the speed of light; p and \(\varphi\) denote the pseudorange and carrier phase observations, respectively; \(\rho\) refers to the geometric distance between the satellite and receiver; \(d{t_r}\) refers to the receiver clock error; \(dt\) refers to the satellite clock errors, which are corrected using precise clock product; \(ISB\) denotes the inter-system bias, when the satellite system is reference system, \(k=0\), and when the satellite system is not reference system, \(k=1\); \(m_{r}^{Q}\) denotes the mapping function of the zenith wet delay of G, E, and C system; \(zwd_{r}^{Q}\) denotes the zenith wet delay (ZWD) of G, E, and C system; \(m_{r}^{L}\) denotes the mapping function of the ZWD of LEO system; \(zwd_{r}^{L}\) denotes the ZWD of LEO system; \({I_{r,i}}\) represents the ionospheric delay; \({d_{r,i}}\) and \({d_i}\) refer to the pseudorang hardware delays at the receiver- and satellite-end, respectively; \({b_{r,i}}\) and \({b_i}\) denote the phase hardware delays at the receiver- and satellite-end, respectively; \({\lambda _i}\) denotes the wavelength; \({\overline {N} _{r,i}}\) refers to the integer ambiguity; \({e_{r,i}}\) and \({\varepsilon _{r,i}}\) denote the observation noise of pseudorange and carrier phase, respectively. The other errors such as Earth solid tides, ocean tides, satellite orbit errors, phase wrapping, PCOs, PCVs, tropospheric dry delays, relativistic effects, Earth rotation and so on, which were corrected using existing models or products such as precise orbit products, antex file, Earth rotation parameters file and so on. In Eq. (2), we estimated the ZWD of G, E, C and LEO satellites as two parameters. Because in the simulation process, the Sasstamoninen model was used to simulate the tropospheric delays of LEO satellites, while the tropospheric delays of G, E, C were real.

The ionosphere-free (IF) combination is one of the commonly used models in PPP, in the experiments covered in this study, the IF combination of G, E, C, L consist of observations at the L1 and L2, E1 and E5a, B1 and B3, L1 and L2 bands, respectively. The IF combination equation is as follows:

$$\left\{ {\begin{array}{*{20}{l}} {p_{{r,{\text{IF}}}}^{Q}=\frac{{f_{i}^{2}p_{{r,i}}^{Q} - f_{j}^{2}p_{{r,j}}^{Q}}}{{f_{i}^{2} - f_{j}^{2}}}=\rho _{r}^{Q}+cd{t_r} - cd{t^Q}+k \cdot ISB+m_{r}^{Q} \cdot zwd_{r}^{Q}+{d_{r,{\text{IF}}}} - d_{{{\text{IF}}}}^{Q}+e_{{r,{\text{IF}}}}^{Q}} \\ {p_{{r,{\text{IF}}}}^{L}=\frac{{f_{i}^{2}p_{{r,i}}^{Q} - f_{j}^{2}p_{{r,j}}^{Q}}}{{f_{i}^{2} - f_{j}^{2}}}=\rho _{r}^{L}+cd{t_r} - cd{t^L}+k \cdot ISB+m_{r}^{L} \cdot zwd_{r}^{L}+{d_{r,{\text{IF}}}} - d_{{{\text{IF}}}}^{L}+e_{{r,{\text{IF}}}}^{L}} \\ \begin{gathered} \varphi _{{r,{\text{IF}}}}^{Q}=\frac{{f_{i}^{2}\varphi _{{r,i}}^{Q} - f_{j}^{2}\varphi _{{r,j}}^{Q}}}{{f_{i}^{2} - f_{j}^{2}}}=\rho _{r}^{Q}+cd{t_r} - cd{t^Q}+k \cdot ISB+m_{r}^{Q} \cdot zwd_{r}^{Q} \hfill \\ {\text{ }}+\lambda _{{{\text{IF}}}}^{Q}\left( {\bar {N}_{{r,{\text{IF}}}}^{Q}+{b_{r,{\text{IF}}}} - b_{{{\text{IF}}}}^{Q}} \right)+\varepsilon _{{r,{\text{IF}}}}^{Q} \hfill \\ \end{gathered} \\ \begin{gathered} \varphi _{{r,{\text{IF}}}}^{L}=\frac{{f_{i}^{2}\varphi _{{r,i}}^{L} - f_{j}^{2}\varphi _{{r,j}}^{L}}}{{f_{i}^{2} - f_{j}^{2}}}=\rho _{r}^{{L,s}}+cd{t_r} - cd{t^L}+k \cdot ISB+m_{r}^{L} \cdot zwd_{r}^{L} \hfill \\ {\text{ }}+\lambda _{{{\text{IF}}}}^{L}\left( {\bar {N}_{{r,{\text{IF}}}}^{L}+{b_{r,{\text{IF}}}} - b_{{{\text{IF}}}}^{L}} \right)+\varepsilon _{{r,{\text{IF}}}}^{L} \hfill \\ \end{gathered} \end{array}} \right.$$
(3)

Where i and j denote the frequency identifier; f represents the frequency; \({d_{r,{\text{IF}}}}\) and \({d_{{\text{IF}}}}\) refer to the pseudorange hardware delay at the receiver- and satellite-end after the IF combination, respectively; \({b_{r,{\text{IF}}}}\) and \({b_{{\text{IF}}}}\) denote the phase hardware delay at the receiver- and satellite-end after the IF combination, respectively; \({\lambda _{{\text{IF}}}}\) denotes the wavelength of the IF combination observations; \({\overline {N} _{r,{\text{IF}}}}\) refers to the integer ambiguity of IF combination observations.

The least-squares and Kalman filter method were used to solve station coordinate and ambiguity parameters, and we weight observations using the stochastic model related to elevation angle. The cut-off elevation angles for the G, E, C satellites are7º and for the LEO satellites are 2º.

UPD products estimation method

UPDs cause the interger ambiguities to lose interger characteristics. If we can determine the UPDs parameters in advance, we can achieve AR successfully, accelerate the convergence time of PPP, and improve the positioning accuracy.

In the PPP AR process, the ambiguity of the IF combination is usually decomposed into WL and NL ambiguities to solve:

$$\tilde {N}_{{r,{\text{IF}}}}^{H}=\left( {\frac{{c{f_j}}}{{f_{j}^{2} - f_{j}^{2}}}\bar {N}_{{r,{\text{WL}}}}^{H}+\frac{c}{{{f_i}+{f_j}}}\tilde {N}_{{r,{\text{NL}}}}^{H}} \right)/{\lambda _{{\text{IF}}}}=\tilde {N}_{{r,{\text{NL}}}}^{H}+\bar {N}_{{r,{\text{WL}}}}^{H}{f_j}/\left( {{f_i} - {f_j}} \right)$$
(4)

Where H represents the G, E, C, and LEO satellite systems, \(\tilde {N}_{{r,{\text{IF}}}}^{H}\) represents the real ambiguity of the IF combination, \(\tilde {N}_{{r,{\text{NL}}}}^{H}\) and \(\bar {N}_{{r,{\text{WL}}}}^{H}\) represents the real ambiguity of the NL and integer ambiguity of the WL, respectively. The WL ambiguity is generally solved using the Melbourne-Wübbena (MW) combination28,29,30:

$$\begin{gathered} \tilde {N}_{{r,{\text{WL}}}}^{H}=\left( {\frac{{\varphi _{{r,i}}^{H}}}{{\lambda _{i}^{H}}} - \frac{{\varphi _{{r,j}}^{H}}}{{\lambda _{j}^{H}}}} \right) - \left( {\frac{{p_{{r,i}}^{H}\lambda _{j}^{H}}}{{\left( {\lambda _{i}^{H}+\lambda _{j}^{H}} \right)}} - \frac{{p_{{r,j}}^{H}\lambda _{i}^{H}}}{{\left( {\lambda _{i}^{H}+\lambda _{j}^{H}} \right)}}} \right)/\lambda _{{{\text{WL}}}}^{H} \hfill \\ {\text{ }}=\tilde {N}_{{r,{\text{WL}}}}^{H}=\bar {N}_{{r,{\text{WL}}}}^{H}+upd_{{r,{\text{WL}}}}^{H} - upd_{{{\text{WL}}}}^{H} \hfill \\ \end{gathered}$$
(5)

Where \(\tilde {N}_{{r,{\text{WL}}}}^{H}\) and \(\bar {N}_{{r,{\text{WL}}}}^{H}\) denote the real ambiguity of the WL and the integer part of the WL ambiguity, respectively; \({\text{~}}\lambda _{{{\text{WL}}}}^{H}\) represents the wavelength of the WL; \(upd_{{r,{\text{WL}}}}^{H}\) and \(upd_{{{\text{WL}}}}^{H}\) refer to the UPDs at the receiver- and satellite-ends of each system, respectively. Because of the large noise of the pseudorange observation, it is necessary to smooth the MW combination value of continuous epochs to improve the reliability. Assuming that each system in a network consisting of m stations can observe a total of \({n^H}\) satellites, the number of satellites that can be observed by each system at the ith station is \(n_{i}^{H}\left( n_{i}^{H} \leqslant {n^H},i=1,2, \ldots ,m\right)\), and the observation equations can be established to solve the WL UPDs parameters from Eq. (6):

$$\left[ {\begin{array}{*{20}{c}} {\tilde {{\varvec{N}}}_{{{\text{WL}}1}}^{H}} \\ {\tilde {{\varvec{N}}}_{{{\text{WL}}2}}^{H}} \\ \vdots \\ {\tilde {{\varvec{N}}}_{{{\text{WL}}m}}^{H}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\varvec{I}}&{}&{}&{}&{{{\varvec{R}}_1}}&{{{\varvec{S}}_1}} \\ {}&{\varvec{I}}&{}&{}&{{{\varvec{R}}_2}}&{{{\varvec{S}}_2}} \\ {}&{}& \ddots &{}& \vdots & \vdots \\ {}&{}&{}&{\varvec{I}}&{{{\varvec{R}}_m}}&{{{\varvec{S}}_m}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\bar {{\varvec{N}}}_{{{\text{WL}}1}}^{H}} \\ {\bar {{\varvec{N}}}_{{{\text{WL}}2}}^{H}} \\ \vdots \\ {\bar {{\varvec{N}}}_{{{\text{WL}}m}}^{H}} \\ {{\varvec{u}}{\varvec{p}}{\varvec{d}}_{{{\text{WL}},r}}^{H}} \\ {{\varvec{u}}{\varvec{p}}{\varvec{d}}_{{{\text{WL}}}}^{H}} \end{array}} \right]$$
(6)

Where \({\tilde {{\varvec{N}}}_{{\text{WL}}i}}\) and \({\bar {{\varvec{N}}}_{{\text{WL}}i}}\) denote the vector of WL real ambiguity and the integer part of the WL ambiguity of each system at the ith station, respectively; \({\varvec{u}}{\varvec{p}}{\varvec{d}}_{{{\text{WL}},r}}^{H}\) and \({\varvec{u}}{\varvec{p}}{\varvec{d}}_{{{\text{WL}}}}^{H}\) represent the WL UPD vector of the receiver- and satellite-end of each system, respectively; \({\varvec{u}}{\varvec{p}}{\varvec{d}}_{{{\text{WL}},r}}^{H}\)is a \(m \times 1\)-dimensional vector; \({\varvec{u}}{\varvec{p}}{\varvec{d}}_{{{\text{WL}}}}^{H}\) is a \({n^H} \times 1\)-dimensional vector; \({{\varvec{R}}_i}\) is a \(n_{i}^{H} \times {n^H}\)-coefficient matrix with the ith column elements of 1 and the remaining elements of 0; \({{\varvec{S}}_i}\) is a \(n_{i}^{H} \times {n^H}\)-coefficient matrix in which the elements of the corresponding satellite in each row are − 1 and the other elements are 0; I is the unit matrix. As the WL UPDs of the satellite- and receiver-end in Eq. (6) are linearly related, there is a rank defect problem in this equation group. the satellite with the most observations of each system is usually selected as the reference satellite of each system, with their WL UPDs fixed to 0, and we can solve Eq. (6) using the least-squares method to obtain the WL UPDs parameters of the satellite- and receiver-end.

Using the fixed WL integer ambiguity (The method for fixing WL ambiguity will be presented in Sect. “Ambiguity resolution method”) and accurately estimated IF real ambiguity, the NL real ambiguity can be obtained from Eq. (7):

$$\tilde {N}_{{r,{\text{NL}}}}^{H}=\tilde {N}_{{r,{\text{IF}}}}^{H} - \bar {N}_{{r,{\text{WL}}}}^{H}{f_j}/\left( {{f_i} - {f_j}} \right)=\bar {N}_{{r,{\text{NL}}}}^{H}+upd_{{r,{\text{NL}}}}^{H} - upd_{{{\text{NL}}}}^{H}.$$
(7)

The NL UPDs are estimated using the Kalman filter according to Eq. (6).

Ambiguity resolution method

The WL ambiguity obtained from Eq. (5) was corrected using the WL UPD of the satellite-end as follows:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} _{{r,{\text{WL}}}}^{H}=\tilde {N}_{{r,{\text{WL}}}}^{H}+upd_{{{\text{WL}}}}^{H}$$
(8)

Where \(\tilde {N}_{{r,{\text{WL}}}}^{H}\) refers to the real WL ambiguity calculated using the MW combination; \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} _{{r,{\text{WL}}}}^{H}\) refers to the real WL ambiguity corrected using the UPD of the satellite-end. We can use the method proposed by Gabor (1999) to average the fractional parts of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} _{{r,{\text{WL}}}}^{H}\) to obtain the WL UPD of the receiver-end31. The obtained WL UPD of receiver-end was used to further correct \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} _{{r,{\text{WL}}}}^{H}\). However, it still not an integer, we can obtain integer WL ambiguity using the direct rounding method:

$$\bar {N}_{{r,{\text{WL}}}}^{H}={\text{round}}(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{N} _{{r,{\text{WL}}}}^{H} - upd_{{r,{\text{WL}}}}^{H})$$
(9)

Where \(\bar {N}_{{r,{\text{WL}}}}^{H}\) is the WL integer ambiguity; \({\text{round}}(\cdot )\) is the rounding function.

We can substitute the fixed WL ambiguity and the accurately estimated IF ambiguity into Eq. (7) to obtain real NL ambiguity. The method similar to that described above was used to further correct NL ambiguity. Because of there is the strong correlation among NL ambiguities, the least-squares ambiguity decorrelation adjustment (LAMBDA) method was used to fix the NL ambiguity32. Because the more the number of ambiguities to be fixed, the greater the amount of calculation, the lower the success fix rate, so we used the method of partial AR (PAR) to fix the NL ambiguities33,34,35. We selected the optimal ambiguity subset using the method proposed by Li and Zhang (2015), which used both bootstrapping success rate and Ratio-test to check the ambiguity integer solution during the subset selection process36,37,38,39. The difference is that we sorted the ambiguities based on the elevation angle. The flowchart of the PAR algorithm is shown below in Fig. 1.

Fig. 1
figure 1

PAR flowchart based on bootstrapping success rate and Ratio-test.

Full size image

After the WL and NL ambiguities are fixed successfully, we can use Kalman filter method to obtain more accurate IF ambiguity.

Results

Performance analysis of UPD products

126 globally distributed stations were used to calculate the WL UPDs on days of year (DOYs) 001–010 and the NL UPDs on DOY 001 in 2022 for G, E, C, LEO, and the distribution of stations is shown in Fig. 2. The wavelength of WL ambiguity is longer, and the noise is reduced after smoothing. WL UPDs are relatively stable and are generally estimated once one day. The wavelength of NL ambiguity is short, and NL ambiguity absorbs other errors. NL UPDs have relatively large changes in a short period of time, typically estimated every 10–30 min5,40. In this study, the WL UPDs were estimated once one day within ten days and the NL UPDs were estimated once 15 min within one day. Figure 3 shows the time series of WL UPDs on DOYs 001–010 for G, E, C, LEO satellites, and the average standard deviation (STD) of WL UPDs for G, E, C, LEO is 0.39, 0.41, 0.37, 0.02 cycles, respectively. Figure 4 shows the time series of NL UPDs on DOY 001 for G, E, C, LEO satellites, and the average STD of NL UPDs for G, E, C, LEO is 0.06, 0.09, 0.17, 0.05 cycles, respectively. In Figs. 3 and 4, lines and symbols in distinct colors within each subplot denote different satellites of respective systems. Table 1 lists the average STDs of WL and NL UPDs of each system. It can be seen from Figs. 3 and 4 that the NL UPD s of each system have good stability within one day, and the WL UPDs of each system have good stability within 10 days, and the WL UPDs of most satellites of each system have similar change tendencies.

Fig. 2
figure 2

Distribution of stations used for UPDs estimation.

Full size image
Fig. 3
figure 3

WL UPDs time series plot on DOY 001–010 in 2022 for G, E, C, LEO satellites. WL: wide-lane; UPD: uncalibrated phase delay; GPS: global positioning system; Galileo: Galileo satellite navigation system; BDS-3: BeiDou-3 navigation satellite system; LEO: low-Earth orbit satellites; DOY: day of year. (In each subplot, lines and symbols in distinct colors denote different satellites within each respective system.).

Full size image
Fig. 4
figure 4

NL UPDs time series plot on DOY 001 in 2022 for G, E, C, LEO satellites. NL: narrow-lane; UPD: uncalibrated phase delay; GPS: global positioning system; Galileo: Galileo satellite navigation system; BDS-3: BeiDou-3 navigation satellite system; LEO: low-Earth orbit satellites; DOY: day of year. (In each subplot, lines and symbols in distinct colors denote different satellites within each respective system.).

Full size image
Table 1 Average STDs of WL and NL UPDs of each system.
Full size table

The posteriori residuals can reflect the quality of the UPD products, Fig. 5 shows the posterior residual distribution of WL and NL UPDs on DOY 001 for G, E, C, LEO satellites. For WL UPDs, more than 89% of the posterior residuals of each system are less than 0.15 cycles and more than 97% are less than 0.25 cycles. For NL UPDs, more than 87% of the posterior residuals of G, E, LEO system are less than 0.15 cycles and more than 95% are less than 0.25 cycles, and 68% of the posterior residuals of BDS-3 system are less than 0.15 cycles and 86% are less than 0.25 cycles. The WL and NL UPDs of each system show good quality.

Fig. 5
figure 5

Distribution of posterior residuals of WL and NL UPDs on DOY 001 in 2022 for G, E, C, LEO satellites. WL: wide-lane; NL: narrow-lane; GPS: global positioning system (orange); Galileo: Galileo satellite navigation system (green); BDS-3: BeiDou-3 navigation satellite system (blue); LEO: low-Earth orbit satellites (purple); DOY: day of year.

Full size image

Performance analysis of multi-system tight combination PPP-AR

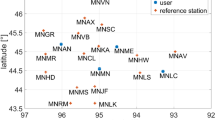
In order to better study the enhancement effect of LEO on G, E, C, we selected stations in diverse locations, including 10 stations in high latitudes (60º−90º), 10 stations in medium latitudes (30º−60º) and 10 stations in low latitudes (0º−30º), and the distribution of stations is shown in Fig. 6.

The sampling rate of the G, E, C, LEO observations are all 30 s. We performed PPP float and fix solutions from Universal Time Coordinated (UTC) 1:00 to UTC 24:00 on DOY 001 in 2022 at these stations, and in order to ensure more experiments, we initialized every 30 min. We defined the convergence time as the time taken for the positioning bias to be better than 10 cm in the east, north, up components for 35 current and subsequent epochs. We defined the time to first fix (TTFF) as the time taken to fix ambiguity successfully for 10 current and subsequent epochs. We defined the ambiguity fixing rate as the number of fix solution epochs as a percentage of the total number of epochs.

Figure 7 shows the average RMSEs of PPP fix solution of high, medium and low altitudes in the east, north and up components. It can be seen from Fig. 7 that for G, E, C systems, the positioning accuracy of the dual-system combination was better than that of the single-system in three directions, and the positioning accuracy of the three-systems was better than that of the dual-system. After adding the LEO satellite, the positioning accuracy had been greatly improved, which was around 1.5 cm in the east and north components and around 3 cm in the up component. Table 2 lists the average RMSEs of PPP float and fix solutions in the 3-dimension (3-D) direction. In high, medium and low latitudes, ambiguity resolution improved the positioning accuracy no matter single-system, dual-system or multi-system combination. The 3-D positioning accuracy was improved by 15.36%, 18.17%, 13.32% with AR in high, medium and low latitudes, respectively.

Figure 8 shows the average convergence time of PPP float and fix solutions of high, medium and low altitudes in the east, north and up components. It can be seen from Fig. 8 that for G, E, C systems, the dual-system combination positioning accelerated the convergence time compared with single-system, the three-system combination positioning accelerated the convergence time compared with dual-system. The addition of the LEO satellites accelerated the convergence time considerably, the convergence time was within 2 min in the east and north components and within 2.5 min in the up component. Table 3 lists the average convergence time of PPP float and fix solutions in the 3-D direction. In high, medium and low latitudes, ambiguity resolution accelerated the convergence time no matter single-system, dual-system or multi-system combination. The 3-D convergence time was improved by 12.95%, 10.19%, 7.25% with AR in high, medium and low latitudes, respectively. Table 4 shows the average TTFF and success fix rate of PPP fix solutions. It can be seen from Table 4, the multi-system combination also shorten the TTFF and increased the success fix rate of AR.

Fig. 6
figure 6

The distribution of 10 stations in high latitudes, 10 stations in medium altitudes and 10 stations in low latitudes. .

Full size image
Fig. 7
figure 7

The average RMSEs of PPP fix solution of high, medium and low altitudes in the east, north and up components. G: global positioning system (GPS); E: Galileo satellite navigation system (Galileo); C: BeiDou-3 navigation satellite system (BDS-3); L: low-Earth orbit satellites (LEO); RMSE: root mean square errors.

Full size image

Table 5 shows the positioning performance of float and fix solutions and the AR performance for all stations. Compared with float solutions, the 3-D positioning accuracy and convergence time was improved by 15.69% and 9.73%, respectively. Whether single system or multi-system GNSS tight combination positioning, whether float solution or fix solution, after adding LEO satellites, the positioning performance and AR performance were improved to a large extent. The positioning accuracy and convergence time was improved by 49.17% and 77.87%, respectively. For the AR performance, the TTFF and success fix rate was improved by 24.15% and 53.83%, respectively.

Table 2 The average RMSEs of PPP float and fix solutions in the 3-D direction.
Full size table
Fig. 8
figure 8

The average convergence time of PPP fix solution of high, medium and low altitudes in the east, north and up components. G: global positioning system (GPS); E: Galileo satellite navigation system (Galileo); C: BeiDou-3 navigation satellite system (BDS-3); L: low-Earth orbit satellites (LEO).

Full size image
Table 3 The average convergence time of PPP float and fix solutions in the 3-D direction.
Full size table
Table 4 The average TTFF and success fix rate of PPP fix solution.
Full size table
Table 5 The positioning performance of float and fix solutions and the AR performance.
Full size table

Conclusion

In this study, we simulated LEO observations, estimated the WL and NL UPDs of G, E, C, LEO, and performed multi-system tight combination PPP float and fix solutions based on G, E, C, LEO. The WL UPDs we calculated have good stability within 10 days and the NL UPDs have good stability within one day. For WL UPDs, more than 97% of the posterior residuals of each system are less than 0.25 cycles. For NL UPDs, more than 95% of the posterior residuals of G, E, LEO are less than 0.25 cycles, and 86% of the posterior residuals of BDS-3 system are less than 0.25 cycles. Both WL UPDs and NL UPDs have good quality.

We selected 10 stations in high, medium and low latitudes to study the improvement of positioning performance by multi-system tight combination and ambiguity resolution on a global scale. Compared with float solutions, the 3-dimension positioning accuracy and convergence time of fix solutions were improved by (15%, 18%, 13%), (13%, 10%, 7%) in the high, medium and low latitudes, respectively. For all stations, the positioning accuracy and convergence time was improved by 15.69% and 9.73%, respectively. AR improved positioning accuracy and accelerated convergence time. Multi-system tight combination increased the number of observable satellites and optimized the spatial geometry configuration between stations and satellites. In particular, the number of LEO satellites is large, the operation speed is fast, and the orbital altitude is low, which obviously accelerated the convergence time and improved the positioning accuracy and the success fix rate of ambiguity resolution to a large extent.

In this study, we used the estimated UPD products to realize multi-system tight combination PPP-AR, which accelerated the convergence time and improved the positioning accuracy. The addition of LEO satellites provided technical support for fast real-time precise positioning. Multi-system tight combination positioning increased the number of observable satellites, however, it also increased alternative values of ambiguities and the difficulty of AR. Therefore, we will focus on achieving a better AR strategy in future study. In this study, the LEO observations we used were simulated, so the results were more satisfactory, however, when using LEO observations in the future, we also need to pay attention to the accuracy of the clock error and orbit. Therefore, the G, E, C, and LEO multi-system tight combination PPP still faces challenges.