Introduction

Direct Instantaneous Torque Control (DITC)1,2,3,4 as a new type of control strategy for Switched Reluctance Motors (SRM), targets the instantaneous torque at any given moment. As a new type of electric motor with tremendous development prospects, the SRM system boasts high efficiency and excellent starting and braking performance, making it one of the most ideal power sources for various electric vehicles5. Due to its stable control performance, simplicity, and excellent suppression of torque ripple, it is very suitable for application in vehicle SRM drive systems. However, DITC still has the drawbacks of slow system response and poor dynamic performance6. To address this issue, researchers have applied sliding mode control strategies to the speed outer loop of DITC. Sliding mode control systems are simple in structure, superior in performance, and strong in robustness7,8 and they have excellent control effects in DITC systems. However, with the development of the industry, the SRM system has put forward higher requirements for the response speed, dynamic performance, robustness, and other key performance indicators of the control strategy. The improvement of the sliding mode control strategy has become a hot topic in today’s research. Although sliding mode speed control strategies have excellent control effects, they suffer from system chattering and long response times9,10. The chattering in speed control can further cause significant torque ripple in the DITC torque loop. To address these issues, this paper proposes a DITC strategy for vehicle SRM based on an improved convergence rate sliding mode control. First, an improved sliding mode convergence rate is introduced, which incorporates system state variables into the traditional exponential convergence rate of the sliding mode control strategy. This allows the convergence speed to be dynamically adjusted according to the system state, accelerating the rate at which the system approaches the sliding surface when it is far away and enhancing the system’s response speed in the face of sudden parameter changes. Then, a continuous piecewise switching function is introduced to replace the sign function, suppressing the chattering phenomenon caused by the discontinuous switching of the sign function when the state variables cross the sliding surface. Finally, the effectiveness of the proposed control strategy is verified through the establishment of an 8/6-pole SRM simulation model.

SRM control strategy based on traditional sliding mode control

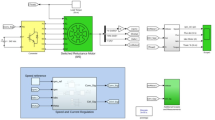
The switched reluctance motor (SRM) system mainly consists of the SRM itself, a power converter, a torque estimation module, a torque hysteresis controller, and so on. The operation of the SRM follows the “principle of minimum reluctance“11 where the phase windings are excited in a reasonable sequence to generate electromagnetic torque. The excitation of the windings can be achieved by controlling the state of the power converter. Figure 1 illustrates the direct instantaneous torque control strategy for SRM based on sliding mode control. The system consists of a speed outer loop and a torque inner loop. The speed outer loop can obtain the reference torque through a sliding mode controller by calculating the difference between the actual speed and the reference speed. The torque inner loop distributes the total reference torque to each phase using a torque allocation function, calculating the difference between the single-phase reference torque and the actual torque. The torque hysteresis controller generates control signals based on the torque difference information to control the commutation of the power converter, thereby adjusting the motor torque.

Fig. 1
figure 1

Sliding mode control-based ditc strategy.

Full size image

As shown in Fig. 2, for each phase winding of the motor, the corresponding power converter has three operational states, specifically: when both the upper and lower arm power switches of the phase winding are conductive, the phase current rises rapidly under the influence of a positive voltage, and the operational state of the phase winding is “S = 1”; when the upper and lower arm power switches of the phase winding are in a conductive and non-conductive state, respectively, the phase current slowly decreases under the influence of zero voltage, and the operational state of the phase winding is “S = 0”; and when both the upper and lower arm power switches of the phase winding are non-conductive, the phase current quickly decreases under the influence of a reverse voltage, and the operational state of the phase winding is “S=−1"12.

Fig. 2
figure 2

Illustration of the three operating states of the power converter.

Full size image

The voltage balance equation for the k-th phase of the motor can be expressed as follows:

$${U_k}={R_k}{i_k}+\frac{{d{\psi _k}}}{{dt}}$$
(1)

Where the flux linkage \({\psi _k}\) of the phase winding is a function of the winding current \({i_k}\) and the rotor position angle \(\theta\), which can be expressed as follows:

$${\psi _k}\left( {\theta ,{i_k}} \right)={L_k}\left( {\theta ,{i_k}} \right){i_k}$$
(2)

Neglecting the effect of mutual inductance between phases, the voltage balance equation for SRM can be determined as follows:

$${U_k}=R{i_k}+\frac{{d{\psi _k}}}{{dt}}=R{i_k}+\frac{{\partial \psi \left( {{i_k},\theta } \right)}}{{\partial {i_k}}}\frac{{d{i_k}}}{{dt}}+\frac{{\partial \psi \left( {{i_k},\theta } \right)}}{{\partial \theta }}\frac{{d{i_k}}}{{dt}}$$
(3)

The mechanical balance equation for the motor can be expressed as follows:

$${T_k}=J\frac{{d\omega }}{{dt}}+{T_L}+F\omega$$
(4)

Where \({T_k}\) represents the electromagnetic torque of the k-th phase; \(\omega\) represents the rotor angular velocity;\(J\) represents the moment of inertia; \({T_L}\) represents the load torque; and \(F\) represents the damping coefficient.

Design of an improved sliding mode controller

The traditional Direct Instantaneous Torque Control (DITC) strategy employs a Proportional-Integral (PI) speed control, which finds it challenging to meet the control requirements of automotive motors. Sliding mode control systems are simple in structure, offer superior performance, and possess strong robustness, making them suitable for the frequent starting, stopping, and speed variation conditions of new energy vehicles. Improving the sliding mode control strategy can enhance the performance of automotive Switched Reluctance Motors (SRM), thereby improving the performance of new energy vehicles as well.

Principle and drawbacks of traditional sliding mode controllers

Take the system state variables of the SRM (Switched Reluctance Motor) to be

$$\left\{ \begin{gathered} {x_1}={\omega _{ref}} - \omega \hfill \\ {x_2}=\int {\left( {{\omega _{ref}} - \omega } \right)dt} \hfill \\ \end{gathered} \right.$$
(5)

In the given expression, \({x_1}\)​ and \({x_2}\)​ represent the system state variables, \({\omega _{ref}}\) denotes the reference rotational speed, and \(\omega\) signifies the actual rotational speed.

From Eq. (5), it follows that:

$${x_1}={\dot {x}_2}$$
(6)

The traditional sliding mode control strategy has a sliding surface given by:

$${\text{s}}={x_1}+c{x_2}$$
(7)

Where c is a coefficient. Setting s = 0 in the above equation and differentiating, we get:

$${\dot {x}_1}+c{x_1}=0$$
(8)

In the given expression, \({x_1}\)​ and \({x_2}\)​ represent the system state variables, \({\omega _{ref}}\) denotes the reference rotational speed, and \(\omega\) signifies the actual rotational speed.

Solving the differential equation yields:

$${x_1}={e^{ - ct}}$$
(9)

Once the system reaches the sliding surface, the tracking error of the motor will gradually decrease to 0 in an exponential manner with a coefficient of c, a process that is not affected by internal or external disturbances. If the coefficient c is set too small, the tracking response of the motor on the sliding surface will become sluggish; whereas if c is set too large, it may jeopardize the stability of the system. Therefore, to maintain good dynamic characteristics of the system while sliding on the sliding surface, it is crucial to precisely select the coefficient c.

Differentiating the sliding surface function yields:

$$\dot {s}={\dot {x}_1}+c{\dot {x}_2}$$
(10)

.

Substituting into the mechanical motion equation, we obtain:

$$\dot {s}=\left( {{{\dot {\omega }}_{ref}} - \frac{{{T_e} - {T_L} - F\omega }}{J}} \right)+{\text{c}}\left( {{\omega _{ref}} - \omega } \right)$$
(11)

The exponential convergence rate of the traditional sliding mode control is given by:

$$\dot {s}= - \varepsilon \operatorname{sgn} \left( s \right) - ks$$
(12)

Where \(\varepsilon\) and \(k\) are the convergence rate coefficients; \(\operatorname{sgn} \left( s \right)\) is the sign function, expressed as:

$$\operatorname{sgn} \left( s \right)=\left\{ {\begin{array}{*{20}{c}} {1,}&{{\text{s}}>0} \\ {0,}&{s=0} \\ { - 1,}&{s<0} \end{array}} \right.$$
(13)

Figure 3 illustrates the sliding mode convergence trajectory. The traditional sliding mode process is divided into two stages13 and the traditional exponential convergence law is composed of \(- ks\) and \(- \varepsilon \operatorname{sgn} \left( s \right)\). Pure exponential convergence means that the motion point approaches the sliding surface asymptotically, with the convergence rate gradually decreasing from a larger value to zero. By adding a constant velocity convergence term on the basis of the exponential convergence term, the convergence rate does not become zero when approaching zero.

Fig. 3
figure 3

Schematic diagram of the sliding mode trajectory.

Full size image

By combining Eqs. (4), (5), and (12), we obtain:

$$\begin{gathered} \dot {s}=\left( {{{\dot {\omega }}_{ref}} - \frac{{{T_e} - {T_L} - F\omega }}{J}} \right)+c\left( {{\omega _{ref}} - \omega } \right) \hfill \\ = - \varepsilon \operatorname{sgn} \left( s \right) - ks \hfill \\ \end{gathered}$$
(14)

Then, the reference torque is:

$$\begin{gathered} {T_e}=J\left[ {{{\dot {\omega }}_{ref}}+c\left( {{\omega _{ref}} - \omega } \right)+\varepsilon \operatorname{sgn} \left( s \right)+ks} \right] \hfill \\ +{T_L}+F\omega \hfill \\ \end{gathered}$$
(15)

In traditional sliding mode control, the sliding rate of the system state variables is significantly influenced by the approach law parameters in the traditional sliding mode controller. However, this key parameter lacks the ability to adaptively adjust according to changes in operating conditions or different stages of approach. The coefficients of the approach law often start from a larger initial value and gradually decrease, a strategy that may lead to non-ideal convergence rates under different operating conditions. Furthermore, the discontinuity of the sign function can cause sudden changes in control parameters, resulting in chattering phenomena, which in turn can lead to significant speed errors and adversely affect the suppression of torque pulsations.

In practical application environments, vehicles need to operate under conditions of frequent starts and stops as well as speed variations. The slow convergence speed of traditional sliding mode control strategies is detrimental to the normal operation of vehicles. Another challenge for the application of SRM (Switched Reluctance Motor) in vehicles is the suppression of torque ripple. The magnitude of torque ripple directly affects the comfort and operational stability of the vehicle. Therefore, improving the sliding mode approach law to increase the system’s convergence rate and suppressing the chattering phenomenon in the sliding mode system are beneficial for enhancing the critical performance of vehicles.

Improved sliding mode control strategy

To enhance the anti-interference capability of SRM (Switched Reluctance Motor) in the face of system parameter variations and to improve system stability, this paper introduces a new approach law:

$$\dot {s}= - \varepsilon \left| {{x_1}} \right|sat\left( {s/a} \right) - ks$$
(16)

In the system design, the dynamic adjustment of the approach velocity is achieved by introducing system state variables, a process that closely depends on the real-time changes of these state variables. To further enhance system performance, this paper integrates the absolute value of the speed error, denoted as \(\left| {{x_1}} \right|\), into the constant velocity approach term and establishes a direct relationship between it and the approach velocity \(\varepsilon\), ensuring that the approach velocity accurately reflects the current state of the system. The specific method is as follows:

  • When the system state is far from the sliding surface, \(\left| {{x_1}} \right|\)exhibits a large value. In this scenario, the approach velocity is jointly dominated by parameters \(- \varepsilon \left| {{x_1}} \right|\operatorname{sgn} \left( s \right)\) and \(- ks\), effectively accelerating the system’s convergence towards the sliding surface.

  • As the system state gradually approaches the sliding surface, both \(\left| {{x_1}} \right|\) and \(- ks\) tend towards zero. At this point, the approach velocity is primarily controlled by the parameter \(- \varepsilon \left| {{x_1}} \right|\operatorname{sgn} \left( s \right)\), leading to a deceleration in the speed.

This method successfully implements an adaptive adjustment mechanism for the approach velocity. Compared to the traditional exponential approach law, it significantly mitigates the performance degradation caused by chattering and effectively enhances the approach velocity, providing strong support for the stable operation and performance optimization of the system.

When the state variables cross the sliding surface, the discontinuity of the sign function may cause sudden changes in control inputs and chattering [13]. To reduce chattering, an effective strategy is to set up a boundary layer near the sliding surface, converting the discontinuous switching control into a piecewise switching function, combined with linear feedback control, so that the control function mainly varies within the boundary layer, effectively suppressing chattering. Therefore, this paper proposes a continuous piecewise switching function to replace the sign function, as expressed in Eq. (17). The function diagram is shown in Fig. 4.

$$sat\left( {{s \mathord{\left/ {\vphantom {s a}} \right. \kern-\nulldelimiterspace} a}} \right) = \left\{ {\begin{array}{*{20}c} {\text{sgn} \left( {{s \mathord{\left/ {\vphantom {s a}} \right. \kern-\nulldelimiterspace} a}} \right),} & {\left| {{s \mathord{\left/ {\vphantom {s a}} \right. \kern-\nulldelimiterspace} a}} \right|> 1} \\ {{s \mathord{\left/ {\vphantom {s a}} \right. \kern-\nulldelimiterspace} a},} & {\left| {{s \mathord{\left/ {\vphantom {s a}} \right. \kern-\nulldelimiterspace} a}} \right| \le 1} \\ \end{array} } \right.$$
(17)
Fig. 4
figure 4

Illustration of a continuous piecewise function.

Full size image

In the equation, a > 0 represents the thickness of the boundary layer, a fixed positive value. An excessively thick boundary layer can lead to an increase in the system’s steady-state error, and a fixed thickness is not adaptive to changes in the system state, affecting stability. This limits the fluctuation range of the output variables, and even under maximum approach conditions, it is impossible to reach the ideal switching plane where s = 0, reducing the system’s robustness.

To address the aforementioned issues, this paper proposes a sliding mode control strategy that dynamically adjusts the thickness of the boundary layer to adapt to changes in system states, achieving precise and efficient control. The strategy initially sets a wider range for the boundary layer thickness and then, through piecewise processing of the system states, gradually reduces the boundary layer thickness until it converges to an optimized value a∗. This strategy, by adjusting the boundary layer thickness in real-time to accommodate the continuous changes in system states, can effectively guide the system to the predetermined sliding surface and equilibrium point regardless of the initial state, achieving more precise and efficient control of the system.

$$a^{ * } = \left\{ {\begin{array}{*{20}c} {a,} & {\left| s \right|> a_{1} ,} \\ {\frac{1}{2}e^{{k\left( {s - a_{1} } \right)}} ,} & {0 \le s < a_{1} ,} \\ {\frac{1}{2}e^{{ - k\left( {s - a_{1} } \right)}} ,} & { - a_{1} \le s < 0,} \\ \end{array} } \right.$$
(18)

By appropriately selecting the threshold values, the smooth transition and continuity of system states can be ensured, effectively avoiding severe fluctuations. This paper sets the boundary layer thickness a to 0.05 and the threshold value a1 to 0.01. By improving the switching function and controlling the boundary layer thickness, the system chattering is confined to a smaller range as the boundary layer gradually narrows. Compared with fixed boundary layer control, this approach mitigates the chattering of output variables, enhances the accuracy of system control, and ensures stable system operation.

By combining Eqs. (4), (5), and (16), the reference torque under the sliding mode control strategy proposed in this paper is obtained as:

$$\begin{gathered} {T_e}=J\left[ {{{\dot {\omega }}_{ref}}+c\left( {{\omega _{ref}} - \omega } \right)+\varepsilon \left| {{x_1}} \right|sat(s/a)+ks} \right] \hfill \\ +{T_L}+F\omega \hfill \\ \end{gathered}$$
(19)

The control principle diagram is shown in Fig. 5:

Fig. 5
figure 5

Schematic diagram of sliding mode control strategy.

Full size image

System stability analysis

A Lyapunov function is selected to verify the system stability. The Lyapunov function is given by:

$$V=\frac{1}{2}{s^2}$$
(20)

Differentiating Eq. (20) yields:

$$\dot {V}=s \cdot \dot {s}$$
(21)

By combining Eqs. (16) and (21), we obtain:

$$\begin{gathered} \dot {V}=s\dot {s} \hfill \\ {\text{ }}= - s\varepsilon \left| {{x_1}} \right|sat(s/a) - k{s^2} \hfill \\ \end{gathered}$$
(22)

To determine the signs of the coefficients in Eq. (22), the equation can be equivalently expressed as Eq. (23).

$$\dot {V}= - s\left( {Asat(s/a)+Bs} \right)$$
(23)

In the formula, A and B are two coefficients, which can be expressed as:

$$\left\{ {\begin{array}{*{20}{c}} {A{\text{=}}\varepsilon \left| {{x_1}} \right|} \\ {B=k} \end{array}} \right.$$
(24)

From Eq. (24), it can be seen that coefficients A and B are positive. From Eq. (20), \(sat(s/a)\) has the same sign as s. Thus, s and \(\left( {Asat(s/a)+Bs} \right)\) have the same sign, making\(- s\left( {Asat(s/a) + Bs} \right)<0\)

Results

To validate the effectiveness of the control strategy proposed in this paper, a SRM-DITC (Switched Reluctance Motor-Direct Torque Control) control system simulation model is established based on Fig. 1. To detect the torque parameters of the SRM in real-time and with precision, this paper employs finite element analysis to obtain the motor torque characteristics. The SRM model is constructed based on these torque characteristics. Figure 6 shows the motor torque characteristic diagram, and the structural parameters of the SRM are presented in Table 1.

Table 1 SRM structural parameters.
Full size table
Fig. 6
figure 6

SRM torque characteristic diagram.

Full size image

To validate the performance of the improved sliding mode control strategy, this paper selects a traditional sliding mode control system as a comparative object for simulation. The following two sets of simulation experiments were designed to verify the performance of the improved sliding mode control strategy under constant and variable operating conditions. Parameters of the sliding mode controller: \(\varepsilon {\text{ = }}0.1\), \(c{\text{=}}10\), \(k{\text{=}}8\)。 Table 2 provides the simulation parameters.

Table 2 Simulation parameters Table.
Full size table

In this paper, the torque ripple ratio is used to describe the torque ripple of the SRM, which is expressed as:

$${T_{ripple}}=\frac{{{T_{\hbox{max} }} - {T_{\hbox{min} }}}}{{{T_{av}}}}$$
(23)

.

In the formula, \({T_{\hbox{max} }}\) represents the maximum torque value, \({T_{\hbox{min} }}\) represents the minimum torque value, and \({T_{av}}\) represents the average torque value.

Constant condition simulation

Low-speed simulation experiment: The motor load torque is set to 5 Nm, and both control strategies are applied at a speed of 500 rpm. The simulation results when the motor is operating stably are shown in Figs. 7 and 8.

The simulation results indicate that when the load torque is 5 Nm and the speed is 500 rpm, the SRM system using the traditional sliding mode control strategy takes 0.25 s to stabilize at 500 rpm after startup, while the SRM system using the sliding mode control strategy proposed in this paper takes 0.17 s to stabilize at 500 rpm after startup, which is a 32% reduction in time from startup to stabilization compared to the traditional sliding mode control strategy. The total torque ripple ratio during stable operation for the sliding mode control strategy proposed in this paper is 9.08%, while for the traditional sliding mode control strategy, it is 12.84%. The torque ripple ratio of the control strategy proposed in this paper is 29.28% lower than that of the traditional sliding mode control strategy.

Fig. 7
figure 7

Simulation diagram of traditional sliding mode control strategy at 500 rpm and 5 nm.

Full size image
Fig. 8
figure 8

Simulation diagram of improved sliding mode control strategy at 500 rpm and 5 nm.

Full size image

High-speed simulation experiment: The motor load torque is set to 5 Nm, and both control strategies are applied at a speed of 1000 rpm. The simulation results when the motor is operating stably are shown in Figs. 9 and 10.

From the simulation results, it can be seen that when the load torque is 5 Nm and the speed is 1000 rpm, the SRM system using the traditional sliding mode control strategy takes 0.31 s to stabilize at 1000 rpm after startup, while the SRM system using the sliding mode control strategy proposed in this paper takes 0.22 s to stabilize at 1000 rpm after startup, which is a 29.03% reduction in time from startup to stabilization compared to the traditional sliding mode control strategy. The total torque ripple ratio during stable operation for the sliding mode control strategy proposed in this paper is 9.08%, while for the traditional sliding mode control strategy, it is 12.84%. The torque ripple ratio of the control strategy proposed in this paper is 22.99% lower than that of the traditional sliding mode control strategy.

Fig. 9
figure 9

Simulation diagram of traditional sliding mode control strategy at 1000 rpm and 5 nm.

Full size image
Fig. 10
figure 10

Simulation diagram of improved sliding mode control strategy at 1000 rpm and 5 nm.

Full size image

According to the simulation results, the improved sliding mode control strategy has a shorter startup time and more stable system operation with less torque ripple during both low-speed and high-speed running compared to the traditional sliding mode controller.

Variable condition simulation

Acceleration simulation experiment: The motor load torque is set to 5 Nm, with an initial speed of 500 rpm. At time t = 1 s, the speed suddenly changes to 1000 rpm. Both control strategies are applied, and the motor speed and torque simulation diagrams are shown in Figs. 11 and 12.

The simulation results indicate that when the given speed changes from 500 to 1000 rpm at t = 1 s with a load torque of 5 Nm, the acceleration time for the motor using the traditional sliding mode control strategy is 0.18 s, whereas with the sliding mode control strategy proposed in this paper, the acceleration time is 0.13 s. The sliding mode control strategy proposed in this paper reduces the time from speed mutation to stabilization by 27.78% compared to the traditional sliding mode control strategy. Additionally, the torque ripple of the motor is reduced with the improved sliding mode control strategy. After accelerating to 1000 rpm and stabilizing again, the total torque ripple ratio during stable operation for the sliding mode control strategy proposed in this paper is 8.45%, while for the traditional sliding mode control strategy, it is 10.88%. The torque ripple ratio of the control strategy proposed in this paper is 22.33% lower than that of the traditional sliding mode control strategy.

Fig. 11
figure 11

Traditional sliding mode control strategy acceleration simulation diagram.

Full size image
Fig. 12
figure 12

Improved sliding mode control strategy acceleration simulation diagram.

Full size image

Deceleration simulation experiment: The motor load torque is set to 5 Nm, with an initial speed of 500 rpm. At time t = 1 s, the speed suddenly changes to 1000 rpm. Both control strategies are applied, and the motor speed and torque simulation diagrams are shown in Figs. 13 and 14.

The simulation results indicate that when the given speed changes from 1000 to 500 rpm at t = 1 s with a load torque of 5 Nm, the deceleration time for the motor using the traditional sliding mode control strategy is 0.17 s, whereas with the sliding mode control strategy proposed in this paper, the deceleration time is 0.13 s. The sliding mode control strategy proposed in this paper reduces the time from speed mutation to stabilization by 23.53% compared to the traditional sliding mode control strategy. Additionally, the torque ripple of the motor is reduced with the improved sliding mode control strategy. After decelerating from 1000 rpm and stabilizing again, the total torque ripple ratio during stable operation for the sliding mode control strategy proposed in this paper is 8.98%, while for the traditional sliding mode control strategy, it is 11.28%. The torque ripple ratio of the control strategy proposed in this paper is 20.39% lower than that of the traditional sliding mode control strategy. This further validates that the proposed improved strategy has better dynamic performance.

Fig. 13
figure 13

Traditional sliding mode control strategy deceleration simulation diagram.

Full size image
Fig. 14
figure 14

Improved sliding mode control strategy deceleration simulation diagram.

Full size image

Variable Loading Simulation Experiment: Another typical operating condition for electric vehicles is hill climbing and other complex conditions. To verify the advantages of the control strategy proposed in this paper, it is compared with the traditional sliding mode control strategy. The system performance of the proposed strategy under sudden load variation conditions is analyzed. The motor speed is set at 1,500 r/min with an initial torque of 10 Nm. At t = 1.5 s, the torque suddenly increases to 30 Nm under stable - state conditions. The two control strategies are used to analyze torque and speed responses under load mutations. Motor simulation diagrams are shown in Figs. 15 and 16.

From Figs. 15 and 16, for the traditional SRM sliding - mode speed control strategy, set the reference speed at 1500r/min. When the SRM operates stably and the load torque suddenly rises from 10 N·m to 30 N·m, speed drops slightly but recovers to stability after 0.06s. For the improved strategy under the same conditions, speed recovery takes just 0.03s. The improved sliding - mode speed control strategy shows faster response, with rapid current waveform response and significantly reduced torque ripple compared with the traditional one.

Fig. 15
figure 15

Simulation diagram of improved sliding mode control strategy under variable load.

Full size image
Fig. 16
figure 16

Simulation diagram of traditional sliding mode control strategy under variable load.

Full size image

From the two sets of simulation experiments, it can be observed that the control strategy proposed in this paper exhibits better torque ripple suppression effects and shorter startup times compared to the traditional sliding mode control strategy under constant operating conditions. When dealing with sudden changes in operating conditions, the sliding mode control strategy proposed in this paper can respond quickly and exhibit ideal waveforms, demonstrating superior dynamic performance compared to the traditional sliding mode control strategy.

Conclusion

This paper addresses the issues of large chattering and long response times associated with traditional sliding mode control strategies by proposing an improved sliding mode control strategy based on an improved approach rate for direct instantaneous torque control of vehicle SRM (Switched Reluctance Motor). Through simulation comparisons with traditional sliding mode control strategies, the following conclusions were drawn:

  • The improved sliding mode control strategy, by incorporating system state variables into the conventional exponential reaching law, significantly reduces system response time, cutting motor startup time in low - and high - speed conditions by 32% and 29.03% respectively; it also strengthens the system’s anti - disturbance capability, lowering system response time during acceleration and deceleration by 27.78% and 23.53%, thus enhancing system dynamic performance.

  • The improved sliding mode control strategy, by introducing a continuous piecewise switching function, effectively suppresses system chattering. The system’s torque ripple is significantly reduced: during low - and high - speed operation, the torque ripple ratio in stable system operation drops by 29.28% and 22.99%, and during acceleration and deceleration, when the system restabilizes, the torque ripple ratio decreases by 22.33% and 20.39%.