Enhanced intrusion detection in cybersecurity through dimensionality reduction and explainable artificial intelligence

Abstract

Cybersecurity is one of the applications of controls, procedures, and technologies for protecting data, networks, programs, and systems from potential cyber threats. Malicious threats have become complex, and the leading task is to recognize obfuscated and mysterious malware, as the malware inventors utilize dissimilar evasion models for data covering to avert recognition by intrusion detection systems (IDSs). Artificial intelligence (AI) usage in cybersecurity is gradually becoming familiar, but the main task is the absence of interpretability and transparency of AI methods. Explainable AI (XAI) can tackle this problem by improving the understandability of AI techniques, permitting cyber-security experts to comprehend the decisions created by these methods and to recognize biases or errors. Recently, Machine learning (ML) and deep learning (DL) models have delivered automatic analytical intrusion detection procedures, providing numerous advantages. This study proposes an Enhanced Intrusion Detection in Cybersecurity through Dimensionality Reduction and Explainable Artificial Intelligence with Attention Mechanism in Deep Learning (EIDCDR-XAIADL) model. The main intention of the proposed EIDCDR-XAIADL model is to deliver a robust cybersecurity system that combines XAI to address the attacks. Initially, the proposed EIDCDR-XAIADL technique performs data normalization by using mean normalization to ensure uniform scaling of network traffic data. The multiverse optimization (MVO) technique selects the most appropriate and discriminative features. For the cybersecurity attack classification process, the hybrid of convolutional neural network (CNN), bi-directional gated recurrent unit (BiGRU), and attention mechanism (CNN-BiGRU-AM) technique is implemented. Moreover, the antlion optimization (ALO) technique adjusts the hyperparameter values of the CNN-BiGRU-AM method optimally and results in more excellent classification performance. Finally, Shapley Additive Explanations (SHAP) is utilized as an XAI technique to enhance threat detection and decision-making by providing trustworthy insights into AI-driven security systems. The experimental evaluation of the EIDCDR-XAIADL approach is examined under dual datasets. The experimental validation of the EIDCDR-XAIADL approach demonstrated a superior accuracy value of 99.19% and 99.12% under NSLKDD and CICIDS 2017 datasets.

Introduction

Cyber Security is an attempt to secure devices, data, and networks besides illegal usage or unauthorized access, along with keeping data integrity, availability, and confidentiality, while cyber defensive devices develop the network, application, and host data levels¹. As the Internet became a vital tool in people’s everyday existence, many systems related to the Internet al.so developed². Nevertheless, extensive Internet usage also induces cyber attackers to improve more effective and advanced cyberattack models for their profit. Consequently, a secure and stable cybersecurity computer system should be determined to guarantee data integrity, privacy, and availability on the Internet³. However, traditional rule-based and signature-based cyber defensive mechanisms face problems expanding some of the data spread through the Internet⁴. Conversely, cyber hackers often struggle to maintain a single step ahead of law enforcement in producing intricate, new, and smart attacking models and applying technological progressions comprising AI to establish their adversarial behaviours more effectively and advanced. Faster development in AI models has generated substantial growth in their utilization in an expanding and different set of applications⁵.

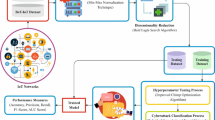
Whereas unique successes were in fields with relatively lower consequences, like movie and product suggestions, AI models are being utilized in gradually higher-consequence applications like clinical diagnoses. Extensive usage is limited, nevertheless, as there is an identification that requires understanding and belief in the decision processes of AI techniques before they are integrated and deployed into massive systems⁶. Several XAI models are developed to enhance confidence and guarantee that a method is not biased. Utilizing AI techniques in cybersecurity operations is increasing, as it promises a process to handle rising cyberattacks and traffic. Cyberattacks cause substantial loss of monetary and/or system resource accessibility⁷. AI approaches improve cyber infrastructure protection by operating at machine speeds while effectively preserving resources. AI has been extensively explored in diverse cybersecurity fields, including detecting malicious activities and malware⁸. XAI is studied systematically utilizing DL approaches in cyber defence, independent of the cybersecurity experts. Figure 1 represents the general architecture of IDS.

Fig. 1

General structure of IDS.

AI has been accepted in the present IDS to identify anomalies, classify attacks, and remove significant features⁹. DL and ML mainly developed favourable security solutions while incorporating IDS to reduce several cyber-attacks. Recently, DL-based IDS have been broadly utilized as they give higher precision and a lower false positive rate, with more excellent performance while functioning with massive amounts of data¹⁰. Nevertheless, DL-based IDS are still examined as effective devices owing to the complications in recognition techniques and the absence of explanation in the general decision-making process. XAI is a novel AI paradigm that enables models to interpret ML-based IDS, allowing such methods to elucidate the reason behind their prediction.

This study proposes an Enhanced Intrusion Detection in Cybersecurity through Dimensionality Reduction and Explainable Artificial Intelligence with Attention Mechanism in Deep Learning (EIDCDR-XAIADL) model. The main intention of the proposed EIDCDR-XAIADL model is to deliver a robust cybersecurity system that combines XAI to address the attacks. Initially, the proposed EIDCDR-XAIADL technique performs data normalization by using mean normalization to ensure uniform scaling of network traffic data. The multiverse optimization (MVO) technique selects the most appropriate and discriminative features. For the cybersecurity attack classification process, the hybrid of convolutional neural network (CNN), bi-directional gated recurrent unit (BiGRU), and attention mechanism (CNN-BiGRU-AM) technique is implemented. Moreover, the antlion optimization (ALO) technique adjusts the hyperparameter values of the CNN-BiGRU-AM method optimally and results in more excellent classification performance. Finally, Shapley Additive Explanations (SHAP) is utilized as an XAI technique to enhance threat detection and decision-making by providing trustworthy insights into AI-driven security systems. The experimental evaluation of the EIDCDR-XAIADL approach is examined under dual datasets. The key contribution of the EIDCDR-XAIADL approach is listed below.

• The EIDCDR-XAIADL model utilizes mean normalization to pre-process the data, enhancing the quality and consistency of input features. This step ensures that all features are scaled to a similar range, mitigating biases in model training. The model attains more accurate and reliable results in cybersecurity attack classification by improving feature representation.

• The EIDCDR-XAIADL technique employs the MVO method for feature selection, effectually detecting the most relevant features for the model. This process improves the accuracy by mitigating dimensionality and removing irrelevant data. As a result, the model becomes more efficient, with enhanced classification performance in detecting cybersecurity threats.

• The EIDCDR-XAIADL approach integrates CNN, BiGRU, and CNN-BiGRU-AM models to improve the classification of cybersecurity attacks. This hybrid approach effectively captures spatial and temporal patterns in the data. The model prioritizes crucial features by incorporating AM, improving detection accuracy and robustness.

• The EIDCDR-XAIADL methodology implements the ALO technique for hyperparameter tuning and refining model parameters to attain optimal performance. This method improves the technique’s accuracy and efficiency by exploring and selecting the most appropriate parameter values. As a result, the model’s overall performance in detecting cybersecurity threats is significantly improved.

• The EIDCDR-XAIADL method utilizes SHAP as an XAI technique to offer transparent and interpretable insights into the model’s decision-making. This approach assists in clarifying how features influence predictions, increasing trust in the model’s outputs. By improving transparency, SHAP supports more effective and reliable cybersecurity threat detection.

• The novelty of the EIDCDR-XAIADL model is due to its hybrid approach, which integrates CNN, BiGRU, and CNN-BiGRU-AM methods and AM for advanced cybersecurity attack classification. It also integrates MVO for feature selection and ALO for hyperparameter tuning to optimize performance. The inclusion of SHAP for explainable AI additionally improves and enhances the transparency of the model, giving interpretable insights into the decision-making process. This unique integration improves both detection accuracy and model interpretability.

Literature survey

Alotaibi et al.¹¹ introduced an XAI with an Aquila optimizer algorithm in the web phishing classification (XAIAOA-WPC) method. Initially, pre-processing is implemented on three levels: text pre-processing, standardization, and data cleaning. The Harris Hawks Optimizer-based feature selection (HHO-FS) approach was also utilized to originate feature sub-sets. The multi-head attention-based LSTM (MHA-LSTM) method is applied for web phishing detection. Moreover, the recognition results are improved by using the AOA technique. Kumar et al.¹² incorporate smart contracts with XAI to intend a strong cybersecurity structure for ZTN. The digital twin (DT) is intended to simulate attack recognition with the gathered data. A Self-attention-based LSTM (SALSTM) technique calculates the attack recognition capable of projected structure. In addition, the interpretability of the presented AI-based IDS is attained by utilizing the SHAP device. Trivedi et al.¹³ developed an approach for pre-processed data and understanding the implementation of progressive ML techniques. This structure employs SHAP for XAI to explain the ML learning process. Formerly, a CIGRE lower voltage microgrid system was experimented with for data collection through cyberattacks, which was succeeded by data pre-processing. Moreover, data augmentation is achieved utilizing ENN and SMOTE, and feature extraction is implemented to employ the Boruta Python package. Eventually, hyper-parameters are tuned by applying the TPE method. Filali et al.¹⁴ examined the role of XAI in spam recognition, focusing on the interpretability of AI-driven methods over SHAP. This paper also introduces a hybrid method associating BERT with ANN and RF for spam recognition and utilizes SHAP values to explain the decision-making process. Shoukat et al.¹⁵ developed and designed an XAI-incorporated DL-based threat detection system (XDLTDS). An LSTM-AutoEncoder (LSTM-AE) technique is primarily applied to encode IIoT data and reduce inference threats. Formerly, an attention-based GRU (AGRU) with softmax is developed for multi-class threat classification in IIoT systems. The method also projects an SDN-based employment framework for the XDLTDS structure. Sharma et al.¹⁶ propose a DL model for intrusion detection, utilizing feature selection and two models, namely deep neural network (DNN) and CNN, to classify attacks while integrating XAI techniques such as Local Interpretable Model-agnostic Explanations (LIME) and SHAP to enhance model interpretability.

Naif Alatawi¹⁷ develops a novel IDS framework that integrates ensemble learning, transfer learning (TL), and feature engineering to improve detection accuracy, adaptability, and interpretability while incorporating XAI methods like LIME and SHAP to improve model transparency. In¹⁸, a privacy-preserving, explainable IDS utilizing DL and federated learning (FL) models is projected. In particular, SHAP and ANN have been incorporated to improve interpretability. This method can effectively examine complicated system traffic designs by employing Transformers, which are known for their superior accomplishment in anomaly detection and modelling sequence. The FL-based method maintains data confidentiality by trained methods locally, whereas collaborative learning enhances method sturdiness. Muthamil Sudar and Deepalakshmi¹⁹ propose a two-level security mechanism for detecting and reducing DDoS attacks in software-defined networks (SDN). Level one utilizes entropy-based detection, while level two employs a C4.5 ML method. Et-Tolba, Hanin, and Belmekki²⁰ improve cross-site scripting (XSS) attack detection by optimizing a DNN using Genetic Algorithms (GA). The approach integrates advanced feature extraction techniques like Term Frequency-Inverse Document Frequency (TF-IDF) and N-grams to effectually detect obfuscated or encoded payloads. Sudar et al.²¹ present a TCP Flooding Attack Detection (TFAD) technique integrating proxy-based and ML mechanisms (ML-TFAD) with SYN and ACK proxies to defend against TCP SYN and ACK flood attacks. Alabbadi and Bajaber²² propose a novel IDS architecture using DL models and XAI techniques to improve network intrusion detection. Three DL models namely customized 1-D CNNs, DNNs, and pre-trained TabNet are also employed. Sudar, Rohan, and Vignesh²³ develop an advanced phishing URL detection model utilizing web-scraped features and feature selection methods. The model utilizes ensemble learning techniques like Random Forest (RF), AdaBoost, GradientBoost, and XGBoost for accurate classification. Jaganraja and Srinivasan²⁴ improve cyberattack detection in IoT networks using a privacy-preserving DL approach. The proposed deep attention network (DAN) technique employs multiple distributions and whale optimization algorithm (WOA) method for improved performance and privacy. Sarker et al.²⁵ propose an attention-based 1D-CNN-GRU methodology optimized with particle swarm optimization (PSO). Additionally, FL is used to ensure privacy and efficiency in the collaborative training process.

Lipsa, Dash, and Ivković²⁶ propose an interpretable feature selection technique for IoMT intrusion detection, utilizing a RF-based explainable AI model. Turaka and Panigrahy²⁷ develop an Ensemble Learning-based attack detection system for IoT networks. The system utilizes network logs, feature extraction with moth flame optimizer (MFO), and an ensemble of classifiers. It incorporates Q-learning and XAI with XceptionNet and TL for continuous enhancement in dynamic attack mitigation. Oyinloye, Arowolo, and Prasad²⁸ introduce an updated learning strategy for artificial neural networks (ANN). Markkandeyan et al.²⁹ proposed a hybrid detection model that incorporates Adaptive TensorFlow DNN (ATFDNN), improved PSO (IPSO), and enhanced long short-term memory (E-LSTM) to accurately identify malware and software piracy. Sumathi and Rajesh³⁰ proposed a hybrid neural network-based IDS to improve DDoS detection accuracy in cloud environments. Behera, Pradhan, and Mishra³¹ developed a hybrid CNN model integrating VGG-16 and ResNet50 techniques. Al-Hawawreh and Moustafa³² proposed an attack intelligence framework utilizing ML, DL, and XAI for cyber–physical attack detection and intelligence extraction. Garikapati et al.³³ presented an explainable hybrid ensemble model for intrusion detection with improved transparency and accuracy. Bahadoripour et al.³⁴ proposed a deep federated multi-modal model with SHAP for enhanced cyber-attack detection in industrial control systems (ICS). Ambekar et al.³⁵ proposed TabLSTMNet, an explainable Android malware classifier integrating TabNet and LSTM features. Ahmed et al.³⁶ proposed a hybrid adaptive ensemble for intrusion detection (HAEnID) using multiple ensemble techniques, including stacking ensemble method (SEM), bayesian model averaging (BMA), and conditional ensemble method (CEM), along with Shapley Additive Explanations (SHAP) and local interpretable model-agnostic explanations (LIME) for enhanced detection and interpretability. Solanki and Chaudhari³⁷ introduced an integrated forensic model combining network forensic analysis and investigation, utilizing deep Q-network (DQN), XAI, and enhanced deep CNN (EDCNN) for enhanced distributed denial-of-service (DDoS) attack detection and analysis. Nkoro et al.³⁸ proposed an explainable DNN for detecting network intrusions in Metaverse learning environments, utilizing SHAP and LIME models for improved accuracy and interpretability.

While the existing studies demonstrate promising results in IDS, various limitations still exist. Many methods depend heavily on specific feature selection techniques or require extensive data preprocessing, which can be computationally expensive and time-consuming. Some models, such as those integrating DL and XAI, face scalability issues when applied to large-scale or real-time network traffic. Moreover, diverse methods still face difficulty with handling hybrid attack scenarios and the trade-off between model complexity and interpretability. The performance of these systems can be inconsistent across several network environments, and issues related to data imbalance in training sets are often not adequately addressed. Furthermore, while privacy-preserving techniques like FL are utilized, they may still encounter threats related to model performance and data security in collaborative learning environments. A key research gap is in the absence of adaptive IDS models that can update in real-time, maintaining accuracy and efficiency. Existing studies struggle to handle the dynamic nature of cyberattacks, restricting their capability to quickly adapt to new and growing threats.

Materials and methods

In this study, the EIDCDR-XAIADL model is proposed. The main intention of the proposed EIDCDR-XAIADL model is to deliver a robust cybersecurity system that combines XAI to address the attacks. The EIDCDR-XAIADL approach has data normalization, MVO-based feature selection, hybrid classification models, ALO-based parameter selection, and XAI-based SHAP to accomplish that. Figure 2 represents the complete workflow of the EIDCDR-XAIADL approach.

Fig. 2

Overall workflow of EIDCDR-XAIADL model.

Mean normalization

At first, the proposed EIDCDR-XAIADL technique applies data normalization using mean normalization to ensure uniform scaling of network traffic data³⁹. This is chosen as it ensures that all input features are scaled to a similar range, enhancing the stability and efficiency of the model during training. Centring the data around zero mitigates the influence of outliers and makes the model less sensitive to discrepancies in feature magnitudes. Compared to other normalization techniques, such as min-max scaling, mean normalization assists in preserving the distribution of the data, which is specifically beneficial when the features have varying units or scales. Additionally, it helps speed up the convergence of optimization algorithms, improving the overall performance. This technique is specifically effective in DL models, where consistent input ranges are significant for successfully training complex architectures. Compared to standardization or other methods, mean normalization assists in attaining faster and more reliable model training with better accuracy.

Mean normalization is a pre-processing method for standardizing data by fine-tuning their distribution and scale. The formulation for mean normalization is Eq. (1).

$$\:F\left(x\right)=\frac{(x-\mu\:)}{R}$$

(1)

Whereas $\:x$ characterizes the unique data point, $\:\mu\:$ refers to the dataset mean, and $\:R$ signifies range, computed as the change amongst the minimum and maximum values within the dataset. This model is mainly beneficial in decreasing the influence of the outlier and guaranteeing that the data are centralized at about $\:zero$, which could improve the performance of ML methods by increasing convergence in training.

Dimensionality reduction process

The MVO technique is used to select the most appropriate and discriminative features. This model was chosen due to its capability to effectively select the most relevant features while mitigating the dimensionality of the dataset. By using MVO, the model explores multiple potential solutions in parallel, ensuring that it selects features with high discriminatory power. Unlike conventional methods like principal component analysis (PCA) or recursive feature elimination (RFE), MVO does not require linear assumptions and can handle complex, non-linear relationships between features. Furthermore, MVO optimizes the feature selection process by averting overfitting and enhancing model performance on unseen data. It is specifically effective in high-dimensional datasets, mitigating computation time and complexity without sacrificing accuracy. The capability of MVO to balance exploration and exploitation makes it a robust technique for dimensionality reduction, ensuring high detection accuracy and model efficiency. Figure 3 depicts the working flow of the MVO method.

Fig. 3

Working flow of the MVO methodology.

MVO is a meta-heuristic subjective by nature derived from a multiverse theory in physics⁴⁰. The optimizer includes three phases: local search, exploration, and exploitation, according to the essential concepts and computation structures of wormholes, black holes, and white holes. Similar to other meta-heuristic models, which work according to the population, the search procedure was divided into dual stages: exploitation and exploration. The principles and theories are applied to perform exploration in searching spaces. In solutions, natures are considered solutions characterized by the magnitudes of their populations. Additionally, all entities worldwide are selected as a variable inside the population’s exploration area. The optimizer uses these sets of principles over an optimizer process.

• A stronger direct relationship occurs between the white holes and the inflation level.

• A reverse relationship occurs between the black holes and the level of inflation.

• Worlds with improved inflation are vulnerable to transferring objects over white holes.

• Worlds with reduced inflation tend to adapt many objects via black holes.

• The objects in the world may follow cyclic movement towards the solution region through wormholes, irrespective of the inflation level.

During the initial stage, a roulette wheel approach has been designated to computationally imitate the black and white holes and exchange the object solutions. The solutions are successively organized based on their level of inflation at all iterations. Assume that $\:G$ characterizes the complete universe (solution), as in Eqs. (2) and (3), correspondingly.

$$\:G=\left(\begin{array}{ccc}{x}_{1}^{1}&\:\cdots\:&\:{x}_{1}^{c}\\\: \vdots &\:\ddots\:&\: \vdots \\\:{x}_{n}^{1}&\:\cdots\:&\:{x}_{n}^{c}\:\end{array}\right)$$

(2)

$$\:{x}_{i}^{i}=\left\{\begin{array}{c}{x}_{k}^{j}\:if\:{r}_{1}<NI\left({G}_{i}\right)\:\\\:{x}_{i}^{j}\:if\:{r}_{1}\ge\:NI\left({G}_{i}\right)\end{array}\right.$$

(3)

Whereas $\:c$ signifies the percentage of the variables, $\:n$ represents solution counts (world), $\:xji$ refers to the $\:jth$ variable of the $\:ith$ solution (world), $\:Gi\:$symbolizes the $\:ith$ solution (world), $\:NI$ ($\:Gi$) signifies the $\:ith$ universe’s standardized level of inflation, $\:{r}_{1}$ stands for random number distributed uniformly in the range $\:\left[\text{0,1}\right]$, and $\:xjk$ symbolizes the $\:jth$ variable of the $\:kth$ world as designated by a roulette wheel method.

During the exploitation stage, wormholes are recognized amongst a solution, and the advanced, more successful solution is used to ensure slight changes for all solutions and to improve the probability of speeding up the level of inflation over wormholes. This stage is defined in Eqs. (4)-(6).

$$\:{x}_{i}^{i}=\left\{\begin{array}{c}{x}_{j}+TDR\times\:\left(\left(g{a}_{j}-l{a}_{j}\right)\times\:{r}_{4}+l{a}_{j}\right)if\:{r}_{3}<0.5\:and\:{r}_{2}<WEP\:\\\:{x}_{j}-TDR\times\:\left(\left(g{a}_{j}-l{a}_{j}\right)\times\:{r}_{4}+l{a}_{j}\right)if\:{r}_{3}\ge\:0.5\:and\:{r}_{2}\ge\:WEP\end{array}\right.$$

(4)

Here, $\:xj$ represents the $\:jth$ variable of the best promising solution made, $\:laj$ refers to the smallest value of $\:a\:jth$ variable, $\:g{a}_{j}$ means $\:jth$ variable’s most significant value, $\:{x}_{ji}$ signifies $\:ith$ solution’s $\:jth$ variable, and $\:r2,r3,r4$ refers to numbers generated at random, which follows a rectangular distribution in the range of zero and one$\:.$ The wormhole existence probability (WEP) states the likelihood of a wormhole’s occurrence. The travelling distance rate (TDR) is a parameter that characterizes the rate at which a wormhole moves an object over the found best-fit universe.

$$\:WEP=min+l\times\:\left(\frac{max-min}{L}\right)$$

(5)

$$\:TDR=1-\frac{{l}^{1/p}}{{L}^{1/P}}$$

(6)

Now $\:min$ means lower limit, $\:max$ refers to an upper limit, $\:l$ epitomizes the present iteration, $\:L$ symbolizes the maximal iteration counts, and $\:p$ signifies the exploitation reliability during the iterations.

The fitness function (FF) reveals the classifier’s accuracy and the sum of preferred features. It exploits classification accuracy and decreases the set dimension of chosen features. Therefore, the FF mentioned below was applied to evaluate discrete solutions, as formulated in Eq. (7).

$$\:Fitness=\alpha\:\times\:\:ErrorRate+\left(1-\alpha\:\right)\times\:\frac{\#SF}{\#All\_F}$$

(7)

Here, $\:ErrorRate$ denotes the classifier rate of error. $\:ErrorRate$ is computed as the ratio of improper that is classified into the number of classifications set among 0 and 1. $\:\#SF$ and $\:\#All\_F$ refer to a quantity of preferred and total amount of features, respectively. $\:\alpha\:$ is utilized for controlling the significance of classification excellence and sub-set length. In the experimentations, $\:\alpha\:$ is fixed as 0.9.

Hybrid classification models

For the cybersecurity attack classification process, the hybrid CNN-BiGRU-AM technique is employed⁴¹. This technique is chosen because it can effectively capture spatial and temporal features of network traffic data. The CNN component outperforms extracting spatial hierarchies and patterns, making it appropriate for recognizing patterns in raw data, such as attack signatures. The BiGRU model, with its ability to capture long-term dependencies in time-series data, complements CNN by handling the sequential nature of network traffic and attacks. The AM model additionally improves the model by concentrating on the most relevant features, enhancing its sensitivity to critical attack indicators. This hybrid approach outperforms conventional techniques by utilizing the merits of every model, enabling improved accuracy in classifying complex attack patterns. Additionally, it gives robustness against varying attack types and growing strategies in cybersecurity, making it more adaptable than standalone CNN or RNN-based models. Figure 4 portrays the structure of the CNN-BiGRU-AM technique.

Fig. 4

Structure of CNN-BiGRU-AM technique.

CNNs have robust grid data handling abilities and are extensively applied to image analysis tasks. CNNs are feed-forward neural networks with intricate frameworks that efficiently handle higher‐dimensional data and spontaneously remove features. The significant frameworks of a CNN comprise a convolutional, input, output, pooling, and fully connected layer (FC). During the convolutional layer, input data is convoluted with filters of changing weights to remove basic features, allowing the calculation of how many dissimilar data locations match the features. The CNN handles input data over feature extractions and transformations carried out by the pooling and convolutional layers for deriving higher‐level characteristics.

The processes for feature extraction are as shown:

$$\:{x}_{j}^{m}=f\left({w}_{j}^{m}\times\:{X}^{m-1}+{b}_{j}^{m}\right)$$

(8)

Whereas $\:{w}_{j}^{m}$ represents a weighted matrix of the initial convolutional kernel of the layer; $\:{X}^{m-1}$ signifies $\:m$-1 layer output; $\:{x}_{j}^{m}$ means $\:j$ feature of the $\:m$ layer; $\:*$ refers to the convolutional operator; $\:{b}_{j}^{m}$ denotes biased term.

During this study, the activation function of the $\:ReLU$ is applied for the CNN, which transforms the linear components of the convolutional layer based on the succeeding representation:

$$\:f\left(z\right)=max\left(0,z\right)$$

(9)

Next, numerous feature matrices are produced with data extraction from the convolutional layer. The pooling layer is successively used to remove the most important features while decreasing computational efficiency. The pooling layer handles the feature matrices gained from the convolutional layer utilizing a pooling kernel, as described by the succeeding Eq. (10):

$$\:{x}_{j}^{m}=f\left({w}_{j}^{m}\times\:{X}^{m-1}+{b}_{j}^{m}\right)$$

(10)

Whereas $\:{X}_{j}^{m}\left(v\right)$ denotes the component of the $\:j\:$feature matrix of the $\:m\:$layer in the pooling kernel area; $\:{y}_{j}^{m+1}\left(w\right)$ represents a component of the $\:j$ feature matrix of the $\:m+1\:$layer after pooling; $\:{D}_{w}$ denotes the area enclosed by $\:jth\:$pooling kernel.

At last, the FC layer combines these features by mapping the pooled data to the output layer. The individual convolutional architecture of the CNN can decrease computational costs and improve execution speed. This minimizes the requirement for physical feature engineering by constantly removing high-value features from raw data utilizing convolutional layers. During this maximal fusion layer, feature spectrograms of convolutional data are joined, and local information is filtered to remove maximal values while decreasing feature sizes. The FC layer then processes the removed higher-level features to produce the CNN output.

The GRU is a basic version of the LSTM, highlighting only the update gate and reset gate. The reset gate mainly forgets unrelated data from the preceding time step, decreasing interference with main characteristics. The update gate defines several preceding state information retained, thus enhancing the correlation between temporal features. For the same prediction precision, the structural design of GRU outcomes in smaller training parameters and quicker convergence compared to LSTM. The calculation procedure for all GRU units is defined below.

$$\:{x}_{i}^{i}=\left\{\begin{array}{c}\sigma\:\left({W}_{r}{x}_{t}+{U}_{r}{h}_{t-1}\right)\:\\\:{z}_{t}=\sigma\:\left({W}_{Z}{x}_{t}+{U}_{Z}{h}_{t-1}\right)\\\:\:\stackrel{\sim}{{h}_{t}}=\text{tanh}\left({r}_{t}\circ\:\left(U{h}_{t-1}\right)+W{x}_{t}\right)\\\:{h}_{t}=(1-{z}_{t})\circ\:\stackrel{\sim}{{h}_{t}}+{z}_{t}\circ\:{h}_{t-1}\end{array}\right.$$

(11)

Whereas $\:{r}_{t}$ denoted reset gate, the nearer its value is to $\:0$, the more information from the preceding moment must be forgotten. $\:z$ represents the update gate, and the nearer its value is to $\:1$, the more information from the prior moment is reserved. $\:\stackrel{\sim}{{h}_{t}}$ signifies the candidate hidden layer (HL) state, replicating the input information at moment $\:t$ and partially preserving the output at moment $\:t-l$. $\:{h}_{t-1}$ and $\:{h}_{t}\:$stands for output of the HL at $\:tth$ instant.$\:\sigma\:$ and $\:tanh$ denotes Sigmoid and activation function; $\:{W}_{t},\:Ur,\:Wz,\:Uz,\:W,\:U$ represents training parameter matrices in the network.

Bi-GRU seizures depend on the start and end of a sequence by transmitting information either forward or backwards concurrently. Compared with conventional unidirectional GRUs, Bi-GRU takes additional contextual data and improves the model’s performance by reflecting forward or backward information within the sequence. Fundamentally, Bi-GRU is a bidirectional recurrent network incorporating dual GRUs with inverse flow direction. It integrates the flow of information from previous to future and, conversely, improves the ability of the model to take dependencies in either direction.

The bias at moment $\:t$, $\:\overrightarrow{{h}_{t}}$ and ${h_t}^ \leftarrow$ represents the output of all Bi-GRU component moments, representing the forward and backwards-propagating GRU output. The three modules are cooperatively influenced. The particular computation procedure is described below.

$$\:\{\overrightarrow{{h}_{t}}=GRU\left({x}_{t},\overrightarrow{{h}_{t-1}}\right)\:\overleftarrow{{h}_{t}}=GRU\left({x}_{t},{h}_{t-1}^ \leftarrow \right)\:{h}_{t}=\alpha\:\overrightarrow{{h}_{t}}+\beta\:\overleftarrow{{h}_{t}}+{c}_{t}$$

(12)

Here, $\:GRU(\cdot\:)$ refers to the computing process for $\:GRU$, the $\:\overrightarrow{{h}_{t}}$, and ${h_t}^ \leftarrow$ signifies forward and backward GRU HL outputs, correspondingly; $\:{\alpha\:}_{t},{\beta\:}_{t}$ signifies consistent HL outputting weights, individually; $\:{c}_{t}$ stands for HL offset consistent with $\:{h}_{t}.$

The attention mechanism (AM) has established its efficiency in many DL applications, comprising image processing, time series, and machine translation prediction. The AM permits the method to discriminate concentration on various portions of the input sequence and approximate the dependences amongst these components. This study calculates attention weights according to the similarities amongst input vector pairs and is autonomous of outside elements. The major mathematic expression of the AM is defined below:

$$\:{h}_{t,{t}^{{\prime\:}}}=tanh\left({W}_{g}{h}_{t}+{W}_{g}^{{\prime\:}}{h}_{{t}^{{\prime\:}}}+{b}_{h}\right)$$

(13)

$$\:{e}_{t,{t}^{{\prime\:}}}=\delta\:\left({W}_{e}{h}_{t,{t}^{{\prime\:}}}+{b}_{e}\right)$$

(14)

$$\:{a}_{t,{t}^{{\prime\:}}}=softmax\left({e}_{t,{t}^{{\prime\:}}}\right)$$

(15)

$$\:{l}_{t}={\sum\:}_{{t}^{{\prime\:}}}^{}{a}_{t,{t}^{{\prime\:}}}{h}_{{t}^{{\prime\:}}}$$

(16)

Among others, $\:{h}_{t,{t}^{{\prime\:}}}$ represents hidden node output of the Bi-GRU layers; $\:{W}_{g}$ and $\:{W}_{g}^{{\prime\:}}$ are similar to the weighted matrices of the hidden states $\:{h}_{t}$ and $\:{h}_{{t}^{{\prime\:}}}$ correspondingly; $\:{e}_{t,{t}^{{\prime\:}}}$ signifies sigmoid activation output; $\:\delta\:$ symbolizes element-wise sigmoid function; $\:{W}_{e}$ mean weighted matrix of the attention network; $\:{a}_{t,{t}^{{\prime\:}}}$ denotes softmax activation of $\:{e}_{t,{t}^{{\prime\:}}}.$ $\:{l}_{t}$ calculates a token’s importance or attention in the AM’s hidden state to dissimilar neighbouring tokens at a specific time step. $\:{l}_{t}$ seizures-related information from the HL in the present token input sequence at time step $\:t$; it assists the approach in utilizing either succeeding or preceding information to improve its representation and understanding of input data. For calculating the attention-concentrated hidden state representation $\:{l}_{t}$, the method typically integrates data from every time step, predicated on their significance to the present token at $\:t$he time step$\:.$

The AM incorporated with Bi-GRU efficiently captures the Bi-GRU’s output sequence information. Here, $\:x$ characterizes the inputs to the Bi-GRU model, $\:h$ symbolizes the HL outputs after training, $\:w$ specifies the weights allocated by the AM to all HL outputs (standardized utilizing softmax), and $\:y$ refers to the last output of the approach.

Hyperparameter tuning using ALO model

Moreover, the ALO method optimally adjusts the hyperparameter values of the CNN-BiGRU-AM approach and outcomes in more excellent classification performance⁴². This method is chosen because it can efficiently explore large search spaces and find optimal or near-optimal hyperparameter configurations. ALO replicates the predatory behaviour of antlions, allowing it to balance exploration and exploitation during the search process. Unlike conventional grid or random search methods, ALO can more accurately handle complex, high-dimensional, non-linear hyperparameter optimization. It is less prone to getting trapped in local minima, making it more effective in discovering better-performing hyperparameters for DL models. Moreover, the flexibility and adaptability of the ALO method make it appropriate for a wide range of models and tasks, including cybersecurity attack classification, where high precision and efficiency are crucial. This method improves model accuracy and mitigates training time by finding optimal hyperparameters more efficiently than conventional techniques. Figure 5 specifies the steps of the ALO approach.

Fig. 5

Steps involved in the ALO technique.

It presents short descriptions of the ALO model, primarily proposed; the consistent pseudocode is imitated in Algorithm 1. Like the swarm/flock kind model, ALO uses $\:{n}_{S}$ ant agents and $\:{n}_{S}$ AL-agents inside a $\:d$-dimensional area. The ants pass over the area and follow random walks in their coordinates. Conversely, antlions construct sandpit pitfalls, with dimensions more excellent than the lowest objective function value (fitness) at a particular place. The ant’s movement must observe the limitations set by the upper $\:{b}_{h}$ and lower $\:{b}_{l}$ Coordinate vectors. This is attained by a random walk provided by:

$$\:{A}^{k}=\left[0,cumsum\left(2r\left({t}_{1}\right)-1\right),\dots\:cumsum\left(2r\left({t}_{IierMax}\right)-1\right)\right],$$

(17)

When the function $\:r\left(t\right)$ is described regarding uniform variables $\:Z\sim\:U\left[\text{0,1}\right]$ at random, thereby $\:r\left(t\right)=1$ if $\:z\in\:\left(\text{0.5,1}\right]$ and $\:0$ formerly. The model guarantees that each of the agents stays in the searching region $\:[{b}_{l},\:{b}_{h}]$ by resorting to the normalization:

$$\:{A}_{i}^{k}={c}_{i}^{k}+\frac{{d}_{i}^{k}-{c}_{i}^{k}}{{b}_{i}-{a}_{i}}\left({A}_{i}^{k}-{a}_{i}\right)$$

(18)

Whereas $\:{a}_{i}$ and $\:{b}_{i}$ represent the maximum and minimum random walking for the $\:ith$ variable, and $\:{c}_{i}^{k}y$ $\:{d}_{i}^{k}$ are the maximum and minimum of the $\:ith$ variable at the$\:\:kth\:$stage.

The ALO model initiates arbitrary distribution of the $\:{n}_{s}$ antlions and the $\:{n}_{s}$ ants above the possible solution area. Then, the top antlion $\:A{L}^{*}$ is recognized, such as the antlion that $\:\:minf\left(A{L}_{j}\left(k=0\right)\right).$ Formerly, due to iteration counts selected a priori, $\:{n}_{MaxIier},$ the ants roam in the searching region while the antlions try to search them down. In contrast, the exploitation of the area of interest was assured by the advanced reduction of antlion sand pit traps that are shown as:

$$\:{c}^{k}=\frac{{c}^{k}}{I},\:y{d}^{k}=\frac{{d}^{k}}{I}$$

(19)

$\:I$ signify the compression ratio, and $\:{c}^{k}/{d}^{k}$ represents the maximum/minimum of each variable inside the $\:kth$ iterations.

Determine how incorporating the ant random walking by the roulette wheel choice of the antlions facilitates evade, by higher possibility, deteriorating into local maxima. Furthermore, the random walks of all ants alongside all dimensions make the agent’s diversity complicated. In addition, the sandpit traps transfer to the location of the best ant discovered in the optimization, guaranteeing regions of the searching area are well-maintained.

Finally, elitism has been utilized. The better antlion at all iterations is kept and compared to the best antlion thus far (the elite).

$$\:{A}_{i}^{k}=\frac{{R}_{A}^{k}+{R}_{E}^{k}}{2}$$

(20)

Here, $\:{R}_{A}^{k}$ represents the path of the antlion dynamic in the present iteration, while $\:{R}_{E}^{k}$ signifies the path of the leading antlion. The detailed process designated above is formalized in the succeeding application of 3 operators.

Algorithm 1

Pseudocode of ALO approach.

The ALO technique originates from an FF to acquire an enhanced performance of a classifier. It expresses a positive number to suggest better results for candidate performance. At this time, the reduction of the classifier error rate has been reflected in FF. Its mathematical formulation is expressed below in Eq. (21).

$$\begin{aligned}fitness\left({x}_{i}\right) & =ClassifierErrorRate\left({x}_{i}\right) \\ &=\frac{no.\:of\:misclassified\:instances}{Total\:no.\:of\:instances}\times\:100\end{aligned}$$

(21)

XAI using SHAP

Finally, SHAP is utilized as an XAI technique to enhance threat detection and decision-making by providing trustworthy insights into AI-driven security systems⁴³. This is chosen due to its robust theoretical foundation rooted in cooperative game theory, which allows it to provide a fair and consistent explanation of model predictions. SHAP values clearly understand how individual features contribute to the model’s global and local output, making it easier for security analysts to interpret complex ML models. Unlike other techniques, such as LIME, which approximate local models, SHAP gives reliable, consistent explanations across diverse models, improving trust in decision-making. Its capability to quantify feature importance and explain interactions between features makes it specifically useful for complex, high-dimensional datasets in cybersecurity. The global interpretability of SHAP also assists in detecting biases or errors in the model, thus enhancing its robustness. Compared to other methods, SHAP ensures that each feature’s contribution is pretty distributed, which is critical in high-stakes domains such as cybersecurity.

Recent advancements in XAI have demonstrated the efficiency of SHAP in improving the transparency and performance of security systems, specifically in complex models such as ensemble and hybrid architectures for intrusion detection. SHAP, based on cooperative game theory, assigns a fair and consistent value to each feature based on its contribution to a model’s prediction, enabling both global and local interpretability. In several advanced approaches, SHAP is employed not only for interpreting feature importance but also as a feature selection mechanism to mitigate dimensionality while preserving critical threat indicators. This dual role significantly enhances both the accuracy and its trustworthiness of the model. Additionally, integrating SHAP with other XAI methods like LIME has proven to provide complementary insights, additionally strengthening the interpretability of DL models.

In the proposed work, SHAP is applied to calculate the contribution of each feature within the deep learning (DL) framework to better understand the distribution of attribute influence on the target outcomes. The SHAP value for each feature is derived using the concept of conditioned expected prediction, which reflects how the inclusion or exclusion of a specific feature impacts the model’s output. Mathematically, the SHAP value$\:{\varphi\:}_{i}\left(f\right)$ is computed using the Shapley value formula depicted in Eq. (22) from cooperative game theory:

$$\:{\varphi\:}_{i}\left(f\right)={\sum\:}_{S\subseteq\:\left\{1,\dots\:,M\right\}\setminus\:\left\{i\right\}}^{}\frac{\left|S\right|!\left(M-\left|S\right|-1\right)!}{M!}\left[f\left(S\cup\:\left\{i\right\}\right)-f\left(S\right)\right],$$

(22)

Whereas $\:{\varphi\:}_{i}\left(f\right)$ refers to the SHAP value of feature or attribute $\:i$ for the method $\:f,M$ stands for complete feature counts, $\:S$ signifies part of characteristics eliminating feature $\:i,\left|\:S\right|$ symbolizes the subset cardinality $\:S,$ $\:f\left(S\right)$ denotes the output of the method after considering only the attributes in $\:S$, and $\:f(S\cup\:\{i\left\}\right)\:$ represents the model’s output after comprising feature $\:i$ along with the features in $\:S.$

Result analysis and discussion

The NSLKDD dataset⁴⁴ examines the performance validation of the EIDCDR-XAIADL model. It consists of 50,000 samples below 2 class labels, standard and anomaly, with 25,000 samples individually illustrated in Table 1. The total number of features is 42, but only 24 are selected in this dataset.

Table 1 Details of the NSLKDD dataset.

Figure 6 validates the confusion matrix established through the EIDCDR-XAIADL method under the NSLKDD dataset below different epochs. The performances indicate that the EIDCDR-XAIADL approach has effectual detection and identification of all classes specifically.

Fig. 6

NSLKDD dataset (a–f) epochs 500–3000 of the confusion matrix.

Table 2; Fig. 7 underscored the cybersecurity detection of the EIDCDR-XAIADL technique under the NSLKDD dataset below distinct epochs. The performance showed that the EIDCDR-XAIADL technique efficiently identified normal and anomaly classes. According to epoch 500, the EIDCDR-XAIADL approach obtains an average $\:acc{u}_{y}$ of 99.00%, $\:pre{c}_{n}$ of 99.01%, $\:rec{a}_{l}$ of 99.00%, $\:{F}_{score}\:$of 99.00%, MCC of 98.01%, and Kappa score of 98.17%. In addition, on epoch 1000, the EIDCDR-XAIADL approach reaches an average $\:acc{u}_{y}$ of 99.10%, $\:pre{c}_{n}$ of 99.10%, $\:rec{a}_{l}$ of 99.10%, $\:{F}_{score}\:$of 99.10%, MCC of 98.20%, and Kappa score of 98.23%. Besides, on epoch 2000, the EIDCDR-XAIADL model obtains an average $\:acc{u}_{y}$ of 99.16%, $\:pre{c}_{n}$ of 99.16%, $\:rec{a}_{l}$ of 99.16%, $\:{F}_{score}\:$of 99.16%, MCC of 98.32%, and Kappa score of 98.31%. At last, on epoch 3000, the EIDCDR-XAIADL model obtains an average $\:acc{u}_{y}$ of 99.19%, $\:pre{c}_{n}$ of 99.19%, $\:rec{a}_{l}$ of 99.19%, $\:{F}_{score}\:$of 99.19%, MCC of 98.39%, and Kappa score of 98.41%.

Table 2 Cybersecurity detection of EIDCDR-XAIADL method under the NSLKDD dataset.

Fig. 7

Average of EIDCDR-XAIADL method under the NSLKDD dataset.

Figure 8 depicts the training (TRA) $\:acc{u}_{y}$ and validation (VAL) $\:acc{u}_{y}$ performances of the EIDCDR-XAIADL technique under the NSLKDD dataset. The values of $\:acc{u}_{y}\:$Are computed across a period of 0-3000 epochs. The figure underscored that the values of TRA and VAL $\:acc{u}_{y}$ show an increasing trend, indicating the proficiency of the EIDCDR-XAIADL approach with enhanced performance across numerous repetitions. In addition, the TRA and VAL $\:acc{u}_{y}$ values remain close through the epochs, notifying lesser overfitting and showing the maximum outcome of the EIDCDR-XAIADL approach, guaranteeing reliable calculation on unseen samples.

Fig. 8

$\:Acc{u}_{y}$ curve of EIDCDR-XAIADL method under the NSLKDD dataset

In Fig. 9, the TRA loss (TRALOS) and VAL loss (VALLOS) graph of the EIDCDR-XAIADL method under the NSLKDD dataset is exhibited. The loss values are computed through a period of 0-3000 epochs. It is depicted that the TRALOS and VALLOS values demonstrate a diminishing trend, which indicates the competency of the EIDCDR-XAIADL technique in harmonizing a tradeoff between generalization and data fitting. The consecutive dilution in values of loss and assurances of the superior performance of the EIDCDR-XAIADL technique and tuning of the prediction results afterwards.

Fig. 9

Loss curve of EIDCDR-XAIADL method under the NSLKDD dataset.

Table 3; Fig. 10 study the comparison results of the EIDCDR-XAIADL methodology under the NSLKDD dataset with the existing methods^{29,46,47,48,49}. The performances indicated that the ATFDNN, IPSO, E-LSTM, XAIID-SCPS, LIB-SVM, Supervised NIDS, MCA-LSTM, GRU, Simple RNN, and FFDNN techniques attained poorer performance. The proposed EIDCDR-XAIADL technique attained higher performance with improved $\:pre{c}_{n}$, $\:rec{a}_{l},$ $\:acc{u}_{y},\:$and $\:{F1}_{score}$ of 99.19%, 99.19%, 99.19%, and 99.19%, respectively.

Table 3 Comparative analysis of the EIDCDR-XAIADL model under the NSLKDD dataset^{29,46,47,48,49}.

Fig. 10

Comparative analysis of the EIDCDR-XAIADL model under the NSLKDD dataset.

Table 4; Fig. 11 illustrates the computational time (CT) analysis of the EIDCDR-XAIADL approach with the existing models. the EIDCDR-XAIADL approach specifies the most efficient performance with a CT of 8.78 s. In contrast, methods such as LIB-SVM and ATFDNN recorded significantly higher times of 19.33 and 18.30 s respectively. Other techniques like E-LSTM and MCA-LSTM followed closely with CTs of 17.54 and 17.98 s. Moderate CT depicted moderately lesser CTs of IPSO at 10.81 s, XAIID-SCPS at 10.03 s, and Supervised NIDS at 11.41 s. GRU and simple RNN required 11.83 and 15.10 s, while FFDNN recorded 16.47 s. These results highlight the superior efficiency of the EIDCDR-XAIADL method, making it a robust candidate for time-sensitive network intrusion detection applications.

Table 4 CT assessment of the EIDCDR-XAIADL approach under the NSLKDD dataset.

Fig. 11

CT assessment of the EIDCDR-XAIADL approach under the NSLKDD dataset.

The simulation validation of the EIDCDR-XAIADL approach is studied using the CICIDS 2017 dataset⁴⁵. It contains 50,000 samples below 2 class labels, such as standard and anomaly, with 25,000 samples each, as depicted in Table 5. This dataset holds 78 features in total, but only 46 features have been selected.

Table 5 Details of the CICIDS 2017 dataset.

Figure 12 states the confusion matrix made by the EIDCDR-XAIADL technique with the CICIDS 2017 dataset below distinct epochs. The performances imply that the EIDCDR-XAIADL model effectively detects and identifies all classes accurately.

Fig. 12

CICIDS 2017 dataset (a–f) epochs 500–3000 of the confusion matrix.

Table 6; Fig. 13, the cybersecurity detection of EIDCDR-XAIADL methodology under the CICIDS 2017 dataset below different epochs is underscored. The performance showed that the EIDCDR-XAIADL model gained efficacious identification of standard and anomaly class labels. With epoch 500, the EIDCDR-XAIADL model obtains an average $\:acc{u}_{y}$ of 98.83%, $\:pre{c}_{n}$ of 98.83%, $\:rec{a}_{l}$ of 98.83%, $\:{F}_{score}\:$of 98.83%, MCC of 97.67%, and Kappa score of 97.71%. Moreover, with epoch 1000, the EIDCDR-XAIADL model obtains an average $\:acc{u}_{y}$ of 98.88%, $\:pre{c}_{n}$ of 98.88%, $\:rec{a}_{l}$ of 98.88%, $\:{F}_{score}\:$of 98.88%, MCC of 97.76%, and Kappa score of 97.79%. Also, with epoch 1500, the EIDCDR-XAIADL model obtains an average $\:acc{u}_{y}$ of 98.97%, $\:pre{c}_{n}$ of 98.97%, $\:rec{a}_{l}$ of 98.97%, $\:{F}_{score}\:$of 98.97%, MCC of 97.94%, and Kappa score of 97.97%. Besides, with epoch 2500, the EIDCDR-XAIADL model obtains an average $\:acc{u}_{y}$ of 99.07%, $\:pre{c}_{n}$ of 99.07%, $\:rec{a}_{l}$ of 99.07%, $\:{F}_{score}\:$of 99.07%, MCC of 98.13%, and Kappa score of 98.17%.

Table 6 Cybersecurity detection of EIDCDR-XAIADL method under the CICIDS 2017 dataset.

Fig. 13

Average of EIDCDR-XAIADL method on CICIDS 2017 dataset.

Figure 14 shows the TRA and VAL $\:acc{u}_{y}$ performances of the EIDCDR-XAIADL model under the CICIDS 2017 dataset. The values of $\:acc{u}_{y}\:$are computed through a period of 0-3000 epochs. The figure underscored that the values of TRA and VAL $\:acc{u}_{y}$ reveal a growing tendency indicating the capacity of the EIDCDR-XAIADL technique with maximum performance through multiple repetitions. Also, the TRA and VAL $\:acc{u}_{y}$ values remain close across the epochs, notifying diminished overfitting and expressing the superior performance of the EIDCDR-XAIADL technique, which assurances reliable calculation on hidden samples.

Figure 15 depicts the TRALOS and VALLOS graph of the EIDCDR-XAIADL method under the CICIDS 2017 dataset. The loss values are computed throughout 0-3000 epochs. The values of TRALOS and VALLOS represent a diminishing trend, which indicates the competency of the EIDCDR-XAIADL technique in equalizing a tradeoff between data fitting and generalization. The consecutive dilution in loss and securities the maximal performance of the EIDCDR-XAIADL technique and tune the prediction results gradually.

Fig. 14

$\:Acc{u}_{y}$ curve of EIDCDR-XAIADL method on CICIDS 2017 dataset

Fig. 15

Loss curve of EIDCDR-XAIADL method on CICIDS 2017 dataset.

Table 7; Fig. 16 compare the EIDCDR-XAIADL technique’s comparison study under the CICIDS 2017 dataset with the existing methodologies^{31,46,47,48,49}. The values in the table underscored that the VGG-16, ResNet50, Hybrid CNN, XAIID-SCPS, LIB-SVM, Supervised NIDS, LSTM, Bi-LSTM, GRU, and Modified Bi-LSTM approaches attained poorer performance. The proposed EIDCDR-XAIADL method illustrated superior performance with higher $\:pre{c}_{n}$, $\:rec{a}_{l},$ $\:acc{u}_{y},\:$and $\:{F1}_{score}$ of 99.12%, 99.12%, 99.12%, and 99.12%, respectively.

Table 7 Comparative analysis of the EIDCDR-XAIADL model under the CICIDS 2017 dataset^{31,46,47,48,49}.

Fig. 16

Comparative analysis of the EIDCDR-XAIADL model under the CICIDS 2017 dataset.

Table 8; Fig. 17 indicates the CT assessment of the EIDCDR-XAIADL method with the existing techniques. The EIDCDR-XAIADL method is the most efficient, with a CT of 10.52 s. In comparison, popular DL models such as VGG-16 and ResNet50 take significantly longer, with CTs of 16.93 and 24.58 s respectively. The hybrid CNN approach also exhibits a high CT of 23.43 s, while the modified Bi-LSTM and XAIID-SCPS methods are nearly identical, needing 23.65 and 23.66 s. Conventional models namely LIB-SVM and supervised NIDS exhibit CTs of 27.77 and 21.95 s. Meanwhile, Bi-LSTM and GRU method perform moderately with 15.15 and 17.46 s. LSTM exhibits the highest CT at 28.08 s. These results highlight the computational efficiency of the EIDCDR-XAIADL approach, making it appropriate for real-time intrusion detection scenarios.

Table 8 CT evaluation of the EIDCDR-XAIADL methodology under the CICIDS 2017 dataset.

Fig. 17

CT evaluation of the EIDCDR-XAIADL methodology under the CICIDS 2017 dataset.

Conclusion

In this study, the EIDCDR-XAIADL model is proposed. The main intention of the proposed EIDCDR-XAIADL model is to deliver a robust cybersecurity system that combines XAI to address the attacks. Initially, the proposed EIDCDR-XAIADL technique applies data normalization using mean normalization to ensure uniform scaling of network traffic data. The MVO technique is employed to select the most appropriate and discriminative features. For the cybersecurity attack classification process, the hybrid CNN-BiGRU-AM technique is implemented. Moreover, the ALO technique optimally adjusts the hyperparameter values of the CNN-BiGRU-AM method and results in more excellent classification performance. Finally, SHAP is utilized as an XAI method to enhance threat detection and decision-making by providing trustworthy insights into AI-driven security systems. The experimental evaluation of the EIDCDR-XAIADL approach is examined under dual datasets. The experimental validation of the EIDCDR-XAIADL approach demonstrated a superior accuracy value of 99.19% and 99.12% under NSLKDD and CICIDS 2017 datasets. The limitations of the EIDCDR-XAIADL approach comprise the reliance on a relatively simplistic model for handling complex, high-dimensional data, which could affect performance in more complex real-world scenarios. Additionally, the approach may not generalize well to highly diverse datasets, potentially resulting in reduced accuracy when dealing with outliers or noisy data. The efficiency of the model in terms of computational resources remains another limitation, specifically in large-scale applications. Furthermore, while the method illustrates satisfactory performance in specific use cases, it may require further optimization to attain robustness across varying conditions. Future work should concentrate on improving the scalability of the model, improving its robustness to noise, and extending its application to more complex tasks. Additionally, the exploration of alternative architectures for enhanced feature extraction and the incorporation of hybrid models may result in crucial performance improvements. Moreover, integrating real-time data processing capabilities and improving interpretability could additionally improve the practical applicability of the methodology in dynamic environments.