Capabilities of battery and compressed air storage in the economic energy scheduling and flexibility regulation of multi-microgrids including non-renewable/renewable units

Abstract

Economic scheduling of multi-microgrids containing distributed units and storage devices is expressed in this scheme according to the multi-objective energy management system. Microgrid operator considers the economic, security, flexibility and operation objectives. The present method minimizes the weighted sum of voltage security index, energy loss, and energy cost. Constraints consider the optimal power flow formulation, flexibility and voltage stability limits in microgrids, and mathematical formulation of sources and storages operation. Microgrid includes non-renewable and renewable units, and storage system in network are battery and compressed air storage. Unscented Transformation approach models the uncertainties of the renewables output, price of energy, and demand. Fuzzy decision approach obtains a compromise point between economic, security and operation objectives. Combining grey wolf and red panda optimizers is able to obtain an optimal solution with low value for variance of the final point. Energy management according to various technical and economic indicators in the several renewable multi-bus microgrids considering battery, compressed air storage and non-renewable unit as flexibility sources based on the Unscented Transformation model and hybrid solver are the advantage, goal and innovation of this project. According to simulation results, the energy management of the energy storage and non-renewable sources in the microgrids with renewable sources can be improved the various indicators, such as reducing the energy cost and loss as well as voltage drop about to 30–60%, 46%, 46–50%, and improving voltage security equal to 10.55% compared with power flow studies. Flexibility of 100% is also reached for microgrids thanks to the incorporation of storage equipment and non-renewable power sources.

Introduction

Motivation

Incorporating renewable energy sources (RESs), i.e. photovoltaics (PV) and wind turbines (WT), in electricity industry and power grids has become popular from the perspective of minimizing environmental pollution¹. Another type of RESs is the biomass energy unit (BEU), which converts waste into methane gas and can generate electrical energy from this gas. This resource is also known as an environmentally-friendly technology due to the consumption of waste². Also, as waste is continuously produced, its exhaustion seems impossible. Hence, BEU can be considered part of RESs². Not only are RESs effective in minimizing environmental pollution, but they can also take steps in reducing the network operating cost due to their small cost of operation. They are also generally located at demand sites, so they can be suitable for boosting technical indicators like operation and security indicators¹. Nonetheless, their output power is uncertain, which may lead to reducing the network flexibility³. To solve this issue, flexible resources such as energy storage systems (ESSs) should be include in the mentioned system³. By controlling its active power, the storage device can deal with the variations in the output power of the RESs system in different scenarios. In other words, in high flexibility situations, the system with ESS and RES can show constant power for different scenarios of RESs output power³. Furthermore, storage devices can help peak-shaving, which is effective in enhancing various technical and economic indicators of the network³. Nonetheless, the above-mentioned advantages, such as improving the network technical and economic states with ESS and RES, depend on the provision of an energy management system (EMS) in the network⁴. In line with this issue, the smart grid assists in inclusion of the mentioned elements in an integrated form such as a microgrid (MG), whose operator should be in mutual coordination with the distribution system operator (DSO)⁵. Therefore, it is expected that a distribution network will include several MGs. The next issue is that there are various technical and economic indicators in a network, in which all of these indicators must be enhanced together. Hence, it is predicted that the optimal operation of the multi-microgrid (MMG), by taking into account the multi-criteria objectives of the MG operator or DSO, can achieve the optimal compromise conditions for economic and technical (like operation, security, and flexibility) indicators in several MGs at the same time.

Literature review

One application to EMS was introduced for an MG located at a house⁶. In this design, one MG was adopted to feed the demand via output power of PV, fuel cell, and battery storage, where the MG operated either in grid-connected or grid-disconnected operating modes. To cope with the uncertain nature of the demand and RESs and their impact on the operation of an MG, Ref ⁷. suggested an optimal scheduling model, by taking into account the demand response, to operate several MGs. The design was able to predict the power output of RESs and the amount of demand. Different types of MGs, including WT, PV, and hydrogen storage were discussed in⁸. The paper also proposed an EMS concerning the uncertain output of RESs. The design minimized the operating cost imposed by battery and hydrogen storage equipment and the energy excess and shortage based on gray wolf optimization (GWO) algorithm. Another design was connecting several MGs containing PV, battery, and load to the main grid using a DC/AC converter, in which the operation of MGs is realized with the control of the operation of the main grid converter and storage converter⁹. Ref ¹⁰. proposes a novel optimization method to enhance the operating status of MGs according to improved Archimedes optimization algorithm (IAOA). The paper formulated a multi-objective function based on the imposed cost and emission level concerning the operation of the MG.

The operation of an MG that consists of renewables, storage, and thermal units was discussed in¹¹, where a stochastic model with two short-term and long-term planning was used. A Stackelberg stochastic model was incorporated in¹² to consider various uncertainty parameters. The model assumes MGs in an upper-level problem that is prone to uncertainties originating from the output power of WT and PV sources, as well as energy price. Chance constrained were also used to provide a modeling of RESs. Also, the uncertain price of energy was modeled using several demand scenarios. The power flow problem was also solved in the lower-level problem. The operation of an MG considering the real situation was discussed in¹³, where two sets of strategies were considered for MGs. The first set optimizes the decisions according to the predictions made on the demand and supply of electrical energy. The second set takes decisions concerning the operation of the MG while taking into account the current situation of the MG. The authors in¹⁴ presented the operation of an MG in grid-connected mode, which is considerably impacted by RES and electric vehicles. The EMS adopted for the MG includes several layers. The MGs, in the proposed design, are either single or interconnected, which are finally in connection with the distribution system. The first layer concerns the operation of single MGs, while the second layer addresses the interconnected MGs. Also, MG’s operating cost is minimized in the first layer while subject to some constraints. The expected operating cost and risk cost imposed by interconnected MGs is minimized in the second layer and the constraints are the same as those of the first layer. Another EMS for interconnected MGs with RESs and flexibility sources was discussed in¹⁵, where flexibility sources include a combination of electric springs, parking lots of electric vehicles, and demand response. An optimization formulation was also structured to find the minimum difference of cost and profit of such flexibility sources. Ref ¹⁶. presents the energy management of multi-carrier water and electricity system by taking into account the considerable number of RESs involved and the seawater desalinization mechanism for meeting water demanded by end-users. This approach has several power, gas and water demand layers to provide electrical energy, thermal energy and drinkable water to the smart island. Ref ¹⁷. expresses the machine learning-based integer linear programming method for the smart grids including the allocation of micro-synchrophasor units considering the reconfigurable distribution networks. In¹⁸, it proposes a novel EMS for a MG relying on the primal–dual method of multipliers. Ref ¹⁹. presents a distributed EMS that utilizes a relaxed consensus mechanism alongside an additional way to align both the trading price and transaction power among MGs and the smart grid. Ref ²⁰. introduces an advanced Golden Jackal Optimization method for the energy management of dispersed sources, battery storage systems, and hybrid energy sources. The goals are to reduce operating costs and address the MG operational issue. Ref ²¹. introduces an operational platform utilizing a clever probabilistic wavelet Petri neuro-fuzzy inference algorithm to regulate the voltage/frequency index amid RESs and battery systems, addressing various risks. Ref ²². presents a distributionally robust optimization framework for microgrids with ambiguous chance constraints. This method utilizes mixed integer linear programming, solved by CPLEX. Table 1 reviews the literature in a summarized way.

Table 1 A summary of the works presented by the literature.

Research gaps and contributions

Regarding the research background presented previously and Table 1, there are main research gaps as follows regarding the operation of MGs:

• In most research, the operation of the distribution network or an MG is formulated. Yet, a distribution network can include several MGs. This issue has been included in few studies such as^6,14. Generally, an MG similar to a distribution network has several buses⁵. However, references^6,14 consider only the single-bus model of MGs.

• There are various technical and economic indicators in an MG. However, according to Table 1, in most of the research, the operating status of the network has been considered, and in a few studies, such as^14,15, the economic index has also been taken into account. Nevertheless, the improvement of a single indicator cannot guarantee the improvement of other indicators. For instance, to make the energy cost of an MG minimized, it is necessary to inject high power of RESs into consumption points. Yet, this may increase the occurrence probability of overvoltage and increase energy loss in the network¹. Furthermore, an MG with RESs requires flexibility management³. Most of the research on this issue has used flexibility sources in the network, but flexibility modeling has been discussed in rare works like¹⁵. Nonetheless, to know the status of an indicator, it should be measured, which can be accessed if its mathematical modeling is extracted. Also, power sources and storage devices are generally located at the consumption points, and their optimal energy management can be effective in enhancing other technical indicators of grid such as security. This subject has also been addressed in few papers.

• Energy management of MGs is one of the operational problems in the power network, where the execution step is short so that, in some cases, it is less than one hour¹⁵. Thus, the computing time is expected to be low in such cases. One approach to reducing the computational time is to reduce the size of the problem. But, as the literature shows, most of the research has used scenario-based stochastic optimization (SBSO) to model uncertain quantities. Since the different uncertainties may appear in the mentioned problem, the number of uncertainties in this problem is considerable. In this situation, SBSO creates a significant number of scenarios for the mentioned problem, which increases the problem volume. To deal with this issue, certain studies, including⁹, have employed robust programming to model uncertainty. This strategy presents a scenario that diminishes the magnitude of the issue. To assess the condition of specific indices, such as flexibility, it is essential to analyze several scenarios of uncertainty, including the output power of RESs¹⁵. This cannot be examined within the comprehensive modeling of uncertainty that encompasses simply a single scenario. Therefore, to precisely compute the indicators and mitigate the problem’s complexity, uncertainties must be represented with approaches that utilize a minimal number of scenarios, a topic that has received limited scholarly attention.

• The problem of energy management of MGs has a non-linear formulation. To solve it, mathematical methods or non-hybrid evolutionary algorithms have been incorporated, which update the decision-making variables in a specific process. However, according to²³, the optimization of decision-making variables in several stages is capable of extracting a more optimal solution at a lower convergence time than non-hybrid solvers. So, according to²³, the genetic algorithm (GA) with a mutation process obtained a more optimal solution including a lower convergence time than the GA without mutation. Therefore, it is expected that the mentioned features are provided by hybrid algorithms, which have been discussed in less works.

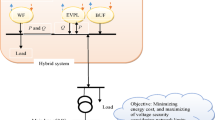
In an attempt to remove the first two research gaps, the present study analyzes the flexi-securable operation of an MMG with distributed generation (DG) and ESS based on DSO multi-criteria objectives using multi-objective EMS (refer to Fig. 1). This approach finds the minimum weighted sum of the expected value of MGs operating cost, MGs energy losses, and the voltage security index (VSI) to model economic, security, and operational indicators at the same time. Also, flexibility index models as a constraint. Constraints of the scheme include AC power flow formulation, operating limits, voltage stability, and flexibility of MGs, as well as operating models of DGs and ESSs. In this paper, a DG is presented in two types, RESs and non-renewable energy sources (NRESs). RES includes BEU, PV, and WT. NRES includes microturbine (MT). Also, ESS is in the form of battery and compressed air energy storage (CAES). Determining the compromise solution between different objectives of DSO is carried out using the fuzzy decision technique (FDT). To address and fill the third research gap, the unscented transformation (UT) approach is used to model the uncertainties of renewable power, energy price, and load. This method is one of the stochastic optimization techniques that can find a reliable optimal solution using the least possible number of cases²⁴. To cover the last research gap, this paper adopts the hybrid algorithm of Red Panda Optimization (RPO) and GWO to provide a solution to the problem. This solver updates the decision variables in two steps, so it is expected to provide an optimal solution with a small standard deviation for the final response. Lastly, the following is a summary of the proposed scheme’s novelties:

• Simultaneous energy management of MMGs with a multi-bus model according to the multi-criteria objectives of the DSO and MG operators (MGOs) to simultaneously improve the status of different technical and economic indices,

• Modeling the flexibility of MGs with WT, PV, and BEU renewable sources using non-renewable sources and storage devices,

• Considering capabilities of flexibility regulation and energy management of battery, CAES and NRES,

• Modeling the uncertain energy demand and production along with the energy price based on UT to make the MMG energy management problem smaller and calculate the flexibility index accurately, and

• Determining the optimal solution including a low variance in the final point by updating the decision variables in several steps using the hybrid GWO + RPO solver.

Fig. 1

The framework of multi-objective EMS for grid-connected MGs.

Part 2 provides the formulation of multi-objective energy management of the MMG along with the UT-based modeling of its uncertain parameters. Part 3 presents the method of extracting the compromise solution with the FDT and solving the problem with the hybrid GWO + DE algorithm. Numerical data derived from different cases are presented in Part 4, followed by the conclusions in Part 5.

The proposed operation of MMG based on multi-objective energy management

Problem formulation

Flexi-securable operation of several MGs at the same time is formulated here. The proposed scheme has an objective function of the minimization of voltage stability factor, energy cost and loss and is limited by optimal power flow formulation of MGs along with their security and flexibility limits in addition to the operating model of resources and storage devices. Therefore, the scheme model will be given as follows:

$$\min \,\,\,\,\,F = \xi_{Cost} Cost + \xi_{EEL} EEL + \xi_{VSI} VSI$$

(1)

$$Cost = \sum\limits_{w} {\pi_{w} \sum\limits_{i} {\sum\limits_{t} {\left( {\lambda_{t,w} P_{i,n = ref,t,w}^{DS} + \sum\limits_{n} {\left( {a_{i,n} + b_{i,n} P_{i,n,t,w}^{NR} + c_{i,n} \left( {P_{i,n,t,w}^{NR} } \right)^{2} } \right)} } \right)} } }$$

(2)

$$EEL = \sum\limits_{w} {\pi_{w} \sum\limits_{i} {\sum\limits_{n} {\sum\limits_{t} {\left( {P_{i,n,t,w}^{DS} + P_{i,n,t,w}^{WT} + P_{i,n,t,w}^{PV} + P_{i,n,t,w}^{BU} + P_{i,n,t,w}^{NR} + \left( {P_{i,n,t,w}^{DCA} - P_{i,n,t,w}^{CCA} } \right) + \left( {P_{i,n,t,w}^{DB} - P_{i,n,t,w}^{CB} } \right) - P_{i,n,t,w}^{C} } \right)} } } }$$

(3)

$$VSI = - \sum\limits_{w} {\pi_{w} \sum\limits_{i} {\sum\limits_{t} {WSI_{i,t,w} } } }$$

(4)

Subject to:

$$P_{i,n,t,w}^{DS} + P_{i,n,t,w}^{WT} + P_{i,n,t,w}^{PV} + P_{i,n,t,w}^{BU} + P_{i,n,t,w}^{NR} + \left( {P_{i,n,t,w}^{DCA} - P_{i,n,t,w}^{CCA} } \right) + \left( {P_{i,n,t,w}^{DB} - P_{i,n,t,w}^{CB} } \right) + \sum\limits_{m} {I_{n,m} P_{i,n,m,t,w}^{F} } = P_{i,n,t,w}^{C} \,\,\forall i,n,t,w$$

(5)

$$Q_{i,n,t,w}^{DS} + \sum\limits_{m} {I_{n,m} Q_{i,n,m,t,w}^{F} } \, = Q_{i,n,t,w}^{C} \,\,\,\,\,\,\,\forall i,n,t,w$$

(6)

$$\begin{aligned} & P_{{i,n,m,t,w}}^{F} = G_{{i,n,m}}^{F} \left( {V_{{i,n,t,w}} } \right)^{2} - V_{{i,n,t,w}} V_{{i,m,t,w}} \\ & \quad \left( {G_{{i,n,m}}^{F} \cos \left( {\phi _{{i,n,t,w}} - \phi _{{i,m,t,w}} } \right) + B_{{i,n,m}}^{F} \sin \left( {\phi _{{i,n,t,w}} - \phi _{{i,m,t,w}} } \right)} \right)\;\;\forall i,n,m,t,w \\ \end{aligned}$$

(7)

$$\begin{aligned} & Q_{{i,n,m,t,w}}^{F} = - B_{{i,n,m}}^{F} \left( {V_{{i,n,t,w}} } \right)^{2} + V_{{i,n,t,w}} V_{{i,m,t,w}} \\ & \quad \left( {B_{{i,n,m}}^{F} \cos \left( {\phi _{{i,n,t,w}} - \phi _{{i,m,t,w}} } \right) - G_{{i,n,m}}^{F} \sin \left( {\phi _{{i,n,t,w}} - \phi _{{i,m,t,w}} } \right)} \right)\;\;\forall i,n,m,t,w \\ \end{aligned}$$

(8)

$$\phi_{i,n,t,w} = 0\,\,\,\,\,\,\,\forall i,n = ref,t,w$$

(9)

$$V_{i,n,t,w} = V_{ref} \,\,\,\,\,\,\,\forall i,n = ref,t,w$$

(10)

$$\sqrt {\left( {P_{i,n,m,t,w}^{F} } \right)^{2} + \left( {Q_{i,n,m,t,w}^{F} } \right)^{2} } \le \overline{S}_{i,n,m}^{F} \,\,\,\,\,\,\,\,\forall i,n,m,t,w$$

(11)

$$\sqrt {\left( {P_{i,n,t,w}^{DS} } \right)^{2} + \left( {Q_{i,n,t,w}^{DS} } \right)^{2} } \le \overline{S}_{i,n}^{DS} \,\,\,\,\,\,\,\,\forall i,n = ref,t,w$$

(12)

$$V^{\min } \le V_{i,n,t,w} \le V^{\max } \,\,\,\,\,\,\,\forall i,n,t,w$$

(13)

$$\begin{aligned} & WSI_{{i,t,w}} = \left( {V_{{i,n,t,w}} } \right)^{4} - 4\left( {V_{{i,n,t,w}} } \right)^{2} \left( {R_{{i,n,m}} P_{{i,n,m,t,w}}^{F} + X_{{i,n,m}} Q_{{i,n,m,t,w}}^{F} } \right) \\ & \quad - 4\left( {X_{{i,n,m}} P_{{i,n,m,t,w}}^{F} - R_{{i,n,m}} Q_{{i,n,m,t,w}}^{F} } \right)^{2} \;\;\forall i,n = p,m = p - 1,t,w \\ \end{aligned}$$

(14)

$$WSI_{i,t,w} \ge WSI^{\max } \,\,\,\,\,\,\,\forall i,t,w$$

(15)

$$\left| {P_{i,n,t,w}^{DS} - P_{i,n,t,w = 1}^{DS} } \right|\, \le \varepsilon_{F} \,\,\,\,\,\,\,\forall i,n,t,w$$

(16)

$$\underline{P}_{i,n}^{NR} \le P_{i,n,t,w}^{NR} \le \overline{P}_{i,n}^{NR} \,\,\,\,\,\,\,\,\forall i,n,t,w$$

(17)

$$0 \le P_{i,n,t,w}^{CB} \le \,\overline{P}_{i,n}^{CB} x_{i,n,t}^{B} \,\,\,\,\,\,\,\forall i,n,t,w$$

(18)

$$0 \le P_{i,n,t,w}^{DB} \le \,\overline{P}_{i,n}^{DB} \left( {1 - x_{i,n,t}^{B} } \right)\,\,\,\,\,\,\,\forall i,n,t,w$$

(19)

$$\underline{E}_{i,n}^{B} \le \hat{E}_{i,n}^{B} + \sum\limits_{h = 1}^{t} {\left( {\eta^{CB} P_{i,n,h,w}^{CB} - \frac{1}{{\eta^{DB} }}P_{i,n,h,w}^{DB} } \right)} \le \,\overline{E}_{i,n}^{B} \,\,\,\,\,\,\,\forall i,n,t,w$$

(20)

$$0 \le P_{i,n,t,w}^{CCA} \le \,\overline{P}_{i,n}^{CCA} x_{i,n,t}^{CA} \,\,\,\,\,\,\,\forall i,n,t,w$$

(21)

$$0 \le P_{i,n,t,w}^{DCA} \le \,\overline{P}_{i,n}^{DCA} \left( {1 - x_{i,n,t}^{CA} } \right)\,\,\,\,\,\,\,\forall i,n,t,w$$

(22)

$$\underline{E}_{i,n}^{CA} \le \hat{E}_{i,n}^{CA} + \sum\limits_{h = 1}^{t} {\left( {\eta^{CCA} P_{i,n,h,w}^{CCA} - \frac{1}{{\eta^{DCA} }}P_{i,n,h,w}^{DCA} } \right)} \le \,\overline{E}_{i,n}^{CA} \,\,\,\,\,\,\,\forall i,n,t,w$$

(23)

Objective function

In this scheme, the sum of weighted functions including the expected value of operation cost of non-renewable sources and MGs (Cost), the expected energy loss (EEL) of MGs, and VSI are minimized to consider the economic, operation, and security objectives of DSO as the objective function (1). Cost formulation is stated in Eq. (2), which consists of two expressions. The first one gives the expected cost of purchasing energy of MGs from the upstream network (distribution network)²⁴. In the second expression, the operating cost or fuel of RESs is presented, which is a parabolic function²⁴. In Eq. (3), the EEL of all MGs is modeled, which is equal to the produced energy minus the consumed energy in MGs. The VSI is also given in Eq. (4). The present study uses the worst security index (WSI) to examine the voltage security of MGs²⁵, which is obtained for a poor bus (a bus with the lowest voltage magnitude) whose value is in the range [0, 1]; 0 represents voltage collapse, and 1 represents the no-load operating mode of the MG²⁵. Thus, to benefit high voltage security, a high value for WSI should be achieved. So, in Eq. (3), VSI is equal to the additive inverse of the sum of WSI because the term min is used for the objective function (F) in Eq. (1).

Constraints of MGs

Equations (5)-(16) express the constraints of MGs. In Eqs. (5)-(10), AC power flow formulation for MGs are the active-reactive power balance, (5) and (6)^26,27,28,29, the flow of active and reactive power on the MG lines, (7) and (8), voltage angle and amplitude of the slack bus, (9) and (10). The limitation of network operation is stated in constraints (11)-(13)^24,25. The boundary of capacity in the distribution line and post is formulated in Eqs. (11)-(12), and the boundary on voltage magnitude of the bus is modeled in Eq. (13) ^30,31,32,33. The lower boundary on the voltage magnitude is to prevent blackout caused by high voltage drop, and the upper boundary is to eliminate insulation breakdown caused by high overvoltage³. Also, MGs were linked to the distribution grid by a post located in the reference bus. So, P^DS and Q^DS appear only on the slack bus. Voltage security constraints are shown in (14) and (15). In constraints (14), the amount of WSI for a poor bus (p) is obtained based on the magnitude of voltage²⁵. To establish high voltage security in the network, the WSI must have a high value; therefore, a limitation similar to (15) is presented in the suggested scheme.

In Eq. (4), there are active power variables of RESs, including WT, PV, and BEU. The generated power generation by these resources is uncertain^34,35,36,37. Hence, real-time and day-ahead operation of MGs are not the same¹⁴. This issue, in turn, is likely to disturb the demand–supply balance in the real-time scheduling of the MG¹⁴. This condition is known as the lack of flexibility of MG³. To address this challenge, flexible resources such as storage devices and non-renewable units that can control their active power can compensate for the power variations of RESs in real-time operation¹⁴. This issue can also be estimated in such a way that the flexibility sources should compensate the RESs power oscillations in various cases in comparison to the case with the expected values ​​of the RESs power (here considered as scenario 1). Therefore, in this paper, the flexibility limit of MGs is formulated in constraint (16). So, if the MG active power deviation (the power flow on the distribution substation) is minimal in different cases than in scenario 1, then the MG can inject/receive both day-ahead and real-time almost constant active power into/from the distribution network. This condition corresponds to high flexibility in MG. In Eq. (16), the parameter ε_F expresses the flexibility tolerance; ε_F = 0 shows 100% flexibility, and its high value represents lower flexibility.

Operating formulation of resources and storage systems

Concerning the operating model of RESs, it is assumed that they supply a specific active power into MG. Therefore, their active power generation is considered as a parameter in Eq. (4)^38,39,40,41. In Eq. (17), the non-renewable source operating model is included, referring to the active limitation of the power output of such power sources²⁴. In constraints (18)-(20), the battery operating model is presented. In Eqs. (18)-(19), the battery charge and discharge rate limits are presented, respectively. These limits respectively refer to the maximum capability to control the active power of the storage in charge and discharge operation^42,43,44,45. In Eq. (20), the limit of stored energy in the battery is given³. In order for the useful life of the battery not to be severely reduced during charging and discharging, the state of discharge (DOD) should be less than a certain limit, such as 0.9. DOD is equal to 1 minus the ratio of the energy stored in the battery to the maximum battery capacity. To estimate the DOD limit, it is necessary that the energy stored in the battery is greater than a certain limit. This is taken into account in Eq. (20). In this regard, the battery energy must be greater than $\underline{E}_{{}}^{B}$. $\underline{E}_{{}}^{B}$ is also about 10 to 20 percent of the maximum battery capacity. Finally, the CAES operating model is presented in constraints (21)-(23)⁴⁶. Its formulation is also the same as the battery performance model. In CAES charging mode, an electric motor receives electrical energy from the grid and stores it as compressed air in a tank. In the CAES discharge mode, the compressed air hitting the generator turbine causes the generator to produce electrical energy and injects this energy into the grid⁴⁶. Therefore, the boundary on the active power of the electric motor for producing compressed air is stated in (21). In (22), the limitation of the generator’s active power output is presented. In (23), the limitation of the compressed air stored in the CAES tank is included. In formulation (18)-(23), the binary variables x^B and x^CA are to prevent the simultaneous charge and discharge of the battery and CAES, respectively. Thus, if they have a value of 1 (0), the charging (discharging) mode is adopted for the mentioned storage devices. The state of charge (SOC) is equal to the ratio of the stored energy to the maximum capacity of the storage device. If constraints (20) and (23) are divided by the maximum capacity of the storage device, the SOC constraint will be presented in the aforementioned relations. Therefore, if the stored energy constraint is satisfied, then the SOC constraint is also satisfied.

UT-based uncertainty modeling

The problem (1)-(23) is subject to uncertainties related to the load, P^C and Q^C; renewable power, P^WT, P^PV, and P^BU; and energy price, λ. In this scheme, to evaluate the flexibility of MGs, different scenarios of P^WT, P^PV, and P ^BU need to be evaluated. Therefore, in the stochastic optimization section, it is incorporated to provide a proper modeling of the uncertain parameters. As another point, the problem is an operation problem. As the executive step in such problems is small, short computational time is of particular importance¹⁵. To achieve this purpose, the size of the problem should be reduced, so UT-based stochastic optimization⁴⁷ has been adopted for uncertainty modeling, in which the least possible number of scenarios can extract a reliable optimal solution. Consequently, for b uncertainty parameters, 2b + 1 scenarios will be required. For the proposed scheme, b = 6, it means that 13 scenarios are needed.

Here we present the problem in the form of y = f(z), where y ∈ R^r shows an uncertain output vector that has r entries while z ∈ Rⁿ is a vector containing uncertain inputs. Moreover, mean and covariance of z are given by μ_z and σ_z. Symmetric and asymmetric entries of the covariance can be adopted when one aims to obtain the covariance and variance of uncertainties. Besides, the UT technique was used to calculate the average (μ_y) and covariance (σ_y) of outputs⁴⁷. The step-by-step process of problem solution is provided as follows.

Step 1: Input 2b + 1 samples (z_s) from the uncertainty data:

$$z_{0} = \mu_{z}$$

(24)

$$z_{s} = \mu_{z} + \sqrt {\frac{b}{{1 - W^{0} }}\sigma_{z} } \,\,\,\,\,\,\,\forall s = 1,2,...,b$$

(25)

$$z_{s} = \mu_{z} - \sqrt {\frac{b}{{1 - W^{0} }}\sigma_{z} } \,\,\,\,\,\,\,\forall s = 1,2,...,b$$

(26)

W⁰ represents the weight of μ_z.

Step 2: Check the weighting coefficient of each of scenarios:

$$W^{0} = W^{0}$$

(27)

$$W_{s} = \frac{{1 - W^{0} }}{2n}b\,\,\,\,\,\,\,\forall s = 1,2,...,b$$

(28)

$$W_{s + b} = \frac{{1 - W^{0} }}{2b}\,\,\,\,\,\,\,\forall s + b = b + 1,b + 2,...,2b$$

(29)

$$\sum\limits_{s = 1}^{b} {W_{s} } = 1$$

(30)

Step 3: Input 2b + 1 scenarios from the nonlinear function so that output samples are found based on Eq. (31).

$$y_{s} = f(z_{s} )$$

(31)

Step 4: Check μ_y and σ_y for output variable, θ.

$$\mu_{y} = \sum\limits_{s = 1}^{b} {W_{s} \theta_{s} }$$

(32)

$$\sigma_{y} = \sum\limits_{s = 1}^{b} {W_{s} \left( {\theta_{s} - \mu_{y} } \right)} - \left( {\theta_{s} - \mu_{y} } \right)^{T}$$

(33)

In this article, the UT technique was used to model uncertainties. Scheme has 6 uncertain parameters. Therefore, UT method creates 13 scenarios. In other words, it creates 13 different values ​​based on relations (24) to (26) for each uncertainty. Then UT method applies these 13 scenarios to the problem. This means that problem (1)-(23) receives 13 scenarios from the UT method, and then extracts the optimal solution for the 13 scenarios. Finally, based on Eq. (1), the expected value of the objective function and variables are calculated.

Solution procedure

Determining a compromise solution using FDT

Problem (1)-(23) is a multi-objective optimization^{48,49,50,51,52} formulated as the Pareto technique using the sum of weighted functions⁵³. In Eq. (1), ξ_Cost, ξ_EFL, and ξ_VSI are respectively the weighting coefficients of Cost, EEL, and VSI functions, the sum of which should be equal to 1⁵³. For various values ​​of ξ_Cost, ξ_EFL, and ξ_VSI, different values ​​are found for the mentioned functions. Plotting these values ​​of the objective functions in a 3D coordinate shows the Pareto front of the suggested scheme. In the following, the FDT helps to extract an optimal compromise solution between different objective functions¹. The details of the FDT process are shown in Algorithm 1. In this algorithm, F^min and F^max are the minimum and maximum values of an objective function. These parameters ​​for Cost, EEL, and VSI functions for three problems are obtained with the weighting coefficients ξ_Cost = 1, ξ_EEL = 1, and ξ_VSI = 1, respectively.

Algorithm 1

FDT Steps.

Problem solution using GWO + RPO

Problem (1)-(23) is based on mixed-integer nonlinear programming (MINLP). To address the last research stated in subsection 1.3, and to estimate the last contribution, introduced in Sect. 1.4, the hybrid algorithm of GWO⁵⁴ and RPO⁵⁵ were adopted for solving the problem. Both GWO and RPO algorithms, according to^54,55, have a favorable ability in solving intricate engineering problems. So, combining these two algorithms helps find the optimal solution to, which will be examined in subsection 4.2.

When the evolutionary algorithm or the GWO + DE solver is used for solving the problem, this algorithm initially selects N (size of the population) random values for P^NR, P^CCA, P^DCA, x^CA, P^CB, P^DB, and x^B based on constraints (34)-(40). These variables refer to the decision variables^{56,57,58,59,60}. Then, these N values ​​for Cost, EEL, VSI, WSI, Q^DS, P^DS, Q^F, P^F, ϕ, and V (dependent variables^{61,62,63,64,65}) are calculated by (2)-(10) and (14). To solve AC power flow equations, (4)-(10), the backward-forward load flow approach⁶⁶ is applied. To estimate the technical limitations of MGs, (11)-(13) and (15)-(16), and the energy stored in storage devices, (20) and (23), the penalty function method⁶⁷ is adopted. In this technique, the penalty function for the limit a ≤ b is equal to μ.max (0, a − b), where μ ≥ 0 as a decision variable denotes the Lagrange multiplier. Then, in this technique, the fitness function^68,69 will be equal to the sum of the penalty functions and objective function F in the form of (41). In the next step, N values are calculated for FF, then its optimal (minimum) value is determined. Next, GWO + RPO is in charge of updating the decision variables. First, RPO calculates new values ​​for N decision variables based on their allowed limits and the optimal FF in previous step. Next, N values ​​for FF and dependent variables are obtained. In the following, GWO updates decision variables using the optimal FF obtained from RPO. The mentioned process advances until the problem converges. The convergence is assumed to be achieved after the maximum update iterations (iter_max). Eventually, Fig. 2 illustrates the solution flowchart. Finally, to implement the proposed formulation on the network, the network needs to have an intelligent platform. An smart network has intelligent algorithms and telecommunication devices^{70,71,72,73,74}.

$$P_{i,n,t,w}^{NR} \in \left[ {\underline{P}_{i,n}^{NR} \,\,\overline{P}_{i,n}^{NR} } \right]\,\,\,\,\,\,\,\,\forall i,n,t,w$$

(34)

$$P_{i,n,t,w}^{CCA} \in \left[ {0\,\,\overline{P}_{i,n}^{CCA} } \right]\,\,\,\,\,\,\,\,\forall i,n,t,w$$

(35)

$$P_{i,n,t,w}^{DCA} \in \left[ {0\,\,\overline{P}_{i,n}^{DCA} } \right]\,\,\,\,\,\,\,\,\forall i,n,t,w$$

(36)

$$x_{i,n,t}^{CA} \in \left\{ {0,1} \right\}\,\,\,\,\,\,\,\forall i,n,t,w$$

(37)

$$P_{i,n,t,w}^{CB} \in \left[ {0\,\,\overline{P}_{i,n}^{CB} } \right]\,\,\,\,\,\,\,\,\forall i,n,t,w$$

(38)

$$P_{i,n,t,w}^{DB} \in \left[ {0\,\,\overline{P}_{i,n}^{DB} } \right]\,\,\,\,\,\,\,\,\forall i,n,t,w$$

(39)

$$x_{i,n,t}^{B} \in \left\{ {0,1} \right\}\,\,\,\,\,\,\,\forall i,n,t,w$$

(40)

$$\begin{aligned} & FF = F + \sum\limits_{{i,n,m,t,w}} {\bar{\mu }_{{i,n,m,t,w}}^{F} \max \left( {0,\sqrt {\left( {P_{{i,n,m,t,w}}^{F} } \right)^{2} + \left( {Q_{{i,n,m,t,w}}^{F} } \right)^{2} } - \bar{S}_{{i,n,m}}^{F} } \right)} \\ & \quad + \sum\limits_{{i,t,w}} {\bar{\mu }_{{i,n = ref,t,w}}^{{DS}} \max \left( {0,\sqrt {\left( {P_{{i,n = ref,t,w}}^{{DS}} } \right)^{2} + \left( {Q_{{i,n = ref,t,w}}^{{DS}} } \right)^{2} } - \bar{S}_{{i,n = ref}}^{{DS}} } \right)} \\ & \quad + \sum\limits_{{i,n,t,w}} {\left( {\underline{\mu } _{{i,n,t,w}}^{V} \max \left( {0,V^{{\min }} - V_{{i,n,t,w}} } \right) + \bar{\mu }_{{i,n,t,w}}^{V} \max \left( {0,V_{{i,n,t,w}} - V^{{\max }} } \right)} \right)} \\ & \quad + \sum\limits_{{i,t,w}} {\underline{\mu } _{{i,t,w}}^{{WSI}} \max \left( {0,WSI^{{\max }} - WSI_{{i,t,w}} } \right)} \\ & \quad + \sum\limits_{{i,n,t,w}} {\bar{\mu }_{{i,n,t,w}}^{F} \max \left( {0,\left| {P_{{i,n,t,w}}^{{DS}} - P_{{i,n,t,w = 1}}^{{DS}} } \right|\, - \varepsilon _{F} } \right)} \\ & \quad + \sum\limits_{{i,n,t,w}} {\left( \begin{gathered} \underline{\mu } _{{i,n,t,w}}^{{ECA}} \max \left( {0,\underline{E} _{{i,n}}^{{CA}} - \hat{E}_{{i,n}}^{{CA}} - \sum\limits_{{h = 1}}^{t} {\left( {\eta ^{{CCA}} P_{{i,n,h,w}}^{{CCA}} - \frac{1}{{\eta ^{{DCA}} }}P_{{i,n,h,w}}^{{DCA}} } \right)} } \right) + \hfill \\ \bar{\mu }_{{i,n,t,w}}^{{ECA}} \max \left( {0,\hat{E}_{{i,n}}^{{CA}} + \sum\limits_{{h = 1}}^{t} {\left( {\eta ^{{CCA}} P_{{i,n,h,w}}^{{CCA}} - \frac{1}{{\eta ^{{DCA}} }}P_{{i,n,h,w}}^{{DCA}} } \right)} - \,\bar{E}_{{i,n}}^{{CA}} } \right) \hfill \\ \end{gathered} \right)} \\ & \quad \, + \sum\limits_{{i,n,t,w}} {\left( \begin{gathered} \underline{\mu } _{{i,n,t,w}}^{{EB}} \max \left( {0,\underline{E} _{{i,n}}^{B} - \hat{E}_{{i,n}}^{B} - \sum\limits_{{h = 1}}^{t} {\left( {\eta ^{{CB}} P_{{i,n,h,w}}^{{CB}} - \frac{1}{{\eta ^{{DB}} }}P_{{i,n,h,w}}^{{DB}} } \right)} } \right) + \hfill \\ \bar{\mu }_{{i,n,t,w}}^{{EB}} \max \left( {0,\hat{E}_{{i,n}}^{B} + \sum\limits_{{h = 1}}^{t} {\left( {\eta ^{{CB}} P_{{i,n,h,w}}^{{CB}} - \frac{1}{{\eta ^{{DB}} }}P_{{i,n,h,w}}^{{DB}} } \right)} - \,\bar{E}_{{i,n}}^{B} } \right) \hfill \\ \end{gathered} \right)} \\ \end{aligned}$$

(41)

Fig. 2

Flowchart for RPO + GWO algorithm.

Numerical results

Data

The scheme is used on a distribution system with IEEE 33-bus and 69-bus radial microgrids, namely, MG1 and MG2^66,67 as shown in Fig. 3. The base voltage for these two MGs is 12.66 kV. The base power is also assumed to be 1 MVA. The data of the lines and the distribution substations of the MGs are reported in^66,67. The voltage magnitude and phase angle for the slack bus are respectively 1 p.u. and zero radians. The voltage magnitude has allowed boundaries of [0.9 10.1] p.u.^{75,76,77,78,79}. The peak load data of consumers in different buses are also presented in^66,67. Hourly load data equals the multiplication of peak load and daily load factor^80,81,82. The daily load factor curve can be found in Fig. 4. Energy price is 16, 24, and 30 $/MWh for [1:00 7:00], [8:00 16:00] and [23:00 24:00], and [17:00 22:00], respectively¹⁸. Also, WSI^max is equal to 0.8²⁴, and to reach high flexibility, the parameter ε_F is considered equal to 0.03 MW. In the mentioned MGs, a renewable source, i.e., microturbine (MT) is used, the location of which is shown in Fig. 3. Its minimum and maximum active power output are zero and 0.5 MW, respectively. Coefficients a, b, and c in its fuel cost are equal to $100, $20/MWh, and 0.002 $/MWh², respectively²⁴. The RESs used in MGs include WT, PV, and BEU, whose locations are shown in Fig. 3. Their capacity is equal to 0.5 MW. The daily curve of the active generation power of these sources can be obtained by multiplying the rating of sources and the daily curve of the power generation rate of RESs^83,84,85. This rate is plotted in Fig. 4^2,14. A 4 MWh battery with charging and discharging efficiencies of 92% and 93% was installed in MGs ¹⁴. The minimum storable energy and its initial energies are 0.4 MWh and 0.4 MWh, respectively. Its charging and discharging rates are 1 MW. Such specifications are assumed for CAES, except for its charging and discharging efficiencies are 75% and 76%⁴⁶. The location of batteries and CAES is given in Fig. 3.

Fig. 3

The test system with 33- and 69-bus MGs^66,67.

Fig. 4

Hourly rate value of RESs power and network load ²⁴.

Results and discussion

Scheme with its information given in part 4.1 and RPO + GWO algorithm is coded and simulated in the MATLAB software environment. Total number of variables (equations) for the proposed scheme with case study in Sect. 4.1 is 414,027 (604,660).

A) Determining the compromise point between operating, economic, and security goals: Table 2 provides the Pareto front of the proposed scheme for ε_F = 0.03 MW. In this table, six values ​​are included for each weight coefficients, which are equal to 0, 0.25, 0.33, 0.5, 0.75, and 1. For the weighted coefficients ξ_Cost = 1, ξ_EFL = 1, and ξ_VSI = 1, the minimum value of Cost, EEL, and VSI has been obtained, which are equal to $1468.7, 2.151 MWh, and − 44.72, respectively. Also, for ξ_Cost = 1, the maximum values ​​of EEL and VSI have been extracted, which are 2.913 MWh and − 41.08, respectively. The maximum value of Cost is $1985.9, which is obtained for ξ_VSI = 1. So, the boundary of changes (the difference between upper and lower values) for Cost, EEL, and VSI is equal to $517.2, 0.762 MWh, and 3.64, respectively. As another point, the process of changes (in terms of increase or decrease) of the mentioned functions based on Table 2 is not the same. For example, generally, as EEL increases, Cost decreases. This is because, to minimize the cost, RES and non-RES and storage located at the point of consumption should feed high energy into the network. Nevertheless, this case increases the current flow from their side to the upstream network, which further increases the power and energy losses in MGs. In the next step, FDT is used to extract the compromise solution between EEL, Cost, and VSI, the process of which is presented in Algorithm 1.

Table 2 Pareto front in the scheme for ε_F = 0.03 MW.

The results of FDT obtained from different solvers and their convergence status for ε_F = 0.03 MW are presented in Table 3. The report for GWO + RPO, GWO, RPO solvers, the krill herd optimizer (KHO)⁸⁶, the sine–cosine algorithm (SCA)⁸⁷, the teaching–learning-based optimization (TLBO)⁸⁸, particle swarm optimizer (PSO)⁶⁷, and GA²³ are described. The population size and maximum update iterations are adopted as 80 and 4000, respectively. The rest of parameters of the algorithms can be found by referring to^{23,54,55,67,86,87,88}. This problem was solved 25 times with each algorithm to find the standard deviation of the final response. The hybrid GWO + RPO algorithm at the compromise point was able to obtain values ​​of $1591.6, 2.357 MWh, and − 44.28 for Cost, EEL, and VSI, respectively, as is shown in Table 3. Juxtaposing Tables 2 and 3, the values ​​of these functions at the compromise point are close to their minimum value. So, Cost at the compromise point is far from its minimum value that was roughly 23.8% ((1591.6–1468.7)/517.2). This value for EEL and VSI is 27% and 12.1%, respectively. It should be noted that the GWO + RPO algorithm has extracted this compromise point for 1264 convergence iterations, which corresponds to the computing time of 129.1 s. Based on Table 3, non-hybrid algorithms have obtained higher values ​​for the mentioned functions in more convergence iterations and longer computing time than the hybrid GWO + RPO solver. Therefore, among the advantages of the mentioned hybrid algorithm is its high convergence speed than non-hybrid algorithms. As another point, the standard deviation of the final response with GWO + RPO is about 0.97%, while it is more than 1.6% for other algorithms. Another advantage of the mentioned hybrid algorithm is the low dispersion in its final point. This confirms the last contribution presented previously in subsection 1.4. The proposed scheme is solved by evolutionary algorithms. For these algorithms, there is a maximum convergence iteration, so that the solution results are printed after the last iteration of the solution steps. The maximum convergence iteration is considered to be 4000 for all evolutionary algorithms in this section. The convergence iteration which the algorithm reaches the convergence point is calculated in Table 3. At the convergence point, the fitness function, Eq. (41), should be the same in the new iteration compared to the previous iteration. For example, in Table 3, the convergence iteration for GWO + RPO is 1264. This means that the fitness function is the same in iterations 1264 to 4000 in the GWO + RPO algorithm. Therefore, the lowest iteration is considered as the convergence iteration, and for iterations higher than 1264, there was a convergence point for the mentioned solver.

Table 3 Convergence situation in the compromise solution based on different solvers and uncertainty modeling for ε_F = 0.03 MW.

The proposed design with the formulation in section "Numerical results" is a non-linear optimization, which is non-convex because of the use of power flow equations. Special solvers for this problem generally obtain the local optimal solution. Therefore, in this problem, an algorithm that obtains the most optimal solution is suitable. For the proposed scheme, a solver that obtains the minimum point for the objective function is suitable. In Table 3, the numerical results of different solution algorithms were presented. Finally, it was observed that the hybrid algorithm of GWO + RPO has the minimum value for the objective function. It can be stated that the distance of the solution obtained in the combined algorithm from the global optimal point is less than other algorithms. Hence, it will be a popular solver for the proposed nonlinear problem.

Table 3 shows the compromise point results obtained by the hybrid GWO + RPO algorithm for modeling uncertainties with UT and SBSO. According to subsection 2.2, there are 13 scenarios with UT for the suggested scheme. The results of the SBSO method are also presented for 40, 60, 80, and 100 scenarios in this table. SBSO is according to the combination of Monte Carlo simulation and the Kantorovich approach. Monte Carlo simulation produces high scenario samples, and the Kantorovich approach is a scenario reduction technique. Details of this SBSO are given in⁸⁹. Based on Table 3, SBSO results have small changes for the number of scenarios above 80 and it is close to UT results. So, the UT has obtained a reliable solution with 13 scenarios, while SBSO achieves the mentioned conditions with at least 80 scenarios. Therefore, according to Table 3, the UT by reducing the problem volume requires a lower computational time compared to SBSO. This also confirms the third contribution presented in subsection 1.4.

The proposed scheme in Section "Numerical results" is a comprehensive model that can be used on different information of network, storages and units. In the present article, evolutionary algorithm helps solve the problem. This algorithm first gives different values ​​to decision variables and then obtain the amount of dependent variables. Next, it determines the best value of the decision variables using the most optimal fitness function. This advances to the convergence point and terminates. The only problem is the increase in computing time for solving the proposed scheme in large comparative networks. This issue can be solved with powerful computing systems. This issue will also increase the cost of solving the problem. Of course, this condition exists for different solvers.

B) Analysis of the operating status of MGs: Figs. 5 and 6 show the performance curves of sources and storage devices, as well as the state of operation of MGs 1 and 2 for ε_F = 0.03 MW. Figures 5a and 6a depict the expected daily curve of the active power of sources and storage in MG1 and MG2, respectively. Based on these figures and their comparison with Fig. 4, it can be seen that RESs such as WT, PV, and BEU systems inject their maximum active power into MG every hour. For example, in MG1, there is a PV with a capacity of 0.5 MW, and its power rate at 12:00 is equal to 1 based on Fig. 4. In Fig. 5a, PV injects active power of 0.5 MW to MG1 at 12:00. This is also true for BEU and WT. In the case of MTs, they inject active power equal to their maximum capacity to MG during 8:00–00:00. There are two MTs in MG1 with a capacity of 0.5 MW. Therefore, they inject active power of 1 MW to MG1 during the mentioned hours. It is noteworthy that in these hours the price of energy is more than the price of fuel of the MT (20 $/MWh according to subsection 4.1). Therefore, to minimize Cost, consumers are expected to receive energy from MT. In the hours 1:00–7:00, when the price of energy is lower than the fuel price of MT, MTs inject low active power. It should be noted that if only Cost was equal to the objective function, MTs would not produce power during these hours. However, as the goals of the problem are extracting the optimal states of operation, flexibility, and voltage security, the MTs are not switched off during the mentioned hours and they always inject active power to the MGs. Concerning the operation of storage devices, batteries and CAES perform charging operations during low energy price hours (1:00–16:00 and 23:00–00:00) and receive active power from MGs. The amount of active power they receive from MGs in the hours of 1:00–7:00 is more than in the hours of 8:00–16:00 and 23:00–00:00. This is because, according to subsection 4.1, the price of energy for the hours 1:00–7:00 (8:00–16:00 and 23:00–00:00) is $16 (24)/MWh. Since their performance should lead to Cost minimization, it is expected that storage devices will receive more power from MGs during the hours of 1:00–7:00 than during other hours. Of course, if the only objective function was equal to Cost, it would be possible for the storage devices to be switched off during the hours of 8:00–16:00 and 23:00–00:00. Nonetheless, the presence of flexibility, operation, and voltage security indicators in the proposed problem has prevented the outage of storage devices during the mentioned hours. For example, according to the performance curve of RESs in Fig. 5a and 6a, these sources altogether generate active power in all operating hours. Therefore, there is uncertainty in the power output of these sources at all hours, and there is a possibility of a lack of flexibility in all operating hours. Hence, flexible sources such as MT, battery, and CAES can control power at all hours and do not switch off to boost the flexibility of MGs. In continuation of the operation of storage devices, they inject active power to MGs during peak hours, 17:00–22:00, in the case the price of energy is the highest. This is how they work to minimize Cost, EEL, and VSI functions. In addition to this, since the capacity of CAES and batteries is equal, but at all hours, the active power of CAES is less than that of batteries, the efficiency of CAES is lower than that of batteries, therefore the energy loss is higher in them. So, CAES exchange less energy with MGs than batteries.

Fig. 5

Hourly curve of (a) active power for storage and sources, (b) station apparent power, and (c) network power loss, and (d) expected curve of voltage profile at 20:00 for MG1 and ε_F = 0.03 MW.

Fig. 6

Hourly curve of, (a) active power for storage and sources, (b) station apparent power, and (c) network power loss, and (d) expected curve of voltage profile at 20:00 for MG2 and ε_F = 0.03 MW.

Figures 5b and 6b show the daily curve of apparent power passing through the distribution substation in MG1 and MG2 for two case studies: power flow and the suggested scheme. As the figures show, during 1:00–7:00, the apparent power in the distribution substation in the proposed scheme may be more than that in the power flow studies. This is more evident for MG2 because according to Figs. 5a and 6b, the storage devices are in charging mode during these hours, and the sources also produce low active power. However, in other hours, the scheme succeeded to decrease the apparent power of MGs significantly in comparison to power flow cases. This issue shows the ability of the proposed plan to release the capacity of MGs to feed more consumers. Figures 5c and 6c illustrate the expected daily curve of active power loss of MGs for the aforementioned study cases. Based on these figures, as the active power consumption of MGs is high in the hours of 1:00–7:00 based on Figs. 5a and 6a, power losses in these hours are higher for the proposed scheme than that of power flow studies. However, in other hours, the opposite is the case. The voltage profiles of MGs 1 and 2 at peak hour (20:00) are drawn in Figs. 5d and 6d, respectively. Based on these figures, the scheme provides a smoother voltage profile (that is, the distance between the maximum and minimum voltage is low) compared to power flow studies. This is due to the injection of the active power of sources and storage during peak hours according to Figs. 5a and 6a. Based on Figs. (5) and (6), it can be stated that the performance of renewable sources and storage devices has led to a decrease in apparent power and power losses than in power flow studies. Also, the smoother voltage profile is obtained. Such conditions provide the distribution lines and substations free capacity in all operating hours. Therefore, these MGs is called to feed more consumers.

C) Evaluation of technical and economic indicators of MGs: To examine the potential of scheme and the effectiveness of power sources and storage devices concerning operation, flexibility, security, and economy, the following study cases are analyzed:

• Case I: Load flow study

• Case II: Power flow study on MGs that contain only RESs

• Cases III, IV, V: Optimal power flow analysis of Case II but taking into account only MTs, battery storage, or CAES

• Case VI: The suggested scheme

The results of this section for operation indicators (maximum over-voltage drop (MOV) and voltage drop (MVD), and EEL), flexibility (minimum value of ε_F), economy (Cost), and voltage security (|VSI| and weak bass) for different study cases for MG1 and MG2 are given in Table 4. Values ​​of operation, economic, and security indicators are presented for ε_F = 0.03 MW. As the table tabulates, RESs (Case II) are more capable than that in Case I compared to other elements of MGs in terms of reducing energy costs and energy losses. This is because their capacity is high, and also their operating cost is negligible (zero). Among MTs, CAES and batteries, batteries (Case IV) have had the greatest reduction in energy cost compared to Case II. In CAES, energy losses are more than batteries, and in MTs, there is an operating cost for energy production. Therefore, compared to MTs and CAES, batteries provide a greater reduction in energy cost than in case II. MTs are only active power injectors, but storages are in charge mode in some hours, and in discharge mode in other hours. Therefore, MTs (Case III) have led to a greater reduction in energy losses compared to Case II. In terms of voltage security, the weak bus in MG1 is Bus 65 for different study cases, but in MG1, it is Bus 18 or Bus 33 for different study cases. Due to their higher capacity compared to other elements, RESs (Case II) have succeeded to obtain a higher VSI than other elements of MGs (compared to cases I, III, IV, and V). In terms of reducing voltage drop, renewable and non-renewable sources together (Case III) reduced the voltage drop the most compared to cases I-II and IV-V, which is more evident in MG 2. This has been achieved by creating a negligible maximum overvoltage (0.001 p.u.). Finally, the simultaneous presence of power sources and storage devices, taking into account their performance based on the proposed scheme, (1)-(23), or Case VI, is more capable than other study cases of improving economic, operation, and voltage security indicators. So, the present scheme (Case VI) reduced the energy cost by about 30.3% ((1426.8–994.3)/1426.8) and 59.1% decrease for MG 1 and MG 2, respectively, compared to Case I. The energy losses in Case VI compared to Case I for MG 1 and MG 2 have decreased by about 45.6% and 46.7%, respectively. VSI has been improved by 10.8% and 10.3% respectively for two MG 1 and MG 2 in the mentioned conditions. MVD for the mentioned MGs is decreased by approximately 50% and 46.2%, respectively. Further, based on Table 4, the batteries have a better ability to improve flexibility than CAES and MTs because they have the lowest flexibility tolerance value (ε_F) among cases III–V. However, the present scheme (Case VI) depending on non-RES and storage equipment achieved 100% flexibility (ε_F = 0) for MGs.

Table 4 Value of technical and economic indicator for various cases and MGs.

Figure 7 depicts Cost, EEL, and |VSI| curves with respect to flexibility tolerance, where the highest energy cost and energy losses, and the lowest VSI have been obtained in the case of 100% flexibility (ε_F = 0). In this situation, based on Figs. 5a and 6a, it is expected that the storage can control higher amounts of active power in charging mode during 8:00–16:00 and 23:00–00:00 compared to the case the flexibility is removed. This increases the energy consumption of MGs compared to the condition of eliminating flexibility, which increases the cost of energy and energy losses. Also, based on Eq. (14), the increase in power consumption (generation) decreases (increases) the WSI. Therefore, as in the mentioned conditions, the energy consumption increases compared to the case of removing flexibility, and the VSI has the lowest value. Next, with the increase of ε_F, the energy cost and energy losses decrease compared to the case of ε_F = 0, but VSI increases. In general, with the increase of flexibility tolerance, the status of economic, operation and voltage security indicators in microgrids are improved. Because increasing flexibility tolerance means reducing the importance of flexibility in scheme. Therefore, the performance of storage systems and production units in the MGs is to improve other technical and economic indicators.

Fig. 7

Curve of (a) Cost (b) EEL, and (c) |VSI| in flexibility tolerance (ε_F) for all MGs.

D) Sensitivity analysis: In Table 5, the effect of changes for price of energy, power of RESs, and load on the cost of operation, energy loss and voltage stability has been examined. In this table, the expression ψ is the rate of change of a parameter. For example, ψ = 0.1 means that the parameter value such as price of energy, power of RESs, and load has been increased by 10% compared to the data in Sect. 4.1. As the table tabulates, increasing the load results in escalated operating costs and energy losses; and the voltage security situation becomes weaker. This is due to the increase in energy consumption in MGs. By increasing the capacity of renewable sources, the operating cost and energy losses are reduced, and the voltage security situation is improved. Finally, increased energy price increases the operating cost and energy losses, but the security of the voltage remains unchanged. Based on this table, for 10% changes in price of energy, power of RESs, and load, the operating cost changes by 8.1%, − 6.2% and 7.2%, respectively. According to the mentioned conditions, the energy loss (voltage security) varies around 3.2% (0.9%), − 2.1% (0.6%) and 0.6% (0%), respectively. The positive (negative) sign in these values ​​indicates the increase (decrease) of the objective function for changes in the mentioned parameters.

Table 5 Sensitivity of objective functions to changes in load, renewable power and energy price for ε_F = 0.03 MW.

Conclusion

In this paper, the economic operation of MMGs in the presence of RES and non-RES, in addition to storage, was expressed based on the flexibility and voltage security using the multi-objective EMS. The proposed scheme minimized the sum of the weighted functions of the expected operating cost of the MG and non-renewable sources, the expected energy loss, and the voltage security index. The scheme was also constrained by optimal power flow constraints of the MGs, the boundary of their flexibility, voltage security, and the formulation of the operation of sources and storage devices. In this study, to accurately evaluate flexibility, stochastic optimization was adopted to give a suitable modeling the uncertain quantities including the amount of load, energy price, and renewable power. Also, to reduce the volume of the problem, stochastic optimization was based on the UT. Moreover, to extract a reliable optimal solution, the hybrid GWO + RPO algorithm was adopted to address the problem. As the findings report, the mentioned hybrid algorithm can obtain the most optimal and accurate solution at a higher convergence speed compared to non-hybrid algorithms so that the standard deviation of its final response is about 0.97%. Power sources compared to storage led to a greater reduction in energy losses and voltage drop and the greatest increase in voltage security. Compared to non-RES, storage equipment and RESs provided the greatest reduction in energy costs. Storage devices, especially batteries, are more capable of improving MG flexibility than non-renewable sources. In total, the simultaneous presence of sources and storage in the suggested scheme reduced the energy cost by 30–60% compared to load flow analysis. It has reduced energy loss and voltage drop by about 46% and 46%-50% than in the power flow case. The voltage security has been improved by about 10.5%, and 100% flexibility conditions can be reached by the proposed scheme.

It is noteworthy that in this article, the market model for the proposed plan was not considered. Only the MG operator expects to receive energy from the distribution network at the lowest cost to upgrade MG’s energy management. But, the conceptual framework developed in this manuscript is very similar to existing structures in peer-to-peer markets. It can be said that these markets on a retail-scale can be developed on a wholesale-scale as well. In this regard, power and information flows can be modeled and implemented according to the mentioned objectives. Therefore, this issue is considered as future work. In this article, MGs are connected to the distribution system. They are connected to each other through the distribution network. So that if the consumed energy in one MG is high, and the produced energy in the other microgrid is high, these two MGs can establish optimal energy management by exchanging power between themselves through the distribution network. But, implementing a shared energy storage model between MGs can significantly enhance overall system efficiency. By allowing multiple MGs to share resources, it reduces the need for each MG to maintain high storage levels, thereby optimizing costs and improving resilience during peak demand periods. This issue is considered as the future work. In this article, the capability of resources and storage in electricity energy management of microgrid was investigated. In other words, the mentioned elements were used to improve electrical indicators such as voltage profile, voltage security, flexibility and other things. But, implementing multiple energy sources, such as thermal energy storage alongside electricity, can improve the flexibility and operational resilience of MGs. This approach is increasingly being adopted in complex, multi-energy grids to enhance overall system performance. This scheme is considered as the future work. In the proposed design, the charging and discharging rate limit, limitations of DOD and the energy stored in the battery are considered. However, the charging and discharging performance of the battery can reduce the useful life of the battery and lead to a cost for the battery. There is a need to calculate this cost and the effect of the charging and discharging performance on the useful life of the battery. This issue was included as future work in the proposed design.