Abstract
Carbon-based nanomaterials, such as graphene and graphene nanoribbons (GNRs), have attracted researchers because of their optoelectronic properties. One of the most intriguing properties of GNRs is their tunable bandgap. Unlike inherently metallic graphene sheets, GNRs can exhibit a bandgap, a crucial property for electronic devices. By controlling the width and edge configuration of GNRs, researchers can precisely tailor their electronic properties to meet specific requirements. Chevron-like graphene nanoribbons (ChGNRs) are a class of nanomaterials with unique properties due to their wavy morphology. The electrical conductivity of ChGNRs makes them potentially useful in devices like organic solar cells and transistors. In this study, we computed the Shannon’s information entropy measures of ChGNRs using a variety of degree-based topological descriptors (TDs). The basic graph theoretical approach was utilized to derive the explicit mathematical equations of the TDs for the ChGNRs. The results were compared with cove-edged graphene nanoribbons (cGNRs) to analyze the thermodynamic stability of both ChGNRs and cGNRs and the different trends were pointed out.
Similar content being viewed by others
Introduction
Graphene is an essential and fascinating material that draws theoretical and practical research because of its unique properties and applications; graphene is helpful in material research1,2,3. However, researchers are interested in atomically precise graphene nanoribbons (GNRs) because of their intriguing electrical properties and prospective uses in electronics, sensors, spintronics, and photovolatics4. The properties of GNRs are well known to be substantially influenced by structural parameters like width, edge type, and chemical bioactivity. Nanographenes include quasi-one dimensional graphene nanoribbons (GNRs) and quasi-zero dimensional graphene quantum dots (GQDs), which are described as graphene cutouts on a nanoscale5,6,7. Both top-down and bottom-up methods can synthesize GNRs are shown in8,9,10,11,12. The bottom-up GNR structures have a significant advantage over conventional top-down GNRs because they are made from small molecular building blocks that self-assemble to produce atomically smooth, well-defined edges and terminations13,14,15,16,17. Because of the molecular building blocks’ adaptability, it is possible to create a variety of GNRs with atomic precision. This includes adjusting the width and edge structures and doing atomic doping and chemical functionalization inside the GNRs or on their edges18,19,20. Consequently, a wide range of GNR structures realized through bottom-up synthesis have shown great potential for band gap engineering, one-dimensional (1D) heterojunctions, and other technologies in nanoelectronics and other fields21,22,23,24,25.
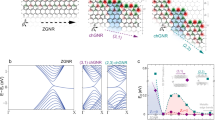
GNRs can be broadly classified into four categories: armchair, zigzag, chiral, and chevron GNRs. The width is the only distinguishing factor between armchair and zigzag GNRs. However, two factors are needed to distinguish chiral GNRs from one another: their width and edge orientation. Along the edge of the chiral GNRs unit cell, the number of graphene unit cell vectors (ma1 and na2) determines the edge orientation. There isn’t a widely accepted classification system for chevron GNRs. Chevron GNRs are topologically meandering GNRs which is shown in Figure 1, where unit of ChGNR(m, n) consists of m copies of hexabenzocoronene (HBC) with varying length n. They may have an assortment of zigzag and armchair edge terminations. As shown in Figure 1,the rings colored with pink indicates the number of aromatic sextets in the Clar formula26.
GNR heterostructures might theoretically be created to further alter GNR characteristics. Variations in breadth, edge topology, or controlled chemical composition can be used to modify band gap and edge-related electronic states along the GNR axis. Nevertheless, this approach relies on the meticulously controlled addition of different precursor monomers to a targeted sequence, which has not yet been achieved. The chevron GNR class has a lot of potential to be successful along this path since it is possible to achieve an alternation of width, edge perspective, and chemical composition at the precursor monomer level. This enables the creation of homogenous GNRs with an incredible range of physical characteristics. There has been lot of research going in the field of various graphene and GNRs applications in the field of material science, structure property modelling, optical, spectral and nuclear magnetic resonance (NMR) are shown in27,28,29,30,31,32,33,34,35.
Chemical graph (CG) modelling is based on graph theory (GT). GT is applied chemically to investigate a variety of characteristics, including chemical, physical, and bio activities. These features are investigated using numerical invariants called topological indices. Chemical graph theory (CGT) is a branch of mathematics concerned with the study of CG’s. The tools of GT are used to mathematically express chemical phenomena. It connects the uses of GT to solve molecular problems, which is important in the chemical sciences. The graph theoretically obtained parameters are useful in predicting various physical and chemical properties. For example graph spectrum is very useful in calculating \(\pi\)- electron energy and HOMO-LUMO gap. In this study, we have obtained various degree-based topological descriptors and their corresponding information entropy measures with the help of simple graph theoretical parameters. Then the spectrum of ChGNRs are used to compute the \(\pi\)-electron energy and algebraic structure counts (ASC) are used to compute the RE. Finally the computed entropy measures are compared with cove-edged graphene nanoribbons (cGNR’s) and it is observed that the cove-edged GNRs exhibits greater entropy than chevron-like GNRs. Also it is shown that cGNR’s are thermodynamically more stable than ChGNR’s.
The novelty of this study lies in using degree-based topological descriptors (TDs) to apply Shannon’s information entropy to chevron-like graphene nanoribbons (ChGNRs). This innovative approach allows for a deeper understanding of the electronic properties and stability of ChGNRs. By analyzing the topological features through entropy measures, we can uncover correlations that may enhance their performance in various applications, such as nanoelectronics and materials science. This methodology provides a novel perspective for assessing the structural complexity and thermodynamic stability of nanomaterials. This study presents a graph-theoretical method for measuring and comparing the information content of ChGNRs and cove-edged GNRs (cGNRs), whereas prior research has mostly concentrated on the electronic and morphological characteristics of GNRs36,37. This study offers a novel framework for comprehending the connection between stability and nanoribbon topology, an area with important implications for the design of next-generation optoelectronic devices, by analyzing the entropy measures of various TDs and deriving explicit mathematical formulations for them.
Methodology
Throughout this study chevron-like graphene nanoribbons (ChGNRs) are considered as a simple graph \(G\in \displaystyle \bigcup _{m\ge n\ge 1}ChGNR(m,n)\) in which the vertices (atoms) and edges (bonds) of G are denoted as the V(G) and E(G), respectively. We define the neighborhood of a vertex p as \(N_{p}(G)=\{q\in V(G)\mid (p,q)\in E(G)\}\). For a vertex \(p\in V(G)\), the degree of p is defined as \(\gamma _{p}(G) = |N_{p}(G)|\). Consider the following set \(D(G)=\{(\alpha ,\beta ) \ ; \ 1< \alpha \le \beta \le \max \limits _{p}\gamma _{p}(G)\}=\{1< \alpha \le \beta < 4 \}\). Let \(\gamma _{(\alpha ,\beta )}(G)=|\{(p,q)\in E(G) \ ; \ \gamma _{p}(G)=\alpha\) and \(\gamma _{q}(G)=\beta \}|\). Then the degree-based topological index function \(\Omega\) is defined as,
Chemistry has extensively used Shannon’s information entropy (SIE), especially in molecular structure and quantum chemistry, because of its capacity to measure properties of information theory38,39. The SIE using these TDs of any molecular structure is given below
The indices and their index expressions are shown in Table 1.
Main results
We consider chevron-like graphene nanoribbons which has both zigzag and armchair edge terminations and it is denoted as ChGNR(m, n). The ChGNR(m, n) consists \(18mn^{2}-24mn+6m+6n\) atoms (vertices) and \(27mn^{2}-40mn+13m+7n-1\) bonds (edges). The degree-based topological descriptors and their corresponding entropies of the ChGNRs are explained in the following sections.
Degree-based topological descriptors
The different degree-based TDs of ChGNRs, namely ChCGNR(m, n) for \(m,n\ge 1\), are calculated with the help of edge distributions shown in Tables 1-2 in which \(\Psi ^{d}(G)\in \{R,RR,M_{1},M_{2},ABC,SC,GA,H,HM,F,AZ\}\). The degree-based TDs are calculated by the equation
Result 1
The TDs of chevron-like graphene nanoribbon ChGNR with size (m, n) are given by
-
(i)
\(R^{\gamma }(ChGNR(m,n))=3.0673m + 2.9663n - 12.0673mn + 9mn^2 + 0.0337\).
-
(ii)
\(RR^{\gamma }(ChGNR(m,n))=47.4041m + 16.7980n - 128.4041mn + 81mn^2 - 4.7980\).
-
(iii)
\(M_{1}^{\gamma }(ChGNR(m,n))=94m + 34n - 256mn + 162mn^2 - 10\).
-
(iv)
\(M_{2}^{\gamma }(ChGNR(m,n))=161m + 41n - 404mn + 243mn^2 - 17\).
-
(v)
\(ABC^{\gamma }(ChGNR(m,n))=8.1814m + 4.9093n - 26.1814mn + 18mn^2 - 0.6667\).
-
(vi)
\(H^{\gamma }(ChGNR(m,n))=3.1333m + 2.9333n - 12.1333mn + 9mn^2 + 0.0667\).
-
(vii)
\(SC^{\gamma }(ChGNR(m,n))=4.6285m + 3.1971n - 15.6512mn + 11.0227mn^2 - 0.1971\).
-
(viii)
\(GA^{\gamma }(ChGNR(m,n))=13.1616m + 6.9192n - 40.1616mn + 27mn^2 - 0.9192\).
-
(ix)
\(HM^{\gamma }(ChGNR(m,n))=636m + 168n - 1608mn + 972mn^2 - 72\).
-
(x)
\(F^{\gamma }(ChGNR(m,n))=86m+10n+324mn-38\).
-
(xi)
\(AZ^{\gamma }(ChGNR(m,n))=188.7656m + 59.3906n - 496.3125mn + 307.5469mn^2 - 11.3906\).
Theorem 3.1
For the chevron-like GNR, Randić entropy is:
Proof
\(\square\)
Theorem 3.2
For the chevron-like GNR, reciprocal Randić entropy is:
Proof
\(\square\)
Theorem 3.3
For the chevron-like GNR, first Zagreb entropy is:
Proof
\(\square\)
Theorem 3.4
For the chevron-like GNR, second Zagreb entropy is:
Proof
\(\square\)
Theorem 3.5
For the chevron-like GNR, ABC entropy is:
Proof
\(\square\)
Theorem 3.6
For the chevron-like GNR, geometric arithmetic entropy is:
Proof
\(\square\)
Theorem 3.7
For the chevron-like GNR, harmonic entropy is:
Proof
\(\square\)
Theorem 3.8
For the chevron-like GNR, sum connectivity entropy is:
Proof
\(\square\)
Theorem 3.9
For the chevron-like GNR, hyper Zagreb entropy is:
Proof
\(\square\)
Theorem 3.10
For the chevron-like GNR, forgotten entropy is:
Proof
\(\square\)
Theorem 3.11
For the chevron-like GNR, augmented Zagreb entropy is:
Proof
\(\square\)
Numerical results and applications
The various DBTD’s and the corresponding entropies calculated in this study are very much useful in predicting the physical and chemical properties of the molecules under study. For example Zagreb type indices like \(M_{1}(G),M_{2}(G),HM(G),AZ(G)\) have shown very high correlation coefficient \(r=0.9994\) with \(\pi\)- electron energy \((E_{\pi })\) values which is shown in Table 5 and the pictorial representation was given in Figure 3. Where as the \(E_{\pi }\) values are computed from its spectrum. Hence it is observed that graph theoretically derived indices are meaningful in predicting the numerous properties of the molecules.
Since entropy plays a vital role in various fields of science, such as software, engineering, medication, and pharmaceutical, its numerical values and graphical representation are essential for researchers. Here, we calculate some exact values of degree-based entropies of ChGNRs, which are shown in Table 3. Furthermore, to compare and contrast these numerical entropies of ChGNRs, we adopted the technique called scaled entropies, which is obtained from Table 3, dividing it by the total number of bonds (edges) of G will give the normalized entropy values or scaled entropies which is used in meaningful predictions of the thermodynamic stability of the chemical structures considered in this study are shown in Table 4. Then we have carried the comparative analysis of scaled entropies which is shown in Table 4 with the scaled entropies of cove-edged graphene nanoribbons (cGNR’s) studied in28. This comparision clearly shows that for given \(m=2,4\) and \(n=3,6\), the cGNRs exhibit greater entropy than ChGNRs which is shown in Figure 2. Hence the ChGNRs are predicted to be thermodynamically stable than cGNRs. Also there are several studies in the literature which focus on entropy based energy prediction models are shown in50,51,52,53.
Another idea of measuring the thermodynamic stability is the Resonance Energy (RE). There are several literature’s available to calculate the RE, which plays a vital role in predicting the aromaticity of a molecule. In this study we have used Herdon’s approach \(RE=A\times \ln (ASC)\). Where \(A=1.185\) is an empirical parameter and ASC is an algebraic structure count which is directly calculated from the constant coefficient of the characteristic polynomial for bipartite graphs. Hence the RE measures obtained in Table 5, gives the idea about the thermodynamic stability ChGNRs. Next we have done the comparative study of thermodynamic stability of ChGNR’s and cove-edged graphene nanoribbons cGNR’s with the help of RE. Once again this study reveals that cGNR’s exhibit greater RE when it is compared with ChGNR’s. Hence it is concluded that Shannon’s information entropy and RE measures both reveals that cGNR’s are thermodynamically more stable than ChGNR’s because both the molecules consists of same number of atoms on different stages but while comparing the total number of bonds (edges) between these two molecules cGNR’s holds the greater number of bonds than ChGNR’s.
Conclusion
In this study, we have computed various degree-based topological descriptors and their corresponding information entropy measures for ChGNR’s with the help of chemical graph theory techniques. Our computed entropies reveals that cove-edged graphene nanoribbons are thermodynamically more stable than chevron-like graphene nanoribbons. Also the resonance energies are computed with the use of algebraic structure count. This study also shows the same trend in thermodynamic measures of ChGNR’s and cGNR’s. Hence it is clear that chemical graph theoretical measures are useful in predicting the structural properties of the molecules. From Table 5, we can observe the stability order of ChGNR(m, n) as follows \(ASC(ChGNR(2,2))\ge ASC(ChGNR(4,2))\ge ASC(ChGNR(6,2))\ge ASC(ChGNR(4,3))\)\(\implies E_{\pi }(ChGNR(2,2)) \ge (ChGNR(4,2))\ge (ChGNR(6,2))\ge (ChGNR(4,3))\). Consequently this relations satisfies the Dewar and Longuet-Higgins rule.
Data availability
All data generated or analysed during this study are included in this published article.
References
Neto, A. C., Guinea, F., Peres, N. M., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Reviews of Modern Physics. 81(1), 109. https://doi.org/10.1103/RevModPhys.81.109 (2009).
Balandin, A. A. et al. Superior thermal conductivity of single-layer graphene. Nano Letters. 8(3), 902–907. https://doi.org/10.1021/nl0731872 (2008).
Rozhkov, A., Sboychakov, A., Rakhmanov, A. & Nori, F. Electronic properties of graphene-based bilayer systems. Physics Reports. 648, 1–104. https://doi.org/10.1016/j.physrep.2016.07.003 (2016).
Johnson, A. P., Gangadharappa, H. V. & Pramod, K. Graphene nanoribbons: A promising nanomaterial for biomedical applications. Journal of Controlled Release. 325, 141–162. https://doi.org/10.1016/j.jconrel.2020.06.034 (2020).
Gu, Y., Qiu, Z. & Müllen, K. Nanographenes and graphene nanoribbons as multitalents of present and future materials science. Journal of the American Chemical Society. 144(26), 11499–11524. https://doi.org/10.1021/jacs.2c02491 (2022).
Narita, A., Chen, Z., Chen, Q. & Müllen, K. Solution and on-surface synthesis of structurally defined graphene nanoribbons as a new family of semiconductors. Chemical Science. 10(4), 964–975. https://doi.org/10.1039/C8SC03780A (2019).
Ali, I., Hasan, S. Z., Garcia, H., Danquah, M. K. & Imanova, G. Recent advances in graphene-based nano-membranes for desalination. Chemical Engineering Journal. 483, 149108. https://doi.org/10.1016/j.cej.2024.149108 (2024).
Wu, D. et al. Giant spin caloritronic properties in spin-semiconductor graphene nanoribbons via zigzag edge extensions. Applied Physics Letters. 125(9) 093901. https://doi.org/10.1063/5.0226405. (2024).
Cheng, Y., Xu, J., Xiang, J., Liu, W. & Miao, M. Bipolar magnetic semiconductors emerging in graphene nanoribbons with zigzag edges and internal defects. Physical Review B. 110(8), 085141. https://doi.org/10.1103/PhysRevB.110.085141 (2024).
Lou, S. et al. Graphene nanoribbons: current status, challenges and opportunities. Quantum Frontiers. 3(1), 3. https://doi.org/10.1007/s44214-024-00050-8 (2024).
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature. 466(7305), 470–473. https://doi.org/10.1038/nature09211 (2010).
Hu, J. et al. Graphene nanoribbon core thermotropic liquid crystal with a well-defined molecular structure. Angewandte Chemie. e202501161 https://doi.org/10.1002/ange.202501161. (2025).
Lyu, B. et al. Graphene nanoribbons grown in hBN stacks for high-performance electronics. Nature. 628 758–764. https://doi.org/10.1038/s41586-024-07243-0. (2024).
Datta, S. S., Strachan, D. R., Khamis, S. M. & Johnson, A. T. C. Crystallographic etching of few-layer graphene. Nano Letters. 8, 1912–1915. https://doi.org/10.1021/nl080583r (2008).
Yang, X. et al. Two-dimensional graphene nanoribbons. Journal of American Chemical Society. 130(13), 4216–4217. https://doi.org/10.1021/ja710234t (2008).
Dong, W. et al. Unzipping carbon nanotubes to sub-5-nm graphene nanoribbons on Cu (111) by surface catalysis. Small. 20(21), 2308430. https://doi.org/10.1002/smll.202308430 (2024).
Kuzmany, H. et al. Well-defined sub-nanometer graphene ribbons synthesized inside carbon nanotubes. Carbon. 171, 221–229. https://doi.org/10.1016/j.carbon.2020.08.065 (2021).
Narita, A., Feng, X. & Müllen, K. Bottom-up synthesis of chemically precise graphene nanoribbons. The Chemical Record. 15, 295–309. https://doi.org/10.1002/tcr.201402082 (2015).
Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature. 531, 489. https://doi.org/10.1038/nature17151 (2016).
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature. 466, 470. https://doi.org/10.1038/nature09211 (2010).
Niu, W., Ma, J. & Feng, X. Precise structural regulation and band-gap engineering of curved graphene nanoribbons. Accounts of Chemical Research. 55(23), 3322–3333. https://doi.org/10.1021/acs.accounts.2c00550 (2022).
Bennett, P. B. et al. Bottom-up graphene nanoribbon field-effect transistors. Applied Physics Letters. 103, 253114. https://doi.org/10.1063/1.4855116 (2013).
Cai, J. et al. Graphene nanoribbon heterojunctions. Nature Nanotechnology. 9, 896. https://doi.org/10.1038/nnano.2014.184 (2014).
Chen, Y.-C. et al. Molecular bandgap engineering of bottom-up synthesized graphene nanoribbon heterojunctions. Nature Nanotechnology. 10, 156. https://doi.org/10.1038/nnano.2014.307 (2015).
Durr, R. A. et al. Orbitally matched edge-doping in graphene nanoribbons. American Chemical Society. 140, 807–813. https://doi.org/10.1021/jacs.7b11886 (2018).
Randić, M. & Balaban, A. T. Local aromaticity and aromatic sextet theory beyond Clar. International Journal of Quantum Chemistry. 118(17), e25657. https://doi.org/10.1002/qua.25657 (2018).
Govardhan, S. & Roy, S. Topological analysis of hexagonal and rectangular porous graphene with applications to predicting \(\pi\)-electron energy. European Physical Journal Plus. 138(7), 670. https://doi.org/10.1140/epjp/s13360-023-04307-4 (2023).
Govardhan, S., Roy, S., Prabhu, S. & Arulperumjothi, M. Topological characterization of cove-edged graphene nanoribbons with applications to NMR spectroscopies. Journal of Molecular Structure. 1303, 137492. https://doi.org/10.1016/j.molstruc.2024.137492 (2024).
Wang, X., Yao, X., Narita, A. & Müllen, K. Hetero atom-doped nanographenes with structural precision. Accounts of Chemical Research. 52, 2491–2505. https://doi.org/10.1021/acs.accounts.9b00322 (2019).
Cai, J. M. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature. 466, 470–473. https://doi.org/10.1038/nature09211 (2010).
Gu, Y., Qiu, Z. & Müllen, K. Nanographenes and graphene nanoribbons as multitalents of present and future materials science. Journal of the American Chemical Society. 144(26), 11499–11524. https://doi.org/10.1021/jacs.2c02491 (2022).
Lv, Y. et al. Activating impurity effect in edge nitrogen-doped chevron graphene nanoribbons. Journal of Physics Communications. 2(4), 045028. https://doi.org/10.1088/2399-6528/aab8df (2018).
Teeter, J. D. et al. On-surface synthesis and spectroscopic characterization of laterally extended chevron graphene nanoribbons. Chem Phys Chem. 20(18) 2281–2285. https://doi.org/10.1002/cphc.201900445 (2019).
Vo, T. H., Shekhirev, M., Lipatov, A., Korlacki, R. A. & Sinitskii, A. Bulk properties of solution-synthesized chevron-like graphene nanoribbons. Faraday Discussions. 173, 105–113. https://doi.org/10.1039/C4FD00131A (2014).
Zhou, B. & Trinajstic, N. On general sum-connectivity index. Journal of Mathematical Chemistry. 47, 210–218. https://doi.org/10.1007/s10910-009-9542-4 (2010).
Raza, Z., Arockiaraj, M., Maaran, A., Kavitha, S. R. J. & Balasubramanian, K. Topological entropy characterization, NMR and ESR spectral patterns of coronene-based transition metal organic framework. ACS omega. 8(14), 13371–13383. https://doi.org/10.1021/acsomega.3c00825 (2023).
Arockiaraj, M., Jency, J., Abraham, J., Kavitha, S. R. J. & Balasubramanian, K. Two-dimensional coronene fractal structures: topological entropy measures, energetics, NMR and ESR spectroscopic patterns and existence of isentropic structures. Molecular Physics. 120(11), e2079568. https://doi.org/10.1080/00268976.2022.2079568 (2022).
Shanon, C. E. A mathematical theory of communication. The Bell System Technical Journal. 27, 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x (1948).
Chen, Z., Dehmer, M. & Shi, Y. A note on distance-based graph entropies. Entropy. 16, 5416–5427. https://doi.org/10.3390/e16105416 (2014).
Gutman, I. Degree-based topological indices. Croatica Chemica Acta. 86(4), 351–361. https://doi.org/10.5562/cca2294 (2013).
Gutman, I., Furtula, B. & Elphick, C. Three new/old vertex degree-based topological indices. MATCH Communications in Mathematical and in Computer Chemistry. 72(3), 617–632 (2014).
Gutman, I. & Trinajstić, N. Graph theory and molecular orbitals: Total \(\pi\)- electron energy of alternant hydrocarbons. Chemical Physics Letters. 17(4), 535–538. https://doi.org/10.1016/0009-2614(72)85099-1 (1972).
Estrada, E. Atom-bond connectivity and the energetic of branched alkanes. Chemical Physics Letters. 463(4), 422–425. https://doi.org/10.1016/j.cplett.2008.08.074 (2008).
Zhou, B. & Trinajstić, N. On general sum-connectivity index. Journal of Mathematical Chemistry. 47, 210–218. https://doi.org/10.1007/s10910-009-9542-4 (2010).
Vukičević, D. & Furtula, B. Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. Journal of Mathematical Chemistry. 46, 1369–1376. https://doi.org/10.1007/s10910-009-9520-x (2009).
Zhong, L. The harmonic index on unicyclic graphs. Ars Combinatoria. 104, 261–269 (2012).
Shirdel, G., Rezapour, H. & Sayadi, A. The hyper-Zagreb index of graph operations. Iranian Journal of Mathematical Chemistry. 4(2) 213–220. https://doi.org/10.22052/ijmc.2013.5294 (2013).
Furtula, B. & Gutman, I. A Forgotten topological index. Journal of Mathematical Chemistry. 53, 1184–1190. https://doi.org/10.1007/s10910-015-0480-z (2015).
Furtula, B., Graovac, A. & Vukičević, D. Augmented Zagreb index. Journal of Mathematical Chemistry. 48, 370–380. https://doi.org/10.1007/s10910-010-9677-3 (2010).
Prabhu, S., Arulperumjothi, M., Salu, S. & Jose, B. K. Computational analysis of linear chain of holey nanographene and their molecular characterizations. Journal of Molecular Modeling. 31, 62. https://doi.org/10.1007/s00894-024-06261-z (2025).
Prabhu, S., Arulperumjothi, M., Manimozhi, V. & Balasubramanian, K. Topological characterizations on hexagonal and rectangular tessellations of antikekulenes and its computed spectral, nuclear magnetic resonance and electron spin resonance characterizations. International Journal of Quantum Chemistry. 124(7), e27365. https://doi.org/10.1002/qua.27365 (2024).
Prabhu, S. et al. Several distance and degree-based molecular structural attributes of cove-edged graphene nanoribbons. Heliyon. 10, e34944. https://doi.org/10.1016/j.heliyon.2024.e34944 (2024).
Balasubramanian, K. Density functional and graph theory computations of vibrational, electronic, and topological properties of porous nanographenes. Journal of Physical Organic Chemistry. e4435 https://doi.org/10.1002/poc.4435 (2022).
Author information
Authors and Affiliations
Contributions
S.M.P.: Conceptualization, Methodology, Writing–original draft, A.R.V.: Supervision, Methodology, Writing–review and editing S.G.: Validation, Software, Investigation, Methodology S.P.: Supervision, Writing–review and editing, Validation, Methodology.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Prabhu, S.M., Vijayalakshmi, A.R., Govardhan, S. et al. Molecular characterization and information entropies of chevron-like graphene nanoribbons with chemical applications. Sci Rep 15, 20632 (2025). https://doi.org/10.1038/s41598-025-06823-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-06823-y