Introduction

The terahertz (THz) frequency range of the electromagnetic spectrum (EM) has gained significant attention due to its ability to investigate basic principles of physics at the millielectron volt (meV) energy scale1,2. With the advancements in terahertz technologies, this frequency range has opened up new possibilities for wireless communication, security, imaging, biosensing, and other applications3,4,5,6,7. As the demand for higher transmission rates in communication systems continues to increase, there is a need for short-range wireless communication that can support data transmission speeds of up to 1 Tbps.8,9,10. To harness the terahertz properties for communication systems, robust terahertz components such as wave plates, amplitude and phase modulators, switches, and filters are needed11,12. One potential method for developing these terahertz devices is through the use of metamaterials (MMs), which are artificial structures with periodic arrangements and subwavelength dimensions. The optical properties of these engineered media are primarily governed by their subwavelength geometries and the materials they are composed of13,14. Studies have been conducted on different types of metamaterials, such as split-ring resonators (SRRs)15, single-strip resonators16, fishnet resonators17, and cross-shaped structures18, for various applications such as frequency selection, narrow frequency filtering and sensing19,20,21. Specific applications such as wireless communication and the Internet of Things (IoT) require terahertz transmission over a wideband spectrum. Researchers have used nested and coupled resonator-based metamaterial structures for broadening resonances in the planar configuration22,23. Although the approach is promising and easy to fabricate, it provides a limited enhancement in bandwidth without compromising resonance amplitude. To overcome this limitation, multi-stacking of metamaterials can be employed to broaden the bandwidth without significantly affecting the resonance strength24,25,26.

The rising demand for terahertz wave modulation has prompted the development of tunable terahertz broadband modulators. A range of techniques, including electrical, mechanical, optical, and thermal, are available for achieving terahertz modulation. Optical modulation, while capable of modulating THz waves effectively, often requires high-power laser sources, which increases system complexity and reduces overall cost-effectiveness. Mechanical modulation, using micro-electro-mechanical systems (MEMS)27, aligns well with integrated circuit fabrication and is particularly useful for tunable THz filters, but it is limited by narrow bandwidth and complex manufacturing processes. Electrical modulation28,29,30, employing elements such as Schottky junctions and 2D materials like graphene, provides compact integration with electronics but suffers from restricted modulation depth and frequency-dependent shifts. Among thermal techniques, vanadium dioxide (VO₂) has garnered significant attention due to its unique insulator-to-metal phase transition around 68 °C. This transition enables dynamic control of terahertz wave propagation with both broad bandwidth and deep modulation. VO₂ is especially notable for its large changes in conductivity and permittivity between its amorphous and crystalline phases, along with high-speed switching capabilities31,32,33, making it a promising material for next-generation actively tunable THz metamaterials.

In this study, we introduce an ultra-broadband terahertz transmission modulator using a hybrid metamaterial that integrates multi-stacked metasurfaces with a VO₂ thin film. The flexible metamaterial is fabricated via photolithography and transferred onto a VO₂ film on quartz, creating tunable metamaterials without damaging the VO₂. We begin by reporting the VO₂ film’s characteristics, including temperature-dependent thermal conductivity, phase change, plasma frequency, and relaxation time. We then showcase the hybrid metamaterial’s broadband modulation capability through THz-TDS and use a transmission line model to elucidate the VO₂ phase transition mechanism and the coupling behaviour of the multi-stacked metamaterial.

Results

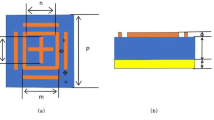
To demonstrate active terahertz broadband modulation in VO2-deposited multistacked MM, we prepared three samples. The first sample was a VO₂ thin film deposited on a quartz substrate via chemical vapour deposition (CVD), with a thickness of d = 1.5 µm. The second sample is a flexible, multi-layered metamaterial comprising five layers: A Polyethylene Terephthalate (PET) substrate, a polyimide spacer, a complementary cross-shaped aluminium resonator (conductivity of 3.5 × 10⁷ S/m), and another identical resonator layer separated by polyimide as shown in Fig. 1a (step 5). Each metallic resonator is 0.2 µm thick, exceeding the skin depth of aluminium in the terahertz range34. Complementary cross-shaped resonators were chosen for their ease of fabrication and symmetric nature, providing polarization-insensitive transmission responses due to fourfold rotational symmetry. The unit cell periodicity was set at p = 95 µm, with resonator dimensions of l = 80 µm and w = 20 µm (see inset of bottom Fig. 1c). The polyimide spacer thickness was optimized to tp = 50 µm to achieve a balance between a higher full width at half maximum (FWHM) and a relatively flat transmission band. Increasing the thickness beyond 50 μm further enhanced the FWHM but compromised the flatness of the transmission band. For a detailed discussion of the optimization process and its impact on the terahertz response, please refer to Section 4 of the Supplementary Material. For Sample 3, we peeled off the multi-layered metamaterial from Sample 2 and transferred it onto the VO₂ layer of Sample 1, as illustrated in Fig. 1 (see steps 6–8). Thus, the final sample consists of two functional components: the VO₂ thin layer on the quartz substrate and the multistacked resonators separated by the polyimide layer. The metamaterial fabrication was carried out using standard photolithography techniques. The multi-stacking, peeling-off, and transfer processes are depicted schematically in Fig. 1a,b, illustrated in steps 1 to 8. The fabricated samples are shown in Fig. 1c. Detailed descriptions of the fabrication and characterization processes can be found in the supplementary material (Sections 2 and 3).

Fig. 1
figure 1

(a) Schematic of the multi-stacking and peel-off process of the metamaterial. (b) Transfer of the flexible metamaterial onto a VO₂ thin film on quartz, with the terahertz characterization scheme of the final MM. (c) Images of the flexible metamaterial, the peel-off process, and the fabricated sample.

Full size image

Prior to combining the VO2 thin film with the multi-layered metamaterial (MM), we conducted an in-depth analysis of its basic properties within the terahertz spectrum. The temperature-dependent complex terahertz conductivity of the VO2 thin film during the metal–insulator transition was assessed by THz-TDS. To compute this conductivity, the complex refractive index of the VO2 thin film was initially obtained by using Eq. (1) 35:

$$T_{{VO_{2} }} = \frac{{F_{sample\left( \omega \right)} }}{{F_{ref\left( \omega \right)} }} = \frac{{2\eta_{2} \left( {\eta_{1} + \eta_{3} } \right)}}{{\left( {\eta_{2} + \eta_{1} } \right)\left( {\eta_{2} + \eta_{3} } \right)}}\exp \left[ { - j\left( {\eta_{2} - \eta_{1} } \right)\frac{\omega d}{c}} \right]FP\left( \omega \right),$$
(1)

where \(FP\left( \omega \right)\) represents the Fabry–Perot term given by:

$$FP\left( \omega \right) = \left[ {1 - \left( {\frac{{\eta_{2} - \eta_{1} }}{{\eta_{2} + \eta_{1} }}} \right)\left( {\frac{{\eta_{2} - \eta_{3} }}{{\eta_{2} + \eta_{3} }}} \right)exp\left( { - 2j\eta_{2} \frac{\omega d}{c}} \right)} \right]^{ - 1}$$
(2)

here \(\eta_{1} ,\eta_{2} and \eta_{3}\) are the complex refractive indices of the air, VO2 thin film and quartz substrate, respectively. The complex transmission coefficient of the sample \(T_{{VO_{2} }}\) were measured experimentally by THz-TDS. During THz-TDS measurements, the temperature was controlled with a stability of ± 1 °C, using a programmable power supply and temperature monitoring via a thermocouple placed in close proximity to the VO₂ film. To ensure uniform and repeatable phase transition behaviour, the heating and cooling rates were maintained at approximately 5 °C/min. These moderate ramp rates were chosen to minimise thermal gradients across the sample and reduce the effects of thermal hysteresis, thus ensuring consistent modulation depths across repeated cycles. This thermal protocol was critical for achieving reliable and reproducible switching characteristics in the VO₂-based modulator. Subsequently, the complex refractive(\(\eta_{2 }\)) index was determined using an algorithm referred to as the ‘downhill method’, as mentioned in the work of Da-Xiang Zhou35. Since VO2 is a non-magnetic material \((\eta_{2} = \sqrt {{\varvec{\varepsilon}}_{2} )}\), complex conductivity \(\user2{ }\left( {{\varvec{\sigma}} = \sigma_{1} + {\varvec{i}}\sigma_{2} } \right)\) can be calculated by the well-known formula derived from Maxwell’s equations given by36.

$${\varvec{\sigma}} = \omega \varepsilon_{o} \left( {\varepsilon^{\prime } - j\left( {\varepsilon^{\prime \prime } - 1} \right)} \right),$$
(3)

where \(\varepsilon^{\prime }\) and \(\varepsilon^{\prime \prime }\) is the real and imaginary components \(\left( {{\varvec{\varepsilon}}_{2} = \varepsilon^{\prime } + j\varepsilon^{\prime \prime } } \right)\) of the permittivity of the VO2 thin film. A detailed analysis is provided in the supplementary material in Section (3). The real(σ1) and imaginary(σ2) components are plotted in Fig. 2b for temperatures ranging from T = 50 °C to T = 90 °C. It is observed that σ1 is nearly flat with a slightly positive slope, consistent with terahertz studies of VO2 conducted by other groups31,33,37. Meanwhile, σ2 remains negative at all temperatures. The behaviours of σ1 and σ2, persisting into the fully metallic state, are characteristic of localized charge carriers32. To describe the conductivity in relation to temperature changes, the conductivity calculated from Eq. (3) is fitted with the Drude-Smith model, a classical generalization of the Drude model. The most common form of the Drude-Smith model is given in Eq. (4)37:

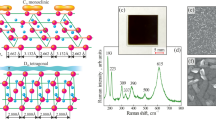
$$\sigma_{DS} \left( \omega \right) = \frac{{ne^{2} \tau }}{{m^{*} \left( {1 - j\omega \tau } \right)}}\left( {1 + \frac{c}{{\left( {1 - i\omega \tau } \right)}}} \right),$$
(4)

where n represents the electron density, τ denotes the Drude-Smith scattering time (often referred to as the relaxation time of electrons), m* = 2me is the effective mass of electrons in VO2, and c is a parameter varying between 0 for free carriers and − 1 for fully localized charges. The fitting results, displayed in Fig. 2b, illustrating the conductivity fitting from the Drude-Smith model (dotted line). It is evident from Fig. 2b that both the dielectric and metallic phases of VO2 are consistent with the Drude-Smith model. The obtained scattering time from the best fit for the VO2 thin films is approximately 14 ± 2 fs, while the c factor is around -0.95 ± 0.03 for the VO2 thin film. Notably, the c values being close to − 1 suggest that strong carrier backscattering and localization may dominate electron transport in the THz range32,37. VO2 deposition via Chemical Vapor Deposition leads to smaller grains compared to other techniques, and these smaller grain sizes result in stronger backscattering. The plasma frequency, calculated from the fitting for the different temperatures, is plotted in Fig. 2d. These values fall within a reasonable range and are consistent with the findings reported by James Lourembam33. Finally, the Raman shift data presented in Fig. 2c further confirm the phase transition properties of VO2 materials as a function of temperature38. The detailed analysis of the VO2 deposition and characterization can be found in the supplementary material (Section 1).

Fig. 2
figure 2

(a) FESEM image of VO₂ thin film surface morphology; insets show zoomed and cross-sectional views, with thickness calculated as 1.5 µm. (b) Real and imaginary components of conductivity fitted using the Lorentz–Drude model. (c) Temperature-dependent Raman data revealing the phase transition behaviour of the VO₂ thin film. (d) Plasma frequency and relaxation time from Drude-Lorentz fitting.

Full size image

To demonstrate thermally active modulation in a VO₂ thin-film-based multistacked metamaterial, numerical simulations were conducted using CST Microwave Studio software, which operates in the frequency domain and employs finite integral techniques to solve Maxwell’s equations. Three simulation sets were performed: Sample 1 (VO₂ thin film), Sample 2 (flexible multistacked metamaterial), and Sample 3 (VO₂ thin film integrated with multistacked metamaterial). The permittivities of quartz and PET substrates were set at 3.7 and 3.5, respectively, while the permittivity of the polyimide spacer was calculated using THz-TDS as 2.89. The conductivity of the VO₂ material, derived from Drude fitting, was utilized in the simulations, with both real and imaginary parts extracted at different temperatures (as shown in Fig. 2b) to modulate the transmission amplitude. Boundary conditions for all cases were taken as unit cells in the X and Y directions.

Figure 3 presents the simulated and corresponding experimental results for each set of samples. Figure 3a depicts the simulated and experimentally calculated transmission amplitudes of the flexible multistacked filter. FWHM for this bandpass filter, calculated from THz-TDS and obtained from CST simulation, is found to be 0.90 THz and 0.76 THz, respectively, which is substantially higher compared to earlier reported works18,26,39,40,41. This broader transmission response is attributed to the multi-stacking of the metamaterial layers and the optimized polyimide spacer thickness, which enhances the coupling between the resonators in adjacent layers. Figure 3b shows the simulated and experimentally calculated transmission amplitudes of the VO2 thin film. It indicates that when the temperature of the VO2 thin film changes from T = 50֯C to T = 90֯C, the conductivity of the VO2 film changes from 15 S/m to 14,000 S/m. As a result, the transmission amplitude calculated from THz-TDS (and obtained from CST simulation), decreases from a maximum of 85% (95%) to a minimum of 27% (25%). The final sample, multistacked metamaterial on the VO2 thin film, is shown in Fig. 3c. The FWHM for this hybrid metamaterial, calculated through THz-TDS (and obtained via CST), is 1.02 THz (0.76 THz). The discrepancies between the FWHM and minor frequency shift of the resonance peak in the simulated and measured spectra may be due to factors such as non-uniform polyimide thickness, differences in the permittivity of the polyimide and metallic resonators compared to simulation parameters, and plasmonic losses from the metallic resonators. Another factor affecting the FWHM is the thickness of the polyimide spacer. If it exceeds the optimized thickness (tp = 50 μm), the FWHM of the transmission can increase, but the band flatness of the terahertz filter may be compromised. More details on optimising the polyimide thickness are provided in the supplementary material, Section 4. As indicated in Fig. 3c, as the temperature of the multistacked MM integrated with the VO2 thin film changes from T = 50–90 °C, the transmission amplitude calculated through THz-TDS (and obtained from CST simulation) changes from 78% (92%) to 24% (27%) at the central frequency (Fc = 1.15 THz). To understand the modulation characteristics, we define the intensity modulation depth41 as \(M_{d} = \left\{ {\left( {\left| {T - T_{0} } \right|} \right)/T_{0} } \right\} \times 100\%\), where T is the transmittance of the sample when the temperature is highest i.e. T = 90 °C and T0 is the transmittance when the temperature is the below phase transition that is T = 50 °C. As the temperature increases from T = 50 °C to T = 90 °C, the modulation depth at the center frequency (fc = 1.15 THz) achieved through the experiment (and from CST simulation) was 55% (77%), which is reasonably higher for the multi-stacked bandpass filter spanning in the range of more than 200 GHz.

Fig. 3
figure 3

(a) Simulated, theoretically calculated, and experimentally measured transmission characteristics for a flexible MM, alongside their schematic and fabricated sample image. (b) VO2 thin film, deposited on the quartz substrate, where the transmission amplitude decreases as the temperature changes from 50 to 90 °C. (c) Illustration of the multi-stacked MM integrated with the VO2 thin film and transmission modulation w.r.t change in temperature.

Full size image

Modulation speed of the device

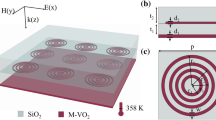
To investigate the dynamic modulation performance of VO₂-based metamaterial device, we performed time-resolved measurements by monitoring the transmission response under controlled electrical pulsing. The applied electrical pulse was used to heat a micro ceramic heater (MCH) integrated beneath the metamaterial device, as shown in Fig. 4b. The heater used in our setup has the following specifications: outer diameter 23 mm, inner diameter 4 mm, thickness 1.2 mm, and resistance of 27.33 Ω. When operated at a constant current of 2.5 A, the system consumed approximately 4.2 W of power, which was sufficient to trigger the insulator-to-metal phase transition in the VO₂ layer. A photographic image of the heating element is shown in the inset of Fig. 4b.

Fig. 4
figure 4

Dynamic and long-term stability of the VO₂-based flexible metamaterial (MM). (a) Time-resolved transmission at 1.1 THz under periodic 2.5 A, 6 s current pulses, showing repeatable modulation. (b) Schematic of the MM placed on a heating control element; inset shows the micro ceramic heater. (c) Transmission spectra at 50 °C and 90 °C after fabrication and 1 year later, confirming stable performance over time.

Full size image

In the experimental protocol, a rectangular-shaped current pulse with an amplitude of 2.5 A and a duration of 6 s was applied periodically at one-minute intervals. The resulting Joule heating modulated the transmission of terahertz waves through the VO₂-based structure. The switching behaviour was evaluated by tracking the time-dependent change in transmission amplitude, as illustrated in Fig. 4a. The switching response exhibits a rise time of approximately 3.4 s and a fall time of around 2 s, indicating efficient and reasonably fast electro-thermal modulation performance under moderate power input. Further enhancement of switching speed could be achieved by using integrated microheaters or through optimised thermal engineering to reduce the device’s thermal mass.

Furthermore, the long-term stability of the device was evaluated by comparing the transmission modulation characteristics of the VO₂-integrated hybrid metamaterial at two time intervals, initially after fabrication and again after 1 year. As shown in Fig. 4c, the modulation depth and transmission behaviour remain nearly identical, indicating excellent long-term operational stability. During this period, the device was stored at room temperature under a controlled ambient humidity of approximately 50%. The component most susceptible to degradation in such devices is typically the VO₂ layer, due to its volatile nature when directly exposed to environmental conditions. However, in our case, the VO₂ is encapsulated beneath the first layer of the polyimide-coated metamaterial structure, effectively protecting it from environmental exposure. This encapsulation strategy has proven critical in preventing material degradation, thereby ensuring the long-term durability and performance consistency of the device.

Discussions

To elucidate the impact of subwavelength micro-resonator structures on the broadening of the transmission amplitude bandwidth, we computed electric field distributions for TE-polarised light using numerical simulations in CST software. Field distributions at four frequencies F1 = 0.24 THz, F2 = 1.05 THz, F3 = 1.34 THz, and F4 = 1.90 THz were examined. Frequencies F2 and F3 exhibited maximum transmission amplitude, whereas F1 and F4 showed minimum amplitude, as indicated by dashed lines in Fig. 5a. The cross-sectional field distribution (along the X–Z plane intersecting the resonators’ edge) and the excited resonators for each layer (front view) are depicted in Fig. 5c–f, with dashed circles representing the excitation of the individual resonators at different frequencies. The orientation of the cutting plane is shown in Fig. 5b. Analysis of the field distribution at these frequencies reveals that resonator excitation is predominantly due to electric dipoles, evident from the front view of the excited resonators in Fig. 5c–f. Both metallic resonators(top and bottom) distinctly contribute to bandwidth broadening and resonance strength. Specifically, the resonance peak at F2 is primarily due to excitation of the upper layers, with minimal contribution from the bottom layer (Fig. 5d), while the resonance dip at F3 is mainly due to excitation of the lower resonators, with negligible upper resonator contribution. The simultaneous excitation of both resonators at F2 and F3 signifies the role of coupling in broadband enhancement. Figure 5d,e confirm that the broadening in terahertz transmission amplitude results from the superimposition of resonance frequencies due to individual resonators and their coupling. The electric field distribution at frequencies F1 and F4 indicates that excitation occurs only within the transmission band (F3–F2), and the broadening is primarily due to the excitation of resonators within this band range. To further understand the role of different resonators and their contributions to bandwidth broadening, transmission line models have been explored in the subsequent section.

Fig. 5
figure 5

(a) Electric field distributions at four frequencies: F1 = 0.24 THz, F2 = 1.05 THz, F3 = 1.34 THz, and F4 = 1.90 THz. (b) Cross-sectional plane of the field distribution (along the x–z plane cutting through the edge of the resonators). (c–f) Side view of the MM and field distributions of the excited resonators at the four frequencies, illustrating coupling between the resonators.

Full size image

Transmission line model of hybrid metamaterial

Building on the previous discussion, VO2 transitions from an insulating to a metallic phase near 68 °C, altering its lattice structure from monoclinic to tetragonal38. In its dielectric phase (σ = 15 S/m), the VO2 film can be modelled as a transmission line comprising a shunt capacitor (CD) and a resistor (RD). Conversely, in the metallic phase (σ = 14,000 S/m), it can be represented by a shunt inductance (LM) and a series resistance (RM). The capacitance CD in the dielectric phase can be calculated using Eq. (5) 42,43:

$$C_{D} = \frac{{\varepsilon_{0} \varepsilon_{r} A}}{d} = \frac{{\varepsilon_{0} \varepsilon_{r} \left( {p \times p} \right)}}{d}$$
(5)

where \(\varepsilon_{0}\) is the permittivity of free space, \(\varepsilon_{r}\) = 36 is the dielectric constant43 of VO2, A is the meta-atom’s area, and d is the film thickness. RD accounts for dielectric losses and is determined by fitting the simulated transmission amplitude to the transmission line model. Figure 6a,b show the simulated transmission amplitudes fitted with the transmission line model for the dielectric and metallic phases, respectively, along with their circuit representations and structural phases.

Fig. 6
figure 6

(a,b) Simulated and circuit-modeled transmission amplitudes for VO₂ in its dielectric (monoclinic) and metallic (tetragonal) phases, respectively, including their circuit representations. (c) Unit cell MM with its equivalent lumped circuital model. (d) Circuital model of the multistacked MM without the VO₂ layer, and (e) its corresponding simulated and calculated transmission amplitude. (f,h) Equivalent circuit representations of the multistacked MM when VO₂ is in the dielectric and metallic phases, respectively. (g,i) Corresponding transmission amplitudes fitted with circuit theory for the dielectric (DP) and metallic phases (MP).

Full size image

To gain a better understanding of the resonance mechanism of the broadband active modulator, a circuital model of coupled resonators, with and without the integration of the VO₂ thin film, was employed. Two identical resonators, when multistacked and coupled to each other, enhance the bandwidth of the transmission spectrum. The VO₂ layer modulates the transmission amplitude in response to temperature changes. The polyimide spacer and quartz substrate are treated as short-length transmission lines with impedances calculated as \(z = z_{0} /\sqrt {\varepsilon_{s} }\) (where \(\varepsilon_{s}\) is the permittivity of the material), yielding 221 Ω for polyimide and 196 Ω for quartz. Figure 6c presents the circuit representation of a single complementary cross-shaped resonator. Inductors (L) and capacitors (C) are added in parallel for the metamaterial (MM) unit cell, with resistance (R) in series with inductors to account for optical losses25,26,44,45. Figure 6d shows the circuit representation of the multistacked MM without the VO₂ film. The simulation results closely match the Transmission Line Model, as depicted in Fig. 6e.

Figure 6f,h illustrate the circuit models for the coupled MM with VO2 in its dielectric and metallic phases, respectively. The transmission responses from simulations align well with the TL models, shown in Fig. 6g,i. In the dielectric phase (Fig. 6f), VO₂ is represented by a shunt capacitor (CD) and resistor (RD), resulting in maximum transmission amplitude due to higher RD, indicating insulating behaviour. In the metallic phase (Fig. 6h), VO2 is modelled with a shunt inductor (LM) and a series resistor, leading to a decrease in transmission amplitude. A higher LM value signifies the metallic behaviour of the VO2 film. The fitting parameters L, C, and R are provided in Table 1.

Table 1 Circuit parameters for calculating the electromagnetic response of the TL models.
Full size table

In conclusion, we have developed an ultra-broadband, multistacked, tunable metamaterial-based modulator integrated with a VO₂ thin film. This hybrid MM provides ultra-broadband transmission with an FWHM of 1.02 THz and a modulation depth of 55% at the center frequency of 1.15 THz, observed with a temperature change from 50 to 90 °C. Our simulations indicate an FWHM of 0.76 THz and a modulation depth of 75%. The difference between calculated and simulated spectra is primarily due to variations in the polyimide spacer thickness, non-uniformity in polyimide thickness, discrepancies in permittivity values, and plasmonic losses from metallic resonators. Prior to integration, we thoroughly examined the thermal properties of the VO₂ film. The metamaterial on the PET substrate exhibited an FWHM of 0.90 THz (0.76 THz) through THz-TDS (and CST simulation). Using a transmission line model, we analysed the role of resonators in bandwidth broadening and the effect of the VO₂ thin film on transmission amplitude modulation. This adaptable approach can be applied to various terahertz wave control applications by adjusting resonator designs and thin films, including 2D materials. The straightforward fabrication process allows for metamaterial translation onto different substrates. Our versatile and scalable hybrid phase-change photonic framework holds promise for future advancements in phase-change terahertz photonics.