Abstract
The problem of L2-gain analysis and anti-windup (AW) fault-tolerant controller design of a class of time-varying delay discrete-time switched systems with actuator saturation and external disturbances is investigated by using the multiple Lyapunov functionals method. Firstly, for each subsystem, we construct an AW fault-tolerant controller consisting of a dynamic state feedback (DSF) controller and an AW compensator, such that the closed-loop system with actuator faults can meet the disturbance attenuation performance index and ensure that the state trajectories of the closed-loop system are bounded under the action of external disturbances. Then, the problem of estimating the allowable interference capacity is transformed into a constrained optimization problem. Next, a sufficient condition on the existence of the restricted L2-gain is established, and the minimum upper bound of the restricted L2-gain is obtained by solving the constrained optimization problem. Finally, the DSF controller gain and AW compensator gain of the AW fault-tolerant controller are obtained by solving the above two optimization problems which have been further handled. A numerical example is given to show the effectiveness and feasibility of the proposed method.
Similar content being viewed by others
Introduction
Switched systems are a very important class of hybrid systems that consist of a finite number of subsystems and a switching signal for autonomously selecting a particular subsystem at different moments1,2,3. Due to the wide application of switched system in practical engineering, in recent years, it has attracted extensive attention from scholars4,5,6. The main analysis tools for studying switched systems are multiple Lyapunov functions method7, the switched Lyapunov function method8, and the average dwell time scheme9. The multiple Lyapunov functions method was used to study the fault estimation problem of non-uniformly sampled systems with actuator faults and bounded disturbances in7. By utilizing switched Lyapunov function method8, considered the control problem of dynamically disturbed partially unknown nonlinear switched systems. By using the slow state feedback control method, the persistent dwell time (PDT) switching law was first proposed for a class of discrete-time singularly perturbed switched systems in9. Specifically, the multiple Lyapunov functions method has been demonstrated as a more powerful and effective tool for identifying a class of useful switching laws.
What’s more, switched systems will inevitably encounter various external disturbances in practice, so L2-gain analysis and design of switched systems have become a very meaningful research topic10. Ref11. considered the multiple Lyapunov functions method to study the stability and L2-gain analysis of a class of switched linear systems. The multiple Lyapunov functions method was used to study the finite-time analysis of stability and L2-gain for mode unstable switched systems in12. Meanwhile, it is well known that actuator saturation is unavoidable for practical control systems, because the device as the actuator is subjected to a certain physical limit or the output amplitude of the actuator reaches the limit, which affects the performance of the system and even leads to the instability of the closed-loop system13,14,15,16. In recent years, with the deep research of the switched systems, it is necessary to consider actuator saturation in the L2-gain analysis and control design of the switched systems. Therefore, more and more scholars pay attention to the L2-gain problem of switched system with actuator saturation17,18. Ref19. investigated the L2-gain analysis and synthesis problem for a class of uncertain switched systems with actuator saturation, by using the switched Lyapunov function approach20. investigated the problem of L2-gain analysis and anti-windup control for a class of switched systems with actuator saturation by using the single Lyapunov function method.
On the other hand, the effect of actuator failure on system stability is huge, or even brings disastrous consequences. Thus, the fault-tolerant control of switched systems has received extensive attention and the fault-tolerant control strategy is proposed from many scholars in recent years21,22,23,24. In25 a fault tolerant control strategy for uncertain switched systems that can be used in the case of additive actuator faults was proposed by using the multiple Lyapunov functions method26. considered fault-tolerant control of a class of uncertain switched nonlinear systems against partial actuator failures by using the common Lyapunov function technique27. used convex combination technology and linear matrix inequality to design the reliable controller and the corresponding switched strategy. In28, an average dwell time method for fault-tolerant control of a class of uncertain switched linear time-delay systems was proposed, and the proposed control strategy ensures exponential stabilization of this type of time-delay systems with actuator faults.
In addition, time delay occurs frequently in practical engineering systems, and it is often a major factor causing system instability and performance decay. In29, static anti-windup compensators for a class of saturated constrained nonlinear systems with both state and input time-varying delays were designed, by using the augmented Lyapunov–Krasovskii and sector conditions30. was concerned with the anti-windup design problem for linear time-delay systems with actuator saturation by utilizing the information of the time delay sufficiently and the generalized delay-dependent sector conditions. Meanwhile, the control problem of time-delay switched systems has attracted the attention of scholars and some beneficial research results are obtained. For instance31, This article is concerned with the stability and stabilization of switched time-delay systems with exponential uncertainty based on an improved state-dependent switching strategy32. studied the problem of fault estimation for a class of discrete-time switched nonlinear systems with mixed time delay by using the multiple Lyapunov–Krasovskii functionals and the average dwell time methods. In33, stability analysis and stabilization control of discrete-time impulsive switched time-delay systems with all unstable subsystems are discussed by the mode-dependent interval dwell-time switching rule.
To sum up, many control problems have been studied for switched systems by scholars. At present, there is less research on the problem of L2-gain analysis and anti-windup fault-tolerant control of discrete switched systems with time-varying delay and actuator saturation. However, the performance analysis and design of switched systems have become more complicated when switching signal, actuator failure, time delay and actuator saturation interact, which poses a great challenge to analysis and controller design. Switching signals can amplify the effects of actuator faults and saturation, particularly in the presence of time delays. Actuator faults, such as partial or complete loss of effectiveness, reduce the available control authority, while saturation limits the control input, leading to compounded performance degradation and potential instability. Time delays further exacerbate these issues by introducing additional dynamics that may destabilize the system or obscure fault symptoms. These interactions create a complex, nonlinear, and time-varying control environment, making it challenging to ensure stability and performance.
Thereby, we will study the L2-gain analysis and anti-windup fault-tolerant control of a class of discrete-time switched systems with time-varying and actuator saturation by using the multiple Lyapunov functionals approach. Firstly, the AW fault-tolerant controller consisting of a DSF controller and an AW compensator is constructed for each subsystem, and then a sufficient condition for the system state to be bounded with actuator faults and external disturbances is derived by using the multiple Lyapunov functionals method, and the maximum allowable level of disturbances is obtained by solving the constrained optimization problem. Then on this basis, the constrained L2-gain is analyzed for the closed-loop system. Next, the DSF controller and the anti-windup compensator are designed to ensure the maximization of the system tolerant interference capability and the minimization of the upper bound of the restricted \(L_{2}\)-gain. Finally, a numerical example is given to show the effectiveness and feasibility of the proposed method.
Problem formulation and preliminaries
Consider a class of discrete-time time-varying delay switched systems with actuator saturation and external disturbances as follows
where \(\varphi (\theta )\) is the vector-valued initial function, \(d(k)\) is a time-varying delay satisfying \(0 \le d_{1} \le d(k) \le d_{2}\). \(A_{\sigma }\), \(A_{d\sigma }\), \(B_{1\sigma }\), \(H_{1\sigma }\) and \(C_{\sigma }\) are constant matrices with appropriate dimensions, \(x(k) \in {\text{R}}^{n}\) is the system state vector, \(u(k) \in R^{q}\) is the control input vector, \(w(k) \in R^{h}\) is the external disturbance input vector and \(z(k) \in {\text{R}}^{p}\) denotes the controlled output vector. \(\sigma :[0,\:\infty ) \to I_{N} = \{ 1,\: \cdots ,\:N\}\) denotes switching signal and it is a piecewise right continuous constant, and \(\sigma = i\) means that the \(i{\text{ - th}}\) subsystem is activated.
It is well known that the L2-gain can be used to analyze the disturbance attenuation ability of systems. However, for systems with actuator saturation, the large external perturbations will result in unbounded states and thus we make the following assumption
where \(\beta\) is a positive number which indicates the allowable interference capability of the system. \(sat:R^{q} \to R^{q}\) is the standard vector-valued saturation function. The definition is as follows
Obviously, without loss of generality, we assume unit saturation limits, since non-standard saturation functions can always be obtained by altering the matrix by employing appropriate transformations, and for simplicity, and in accordance with the notation prevalent in the literature, we adopt the notation \(sat( \bullet )\) to denote both scalar and vector saturation functions.
Considering actuator failures, we introduce a fault matrix \(M{}_{i}\), in which
where \(m_{ijl}\) and \(m_{iju}\) are given constants, \(m_{ij} = 0\) means that the \(j - th\) actuator is completely disabled, and \(m_{ij} = 1\) indicates that the \(j - th\) actuator is normal. Further \(0 < m_{iju} < m_{ij} < m_{ijl} < 1\) represents the \(j - th\) actuator partial failure.
Let \(M_{0i} = diag\left\{ {m_{0i1} ,m_{0i2} ,...m_{0iq} } \right\},\;m_{0ij} = \frac{{m_{ijl} + m_{iju} }}{2},\)
Then, the resulting matrix \(M_{i}\) can be written as
where \(\left| {L_{i} } \right| = diag\left\{ {\left. {\left| {l_{i1} } \right|,\left| {l_{i2} } \right|,...\left| {l_{iq} } \right|} \right\}} \right.\).
From the above Eq. (5), it can be seen that for the subsystem \(i\), the matrix \(M_{0i}\) is a constant matrix and the uncertainty of fault matrix \(M_{i}\) is only related to the matrix \(L_{i}\), then the closed-loop system containing actuator faults is
From34, we construct the following AW fault-tolerant controller containing DSF controller and AW compensator
where \(u(k)\) is the controller state, \(E_{ci} \in R^{q \times q}\) is the AW compensator gain, and matrices \(F_{i} \in R^{q \times n}\) and \(G_{i} \in R^{q \times q}\) are the DSF controller gain.
From (6) and (7) the above closed-loop system can be rewritten as the following form
Then, we define some new variables and matrices as follows
The resulting closed-loop system can be rewritten as
where \(\psi (v) = (sat(v) - v)\), \(v = \hat{N}_{i} \zeta = u(k),\) and the vector-valued initial function \(\hat{\phi }(\theta )\) is magnitude and difference bounded or say that the initial function \(\hat{\phi }(\theta )\) belongs to the following domain.
.
The following definitions and mathematical notation will be used for system (9):
Definition 1
Ref35,36.: Given \(\gamma> 0\). The system (9) is said to have a restricted L2-gain less than \(\gamma\), if there exists a switching law \(\sigma\), the following condition is satisfied under the zero initial condition,
for all non-zero \(w(k) \in W_{\beta }^{2}\).
Definition 2
Ref37.: Let \(P \in {\text{R}}^{{\left( {q + n} \right) \times \left( {q + n} \right)}}\) represent the positive definite matrix and define the ellipsoid:
Definition 3
Ref37.: For the matrix \(\hat{N}_{i} ,H_{i} \in R^{{q \times \left( {q + n} \right)}}\), we define the following symmetric polyhedron.
where \(\hat{N}_{i}^{j}\),\(H_{i}^{j}\), denote the \(j - th\) row of the matrices \(\hat{N}_{i}\) and \(H_{i}\), respectively.
Lemma 1
Ref38.: For the symmetric matrix.
where \(S_{11} \in {\text{R}}^{n \times n} ,S_{12} = S_{21}^{{\text{T}}} \in {\text{R}}^{n \times q} ,S_{22} \in {\text{R}}^{q \times q} ,\) the following three conditions are equivalent
Lemma 2
Ref39.: Consider the function \(\psi (v)\) defined above, if \(\zeta \in L(\hat{N}_{i} ,H_{i} )\), then the relation.
holds for any matrix \(J_{i} \in R^{q \times q}\) diagonal and positive definite.
Lemma 3
Ref40.: Let \(Y\), \(U\) and \(V\), be given matrices of appropriate dimensions, then for any matrix \(\Gamma\) satisfying \(\Gamma^{{\text{T}}} \Gamma \le I\),
if and only if there exists a constant \(\lambda> 0\) such that
Disturbance tolerance
In this section, by using the multiple Lyapunov functionals approach, a sufficient condition for the state trajectory of the closed-loop system (9) to be bounded is given under the assumption that the AW fault-tolerant controller gains are known. How to design the AW fault-tolerant controller problem will be given in section"Control synthesis solution".
Theorem 1:
Consider the closed -loop switched system (9). For a given positive scalar \(\rho_{1}\), if there exist positive definite matrices \(P_{i} , \, Q_{1} , \, Q_{2} , \, Q_{3} , \, Z_{1} , \, Z_{2}\), positive definite diagonal matrices \(J_{i}\), and a set of scalars \(\beta_{ir}> 0\), such that.
and
where
and the initial conditions are satisfied
where \(\lambda_{\iota }\), \(\iota = 1,\,\,2,\;3 \cdots 6\), are positive scalars satisfying
then any trajectory of the system (9) starting from the region \(\cup_{i = 1}^{N} (\Omega (P_{i} ,\:\rho_{1} ) \cap \Phi_{i} )\) will remain inside the region \(\cup_{i = 1}^{N} (\Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} )\) for every \(\forall w \in W_{\beta }^{2}\), under the sate-dependent switching law
Proof:
By condition (15), if \(\forall \zeta \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i}\), then \(\zeta \subset L(\hat{N}_{i} ,H_{i} ),\) therefore in view of Lemma 2, for \(\forall \zeta \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i}\) it follows that \(\psi (v) = (sat(v) - v)\) satisfies \(\psi (\hat{N}_{i} \zeta )J_{i} (\psi (\hat{N}_{i} \zeta ) - H_{i} \zeta ) \le 0,\forall i \in I_{N}\).
In view of the switching law (17), for \(\zeta \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\), the \(i - th\) subsystem is active.
Choose the Lyapunov–Krasovskii functionals of the closed-loop system (9) as
where
Case 1:\(\sigma (k + 1) = \sigma (k) = i\),for \(\forall \zeta (k) \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\). It follows that
Then, combining with Lemma 2 and condition (15), we have
Multiplying (14) from the left by \(\left[ {\begin{array}{*{20}c} {\zeta \left( k \right)} \\ {\zeta \left( {k - d\left( k \right)} \right)} \\ {\zeta \left( {k - d_{1} } \right)} \\ {\zeta \left( {k - d_{2} } \right)} \\ {\psi (v)} \\ {w(k)} \\ \end{array} } \right]^{T}\) and then from the right by \(\left[ {\begin{array}{*{20}c} {\zeta \left( k \right)} \\ {\zeta \left( {k - d\left( k \right)} \right)} \\ {\zeta \left( {k - d_{1} } \right)} \\ {\zeta \left( {k - d_{2} } \right)} \\ {\psi (v)} \\ {w(k)} \\ \end{array} } \right]\), we have.
Then, according to the above two inequalities, we can obtain
By switching law (17) again, we can get
therefore
Case 2:\(\sigma (k) = i,\) \(\sigma (k + 1) = r\) and \(i \ne r,\) for \(\forall \zeta (k) \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\). By switching law (17), we can get
From the switching law(17) again, it follows that
which indicates
By combining Eqs. (19) and (20), we can obtain
Thus, it follows that
which in turn gives
Next, it is easy to see that the following inequalities hold.
Thus, we have
Due to \(\sum\limits_{k = 0}^{\infty } {w^{{\text{T}}} (k)w} (k) \le \beta\), we have
Thus, in light of \({\mathbb{Q}}(\zeta (l)) \le \rho_{1}\), it is easy to see that \(\zeta^{T} (0)P_{i} \zeta (0) \le \rho_{1}\), and the control constraints \(L(\hat{N}_{i} ,H_{i} )\) are also satisfied owing to (15). Thus, all the trajectories of closed loop system (9) that start from \(\cup_{i = 1}^{N} (\Omega (P_{i} ,\:\rho_{1} ) \cap \Phi_{i} )\) remain in set \(\cup_{i = 1}^{N} (\Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} )\).This proof is completed.
From the above conclusions, we know that the disturbance tolerance capacity of the closed loop system should be estimated before analyzing the restricted L2-gain. It is obvious that the larger the \(\beta\), the larger the disturbance tolerance capacity is. Thus, the largest disturbance tolerance level \(\beta^{*}\) for the closed-loop system (14) can be obtained by solving the following optimization problem
Applying the lemma 1 to (14), we get
where
Due to \(\tilde{A}_{i} = \hat{A}_{i} + I_{R} K_{i} + \hat{B}_{i} M_{0i} L_{i} I_{R}^{T} ,\)\(V_{1i} = 2(\hat{B}_{i} + I_{R} E_{ci} )M_{0i} \hat{G}_{i}\), the inequality (24) can be arranged as
From Lemma 3, (25) holds if and only if the following matrix inequality holds
where \(\lambda_{1i}\) > 0.
Then, using Lemma 1 to (26), we have
Then, the inequality (27) can be again arranged as
From Lemma 3, (28) holds if and only if the following matrix inequality holds
where \(\lambda_{2i}\) > 0.
Then, in the light of Lemma 1, we can get
where
Next, let \(\varepsilon = \left( {\rho_{1} + \beta } \right)^{ - 1}\) and we will explain that the constraint (15) can be transformed into the following matrix inequality
where \(\delta_{ir}> 0\),and \(\hat{N}_{i}^{j}\),\(H_{i}^{j}\) denotes the \(j - th\) row of \(\hat{N}_{i}\) and \(H_{i}\) respectively.
Let \(G_{i} = P_{i} - \sum\limits_{r = 1,r \ne i}^{N} {\delta_{ir} (P_{r} - P_{i} )}\). For \(\forall \zeta (k) \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i}\), then from switching law (17), it is clear that
and
Then, we get
Finally, we have
or
(34) implies that if \(\forall \zeta (k) \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i}\), then \(\zeta (k) \in L(\hat{N}_{i} ,H_{i} )\). As a result, constraint condition \(\Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} ),\:i \in I_{N}\), can be transformed into (31).
Thus, we can rewrite the optimization problem (23) as follows:
If we do not consider the anti-windup compensation cases, we can get the corollary 1.
Corollary 1:
Consider the closed -loop switched system (9). For a given positive scalar \(\rho_{1}\), if there exist positive definite matrices \(P_{i} , \, Q_{1} , \, Q_{2} , \, Q_{3} , \, Z_{1} , \, Z_{2}\), positive definite diagonal matrices \(J_{i}\), and a set of scalars \(\beta_{ir}> 0\), such that.
and
where
then for the closed-loop system (9), under the sate-dependent switching law (17) and the initial conditions (16), the state trajectory starting from the region \(\cup_{i = 1}^{N} (\Omega (P_{i} ,\:\rho_{1} ) \cap \Phi_{i} )\) will remain inside the region \(\cup_{i = 1}^{N} (\Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} )\) for every \(\forall w \in W_{\beta }^{2}\).
\({L}_{2}\)4. -Gain analysis
In this section, we will use the multiple Lyapunov functionals method to solve the restricted L2-gain problem for the system (9), based on Theorem1, that is, the state trajectories of the system are bounded. Similarly, the design method of anti-windup fault-tolerant controller will be proposed in section"Control synthesis solution".
Theorem 2:
Consider the closed-loop system (9). For a given constant \(\beta \in (0,\:\beta^{*} ]\) and \(\gamma> 0\), suppose there exist positive definite matrices \(P_{i} , \, Q_{1} , \, Q_{2} , \, Q_{3} , \, Z_{1} , \, Z_{2}\), diagonal positive definite matrices \(J_{i}\), and a set of scalars \(\beta_{ir}> 0\), such that.
and
where
Then the restricted \(L_{2}\)-gain from \(w\) to \(z\) over \(w \in W_{\beta }^{2}\) is less than \(\gamma\) under the state-dependent switching law
Proof:
Using the similar method as for proving Theorem 1, we choose the Lyapunov–Krasovskii functionals of the closed-loop system (9) as.
where
Here, we still divide the proof into two parts.
Case 1:\(\sigma (k + 1) = \sigma (k) = i\),for \(\forall \zeta (k) \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\). It follows that:
Thereby,.
Then, combining with Lemma 2 and condition (37), we have
Multiplying (36) from the left by \(\left[ {\begin{array}{*{20}c} {\zeta \left( k \right)} \\ {\zeta \left( {k - d\left( k \right)} \right)} \\ {\zeta \left( {k - d_{1} } \right)} \\ {\zeta \left( {k - d_{2} } \right)} \\ {\psi (v)} \\ {w(k)} \\ \end{array} } \right]^{T}\) and then from the right by \(\left[ {\begin{array}{*{20}c} {\zeta \left( k \right)} \\ {\zeta \left( {k - d\left( k \right)} \right)} \\ {\zeta \left( {k - d_{1} } \right)} \\ {\zeta \left( {k - d_{2} } \right)} \\ {\psi (v)} \\ {w(k)} \\ \end{array} } \right]\), we have
Then, according to the above two inequalities, we can obtain.
\(\Delta V(\zeta (k)) < w^{{\text{T}}} (k)w(k) - \gamma^{ - 2} \zeta^{{\text{T}}} (k)\hat{C}_{i}^{T} \hat{C}_{i} \zeta (k) - \sum\limits_{r = 1,\:r \ne i}^{N} {\beta_{ir} \zeta^{{\text{T}}} (k)(P_{r} - P_{i} )\zeta (k)} .\) By switching law (38), we can get
Therefore
Case 2:\(\sigma (k) = i,\) \(\sigma (k + 1) = r\) and \(i \ne r,\) for \(\forall \zeta (k) \in \Omega (P_{i} ,\:\rho_{1} + \beta ) \cap \Phi_{i} \subset L(\hat{N}_{i} ,H_{i} )\). By switching law (38), we can get
From the switching law (38), it follows that
which indicates
By combining Eqs. (40) and (41), we can obtain
Thus, it follows
which in turn gives
Due to \(\zeta (0) = 0\) and \(V(\zeta (\infty )) \ge 0\), we obtain, we obtain
(44) means that the switched system (9) has the restricted L2-gain from \(w\) to \(z\) over \(w \in W_{\beta }^{2}\) less than \(\gamma\). This proof is complete.
Just as (15) is treated as (31), (37) can also be treated as (31), similar to the processing of (15) into (31), (37) can also be processed into (31).
It follows from Theorem 2 that for each given \(\beta \in (0,\:\beta^{*} ]\), the minimum upper bound on the restricted L2-gain of the closed-loop system (9) can be obtained by solving the following optimization problem
Then, we adopt the similarly method for converting optimization problem (23) into optimization problem (30). If the following matrix inequality holds, then matrix inequality (36) holds.
where
where, \(\varsigma = \gamma^{2}\).
Then, optimization problem (45) can be expressed as
Control synthesis solution
In this section, we consider the anti-windup compensator gain \(E_{ci}\) and the dynamic state feedback controller gain \(K_{i}\) as the variables to be designed, which allows the performance of the closed-loop system (9) to be further improved.
Firstly, set \(P_{i}^{ - 1} = X_{i}\), \(F_{i} = H_{i} X_{i}\),\(J_{i}^{ - 1} = S_{i}\), \(Q_{1}^{ - 1} = U\), \(Q_{2}^{ - 1} = U_{1}\), \(Q_{3}^{ - 1} = U_{2}\), \(Z_{1}^{ - 1} = U_{3}\), \(Z_{2}^{ - 1} = U_{4}\),\(K_{i} X_{i} = Y_{i}\). Multiplying both sides of the inequality (24) by the diagonal matrix \(\{ P_{i}^{ - 1} ,Q_{3}^{ - 1} ,Q_{1}^{ - 1} ,Q_{2}^{ - 1} {,}J_{i}^{ - 1} ,I,P_{i}^{ - 1} ,P_{i}^{ - 1} ,P_{i}^{ - 1} ,I,I\}\) respectively, and using lemma 1, we have
where
A similar process is applied to (31), then we also obtain
where, \(\hat{N}_{i}^{j}\), \(H_{i}^{j}\) denotes the \(j - th\) row of \(\hat{N}_{i}\) and \(H_{i}\) respectively.
Thus, the maximum allowable disturbance level \(\beta^{*}\) can be established by solving the following optimization problems.
Next, multiplying both sides of the inequality (46) by the diagonal matrix \(\{ P_{i}^{ - 1} ,Q_{3}^{ - 1} ,Q_{1}^{ - 1} ,Q_{2}^{ - 1} {,}J_{i}^{ - 1} ,I,P_{i}^{ - 1} ,P_{i}^{ - 1} ,P_{i}^{ - 1} ,I,I\}\) respectively, and using lemma 1, we have
where
where,\(\tau = \gamma^{2} .\)
Therefore, the minimum upper bound on the restricted L2-gain of the closed-loop system (9) can then be obtained by solving the following optimization problem
Then, we can obtain the anti-windup compensator gain matrices \(E_{ci}\) by solving the above two optimization problems (50) and (52), and the corresponding dynamic state feedback controller gain matrices can be calculated as \(K_{i} = Y_{i} X_{i}^{ - 1}\).
Remark 1.
A key feature of the proposed anti-windup approach is that the anti-windup compensator remains inactive when saturation does not occur, thereby preserving the nominal design performance of the system. In practice, systems operate in non-saturated conditions most of the time, meaning that the design performance is unaffected in the majority of cases. The anti-windup compensator only becomes active when saturation occurs, ensuring system stability and performance during saturation. As a result, the anti-windup method has strong practical engineering relevance for the switched systems. However, in the convex hull approach36,38, as the control input dimension and subsystem count increase, the number of linear matrix inequalities (LMIs) grows exponentially, leading to a prohibitively high computational burden.
Numerical simulation
This section presents two numerical examples to demonstrate the effectiveness of the proposed method. We consider the following a class of time-varying delay discrete-time switched systems with actuator saturation and external disturbances.
Example 1
where \(\sigma \in I_{2} = \{ 1,\:2\}\),
Assuming that the range of actuator faults is \(0.1 \le m_{ij} \le 0.9,\) and according to the continuous fault model we can get
Let \(M_{1} = \left[ {\begin{array}{*{20}c} {0.4} & 0 \\ 0 & {0.5} \\ \end{array} } \right],\)\(M_{2} = \left[ {\begin{array}{*{20}c} {0.6} & 0 \\ 0 & {0.5} \\ \end{array} } \right],\)\(d_{1} = 1,\)\(d_{2} = 9,\)\(\rho_{1} = 0.5,\)\(\lambda_{11} = 30,\) \(\lambda_{12} = 0.033.\)
Then, by solving the optimization problem (50) we can obtain the following feasible solutions
and the AW compensator gains for the closed-loop system are
Then, the dynamic state controller gains of the closed-loop system are computed as
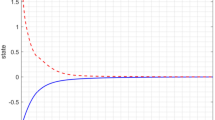
Then, we select \(\omega (t) = \sqrt {2\beta^{*} } e^{ - t}\) as external interference input for simulation. Figure 1 shows the state response curve of the switched system (53). The state response of the controller of the switched system (53) is shown in Fig. 2. Figure 3 shows the switching signal of the closed-loop system. The control input signal for the switched system (53) is shown in Fig. 4. Figure 5 shows the variation of Lyapunov function values of the switched system (53). It can be seen through Fig. 5 that the values of the Lyapunov function for the switched system (53) are consistently less than \(\beta^{*} = 12.2797\). This indicates that the state trajectories of the switched system (53) with the initial conditions always remains within this bounded set.
State response of the switched system (53).
State response of the controller of the switched system (53).
The switched signal for the switched system (53).
The input signal of the closed loop system (53).
Lyapunov function values for the switched system (53).
Then, for each given \(\beta \in (0,\:\beta^{*} ]\), we estimate an upper bound on the restricted L2-gain of the closed-loop system (53). Therefore, we can consider the following scenarios.
-
1. If \(\beta = 0.5,\) we obtain,\(\gamma = 23.0997\),
$$\begin{gathered} K_{1} = \left[ {\begin{array}{*{20}c} { \, 0.1633} & { \, 0.2960} & { \, 0.1014} & { \, 2.8474} \\ { - 1.6428} & { - 2.8632} & { - 1.5806} & { - 17.2502} \\ \end{array} } \right], \, E_{c1} = \left[ {\begin{array}{*{20}c} {0.3791} & { - 3.3134} \\ {0.6843} & { - 5.7767} \\ \end{array} } \right], \hfill \\ K_{2} = \left[ {\begin{array}{*{20}c} { \, 0.7071} & { \, 0.3001} & { - 0.0454} & { - 0.0424} \\ { - 3.4434} & { - 1.2942} & { - 1.0575} & { - 0.5768} \\ \end{array} } \right], \, E_{c2} = \left[ {\begin{array}{*{20}c} {1.5081} & { - 7.1632} \\ {0.6368} & { - 2.6950} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$ -
2. If \(\beta = 1\), we obtain \(\gamma = 23.1065\),
$$\begin{gathered} K_{1} = \left[ {\begin{array}{*{20}c} { \, 0.1626} & { \, 0.2949} & { \, 0.1000} & { \, 2.8581} \\ { - 1.6436} & { - 2.8645} & { - 1.5814} & { - 17.2529} \\ \end{array} } \right], \, E_{c1} = \left[ {\begin{array}{*{20}c} {0.3855} & { - 3.3244} \\ {0.6956} & { - 5.7955} \\ \end{array} } \right], \hfill \\ K_{2} = \left[ {\begin{array}{*{20}c} { \, 0.7086} & { \, 0.3010} & { - 0.0475} & { - 0.0443} \\ { - 3.4567} & { - 1.2986} & { - 1.0657} & { - 0.5794} \\ \end{array} } \right], \, E_{c2} = \left[ {\begin{array}{*{20}c} {1.5000} & { - 7.1100} \\ {0.6343} & { - 2.6733} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$ -
3. If \(\beta = 7.5\), we obtain \(\gamma = 23.1960\),
$$\begin{gathered} K_{1} = \left[ {\begin{array}{*{20}c} { \, 0.1630} & { \, 0.2955} & { \, 0.1008} & { \, 2.8534} \\ { - 1.6431} & { - 2.8636} & { - 1.5808} & { - 17.2503} \\ \end{array} } \right], \, E_{c1} = \left[ {\begin{array}{*{20}c} {0.3851} & { - 3.3222} \\ {0.6949} & { - 5.7918} \\ \end{array} } \right], \hfill \\ K_{2} = \left[ {\begin{array}{*{20}c} { \, 0.7078} & { \, 0.3005} & { - 0.0464} & { - 0.0435} \\ { - 3.4477} & { - 1.2956} & { - 1.0602} & { - 0.5768} \\ \end{array} } \right], \, E_{c2} = \left[ {\begin{array}{*{20}c} {1.5047} & { - 7.1100} \\ {0.6357} & { - 2.6742} \\ \end{array} } \right]. \hfill \\ \end{gathered}$$
Example 2
where \(\sigma \in I_{2} = \{ 1,\:2\}\),
Assuming that the range of actuator faults is \(0.2 \le m_{ij} \le 0.4,\) and according to the continuous fault model, we can get
Let \(M_{1} = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.3} \\ \end{array} } \right],\)\(M_{2} = \left[ {\begin{array}{*{20}c} {0.4} & 0 \\ 0 & {0.3} \\ \end{array} } \right],d_{1} = d_{2} = 1,\rho_{1} = 0.5,\lambda_{11} = 20,\lambda_{12} = 0.5.\)
Then, by solving the optimization problem (50) we can obtain the following feasible solutions.
and the AW compensator gains for the closed-loop system (54) are
Then, the dynamic state controller gains of the closed-loop system (54) are computed as
If we set \(E_{c1} = E_{c2} = 0\), then the optimal solution obtained is \(\beta^{*} = 1.6372\) based on corollary 1. Obviously, this shows that the interference tolerance of the closed-loop system (54) is enhanced under the action of the anti-windup compensator.
Then, we select \(\omega (t) = \sqrt {2\beta^{*} } e^{ - t}\) as external interference input for simulation. Figure 6 shows the state response curve of the switched system (54). The state response of the controller of the switched system (54) is shown in Fig. 7.
State response of the switched system (54).
State response of the controller of the switched system (54).
In the event of actuator failure, the state response is depicted in Figs. 8 and 9 for switched system (54) under the conventional anti-windup controller. Note that the conventional anti-windup controller here refers to a design that does not account for actuator failures. As evident from Figs. 8 and 9, the system states become unbounded when actuator failure occurs under this controller. In contrast, the anti-windup fault-tolerant controller ensures that the state trajectory remains within a bounded region, as demonstrated in Figs. 6 and 7. This confirms that the anti-windup fault-tolerant controller, designed using our proposed method, exhibits superior fault tolerance performance.
State response of system (54) under conventional anti-windup controller.
Additionally, Table 1 presents the relationship between the maximum allowable disturbance \(\beta^{*}\) and varying \(d\) values, obtained by solving optimization problem (50) (where \(d = d_{1} = d_{2}\)). The results demonstrate that the disturbance tolerance of closed-loop system (54) decreases as \(d\) increases.
Conclusion
In this paper, the problem of L2-gain analysis and anti-windup fault-tolerant controller design of a class of discrete-time switched systems with time-varying delay and actuator saturation is investigated by using the multiple Lyapunov functionals method. Firstly, with the anti-windup fault-tolerant controller given in advance, the sufficient conditions to be state bounded under the action of actuator fault and external disturbance are given for the closed-loop system, and then disturbance tolerance problem is transformed into a constrained optimization problem. Then, based on this condition, the constrained \(L_{2}\)-gain of a closed-loop system is analyzed and the minimum upper bound of the restricted \(L_{2}\)-gain is presented by solving a convex optimization problem. Finally, in order to obtain better performance of the closed-loop system, we design the AW controller to maximize the allowable disturbance capability of the closed-loop system as well as to minimize the restricted \(L_{2}\)-gain upper bound. A numerical simulation example is given to verify the effectiveness of the proposed method in this paper.
In this paper, we presuppose the availability of certain unknown parameters beforehand and subsequently reformulate the associated optimization challenges into problems featuring LMI constraints. Nonetheless, in real-world applications, these parameters inevitably influence the outcomes of the optimization processes. Consequently, determining the optimal selection of these parameters to achieve the highest possible level of disturbance tolerance and the lowest feasible upper limit of the constrained L2-gain presents a fascinating and complex area for investigation. Employing advanced optimization techniques, including genetic algorithms and ant colony optimization, could prove effective in identifying the ideal values for these parameters, meriting additional exploration and study. In addition, the Zeno phenomenon induced by minimum switching laws can cause significant issues, potentially resulting in severe harm to real-world engineering systems. As a result, in our forthcoming research, we intend to employ the dwell time approach to explore the fault-tolerant control challenges in switched systems experiencing actuator saturation and failure. The switching law developed using the dwell time method is expected to successfully prevent the occurrence of the Zeno phenomenon.
Data availability
All data generated or analysed during this study are included in this published article.
References
Wang, Z. M., Wei, A. & Zhang, X. Stability analysis and control design based on average dwell time approaches for switched nonlinear port-controlled hamiltonian systems. J. Franklin Inst. 356(6), 3368–3397 (2019).
Wang, J. & Zhao, J. Stabilisation of switched positive systems with actuator saturation. IET Control Theory Appl. 10(6), 717–723 (2016).
Qi, W., Zong, G., Hou, Y. & Chadli, M. SMC for discrete-time nonlinear semi-Markovian switching systems with partly unknown semi-Markov kernel. IEEE Trans. Autom. Control 68(3), 1855–1861 (2023).
Qi, W. H., Li, R. K., Park, J. H., Wu, Z. G. & Yan, H. Observer-based stabilization for discrete nonlinear semi-Markov jump singularly perturbed models with mode-switching delay. Sci. China Inform. Sci. 68(4), 149201 (2025).
Cheng, P., He, S., Stojanovic, V., Luan, X., & Liu, F. Fuzzy fault detection for Markov jump systems with partly accessible hidden information: An event-triggered approach. IEEE Transactions on Cybernetics. (2021)
Zhang, X., Wang, H., Stojanovic, V., Cheng, P., He, S., Luan, X., & Liu, F. Asynchronous fault detection for interval type-2 fuzzy nonhomogeneous higher-level Markov jump systems with uncertain transition probabilities. IEEE Transactions on Fuzzy Systems. (2021)
Zhang, J., Qiu, A., Mao, J., & Gu, J. Observer-based robust fault estimation under non-uniformly sampled measurements. In 2016 IEEE International Conference on Information and Automation (ICIA) (pp. 1290–1295). IEEE. (2016)
Aghababa, M. P. Lyapunov control method for mismatched uncertainty and gain variation compensation in switched systems. IEEE Trans. Syst. Man, Cybern.: Syst. 51(7), 4227–4237 (2019).
Qi, W. et al. Asynchronous Dynamic Output Feedback Control for Discrete Nonlinear Networked Semi-Markov Jump Models With Cyber Attacks and Applications. IEEE Trans. Autom. Sci. Eng. 22, 6316–6326 (2025).
Wang, Y. E., Wu, B. W. & Wu, C. Stability and L2-gain analysis of switched input delay systems with unstable modes under asynchronous switching. J. Franklin Inst. 354(11), 4481–4497 (2017).
Wang, Z. M., Wei, A., Zhao, X., & Zhang, C. Stability and L2-gain analysis based on multiple discontinuous Lyapunov function approaches for switched systems with unstable modes. International Journal of Control, 1–11. (2021)
Zhao, G. & Wang, J. Finite time stability and L2 -gain analysis for switched linear systems with state-dependent switching. J. Franklin Inst. 350(5), 1075–1092 (2013).
Hussain, M., Rehan, M., Ahn, C. K. & Tufail, M. Robust antiwindup for one-sided Lipschitz systems subject to input saturation and applications. IEEE Trans. Industr. Electron. 65(12), 9706–9716 (2018).
Chen, Y., Wang, Z., Fei, S. & Han, Q. L. Regional stabilization for discrete time-delay systems with actuator saturations via a delay-dependent polytopic approach. IEEE Trans. Autom. Control 64(3), 1257–1264 (2018).
Li, Y. & Lin, Z. Stability and performance of control systems with actuator saturation (Birkhäuser, 2018).
Du, D., Tan, Y. & Zhang, Y. Dynamic output feedback fault tolerant controller design for discrete-time switched systems with actuator fault. Nonlinear Anal. : Hybrid Syst. 16, 93–103 (2015).
Zuo, Z., Li, Y., Wang, Y. & Li, H. Event-triggered control for switched systems in the presence of actuator saturation. Int. J. Syst. Sci. 49(7), 1478–1490 (2018).
Zhang, X. Q. & Zhao, J. L2 -gain analysis and anti-windup design of discrete-time switched systems with actuator saturation. Int. J. Autom. Comput. 9(4), 369–377 (2012).
Li, T., Wang, T., Yu, Y. & Fei, S. Static anti-windup compensator for nonlinear systems with both state and input time-varying delays. J. Franklin Inst. 357(2), 863–886 (2020).
Zhao, J. & Hill, D. J. On stability, L2-gain and H∞ control for switched systems. Automatica 44(5), 1220–1232 (2008).
Fu, J., Chai, T., Jin, Y. & Su, C. Y. Fault-tolerant control of a class of switched nonlinear systems with structural uncertainties. IEEE Trans. Circuits Syst. II Express Briefs 63(2), 201–205 (2015).
Benzaouia, A., & Telbissi, K. Fault tolerant control for uncertain switching discrete-time systems with actuator failures. In 2017 6th International conference on systems and control (ICSC) (pp. 383–390). IEEE. (2017)
Jin, Y., Zhang, Y., Jing, Y. & Fu, J. An average dwell-time method for fault-tolerant control of switched time-delay systems and its application. IEEE Trans. Industr. Electron. 66(4), 3139–3147 (2018).
Yang, W. & Tong, S. Adaptive output feedback fault-tolerant control of switched fuzzy systems. Inf. Sci. 329, 478–490 (2016).
Aouaouda, S. & Chadli, M. Robust fault tolerant controller design for Takagi-Sugeno systems under input saturation. Int. J. Syst. Sci. 50(6), 1163–1178 (2019).
Wang, Y., Xu, N., Liu, Y. & Zhao, X. Adaptive fault-tolerant control for switched nonlinear systems based on command filter technique. Appl. Math. Comput. 392, 125725 (2021).
Gu, Z., Yue, D., Peng, C., Liu, J. & Zhang, J. Fault tolerant control for systems with interval time-varying delay and actuator saturation. J. Franklin Inst. 350(2), 231–243 (2013).
Huang, S. & Xiang, Z. Robust L∞ reliable control for uncertain switched nonlinear systems with time delay under asynchronous switching. Appl. Math. Comput. 222, 658–670 (2013).
Yuan, S., Zhang, L. & Baldi, S. Adaptive stabilization of impulsive switched linear time-delay systems: A piecewise dynamic gain approach. Automatica 103, 322–329 (2019).
Park, J. H., Mathiyalagan, K. & Sakthivel, R. Fault estimation for discrete-time switched nonlinear systems with discrete and distributed delays. Int. J. Robust Nonlinear Control 26(17), 3755–3771 (2016).
Liu, C., Liu, F., Yang, T. & Liu, K. Improved stability and stabilisation conditions of uncertain switched time-delay systems. Int. J. Syst. Sci. 55(6), 1073–1088 (2024).
Mohammed, C., Noureddine, C., & El Houssaine, T. Robust stability of uncertain discrete-time switched systems with time-varying delay by Wirtinger Inequality via a switching signal design. In 2019 8th International conference on systems and control (ICSC) (pp. 525–532). IEEE. (2019)
Jiang, N. & Sun, Y. Stability analysis and stabilization control of discrete-time impulsive switched time-delay systems with all unstable subsystems. Nonlinear Anal.: Modelling Control 29(3), 449–465 (2024).
Zhou, L., Wang, C., Wang, Q. & Yang, C. Anti-windup control for nonlinear singularly perturbed switched systems with actuator saturation. Int. J. Syst. Sci. 49(10), 2187–2201 (2018).
Zheng, Q. & Wu, F. Output feedback control of saturated discrete-time linear systems using parameter-dependent Lyapunov functions. Syst. Control Lett. 57(11), 896–903 (2008).
Lu, L., Lin, Z. & Fang, H. L2-gain analysis for a class of switched systems. Automatica 45(4), 965–972 (2009).
Petersen, I. R. A stabilization algorithm for a class of uncertain linear systems. Syst. Control Lett. 8(4), 351–357 (1987).
Wang, J. & Zhang, X. Non-fragile Robust Stabilization of Nonlinear Uncertain Switched Systems with Actuator Saturation. J. Control, Autom. Electr. Syst. 34(1), 18–28 (2023).
Zhang, X. L2-Gain analysis and anti-windup design of switched linear systems subject to input saturation. Asian J. Control 19(2), 672–680 (2017).
Li, Z. M., Chang, X. H., Mathiyalagan, K. & Xiong, J. Robust energy-to-peak filtering for discrete-time nonlinear systems with measurement quantization. Signal Process. 139, 102–109 (2017).
Acknowledgements
This work was supported by the Basic Scientific Research Fund of Education Department of Liaoning Province of China (LJKMZ20220731). This work was supported by the Natural Science Foundation of Liaoning Province of China (No.2020-MS-283).
Funding
Basic Scientific Research Fund of Education Department of Liaoning Province of China, LJKMZ20220731, LJKMZ20220731, Natural Science Foundation of Liaoning Province of China, 2020-MS-283, 2020-MS-283.
Author information
Authors and Affiliations
Contributions
Mengxiang Li and Xinquan Zhang wrote the main manuscript text and Mengxiang Li and Xinquan Zhang prepared figures. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Li, M., Zhang, X. Anti-windup control of discrete time switched delay systems with actuator saturation and failures. Sci Rep 15, 21483 (2025). https://doi.org/10.1038/s41598-025-07143-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-07143-x