Modeling methylene blue removal using magnetic chitosan carboxymethyl cellulose multiwalled carbon nanotube composite with genetic algorithms and regression techniques

Abstract

The purpose of this study was to model and optimize the removal of methylene blue using a novel magnetic chitosan-carboxymethyl cellulose/multiwalled carbon nanotubes and to identify the most significant parameters influencing the adsorption efficiency. Genetic Algorithm and other statistically advanced techniques such as Gradient Boosting Regressor, and Maximum Likelihood Estimation were used to extract the necessary process parameters and the factors that posed a major impact on the adsorption efficiency. The following metrics showed the secondary model, trained using the Gradient Boosting Regressor technique, had a slightly better accuracy of 0.99, Root Mean Square Error of 0.68 and Mean Absolute Error of 0.49 compared to the Maximum Likelihood Estimation of 0.94 in the training sample and 0.95 in testing. Gradient Boosting Regressor model was more stable and did not overfit, there was some sign of overfitting in Maximum Likelihood Estimation. From the feature importance X2 (initial methylene blue concentration) was the most important feature while X1 (contact time) and X4 (adsorbent amount) were not too important and can be eliminated from the models. The result of Genetic Algorithm analysis also proved the model has converged to the optimal solution effectively, the best solution of X1 = 49.41, X2 = 110.62, X3 = 11.85 and X4 = 20 which gives the maximum removal efficiency = 94.64% of methylene blue. These steps also supported the increased importance of X2, with a positive coefficient of 0.72 for improved removal efficiency as well as X3 which correlated positively with a coefficient of 0.66 in this regard. The adsorbent showed stability in residuals in the training set equal to Mean Residual = 0, and Root Mean Square Error of 0.68, while testing gave the Mean residual = 0.15, and the Root Mean Square Error of 2.33. The major conclusion drawn is that the algorithm working on the Gradient Boosting Regressor was more efficient, and had a higher accuracy margin as well as a more stable model than Maximum Likelihood Estimation. The result indicated that the adsorbent possessed a higher removal efficiency of 94.64%, thus, its application in the removal of dyes from wastewater could be seen as possible.

Introduction

Industrial effluent is wastewater produced in the process of industrial activities. It usually includes a range of pollutants, organic and inorganic compounds, heavy metals, suspended solids, toxicants and others that are based on the type of industrial operations¹. The textile, paper, and cosmetic industries are the leading consumers of dyes in the world (about 5–10% of these dyes are discharged as industrial waste)². Currently more than 8000 synthetic chemical substances are used in textile production, the annual world production of synthetic dyes is 7.1 metric tons of which as much as 10% is released into the environment as industrial effluents (according to a World Bank Report, 17–20% of the industrial effluents come from the manufacture of textile materials, one of the most water consuming industries).To state the obvious, synthetic dyes are not easily biodegradable due to their complex molecular structures, which means they are extremely resistant to hydrolysis, oxidation, or light exposure. Dye-contaminated effluents released into aquatic ecosystems tend to reduce dissolved levels of oxygen, a factor that is dangerous to aquatic dwelling species. Dyes also tend to reduce the transmission of sunlight into water bodies hence reducing the ability of aquatic flora to photosynthesize³. One of the main pollutants in some industries such as printing, textile and pharmaceutical industries is methylene blue^4,5, which has attracted the attention of environmental health engineers due to its non-biodegradability and very resistant structure. Thus, there is a need to look for the best and cheapest way to remove these pollutants from water bodies^6,7.

Adsorption is a method of increasing the removal of heavy metals which employs different types of materials that have the ability to attract or hold organic pollutants (such as dyes) to their outer surface from aqueous solution. This process is viewed as a favored approach to environmental remediation because it is quite simple, quite efficient, and not so expensive^8,9,10. Adsorption is identified as being a competitive technique for the removal of pollutants because of its measurability, practicality, and the fact that the approach can decontaminate a lot of pollutants such as inorganic compounds^11,12. Although quite efficient, many of the traditional adsorbents are limited, for example, by instability in aqueous environments with different pH values, and by lack of mechanical strength, and, therefore, their possible reuse is reduced. In this respect, in this sense, composites, especially those of a polymer basis, are advanced materials. They exhibit enhanced stability, durability and adsorption capacity than their unity elements. Polymeric adsorbents are found to be performing exceptionally well in the removal of a large number of pollutants because of the synthetic versatility, functionalization ability, high surface area, microporous structure and intra-pore size distribution. According to a review of research data on poly and non-polymeric adsorbents including carbon based, bio based and inorganic materials, it is evident that polymeric adsorbents are superior to non-polymeric adsorbents, cheaper than non-polymeric adsorbents. In addition, the use of natural polymers increases their biocompatibility and environmental friendliness and makes them attractive for water treatment applications^13,14.

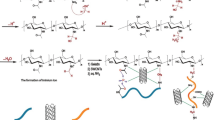
Putting several nanomaterials together improves the ability of the nanocomposite to adsorb pollutants^12,15. This could be due to the increase in the surface area of ​​the adsorbent and consequently the increase in the adsorption capacity of the pollutants. The combination of chitosan (CS), carboxymethyl cellulose (CMC), and multi-walled carbon nanotubes (MWCNTs) as nanocomposite adsorbents has shown high potential for removing dyes from aqueous solutions¹⁶. Chitosan, a biopolymer prepared from the exoskeletons of crustaceans such as shrimp and crabs, is highly demanded in many industries owing to its friendly biological characteristics and excellent compatibility with cells¹⁷. The good affinity of the polymer for engaged functional groups improved contaminant removal. Carboxymethyl cellulose has a good power of water adsorption as well as gel formation, which can enhance the adsorption performance¹⁸. The placement of these two nanocomposites together and in combination with magnetic carbon nanotubes, in addition to improving the adsorption methods, can also increase the recyclability of the adsorbent^16,19. This study focuses on modeling and predicting the performance of magnetic CS-CMC /MWCNT_S in removing methylene blue (MB) from aqueous solutions. In this study, the performance of regression models (Gradient Boosting Regressor (GBR) and Maximum Likelihood Estimation (MLE)) and the Genetic algorithm (GA) for optimization and adsorption yield prediction was applied. Through these methods, key factors affecting adsorption efficiency are identified, and operational parameters are optimized to achieve maximum dye removal efficiency.

Since it is tough to forecast the adsorption of pollutants, AI support software is used to look carefully at the collected data and measure the outcomes. As a result, in this study, the GBR model was applied, and it is considered an excellent member of the ensemble machine learning methods. Thanks to the way it is formed by combining weak decision trees, GBR can manage various and curved relationships between input and output values and produce highly precise predictions using the error reduction technique at every step. So, people often analyze dyes in water using GBR as it clarifies how dyes behave in solution. At the same time, MLE uses a statistical method called model likelihood estimation to obtain the data. As MLE was made to examine probabilities and aims to understand main factors in an adsorption process, it was selected for the study to review machine learning methods. Also, parameters were optimized and the areas best suited for performance were determined with the help of GA. The algorithm based on natural selection and genetic changes can search widely and find the top solution to complex problems with many adjustments. GA is effective in adjusting important aspects like dosage, time, pH, and so on for higher removal of pollutants. New ways of modeling help us observe adsorption more clearly and make its analysis better. Moreover, by using them, the outcome of any water treatment system is made both helpful and harmless to nature. Therefore, the application of GBR and MLE models alongside the Genetic Algorithm as key tools in the present study has played a significant role in advancing knowledge and improving the performance of pollutant adsorption processes^20,21.

In a research, novel PEI/GO/LTH nanocomposite was synthesized and characterized, and subsequently used in the removal of phenolic (bisphenol A) and azo dye (acid red 1) pollutants from wastewater samples. The study proved that the nanocomposite is highly effective against these contaminants and the synthesized composite performed with high reusability with minimal loss in effectiveness. Beyond, experimental investigations were conducted as well. Models of artificial intelligence (AI) such as support vector machine (SVM) and Bayesian optimization were then applied to predict the adsorption capacity for AR1 and BPA and highly accurate results on the testing phase (correlation coefficients of 97.3% and 96.6% for AR1 and BPA, respectively)²². Another study aimed to develop a predictive and optimization model for dye removal efficiency and Gibbs free energy behavior during adsorption. For the removal of anionic dye from aqueous solutions, a composite of chitosan-polyacrylamide/TiO₂ was utilized. The research used elevated modeling tools such as response surface methodology (RSM), artificial neural networks (ANN) and machine learning (ML). The RSM model revealed a high statistical significance (F-value:814.62), and the R²=0.99 that was shown by the ANN model indicated outstanding accuracy, which made it possible to predict both dye removal performance and the Gibbs free energy dynamics²³.

GBR and MLE are chosen because of their high accuracy and robust performance in nonlinear relationships in environmental modeling issues. GBR is an ensemble learning method and is very popular because of its excellent predictive ability from combining weak learners; consider the decision tree, a weak learner, into a strong predictive model, which is very useful in handling complex adsorption systems. On the other hand, MLE is a strong statistical technique used to estimate model parameters such that the likelihood function is maximized, and thereby it suits the analysis of the underlying distributions for adsorption behavior. Also, the GA was used because of its capacity to solve the problem of optimum search in a large and complex parameter space searching for global optima, which is of great value in optimizing operational conditions in adsorption processes. As for justification for the choice of the adsorbent, the magnetic CS-CMC/MWCNT was chosen because aspects of its components provide multiple yet distinct advantages that improve adsorption of dyes. CS provides biocompatibility and those functional groups which are favorable for dye affinity. CMC is responsible for water retention, gel-forming, and supporting the dye capture and finally MWCNTs offer a high surface area and magnetic property to allow easy separation. The combination of these materials results into faster adsorption rate and increased recyclability. Also, some other numerous recent studies investigated similar nanocomposites for dye removal with good results. However, what is new in our work is that we combine it with advanced ML and evolutionary optimization methods to not just assess the qualities of the adsorbent but also predict and optimize it as well which can serve both researchers and engineers who develop the water treatment system design derivatives.

The key benefits of the current work are based on the fact that the new magnetic nanocomposite applied in the study is a mixture of CS, CMS, and MWCNT, resulting in an increase of the surface area and the interaction of functional groups that increases the adsorption capability. Another major benefit is the simple addition of the state-of-the-art ML regression models (GBR and MLE) and a GA, which enables correct prediction and optimization of dye removal efficiency. Through the synergy, the modeling precision is significantly improved and the important operational parameters are identified relatively. Also, the water treatment process has been made to be more sustainable by the fact that it is easy to separate and reusable through the magnetic properties of the said nanocomposite. Also, this method’s accuracy needs further verification in the actual wastewaters, and results from the laboratory experiments cannot fully characterize environmental conditions. Furthermore, the study may need more validation in real wastewater, and laboratory-based results are not adequate to characterize environmental variations.

The selectivity for MB removal by the proposed nanocomposite will be mainly ascribed to the structural and chemical compatibility of the dye molecules with the functional group in the adsorbent components. Chitosan carries amino (-NH₁) and hydroxyl (-OH) groups which establish strong interaction with the cationic nature of MB through electrostatic attraction and hydrogen bonding. Similarly, CMC provides carboxyl (-COOH) which helps to increase binding affinity in case of charged dye molecules, and the addition of the MWCNTs enhances selectivity by offering a π–π interaction platform for π–π electronic groups between the aromatic rings of MB and the conjugated structure of carbon nanotubes. Moreover, increased surface area and voids of the nanocomposite will ensure preferential entry and adsorption of MB over possible contaminants^10,24. The combination of these synergistic effects between the dye and the constituents can be responsible for the high selectivity toward MB, which is proven by the optimized performance models during this research.

The research hypothesis that is used for the present study is that a magnetic nanocomposite created using chitosan, CMC, and MWCNTs will be able to remove MB dye from aquatic solutions reliably and effectively, as the adsorption efficiency can be properly predicted and optimized with high grade regression models (GBR and MLE), when combined with a GA. Based on the provided introduction, the research gap addressed by the present study can be articulated as follows: although the popularity of nanocomposite adsorbents in the removal of dyes increases, there is still a lack of integration approaches that cover new, magnetically separable biopolymer-based nanocomposites combined with superior ML and optimization algorithms for predicting and maximizing the adsorption performance, namely for MB. Most of the past research work has been limited to either the use of traditional adsorbents which they are not very efficient or the lack of appropriate predictive modelling and optimization frameworks furthermore, the possibilities of synthesizing chitosan, CMC and MWCNTs in a single composite structure with a magnetic recovery of advantage has not been studied in-depth for selective dye removal. The gap has been addressed in this study with the proposal of a novel magnetic nanocomposite which has since been combined with predictive modeling using procedures of ML and optimization with GA to enhance the removal and process control efficiency.

The newness of this research is connected to the fact of the development and the actual use of a magnetic nanocomposite consisting of CS, CMC, and MWCNTs for the effective and selective elimination of MB in the aqueous solutions taken together for the first time with the advanced regression model (GBR, MLE) and a GA for prediction and optimization of adsorption performance. This integrated work improves efficiency and selectivity of removal but also introduces a practical, reusable cost cost-effective system for the treatment of wastewater; unlike past studies that focused either on material synthesis only or modeling without any innovative adsorbent, this work, in my opinion spans both in one consistent framework.

Thus, the major purpose of this study is to investigate and model the performance of magnetic CS-CMC/MWCNT_S for MB dyes in aqueous solutions. For this purpose, advanced regression models of GBR and MLE were applied to let the predicted adsorption efficiency fall in the desired mean square error. Through the use of GA, the researchers got to adjust the operational parameters to achieve better dye removal efficiency. The focus of our study is the potential of ML and magnetic nanocomposite adsorbents as assistance for the establishment of a cheap and environmentally-friendly water purification system.

Materials and methods

Materials

This considers utilized different materials, counting atomic weight CS (DDA 80%), CMC (atomic weight 250,000), ferric chloride hexahydrate (FeCl₃⋅6H₂O ≥ 98%), ferrous chloride tetrahydrate (FeCl₂⋅4H₂O ≥ 99%), hydrochloric acid (37%), ammonium hydroxide (99%), glacial acetic acid (98%) (to dissolve chitosan and adjust the pH in the synthesis processes of biopolymeric materials), sodium triphenylphosphine (TPP ≥ 98%) (it is used as an ionic cross-linking agent in chitosan-based formulations, forming a gel structure through interactions with amino groups (-NH₂)), and MWCNTs (> 95%). All these chemicals, sourced from Merck (Darmstadt, Germany), were of reagent grade. Furthermore, all arrangements were made using double-distilled water.

Preparation of chitosan/carboxymethyl cellulose (CS/CMC)

Carboxymethyl cellulose (0.5 g) was dissolved in a 1 wt% NaOH solution with continuous stirring. At that point, 300 µL of epichlorohydrin was gradually added to the mixture while stirring was maintained. In a separate process, 0.5 g of chitosan powder was blended with 1% (v/v) acetic acid solution and mixed attractively at room temperature for 4 h to obtain a homogeneous solution. The solution’s pH was measured and adjusted to 5.0 utilizing 1 N NaOH. A CMC solution (0.5% (w/v)) was at that point included dropwise into the chitosan nanoparticle suspension. To improve the composite’s properties, 25 mL of a 1% w/v TPP solution, as a crosslinking agent, was added. At last, the coming about CS/CMC composite was washed three times with methanol and dried under vacuum at 40 °C²⁵.

Preparation of Fe₃O₄ NPs

A three-necked flask containing 80 mL of deionized water was purged with nitrogen gas for 30 min at 65 °C while being under constant stirring to create an inert atmosphere. Along these lines, 2.4 g of FeCl₃⋅6 H₂O and 0.9 g of FeCl₂⋅4 H₂O were dissolved in the deoxygenated water. The pH was adjusted to a range of 9 to10 by dropwise addition of NH₄OH, with stirring was maintained at 70 °C for 1 h. The Fe₃O₄ nanoparticles were at that point collected using a magnetic bar and altogether washed with deionized water and methanol until the pH of the washing solution reached approximately 7. Finally, the nanoparticles were freeze-dried^26,27.

Functionalization of MWCNTs

In a conventional method, 1 g of MWCNTs was oxidized by refluxing in 60 mL of concentrated HNO₃:H₂SO₄ (1:3, v/v) mixture at 100 °C for 12 h to induce oxidation. After the reaction, the reaction mixture was filtered and washed repeatedly with deionized water after cooling to room temperature. The washing proceeded until the pH of the final rinse reached a neutral pH. Finally, the resulting oxidized product was dried under vacuum to obtain carboxylated multi-walled carbon nanotubes²⁸.

Synthesis of magnetic CS/CMC/MWCNTs nanocomposite

In the final fabrication process of the magnetic CS/CMC/MWCNTs nanocomposite, the following materials and proportions were used: chitosan (CS) 0.5 g dissolved in a 1% acetic acid solution, carboxymethyl cellulose (CMC) 0.5 g dissolved in a 1% w/w NaOH solution, epichlorohydrin as a crosslinking agent for CMC in the amount of 300 µL, TPP as a crosslinking agent for chitosan with 25 mL of a 1% w/v solution, functionalized multi-walled carbon nanotubes (MWCNTs) 0.1 g dispersed in the prepared CS/CMC solution, and Fe₃O₄ nanoparticles 20 mg added to the solution after the ultrasonication step. All chemicals used in this study were of reagent grade and utilized without further purification. Chitosan (medium molecular weight, ≥ 75% deacetylated), carboxymethyl cellulose (low viscosity, sodium salt), epichlorohydrin (≥ 99%), sodium tripolyphosphate (TPP, ≥ 98%), and functionalized multi-walled carbon nanotubes (outer diameter 10–20 nm, > 95% purity) were purchased from Sigma-Aldrich (USA). Fe₃O₄ nanoparticles (average size ~ 50 nm, ≥ 99% purity) were obtained from Merck (Germany).

To synthesize the magnetic-CS-CMC/MWCNTs, functionalized MWCNTs were dispersed into a CS/CMC aqueous solution. After being stirred continuously for 6 h, the blend was ultrasonicated for 30 min. At that point, 20 mg of pre-synthesized Fe₃O₄ nanoparticles were added to the viscous solution, which was mixed mechanically for an extra hour at 25 °C. The resulting nanocomposite was magnetically separated using an external magnetic field, washed twice with ethanol and deionized water, and dried at 80 °C in an oven to obtain a stable magnetic product^28,29.

Characterization of nanocomposite

The basic and morphological characteristics of the magnetic CS-CMC/MWCNTs were explored utilizing progressed analytical strategies. The analysis of sample spectra required the use of Bruker Vertex-22 FTIR spectrometer. The FTIR spectra were obtained within the wavenumber extend of 500–4000 cm⁻¹ utilizing KBr pellets containing the nanocomposite. Morphological investigation was carried out utilizing Field Emission Scanning Electron Microscopy (FE-SEM, MIRA3 TESCAN, Czech Republic), prepared with Energy Dispersive X-ray Spectroscopy (EDS). The crystallinity of the nanoparticles was analyzed utilizing an X-ray diffractometer (Rigaku-12 KW) within the 2θ range of 10–80°. Magnetic properties were measured with a Vibrating Test Magnetometer (VSM, Lakeshore).

Batch adsorption experiments

In order to assess the efficiency of magnetic CS-CMC/MWCNTs to eliminate MB from water, batch adsorption experiments were carried out. These experiments were aimed at establishing the influence of different operational factors such as initial MB concentration (mg L^− 1) (X1 = 10 to 50), time (min) (X2 = 5 to 120) solution pH (X3 = 2 to 12) and amount of adsorbent (mg L^− 1) (X4 = 5 to 120). The experiments were carried out in 250 mL erlenmeyer flasks with 100 mL MB solution of the stated concentration and the pH of the solution was regulated using HCl or NaOH solutions. To obtain uniformity in the solution, from time to time, the flasks were rotated with a mechanical shaker (Model: KS-15 A, Pars Azma Co., Iran) at an optimal speed. When the equilibrium condition was attained, only a small volume of samples was collected, and the adsorbent was separated by filtration (Whatman No. 42)^30,31. The remaining MB was assessed via UV-Vis spectrophotometry (Model: UV-1600PC, MAPADA Instruments, China) at the wavelength of the maximum absorbance, 664 nm³¹.

Advanced regression techniques (GBR, MLE) and genetic algorithms optimization

To implement advanced regression models (GBR and MLE) for predicting the adsorbent’s performance in MB removal, the following steps were performed³².

Data preparation

Experimental adsorption parameters such as initial MB concentration, contact time, pH, and adsorbent dosage as independent variables and also the rate of MB removal as the dependent variable were grouped into training and testing datasets. The data were standardized to remove the effects of scale differences of features.

Modeling with GBR

Model construction

The GBR model was constructed using decision trees as weak learners to reduce the error of the decision made by the previous tree.

Model parameters

Other control factors like the number of trees and depths per tree, learning rate, and minimum threshold of samples per leaf were optimized for performance. This means that these hyperparameters were tuned (commonly with the help of grid search, random search or evolutionary algorithms) with a view to maximizing accuracy while minimizing error in this model.

Model training

The model was trained on the training data, iteratively reducing residual errors to achieve the best fit.

Modeling with MLE

Defining the likelihood function

The likelihood function was discussed concerning the actual data which represents the probability of the actual data under the model parameters.

Parameter optimization

Several model parameters were tuned for achieving maximum likelihood using the optimization algorithms such as Newton Raphson or gradient descent.

Model evaluation

Having estimated the parameters for the fitted model, it was used on the test data to check its accuracy and predictive ability.

Model validation

Metrics such as R² (coefficient of determination), MAE (mean absolute error), and RMSE (root mean square error) were used to evaluate model accuracy.

The performance of GBR and MLE models was compared to select the superior model.

Analysis and interpretation of results

The effects of the individual input parameters on model performance and MB removal were studied. To facilitate the interpretation of their results as well as determine quantitatively the representative power of the models used, the authors devised graphical diagrams from the between predicted and actual values of interest.

Optimization of final model

If needed, the model settings (learning rate or tree depth in GBR and probability distributions in MLE) were examined and optimized to improve the final results. This helped to create an accurate model to perform predictions of the performance of adsorbent, as well as to perform a deep analysis of complicated relationships between input and output variables.

GA optimization

Defining the objective function

Based on the above, the objective function for optimization was defined as a specific performance of the adsorbent (i.e., rate of MB removal). This function depended on operational variables such as initial concentration, adsorbent dosage, pH, contact time, and temperature. The goal of the algorithm was to maximize this function.

Generating the initial population

The algorithm began by generating sets of individuals who had random values of the predictors.

Fitness evaluation

The corresponding degree of fitness to the objective function was assigned to each chromosome in the population. Chromosomes with better performance achieved higher fitness values.

Genetic operations

Selection Therefore, depending on the achieved fitness score, only the best-performing chromosomes were picked to breed the next generation. Methods like Roulette Wheel Selection or Tournament Selection were used.

Crossover Some specified chromosomes were recombined to form new ones by exchanging segments of their parameters. It made sure that the beneficial traits passed from one generation to the next.

Mutation Small random changes were introduced in chromosomes to maintain diversity in the population and prevent the algorithm from being trapped in local optima.

Iterative process

There followed a process of fitness evaluation, selection, exercises in crossover, and mutation until a specified number of generations is reached or a stopping criterion is obtained. The stopping criterion could be achieving a fixed number of generations or stabilizing the objective function value.

Identifying the optimal solution

Finally, the chromosome with the maximum fitness was chosen to be the best solution to the current problem, i.e., optimal operational parameters for the removal of MB.

Analyzing results

All of the features in the set were properly normalized so that the machine learning models could depend on them. Still, the main advantage of this study is combining strong ensemble methods with effective optimization. Scientists applied the hybrid model to find out how all the factors were important for adsorption. They conducted eight theories and checked their outcomes with the tool’s predictions. Employing this strategy greatly aided in studying the complex settings and reaching the best outcomes for better adsorbent capacity.

In this study, all the modeling and optimization analyses were conducted using the programming language Python 3.12.1 supported on the Jupyter Notebook environment. The implementation of GBR and MLE models was carried out using the Python standard package scikit-learn, stats models, pandas, NumPy, matplotlib, and scipy. A total of [70 samples] experimental data points were analyzed. These data included four independent variables (X1(contact time), X2 (initial methylene blue concentration), X3 (solution pH) and X4 (adsorbent amount)) and one dependent variable (Removal of MB).

Before modeling, the features were normalized using the StandardScaler to eliminate scale differences between variables. The dataset was then split into 80% training and 20% testing using random_state = 42 so as to produce repeatable results. For the GBR model, the GBR class from sklearn.ensemble was applied with default parameters. For the MLE approach, OLS from the statsmodels.api library was used. The market price was also set to be constant in the matrix of the features to accommodate the intercept in the linear regression model. By graphing samples that were randomly chosen, the models’ performance was investigated. Scatter plots for the relationship between actual and predicted values for the training and the testing data sets, and residual plots (not actual values, but prediction error) for the two data sets. To quantitatively evaluate model performance, the following statistical metrics were calculated (Eqs. (1) to (3)).

$$R^{2} = \frac{{\sum {(y_{i} - \hat{y}_{i} )^{2} } }}{{\sum {(y_{i} - \overline{y} )^{2} } }}$$

(1)

$$MAE = \frac{1}{n}\sum {\left| {(y_{i} - {\hat{y}}_{i} )} \right|}$$

(2)

$$RMSE = \frac{1}{n}\sum {\left( {y_{i} - \hat{y}_{i} ^{2} } \right)}$$

(3)

Where y_i​ is the actual value, $\hat{y}_{i}$is the predicted value, $\overline{y}$is mean of the observed values and n is the number of data points. To validate the obtained accuracy, reliability, and generalization ability of the trained models without overfitting, these metrics were calculated for both the training and testing sets.

This study used the GBR algorithm, which is available in the sklearn.ensemble library, in modeling as well as predicting the MB removal efficiency. The addition code shows that it constructed the initial model with default parameters by using the command gradient_boosting_model = Gradient Boosting Regressor (). So, for quick model evaluation and safe results, n_estimators = 100, learning_rate = 0.1, max_depth = 3, min_samples_split = 2, and subsample = 1.0 were adopted as the initial parameters. Setting default values is a smart choice for science and efficiently measures the effectiveness of a model with a lower chance of overfitting. Before any training is done, data is standardized using StandardScaler to help reduce problems related to different input attributes. This positively affects the model’s speed of learning and prevents unnecessary changes in gradient parameters while it is learning, as seen from the command scaler = StandardScaler(), followed by X = scaler.fit_transform (X). When random_state = 42 is used to split the data, the outcomes can be replicated and made comparable to other models, as directed by the line X_train, X_test, y_train, y_test = train_test_split (…, random_state = 42). Performance analysis using residuals in both training and testing sets, supported by appropriate plots, enables a detailed examination of the model’s level of overfitting or underfitting. A small difference between the expected and the actual values in the testing data shows that the model works well and backs up the choice of initial values. While the topic of using R², MAE, and RMSE for assessing models using data was discussed in the document and not in the code, this method can be added to value the model’s results and gain exact insights. Default parameters are being used now so that we have a basic set of rules to check our initial results; it is a common practice in data science as researchers examine after setting grid or random search. Summing up, it did not experiment with any settings in this step and yet the process ran well using the original settings and clear data models. Therefore, this result proves that GBR can handle the type of data at hand.

Results and discussion

Characterization

Magnetic-CS-CMC/MWCNT_S were characterized using FTIR, XRD, VSM, and FE-SEM/EDS analyses, and are presented in Figs S1 to S3 in the supporting information file.

GBR model

Performance evaluation of a GBR model for predicting removal and evaluation of generalization performance of GBR model using 5-fold cross-validation

The given charts (Fig. 1) illustrate the performance of the GBR model used on a dataset for forecasting an ongoing target variable, the removal predicted based on several predictors. As shown in Fig. 1a, the scatter plot presents the true value of the target variable on the horizontal axis and the predicted value by the model on the vertical axis. The diagonal line shows ideal alignment of actual and predicted, and the number closer to the line point predicts more accurate models. For training data, as shown in the top-left scatter plot, the points are well-concentrated around the diagonal, indicating that the model performs well on the training data. For the test data shown on the top-right scatter plot, points are relatively close to the diagonal line, yet they are a bit scattered compared to the training data; thus, the model generalizes well to new data. In the residual plots (Fig. 1b) the x-axis is the independent axis which contains the actual values of the target variable and the y-axis is the dependent axis which contains the residual values. The residual values are the difference between the actual and the predicted values. A straight line across the center of the page represents zero residuals and points surrounding the line show no particular relationship between the errors of the model. For the residuals for the training data (on the bottom left residual plot), residuals are uniformly scattered around the zero line, thus indicating that the error is distributed uniformly and in addition there is no systematic bias in the model. For the test data, shown in the bottom-right residual plot, the residuals also appear random but are slightly more dispersed, implying reduced accuracy on unseen data. Comparing the training and test data results shows a very near-zero mean residual for the training data, which indicates there is no bias towards estimates, while the case in the test data is slightly biased away from zero. The training data possesses a standard deviation of the residuals which is lower, demonstrating better precision, while the test data has higher variation and more scattered prediction errors. For the case of training data, the residual skewness is positive; thus, there is a slight tendency towards positive errors, while, for the case of test data, the residual skewness is negative; there is a tendency towards negative errors. Kurtosis for the training data is a tad higher than 3, an indication of a sharper peak than an actual normal distribution, but the test data gives negative kurtosis to indicate wider residual distribution. For the training data, the MAE, the MSE and the RMSE are 0.49, 0.46 and 0.68, respectively; all of which are significantly lower than the corresponding values for the test data, where MAE, MSE, and RMSE are 2.09, 5.46 and 2.33, respectively. These metrics suggest the model performs better on training data with smaller errors. The R-squared value for the training data is 0.998, indicating an excellent fit, explaining 99.8% of the variability in the target variable, while the test data R-squared value is slightly lower at 0.97, indicating a slight reduction in explanatory power when generalizing to unseen data. Overall, the model shows high accuracy on training data but reveals some limitations and increased error variability on test data, emphasizing areas for potential improvement in generalization. The GBR model was applied with 5-fold cross-validation in order to predict the removal (Fig. S4 in Supporting Information File). The results demonstrate good performance of the model in estimating the target values. Specifically, the MAE was 2.49, the RMSE was 3.27, and the R² reached 0.96. The fact that a high R² value indicates that the model can explain most of the variance in the actual data is important. Furthermore, the scatter plot which compares the predicted and actual values demonstrates that most of the points lie close to the identity line (y = x) which is desirable and reflects a high degree of consensus between the model predictions and the real values. Such conclusions indicate the high ability of the GBR model to learn and generalize in this problem. Therefore, it can become a useful tool to predict the removal.

To further test the generalization capabilities of the model the authors used an Out-of-Bag (OOB) error estimation via a random forest regression variation. The OOB R² score was 0.907, corresponding to an OOB error estimate of 0.09. This outcome means that roughly 90.7% of the variance in unseen data can be accounted for without a separate validation set, serving as corroboration of the model’s effectiveness on new data; apart from OOB assessment, the general performance metrics of the system were as follows: for the training set, MAE = 1.49; RMSE = 1.92; R²=0.9879; test set, MAE = 3.42; RMSE = 4.17; R²=0.93. These results, while slightly lower in accuracy compared to the original GBR model’s 5-fold evaluation, still confirm its high predictive power and robustness. Once again, the magnified error values in the test data relative to the training set again illustrate the typical trade-off between model complexity and generalization. Overall, the GBR model demonstrates notable predictive performance as well as useful generalization as evidenced by the 5-fold cross-validation metrics, the nature of the residuals and OOB error profile. The model explains most of the variation, with a truly remarkable R² value of 0.93 or more, in both the training and test datasets the addition of the OOB error confirms the model’s reliability hence reinforcing its continued importance in predicting percentage removal accurately, beyond any reasonable doubt^33,34,35.

Fig. 1

Scatter (a) and Residual (b) plots for training and test data performance.

Analysis of residual distributions for training and testing datasets

Residual distribution plot (Fig. 2) shows mean residual in training dataset is almost zero, which means we have unbiased predictions all around with the model not being consistently over- or under-estimating the values. The standard deviation (0.68) proposes direct scattering, meaning a few forecasts are exact whereas others deviate significantly. The interquartile extend (IQR) is from − 0.35 to 0.27, showing that 50% of the residuals fall inside this extend, indicating direct changeability. The middle leftover (-0.05) is close to zero, highlighting a symmetric dispersion around zero. The skewness (1.03) shows a slight right-skew, proposing more positive residuals, and the kurtosis (1.72) recommends a marginally more honed top than a typical dispersion, demonstrating the next recurrence of residuals close to zero. For the testing dataset, the mean residual (0.15) is near zero but marginally positive, indicating a gentle inclination to overpredict on normal. The standard deviation (2.3) is altogether bigger than that of the training dataset, showing higher spread and more prominent variability in residuals. The IQR ranges from − 1.96 to 2.01, indicating that residuals within the testing dataset are more spread out compared to the training dataset. The middle remaining (0.42) is somewhat positive, reinforcing the tendency to overpredict. The skewness (-0.2) shows a slight left skew, proposing more negative residuals, whereas the kurtosis (-1.2) reflects a compliment distribution compared to the ordinary distribution, demonstrating greater variability in residuals. Comparing the datasets, both appear to have near-zero means, suggesting in general fair expectations, but the testing dataset includes a marginally positive predisposition. The testing dataset al.so has a much bigger spread (higher standard deviation), implying diminished accuracy on concealed information. The prepared dataset appears to have a slight right-skew, whereas the testing dataset appears to have a slight left-skew, demonstrating diverse designs in remaining conveyances. The training dataset is slightly more peaked (higher kurtosis), while the testing dataset shows a flatter distribution, reflecting more variability. Overall, the training dataset reflects better residual symmetry and lower dispersion, indicating a well-fitted model. The testing dataset shows higher variability, suggesting challenges in generalizing to unseen data, which could be addressed by refining the model or using techniques like cross-validation and hyperparameter tuning³⁶.

Fig. 2

Residual density plot for training and testing datasets.

Data distribution analysis using box plot: examining key characteristics and dispersion

The box plot (Fig. 3) may be an effective visual device in clear measurements, utilized to show the distribution of a dataset. It contrasts to quickly get it how the data is scattered and its key characteristics. The box is the central part of the plot and contains 50% of the data. The lower edge of the box talks to the essential quartile (Q1), even though the upper edge talks to the third quartile (Q3). The line interior the center of the box appears up the center of the information. Bristles are lines that expand from the box upward and descending, ordinarily to the greatest and least information focuses that are not exceptions. In this plot, most of the information falls between 50% and 70%, showing that expulsion rates are regularly within this range. The modestly brief length of the box suggests that the data is tightly clustered around the center, meaning most data points are close to it. No particular exceptions are observed in this plot, recommending that most data points are inside a satisfactory run, with exceptionally few extraordinary values. The line plotted right in the middle of the box indicates that the middle is about 60%, that is, 50% of the data centers lie below 50%, while the other 50% lie beyond that. Most information focuses drop between 52 and 75.3, affirming a moderate limit information spread. The near-equal removal from Q1 to the middle and the middle to Q3 suggests that the information conveyance is approximately symmetric. Any data point outside the range of 25 to 93.5 is considered an outlier. This box plot uncovers a symmetric distribution with most information concentrated close to the middle (63.5) and no significant outliers. This demonstrates reliable and solid information within a contract extent of changeability^34,37,38.

Fig. 3

Box plot analysis of removal rate distribution and variability.

Understanding feature importance in ML models

A significance chart (Fig. 4) may become an efficient technique for enhancing ML models understanding. This chart outwardly illustrates the effect of each input included on the target variable and makes a difference in distinguishing which highlights perform way better in forecast. The vertical position of a bar in that chart refers to the importance of such a include relatively: the taller the bar, the greater its influence on the prediction of the target variable. By comparing the bar statures, highlights can be positioned from the foremost imperative to the slightest vital. Highlights with taller bars are considered key features of the demonstration, shaping the spine of its predictions, whereas highlights with exceptionally brief bars likely have a negligible impact on the prediction and can be removed from the model. In the presented chart, X2 receives the greatest noteworthy significance, that is, changes in X2 exhibit the most pronounced effects on varieties in target variable. To make strides in forecasting precision for the target variable, extraordinary consideration ought to be given to changes in X2. On the other hand, features X1 and X4 have exceptionally low significance, demonstrating that changes in their values don’t altogether influence the target variable, and these features can be removed to rearrange and upgrade the model’s productivity. X3 has direct importance, with an effect less than X2 but greater than X1 and X4.

According to the feature importance analysis, X2 (contact time) influenced the dye removal process more than other methods. This result agrees with scientific facts since the longer the contact between dye and adsorbent, the more chances dye molecules have to enter and stick to the adsorbent pores. An increased contact time generally leads to a higher adsorption capacity until equilibrium is reached. For this reason, the key nature of this variable is in line with current adsorption theories and chemical properties. The next most important factor was X3 (pH of the solution), which is very important for adsorption. Depending on the acidity, each dye may behave differently on the fabric. At higher pH levels, the surface negatively charges, so the dyes stick to it more strongly. So, the model’s sensitivity to pH changes proves how vital it is in adsorption. Conversely, the other two parameters, dosage and initial concentration of methylene blue, had lower influence on the outcome. A reason for this might be that the data points are limited, and hence, the machine learning algorithm does not see a clear effect of these factors. Moreover, regarding X1 (adsorbent dosage), it is possible that the system reached saturation at low adsorbent levels, meaning the available active sites for methylene blue adsorption were sufficiently occupied even at the initial doses. This is why there was not much gain in performance after raising the adsorbent above a certain point. Eventually, the model saw that the parameter had little impact on the target. For X4 (initial methylene blue concentration), although increasing the initial concentration generally enhances the concentration gradient and thus the adsorption rate, early saturation of the adsorbent’s active sites may leave the excess dye in the solution unadsorbed. Consequently, the model in such a case disregards the level of initial concentration because it barely affects the result. In short, the detailed analysis of feature importance shows what role each variable plays and points out the way to optimize the experiment, making the behavior and control of adsorption clearer. This analysis allows researchers to allocate resources more efficiently to the most influential variables in future experiments, thereby improving process performance with reduced cost and time^33,39,40.

Fig. 4

Visual representation of feature importance.

MLE model

Evaluating the performance of a linear regression model for predicting removal efficiency and evaluation of generalization performance of MLE model using 5-fold cross-validation

The displayed charts (Fig. 5) outline the occurrence of a direct relapse demonstrating connected to a dataset. Linear regression may be a measurable demonstrate utilized to predict a continuous variable (here, the response variable) based on one or more indicator variables. In this case, the model aims to predict the “removal " based on the autonomous factors X1, X2, X3, and X4. The charts are separated into scatter plots and residual plots. In the scatter plots, the horizontal axis is the real values of the reaction variable (removal), with the vertical axis being values expected by the model. A 45-degree line passes through the origin that has a slope of 1 represents a case where the predicted values are equal to actual values. Each point on the chart represents an observation and the vertical distance of a point from the 45-degree line depicts the prediction error of that observation. From the available table values several conclusions are drawn. The general performance of the model is good as indicated by low MAE and RMSE values for the training and test datasets, suggesting a good prediction model. The model also generalizes well with small but not significantly different MAE and RMSE values in the test dataset than in the training dataset. The model shows a good fit; the R² values for both datasets are very close to 1, which means that the model explains most of the variance in the dependent variable. There is no bias in the model because this is reflected in the low mean residuals of both datasets close to zero values. The distribution of error is reasonable and the variances of residuals are reasonable, showing a good spread of errors around the regression line. With such findings, the linear regression model shows excellent performance in predicting the target variable and can accurately estimate the target values given the independent variables.

The 5-fold cross-validation was used to evaluate the performance of the MLE model in predicting removal (Fig. S5 in the supporting information file). The results showed the model is good according to the average MAE of 3.29, RMSE of 3.89 and R² of 0.94 meaning it can explain approximately 94.4% of the variation in the actual data. However, the scatter plot shows that most predicted values are close to the ideal y = x line; the slightly wider spread of points compared to the GBR model suggests that the MLE model has slightly lower predictive accuracy and generalization performance. From evaluating the MLE model for the prediction of removal using 5-fold cross-validation, the results indicate that the model performs well. The results indicate that the average MAE, RMSE, and R² were 3.29, 3.89, and 0.94, respectively. These results reveal that the model explains about 94.4% of the variation in the actual data. This level of fit represents the high ability of the model in predicting the target values accurately. However, based on the scatter plot, which displays the predicted values against the actual values, it can be observed that most predicted values are close to the ideal y = x. While there is a somewhat larger spread of points than of the GBR model, it means that the point estimates for the MLE model have slightly lower predictive accuracy and generalization performance. These differences are however, very small and do not pose a significant problem for the performance of the MLE model, especially considering that its overall outputs are favorable. This small spread implies that there are minor variations between models that may be influenced by the nature of the data or modeling choices. Nevertheless, a considerable portion of the data variance was already explained by the MLE model and during the tests, it demonstrated good performance, which means that it has high predictive and generalization capabilities for the new data, ultimately, it should be emphasized that although such spread differences in the predictions are noticeable they do not make a significant impact on the predictive and generalization abilities of the model overall and demonstrate the strength of the MLE model.

The AIC (Akaike Information Criterion) for the training data is 165.6 and for the test data is 47.02. AIC is a measure of balances model fit and complexity, and is a tradeoff between how well a model fits data and how complex the model is. A lower AIC value indicates a more optimal model. In this case, the AIC value for training data is greater than test data, which means that the model is more complex when fitting the training data. The BIC (Bayesian Information Criterion) for the training data is 177.7 and for the test data is 50.8. Similar to AIC, BIC is also used to evaluate model quality, but it penalizes model complexity more heavily. As with AIC, the BIC is higher for the training data than for the test data. The linear regression model is effective for both the training and test datasets; R² values near 1 indicate an excellent fit of the model to the data; the error metrics (MAE and RMSE) are suitable for both the test and train datasets with only a small difference between them indicating good generalization to new data. AIC and BIC values are higher for the training data compared to the test data, suggesting greater model complexity when fitting the training dataset^{33,41,42,43,44}.

Fig. 5

Predicted vs. actual values and residual distribution for removal efficiency.

Evaluating the performance of the linear regression model through residual analysis

The residuals histogram (Fig. 6) will likely be an efficient tool for checking regression models. That is the distribution of forecast errors of the model. Residuals are differences between actual and model predicted data. On the shown chart there are two histograms for residuals of the training dataset (training residuals) and the test dataset (test residuals) plotted. Both histograms indicate that the residuals are generally regularly distributed, meaning most residuals are near zero, and their recurrence steadily diminishes as they move absent from zero. Desirable since one of the most common assumptions of linear regression is the typical conveyance of residuals. The residuals are scattered close to zero and thus reveal the average low prediction error and its absence of systematic tendency to overestimate or underestimate values. Both histograms have a comparative in general shape, suggesting that the demonstrate performs essentially on both datasets. This shows great generalizability. To any extent, it is possible, though, for minor discrepancies in shape and dispersion of residuals between the two sets to be present, possibly because there are small differences between the training and test datasets. In the measurements, the mean for the training dataset is surprisingly close to zero, indicating that the model has low normal expectation error, and does not systematically over or under estimate numbers. The mean for the test dataset deviates slightly from zero but remains generally small, indicating that the model is by and large fair-minded for the test dataset as well. There is a level of scattering of the data about the mean. Close to equal standard deviation from two datasets indicates identical errors. Skewness values of close to zero for both datasets indicate a symmetric error distribution. Kurtosis values for both datasets are close to zero, recommending that the residual distributions are about as level or peaked as a typical dispersion. The minimum and most extreme values appear in the extent of residuals, giving bits of knowledge into the spread of forecast errors. The Shapiro-Wilk test for typicality appears to yield p-values more noteworthy than 0.05 for both datasets, demonstrating insufficient evidence to reject the presumption of ordinariness. Generally, residuals are approximately normally distributed, with skewness and kurtosis values near to zero. The model is largely unbiased, with mean residuals near zero, appearing low normal forecast errors. Residual distribution is consistent across datasets with comparable standard deviations. This linear regression model performs well, and its key assumptions, such as normality of residuals, are largely satisfied³⁶.

Fig. 6

Distribution of residuals and statistical characteristics of the linear regression model.

Evaluating residual distribution using Q–Q plots in linear regression model

Figure 7 demonstrates that Q-Q (Quantile-Quantile) plots are strong devices for assessing the dispersion of knowledge. In regression modeling contexts, these plots help us in comparing the distribution of the model’s residuals with a theoretical distribution (usually a normal distribution). One of those assumptions governing linear regression is that the residuals are normally distributed. If residuals are also approximately normally distributed, we can be more confident about the model results. In the provided plots, two Q-Q plots for the residuals of the training and test datasets are displayed. The horizontal axis in each plot corresponds to the quantiles of standard typical dispersion, while the vertical axis shows the quantiles of the test (i.e., the model residuals). The red 45-degree line is something to compare to in respect to correlation. In case the data points generally lie on the 45-degree line, this demonstrates that the residual distribution is approximately normal. If the information deviates from the 45-degree line, this shows that the remaining dispersion deviates from normality. For the training data, most of the data points generally lie on the 45-degree line, showing that the residual distribution in the training dataset is approximately normal. However, at the tails of the conveyance, a few points deviate from the 45-degree line, which may show a slight deviation from normality. This deviation might be due to the presence of some outliers or the expanded complexity of the actual residual distribution. Within the test information plot, most of the data points generally lie on the 45-degree line, but compared to the training data plot, there is a greater deviation from the line. This proposes that the residual distribution in the test dataset might slightly deviate from ordinariness. Based on the given Q-Q plots, we will conclude that the residual distribution is for the most part ordinary, as both plots appear that most of the data points are near the 45-degree line. Either way there are small variations in both plots indicating insignificant departures from normality. These deviations could be due to different components, such as outliers, expanded complexity of the actual residual distribution, or a limited sample size^43,44,45,46.

Fig. 7

Comparing residual distribution with normal distribution through Q–Q plots.

Analyzing actual and predicted distributions using kernel density estimation (KDE)

Figure 8 shows (computed using Kernel Density Estimation (KDE)) the real and expected distributions on training and test data sets. Furthermore, a “statistics Table” is provided with various quantities of metrics for these distributions. Overall, the predicted distributions for both the training and test datasets closely follow the distribution of the actual values, demonstrating that the regression can learn the general pattern of the data and make reliable predictions for new (test) datasets. On inspection, small differences between the predicted and actual distributions can be observed. The anticipated distribution in both datasets seems to be slightly right skewed but the actual distribution is symmetric. This right skewness proposes that the model might slightly overpredict values compared to the real ones. The statistics table gives different measurements for the distributions of actual and predicted. The actual means that both the training and test datasets are near to each other. The estimates mean for the two datasets is, however, slightly larger than the mean as expected from the KDE plot representation. The actual standard deviation in both datasets is broadly similar. The predicted standard deviation in both datasets is slighter smaller than expected of the actual standard deviation, showing that the model may make slightly conservative predictions. Variance reflects the spread of the information around the mean and is related to the square of the standard deviation, following a similar interpretation. As shown within the KDE chart, the skewness values for the predicted distribution are somewhat positive, showing a right skew. The skewness values for the actual distribution approach zero with a nearly symmetric distribution. Kurtosis indicates the extent to which a distribution is more peaked or flat compared to a normal distribution. The kurtosis values within the table are near 2, suggesting that the distributions are near normal. Using the KDE graph and insights table, it is possible to conclude that the regression model is competent enough to extract the general outline of real data and provide a plausible prediction. Anticipated dispersions in training and test sets are more or less close to actual distributions, but there are minor discrepancies. The predicted distributions show up somewhat right-skewed, and the predicted means are marginally higher than the actual means. These observations show that the model tends to overpredict values slightly, higher than actual values. Depending on the nature of the issue, this inclination may or may not be a concern^43,45,47,48.

Fig. 8

KDE visualization of actual vs. predicted distributions for training and test datasets.

Analysis of feature importance in the linear regression model

The relative importance of each variable adopted by the linear regression model and the way each feature affects the dependent variable is presented by Fig. 9. The horizontal axis speaks to the names of features used in the model, whereas the vertical axis speaks to the magnitude of the given feature’s coefficient. The coefficient demonstrates how much the dependent variable changes with a one-unit alter within the individual included. The effect of that feature on the dependent variable is shown by the height of each bar; the higher the bar the more the effect. In case a bar is over the x-axis, it implies that an increase in the feature’s value leads to an increase in the dependent variable, illustrating a positive relationship. On the other hand, in case a bar is underneath the x-axis, it implies that an increment within the feature’s value diminishes the dependent variable, showing a negative relationship. In this chart, all bars are above the x-axis, so all features are positively related to the dependent variable. According to the chart, the most prominent effect belongs to X2, followed by X3 which has a considerable impact but still less than X2. X1 and X4 have the least effect because they have the shortest bars, hence less impact on the dependent variable.

The results indicate that the residuals largely follow a normal distribution. The presented histograms of residuals about both training and test data sets show that the majority of errors are clustered around zero with a bell-shaped distribution. In addition, both datasets’ skewness and kurtosis values are close to zero, which implies that the residual distribution is almost symmetrical with a peak that resembles a normal distribution. Results of the Shapiro-Wilk test with p-values in both sets greater than 0.05 confirm the inadequate evidence to reject the normality assumption. The Q-Q plots also show that most of the data points lie on the 45-degree reference line, with only some deviations near the tails, which could be outliers or some form of extra complexity of the true residual distribution. For the homoscedasticity assumption, the plots of residual scatter demonstrate that the distribution of residuals is roughly uniform along predicted values with no established pattern of variance growth or decay. In addition, there are comparable variations in the residuals of both the training and testing sets, corresponding to the fact that there will be a similar distribution of errors in the two sets, and the model performs consistently across the entire range of predictions. Thus, it can be concluded that the model behaves reliably from the point of a statistical perspective and the major assumptions of regression are met satisfactorily. However, if in the course of future applications more serious violations of these assumptions are detected, then such techniques as logarithmic or Box–Cox transformations can be used for stabilizing the variance and normalizing residuals; Weighted Least Squares regression can also be used for cases of heteroscedasticity; the methods of robust regression or bootstrapping can also be implemented. Generally, the current findings suggest that the MLE model is sufficiently calibrated to statistical assumptions, and significant corrections are not required³⁹.

Fig. 9

Relative impact of features on the dependent variable.

GA method

Analysis of absolute change in best fitness across generations in an evolutionary algorithm

Figure 10 shows the absolute change in an evolutionary algorithm of the best fitness through the generations. The horizontal axis speaks to the number of generations, whereas the vertical axis represents the absolute change in the best solution of each era compared to the previous one. Each point on the chart demonstrates how much better the solution has changed in the current generation as compared to the previous one. A higher value signifies a greater change in the best solution. Generally, as the number of generations increases, the absolute changes in the best fitness decrease. This suggests an approximation of the algorithm to an optimal solution with smaller changes in every generation. Although, over the whole, changes in every generation are reduced, fluctuations are still visible in the chart. These fluctuations relate to the stochastic character of evolutionary algorithms and may be caused by mechanisms such as mutation or crossover. If the chart flattens into a horizontal line, the algorithm has converged to a local optimum solution, with minimal changes in the best solution over successive generations^35,49,50.

Fig. 10

Absolute change in best fitness over generations.

Visualization of variable relationships using a correlation heatmap

Heatmap (Fig. 11) is a strong visual way to find the connection of various features. It illustrates the strength and type of relationship between each combination of factors by color. More warm colors (e.g., red) indicate a stronger positive relationship, while cooler colors (e.g., blue) indicate a stronger negative relationship. White typically represents no relationship or a weak relationship. The given heatmap shows a correlation structure among the factors X1, X2, X3, X4 and removal. Each cell in this matrix shows the Pearson correlation between two factors; values range from − 1 to + 1, showing the strength and direction of a linear relationship. Warmer colors represent strong positive correlations, cooler colors strong negative correlations, while the white indicates weak or no relationship. Diagonal values are always 1, as the relationship of a variable with itself is idealized. The arrangement is symmetric, as the relationship between x and y is the same as between y and x. The relationship coefficient close to 1 illustrates a strong positive relationship, meaning that as one variable increases, the other tends to increase as well. A correlation coefficient near − 1 indicates a strong negative relationship, where one variable increases as the other reduces. A coefficient near 0 suggests no or very weak linear relationship. From the heatmap, the correlation between X1 and removal is about 0.08, showing a weak positive relationship, meaning that an increase in X1 slightly increases removal. X2 and removal have a strong positive relationship, with a coefficient of 0.72. This suggests that an increase in X2 significantly increases removal. The association between X3 and X4 is just about 0.03, which shows a strong positive relationship between these factors. The relationship between X3 and removal is 0.66, indicating a strong positive relationship, marginally weaker than X2 and removal. Weak negative relationships are observed, such as between X1 and X3, where an increase in X1 slightly decreases X3. In conclusion, X2 has the strongest positive impact on removal, followed by X3. Other factors, such as X1, appear to have a negligible effect. Certain sets of factors, like X3 and X4, show almost no relationship. This heatmap provides a clear overview of variable relationships and provides a foundation for prioritizing the most influential ones.

Under a model that helps in optimal removal efficiency, the respective optimal values of these parameters were chosen. As we can see it from the heatmap, X2 variable is more correlated with removal (r ≈ 0.72), while X3 has a weak positive correlation (r ≈ 0.66); these large correlation coefficients are used to conclude that both these variables have some significant effects on performance and variance in their value can affect the outcome. To assess whether the performance is sensitive to small changes around the optimal values, attention must be paid to the slope of the response surface near the optimum points. If, around such points if the flatness of the surface is moderate, it is a sign of system stability, which means that even slight fluctuations in X2 or X3 will not cause a sharp decline in performance, however if a sharp peak is formed with the shape of the response curve, then the optimum zone is rather shallow and any deviation from the optimum values can be very sharp in reducing performance. Given the high correlation coefficient and the model’s reasonably accurate predictive performance, it can be concluded that its performance remains relatively stable around the optimum values, even within a narrow range of variation. In other words, while X2 and X3 are influential variables, the model likely has good tolerance to slight fluctuations in their values unless those exceed acceptable operational limits. If the surroundings around these points are more or less flat, it implies system stability, meaning that small oscillations around X2, X3 will not lead to a significant loss of performance. However, if the curve of the response takes the shape of a sharp peak, indicating a narrow optimal region, then even small departures from the optimum values could dramatically reduce the performance of the system^{33,51,52,53,54,55}.

Fig. 11

Correlation matrix of X1, X2, X3, X4​, and removal.

Exploring variable relationships using a pairplot

A pair plot (Fig. 12) is a powerful visualization tool in Python, especially in the Seaborn library to exploring the relationships between variables of the dataset. Such a plot is arranged as a matrix of scatter and distribution plots (histogram or kernel density estimate) and the relations between two factors are shown in each cell of the matrix. Off-diagonal cells display a scatter plot that demonstrates the association between two numeric variables with every point representing an observation about specific values for both variables. There are inclining cells which show the univariable distribution plots and demonstrate the distribution of each variable individually. Data points are color-coded based on the values of a specific variable (e.g., removal) whereby we can see how other factors correspond with changing values of removal. A positive relationship is observed when an increase in one variable generally corresponds to an increase in another, appearing by focusing corner to corner from the bottom-left to the top-right. A negative relationship occurs when an increment in one variable corresponds to a decrease in another, appearing as points aligned from the top-left to the bottom-right. In case no recognizable straight relationship exists between two factors, the scatter plot will appear random or dispersed.

Several important insights can be drawn from this plot.

The strongest positive relationships with the removal efficiency are observed for X2 (contact time) and X4 (adsorbent amount). With an increase in values of these two variables, the color of points shown gradually changes from blue to red with this reflecting that longer contact times and higher adsorbent doses considerably improve the removal of MB.

X3 (solution pH) also shows a moderately positive trend. In the subplots of X3 versus X4 and X3 versus X2, however, an increase in pH is accompanied by warmer colors (red), meaning that an alkaline condition is more effective for dye adsorption.

X1 (initial dye concentration) shows a negative or weak correlation with the removal efficiency. At higher X1 values (about 50 mg L^− 1), most data points are represented in shades of blue or light blue indicating the reduction in removal performance with higher initial concentrations, probably caused by saturation of the adsorbent’s active sites.

In addition, the histograms on the main diagonal provide a distribution of each variable individually and show that the experimental design captures the full range of variation of values for each parameter. This visual analysis assists in identifying the primary parameters for optimization and gives ways of possible inter-parameter interactions that can be modelled in the future^33,56,57.

Fig. 12

Pairplot of variables X1, X2, X3, X4​, and removal.

Visualizing optimal parameter values using a histogram chart

The histogram chart Fig. 13 presents a clear and informative visualization of the optimal parameter configuration. It adds the parameter values and their best values in intervals to bring out the best configuration in the model. Comparing the central values to the target values reveals variability in the data. The chart is concerned with five parameters (X1, X2, X3, and X4), and their optimal results are shown. It is also useful in explaining why some parameters are better, outlining the acceptable boundaries for each variable. The horizontal axis shows the calculated values, i.e., the vector means of a dataset, while the vertical axis shows the range of numerical values of each parameter.

Based on four input parameters: Contact time (X2), solution pH (X3), initial dye concentration (X1), and adsorbent amount (X4). The algorithm identified the optimal values of X1 = 49.41 mg L^− 1, X2 = 110.62 min, X3 = 11.84, and X4 = 20 mg L^− 1. These are the results of the best parameter combination that delivered the greatest removal efficiency based on the fitness function developed. Therefore, it is possible to conclude that the optimal conditions for the removal of MB have been determined.

These experiments were useful for determining the effect of different operational parameters, such as initial dye concentration (mg L^− 1) (X1), contact time (min) (X2), solution pH (X3) and adsorbent dosage (mg L^− 1) (X4). The best values of these parameters derived from the model were either conditions that minimized prediction errors or best conditions for achieving optimal performance as desired, such as “removal”. These values are, however, mainly optimal from a statistical or model point of view, but they may face practical limitations in the real process environment, e.g., operational constraints, physical availability of equipment or availability of resources. Particular values of parameters, such as, X2 and X3, could mean a setting or input value that needs a specific resource or raw material. For example, if a higher X2 value (e.g., 110.62) causes greater material use, this may raise costs (in practice these values need to be balanced with cost-saving): in many industries (manufacturing/chemical processing) where further parameter increases improve performance it is also possible that costs related to raw materials, energy, or time may increase. Being able to find the best values may mean needing to change equipment settings, increase in maintenance, or change in production rate; all of these options will increase the cost of operation. Even values such as X3 = 11.84 may represent operational settings that require more frequent adjustment or heightened monitoring leading to higher labor or observation costs. The process environment can have physical constraints such as temperature or pressure or flow rate limiting values of the specific parameters: e.g., although X2 = 110.62 may be optimal, the equipment may only be able to handle limited values of this parameter. Therefore, optimal model values should be compared and aligned with these operational constraints as well; further, certain parameters may be controlled by safety rules or industry standards, e.g., if X3 is the dose of a chemical in a treatment process, it may be governed by safety standards and regulations to avoid the overuse of toxic substances. Such legal restrictions may make it impossible to implement the model’s optimal values necessitating some modifications, the translation of optimal values into actual processes is generally a compromise between performance and feasibility; optimal parameter values should be treated as a starting point, but to adapt to changes in the environment such as weather conditions or changes in inputs or to optimizing the cost-performance trade-off may require further adjustments. Even a powerful process that best utilizes optimal values in the model cannot work best on the real world without further tuning. The model suggests optimal values that serve as starting points for experimentation and tuning of the real-world process environment. For instance, as starting point, X2 = 110.62, X3 = 11.84 can be chosen, and further adjustments made based on practical considerations, like yield, cost or any unexpected constraints. In conclusion though the optimal parameter value that was arrived at across the model, like X2 = 110.62, X3 = 11.84, work wonderfully for optimization of performance or efficiency, it needs to be carefully put into consideration and adapted to reflect in the real process environment. Cost constraints, physical limitations, legal considerations and process flexibility are among the factors that determine practically the way the optimal values can be implemented. Additional adjustments in this regard will guarantee that the proposed parameters by the model become the reality of sustainable and cheap operations. While a data-driven approach can provide statistically valid insights into optimal parameters, including a mechanistic understanding, especially about time (X2), and pH (X3), would fortify the scientific rationale of the model and enhance its applicability in a real-world setting. Regarding X2 (time), adsorption is inherently a time-dependent process governed by mass transfer dynamics. Methylene blue molecules get more opportunities to cross the boundary layer and reach the active sites on the surface of the adsorbent as the contact time increases. In the initial stages, the adsorption rate is high due to the abundance of available sites. However, as these sites become occupied, the rate slows down and the system reaches equilibrium. The optimal value of time (X2 = 110.62 min) may be a point at which the adsorption capacity is close to saturation without high time or energy costs. In other words, time directly affects the completeness of adsorption and the accessibility of less active or internal sites. As to X3 (pH), such a factor is of great importance for the surface chemistry of the adsorbent and the ionic form of methylene blue. At different pH levels, the surface charge of the adsorbent and the status of ionization of the dye would change, directly influencing electrostatic interactions and chemical bonds. For instance, in acidic conditions, excess H ⁺ ions may compete with dye molecules for access to active sites upsetting the adsorption efficiency; conversely in alkaline conditions (X3 = 11.84), the adsorbent surface may carry a negative charged thus positive dye molecules could be further electrostatically attracted to the adsorbent. The high positive correlation recorded between pH and removal efficiency in the model is attributed quantitatively to the quantum electrostatic effect. In conclusion, time affects kinetic and accessibility parameters of adsorption; pH, On the other hand, it governs electrostatic interactions and ionic behavior. By including such mechanistic information, the level of analysis deepens, and confidence in the applicability of the model to actual process conditions increases. To provide the prediction interval for the estimated rate of removal and to describe the confidence of each predicted value, it should be noted that, in the present study the prediction interval for the optimal removal rate was calculated with the use of the Monte Carlo simulation method. In contrast with sampling from the whole parameter space, random sampling with 5% deviation was made only around the optimum parameter combination (the coefficient values are X1 = 49.41 mg L^− 1, X2 = 110.62 min, X3 = 11.84, and X4 = 20 mg L^− 1). New removal rates at each iteration were determined by applying the objective function with these limited perturbations to yield a total of 1,000 removal values. The 95% prediction interval was then obtained through the 2.5th and 97.5th percentiles of these simulated values, giving a numerical range of (94.47%, 94.83%). The smaller the gap between the upper and lower bounds of this interval, the higher the robustness and precision of the model around the optimal point, in other words, the reliability of the predicted removal rate under its optimal conditions is statistically very reliable. This suggests that in an operational environment where small deviations or input errors may occur, the output of the model would remain relatively stable. More specifically, the optimal removal rate was estimated to be 94.64% and if the computed interval for prediction was utilized, then the deviation should be less than ± 0.2%. This means that the model, at the same time, is consistent even in the presence of small changes in the parameter value implying that similar results can be expected under real-world conditions. Thus, the best established values by the model may be regarded as a proper starting point for process optimization in practice, although secondary corrections may be required due to actual operational and implementation limitations^58,59.

Fig. 13

Histogram of best solution parameters X1 to X4.

Scalability, regeneration, and environmental considerations of magnetic-CS-CMC/MWCNT nanocomposites for industrial applications

When scaling the magnetic-CS-CMC/MWCNT nanocomposites in industrial application for MB removal, a number of vital things should be considered in order for the laboratory scale behavior to be transferable to large-scale processes. Firstly, when it comes to scalability, the nanocomposite is produced from materials that are technically available for mass production. CS and CMC are both biobased and rather inexpensive materials, which are thus omnipresent in various branches. In addition, MWCNTs are currently produced on an industrial scale by means of CVD (Chemical Vapor Deposition) and other methods, but the cost issue and even the problem of uniformity may appear in real applications. Unlike the magnetic properties of the nanocomposite, which enable easy recovery from solution thereby simplifying the filtration process at large quantities and getting rid of the need for complex filtration. Regarding membrane fouling, while the nanocomposite was used in suspension in this study, in industrial applications, it may be applied as a coating on membranes or in packed columns. In such situations, membrane fouling may arise from a buildup of either nanoparticles, dye or organic pollutants. To rectify this situation, appropriate design of the bed, pretreatment processes, and periodic washing with proper solutions, for example, mild acid or hydrogen peroxide, are recommended. The regeneration process is made easy by the nanocomposite’s magnetic property for recovery after utilization and several studies have proven that chitosan and magnetic nanoparticles can be reused after washing with suitable solutions (e.g., ethanol or gentle acids) and will hold their properties in successive cycles. However, in industrial environments, performance after repeated cycles must be emphasized to avoid; significant drop in adsorption capacity or structural degradation over some time concerning its disposal, the base materials of this nanocomposite (CS and CMC) are indeed biodegradable and of slight hazard; but presence of MWCNT_S calls for special attention as they may remain stable in some environmental conditions or have special biological effect. On completing the nanocomposite’s life cycle, controlled incineration or stabilization in solid matrices may be considered as a possible disposal method. In conclusion, this nanocomposite has great potential for scalability with respect to structure, performance and separability aspect; however, the drawback lies in further study on the durability, regeneration and the environmental issues in longer use cycles for the successful industrial implementation.

Potential of the synthesized nanocomposite for removing a wide range of dyes

While the main aim of this study was to look at MB, the special properties of the magnetic CS/CMC/MWCNTs suggest that it may effectively remove many different types of dyes. FTIR analysis has shown that the adsorbent contains –OH, –NH₂, –COOH, and –C–O– groups on the surface. Electrostatic attractions with cationic dyes such as crystal violet, malachite green, and rhodamine B, play a key role in the adsorption process. Hydrogen bonding with anionic dyes such as methyl orange and Congo red contributes significantly to the adsorption mechanism. And π–π interactions with aromatic ring-containing dye molecules further enhance the adsorption capacity of the nanocomposite.

In addition, MWCNTs make adsorption happen over a larger area, improve how dyes are removed, and favor interactions between the dye and MWCNTs that involve π-bonds. It is found that if an external magnet is added, the easy recovery of the nanocomposite can be achieved from aqueous fluids. Such simplicity plays an important role in industry and repeatedly using the adsorbents. Our images and the results prove that CS and CMC layers separated close MWCNTs. As a result, the material can take care of more dyes and act faster and better. Although the study did not experiment with different dyes, the discovered features indicate that the synthesized nanocomposite is very likely to be effective at cleaning up a range of dye pollutants in real wastewater treatment.

Also, the reusability of the synthesized adsorbent was thoroughly investigated in the present study to assess its potential for practical applications. After five consecutive adsorption-desorption cycles, the removal efficiency decreased from 94.64 to 78.2%, indicating only a 16.4% reduction in performance. This demonstrates that the material maintains considerable adsorption capacity even after multiple uses, confirming its potential for cost-effective and sustainable application in dye removal processes (Fig. S6 in the supporting information file).

A comparative study was conducted between the adsorbent used in this research and other nano-adsorbents for the removal of MB from aqueous solutions. The results showed that this adsorbent demonstrated significantly higher efficiency in removing MB compared to other nano-adsorbents (Table S1 in the supporting information file).

Conclusion

This study successfully showed that a magnetic-CS-CMC/MWCNT nanocomposite has excellent performance for the removal of MB from aqueous solutions. Using the advanced regression models, GA optimization, the most influential parameters, and optimal conditions for the maximum dye removal have been determined. The applied models include GBR with better predictive accuracy, which overperformed the MLE (R²=0.949 (training) and R²=0.951 (test), RMSE = 5.77, and MAE = 3.83) which produced R²=0.999, RMSE = 0.92, and MAE = 0.6. Residual analysis confirmed that GBR predictions were more stable and normally distributed. Feature importance analysis consistently identified X2 (amount of CMC) as the most significant factor in both models, with a correlation coefficient of 0.72 with removal efficiency, followed by X3 (amount of MWCNT) with 0.66. Variables X1 (pH) and X4 (initial dye concentration) had minimal impact and may be excluded to simplify future models. The solution even confirms these results, as evaluated using the GA, by converging to an optimal solution of the system that has X1 = 49.41, X2 = 110.62, X3 = 11.84, and X4 = 20 that in turn maximize the removal efficiency under these settings. These results underpin the fact that the proposed approach, along with its contribution towards a deeper understanding of the adsorption mechanism, provides a reliable and optimized predictive model for available dye removal, hence advocating for its universality in cost and large-scale water treatment technologies.

In the short term, future studies may simplify the proposed model by removing the less significant variables (for example, X1 and X4) and thereby reducing the computational complexity. Still, the prediction accuracy will not suffer as a result of such a reduction in the complexity of computation. Also, the adsorbent’s performance within real wastewater matrices should be validated in order to determine the applicability of the obtained adsorbent under complex or real-life conditions. A further measure to establish the effectiveness of the model is the experimental verification of the (GA) found optimal values. In the long term, scaling up the synthesis of the magnetic-CS-CMC/MWCNT nanocomposite for pilot-scale or industrial applications can be pursued. Further, expansion of the model into multi-contaminant systems, followed by testing the selectivity and reusability of the nanocomposite over a series of cycles, would increase its practicality for sustainable reactor systems for wastewater treatment. Incorporation of this framework with online monitoring/control systems utilizing the latest machine learning enabled algorithms in real time is another intriguing future course of study.