PM_2.5 concentration 7-day prediction in the Beijing–Tianjin–Hebei region using a novel stacking framework

Abstract

High-precision prediction of near-surface PM_2.5 concentration is a significant theoretical prerequisite for effective monitoring and prevention of air pollution, and also provides guiding suggestions for the prevention and control of PM_2.5-related health risks. It has been acknowledged that existing PM_2.5 prediction models predominantly rely on variables influenced by near-surface factors. This inherent limitation could hinder the comprehensive exploration of the continuous spatio-temporal characteristics associated with PM_2.5. In this study, an optimal 7-day prediction model for PM_2.5 concentration based on the Stacking algorithm was constructed based on multi-source data mainly including atmospheric environment ground monitoring station data, MODIS remote sensing-derived aerosol optical depth (AOD) daily data and meteorological factors. The findings indicated that the PM_2.5 forecasting outcomes derived from this integrated RF-LSTM-Stacking model exhibited a superior fit, with R², RMSE, and MAE values of 0.95, 7.74 µg/m³, and 6.08 µg/m³, correspondingly. This approach enhanced the accuracy of prediction to a degree of approximately 17% in comparison with a solitary machine learning model. The findings of this study demonstrated that the integration of the LSTM-RF model with the fusion-based Stacking algorithm led to a substantial enhancement in the accuracy of PM_2.5 predictions. This model was found to serve as an effective reference for the monitoring of PM_2.5 prediction and early warning systems.

Introduction

Particulate matter 2.5 (PM_2.5) refers to particles in the atmosphere with an aerodynamic equivalent diameter of no more than 2.5 μm, which are capable of entering human lungs via the respiratory tract. This has the potential to cause harm to the human immune system and to have adverse effects on human health^1,2. In the interim period, studies have demonstrated that atmospheric concentrations of PM_2.5, which remain elevated for protracted durations, have a deleterious effect on the visibility of the atmosphere. Moreover, evidence has indicated that this phenomenon can have significant consequences for ecosystem integrity and crop productivity^3,4. In recent years, the implementation of various measures aimed at the prevention, control, and management of air contamination has resulted in a notable decreased in PM_2.5 concentration pollution across the majority of regions within the country. Nevertheless, instances of pollution remain relatively prevalent during the autumn and winter periods^5,6. It is therefore crucial that accurate prediction of near-surface PM_2.5 concentration and in-depth exploration of its spatial distribution are of great significance in guiding with the refined management of air pollution prevention and control, as well as the safeguarding of population health and safety⁷.

At present, the principal methodologies for the high-precision prediction of near-surface PM_2.5 concentrations include atmospheric physical transport models and statistical theory models⁸. Atmospheric physical transport models typically rely on emission inventories and a range of historical meteorological data, incorporating comprehensive considerations of chemical reactions between pollutants, the diffusion of atmospheric pollutants, and the process of gaseous solid-state interconversion⁹, such as WRF-CMAQ¹⁰, WRF-Chem¹¹. Nevertheless, these techniques were constrained by inadequate temporal precision, the necessity for a considerable number of parameters for model construction, the prolonged process of forecasting PM_2.5 concentrations, and the requirement for a specialized background in meteorology¹². By way of comparison, statistical theory models did not require consideration of complex and varied chemical-physical evolution processes, as the case with atmospheric physical transport models. The potential existed to exploit the characteristics of the non-linear relationship between atmospheric pollutants, meteorological factors, the natural environment, and socio-economic factors, in order to achieve more accurate predictions of PM_2.5^13,14. The prevailing statistical theory models were as follows: the linear regression model¹⁵, the machine learning model¹⁶, and the deep learning model¹⁷. The linear regression model was advantageous in terms of simplicity, interpretability, and ease of comprehension. Nonetheless, it was less efficacious in the context of fitting non-linear relationships and data sets with extensive feature spaces, was vulnerable to the influence of outliers, and was incapable of accommodating high-dimensional features¹⁸. The most commonly adopted machine learning models, such as Random Forest (RF)¹⁹ and Support Vector Machines (SVM)²⁰, were preferred due to their underlying mathematical theory. However, the efficacy of these models was constrained by limitations in their data feature extraction abilities and a tendency to overfit, particularly when the available data was insufficient for effective training. The most common deep learning models currently in use are Long Short-Term Memory Neural Networks (LSTM) and Convolutional Neural Networks (CNNs)²¹. These models were demonstrated proficiency in temporal feature extraction; however, they are vulnerable to challenges such as local optimality and sluggish iteration speeds²².

Ensemble learning is a machine learning approach that has been shown to enhance the predictive accuracy and the robustness of the models involved by means of a combination of multiple underlying models. Common integrated learning algorithms include bagging, boosting, and stacking²³. The Stacking algorithm is notable for its employment of a hierarchical structure, which is instrumental in the effective synthesis of the characteristics of various base learners. This process is further augmented by the utilization of data for model training and optimization, thereby ensuring the efficacy of the algorithm. This approach enhances the prediction accuracy and stability of the integrated model, while circumventing the limitations associated with overfitting and slow iteration speed, which are commonly observed in conventional models. A considerable body of research has utilized ensemble learning algorithms to predict ground-level PM_2.5 concentration, yielding specific research outcomes²⁴. Nevertheless, the control variables employed in these prediction studies were generally near-surface influences with large spatial limitations. The advent of satellite remote sensing observation technology has led to the availability of a greater number of continuous parameters that are indicative of spatial distribution for the purpose of PM_2.5 concentration monitoring. This development has resulted in the provision of continuously varying remotely derived parameters on a large-scale spatial scale, and to a certain extent, has facilitated the generation of a continuous sequence of reliable eigenvectors for the prediction of near-surface PM_2.5 concentration²⁵. The principal remote sensing satellite-derived products employed for the monitoring of atmospheric aerosols are the Aerosol Optical Depth (AOD) and the Angstrom Index^26,27. Aerosol optical depth (AOD) is a pivotal parameter in the study of atmospheric columnar aerosols, and it has emerged as a prevalent derivative of remotely sensed aerosols^28,29. The temporal-spatial variability characteristics of aerosol optical thickness data would be combined with integrated learning algorithms with the objective of improving the prediction accuracy of PM_2.5 to a certain extent.

The Beijing-Tianjin-Hebei region is of significant importance in northern China. The region is facing severe environmental challenges related to PM_2.5 concentrations, which are a result of high-density industrial activities, energy consumption and traffic congestion. The accurate prediction of regional PM_2.5 concentration is of significant scientific importance, as it would provide a robust foundation for decision-making and strategic management of air pollution control measures. In this study, a 7-day prediction model of PM_2.5 concentration based on LSTM-RF- Stacking Integrated Learning Framework was constructed based on the atmospheric monitoring data from 80 national air quality monitoring stations and their corresponding AOD and meteorological data, which was able to capture the spatial and temporal characteristics of the future changes of PM_2.5 concentration, and would provide an accurate reference for the prediction of and early warning for PM_2.5.

Materials and data sources

Study area

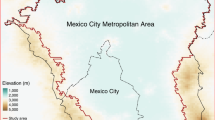
The Beijing-Tianjin-Hebei region encompasses the municipalities of Beijing and Tianjin, as well as 11 prefecture-level cities located within Hebei Province, spanning from 36°00’ to 42°40’ north latitude and 113°27’ to 119°50’ east longitude (Fig. 1). It is situated at the north-eastern extremity of the North China Plain, with the terrain exhibiting a marked elevation from west to east, with highlands in the north-west and lowlands in the south-east. The region encompasses by a diverse range of landforms, including plains, mountains, hills, and is classified as exhibiting a temperate continental climate³⁰.

Fig. 1

Schematic distribution of the study area and monitoring stations.

With the implementation of a series of measures to control and prevent the proliferation of air pollutants, PM_2.5 has decreased significantly in the Beijing-Tianjin-Hebei region recently. The annual average PM_2.5 in this area rapidly decreases from 106 µg/m³ to 37 µg/m³ between 2013 and 2022, with an average annual decrease of 7.67 µg/m³. The proportion of polluted days with PM_2.5 decreased from 37.5% in 2013 to 12% in 2022, a decrease of approximately 4.4%. The cumulative decrease will be approximately 37.4%, with the proportion of good days averaged annually at 65.5%³¹.

Data source

In this study, the stacking dataset ensemble model used comprises three constituent parts: air pollution data, meteorological data, and AOD. Among them, the observed time series data of air pollutants were obtained from the China Environmental Monitoring General Station (http://www.cnemc.cn/sssj/), including seven types of PM₁₀, NO₂, AQI, SO₂, O₃, and CO, and the PM_2.5 data from the National Tibetan Plateau Science Data Centre^32,33. The meteorological data were obtained from the ERA5 global climate reanalysis dataset, published by the European Centre for Medium-Range Weather Forecasts. The meteorological variables included in the analysis were atmospheric pressure (PAIR), relative humidity (EH), temperature (TEM), and wind speed (WS), which are denoted by the following abbreviations; The AOD dataset was obtained from MODIS which is mounted on the Aqua and Terra satellite probes of the EOS series (https://ladsweb.modaps.eosdis.nasa.gov/); The Optical_Depth_550 dataset from the MCD19A2 data was employed to extract daily hourly AOD values within the study area at a wavelength of 550 nm, with the objective of contributing to the model predictions.

The dataset adopted a tabular structure with hierarchical organization by monitoring stations, where each row encapsulated daily observations of air quality parameters, meteorological variables, and aerosol optical depth (AOD) measurements, systematically timestamped by date and local time. Spanning the Beijing-Tianjin-Hebei region from January 1 to December 31, 2020, this comprehensive collection comprised 29,263 hourly records obtained from 80 environmental monitoring stations. These temporally resolved measurements were specifically curated for time series analytical applications in atmospheric research.

Data reprocessing

The AOD dataset with the primary processing, including the extraction of the dataset, filtering of the QA values, and other processes. The MCD19A2 dataset was extracted by first filtering the AOD multivalue data in the 550 nm band that had passed the quality control from the raw data and converting it to real data, which in turn led to the acquisition of daily 550 nm_AOD averages. Subsequently, the data underwent a series of processing stages, including image stitching, conversion of the projection system, and other procedures, in order to get the daily AOD data.

In case a single missing value within the dataset, the preceding moment of data for that specific missing value was employed in its place. The min-max normalization was used to mitigate the adverse effects on the prediction outcomes resulting from discrepancies in the magnitude and value ranges between individual characteristics. Consequently, this approach accelerated the training process of the model to a certain extent, while ensuring a uniform transformation of the feature range between 0 and 1⁷. The formula was as shown:

$$\bar{x} = \frac{{x - x_{{\min }} }}{{x_{{\max }} - x_{{\min }} }}$$

(1)

where $\bar{x}$ denotes the normalized independent variable, x_max denotes the maximum value of the original independent variable, and x_min denotes the minimum value of the original independent variable.

Research methods

Stacking ensemble learning model

The stacking learning ensemble model is a multi-layer learning system that organizes different learners through a hierarchical structure (Fig. 2). The model consists of several base learners as the first layer of the prediction model, a meta learner as the second layer of the prediction model, and a feature extractor that trains the features included from the base learner model on the dataset again as inputs to the meta learner³⁴. This process enables the learner model to synthesize and stack features²³. Furthermore, the findings demonstrate that the robustness and generalizability of the stacking ensemble learning model is considerably enhanced in comparison to a solitary model³⁵. In this study, the Multiple Linear Regression Model (MLR) is selected as the meta-learner. MLR is responsible for identifying the relationship between the input features and the target variable PM_2.5 by employing a linear combination of the prediction results of the base learner model. The prediction results output from the base learner model are utilized as the input feature matrix, and the coefficients of the linear regression equation are determined by minimizing the error between the predicted value and the actual value. The advantages of each base learner are combined to enhance the overall prediction accuracy and generalization ability of the model, thereby facilitating highly accurate prediction of PM_2.5³⁶.

Fig. 2

Stacking network architecture.

Long short-term memory

Long Short-Term Memory (LSTM) is an improved version of the Recurrent Neural Network (RNN) model, which enables the storage and regulation of temporal data by adding memory units to the hidden unit layer. LSTM networks facilitate the transfer of information between units in the hidden layer through the incorporation of three storage unit structures: the forgetting gate, input gate, and output gate. This unit structures design facilitates the effective filtering and memorization of information³⁷. In comparison to conventional RNN models, LSTM models are capable of addressing issues such as gradient vanishing or gradient explosion, which are inherent to RNN¹⁸, the network architecture is shown in Fig. 3.

Fig. 3

LSTM network architecture.

Among them, i_t, f_t, and o_t are three gating structures: input gate, forgetting gate, and output gate, respectively. The input gate is responsible for the regulation of information input, the forgetting gate for the retention of information regarding the historical state of the cell, and the output gate for the control of information output. And σ()is the sigmoid function, and tanh()is the activation function.

Random forest

Random Forest (RF) is a combinatorial model consisting of a set of regression decision trees. In accordance with the idea of Bagging (Bootstrap Aggregating), the Random Forest model acquires a multitude of subsets of training samples, each distinct from the others. This is achieved through the random extraction of features from the original samples on multiple occasions, followed by their subsequent reintroduction³⁸. The Random Subspace Method (RSM) is employed for the construction of decision trees utilizing various sample subsets³⁹. The features incorporated into the decision tree are randomly extracted from the data features. When the nodes of the decision tree are split, the best feature nodes within the randomly generated feature subset are selected for splitting. Ultimately, the final prediction result of the RF model is obtained by averaging the prediction results of each decision tree, as illustrated in Fig. 4. Compared with the base learner, the RF model exhibits a greater capacity for randomness in the selection of samples and feature nodes. This can enhance the model’s generalization ability to a certain extent. Furthermore, the RF model exhibits a notable advantage over other algorithms in its ability to process multidimensional data without the necessity of feature selection⁴⁰.

Fig. 4

RF network architecture.

Inverse distance weighting

Inverse Distance Weighting (IDW) is based on the improvement and optimisation of distance-weighted interpolation. The method is predicated on the assumption that each measurement point is subject to local effects that diminish with distance^41,42. In the event that a test site is divided into multiple regions, neighbouring points within each region are employed for the estimation of unknown points, provided that the locations of all measurement points are known. This method assigns higher weights to points in close proximity to the predicted location, with the weights gradually decreasing as the distance from the predicted location increases. The topography of the Beijing-Tianjin-Hebei region is complex, and the PM_2.5 concentrations in different regions are greatly influenced by pollution sources, meteorological conditions and other factors. The IDW method is a geostatistical interpolation technique that can fully take into account the influence of spatial location on PM_2.5 concentrations. In order to predict the PM_2.5 concentration at a specific location, greater reliance is placed on data from neighbouring monitoring stations. This approach ensures that the prediction results accurately reflect the local pollution situation and facilitates the assessment of the reasonableness of the interpolation results. The formula is as follows:

$$Z = \frac{{\sum\nolimits_{i}^{n} {\frac{{z_{i} }}{{d_{i}^{k} }}} }}{{\sum\nolimits_{i}^{n} {\frac{1}{{d_{i}^{k} }}} }}$$

(2)

Assessment indicators

The Mean Square Error (MSE), Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Determination Coefficient (R²), and Mean Absolute Percent Error (MAPE) were employed to assess prediction results of each predicted model. The relevant assessment indicators are as shown:

$$R^{2} = 1 - \frac{{\sum\limits_{{i = 1}}^{n} {y_{i} - \hat{y}_{i} ^{2} } }}{{\sum\limits_{{i = 1}}^{n} {y_{i} - \bar{y}_{i} ^{2} } }}$$

(3)

$$MAE = \frac{{\sum\limits_{{i = 1}}^{n} {\left| {y_{i} - \hat{y}_{i} } \right|} }}{n}$$

(4)

$$RMSE = \sqrt {\frac{{\sum\limits_{{i = 1}}^{n} {y_{i} - \hat{y}_{i} ^{2} } }}{n}}$$

(5)

$$MAPE = \frac{{100\% }}{n}\sum\limits_{{i = 1}}^{n} {\left| {\frac{{(\hat{y}_{i} - y_{i} )}}{{y_{i} }}} \right|}$$

(6)

Where y_i denotes the actual measurement value of the i-th PM_2.5, $\hat{y}_{i}$ denotes the predicted value of the i-th PM_2.5, $\bar{y}_{i}$ denotes the actual mean measurement value of the i-th PM_2.5.

Results

RF-LSTM-stacking model construction

The various influencing factors were illustrated by Pearson’s correlation coefficients (Fig. 5). It was evident that there was a significant positive correlation between the data on air pollution and AOD, with a correlation coefficient of 0.39 between O₃ and PM_2.5, indicating a robust correlation and a more intricate non-linear change rule. Moreover, the correlation between PM_2.5 and meteorological data proved to be significantly low, with the correlation coefficient between PAIR and PM_2.5 displaying the least substantial correlation among all variables. Consequently, the present study selected air pollution data and AOD data for incorporation into the model construction process.

Fig. 5

Correlation between characteristics of independent variables.

The PM_2.5 prediction model was on the basis of the stacking ensemble learning algorithm, the base learners were LSTM and RF, while MLR was employed as a meta-learner. Among them, LSTM showed a superior prediction accuracy for long time series and was suitable for PM_2.5 prediction on the basis of historical data⁴³; The RF model was good at dealing with data with high-dimensional features and did not require characteristics selection, and usually had fast model training and high prediction accuracy, so it was suitable for multivariate PM_2.5 prediction⁴⁴.

The primary steps were: 1) The first 25,000 sets of data in the original dataset were taken as the training set M, and the last 4263 sets of the dataset were taken as the testing set N. The total length of the sequences in the training set l₁ and testing set l₂, the sliding time window input was defined as 7, and the step size was defined as 1. The process generated l₁−7, l₂−7 sets of subsequences of length 7 for both the training set and testing set. The base learner models were trained using the training set M. Furthermore, the Grid Search (GS) was employed to identify the most appropriate hyperparameters for each model⁴⁵. In order to enhance the model’s performance and robustness, this study employed the GS method to systematically tune the key hyperparameters of the base learner LSTM with RF. GS is a method of filtering out the hyperparameter combinations with optimal performance. It performed an exhaustive search for parameter combinations on the training set, using the RMSE of the validation set as an evaluation metric. Specifically, the LSTM model was configured with a two-layer structure comprising hidden units. The first hidden layer contained 30 LSTM units, the function of which is to retain the outputs of all time steps for use in subsequent layers. The second hidden layer contained 20 units, the function of which is to output the hidden state of the last time step. The final stage of the process involves the use of a fully connected layer containing 10 neurons with an activation function of ReLU to output a single continuous value for the purpose of regression prediction of PM_2.5 concentration. The configuration was developed to ensure equilibrium between the temporal feature extraction capability and the model complexity. In the context of the RF model, the optimal hyperparameters that were determined through grid search were as follows: the number of decision trees was set to 200, the minimum number of leaf node samples was 1, and the minimum number of division samples was 2. This parameter design ensured the model’s ability to fit the data while effectively controlling the training time, thereby achieving the minimum RMSE on the validation set. This set of parameters was then used to construct the base learner(Table 1). 2) Following the training of each base learner model, the prediction results (M₁, M₂) for M and (N₁, N₂) for N were obtained, respectively. 3) The data in the training set M₁ were used as the input feature matrix X, and the corresponding real PM_2.5 values were used as the output matrix Y. Subsequently, X and Y were employed as the input feature matrices of the meta-learner model. The sample data constructed with X and Y were used to train the meta-learner model in the second layer. During the training process, the regression coefficients were continuously adjusted by minimizing the error between the predicted and true values. This process was undertaken to facilitate the identification of the optimal linear mapping relationship between the predicted values and output variables of each base learner. 4)The new feature matrix N₁ was used to test the prediction of the trained meta-learner, so as to capture the effective patterns in the prediction information of multiple base learners, and achieve the synthesis of the learning ability of the base learners’ model. This process enabled the meta-learner to effectively extract and integrate the prediction ability of multiple base learners in the prediction ability of the different data features, and improved the prediction accuracy and generalization ability of the overall model(Fig. 6).

Table 1 Grid search results for the main parameters of each model.

Fig. 6

Stacking ensemble learning framework. Among them, P was PM_2.5 concentration data, T was PM₁₀, NO₂, AQI, SO₂, O₃,CO and AOD data.

Comparative analysis of model evaluation indicators

In order to ascertain whether the predictive effectiveness of the stacking model exceeded that of the other single models, the predictive effectiveness of four single prediction models, LSTM, RF, KNN(K-Nearest Neighbours, KNN), and MLR, were selected for evaluation and analysis (Table 2). Overall, all five machine learning models demonstrated an R² value exceeding 0.92, indicating that the selected optimal parameters were capable of effective prediction of PM_2.5. The RF model demonstrated superior predictive performance in the training set, with a correlation coefficient R² of 0.99, outperforming the other four models. However, when the model was applied to the testing set, the predictive performance of the RF model, which had performed well in the training set, was found to decrease. This indicated that the RF model might have been exhibiting problems of overfitting in the training set. In comparison to several other models, the MLR model demonstrated the poorest performance in the testing set, with an R² value of 0.93. The Stacking model demonstrated superior performance when applied to the test set compared to the other four models, exhibiting a correlation coefficient R² of 0.96, MAE and RMSE of 6.08 and 7.74, respectively, and a MAPE of 0.26%. In comparison to the LSTM model, the RMSE and MAE were decreased by 16.18% and 22.47%, respectively. Similarly, in comparison to the RF model, the RMSE and MAE were decreased by 17.13% and 20.59%, respectively. In comparison to the MLR model, the RMSE and MAE were decreased by 22.90% and 23.50%, respectively. Similarly, in comparison to the KNN model, the RMSE and MAE were decreased by 56.5% and 51.04%, respectively. In comparison to other studies that had attempted to predict PM_2.5 concentrations, the Stacking algorithm was capable of effectively combining the advantages of different models. Its results demonstrated an improvement in the RMSE and MAE by approximately 12.40% - 32.89%, which significantly enhanced the accuracy of the predictions.

In summary, a comparison of the predictive performance of the five machine learning models revealed that the Stacking model demonstrates the optimal predictive performance. The LSTM, RF and MLR models exhibited inferior predictive performance, while the KNN model produced the least satisfactory results.

Table 2 Performance of different models on testing and training Sets.

Comparative analysis of model station prediction results

The prediction effects of the five models were evaluated using the monitoring station of Tangshan Lunan University of Electricity as an example from 23 September 2020 to 31 December 2020 (Fig. 7). It was found that the prediction accuracy improved and the predicted values overlapped with the true values more when the PM_2.5 levels ranged from 20 to 70 µg/m³. Conversely, when the PM_2.5 concentration exceeded 70 µg/m³, the discrepancy between the predicted and true values of each model increased. When the PM_2.5 concentration exceeds 10 µg/m³, a discrepancy emerged between the predicted and actual values of each model. When the PM_2.5 concentration continued to rise above 120 µg/m³, the discrepancy between the predicted and actual values of each model further increased, resulting in unsatisfactory prediction results.

Fig. 7

Comparison between predicted and actual values of the five predicted model.

Among them, the Stacking model demonstrated the greatest alignment with the PM_2.5 concentration curve, exhibiting the most precise correspondence between the predicted and actual values, and was the most effective at capturing the evolving trend of PM_2.5. The predicted values of the LSTM and RF models were closer to the actual values, although they exhibited a slight underestimation of PM_2.5 concentrations at high levels and a slight overestimation at low levels, and there was a notable discrepancy between the predicted values and the observed values of the KNN and MLR models. In comparison to the LSTM and RF models, the variance of the PM_2.5 concentration prediction results of the Stacking model was smaller. However, there were instances where the predicted peaks differed from the actual values. Nevertheless, the highest and lowest points of the overall predicted values were closer to the actual values, and the prediction results were superior to those of the LSTM model, particularly at the inflection points.

In order to comprehensively evaluate the performance of the evaluation model, a metric known as annual cumulative prediction bias was utilized to ascertain the effectiveness of the model in predicting PM_2.5 concentration values⁴⁶. This metric enabled the quantification of the predictive accuracy of the model by summing the absolute difference between the predicted and true value concentrations. Adopting this approach yielded a comprehensive understanding of the model’s predictive capacity and facilitated a judicious comparison between models. As demonstrated in Fig. 8, the cumulative bias in the northern part of the study area was, in general, smaller than that in the southern part of the study area across the models. The annual cumulative prediction bias of the Stacking model was approximately 1300 µg/m³- 5300 µg/m³ across the PM_2.5 monitoring stations, followed by the LSTM and RF models, with the annual cumulative prediction bias ranging approximately 1500 µg/m³- 6100 µg/m³. For the KNN and MLR models that demonstrate poorer performance, the range was approximately 1000 µg/m³ - 12,000 µg/m³. The disparate ranges of prediction bias observed for each model furnished a multiplicity of perspectives on the relative performance of the models in predicting PM_2.5 concentration values. The Stacking model was demonstrated to effectively combine multiple base learners and exhibited reduced prediction bias in terms of variability, thus showing higher reliability and stability.

Fig. 8

Annual accumulated bias values for individual PM_2.5 monitoring stations for five models in the Beijing-Tianjin-Hebei (µg/m³).

Comparative analysis of spatial variation characteristics

The spatial distribution of daily average PM_2.5 in the study area was obtained by the IDW interpolation method based on the PM_2.5 concentration prediction results of the LSTM, RF and Stacking models (Fig. 9). As could be seen from the figure, the IDW method can accurately reflect the spatial trend of PM_2.5 concentration in the region according to the distribution of monitoring stations and concentration data. From the results, it successfully captured the distribution of PM_2.5 concentrations in the Beijing-Tianjin-Hebei region, where the concentrations were high in the south and low in the north, as well as the approximate locations of the centers of high and low values, which indicates that the method could effectively handle the data in the present study, and obtain the spatial distribution results consistent with the actual situation. The spatial distribution of PM_2.5 from the Stacking model was found to be the closest to the measured data. Among the models considered, the spatial distribution of PM_2.5 from the Stacking model demonstrated the closest alignment with the measured data, thereby providing a comprehensive overview of the distribution of PM_2.5 within the study area. In comparison, the LSTM model, which employed three gating structures for time-series prediction, yielded results that were more consistent and exhibited an overall trend that was similar to that of the measured data. However, discrepancies were observed at the boundaries between areas with high and low concentrations. Conversely, the RF model utilized a large number of decision trees for prediction and exhibited notable resilience to overfitting. Nevertheless, it should be noted that this approach might have resulted in the emergence of bias in specific local areas. Satellite remote sensing data estimated PM_2.5 concentration through satellite observation of AOD in the atmosphere, which was affected by meteorological conditions, surface albedo, and other factors, and thus showed a slight difference in spatial distribution from the measured data.

Overall, the Stacking model performed best in terms of prediction accuracy and showed high robustness. From the perspective of the accuracy of the comparison of the PM_2.5 concentration prediction results from different models, the spatial distribution of PM_2.5 concentration obtained based on IDW interpolation had a better fit with the prediction results of the Stacking model as well as the measured data, and was able to capture the distribution of PM_2.5 concentration in the region in a more comprehensive way, which in turn demonstrated the validity of the method in this study.

Fig. 9

Daily spatial variation of PM_2.5 employing the IDW interpolation method in the Beijing-Tianjin-Hebei region in 2020 (µg/m³).

Discussion

The influence of meteorological data

There was a positive correlation between PAIR, EH and TEM and PM_2.5, whereas WS displayed a negative correlation (Fig. 4). This suggested that meteorological conditions exerted some influence on PM_2.5. Among the variables under consideration, the correlation between PAIR and PM_2.5 was the weakest, with a coefficient of 0.03. This was due to the fact that the majority of the monitoring stations selected for inclusion in this study were state-controlled stations, with the majority of these located in the main urban areas of each city. The proximity of state-controlled monitoring stations in the same main urban area resulted in minimal variation in the meteorological data extracted, which have limited the ability to fully understand the relationship between meteorological conditions and PM_2.5. Further research could have expanded the distribution of monitoring stations to obtain a more accurate understanding of the influence of meteorological conditions on PM_2.5 concentrations.

Advantages of LSTM-RF-stacking model for predicting PM_2.5 concentration after 7 days

In this study, five PM_2.5 concentration prediction models were constructed and compared. The results demonstrate that there are discrepancies in the extraction ability, structural mechanism, and generalization ability of the models with regard to data features. The RF model is predicated on the Bagging integration learning strategy, which constructs multiple decision trees by randomly extracting samples and features multiple times, and integrates its prediction results. This mechanism facilitates the demonstration of remarkably elevated fitting ability and training efficiency on the training set (R²=0.99). However, it has been observed to demonstrate a propensity for overfitting when confronted with the test set data, resulting in a diminution of its generalization capability due to the overfitting of noise and local patterns present in the training data⁴⁷. In the field of time-series analysis, the LSTM model has been shown to be effective in capturing long-term dependencies through its gating mechanism. Its application in dealing with PM_2.5 concentration series data, characterized by its time-series properties, has yielded relatively robust prediction performance on both the training and test sets. However, the model’s performance is not as comprehensive as the integrated approach in handling complex non-linear relationships. In this regard, the LSTM model exhibits a slight weakness in comparison to the Stacking model on the test set⁴⁸; The KNN model is developed for the purpose of selecting the K nearest neighbours for prediction. This is achieved by comparing the distance between the input samples and the samples in the training set. Within the training set, the model may exhibit a degree of prediction capability due to the local similarity of the data. However, this local similarity-based prediction is deficient in its inability to comprehensively grasp the overall characteristics and trends of the data. In instances where the data distribution in the test set deviates from that of the training set, the prediction capability of the KNN model is compromised, consequently leading to a diminished prediction accuracy in the test set, as evidenced by an R² of 0.76⁴⁹. The MLR model is predicated on the linear relationship between variables, with the regression coefficients being determined by minimizing the discrepancy between the predicted and actual values. This model is uncomplicated and straightforward to comprehend. Nevertheless, when confronted with a complex time-series problem, such as PM_2.5 concentration prediction, its linear assumption frequently falls short of accurately depicting the true relationship between the data, consequently leading to suboptimal prediction accuracy in the test set (R² = 0.93). Conversely, the Stacking model is predicated on a hierarchical structure that integrates the base learner models (LSTM, RF) and trains the prediction outputs of the base learner models with MLR as a meta-learner to derive the final prediction results. This approach enables the comprehensive integration of the strengths inherent in each base learner model, thereby ensuring the enhancement of the model’s prediction accuracy and stability. The Stacking algorithm has been demonstrated to facilitate the capture of complex characteristics and nonlinear relationships in data, thereby enhancing the generalization capability of the model²⁴.

The characteristics of PM_2.5 spatial distribution

The spatial distribution characteristics of the annual average PM_2.5 concentration revealed a significant gradient reduction in the annual average PM_2.5 concentration extending from the northeast to the southwest. Specifically, the northern regions of Zhangjiakou and Chengde have lower annual average PM_2.5 concentrations due to their mountainous topography, which facilitates good air circulation, high natural vegetation cover, a paucity of polluting industries, and well-developed tourism. In contrast, the south-central areas of Beijing, Tianjin, Shijiazhuang, Baoding, and Handan are areas with high PM_2.5 concentrations, with predominantly plain topography, high proportions of agricultural land and urban industrial and mining land, and a serious lack of ecological land coverage. This, in conjunction with the obstruction of PM_2.5 transportation by the Yanshan and Taihang mountain ranges, has resulted in the accumulation of pollution in the mountain front areas, leading to elevated annual mean values for the region. The findings of this study demonstrate that the spatial distribution characteristics of PM_2.5 are consistent with the observations reported by Fu et al.⁵⁰, which indicate that the central and southern regions of Beijing-Tianjin-Hebei are highly polluted areas for PM_2.5, while the northern regions exhibit reduced PM_2.5 concentrations.

Limit and future work

Despite the Stacking model’s demonstrated efficacy in PM_2.5 concentration prediction, it remains constrained in its ability to accommodate extreme pollution scenarios. The study data demonstrate that when the PM_2.5 concentration exceeds 120 µg/m³, the variance between the predicted and actual values of the model increases dramatically, resulting in a significant decrease in prediction accuracy. This phenomenon can be attributed to the fact that the environmental factors affecting PM_2.5 concentration in extreme pollution events present highly nonlinear and complex coupling characteristics, and existing models are unable to comprehensively portray their intrinsic correlation mechanisms. Moreover, the Stacking model is an integrated learning framework that relies on multiple base models and meta-learners. The training process involves constructing a multi-layer model, optimizing hyperparameters and conducting cross-validation. This process is both computationally intensive and time-consuming. This feature imposes significant limitations on the model’s capacity for rapid deployment and real-time update in practical applications. In the future, we need to start from the optimization of algorithms and resource allocation, and improve the application efficiency and environmental adaptability of the model by improving the model structure and adopting distributed computing technology.

Conclusions

Accurate forecasting of PM_2.5 changes was of significance for air pollution warning information. In this study, we employed a multi-source approach, integrating ground-based data from monitoring stations with satellite remote sensing AOD data, to structure a PM_2.5 Stacking prediction model for the Beijing-Tianjin-Hebei region. The model was a combination of time series sliding windows based on LSTM and RF and uses a stacked integration framework, which led to the following conclusions: 1) The selection of model input variables had an impact on the resulting predictions, and the preprocessing of data could enhance the precision of model projections. A positive correlation was evident between AOD and O₃, with O₃ exhibiting the highest correlation with PM_2.5. 2) In comparison to a single prediction model, the integrated learning algorithm fuses multiple base-learner models with the objective of more effectively capturing the nonlinear relation between each input variable and PM_2.5. In the five models, the stacking integration model demonstrated the most favourable predictive performance, exhibiting a notable enhancement in the model’s generalization capabilities and overall performance. 3) The spatial distribution of daily average PM_2.5 in the research region was obtained by IDW, which demonstrated a notable degree of spatial heterogeneity. The south-central region exhibited elevated PM_2.5, while the northern area displayed comparatively lower levels. Among them, the Stacking model was the most consistent with the measured data in predicting the spatial distribution of PM_2.5, and was able to more accurately capture the overall distribution and local variations in the study region.

In conclusion, this research developed a seven-day stacking prediction model for PM_2.5 utilising the integrated learning Stacking algorithm, with the objective of accurately predicting the daily average near-surface PM_2.5 concentration. The optimal Stacking prediction model, when selected and applied to daily ambient air quality forecasting, resulted in a further improvement in the precision of PM_2.5 prediction. Furthermore, this will offer a foundation for strengthening the control of atmospheric pollution and for achieving comprehensive regional environmental management and scientific strategic decisions in the Beijing-Tianjin-Hebei region.