Introduction

Indian mustard (Brassica juncea L. Czern & Coss) is a crucial crop belonging to the Cruciferae (Brassicaceae) plant family, known as the mustard family1. The essential oil of Brassica juncea seeds has been used in cosmetics for hair control, preparation of pickles and medicines, and for flavoring2. The seed contains protein (26 g/100 g), carbohydrates (28 g/100 g), dietary fiber (12 g/100 g), and fat (36%) with oil content ranging from 37 to 49%. Along with major components, it also has an ample number of vitamins like vitamin C and vitamin K, trace minerals such as Fe, Ca, Zn, Cu, Se, Mn, and Mg, as well as electrolytes like Na and K, etc3,4,5. In recent decades, India has witnessed a substantial rise in per capita edible oil consumption, reaching 19.7 kg per year. However, this increasing demand has outpaced domestic production, resulting in a high dependence on imports—nearly 57% of the edible oil consumed in the country is imported DFPD, 20246. This growing reliance emphasizes the need to enhance indigenous oilseed productivity to achieve self-sufficiency. Among the various oilseed crops cultivated in India, rapeseed-mustard holds a significant position. During the 2018–19 cropping season, Indian mustard was grown on 6.23 million hectares, producing about 13.16 million tonnes, and contributing 33.24% of the nation’s total oilseed output DRMR7. This highlights its vital role in meeting the country’s edible oil requirements. Despite its importance, achieving a balance between high seed yield and improved oil quality remains a major breeding challenge, as these traits are often negatively correlated8. Additionally, the productivity and oil composition of mustard are influenced by multiple biotic and abiotic stresses. The effective utilization of diverse germplasm through hybridization plays a crucial role in the genetic improvement of mustard crops to develop the architecture of genotypes having desirable traits, resulting in better performance of genotypes referred to as an ideotype9. The selection of superior genotypes across the traits is a challenging task; that’s why it requires a robust approach for selection which is based on multiple traits. Selecting genotypes having a balance of multiple desirable long-term traits is the aim of the breeder10. The presence of multicollinearity and the choice of weighting coefficients in classical linear multi-trait selection indices depletes the genetic gain11,12. Smith-Hazel Selection Index (SHI), developed by Smith13 and Hazel14 is a weighted selection index that enhances genetic gain by considering multiple traits simultaneously. Breeder faces difficulties in assigning the economic value of traits, converting them into realistic economic weightings with a multicollinearity issue15. Factor Analytic Best Linear Unbiased Prediction (FAI-BLUP) incorporates factor analysis for handling multi-trait to improve accuracy in multi-trait selection. Multi-Trait Selection Index (MTSI) identifies the high-yielding, stable genotypes across the environment. Multi-Trait Genotype –Ideotype Distance Index (MGIDI) ranks the genotypes based on multiple traits simultaneously with balanced trait performance. This MGIDI can effectively be used for multi-trait selection by overcoming the difficulties of SHI10. The combination of these rankings into a single robust decision-making framework, Weighted Rank Aggregation (WRA) using ranker accuracies, is a robust approach for genotype selection when multiple rankings are available. Genotype by Yield×Trait (GYT) Biplot used to visualize and interpret the relationship between genotypes and traits with special emphasis on yield. Genotype-by-trait biplots (GT biplots) have constraints, like failing to explain most of the variation and therefore being unable to give all patterns of data. Along this, it is unable to differentiate the effect of all traits on yield, while in the case of the genotype by yield×trait biplot (GYT biplot), it is able to address all these challenges present in the GT biplot12,16. The GYT biplot method is a comprehensive and effective method that gives the strengths and weaknesses of each genotype graphically and provides the rank of each genotype using superiority index (SI) based on GYT score by including all traits with yield12,16. It is applicable to different kinds of data sets having different agronomic traits, multiple locations or multiple years. Accordingly, the following study aims to understand the reliability of different multi-trait selection index and to select the best genotypes using WRA by utilizing the rank of SHI, FAI-BLUP, MTSI and MGIDI, the association of different multi-trait selection index and the selection of genotypes with special emphasis on yield traits using GYT biplot analysis.

Materials and methods

Materials

The ten parental genotypes of Indian mustard were sourced from the germplasm repository at the Sardar Vallabhbhai Patel University of Agriculture and Technology, Meerut, Uttar Pradesh, India, and selected for their contrasting traits relevant to crop improvement. Ten diverse genotypes, viz., RH-725, Pusa Jai Kisan, PM-28, Pusa Bold, Pusa Agrani, PM-29, CS-60, Kranti, Giriraj, and RH-749, were used for hybridization. Genotype used in hybridization aiming to address the different aspects of crop improvement, like Pusa Agrani and RH-725 used for short-duration and early sowing, respectively. PM-29 was used in crossing as it has lower erucic acid, which plays a crucial role in oil quality. Kranti has resistance to Alternaria blight and aphids, whereas CS-60 has tolerance to salinity and alkalinity. Pusa Bold, PM-28, Pusa Jai Kisan, and Giriraj genotypes have bold seed size, high oil content, and high yield, respectively; genotypes were used in the mating as yield improvement is the main research objective for breeders, and it can be improved by improving yield and its related components like bold seed size, high oil content, and high yield. The details of genotypes are provided in supplementary material (S1 Table).

Experimental details

During the Rabi season of 2022–23, ten genetically diverse Indian mustard (Brassica juncea L.) genotypes were selected and crossed using a half-diallel mating scheme, excluding reciprocals. This crossing program resulted in the development of 45 F1 hybrids. Together with the original ten parents with 45 hybrids, a total of 55 genotypes were further evaluation in the Rabi season of 2023–24, at the Crop Research Centre, of Sardar Vallabhbhai Patel University of Agriculture and Technology, Meerut. The trial was laid out in a randomized complete block design (RCBD) with three replications to ensure statistical reliability. Standard agronomic practices were followed throughout the growing season to maintain uniform crop management and minimize environmental variation.

Observations recorded

Thirteen quantitative characters were recorded during the experiment: (i) days to 50% blooming (DFB), (ii) days to maturity (DM), (iii) plant height (PH), (iv) branches on a main raceme (BMR), (v) siliquae on a main raceme (SMR), (vi) length of a main raceme (LMR), (vii) siliqua length (SL), (viii) seeds per siliqua (SPS), (ix) biological yield per plant (BY), (x) harvest index (HI), xi) oil content (OC), xii) test weight (TW), and xiii) seed yield per plant (SY). Five plants from each parent and hybrid in each replication were randomly selected and tagged before maturity. The mean of particular genotypes was calculated using the average of five plants, except for DFB and DM, which were assessed on a population basis.

Statistical analysis

All statistical analyses were conducted using R version 4.4.3. The work was performed on a cloud-based RStudio environment running Ubuntu 20.04.6 LTS. Analyses were carried out using the metan package17.

Analysis of variance (ANOVA)

The analysis of variance for the experimental design was based on the model: Pijk = µ + vij + bk + eijk. (i, j = 1…t; k = 1…b). Where, Pijk = the phenotype of ijkth observation, µ = the population mean, vij=the progeny effect, bk = the block effect, eijk = the error term for ijkth observation.

Smith–Hazel selection index (SH index)

The Smith–Hazel index13,14 is estimated as follows:

$$\:b={P}^{-1}Gw$$

Where P and G are phenotypic and genetic covariance matrices, respectively and w and b are vectors of index coefficients and economic weightings, respectively.

The genetic worth I of an individual genotype based on traits x, y, …, n, is calculated as:

$$\:I={b}_{x}{G}_{x}+{b}_{y}{G}_{y}+\:\dots\:+{b}_{n}{G}_{n}$$

where b the index coefficient for the traits x, y, …, n, respectively, and G is the individual genotype BLUPs for the traits x, y, …, n, respectively.

Factor analytic best linear unbiased prediction (FAI-BLUP)

Multi-trait index based on factor analysis and ideotype design proposed by Rocha, et al.18.

The formula used for calculating the FAI-BLUP index is as follows:

$$\:{P}_{ij}=\:\frac{\frac{1}{{d}_{ij}}}{{\sum\:}_{i=1;j=1}^{i=n;j=m}\frac{1}{{d}_{ij}}}$$

Where: Pij is the probability the genotype (i = 1, 2,…, n) is similar to ideotype j (j = 1,2,…,m); dij is the genotype j distance, based on the standardized mean Euclidean distance.

Multi-trait selection index (MTSI)

Computes the multi-trait stability index proposed by Olivoto, et al.19. Multi-Trait Selection Index (MTSI) is a quantitative method that facilitates the simultaneous selection of multiple traits by assigning appropriate weights to each trait, reflecting their relative economic or breeding importance20. This approach enables breeders to optimize overall genetic gain by considering the combined value of all targeted traits, rather than improving them individually. The general formula for the selection index (I) is a linear combination of trait values:

$$\:I=\:{b}_{1}{X}_{1}+\:{b}_{2}{X}_{2}+\:\dots\:+\:{b}_{n}{X}_{n}$$

Where, b1 represents the weight assigned to traitX1.By effectively balancing multiple traits, MTSI enhances the efficiency of breeding programs and accelerates the development of superior genotypes21.

Multi-trait genotype–ideotype distance index (MGIDI)

The MGIDI index is computed as following formula10:

$$\:{MGIDI}_{i}=\:\sqrt{\sum\:_{j=1}^{f}{\left({F}_{ij}-{F}_{j}\right)}^{2}}$$

where MGIDIi is the multi-trait genotype-ideotype distance index for the ith genotype;

Fij is the score of the ith genotype in the jth factor (i = 1, 2, …, g; j = 1, 2, …, f), being g and f the number of genotypes and factors, respectively, and Fj is the jth score of the ideotype.

Spearman’s rank correlation coefficient

In our study, Spearman’s Rank Correlation Coefficient is employed to assess the strength and.

direction of associations between various selection indices, such as FAI-BLUP, MTSI, MGIDI, and SHI. This non-parametric measure is particularly suitable for ordinal data or when the assumptions of Pearson’s correlation are not met. By evaluating the rank correlations among these indices, we can identify redundancies and ensure that each index contributes unique information to the selection process. This understanding is crucial for developing a comprehensive selection strategy that effectively balances multiple traits, thereby enhancing the efficiency of breeding programs22. Formulae used for Spearman rank correlation23:

$$\:{\uprho\:}=1-\frac{6\:\:{\text{d}}_{\text{i}}^{2}}{\text{n}\left({\text{n}}^{2}-\:1\right)}$$

Where, di: = Difference between the ranks of two variables for the ith observation, n = Number of observations.

Venn analysis

A venn diagram with four circles was created using Microsoft Excel to visually represent the relationships among different datasets. The diagram was customized by adjusting circle sizes, colors, and overlapping regions to highlight shared and unique elements among the groups.

Weighted rank aggregation (WRA)

Weighted Rank Aggregation (WRA) based on Ranker Accuracies (RA) is a robust statistical approach used to combine multiple ranking methods into a single final ranking by assigning weights to each method based on its reliability. In the context of plant breeding, this method resolves conflicts between selection indices like FAI-BLUP, MTSI, MGIDI, and SHI, ensuring accurate identification of superior genotypes. By giving higher weight to less correlated and more reliable indices, WRA enhances decision-making and improves selection efficiency in multi-trait analysis.

$$\:{w}_{i}=\:\frac{(\:1-\left|{r}_{i}\right|)}{(\:1-\left|{r}_{i}\right|)}$$

Where, ri is the average absolute Spearman correlation of each selection index (FAI-BLUP, MTSI, MGIDI, SHI), wi is the weight assigned to each index based on its Ranker Accuracy (RA)24.

Genotype by yield×trait biplot (GYT biplot)

Genotype by Yield×Trait (GYT) biplot analysis is a novel method that evaluates genotypes based on their combined performance across multiple traits, emphasizing the integration of yield with other agronomic characteristics. By focusing on the combined effect of yield and other traits, GYT biplot analysis provides a comprehensive evaluation of genotypes, aiding in the selection of superior cultivars with balanced performance across multiple characteristics12.

GYT index

$$\:{GYT}_{ij}=\:\frac{{T}_{ij}}{\stackrel{-}{{T}_{j}}}\times\:{Y}_{i}$$

Where: GYTij: GYT Index for the ith genotype and jth trait, Tij: Trait value of genotype i for trait j, \(\:{T}_{j}\): Mean value of trait j across all genotypes, Yi: Yield of genotype i.

GYT standardized value

$$\:{Z}_{ij}=\:\frac{{GYT}_{ij}-G\stackrel{-}{Y}{T}_{j}}{{\sigma\:}_{j}}$$

Where: Zij: Standardized GYT value, \(\:G\stackrel{-}{Y}{T}_{j}\): Mean of GYT value for trait j, \(\:{\sigma\:}_{j}\): Standard deviation of GYT values for trait j.

Results

Analysis of variance

ANOVA for thirteen traits observed highly significant for all 13 traits for genotypes as a source of variation. The ANOVA for 13 quantitative traits is presented (Table 1). It revealed that sufficient variations were present in germplasm, as the presence of heritable variation in germplasm is the key requirement to accomplish any plant breeding program. The presence of variation in the germplasm is essential for accurately estimating heritable values and identifying superior genotypes for use in future breeding programs.

Table 1 Analysis of variance for 13 quantitative traits.
Full size table

Smith–Hazel selection index (SH index)

In the Smith-Hazel index, the genotypes were ranked as per the SH score, in which the high-score genotype was considered superior compared to the low SH score, and it is used by breeders frequently for selecting multi-trait. The ranking of 55 genotypes with score is presented (Table 2), whereas its visual representation is shown (Fig. 1). As per the result observed, the best ten genotypes with the SH index score are C16 (7.02), followed by C3 (6.74), C37 (6.18), C36 (5.89), C15 (5.75), C32 (4.07), C4 (3.65), C7 (3.58), C29 (3.21) and C27 (2.90).

Factor analytic best linear unbiased prediction (FAI-BLUP)

The ranking of 55 genotypes with score according to FAI BLUP is presented (Table 2), whereas its visual representation is shown (Fig. 1). FAI BLUP factor analysis grouped into three factor analyses: FA1, FA2 and FA3. The communality results of three-factor analysis for each trait are DFB (0.74), DTM (0.81), PH (0.35), BMR (0.85), SMR (0.89), LMR (0.78), SL (0.79), SPS (0.87), BY (0.87), HI (0.93), OC (0.75). TW (0.87) and SY (0.91) with an overall mean communality value of 0.80. It revealed the percentage improvement (selection differential percentage) for the trait SY increased by 28.65%, followed by SL (15.49%), HI (15.02%), SMR (14.30%), TW (11.87%), BY (11.64%), SPS (10.85%), LMR (5.09%), OC (2.19%), PH (1.19%), DTM (0.97%), BMR (0.51%) and DFB (−2.58%). The genotypes having a high score are considered superior compared to lower score genotypes. The best ten genotypes ranked with score as per FAI BLUP are C4 (0.146), followed by C7 (0.129), C29(0.122), C27(0.110), C32(0.109), C3(0.106), P9(0.105), C36(0.102), C24 (0.101) and C37(0.100).

Fig. 1
figure 1

Genotype rankings based on (a) Smith-Hazel Index and (b) FAI-BLUP across 13 quantitative traits.

Full size image

Multi-trait selection index (MTSI)

Multi-Trait Selection Index is a quantitative method that facilitates the simultaneous selection of multiple traits by assigning appropriate weights to each trait, reflecting their relative economic or breeding importance (20). This approach enables breeders to optimize overall genetic gain by considering the combined value of all targeted traits, rather than improving them individually. The ranking of 55 genotypes with score is presented (Table 2), whereas its visual representation is shown (Fig. 1). MTSI score ranks the 55 genotypes in the following manner: lower scores are considered desirable genotypes whereas higher scores depict undesirable genotypes. The best ten genotypes observed with score as per MTSI ranks with MTSI scores are C3 (6.06), followed by C27 (8.61), C37 (8.93), C36 (9.05), C4 (9.51), C32 (9.57), C7 (9.84), C29 (9.88), C6 (10.47), C15 (10.45) and C41 (10.53).

Multi-trait genotype–ideotype distance index (MGIDI)

To address shortcomings of the SH index, MGIDI are used for getting significant results (10, 25). MGIDI is a selection index designed to rank genotypes based on multiple traits simultaneously to help in identifying superior genotypes that perform well across the traits. The rank of MGIDI for 55 genotypes with score is presented (Table 2), whereas as visualization are represented (Fig. 2). It is divided into three factors for different traits, like FA1, which includes DFB, DTM, PH, BMR, LMR, and OC; FA2, which includes HI and SY; whereas the remaining traits come under FA3, like SMR, SL, SPS, BY, and TW. The MGIDI revealed a percent increase in Selection Differential for SY (30.76%), followed by SL (18.37%), HI (15.55%), SMR (15.47%), TW (14.61%), SPS (13.64%), BY (13.55%), LMR (9.59), BMR (5.07%), OC (2.99%), PH (1.84%), DTM (0.25%) and DFB (−4.36%). The lower score of MGIDI indicates desirable genotypes compared to the higher score, which is not desirable. The best ten genotypes as per MGIDI ranks with MGIDI scores are C4 (1.36), followed by C27 (2.40), C7 (2.85), C29 (3.15), C32 (3.32), C3 (3.36), C36 (3.66), C30 (3.95), C19 (3.99), C37 (4.00) and C22 (4.05).

Fig. 2
figure 2

Genotype rankings of 55 genotypes based on (a) Multi-Trait Selection Index (MTSI) and (b) MGIDI across 13 quantitative traits.

Full size image

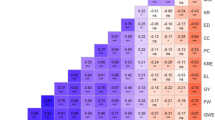
Correlation and venn diagram

Spearman’s rank correlation coefficient was studied to understand the association of different multi-trait selection index to ensure the reliability of these indexes. Correlations were calculated between the ranks of different multi-trait selection index i.e. SHI, FAI-BLUB, MTSI and MGIDI. The results of the correlation are represented (Fig. 3). It showed the highest correlation between SHI and MTSI (0.94), followed by MGIDI and FAI BLUP (0.86), MGIDI and MTSI (0.61), SHI and MGIDI (0.51), MTSI and FAI BLUP (0.35) and SHI and FAI BLUP (0.25). A venn diagram is used to select the desired genotypes, which are the best in all selection indexes. It was created using eight of the best genotypes of all different selection indexes. Venn diagrams for the selection index FAI BLUP, MGIDI, MTSI and SHI with respective genotypes are represented (Fig. 3). The best five genotypes which are superior in all four indexes are C3, C4, C7, C32 and C36. The genotypes C27 and C29 were found superior in MGIDI, FAI BLUP and MTSI. The genotypes C37 was found superior in MSTI and C15 and C16 in SHI. The other two genotypes, P9 and C30, are found superior only in the single selection index FAI BLUP and MGIDI, respectively.

Fig. 3
figure 3

(a) Rank correlation among different selection indices; (b) Venn diagram showing superior genotypes selected by four selection indices.

Full size image

Weighted rank aggregation (WRA) based on ranker accuracies (RA)

Selecting the best genotype from a set of multiple ranking methods is a challenging task in plant breeding and genetic studies. Different selection indices, such as FAI-BLUP, MTSI, MGIDI, and SHI, provide different rankings for the same genotypes. This approach assigns weights to each ranking method according to its reliability and then integrates them into a single final ranking. The final weighted rank aggregation rank of 55 genotypes with score based on the rank of FAI-BLUP, MTSI, MGIDI, and SHI is presented (Table 2). The visualization of WRA of 55 genotypes is represented in (Fig. 4). WRA assigned weights to different statistical analyses: FAI BLUP (0.30), followed by SHI (0.26), MTSI (0.22) and MGIDI (0.20). Lowest weight scores are considered the best genotypes compared to the highest weight scores. The best ten genotypes as per the rank of WRA with WRA scores are C4 (3.46), followed by C3 (3.84), C27 (4.72), C7 (4.89), C32 (5.48), C36 (5.86), C29 (5.89), C37 (6.61), C15 (10.4), C16 (10.6) and C19 (14.5).

Fig. 4
figure 4

Combined rank of 55 genotypes based on four selection indexes (FAI BLUP, MTSI, MGIDI and SHI) using weighted rank aggregation.

Full size image
Table 2 Rank of 55 genotypes for different selection index including final aggregate rank.
Full size table

Genotype by yield×trait biplot (GYT biplot)

Genotype by Yield×Trait (GYT) Biplot is a graphical method used to visualize and interpret the relationship between genotypes and multiple traits, particularly yield-related attributes. Help to select high-yielding genotypes with secondary traits. It used principal component analysis (PCA) to convert multiple trait data into a two-dimensional biplot. PCA of Genotype by Trait Biplot (GT Biplot) revealed the variation of PC1 (63.64%) and PC2 (8.65%) with a total cumulative variance of 72.29%. Similarly, GYT revealed the variation of PC1 (94.53%) and PC2 (2.43%) with a total cumulative variance of 96.96%. It revealed GYT captured more variance compared to the GT biplot. The GYT biplot of genotypes with traits are represented in (Fig. 5), whereas the GYT standardized score of each genotype for all traits with genotype rank and superiority index (SI) are given (Table 3). The best ten genotypes as per GYT standardized score are C3, followed by C37, C36, C16, C15, C4, C32, C29, C37, C36, C16, C15, C4, C32, C29, C7 and C27. The scores of the best three are discussed. The standardized GYT score revealed C3 as rank 1 among 55 genotypes with a total GYT score of 24.42. The C3 GYT score (24.42) comprises the different scores for DFB (1.48), DTM (1.76), PH (2.06), BMR (2.24), SMR (2.22), LMR (2.22), SL (2.03), SPS (2.47), BY (2.46), HI (1.30), OC (1.97) and TW (2.22). The genotype C37 ranks 2nd amongst 55 genotypes with a total GYT score of 24.32, and it comprises DFB (1.40), DTM (1.82), PH (2.27), BMR (2.32), SMR (2.12), LMR (2.27), SL (2.00), SPS (1.98), BY (2.36), HI (1.63), OC (2.03) and TW (2.12).Similarly, the genotype C36 ranks 3rd amongst 55 genotypes with a total GYT score of 23.54 and a comprises of DFB (1.50), DTM (1.78), PH (2.04), BMR (2.07), SMR (1.90), LMR (2.45), SL (2.05), SPS (2.04), BY (2.33), HI (1.44), OC (1.87) and TW (2.07). The different biplot represents the same set of genotypes in a group which was found superior in standardized GYT score. Genotypes set C3, C37, C36, C16 and C15 can be seen in the GT biplot (S1: Fig.) and GYT polygon biplot (S2: Fig.) for better visualization and validation. Average Tester Coordination (ATC) biplot is used in ranking the genotypes, whereas which-won-where biplot is used to highlight genotypes, including their outstanding profiles as presented in supplementary files (S3: Fig.) and (S4: Fig.), respectively.

Fig. 5
figure 5

Representation of genotype by yield*trait biplot for traits and genotypes.

Full size image
Table 3 Standardized Genotype-by-Yield*Trait (GYT) scores for 12 quantitative traits, including combined GYT score, superiority index (SI), and overall rank.
Full size table

Discussion

Selecting superior genotypes based on multiple traits remains a complex and demanding task in plant breeding, requiring robust analytical tools capable of handling trait interdependence and variation. The presence of diverse genetic variation is the foundation of any breeding program, and the ANOVA results (Table 1) confirmed significant differences among genotypes for all studied traits, highlighting the presence of heritable variability. This finding underscores the potential of the studied germplasm for genetic enhancement, aligning with previous results25,26,27. Among the earliest approaches, the selection index proposed by Smith13based on Fisher’s discriminant function28 provided a way to simultaneously select for multiple traits by focusing on phenotypic performance and de-emphasizing fewer desirable traits. The Smith-Hazel index14 further refined this approach by incorporating path coefficients, allowing for more informed selection of genotypes with superior overall performance (Fig. 1a). This index has been effectively utilized in crops like maize to enhance genetic gain29. However, classical indices such as SH often suffer from limitations due to environmental variability and challenges in assigning appropriate economic weights. The FAI-BLUP index, which integrates factor analysis and BLUPs, addresses these issues by improving multi-trait selection accuracy and minimizing environmental noise11,18. In the present study, the FAI-BLUP model revealed communality score of a three-factor analysis 0.91 for seed yield (SY), which was notably higher than the average communality (0.80), and led to a 28.65% increase in selection differential for SY. Its successful application has also been demonstrated in wheat (11) and Brassica juncea for oil content and seed weight improvement30. Identification of superior genotypes was performed by applying the multi-trait selection index for ranking the genotypes as presented (Fig. 2a). Similarly, it was applied to crops like maize for both mean performance and stability analysis31. Multi-trait selection index like MGIDI provide a balanced selection strategy by addressing the weaknesses of SH. Unlike traditional indexes, MGIDI does not rely on economic weights and is well-suited for practical breeding decisions due to its intuitive interpretation and comprehensive selection capabilities10,13,14,18,32,33. The selection-based MGIDI provides more balanced gains, making it more desirable compared to FAI-BLUP and SH indexes (Fig. 2b). It ensures long-term genetic improvement of the primary trait without compromising associated secondary traits, as demonstrated in stress-resilient maize hybrids developed for grain yield under climate change scenarios34. The MGIDI model divided the studied traits into three main factors: FA1 (DFB, DTM, PH, BMR, LMR, OC), FA2 (HI, SY), and FA3 (SMR, SL, SPS, BY, TW). This pattern is consistent with previous studies, such as those conducted in Bush Yam35. Similar MGIDI-based genotype selection has also been implemented in Brassica juncea for oil and yield traits30 Dioscorea rotundata36 and D. praehensilis35 as well as in wheat10,11 eggplant37 and rice for seedling vigor and yield traits38. Spearman rank correlation is a robust statistical tool widely used for comparing rankings obtained from different selection methods, enabling more stable and reliable decision-making in genotype selection. For example, it was effectively used to rank the mean yield of wheat genotypes39. In the present study, the Spearman correlation revealed a strong association between various indexes: a high correlation of 0.94 was observed between SHI and MTSI, and 0.86 between MGIDI and FAI-BLUP. Overall, the correlation ranged from 0.25 to 0.94 (Fig. 3a), supporting the reliability of these methods for multi-trait selection. Similarly, in Indian beans, rank correlation was used to assess the consistency of different economic weighting methods EW (W1, equal weight), GCC (W2, genotypic correlation coefficient), and GPC (W3, genotypic path coefficient) with the ranking of seed yield per plant. The results showed a desirable correlation range of 0.67 to 0.99, confirming the robustness of such indexes40. In wheat, the rank correlation technique has been applied to examine the relationship among three ranking parameters—stability, yield–stability, and yield—across four statistical methods: yield–stability index (YSi), genotype plus genotype-by-environment interaction (GGE), additive main effects and multiplicative interaction (AMMI), and joint regression analysis (JRA). The correlations, particularly among GGE biplots and AMMI, ranged from 0.02 to 0.99 and were statistically significant (P < 0.01), highlighting the similarity in yield ranking results41. The Venn diagram approach (Fig. 3b) was employed to identify genotypes that were commonly ranked superior across the four selection methods. A similar strategy was used by Ambrósio and et al.42 for selecting elite black bean genotypes, demonstrating the value of such integrative techniques. Rank aggregation methods, which are non-parametric and statistical in nature, are particularly effective in consolidating rankings from multiple analytical methods into a single, consensus-based and dependable ranking43,44,45. These methods have been successfully applied across diverse fields including sports competitions43 psychology46 marketing research47 and biological sciences44,48. In plant breeding, Simko and Pechenick49 introduced the concept of rank aggregation to synthesize results from independent varietal trials, which was later adopted by Van Etten and et al.50. In the current study, rank aggregation proved effective in identifying top-performing genotypes (Fig. 4; Table 2), reinforcing its utility for crop genotype evaluation. The Genotype by Yield*Trait (GYT) biplot method further enhanced the selection process by visually displaying the strengths and weaknesses of each genotype. It calculates a superiority index (SI) based on the GYT scores, thereby enabling comprehensive genotype ranking across all traits including yield (Table 3; Fig. 5). This approach was similarly employed12,16 confirming its practical value. The GYT biplot (Fig. 5) was generated by transforming the traditional genotype-by-trait (GT) biplot (S1: Fig.) into a GYT two-way matrix. The polygon view of the GYT biplot is provided in the supplementary material (S2: Fig.) for more intuitive interpretation. The average tester coordination (ATC) view of the GYT biplot (S3: Fig.) allowed for an objective evaluation of each genotype’s strengths and weaknesses, supporting better decision-making through visual ranking of superiority across traits12,51. The practical relevance of GYT has also been demonstrated in sunflower single crosses, where genotypes were evaluated for various agronomic traits across multiple environments52. Comparable success was reported in multi-environment oat datasets, showcasing the method’s broad applicability in plant breeding12.

Conclusion

This study highlights the effectiveness of integrating multi-trait selection indexes SHI, FAI-BLUP, MTSI, and MGIDI with advanced tools like weighted rank aggregation and GYT biplot analysis to identify superior genotypes in Indian mustard. Among these, FAI-BLUP, MTSI, and MGIDI consistently showed strong reliability, with high correlations indicating agreement in genotype rankings. Notably, genotypes C3, C4, C7, and C32 were repeatedly selected across all indexes, WRA, and GYT, demonstrating favourable improvements in key traits such as seed yield, siliqua length, harvest index, and test weight. While the traditional Smith-Hazel index remains foundational, it showed limitations due to sensitivity in trait weighting and multicollinearity. In contrast, FAI-BLUP and MGIDI effectively accounted for genetic correlations, providing balanced selection across yield and related traits. MTSI offered a user-friendly approach for multi-trait improvement. The WRA method further strengthened selection by combining ranks from different index, producing a more robust consensus. Meanwhile, the GYT biplot visually summarized genotype performance, capturing more variance than the GT biplot, thus supporting clearer and objective selection decisions. Practically, breeders are encouraged to combine these indexes with graphical tools like GYT to achieve stable, efficient, and balanced genotype selection. This integrated approach leverages genetic diversity and accelerates breeding progress. Future research could refine weighting schemes and include environmental interactions to enhance selection accuracy further.