Method and experimental verification of spatial attitude prediction for an advanced hydraulic support system under mining influence

Abstract

The mining roadways of fully mechanized mining faces are susceptible to complex disturbances, leading to deformation of the surrounding rock, breaking the mechanical balance of the advanced support section of the mining roadway, and potential roof safety incidents and equipment damage. Accurate prediction of the spatial attitude of the advanced hydraulic support group can provide a foundation for dynamically adjusting the spatial attitude to accommodate the deformation of the roadway’s surrounding rock. The selection of training parameters in the conventional Long Short-Term Memory (LSTM) network is often random and involves a significant amount of effort, which further limits prediction accuracy and real-time performance. Based on this, the WOA algorithm was utilized to search for the optimal number of neurons in the hidden layer and the learning rate. A spatial attitude prediction method for the advanced hydraulic support group based on WOA-LSTM was proposed. Relying on the experimental monitoring platform, the attitude parameters of key nodes during the movement of the support group were obtained, and comparative experiments were carried out. The results indicate that, with 3,200 training samples for the top beam pitch angle and 600 iterations, the Mean Absolute Error (MAE) of the WOA-LSTM prediction model is 0.18°, the Root Mean Squared Error (RMSE) is 0.23°, and the Mean Absolute Percentage Error (MAPE) is 1.3%. Compared to the traditional LSTM model, these three error metrics are reduced by 0.2°, 0.2°, and 1.6%, respectively. This improvement enhances the accuracy and parameter optimization efficiency of the advanced support attitude prediction model, thereby providing robust theoretical and technical support for the intelligent, safe, and efficient mining operations of the advanced coupling support system.

Introduction

The advanced hydraulic support group, as the main supporting equipment of the mining roadway in the fully mechanized coal mining face, together with the surrounding rock - anchor support system of the roadway, constitutes the advanced coupling support system (The rock bolt system (active support) and forepoling support (passive support) jointly withstood dynamic roof loads during strata movement, with the active support mechanism demonstrating predominant load-bearing functionality. The passive support system effectively supplemented the active reinforcement system, resulting in minimal surrounding rock subsidence that remained within the permissible threshold of maximum displacement. ), playing a role in providing safe and stable support for the mining roadway^1,2. With the continuous increase of mining depth, the stress of the surrounding rock of the mining roadway keeps increasing. The complex disturbance is prone to induce the deformation of the surrounding rock, causing the advanced hydraulic support group to be in an abnormal supporting posture during the coupling support process, and further inducing safety accidents such as equipment damage and roof caving^3,4. Thus, the development and application of advanced sensing technologies for real-time monitoring and predictive analysis of hydraulic canopy support postures, coupled with subsequent adaptive adjustments of support configurations, has emerged as a critical technological challenge requiring urgent resolution to ensure safe and efficient roadway support in fully-mechanized longwall mining operations.

Regarding real-time perception of spatial attitudes in advanced hydraulic supports, domestic and international experts have conducted extensive research. Chen HY et al.⁵ established a kinematic measurement model for advanced hydraulic supports and proposed a yaw-roll angle calculation algorithm based on ultrasonic ranging data, achieving multi-sensor-based attitude monitoring. Chen NN et al.⁶ developed an FBG (Fiber Bragg Grating) sensing platform integrated with FBG sensing theory, enabling real-time monitoring and information management of hydraulic support attitudes. However, most current posture monitoring systems rely on manual-sensor collaboration. When sensors malfunction, operators must control critical operations (e.g., lifting, lowering, and shifting) based on environmental judgments and empirical experience. This manual dependency often leads to delayed terrain adaptation, compromising support quality and operational safety.

Accurate prediction of spatial attitudes in advanced supports, considering the hysteresis characteristics of actuator control systems, is critical for ensuring sufficient response time for adjustments. Li YY et al.⁷ employed Kriging surrogate models and polynomial interpolation for hydraulic support dynamics, proposing a tail beam motion prediction model. Zhao YL and Xie JC et al.^8,9 analyzed key parameters affecting support attitudes and introduced a Markov theory-based prediction method for anticipating posture parameters during shifting operations, though spatial feedback remains non-intuitive. Wang YF et al.¹⁰ developed a grey theory-based memory attitude monitoring method, predicting subsequent support postures using historical cyclic data. Pang YH et al.^11,12 investigated template curve library-driven data analysis for abnormal load prediction through feature decomposition. These methods, however, impose significant data transmission demands due to multi-channel monitoring requirements.

Neural network-based models, renowned for high prediction accuracy and stable dynamic characteristics, have gained traction in advanced support state forecasting. Gao TY et al.¹³ proposed a multi-scale feature extraction neural network to capture temporal patterns in hydraulic pressure data. Yao YP et al.¹⁴ designed an LSTM-based tail beam inclination prediction model by establishing factor-angle mapping relationships. Nevertheless, Traditional LSTM architectures struggle to decouple the nonlinear interactions between multiple degrees of freedom (roll, yaw, pitch) and time-varying geological pressures, and inadequately address the complex coupling between time-dependent deformation patterns and spatial constraints in the time-series data of the spatial posture. At the same time, the traditional LSTM implementation fails to take into account the changes in the spatial attitude of the stent caused by pressure fluctuations in actual mining operations, and lacks instantaneous dynamic adaptability. As for the configuration of hyperparameters, manual tuning (e.g., hidden units, learning rates) for LSTM models is labor-intensive and suboptimal. Population intelligence algorithms (e.g., PSO, GA, WOA) offer efficient alternatives for hyperparameter optimization. Compared to PSO and GA, the Whale Optimization Algorithm (WOA)¹⁵ exhibits superior convergence in low-dimensional continuous spaces (e.g., optimizing LSTM’s neuron count and learning rate). To enhance the dynamic adaptation to transient changes and prediction accuracy of the model, and effectively addressing the nonlinear spatiotemporal coupling characteristics of spatial pose sequential data, this study integrates WOA with LSTM to develop a spatial attitude prediction model for advanced hydraulic support groups. The main contributions are as follows:

• A WOA-LSTM-based spatial attitude prediction framework is proposed, replacing manual hyperparameter tuning with WOA to improve prediction efficiency and accuracy.

• An advanced support group perception network is established for dynamic spatial attitude monitoring.

• Comparative experiments between LSTM and WOA-LSTM models validate the proposed method’s effectiveness through error analysis and robustness evaluation.

The rest of this paper is organized as follows: “Analysis of spatial posture characteristics of leading hydraulic support groups” introduces spatial attitude characteristics of advanced hydraulic support groups. “Long short-term memory neural network (LSTM)” details the architecture of LSTM neural networks. “Whale optimization algorithm (WOA)” derives the WOA. “The posture angle prediction model of advanced hydraulic support based on WOA-LSTM” presents the WOA-LSTM prediction model for support attitude angles. “Experimental verification analysis” validates the method through experimental analysis, followed by conclusions in “Conclusion”.

Analysis of spatial posture characteristics of leading hydraulic support groups

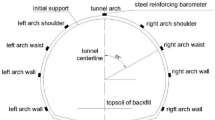
During the combined tunneling process of the advanced hydraulic support group, the anchor cables (rods) and steel wire meshes installed provide safe and efficient support for the advanced section of the roadway. Due to the complex rock stratum movement and the deformation of the roadway surrounding rock induced by the mining and excavation disturbance, the spatial posture of the advanced hydraulic support changes, as shown in Fig. 1, the surrounding rock deformation in the mining face (e.g., floor heave, roof subsidence, and rib deformation) drives deviations in the triaxial attitude angles (pitch$\:\:{\upgamma\:}$ roll $\:{\upalpha\:}$, and yaw$\:\:{\upbeta\:}$ ) of the advanced hydraulic supports.

Fig. 1

Changes in Key Postures of the Advanced Hydraulic Support.

The advancing direction of the roadway is defined as the x-axis, the width direction of the roadway as the y-axis, and the height direction of the roadway as the z-axis. The angle formed between the rotation of the advanced hydraulic support around the z-axis and the x-axis is defined as the yaw angle$\beta$, the angle formed between the rotation of the advanced hydraulic support around the x-axis and the y-axis is defined as the roll angle$\alpha$, and the angle formed between the rotation of the advanced hydraulic support around the z-axis and the x-axis is defined as the pitch angle$\gamma$.

Therefore, during the normal support process of the advanced hydraulic support group, the posture will change in terms of attitude angles such as yaw angle, roll angle, and pitch angle due to the deformation of surrounding rocks and other situations, which seriously affects the stability and safety of the support.

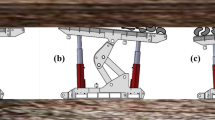
Meanwhile, during the process of supporting the surrounding rock, the advanced hydraulic support group should always maintain a certain safe distance from both sides of the roadway. If the safe distance becomes smaller, the position of the advanced hydraulic support group in the roadway space needs to be adjusted through the balance cylinder to ensure the safe distance. During the adjustment of the balance cylinder, the spatial posture of the advanced hydraulic support will also change, which is likely to cause the inadaptability of the supporting state, as shown in Fig. 2, timely feedback on the spatial attitude of the advanced supports enables precise guidance for the corrective motions of the front/rear traction cylinders and telescopic columns, completing posture transitions (e.g., lifting, lowering, and lateral shifting) from State 1 to State 5 as illustrated in the diagram.

Fig. 2

Schematic diagram of the relative position of the advanced hydraulic support in the roadway.

Long short-term memory neural network (LSTM)

The LSTM (Long Short-Term Memory Network), a specialized type of recurrent neural network (RNN), is capable of capturing long-term dependencies when processing sequential data¹⁶. is capable of capturing long-term dependencies when processing sequential data. Through its gating mechanism, LSTM can learn and retain long-term dependencies, addressing the issue of ordinary RNNs struggling to capture long sequences. The structural design of LSTM facilitates gradient flow maintenance and effectively resolves the problem of vanishing gradients during the training process of traditional RNNs, enabling superior performance in complex sequence prediction tasks. At the same time, the support attitude offset (such as the pitch Angle of the top beam and the expansion of the column) is affected by the historical state of coal mining advance speed and roof pressure distribution, and the window is 15–30 min (the measured data period is 0.5s/ sample), which is far beyond the 10–20 steps effective memory depth of the traditional RNN, and LSTM through special gate structures and cell states, it can better conserve long-term memory and store time-related information in memory cells, replacing the previous iterative transformation. During the moving process of the advanced hydraulic support group, the periodic changes of the floor attitude data have certain information. In the changing data, using LSTM can solve the long-term dependency of the attitude data, and its network structure is shown in Fig. 3.

Fig. 3

The structure diagram of LSTM neural network.

In the figure, ${x_t}$is the input at time t, ${h_{t-1}}$and${h_t}$denote the outputs at times$t - 1$and t, while ${C_{t-1}}$and${C_t}$represent the cell state outputs at times$t - 1$and t. σ denotes the sigmoid activation function, and tanh represents the hyperbolic tangent activation function.

LSTM units can retain information for extended periods in the form of self-cyclic encoded data, comprising a memory unit (Cell) and three “gate” units (forget gate, input gate, and output gate)¹⁷. The memory unit (cell) is the core of the computing node, used to store the current state of time. The forget gate is used to control which information needs to be discarded at a given time and transmit the retained information to the next time step. The value of the forget gate ranges between 0 and 1. When the value of the forget gate is 0, the previous cell state will be completely erased during the calculation of the current cell state. When the value of the forget gate is 1, during the calculation of the current cell state, the previous cell state will be completely preserved¹⁸. The calculation formula is as follows:

$${f_t}=\sigma ({W_f}[{h_{t - {\text{1}}}}, {{\text{x}}_t}]+{b_f}).$$

(1)

In the formula, σ is the sigmoid activation function,${W_f}$stands for the weight of the forget gate layer,${h_{t - {\text{1}}}}$represents the previous output,${x_t}$denotes the current input, ${b_f}$is the threshold of the forget gate layer, and${f_t}$signifies the output of the forget layer.

The input gate is used to determine which types of information will be incorporated into the current cell state. The value of the input gate is between 0 and 1. When the input value is 0, it indicates that the cell state has not been updated with information. When the input value is 1, it indicates that the cell state has been filled with information. The calculation formula is as follows:

$${i_t}=\sigma ({W_i}[{h_{t - 1}},{x_t}]+{b_i})$$

(2)

$${\tilde {C}_t}=\tanh ({W_c}[{h_{t - 1}},{x_t}]+{b_c}).$$

(3)

In the above formula, $\tanh$is the hyperbolic tangent activation function,${i_t}$represents the information that needs to be updated,${\tilde {C}_t}$stands for the new candidate vector in the tanh layer,${W_i}$and ${W_c}$denote the weights corresponding to the input gate, and${b_i}$and${b_c}$refer to the thresholds corresponding to the input gate.

Update the old cell state${C_{t - 1}}$to${C_t}$using the following formula:

$${C_t}={f_t}*{C_{t - 1}}+{i_t}*{\tilde {C}_t}.$$

(4)

In the formula,${C_t}$represents the output state, and${C_{t - 1}}$represents the old state.

The output gate is used to determine the final output value, which ranges from − 1 to 1. When the output value is 0, the final state representing the cell completely discards the current cell state. When the output value is 1, the final state representing the cell state is the current cell state. The calculation formula is as follows:

$$\tanh \left( x \right)=\frac{{1 - {e^{ - 2x}}}}{{1+{e^{ - 2x}}}}$$

(5)

$${o_t}=\sigma ({W_o}*[{h_{t - 1}},{x_t}]+{b_o})$$

(6)

$${h_t}={o_t}*\tanh ({C_t}).$$

(7)

In the formula,$[{h_{t - 1}},{x_t}]$represents the output state feature,${W_o}$represents the weight of the output gate,${b_o}$represents the threshold of the output gate, and${h_t}$represents the final output.

Whale optimization algorithm (WOA)

In recent years, with the rapid advancement of simulation-based intelligent optimization algorithms, scientists, by investigating the behavioral traits exhibited by whales during the hunting process, have summarized them into three categories of predatory behaviors: herding prey, bubble-net feeding, and searching for prey, and have proposed the WOA. When solving for the optimal solution, by referring to the various hunting behaviors among whales in the hunting process of the whale group, each individual whale in this group is regarded as a solution. During the process of herding prey, the whale group rapidly discovers the whale individual that is closest to the prey during the herding process, that is, quickly identifies the optimal solution to the problem. For low-dimensional continuous optimization tasks (e.g., tuning LSTM’s hidden neuron count [1D] and learning rate [1D]), the Whale Optimization Algorithm (WOA) exhibits superior convergence speed compared to Genetic Algorithm (GA, requiring frequent encoding/decoding) and Particle Swarm Optimization (PSO, demanding complex inertia weight adjustments), owing to its shrinking encircling mechanism. This algorithm features high solution accuracy and a fast optimization process and has been widely utilized in domains such as optimal control, parameter optimization, and image segmentation.

(1) Herding prey.

When the whale group herds prey, whales can rapidly identify the location of the prey and surround it. During this process, there exists a whale with the best position within the whale group. As this whale swims towards the prey, other whales continuously track the position of the optimal whale to achieve the herding of the prey. The WOA algorithm references this process of the whale group herding prey to achieve the solution of the optimal parameters¹⁹, and the model of this process is as follows:

$$\vec {D}=\left| {\vec {C} \cdot {{\vec {X}}^*}(t) - \vec {X}(t)} \right|$$

(8)

$$\vec {X}(t+1)={\vec {X}^*}(t) - \vec {A} \cdot \vec {D}.$$

(9)

Here, t is the number of iterations,$\overrightarrow {{X^*}} (t)$is the position of the current optimal whale,$\vec {X}(t)$is the position of the neighboring whales, and$\vec {A}$and$\vec {C}$are the coefficients. By continuously optimizing the values of$\vec {A}$and$\vec {C}$to represent the process of finding the nearest whale, the coefficients$\vec {A}$and$\vec {C}$are calculated as follows.

$$\vec {A}=2\vec {a} \cdot \vec {r} - \vec {a}$$

(10)

$$\vec {C}=2\vec {r}.$$

(11)

Where$\vec {a}$is linearly decreasing from 2 to 0 in the iterative process and$\vec {r}$is a random number in [0,1].

(2) Bubble predation (local search stage).

Taking the process of whales surrounding prey exhalation bubbles as the simulation object, two methods were established to describe the whale predation process, which were contraction surrounding mechanism and spiral updating position, so as to better update the position of the optimal solution.

A surround search is performed by calculating the spatial distance between the positions of other whales and the current optimal solution, followed by a spiral walk ascent. The spiral motion process of the whale is calculated by the spiral equation, and the calculation formula is as follows.

$$\vec {X}(t+1)=\overrightarrow {D'} (t) \cdot {e^{bl}} \cdot \cos (2\pi l)+\overrightarrow {{X^*}} (t)$$

(12)

$$\overrightarrow {D'} (t)=\left| {\overrightarrow {{X^*}} (t) - \vec {X}(t)} \right|.$$

(13)

Where$\overrightarrow {D'}$represents the optimal distance solution in the whale swarm and b is the spiral shape constant, which l is a random number in the range [-1,1].

The whale has two kinds of predatory behaviors when it is close to the prey. Assuming that the probability of the whale choosing the two modes of predation is 50%, the calculation formula can be expressed as follows.

$$\vec {X}(t+1)=\left\{ {\begin{array}{*{20}{c}} {\overrightarrow {{X^*}} (t) - A(t) \cdot \overrightarrow D (t)} & {p < 0.5} \\ {\overrightarrow {{D^ \prime}} (t) \cdot {e^{bl}} \cdot \cos (2\pi l)+\overrightarrow {{X^\ast}} (t)}& {p \geqslant 0.5} \end{array}} \right. .$$

(14)

Here, p is a random probability, and the relationship between probability p and predation mode is shown in Table 1.

Table 1 Correspondence between p and the mode of predation

(3) Search for prey (global search phase).

When the whale is close to the prey, it can select another whale to search for new prey according to the position of each whale in the whale swarm, and the calculation formula can be expressed as follows.

$$\vec {X}(t+1)={\vec {X}_{rand}} - A(t) \cdot \overrightarrow D (t).$$

(15)

Wherein:

$$\overrightarrow D (t)=\left| {C(t) \cdot {{\vec {X}}_{rand}} - \vec {X}(t)} \right|.$$

(16)

Among them,${\vec {X}_{rand}}$denotes the position of a randomly chosen whale in the whale group.

In the WOA, vector A is employed to select the path for whales to search for prey, and probability p is utilized to determine the predation mode. The complete process of the WOA is depicted in Fig. 4.

Fig. 4

Flowchart of the WOA.

The posture angle prediction model of advanced hydraulic support based on WOA-LSTM

The prediction effect in the LSTM neural network is determined by the quality of the sample data and the model training parameters. The model training parameters mainly comprise two types of parameters: the number of neurons in the hidden layer and the learning rate. Among them, the number of neurons in the hidden layer determines the learning capacity of the LSTM network. If the number is set too low, the learning capacity of the network will be reduced. If it is set too high, the learning difficulty of the network will increase. The magnitude of the learning rate determines the convergence speed of the LSTM network. If the learning rate is set too large, the convergence speed will be too fast, and oscillation is prone to occur. If the learning rate is set too small, the convergence speed will be too slow, and overfitting is prone to occur²⁰. Therefore, to achieve the best prediction effect of the LSTM neural network, in this section, the WOA is employed to search for the optimal number of neurons in the hidden layer and the learning rate, replacing the manual parameter optimization process. This enables more efficient and accurate prediction of the position and attitude angle of the advanced hydraulic support, and the model process is depicted in Fig. 5.

Fig. 5

WOA-LSTM pose angle prediction model.

First, the LSTM neural network’s hidden layer neuron number and learning rate are manually adjusted to the network and obtain the ValidationRMSE, which is set as the reference RMSE value. Then, the optimal hidden layer neuron number and learning rate are obtained through the WOA, and the parameters are applied to the LSTM neural network to train the optimized network and obtain the reference RMSE value. The ValidationRMSE of optimized model is compared with the reference value. If the value is greater than the reference value, it is considered that the prediction accuracy of the LSTM network is not met, and the parameters need to be re-optimized. If the value is less than the Reference value, it is considered that the prediction accuracy of the LSTM network is met²¹.

The prediction process of the model is presented as follows:

Step 1: Input the data and initialize the training parameters of the LSTM network.

Step 2: Place the initialized learning rate and the number of hidden layer nodes into the WOA, update the random probability parameters, select the appropriate encirclement approach, and search for the optimal parameters.

Step 3: Incorporate the optimal learning rate and the number of hidden layer nodes found into the LSTM model and commence predictive training.

Step 4: Conduct batch training. Send the initial learning rate and the number of hidden layer nodes to the LSTM model for training to obtain the ValidationRMSE. Subsequently, the train loss of WOA-LTSM is obtained by model training.

Step 5: Compare the ValidationRMSE of the optimized model with that of the reference model. If the ValidationRMSE of the optimized model is less than reference value, it is deemed that the optimized learning rate and the number of hidden layer nodes meet the accuracy requirements. Utilize the optimized parameters for LSTM model prediction and output the optimal predicted value of the leading hydraulic support. Conversely, if the ValidationRMSE of optimized model is greater than reference value search for another set of optimal parameters and re-feed them into the LSTM model for training.

The number of WOA populations is set to 30, the maximum number of iterations is set to 50, and the first 80% of the 4,000 sets of pose sample data are used as the training samples. The LSTM training parameters (numHiddenUnits, LearnRate) are then searched for optimality. The distributions of the candidate parameters in the search space are shown in Fig. 6, with the color depths denoting the size of the RMSE.

Fig. 6

Trajectory of Parameter Space Search. (a) Spatial scatter plot of parameters (b)Contour Map with Hyperparameter Distribution.

As can be seen from the figure, the range of variation of ValidationRMSE within the parameter search space is as low as 0.2306 and as high as 0.8208, and the RMSE contours are asymmetrically distributed, indicating that there is a strong nonlinear interaction between the learning rate and the neurons, and the results show that the low error region (dark blue) is concentrated in the neuron number 110–140, learning rate 0. The number of neurons can be fixed at 006-0.009, which is consistent with the parameters of the optimization result (126 neurons and 0.007 LearnRate).The number of neurons can be fixed at 126 ± 10 and the LearnRate can be dynamically adjusted to adapt to the migration learning needs of different work surfaces. For a more intuitive observation of the parameters in the whole search process, the histogram of the distribution of numHiddenUnits and LearnRate is plotted as shown in Fig. 7.

Fig. 7

Distribution of numHiddenUnits and LearnRate.

The frequency of parameter distribution shows that the algorithm’s search for hidden layer neurons is concentrated in the range of 122–132, the LearRate search range is concentrated in the range of 0.006–0.008, the peak value of the search for the numHiddenUnits appears in the interval of 127.5 ± 5, the peak value of the search for the LearRate appears in the interval of 7.25 × 10 − 3 ± 5 × 10 − 4, and the search process spreads over the entire established parameter space, which suggests that the algorithm effectively explores the parameter space without converging prematurely.

The convergence curve of ValidationRMSE in the iterative process of WOA optimization search is shown in Fig. 8. In the optimization search process with 50 iterations and a population size of 30, the ValidationRMSE converges from 0.3584 to 0.2306, and the optimal search parameter is reached in the eighth iteration to remain stable, which verifies the effectiveness of the WOA optimization algorithm.

Fig. 8

WOA Convergence Curve.

The first 80% of the same 4000 sample sets were selected as training samples, and the number of iterations was set to 600. The network hyperparameters of the WOA optimised network (numHiddenUnits = 126, LearnRate = 0.007) were applied to the LSTM neural network and compared with the pre-optimization model (numHiddenUnits = 150, LearnRate = 0.005). The iterative curve of TrainingRMSE is shown in Fig. 9.

Fig. 9

TrainingRMSE Convergence Comparison.

The results demonstrate that the WOA-optimized LSTM model exhibits superior convergence behavior compared to the baseline LSTM. Specifically, the WOA-LSTM achieves a stable TrainingRMSE of 0.025 after merely 55 iterations, whereas the unoptimized LSTM requires 250 iterations to reach a higher stable value of 0.040. Under identical training conditions, the hyperparameter-optimized network outperforms its counterpart in both convergence rate and precision. These findings substantiate the enhanced reliability of the WOA-LSTM algorithm for spatial attitude prediction in advanced hydraulic supports, confirming its advantages in predictive accuracy and computational efficiency.

Experimental verification analysis

The WOA-LSTM-based spatial attitude prediction model for advanced hydraulic supports is illustrated in Fig. 10. The system operates through a real-time sensory monitoring network that transmits time-series data including Attitude of Advance Supports, Cylinder Displacement, and Support Pushing Speed. After data filtering and encoding, the packaged information is transmitted via industrial Ethernet to the monitoring center in the retreating gateway, enabling real-time data exchange as temporal sample inputs for the WOA-LSTM prediction model.

By comparing the model’s output predictions with both the current spatial attitude measurements from hydraulic supports and the previous time-step’s predicted values, the system generates adaptive adjustment strategies for the electro-hydraulic control signals. This closed-loop implementation achieves predictive regulation of advanced hydraulic support posture.

Fig. 10

The prediction process of spatial posture of advanced hydraulic supports.

To validate the effectiveness and accuracy of the proposed data fusion algorithm, relying on the attitude monitoring experimental platform of the leading hydraulic support at the Robotics Experiment Center of Shandong University of Science and Technology, the relevant attitude data of the leading hydraulic support was collected and brought into the designed pose prediction algorithm for comparative analysis to verify the validity of the research content. The relevant experimental platform is depicted in Fig. 11.

Fig. 11

The overall structure of the advanced hydraulic support experimental system.

The main technical parameters of the advanced hydraulic support experimental platform are shown in Table 2.

Table 2 Main technical parameters of advanced hydraulic support experimental prototype.

The experiment adopted Attitude Sensor, Ultrasonic Distance Sensor, and Cylinder-mounted magnetic displacement sensor to measure the overall attitude of the advanced hydraulic support group. The inclination sensors were installed on the top beam, base, and balance cylinder of the support to collect the attitude information of the corresponding positions. The ultrasonic ranging sensors were installed at both ends of the top beam, both ends of the base, and the lower end of the shielding beam to collect the distances between the support, the two sides of the roadway, and the floor. The cylinder stroke sensor selected the built-in sensor to collect the expansion length of the cylinder. The specific arrangement positions of the position and attitude monitoring sensors are shown in Fig. 12.

Fig. 12

Schematic diagram of the installation layout of the pose monitoring module.

Here, with the lowest position and posture of the advanced hydraulic support as the benchmark (the lowest support height of the prototype is 1 m, and the top beam is parallel to the base), the calibration of each sensor is carried out. Taking the rear end point $\:{O}_{0}$ of the base as the reference coordinate, when installing the inclination sensor, the sensor surface should be attached to the support surface as much as possible, and voids should be avoided as much as possible. The inclination sensors located on the top beam and the base are installed vertically upward perpendicular to the $\:{Y}_{0}{O}_{0}{Z}_{0}$-plane, and the inclination sensor located on the balance shaft is installed parallel to the axial direction. The ultrasonic distance sensors are located on both sides of the base, and the magnetic displacement sensors are built into the front and rear telescopic columns of the hydraulic support. The specific sensor specifications and installation position parameters are shown in Table 3.

Table 3 Sensor specifications and installation position Parameters.

Based on the installation parameters calibrated by the above-mentioned pose monitoring sensor, a spatial pose monitoring platform for the advanced hydraulic support is constructed, as shown in Fig. 13. Comparative experiments are carried out for the LSTM prediction model and the WOA-LSTM prediction model. To fulfill the experimental requirements, the initialization parameter configurations of the two prediction networks and the datasets used for training remained consistent during this process. By comparing the errors between the predicted values and the actual measured values of the two prediction models, the feasibility of the WOA-LSTM prediction model investigated in this paper in the field of advanced hydraulic support posture prediction was demonstrated.

Fig. 13

Installation layout of the pose monitoring module.

In this experiment, the change of the pitch angle of the top beam was taken as an example. The rear traction cylinders and front/rear telescopic columns simulate the advanced support’s poses under varying operational conditions. 4,000 sets of posture data of the top beam variations were collected using a posture sensor and divided into the training set and the validation set at a ratio of 8:2. During the experiment, the first 3,200 sets of top beam pitch angle data were taken as the training samples of the LSTM, and the remaining 800 sets were used as the validation samples of the LSTM. The training parameters of the LSTM neural network were set, among which the number of hidden layer nodes was 150, the initial learning rate was 0.005, the number of iterations was 600, and the learning rate became half of the initial rate at the 300th iteration to enhance the convergence speed of the LSTM neural network. As shown in Fig. 14, the LSTM-based posture prediction results demonstrate stable tracking with minimal fluctuations, albeit slightly overestimating the true values.

Fig. 14

Prediction and tracking curves of the canopy pitch angle based on LSTM.

Based on the aforementioned LSTM model configuration, a spatial attitude prediction method for the advanced hydraulic support group based on WOA-LSTM was proposed. The MAPE loss function was introduced during the training process, and the search range of the training parameters was determined. Specifically, the optimal number of neurons in the hidden layer was sought within the range of [100, 200], the optimal learning rate was sought within the range of [0.001, 0.01], the number of iterations was set to 600, and the first 3,200 sets of top beam pitch angle data were employed as the training samples for the WOA-LSTM. The optimal training parameters were identified, and then the remaining 800 sets of top beam pitch angle data were utilized for pose prediction. The prediction effects of the WOA-LSTM network and the LSTM network were compared, and the comparison results are presented in Fig. 15.

Fig. 15

Comparative curves of attitude prediction and tracking.

The prediction errors of the model are calculated using attitude perception data, yielding the comparative error diagram in Fig. 16.

Fig. 16

Comparative diagram of attitude prediction error analysis.

Analysis of tracking curves and prediction errors reveals that the WOA-LSTM model achieves higher accuracy in tracking the true attitudes of advanced supports compared to standalone LSTM. The LSTM prediction error stabilizes within 0–1°, while WOA-LSTM reduces this range to 0–0.7° with lower volatility, confirming its enhanced precision. For intuitive performance evaluation, 800 test samples are divided into 40-sample groups, and the mean error per group is plotted (Fig. 17).

Fig. 17

Grouped mean error comparison for attitude prediction.

As shown, the LSTM model exhibits a maximum grouped mean error of 0.74233° and a minimum of 0.08725°, whereas WOA-LSTM achieves tighter convergence (max: 0.404665°, min: 0.01831°), maintaining errors below 0.5° for reliable predictions.

To validate the precision of the advanced hydraulic support attitude prediction system and assess the efficacy of WOA-LSTM, statistical analyses are performed on prediction errors before and after LSTM optimization. Results are summarized in Table 4; Fig. 18.

Table 4 Statistical comparison between LSTM and WOA-LSTM.

Fig. 18

Schematic analysis of statistical evaluation metrics for prediction errors.

Under identical experimental conditions (4,000-sample dataset, hidden neuron range: [100, 200], learning rate range: [0.001, 0.01]), WOA-LSTM outperforms LSTM across all statistical metrics. Specifically, WOA-LSTM reduces MAE by 0.2, RMSE by 0.2, and MAPE by 1.6%, while confining maximum prediction error to 0.59° (vs. LSTM’s 0.88°). These results confirm that WOA-LSTM enhances prediction accuracy and reliability, offering theoretical guidance for early warning and safety protocols.

Conclusion

The working conditions in the underground coal mine’s integrated mining face are complex, and there is no effective method to predict the position and orientation of the super-ahead hydraulic support during its support and movement process. This leads to the inability to provide effective safety guarantees for the mine tunnel equipment and personnel. In order to meet the intelligent mining’s requirements for the support of the super-ahead hydraulic support, this paper studies a method of short-term position and orientation prediction for the super-ahead hydraulic support, improving the real-time and reliability of the support, and the main conclusions are as follows:

A method of super-ahead hydraulic support posture prediction based on WOA-LSTM model was studied, which can predict the posture data of the super-ahead hydraulic support for the next cycle based on the trend of the support’s posture change. The precision of the posture data processing method proposed in this paper was verified and analyzed by the super-ahead hydraulic support posture monitoring experimental platform, and the experimental results show that the algorithm has significant effects in short-term posture prediction, and the trend of the predicted value and the experimental value is consistent. The average absolute error of the predicted posture is 0.18°, and the root mean square error is 0.23°, And the model’s prediction error is stable within 0.59°, Compared to existing LSTM-based methods for hydraulic support inclination prediction¹⁴, our approach achieves equivalent monitoring precision while resolving time-cost and optimization challenges inherent in manual LSTM parameter tuning. By integrating real-time spatial feedback into the closed-loop control system of actuators, the model compensates for response hysteresis in drive cylinders, improving both accuracy and timeliness of posture adjustments, and provides technical support for the self-adaptive support of the coal mine underground super-ahead coupled support system. Furthermore, the proposed WOA-LSTM framework is extensible to localization monitoring of coal mining equipment (e.g., armored face conveyors and roadheaders). Future work will integrate digital twin models to enhance system visibility and reliability.