Introduction

The doubly-fed induction motor (DFIM) is emerging as a promising solution, gradually replacing the asynchronous machine for various industrial applications1. In motor mode, it used in traction systems, railways and others. while in generator mode generator mode, it is essential for power generation, in wind turbines, marine systems and other applications. Thanks to its many advantages in these different operating modes, several researchers have endeavored to control this machine despite the complexity of flux-torque decoupling2,3.

The first control developed to translate the behavior of the DFIM into a behavior similar to that of the DC machine is the Field Oriented Control (FOC)4, designed by Hasse and Blachke. FOC can be divided into two types : direct control (DFOC)5, However this type is very sensitive to mechanical vibrations, which can add harmonics to the measurement. The second type, indirect FOC (IFOC)6, which does not require a flux sensor but estimates the flux. The main disadvantage of vector control lies in the controllers used to correct the current and flux variables.Numerous PID correctors within this control reduces its robustness, notably due to the fixed gains of the correctors, which can pose a problem in the event of variations in the machine’s internal parameters under severe operating conditions. To overcome the issues of traditional vector control, researchers have proposed several alternative solutions, each with its advantages and disadvantages7,8,9,10. Sliding mode control (SMC) is a robust technique for efficiently controlling nonlinear systems. By introducing a sliding surface and forcing the system to evolve on this surface, SMC ensures insensitivity to disturbances and variations in system parameters11,12,13. For the DFIM, this method enables more effective management of flux and torque variations, thus offering better performance under variable operating conditions14. However, the phenomenon of chattering generates parasitic oscillations in the system, increasing harmonics and torque ripples15,16,17.

In the same vein, the researchers developed another, more sophisticated control called backstepping control.Based on a recursive approach, this technique, makes it possible to design controllers for non-linear systems by decomposing a complex control problem into simpler sub-problems, based on Lyapunov’s theorem18. Applied to DFIM, backstepping makes it possible to design controllers ensuring good dynamic performance despite the non-linearities and uncertainties of the machine model. This improves system stability and robustness, while simplifying controller synthesis19,20. However, the choice of the degree of the Lyapunov function remains difficult to guarantee system stability21,22,23. Control specialists have also developed a powerful new method called direct torque control (DTC)24,25. DTC enables direct control of machine flux and torque without requiring coordinate transformation. Using flux and torque comparators, DTC instantly adjusts machine voltages to the desired values26,27,28.DTC is an advanced and complex control technique, particularly applicable for non-linear systems such as DFIM drives. DTC offers fast dynamic response and improved transient management, reducing losses and increasing energy efficiency. However, this technique is marked by significant torque ripples, which degrade machine life

The fundamental principle of Direct Torque Control (DTC) is based on a straightforward control structure, typically implemented using a Proportional–Integral–Derivative (PID) controller. While PID controllers are widely recognized for their simplicity and effectiveness in linear systems, their integration into DTC-designed for inherently nonlinear systems-introduces several challenges. The highly dynamic and variable nature of torque and flux in DTC systems demands precise tuning of PID parameters to avoid undesirable phenomena such as significant torque ripple, instability, or degraded transient performance. Furthermore, the system’s nonlinearities and sensitivity to parameter variations often necessitate advanced tuning techniques or adaptive control strategies to ensure optimal performance29,30,31.

Comprehensive studies in the literature indicate that PID controllers can be made robust to nonlinearities through the dynamic optimization of their gains at each control interval, allowing the system to continuously adapt to real-time variations. The application of optimization algorithms has therefore become a key approach to enhancing the robustness of complex, multidisciplinary systems. Among these, Ant Colony Optimization (ACO) has proven particularly effective in meeting the nonlinear demands of many control systems. Numerous studies have shown that ACO outperforms other optimization techniques in terms of efficiency, accuracy, and adaptability.

For example, in the study by32, both ACO and Particle Swarm Optimization (PSO) were used for fault detection and correction in electric transmission lines. The results demonstrated that ACO was faster and more effective for fault identification and reactive power injection. Similarly,33 applied ACO and PSO to tune PID gains in autonomous underwater vehicles, with ACO providing superior results.34 compared ACO and Genetic Algorithms (GA) for optimizing the speed controller of an induction motor powered by a photovoltaic system, concluding that ACO offered better performance in terms of speed, precision, and stability.

35 utilized fuzzy logic rules combined with ACO to regulate concentration in a fermentation process and demonstrated the superiority of ACO over conventional fuzzy controllers.36 showed that a Fractional Order PID (FOPID) controller optimized by ACO achieved optimal speed tracking performance in electric vehicles, outperforming GA- and PSO-based approaches. Similarly,37 concluded that ACO enhances the efficiency and stability of magnetic levitation systems when compared to Ziegler–Nichols tuning, GA, PSO, and evolutionary programming.

Other notable contributions include works by38,39, and40, who employed algorithms such as Grey Wolf Optimization (GWO) and PSO to optimize PID controllers in second-order DC motor systems.40 proposed a multi-objective GA for PID tuning applied to robotic manipulators, while41 developed a GA-based PID to solve a constrained optimization problem in servo systems.42 also highlighted the promising results of ACO in terms of response time and stability.

In the study by43, a control strategy for a Doubly-Fed Induction Machine (DFIM) was proposed using a genetic algorithm to optimize the PID parameters of the stator-side DTC controller. The rotor was supplied with low voltage and frequency (12 V, 5 Hz), which helped reduce torque ripple but limited the full exploitation of the DFIM’s capabilities, particularly overspeed operation.44 extended this method by applying the optimization to both stator and rotor sides, enabling full utilization of the machine’s potential.

To date, only three studies in the literature have applied optimization algorithms to the DTC of DFIMs-those by44,45 and43-all of which relied on genetic algorithms for PID tuning. In this study, and for the first time in the literature, Ant Colony Optimization (ACO) is applied to the DTC of a DFIM. This novel approach offers several advantages, including fast speed response, reduced torque ripple, and zero steady-state error.

To overcome the limitations inherent in conventional DTC schemes, several artificial intelligence-based methods have been developed. Today, optimization algorithms such as Genetic Algorithms (GA)44 and Ant Colony Optimization (ACO)45,46,47 are increasingly regarded as powerful tools for finding optimal solutions. Numerous studies have demonstrated the effectiveness of both techniques. For instance,48 employed a GA to optimize DTC control of an induction motor with the objective of minimizing torque ripple. In49, a GA using “earliest due date” encoding was applied for scheduling operations in the automotive metal stamping industry. Additionally,50 demonstrated the effectiveness of GAs in solving large-scale global optimization problems, while51 examined their impact on artificial neural network learning capabilities.

In the present study, two approaches-based on GA and ACO-are implemented to optimize the speed PID controller gains in the DTC control of a DFIM. The first approach, based on GA, combines the benefits of DTC with the global search capabilities of evolutionary algorithms. Inspired by the principles of natural selection, GA efficiently explores complex search spaces to identify optimal PID parameters, with the main objective of minimizing torque ripple and enhancing the system’s dynamic response.

The second approach employs Ant Colony Optimization, a bio-inspired technique that mimics the collective behavior of ant colonies in finding the shortest path to a food source. Applied to DTC, this method allows for the optimization of control parameters by minimizing system losses and maximizing machine efficiency. The ACO-DTC system is characterized by greater robustness to changes in operating conditions and provides significantly improved accuracy in flux and torque control.

By combining these advanced techniques, researchers aim to transcend the limitations of traditional control methods and propose more robust and high-performance control strategies for DFIMs. These advancements respond to the growing demands of modern industrial applications in terms of performance, energy efficiency, and reliability.

The core principle underlying DTC is its reliance on a simple controller structure, the most commonly employed being the PID controller. While PID controllers are widely recognized for their simplicity and effectiveness in linear systems, their integration into DTC, which is inherently designed for non-linear systems, can lead to challenges. Specifically, the dynamic and highly variable nature of torque and flux in DTC requires precise tuning of PID parameters to avoid issues such as excessive torque ripple, instability, or degraded transient performance. Furthermore, the non-linearities and parameter sensitivities of the system often necessitate advanced tuning methods or adaptive control techniques to maintain optimal performance.29,30,31. To overcome these problems, several artificial intelligence techniques have been developed. At present, optimization algorithms such as genetic algorithms (GA)44,45,46 and ant colony algorithms (ACO)45,47 are becoming increasingly effective in finding optimal solutions. Numerous studies in the literature attest to the effectiveness of these two types of algorithm. For example, in48, the authors developed a GA to optimize the performance of DTC control in order to reduce torque ripples in an induction motor. In49, a GA with earliest due date coding was applied to schedule automotive stamping operations. Furthermore,50 describes the application of a GA to solve large-scale global optimization problems. The influence of GAs on the learning capabilities of artificial neural networks is explored in51. With regard to ACOs,52 shows their use in determining the shortest search route in light food production distribution. New ACO-based MPPT controllers for photovoltaic systems under partial shading conditions are developed in53 and54. In this study, two solutions based on GA and ACO are used to optimize the gains of the PID speed controller of the DTC control of a DFIM. The first solution, based on GA, combines the advantages of DTC with GA optimization. GAs, inspired by the theory of natural evolution, enable optimal solutions to be found in complex search spaces. By applying these algorithms to DTC, it is possible to optimize speed controller parameters to improve overall system performance, particularly in terms of reducing torque ripples and improving dynamic response. The second solution, based on ACO, uses ant colony optimization, a method inspired by the behavior of ants in nature to find the shortest paths to a food source. Applied to DTC, this technique optimizes control parameters, minimizing losses and maximizing machine efficiency. ACO-DTC offers greater robustness in the face of variations in operating conditions, and improves the precision of flux and torque control. By combining these advanced approaches, the researchers aim to overcome the limitations of traditional methods and offer more robust and efficient control solutions for the DFIM. These advances meet the growing demands of modern industrial applications in terms of performance, energy efficiency and reliability.

In this paper, the highlights are as follows:

  1. 1.

    Optimization efficiency:

    • GA-based PI controllers achieve faster convergence and avoid local minima through effective global search.

    • ACO-based controllers use positive feedback and adaptive learning for robust and balanced parameter optimization.

  2. 2.

    Dynamic performance:

    • GA tuning results in faster response with less overshoot.

    • ACO offers smoother torque and speed profiles during transients.

  3. 3.

    Adaptability and robustness:

    • Both methods improve DTC robustness under disturbances.

    • ACO adapts better in real-time due to its decentralized, iterative structure.

  4. 4.

    Torque ripple reduction:

    • ACO slightly outperforms GA in reducing torque ripple, enhancing motor efficiency.

    • GA emphasizes accurate speed tracking with moderate ripple control.

This work is organized as follows:“ DFIM model in (\(\alpha\),\(\beta\)) representation” section presents the mathematical model of the DFIM, “Direct torque control” section is devoted to the modeling of conventional DTC control, “Direct torque control based on genetic algorithm” and “Direct torque control based on ant colony optimization” sections detail the principles of genetic algorithms and ant colonies, and the application of these two solutions to DTC control. “Comparative evaluation of GA-DTC and ACO-DTC: robustness,performance, and industrial feasibility” section presents a comprehensive discussion and comparison between the GA-DTC and ACO-DTC strategies, including robustness testing, a detailed analysis of their respective advantages and limitations, comparison with recent published works, and an evaluation of cost and implementation feasibility for industrial applications. “Conclusion” section concludes with the results obtained with the GA-DTC and ACO-DTC controls.

DFIM model in (\(\alpha\),\(\beta\)) representation

The mathematical model of the three-phase DFIM can be derived using Concordia’s assumptions, while neglecting the DFIM magnetic saturation , as well as slot effect and core losses. Thus, the DFIM model can be represented as indicated by the equations from 1 to 5.44,55:

  • Stator voltage components:

    $$\begin{aligned} \left\{ \begin{matrix} {v_{s\alpha } = R_{s}{\cdotp }i_{s\alpha } + \frac{d\psi _{s\alpha }}{dt}} \\ {v_{s\beta } = R_{s}{\cdotp }i_{s\beta } + \frac{d\psi _{s\beta }}{dt}} \\ \end{matrix} \right. \end{aligned}$$
    (1)

  • Rotor voltage components:

    $$\begin{aligned} \left\{ \begin{matrix} {v_{r\alpha } = R_{r}{\cdotp }i_{s\alpha } + \frac{d\psi _{r\alpha }}{dt} + \omega _{m}{\cdotp }\psi _{r\beta }} \\ {v_{r\beta } = R_{r}{\cdotp }i_{r\beta } + \frac{d\psi _{r\beta }}{dt} - \omega _{m}{\cdotp }\psi _{r\alpha }} \\ \end{matrix} \right. \end{aligned}$$
    (2)

  • Stator flux components:

    $$\begin{aligned} \left\{ \begin{matrix} {\psi _{s\alpha } = L_{s}{\cdotp }i_{s\alpha } + L_{m}{\cdotp }i_{r\alpha }} \\ {\psi _{s\beta } = L_{s}{\cdotp }i_{s\beta } + L_{m}.i_{r\beta }} \\ \end{matrix} \right. \end{aligned}$$
    (3)

  • Rotor flux components:

    $$\begin{aligned} \left\{ \begin{matrix} {\psi _{r\alpha } = L_{r}{\cdotp }i_{r\alpha } + L_{m}{\cdotp }i_{s\alpha }} \\ {\psi _{r\beta } = L_{r}{\cdotp }i_{r\beta } + L_{m}{\cdotp }i_{s\beta }} \\ \end{matrix} \right. \end{aligned}$$
    (4)

  • Mechanical subsystem:

    $$\begin{aligned} \left\{ \begin{matrix} {T_{em} = p{\cdotp }\left( {\psi _{s\alpha }i_{s\beta } - \psi _{s\beta }i_{s\alpha }} \right) } \\ {j\frac{d\Omega }{dt} + f\mathrm {\Omega } = T_{em} - T_{r}} \\ \end{matrix} \right. \end{aligned}$$
    (5)

Direct torque control

DTC is an advanced technique for controlling DFIM, enabling precise torque and flux management by directly manipulating the voltage vectors applied to the voltage source inverter (VSI). This method is based on several key elements: hysteresis controllers, a signal estimation block, and an inverter switching table47,56.

Hysteresis controllers keep flux amplitudes and electromagnetic torque within predefined error limits, by adjusting voltage vectors according to calculated signals such as developed torque and flux amplitudes. The signal estimation block evaluates these parameters for the controllers, while the inverter switching table uses the controller outputs, together with flux position information, to determine the optimum voltage vectors. This approach guarantees efficient DFIM operation with continuously adjusted voltages57,58.

Block of signal estimation

The magnitudes of the stator and rotor fluxes (\(\alpha\), \(\beta\))and torque can be calculated using the following expressions:45,47:

$$\begin{aligned} \psi _{s\alpha \beta } = \int \left( {V_{s\alpha \beta } - R_{s}{\cdotp }I_{s\alpha \beta }} \right) dt \end{aligned}$$
(6)
$$\begin{aligned} \psi _{r\alpha \beta } = \int \left( {V_{r\alpha \beta } - R_{r}{\cdotp }I_{r\alpha \beta }} \right) dt \end{aligned}$$
(7)
$$\begin{aligned} \left| \psi _{s} \right| = \sqrt{\psi _{s\alpha }^{2} + \psi _{s\beta }^{2}} \end{aligned}$$
(8)
$$\begin{aligned} \left| \psi _{r} \right| = \sqrt{\psi _{r\alpha }^{2} + \psi _{r\beta }^{2}}\end{aligned}$$
(9)
$$\begin{aligned} T_{em} = p{\cdotp }\left( {\psi _{s\alpha }{\cdotp }i_{s\beta } - \psi _{s\beta }{\cdotp }i_{s\alpha }} \right) \end{aligned}$$
(10)

The flux sectors are partitioned into six sections, each spanning an angle of \(\pi /3\) radians and represented in a complex two-dimensional plane. The position of the flux space vector within this plane can be illustrated as follows45,47:

$$\begin{aligned} \theta _{s} = \tan ^{- 1}\frac{\psi _{s\beta }}{\psi _{s\alpha }} \end{aligned}$$
(11)
$$\begin{aligned} \theta _{r} = \tan ^{- 1}\frac{\psi _{r\beta }}{\psi _{r\alpha }}\ \end{aligned}$$
(12)

Each sector angle is associated with a numerical value, enabling the voltage vector to be identified.

Hysteresis regulators

Calculated torque and flux values are compared with their respective references. To keep these values within acceptable limits, appropriate controls are generated.

\(\Delta \psi _{s}\) = \({\Delta }\psi _{r} = 1\) for an increase in flux, and \({\Delta }\psi _{s} = {\Delta }\psi _{r} = - 1\) for a decrease45.

$$\begin{aligned} {\Delta }\psi _{s} = 1~if~\left| \psi _{s} \right| \le \left| \psi _{s}^{*} \right| - \left| {hysteresis~limit} \right| \end{aligned}$$
(13)
$$\begin{aligned} {\Delta }\psi _{s} = - 1~if~\left| \psi _{s} \right| \ge \left| \psi _{s}^{*} \right| + \left| {hysteresis~limit} \right| \ \end{aligned}$$
(14)
$$\begin{aligned} {\Delta }\psi _{r} = 1~if~\left| \psi _{r} \right| \le \left| \psi _{r}^{*} \right| - \left| {hysteresis~limit} \right| \end{aligned}$$
(15)
$$\begin{aligned} {\Delta }\psi _{r} = - 1~if~\left| \psi _{r} \right| \ge \left| \psi _{r}^{*} \right| + \left| {hysteresis~limit} \right| \end{aligned}$$
(16)

To increase the torque, \(\Delta T_{e} = 1\); to decrease the torque, \(\Delta T_{e} = -1\); and to keep it constant, \(\Delta T_{e} = 0\). A three-level regulator is used to manage the torque, while a two-level regulator is employed for controlling the flux57,58.

$$\begin{aligned} {\Delta }T_{e} = 1~if~T_{e} \le T_{e}^{*} - \left| {hysteresis~limit} \right| \end{aligned}$$
(17)
$$\begin{aligned} {\Delta }T_{e} = 1~if~T_{e} = T_{e}^{*}\ \end{aligned}$$
(18)
$$\begin{aligned} {\Delta }T_{e} = - 1~if~T_{e} \le T_{e}^{*} + \left| {hysteresis~limit} \right| \end{aligned}$$
(19)

Inverters switching table

The DTC switching table principle for controlling VSI inverter arms is based on the optimum selection of switching states (\(S_a\),\(S_b\) and \(S_c\)) to directly control DFIM torque and flux. First, phase currents and voltages are measured to calculate stator fluxes and electromagnetic torque. Next, flux and torque errors are evaluated, and the stator flux sector is determined. Using a predefined switching table illustrated by Table 1, the errors and sector are combined to select the optimum switching state for the inverters, thereby controlling the power transistors to generate the required voltage vectors. This voltage vector is applied to the inverter arms, adjusting flux and torque in real time. The process is iterative, guaranteeing a fast and accurate response, optimizing motor performance for a variety of industrial applications.44,58.

Table 1 Switching table.
Full size table

Direct torque control based on genetic algorithm

Combining the genetic algorithm with the DTC control creates a hybrid control called GA-DTC. The genetic algorithm is based on a number of terminologies essential to its operation, such as chromosome coding, population creation, selection, crossover and mutation. The following sections detail each part of the process.

Genetic algorithm operating principle

The genetic algorithm is a search method based on natural and genetic selection. It initially generates a random population of potential solutions to a problem with no known solution. Each solution is represented by chromosome-encoded genetic sequences, evaluated for their proximity to an unknown optimal solution. The best-performing individuals are more likely to reproduce, passing on their genetic heritage to the next generation. This evolutionary process repeats itself, combining genes from parents to create new generations with incremental improvements, until an optimal solution is reached59.

Coding

The genetic algorithm is distinguished by the use of coded parameters rather than the parameters themselves. The choice of a suitable encoding method, such as the commonly used binary encoding (represented by (20)), is crucial to effectively represent the problem’s solution space. The literature also explores variants of genetic algorithms using integers and symbolic alphabets for different applications60,61.

$$\begin{aligned} x_{reel}=(\sum ^{n}_{i=1}b(i).2^{n-1}) \end{aligned}$$
(20)

Where b(i) is a bit of rank i and n is the maximum number of bits.

Creating the first population

The genetic algorithm begins by exploring several points to find the optimal solution. It is essential to create initial values for these points, usually at random to cover the entire search space. However, studies show that the quality of this initial population influences the speed of convergence of the algorithm. A high-quality initial population enables the algorithm to converge more rapidly towards the optimum by producing individuals close to the optimal solutions.62.

Population size

The size of the initial population is crucial in genetic algorithms. Too small a population can lead to sub-optimal solutions due to lack of information and rapid but limited convergence. Conversely, too large a population increases computation time without guaranteeing significant improvement. Various researchers have recommended different sizes: Grefenstette ideally suggests 10 to 160 individuals63, but points to non-linear relationships with crossover and mutation probabilities. Odeyato suggests between 100 and 400 individuals, while Robertson has used up to 8000 individuals for classification problems64.

Selection

The essential principle of selection is generally “the best survives”. The aim of selection is to increase the number of offspring with better fitness values. Selection methods can be grouped into 3 types of selection65,66: Selection by roulette wheel, Selection by rank and Selection by tournament. Comparative studies of various selection approaches have revealed that selection by rank and selection by tournament give better results with a good speed of convergence67.

Crossover

The crossover operator attempts to increase population diversity by modifying chromosomal components. The idea of this operator is to create two new individuals, the children, by sharing information between two other individuals called parents. Crossover takes place in two stages. In the first stage, two individuals are selected at random from the population. The crossover procedure exchanges the information from these points between the two chromosomes59. This procedure results in the creation of two genetically modified chromosomes that will be part of the next generation, known as offspring. Crossing methods can be grouped into 3 types:K-Crossing point ,Chain crossing and Uniform crossing. It is difficult to identify the best form of crossover. It is determined by the problem to be solved: there is no universal crossover operator. The type of crossing operator is determined experimentally by controlling the effect of different types of crossing59.

Mutation

Mutation involves the alteration of one or more genes within a series to generate a new offspring. Traditionally, mutation has been a key component of genetic algorithms. Recent studies highlight that the mutation operator plays a crucial role, primarily aimed at enhancing population diversity. This increased diversity improves the likelihood of discovering optimal solutions59.

Performance functions (fitness)

The ISE (Integral of Squared Error) performance function is particularly useful for evaluating a controller’s performance in terms of error minimization. When we talk about speed error in the context of control systems, we mean the difference between the actual speed and the set (or desired) speed. For a system where we control speed, the ISE for speed error can be defined as follows46:

$$\begin{aligned} ISE = \int _{0}^{T}\xi (t)^2\,\textrm{d}t \end{aligned}$$
(21)

Where :

  • \(\xi (t)=\Omega _ {ref}(t)-\Omega (t)\) is the speed error at time t.

  • \(\Omega _ {ref}(t)\) is the target speed at time t.

  • \(\Omega (t)\) is the actual system speed at time t.

  • T is the duration of the time interval over which the error is integrated.

In order to establish equivalence between the error and the gains of the regulator, the ISE is calculated in inverse ratio to obtain its fitness value. This determines the relevance of the chromosomes. The fitness function is defined as follows:

$$\begin{aligned} Fitness=\frac{1}{ISE} \end{aligned}$$
(22)

Controller structure designed and flowchart GA

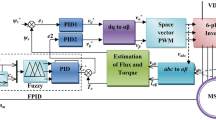
The system studied off-line is the speed loop of the DTC controller. The GA optimizes and generates the \(K_P\), \(K_I\) and \(K_D\) parameters of the PID controller. Figure 1 shows the simplified structure of the GA optimization method used and Fig. 2 shows the operating AG flowchart.

Fig. 1
figure 1

Optimization of the PID regulator by GA.

Full size image
Fig. 2
figure 2

GA flowchart.

Full size image

Simulation procedure and interpretation

Once the hybrid GA-DTC controller has been designed, the same simulation conditions used previously in the DTC controller are used again in this controller in order to compare the results of the different solutions proposed in this article.

Simulation procedure

Figure 3 illustrates the proposed technique for DTC using a PID controller optimized by a Genetic Algorithm (GA). The approach employs separate objective functions and a weighted combination applied to the DFIM.

Within the MATLAB/Simulink environment, the GA-based PID controller is utilized to simulate DTC control of a DFIM, aiming to determine the optimal PID controller parameters. The variation ranges for the PID gains in the GA (\({\textbf {Var}}_{Pmin}\), \({\textbf {Var}}_{Imin}\), \({\textbf {Var}}_{Dmin}\), \({\textbf {Var}}_{Pmax}\), \({\textbf {Var}}_{Imax}\), \({\textbf {Var}}_{Dmax}\)), along with the number of iterations (\({\textbf {n}}_{iter}\)) and population size (\({\textbf {Pop}}\)), are initialized to large values (\({\textbf {Var}}_{Pmax} = {\textbf {Var}}_{Imax} = {\textbf {Var}}_{Dmax} = 100\), \({\textbf {Var}}_{Pmin} = {\textbf {Var}}_{Imin} = {\textbf {Var}}_{Dmin} = -100\), \({\textbf {n}}_{iter} = 100\), \({\textbf {Pop}} = 100\)). This broad initialization increases the likelihood of generating optimal values for \(K_P\), \(K_I\), and \(K_D\), though it may result in extended convergence times (potentially several days). To expedite convergence, the range of these parameters can be narrowed to values closer to the optimal ones, thereby reducing the number of iterations.

This adjustment enables the system to converge more rapidly to the best solution. The PID controller parameters generated by the GA are detailed in Table 2, with values falling within the ranges specified in Table 9 of Appendix. The GA is configured using the parameters listed in Table 10 of Appendix and is tested under reference speed and torque conditions. The objective functions of the proposed GA-DTC strategy are evaluated on a \(1.5\,\text {kW}\) machine, configured as follows:

  1. 1.

    sampling frequency : \(f_s =10 kHz\).

  2. 2.

    Hysteresis band widths : \(\Delta C_{em} =\pm 0,01Nm, \Delta \psi _s=\pm 0,001Wb\) et \(\Delta \psi _r= \pm 0,001Wb\).

Table 2 Optimal gains generated by GA.
Full size table
Fig. 3
figure 3

Global structure of the \(GA-DTC\) control of a DFIM.

Full size image

Simulation results and interpretation

To assess the tracking performance of the proposed GA-DTC control, the ISE function is utilized as the objective function. Speed and torque setpoints are applied to the system under investigation for this evaluation.

Fig. 4
figure 4

Speed responses for GA-DTC control.

Full size image
Fig. 5
figure 5

Speed responses zooms.

Full size image

The responses in Figs. 4 and 5 demonstrate that the proposed controller enables the DFIM to effectively track variations in reference speed, both under no-load and loaded conditions. This is evident when the speed setpoint changes from 78.5 rad/s to 157 rad/s, from -157 rad/s to -78.5 rad/s, and during slope variations. Notably, the motor speed converges to the reference value more efficiently with the GA-DTC control compared to the conventional DTC control, as reflected in the reduced response time. Specifically, the GA-DTC control achieves an 80.83% improvement in the ISE function (27.2 ms for conventional DTC vs. 96.5 ms for GA-DTC) and a 69.55% improvement in zone (Fig. 5b) (83.1 ms for conventional DTC vs. 25.3 ms for GA-DTC). Additionally, an 85.9% improvement is observed in zone (Fig. 5d). The GA-DTC control also eliminates overshoot entirely, achieving a 100% reduction in zones (Fig. 5c and d), while significantly reducing undershoot by 86.73% (from 4.9 rad/s for conventional DTC to 0.65 rad/s for GA-DTC) in zone 1 and by 59.39% in zone (Fig. 5d). Furthermore, the rejection time required for the machine speed to return to its reference after load torque application shows a 94.58 ms improvement for GA-DTC (33.6 ms for conventional DTC vs. 1.82 ms for GA-DTC) in zone 1, with additional improvements of 93.74%, 81.7%, and 43% in zones (Fig. 5b–d), respectively, indicating robust speed adaptation to disturbances.

Table 4 summarizes key performance metrics, including speed response, torque and flux ripples, and stator and rotor current THDs. Figures 6 and 7 reveal that the GA-DTC approach produces fewer torque ripples compared to conventional DTC, with improvements of 12.13% (2.39 Nm for conventional DTC vs. 2.1 Nm for GA-DTC) in zone 1, and 3.77%, 17.14%, and 16.28% in zones (Fig. 7a). This confirms that the GA-DTC approach achieves precise reference tracking without undershoot, unlike conventional DTC.

The torque behavior during startup and abrupt speed changes is similar across control strategies, as it is inherently challenging to eliminate current inrush during these periods. However, the inrush is mitigated using a saturation block with a range of +15 Nm to -15 Nm to ensure the starting torque remains within safe limits.

Figures 8, 9, 10, and 11 illustrate the stator and rotor currents, which remain sinusoidal with harmonic content varying according to load conditions. The impact of optimized GA-DTC gains is evident in the harmonic spectral analysis, which shows significant reductions in THD. For instance, the GA-DTC strategy achieves THDs of 7.89% and 11.07% for stator and rotor currents, respectively, compared to 36.25% and 39.75% for conventional DTC in zone 1. Further improvements ranging from 21.53% to 44.82% are observed in other zones, highlighting the superior performance of the GA-DTC approach.

Fig. 6
figure 6

GA-DTC electromagnetic torque response.

Full size image
Fig. 7
figure 7

Zooms of electromagnetic torque response.

Full size image
Fig. 8
figure 8

isa current (a) isa current zooms (b) of GA-DTC control.

Full size image
Fig. 9
figure 9

isa current FFTs for the GA-DTC control.

Full size image
Fig. 10
figure 10

ira current (a) isa current zooms (b) of GA-DTC control.

Full size image
Fig. 11
figure 11

ira current FFTs for the GA-DTC control.

Full size image
Fig. 12
figure 12

Circular trajectories of stator and rotor fluxes in the GA-DTC control system.

Full size image

The stator and rotor flux waveforms for the proposed GA-DTC control are illustrated in Fig. 12a and b, respectively. The GA-DTC control demonstrates excellent dynamic performance, achieving reductions in flux ripples by 11.1% and 7.37% (0.04784 Wb and 0.01058 Wb for conventional DTC control vs. 0.0415 Wb and 0.0092 Wb for GA-DTC control). These characteristics highlight the suitability of the GA-DTC approach for high-performance applications.

In summary, the GA-enhanced DTC approach provides an effective solution to address the limitations in the robustness of the PID speed controller. It ensures precise control of speed performance and achieves a significant reduction in torque ripples, making it a highly effective control strategy.

Direct torque control based on ant colony optimization

The Ant Colony Optimization (ACO) algorithm, introduced by Marco Dorigo in 199268, is a meta-heuristic approach designed to solve combinatorial optimization problems. It operates by simulating artificial ants that explore paths within a graph, with the goal of identifying minimum-cost solutions. Through collaborative behavior, these artificial ants collectively converge on the most optimal paths69,70,71,72.

Ant colony algorithm

The ACO algorithm is suitable for parallel work, where ants act as intelligent agents exploring at random. In the traveling salesman problem, they visit cities, depositing pheromones to reinforce the best paths. The choice of a city depends on pheromones and visibility, thus optimizing the path.The selection of the most suitable path will be determined randomly based on the probability of choosing city j given by the following probability expression73,74,75:

$$\begin{aligned} P^k_{ij}(t) = \left\{ \begin{array}{rcl} \frac{[\tau _{ij}]^\alpha .\eta ^{\beta }_{ij}}{\sum _{i\in N^{k}_i(t)}[\tau _{il}]^\alpha .\eta ^{\beta }_{il}} & if & j\in N^k_i \\ else & 0 \end{array}\right. \end{aligned}$$
(23)

Where :

  • \(\tau _{ij}(t)\) is the quantity of pheromones deposited on the path linking city i with city j;

  • \(\eta _{ij}\) is the visibility.

  • \(N^k_i\) is the set of cities that ant k has not yet visited when located on city i.

Designing a PID controller using ACO

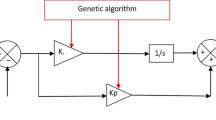
Many researchers have worked on PID parameterization methods using ACO. The authors70 used ACO to determine the controller parameters PID for a second-order system with a cost function. They achieved very satisfactory results compared with the conventional tuning method. The authors in69,70,71,72 also used an improved ACO for a nonlinear PID controller and concluded that their approach was very efficient. Figure 13 shows the block diagram of a PID controller optimized with the ACO.

Fig. 13
figure 13

Optimization of the PID regulator by ACO.

Full size image

To solve the problem of designing the PID controller with the ACO, we represent it as a graph, as shown in Fig. 14. The values of each parameter (\(K_P\), \(K_I\), \(K_D\)) are placed in three different vectors. In order to create a graphical representation of the problem, these vectors can be considered as paths between the nest and the food. The ant must visit three nodes, choosing the path between the starting point (nid) and the end point (food). The ants deposit pheromones in each path. Then, the pheromones are updated, enabling the intelligent ants to reinforce the payoffs (vertices of each vector) to maintain the amount of pheromone on the shortest path, ultimately generating optimal payoffs. Figure 14 shows the graphical structure of the ACO approach used to find the shortest path between the nest and the food.59.

Fig. 14
figure 14

Graphical representation of the ACO for the PID control process.

Full size image

The aim of ACO is to find the best path with the lowest cost function. According to the comparative study of cost functions carried out in the first part of this chapter, ISE is the best cost function, giving very good results. For this reason, ISE must also be used to calculate the speed error47. In the proposed approach, each ant updates the pheromones deposited on the paths it has traversed according to the following expression :

$$\begin{aligned} \tau _{ij}(k)=\tau _{ij}(k-1)+\frac{0.01\theta }{ISE} \end{aligned}$$
(24)

where \(\tau _{ij}(k)\) is the value of the pheromone quantity between nest i and food j at iteration k, \(\theta\) is the general pheromone update coefficient, ISE is the ant’s path cost function. The global pheromone update, with the pheromones of the paths belonging to the best paths (25) and the worst paths (26) of the ant colony, is performed according to the following expressions :

$$\begin{aligned} \tau ^{best}_{ij}(k)=\tau ^{best}_{ij}(k)+\frac{\theta }{ISE^{best}} \end{aligned}$$
(25)
$$\begin{aligned} \tau ^{worst}_{ij}(k)=\tau ^{worst}_{ij}(k)-\frac{0.3\theta }{ISE^{worst}} \end{aligned}$$
(26)

The pheromone levels on paths associated with the colony’s best solution are substantially reinforced, while those on paths linked to the worst solution are reduced. Subsequently, pheromone evaporation, as described in (27), enables the ant algorithm to reset its historical data. This mechanism ensures that the ACO can explore new directions and avoid becoming stuck in suboptimal paths59.

$$\begin{aligned} \tau _{ij}(k)={\tau ^{\lambda }_{ij}}(k)+(\tau ^{best}_{ij}(k)+\tau ^{worst}_{ij}(k)) \end{aligned}$$
(27)

where \(\lambda\) is the evaporation constant59.

ACO parameters

The steps involved in optimizing the PID controller with ACO are described by the flowchart in Fig. 15. The PID parameters have been encoded by 5000 nodes, each node representing a value for \(K_P\), \(K_I\) and \(K_D\). The more nodes, the more precise the gains, but this slows down the algorithm. The choice of parameters is crucial to optimizing the controller quickly. We used a method similar to that of the genetic algorithm, with optimal parameters (\(\theta =0.06\), \(\lambda =0.95\)), obtained after many experiments (see appendix 8)59.

Fig. 15
figure 15

ACO flowchart.

Full size image

After selecting the ACO parameters, equal pheromones were assigned to all available paths, stored in a matrix. The first artificial ant randomly selects a path, then the simulation is run with the selected PID coefficients. Path values are updated by calculating the ISE error of the velocity, and the pheromone table is adjusted to avoid repetition. Ant paths with the minimum ISE error have their pheromone increased, while those with the maximum error have their pheromone reduced. Pheromone evaporation takes place with the constant (\(\lambda\)). At the end, the optimal paths are recorded and the optimal PID parameters are summarized in Table 3.

Table 3 Optimum gains generated by ACO.
Full size table

Simulation procedure and interpretation:

Once the hybrid ACO-DTC control had been designed, we used the same simulation conditions as in the conventional DTC control to compare the results of the different solutions proposed in this document. The ACO configuration parameters are presented in appendix D3. Figure 16 shows the overall structure of the proposed ant colony-based ACO-DTC control.

Fig. 16
figure 16

Global structure of the \(ACO-DTC\) control of a DFIM.

Full size image

ACO-DTC control simulation

The speed and torque setpoints are the same as before. Figures 17 and 18 show the speed responses of the motor with load variations in both directions. The speed responses prove that the motor’s speed characteristic is improved by the optimization technique ACO-DTC. We can see that there is no longer any overshoot in the various zones of the setpoint. There is also a reduction in response time, rejection time and undershoot, with rates of 80.83 \(\%\), 99.88 \(\%\) and 76.12 \(\%\) respectively compared with the classic DTC control in the Fig. 18a zone. We find high improvement rates in the Fig. 18b–d zones. These results prove that the hybrid ACO-DTC control has speed control efficiency with high speed.

Fig. 17
figure 17

Speed responses of ACO-DTC and conventional DTC controls.

Full size image
Fig. 18
figure 18

Zoomed speed responses.

Full size image
Fig. 19
figure 19

Electromagnetic torque response of ACO-DTC and conventional DTC.

Full size image
Fig. 20
figure 20

Zooms of electromagnetic torque responses.

Full size image

Figures 19 and 20 illustrate motor torque responses according to various control strategies, based on the results in Table 4, we can state that the torque response of the intelligent approach ACO-DTC has fewer ripples than the conventional DTC control, which is translated into an improvement rate of 20.08 \(\%\) (2. 39 Nm for conventional DTC control and 1.91 Nm for ACO-DTC control) recorded on the zone (Fig. 20a) and significant improvement rates of 25.93 \(\%\), 27.86 \(\%\) and 24.81 \(\%\) for zones (Fig. 20b–d) respectively. The improvements are almost observed over the entire torque response, confirming the fidelity of the control. ACO-DTC.

Fig. 21
figure 21

ACO-DTC isa current (a) isa current zooms (b).

Full size image
Fig. 22
figure 22

The isa current FFTs of the ACO-DTC control.

Full size image
Fig. 23
figure 23

ACO-DTC control current (a) Zooms of current (b).

Full size image
Figure 24
figure 24

FFTs of the ira current of the ACO-DTC control.

Full size image

Figures 21, 22, 23, 24 illustrate stator and rotor current patterns, as well as their THDs. Based on the figures and the results of the Table 4, we can say that the currents are almost sinusoidal, with low THDs and less torque ripple.

Fig. 25
figure 25

Circular trajectories of stator and rotor fluxes for ACO-DTC control and conventional DTC.

Full size image

Figure 25 illustrates the stator and rotor flux characteristics of the proposed ACO-DTC control, where flux vectors are still maintained within the hysteresis bands but with acceptable reductions in band amplitudes giving improvements in flux values of 16. 17 \(\%\) and 22.5 \(\%\) respectively, demonstrating the effect of flux ripples on torque, which the reduction in torque ripples has brought about. When comparing the ACO-DTC with the conventional DTC, it is evident that the DFIM achieves its reference torque value more rapidly. Additionally, the torque remains well-regulated even under fluctuating load conditions. The ACO-based DTC demonstrates excellent speed response, reaching the target speed quickly and without overshoot. Moreover, the speed can be smoothly controlled during sudden load variations. Overall, the proposed ACO-DTC strategy outperforms the conventional DTC, offering superior performance. This strategy is highly effective for motor control, ensuring minimal torque ripples.

Based on the preceding analysis and the performance metrics outlined in Table 4, the ACO-DTC strategy proposed in this study has successfully achieved the objectives outlined in the introduction. It has demonstrated robustness in terms of speed regulation, flux control, torque ripple reduction, and current THD minimization. The enhancements introduced by ACO to the conventional DTC control enable more reliable and efficient control of the DFIM across a wide range of operating conditions. Furthermore, the ACO-DTC strategy exhibits strong adaptability to parametric variations in the machine, positioning it as a superior option for variable speed drive applications.

Comparative evaluation of GA-DTC and ACO-DTC: robustness, performance, and industrial geasibility

Discussion and comparison between GA-DTC and ACO-DTC

Table 4 Performances of DTC, \(GA-DTC\) and \(ACO-DTC\) controls.
Full size table

  • Performance comparison of DTC, GA-DTC and ACO-DTC controls

    Table 4 presents a detailed comparison of the performance of DTC, GA-DTC and ACO-DTC control in terms of several key parameters in zones 1,2,3 and 4. These results enable us to assess the effectiveness of the optimization techniques compared with conventional DTC control, highlighting the improvements brought about by the GA and ACO algorithms. From Table 4, we can see that similar improvements are seen in the other areas. Consequently, the comparison focuses on zone 1 only.

  • Speed performance (\(\Omega\))

    In terms of response time, GA-DTC and ACO-DTC show a significant improvement over conventional DTC. Response time drops from 96.5 ms for DTC to just 27.2 ms for both optimized techniques, representing an improvement of 80.83%. This drastic reduction in response time enables faster system response, essential for applications requiring greater precision and speed.

    Overshoot is completely eliminated with GA-DTC and ACO-DTC, dropping from 34 rad/s with conventional DTC to 0 rad/s. This 100% improvement indicates superior performance in terms of speed stability and accuracy. In addition, rejection time shows a marked improvement, particularly with ACO-DTC which reduces this time to 0.041 ms, compared with 33.6 ms for DTC, an improvement of 99.88%. Although GA-DTC also offers a significant improvement (94.58%), ACO-DTC demonstrates marginal superiority in this measure.

    Undershoot is also better controlled with the optimized techniques. GA-DTC reduces underdamping to 0.65 rad/s, an improvement of 86.73% over conventional DTC, while ACO-DTC reduces it to 1.17 rad/s, representing an improvement of 76.12%. These results show that both optimized techniques offer improved performance in terms of system stability and responsiveness.

  • Electromagnetic Torque Performance (\(T_{em}\))

    Electromagnetic torque ripples are a crucial indicator of control quality. The results show that GA-DTC and ACO-DTC improve performance over conventional DTC. Ripple is reduced to 2.1 Nm with GA-DTC and 1.91 Nm with ACO-DTC, representing improvements of 12.13% and 20.08% respectively. ACO-DTC demonstrates a greater ability to minimize torque fluctuations, which is essential for smoother, more efficient engine operation.

  • Flux performance (\(\psi _s\) and \(\psi _r\))

    Stator and rotor flux ripples are also better controlled with the optimized techniques. GA-DTC and ACO-DTC reduce stator flux ripples from 0.04784 Wb to 0.04253 Wb and 0.0401 Wb, respectively. This represents improvements of 11.1% for GA-DTC and 16.17% for ACO-DTC, indicating that ACO-DTC is more effective in reducing stator flux ripples.

    For rotor flux ripples, the improvements are even more pronounced with ACO-DTC reducing ripples to 0.0082 Wb, an improvement of 22.5%, compared to 0.0098 Wb with GA-DTC (an improvement of 7.37%). These results suggest that ACO-DTC is particularly effective in improving rotor flux stability.

  • Currents performances (\(i_{sa}\) and \(i_{sa}\))

    Finally, when it comes to the total harmonic distortion (THD) of stator and rotor currents, both optimized techniques show significant improvements. GA-DTC reduces stator current THD from 7.89% to 5.03%, while ACO-DTC reduces it even further to 4.25%, representing improvements of 36.25% and 46.13%, respectively. For rotor current THD, GA-DTC and ACO-DTC offer reductions to 6.67% and 6.13%, respectively, compared to 11.07% for conventional DTC. These results show improvements of 39.75% for GA-DTC and 44.63% for ACO-DTC.

    In summary, both GA-DTC and ACO-DTC controls improve performance over conventional DTC, with ACO-DTC showing marginal superiority in several key parameters, including torque and flux ripples, as well as current THD. These results demonstrate the effectiveness of optimization techniques in improving the performance of doubly-fed induction motor control systems, offering promising prospects for their industrial application.

Robutness test

Direct Torque Control has been extensively validated in the literature for its effectiveness in controlling electrical machines. Building on this foundation, the proposed GA-DTC and ACO-DTC strategies aim to further enhance the performance and robustness of DFIM. To assess the resilience of our approach, the DFIM was subjected to several physical constraints, including thermal and magnetic saturation-factors that directly influence internal machine parameters, particularly stator and rotor resistances and inductances.

Accordingly, the DFIM model was adapted to reflect these variations by adjusting several internal parameters. A series of tests were performed using these modified parameters, and the system’s behavior was analyzed through graphical results presented in Figs. 26 and 27. The results indicated that the machine’s speed response remained closely aligned with the reference values. While a slight increase in response time was noted, it is attributed to the deliberate modifications of the machine’s electrical characteristics. Importantly, the static error was negligible, and both GA-DTC and ACO-DTC controls demonstrated a high degree of insensitivity to variations in stator and rotor parameters.

In conclusion, these findings confirm that the proposed GA-DTC and ACO-DTC strategies exhibit strong robustness against fluctuations in internal machine parameters. This reinforces the practical viability and effectiveness of the proposed control approaches in maintaining high-performance operation of DFIMs under a variety of challenging conditions.

Fig. 26
figure 26

Speed response during variation of stator and rotor resistances of GA-DTC and ACO-DTC.

Full size image
Fig. 27
figure 27

Speed response during variation of stator and rotor inductances of GA-DTC and ACO-DTC.

Full size image

Pros and cons of GA-DTC and ACO-DTC techniques

The implementation of optimization-based PI controllers in Direct Torque Control, namely GA-DTC and ACO-DTC, brings significant improvements in motor performance. However, each technique exhibits distinct advantages and limitations. The Table 5 presents a comparative summary of their respective strengths and drawbacks:

Table 5 Pros and Cons of GA-DTC and ACO-DTC Techniques.
Full size table

Both GA-DTC and ACO-DTC offer promising improvements over conventional DTC. GA-DTC is advantageous in terms of implementation simplicity and fast convergence, making it suitable for applications requiring quick deployment. On the other hand, ACO-DTC excels in smooth torque control and adaptability, especially in environments with frequent parameter fluctuations. The selection between the two should be based on specific application requirements, such as speed of convergence, smoothness of control, and robustness to machine parameter variation.

Comparison with recent published works

The Table 6 compares different DFIM control strategies based on response time, torque ripples, and robustness. FOC and SMG are traditional methods with slow response times (0.56s and 0.19s) and high torque ripples (2.5Nm and 2.4Nm), lacking robustness. Backstepping improves speed (0.11s) and reduces ripples (2Nm) while ensuring robustness. DTC is even faster (0.0507s) but still has noticeable ripples (2.445Nm). Compared to the proposed work (GA-DTC and ACO-DTC), which achieve 0.0272s response time, all previous methods are significantly slower. Additionally, ACO-DTC has the lowest torque ripples (1.91Nm), making it the most efficient. RTO-DTC, despite being robust, performs the worst due to extremely high ripples (12Nm). In conclusion, compared to the proposed work, conventional methods are less effective, while ACO-DTC offers the best balance of speed, stability, and efficiency.

Table 6 Comparison between DFIM’s controls.
Full size table

Cost and implementation feasibility

The proposed approach using GA and ACO for PI speed control in DTC systems is generally feasible for industrial deployment due to its compatibility with standard industrial processors such as DSPs and high-performance microcontrollers. GA has moderate algorithmic complexity, simpler implementation, and faster convergence, while ACO, although more computationally intensive, offers greater adaptability and improved torque ripple reduction. Both methods can be integrated into existing DTC infrastructures without significant hardware modifications, which keeps infrastructure costs low. Their ability to handle parameter variations and load changes enhances system robustness and reduces long-term maintenance costs. In terms of initial deployment, GA tends to be more cost-effective and quicker to implement, whereas ACO may require more resources for fine-tuning and validation. Overall, both approaches are cost-efficient, scalable, and well-suited to industrial motor control applications, Table 7 summarizes the comparison criteria between the GA-DTC and ACO-DTC control strategies.

Table 7 Comparison of GA-based and ACO-based PI controllers for industrial use.
Full size table

Conclusion

This article explores two methods for improving the robustness of DTC control by using optimization algorithms to adjust PID controller gains as a function of the speed error between setpoint and output, evaluated by a fitness function. The GA-DTC strategy, based on the ISE cost function, offers promising results by effectively controlling machine speed while reducing torque ripples. The hybrid ACO-DTC control also demonstrates its effectiveness in terms of speed and torque, confirming the robustness of optimization algorithms for reference tracking. In conclusion, GA-DTC and ACO-DTC outperform conventional DTC, with ACO-DTC showing a slight superiority in key parameters such as torque and flux ripples, as well as the THD of stator and rotor currents represented by improvements 27.86%, 16.17%, 22.5% , 46.13% and 44.63% respectively. These results underline the effectiveness of optimization techniques for improving the performance of doubly-fed induction motor control systems, offering promising prospects for their industrial use.