Introduction

Epilepsy is a neurological disease characterized by recurrent, unprovoked seizures and is estimated to affect ~ 50 million people worldwide1,2. A scalp electroencephalogram (EEG) non-invasively records the electrical activity of the brain, and its findings play a critical role in the clinical diagnosis and management of epilepsy3,4,5. The diagnostic yield of a short 20–40-minute routine EEG is determined by the presence of spontaneous transient interictal epileptiform discharges (IEDs)6,7,8. However, ~ 30–55% of routine EEGs of patients with epilepsy and 9–10% of prolonged video EEGs show no evidence of IEDs and delay the diagnosis of epilepsy9,10,11,12,13,14.

In newly diagnosed epilepsy, anti-seizure medications (ASMs) are the first choice of therapy. However, despite a successful diagnosis, about half the patients do not respond to their first ASM, and about a third continue to have uncontrolled seizures despite multiple ASM trials15,16. Therefore, the determination of drug-resistant epilepsy (DRE) can take several months or years, while the patients continue to experience seizures and comorbidities. Thus, the early identification of DRE is essential to reduce disease burden and to initiate evaluations for additional therapies such as resective surgery and electrical brain stimulation. In focal epilepsy, magnetic resonance imaging (MRI) scans of the brain can help clarify the disease etiology by identifying structural abnormalities that lead to seizures17. In MRI negative, i.e., non-lesional, epilepsy patients, normal EEGs can cause further delays in identifying the epileptogenic brain regions for treatment. Broadly, the inability to identify interictal epileptiform activity during visual review of routine EEGs can delay the initiation of ASMs, increase healthcare costs, and put the patient at an increased risk of seizure-related injuries and comorbidities.

As such, there is a clear need for alternative approaches that can assist with early diagnosis and treatment planning when traditional routine EEG tests are inconclusive. This study aims to develop a quantitative approach to explore automatic analysis of normal interictal EEGs, which could provide early, objective, and inexpensive clinical decision support. Given that the current standard of clinical care relies on the presence of EEG abnormalities, recent quantitative EEG literature has focused primarily on detecting those abnormalities to augment traditional visual EEG review18,19,20,21. However, despite being frequently recorded in practice, normal interictal EEGs remain largely under-utilized in epilepsy classifications. In recent studies, normal or non-IED interictal EEGs have shown promise in detecting focal epilepsy, identifying the epileptic hemisphere, and prognosticating surgical outcomes22,23,24,25,26,27,28,29. However, their clinical value in challenging scenarios such as drug-resistant and non-lesional epilepsy has not yet been fully explored, especially in comparison with non-epileptic neurological patients like those encountered in practice. In this study, we explore the quantitative analysis of normal EEGs and investigate finer classifications of epilepsy, including drug-resistant and non-lesional epilepsy, using a large clinical population database of patients with and without epilepsy. Our approach provides expert-interpretable and patient-specific quantitative descriptors of normal EEG activity that could aid clinical decision-making in the future.

Quantitative analyses of scalp EEGs have primarily used expert-defined time- and frequency- domain features such as Hjorth parameters30,31 zero-crossings32,33 relative power34 power ratios34 entropy35,36 and connectivity37. However, such features may be limited to pre-defined spectral bands or spatial locations and, therefore, fail to capture multivariate EEG patterns. Here, we adopt an unsupervised approach based on tensor decompositions to extract multivariate EEG patterns while fully utilizing the full spectral and spatial extent of scalp EEGs. Prior EEG tensor analyses have mostly focused on spectral power and lacked robustness due to arbitrary initialization conditions38,39,40. In addition, the rank of tensor decomposition, i.e., the number of factors recovered from the decomposition has largely been determined empirically by trial-and-error. Furthermore, the value of such analyses has not been explored in the context of improving epilepsy diagnosis using normal interictal EEGs. Our approach advances large-scale tensor-based EEG analysis by recovering spectral connectivity patterns in an unsupervised fashion and addresses prior limitations using a physiology-informed initialization that allows reproducible decomposition with a meaningfully predefined rank.

In this study, we retrospectively analyzed a large dataset of 13,652 routine EEGs from a diverse neurological population of 12,134 adults and a cohort of 121 adults with confirmed focal epilepsy. Patterns of power spectral density and phase-based connectivity in eyes-closed wakefulness were extracted from the 6,242 normal EEGs in the population dataset using canonical polyadic tensor decomposition. We examined the spatial and frequency distributions of these patterns and investigated their association with age and clinically assigned EEG grades. We then obtained loading scores for an unseen cohort of patients with focal epilepsy by projecting their EEG data onto the normal interictal EEG patterns identified using the population dataset. These loadings served as subject-specific quantitative descriptors (or features) of normal EEG activity in binary classification analyses focusing on focal epilepsy diagnosis and additional clinical classifications, including the epileptogenic lobe (temporal or frontal), drug resistance, and the presence of structural abnormalities.

Fig. 1
figure 1

Cohort selection process flow starting from the overall clinical population dataset. Patients with focal epilepsy and controls without epilepsy were triaged using clinically assigned EEG grades, electronic health record notes/reports, and case reviews. Epochs extracted from their EEGs were reviewed for interictal abnormalities and excessive artifacts. Clinically graded normal EEGs comprise the population set for tensor decomposition.

Full size image

Data & methods

Clinical population dataset and expert EEG review

Our study utilized 13,652 routine clinical EEG recordings obtained from 12,134 adult patients (18 or older) at Mayo Clinic, Rochester, MN, USA between 2016 and 202241. This study and the experimental protocols were approved by the Mayo Clinic Institutional Review Board (IRB#: 15-006530) and were conducted in accordance with the Declaration of Helsinki. All patients and/or legal guardians provided informed consent. The EEGs were recorded using the XLTEK EMU40EX headbox manufactured by Natus Medical Incorporated, Oakville, Ontario, Canada. All EEGs followed the standard 10–20 electrode placement system42 and were sampled at 256 Hz. The patient population comprises individuals presenting with a diverse array of conditions including epilepsy, cognitive impairment, episodic migraines, syncope, and functional spells, among others. Overall, this dataset represents the patient population typically referred for routine EEG assessments at the Mayo Clinic in Rochester, MN, USA. All EEG records were visually reviewed by board-certified epileptologists and graded based on the Mayo Clinic internal EEG grading protocol. EEGs within normal limits and without visible abnormalities were graded as normal. EEGs with asymmetry, persistent delta frequency slowing, and intermittent abnormalities were classified either as Dysrhythmia 1 (mild, non-specific slowing or excess of fast activity), Dysrhythmia 2 (moderate to severe intermittent slowing), or Dysrhythmia 3 (e.g. epileptiform abnormalities, triphasic waves, intermittent rhythmic delta frequency activity). A more detailed summary of this EEG grading protocol is provided in Supplementary Item 7. Normal EEGs comprise the population set used for tensor decompositions. Note that patients corresponding to these normal EEGs may present with the aforementioned conditions including epilepsy.

Focal epilepsy cohort and matched control subjects without epilepsy

Figure 1 depicts the process flow for constructing the epilepsy and control cohorts. Patients with EEGs containing focal epileptiform abnormalities (i.e., Dysrhythmia grade 3) were used to triage focal epilepsy cases in the overall patient population. Based on further review of the electronic health records of those patients including neuroimaging tests, patient seizure diaries, and other clinical evidence, we identified a total of 121 focal epilepsy patients (frontal = 21; temporal = 100; 125 EEGs) who had a confirmed diagnosis of frontal or temporal lobe epilepsy and had no prior history of any cranial surgery. The drug response status was determined by whether two adequate anti-seizure drug trials resulted in a > 50% reduction in baseline seizure frequency within a year of their EEG assessment. Lesional findings of patients with temporal lobe epilepsy were determined by reviewing diagnostic MRI reports available within a year of their EEG assessments. Cases where clinical evidence was either not available or insufficient were excluded from clinical sub-group classifications. Patients with frontal lobe epilepsy were not considered for these sub-group classifications due to low sample size. An age- and sex-matched control cohort of 76 subjects with normal EEGs and without diagnosis of epilepsy or other major neurological disorder was selected for comparisons from the overall set of normal EEGs. Data of patients in focal epilepsy and matched control sets were excluded from the population set during subsequent analyses to prevent statistical data leakage.

Fig. 2
figure 2

Overall analytic workflow of the study. (A) Multiple eyes-closed awake interictal epochs from each EEG recording are identified for data analysis. The average power spectral density (PSD) and phase-based connectivity (PC) between each channel pair are computed and stacked across recordings to obtain 3-d PSD and PC tensors (recordings x channels or channel pairs x frequencies). (B) PSD and PC population tensors are decomposed separately in an unsupervised fashion to obtain multiple interpretable spatio-spectral patterns (i.e., factors). (C) Normal interictal EEG data from focal epilepsy patients are projected on each population-level factor to obtain patient-specific factor loadings. Differences in drug-resistant and non-lesional MRI focal epilepsy are investigated by using these loadings in statistical group/sub-group comparisons and predictive analyses.

Full size image

The complete analytical workflow of this study from processing of raw EEGs to results is illustrated in Fig. 2. Below we describe the methods used in this workflow.

EEG preprocessing and epochs selection

All routine EEGs were preprocessed as follows: (1) selection and ordering of the 19 EEG channels arranged according to the 10–20 system (i.e., Fp1, F3, F7, C3, T7, P3, P7, O1, Fp2, F4, F8, C4, T8, P4, P8, O2, Fz, Cz, and Pz), (2) resampling to ensure a sampling rate of 256 Hz, (3) band-pass filtering between 0.1 and 45 Hz, and (4) transformation to common average reference. Artifact rejection was not performed in this pipeline as we hoped to recover population patterns specific to artifacts in a data-driven manner using tensor decompositions. Next, we applied a heuristic algorithm24 to select a maximum of six 10-second EEG epochs from the full recording representing eyes-closed wakefulness. The algorithm relies on sleep staging43eye blinks, sample entropy, and occipital alpha power to select candidate epochs. These selected epochs are not guaranteed to be contiguous. After preprocessing, all EEG recordings were represented by at most six EEG epochs representing eyes-closed resting-state wakefulness. Preprocessing was done using the numpy44 and MNE45 Python libraries. Epochs selection used the MNE-features46 and YASA43 libraries.

Additional review of EEG epochs extracted from focal epilepsy and control patients

From the extracted EEG epochs of focal epilepsy patients, a board-certified epileptologist visually reviewed and selected ones containing normal interictal activity. Abnormal epochs containing seizures, epileptiform spikes, epileptiform sharp waves, temporal intermittent rhythmic delta activity (TIRDA), and excessive artifacts were excluded from the study. Polymorphic, intermittent delta and theta frequency slowing (0.1 - <8 Hz) events, however, could not be excluded due to their pervasive presence in some EEGs. Similarly, epochs from non-epileptic controls with excessive artifacts were also excluded. We note that this additional review of epochs extracted using the automated algorithm was conducted only for epilepsy and control EEGs.

Constructing tensors of spectral power

Power spectral density (PSD) of EEG data was estimated for all 19 EEG channels using Welch’s algorithm47 yielding log-power values at all integer frequencies between 1 and 45 Hz. We then averaged the PSD measures of each EEG recording across all the identified epochs to obtain a single PSD vector for each channel. The PSD measures of each EEG recording can now be represented as a matrix with shape 19 × 45 (19 channels and 45 frequencies). Stacking this average PSD matrix across recordings produces a 3-d power-spectral tensor (“PSD-tensor”) of the form: N recordings x 19 channels x 45 frequencies. The population PSD-tensor is globally min-max scaled between [0, 1] to maintain non-negativity for subsequent tensor decomposition. Focal epilepsy and control PSD-tensors are scaled similarly but are stacked together first to preserve group differences for downstream analyses. A global scaling scheme, using min-max values computed considering all tensor dimensions, was applied to preserve the variability between channels within the same recording as well as the variability across multiple subjects/recordings.

Constructing tensors of phase-based connectivity

An estimate of phase-based connectivity (PC) between a pair of channels \(\:(i,\:j)\) is computed using the weighted Phase Lag Index48 (wPLI) measure defined as:

$$\:wPLI\left(i,j\right)=\frac{\left|E\left[\mathfrak{I}\left({X}_{ij}\right)\right]\right|}{E\left[\left|\mathfrak{I}\left({X}_{ij}\right)\right|\right]}=\:\frac{\left|E\left[\left|\mathfrak{I}\left({X}_{ij}\right)\right|\:sgn\left(\mathfrak{I}\left({X}_{ij}\right)\right)\right]\right|}{E\left[\left|\mathfrak{I}\left({X}_{ij}\right)\right|\right]}$$

where \(\:{X}_{i,j}\) denotes the cross-spectral density of channels \(\:i\) and \(\:j\), \(\:\mathfrak{I}(.)\) is the imaginary part of the cross-spectrum, \(\:sgn(.)\) is the sign function, and \(\:E[.]\) represents a mean over the selected eyes-closed epochs. wPLI values range between [0, 1]. A positive value reflects an imbalance between leading and lagging relationships, with 1 indicating a perfect lead or lag relationship. At each integer frequency between 1 and 45 Hz, wPLI provides a connectivity value for each of the 171 unique channel pairs. Thus, we obtain a 3-d phase-based connectivity tensor (“PC-tensor”) of the form: N recordings x 171 channel pairs x 45 frequencies.

Representing the normal EEGs as 3-d population tensors

We utilized the clinically graded normal EEGs in the overall population dataset (N = 6,242 out of 13,652) to extract population-level EEG patterns. We estimated the PSD and PC measures for these normal EEGs using their automatically extracted epochs and formed the population PSD-tensor and PC-tensor of shape (6,242 × 19 × 45) and (6,242 × 171 × 45), respectively.

Decomposition of 3-d tensors into factors

The canonical polyadic (CP) decomposition49,50 (also known as the PARAFAC decomposition51) approximates a given tensor as a sum of \(\:R\) rank-1 tensors, where \(\:R\) is the decomposition rank, i.e., the resulting number of factors obtained from decomposing the tensor. The CP decomposition of a 3-dimensional tensor \(\:T\) with rank \(\:R\) is defined as:

$$\:T\approx\:{\sum\:}_{r=1}^{R}{A}_{r}\otimes\:{B}_{r}\otimes\:{C}_{r}$$

where \(\:\otimes\:\) denotes an outer product and \(\:{A}_{r}\), \(\:{B}_{r}\), and \(\:{C}_{r}\) are vectors with shapes matching each of the three dimensions of \(\:T \) (recording, channel, frequency). Each term in the summation, i.e., a combination of \(\:{A}_{r}\), \(\:{B}_{r},\:\)and \(\:{C}_{r\:}\), is a rank-1 tensor and is referred to as a factor. The \(\:A\), \(\:B\), and \(\:C\) factor matrices (containing \(\:{A}_{r}\), \(\:{B}_{r},\:\)and \(\:{C}_{r\:}\)vectors as columns, respectively) are optimized with a non-negativity constraint using the hierarchical alternating least squares51,52 approach.

Determining the initialization and rank for CP decomposition

We provided a physiologically meaningful initialization and rank derived from PSD characteristics of healthy subjects to initialize the decomposition of the PSD-tensor. For this, we fit a parametric model of the EEG PSD, named FOOOF53 (“fitting oscillations and one over f”), to the eyes-closed trials in the MPI Leipzig Mind-Brain-Body dataset54 (N = 207, 8 trials per subject, 60s trial duration). The FOOOF model segments the observed morphology of an EEG PSD into superimposed aperiodic (\(\:L\)) and oscillatory components (\(\:{G}_{n}\)):

$$\:PSD=L+{\sum\:}_{n=1}^{5}{G}_{n}$$

Each \(\:{G}_{n}\) is a Gaussian peak corresponds putatively to a canonical brain oscillation (delta, theta, alpha, beta, or gamma) and is parameterized by height, mean or center frequency, and a standard deviation. \(\:L\) is a function of the form \(\:\text{L}\left(F\right)={10}^{b}\text{*}\frac{1}{\left(k+F{\upchi\:}\right)}\) whose parameters \(\:b\), \(\:k\), and \(\:\mathcal{X}\) capture aperiodic 1/f-like nature of the \(\:PSD\). We refer readers to Donoghue et al. (2020) for additional model details. We fit this six-component model to healthy PSDs in the MPI-Leipzig dataset. The fitted versions of \(\:{G}_{n}\) and \(\:L\) formed the frequency initializations \(\:{B}_{r}\:\)of the decomposition solution and informed the choice of rank \(\:R=6\). These initializations are shown in Supplementary Figure S1.

Decomposing the population tensors

Factor matrix \(\:B\) (containing \(\:{B}_{r}\:\)vectors as columns) was initialized with the six spectral “priors” described above. CP decomposition with non-negativity constraints and \(\:R\)=6 was applied on the min-max scaled population PSD-tensor. The resultant \(\:B\) was then used as an immutable initialization for the subsequent CP decomposition of the population PC-tensor. In other words, only factor matrices \(\:A\) and \(\:C\) were optimized in the PC-tensor decomposition. The use of \(\:B\), i.e., frequency patterns extracted from the PSD-tensor, in PC factors ensured that the frequency dependence of resting-state brain networks55,56 was captured in a data-driven manner and that factor interpretations were aligned across both decompositions. Tensor analyses were done using the tensortools57 Python library.

Visualization of factors derived from the normal EEG population

The \(\:{A}_{r}\), \(\:{B}_{r}\), and \(\:{C}_{r}\) vectors resulting from both CP decompositions represent semantically coherent components: \(\:{A}_{r}\) contains factor’s loadings per recording, \(\:{B}_{r}\) holds the factor’s frequency activations, and \(\:{C}_{r}\) holds the factor’s channel or channel-pair activations. The recording loadings are visualized as histograms, frequency activations as power spectral profiles, and channel activations as topographical distributions over the scalp. Note that we obtain \(\:{A}_{r}\) and \(\:{C}_{r}\) separately from the PSD-tensor and PC-tensor decompositions, while \(\:{B}_{r}\:\)is shared between both as described above. We refer to values in \(\:{A}_{r}\) as “PSD loadings” or “PC loadings” depending on the tensor they are associated with. Factor visualizations with channel and channel-pair values scaled to a consistent range can be found in Supplementary Figure S3.

Computing factor loadings for the focal epilepsy cohort

We computed population factor loadings for the focal epilepsy cohort using a projection operation40,41. Consider the basis matrix \(\:P\) containing vectorized versions of the spatio-spectral factors \(\:{B}_{r}\) \(\:\otimes\:\) \(\:{C}_{r}\). Thus, matrix P has \(\:R\) rows and \(\:C\)*\(\:F\) columns, where \(\:C\) and \(\:F\) is the length of the channel dimension and frequency dimension of the tensor, respectively. Then, for a new EEG recording \(\:{x}_{new}\in\:{R}^{C\times\:F}\), its loadings are computed by \(\:{P}^{+}\times\:\text{vectorized}\left({x}_{new}\right)\), where \(\:{P}^{+}\) is the pseudo-inverse of \(\:P\). This operation provides R weights or loadings that represent how strongly each population factor is expressed in the new EEG recording. Note that this operation does not guarantee non-negative loadings.

Associations and statistical testing

Pearson’s correlation coefficient and Spearman’s rank correlation coefficient were used to quantify associations of factor loadings with patient age and ranked degree of slowing, respectively. The corresponding p-values test the null hypothesis that the distributions underlying the samples are uncorrelated. The Mann-Whitney-Wilcoxon two-sided test58 was used for group-level comparisons with Bonferroni correction59 for multiple comparisons. The test was performed using the stat-annot60 Python library.

Predictive modeling

Patient-specific loadings were robustly scaled (subtract median, scale by interquartile range) and used as features in a logistic regression binary classifier. We explored three sets of features: PSD loadings, PC loadings, and both concatenated together. Nested k-fold cross-validation (CV) was done to assess variability of model performance on different held-out sets (outer CV loop, 10-fold) and to tune the ElasticNet regularization strength61 hyperparameter for each training set (inner CV loop, 5-fold). Grid for the hyperparameter search ranged between [0, 1] with increments of 0.1. Both CV loops used disjoint patient splits with target stratification. Loss values were weighted using target class proportions to handle class imbalance. For each outer CV fold, a classifier was trained using the best hyperparameter setting found by the inner CV loop and evaluated on the corresponding outer test fold. We used the area under receiver operating characteristic curve (AUC) to evaluate model performance across the outer CV folds. Predictive modeling was performed using the scikit-learn62 Python library.

Results

Characteristics of the neurological population, focal epilepsy cohort, and controls

Table 1 provides an overview of the population-level routine EEG dataset. This dataset included 13,652 recordings from 12,134 unique patients. Most routine EEG sessions in this dataset were ~ 50–60 min long (mean: 53.81 (± 9.02) minutes; range: 5.68–119.40 min). Expert visual review of these EEG recordings based on the Mayo Clinic grading criteria resulted in 45.7% (N = 6,242) normal EEGs, 24.9% (N = 3,395) EEGs with mild slowing (Dysrhythmia grade 1), 13.2% (N = 1,800) EEGs with moderate to severe slowing (Dysrhythmia grade 2), and 16.2% (N = 2,215) EEGs with epileptiform abnormalities (Dysrhythmia grade 3). From the population of Dysrhythmia grade 3 EEGs, we identified 121 focal epilepsy patients with clinically confirmed epilepsy in either the frontal (N = 21) or temporal (N = 100) region. In addition, a set of 76 matched non-epileptic controls with normal EEGs and without a diagnosis of any neurological disease were identified for group comparisons. Table 2 summarizes the characteristics of the confirmed epilepsy patients and controls.

Table 1 Characteristics of the overall neurologic clinical population.
Full size table
Table 2 Characteristics of epilepsy cohort and controls used in this study.
Full size table

Tensor decomposition extracts interpretable spatio-spectral patterns from normal EEGs

Figure 3 shows the factors obtained by decomposing the normal EEGs in the population dataset, i.e., the population PSD-tensor and PC-tensor. The frequency profiles are largely distinct, except in the case of factors 2 and 6, where their spatial distributions uniquely characterize the overall pattern.

Factor 1 shows the characteristic 1/f frequency profile with minor deviations around the oscillatory bands and spatial activations in the fronto-temporal and posterior regions, characterizing the background non-oscillatory (i.e., aperiodic) brain activity. Factor 2 shows high frequency activations (> 25 Hz) in the prefrontal region, suggesting eye-movement-related artifacts. Factor 3 predominantly contains high-theta/low-alpha activity (6–9 Hz) in fronto-parietal regions, possibly indicating the high theta rhythm or slow alpha rhythm. Factor 4 shows occipital activations in 8–13 Hz, resembling the characteristic posterior dominant rhythm. Factor 5 shows centro-parietal activations in 13–25 Hz, capturing the Rolandic beta activity. Lastly, factor 6 shows high-frequency activations (> 25 Hz) in the temporal regions, which may represent muscle artifacts. The analyses and findings presented in the remaining text focus on the four putatively physiologic factors (1, 3, 4, and 5).

Fig. 3
figure 3

Data-driven population-level patterns of eyes-closed awake EEG data extracted from 6,242 normal EEGs. Three-dimensional tensors containing spatio-spectral information were decomposed using non-negative Canonical Polyadic Decomposition to yield six factors. Each row corresponds to a combination of a power spectral and connectivity-based factors, which is defined by the common spectral profile, the spatial power distribution over the 19 channels, the pair-wise channel connectivity, and loadings of EEG recordings in the PSD-tensor and PC-tensor. Recording loadings are visualized as histograms, spatial activations are visualized as scalp topographical distributions, and spectral activations are visualized as power spectral density. Note that the PSD-tensor was decomposed first, and the resulting frequency factors were kept frozen during the decomposition of the PC-tensor to align interpretation of the factors (a.u. refers to absolute units.)

Full size image
Fig. 4
figure 4

Associations of PSD and PC loadings of the four putatively physiologic factors (1, 3, 4, and 5) with physiological (aging) and pathological (slowing, epileptiform activity) variables. Factor numbers correspond to those in Fig. 3. Loadings describe activity found in eyes-closed awake EEG segments selected from expertly graded routine EEGs in the population-level dataset. (A) Correlations of PSD and PC loadings of normal EEGs with patient age. (B) Correlations of PSD and PC recording loadings with expert-assigned severity of slowing. The ranked severity levels are 0 (normal EEG, no slowing), 1 (Dysrhythmia 1 EEG, mild slowing), and 2 (Dysrhythmia 2 EEG, moderate to severe slowing (C) Correlations of PSD and PC recording loadings with the presence of epileptiform activity (Dysrhythmia 3 EEGs abbreviated as “Dys3”). Significance levels correspond to the Mann-Whitney-Wilcoxon test. Loading values along y-axes are in arbitrary units. * indicates a significant correlation with p < 0.05 and **** indicates a significant correlation with p < 1e-4.

Full size image

Patient loadings show sensitivity to aging and EEG dysrhythmia grades

Figure 4 shows the associations between the loadings of population EEGs for factors 1, 3, 4, and 5 against patient age and expert-assigned EEG grades.

Trends with patient age (Fig. 4A): Factor 3 is positively correlated with age (p < 1e-4), while factors 1 (PSD: p < 1e-4, PC: p < 0.01) and 4 (p < 1e-4) are negatively correlated. Although the correlation strength varies between the PSD and PC loadings of the same factor, they are directionally consistent. Correlations of factor 5 are either marginally significant (PSD: p < 0.05) or not significant (PC).

Trends with expert-ranked degree of slowing (Fig. 4B): Factor 1 is positively correlated with severity of slowing (p < 1e-4), while factor 4 is negatively correlated (p < 1e-4). Correlation of factor 3 is either low (PSD: p < 0.05) or not significant (PC). The correlation of factor 5, although significant (p < 1e-4), is directionally divergent between the PSD and PC loadings.

Differences in presence of epileptiform activity (Fig. 4C): Here, loadings of EEGs with epileptiform activity were compared against those of normal EEGs. PSD loadings of factor 1 increase under presence of epileptiform activity, while those of factors 4 and 5 decrease (p < 1e-4 in every case). Factor 3 PSD loadings show no significant change. PC loadings of factors 1 and 4 show trends consistent with corresponding PSD loadings (p < 1e-4 in both cases). However, the PC loadings of factors 3 and 5 show slight increases (p < 1e-4).

Fig. 5
figure 5

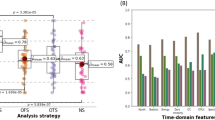
Differentiation of focal epilepsy and epileptogenic. (A-B) PSD and PC loadings of focal epilepsy patients (FOCAL-EPI) are compared to those of non-epileptic controls (CTL) across the four physiologic population factors. Loading values along y-axes are in arbitrary units. * indicates a significant difference with p < 0.05 and **** indicates a significant difference with p < 1e-4 in the Mann-Whitney-Wilcoxon test. (C) PSD and PC loadings are used as features to classify focal epilepsy vs. non-epileptic controls within a binary classification framework. (D-E) The same classification is broken down by temporal (TLE) and frontal (FLE) sub-types of focal epilepsy. (F) Differential diagnosis of the epileptogenic lobe, i.e., TLE vs. FLE, within the focal epilepsy cohort. Note that all classifications used only the four putative physiologic factors (1, 3, 4, and 5) and were conducted with three sets of features/loadings - only those of PSD factors (“PSD only”), only those of PC factors (“PC only”), or both concatenated (“PSD + PC”).

Full size image

Quantitative analysis of normal interictal EEG reveals differences in focal epilepsy

Figure 5 shows results for group differences and binary classifications between non-epileptic controls and the focal epilepsy cohort using patient-specific PSD and PC loadings of the physiologic factors. We find focal epilepsy patients to have elevated factor 1 (p < 0.001) and factor 3 (p < 0.05). in both PSD and PC comparisons (Fig. 5A-B). In addition, we find PC loadings for factor 5 (p < 0.05) significantly different in focal epilepsy relative to non-epileptic controls. Factor 4 loadings do not show significant differences in either the PSD or PC comparisons.

Figure 5C shows classification of focal epilepsy vs. non-epileptic patients is possible above chance levels, with PC loadings providing the largest contribution to the average classification performance (AUC = 0.76). This performance is marginally improved by using a combination of PSD and PC loadings (AUC = 0.78). Supplementary Figure S4 shows the relative contribution of the PSD and PC loadings towards the classification. All feature sets show high variability in performance across the held-out folds (0.09–0.13). Figure 5D-E show results for the classification of frontal (FLE) and temporal lobe epilepsy (TLE) against non-epileptic controls. TLE is better differentiated from non-epileptic patients than FLE (top mean AUC = 0.8 vs. 0.7). TLE is best differentiated by combined PSD and PC loadings (AUC = 0.80), with PC loadings contributing the most to classifier performance (AUC = 0.77). FLE is best differentiated using PC loadings alone (AUC = 0.70), and the addition of PSD loadings slightly worsens the performance (AUC = 0.68). Variability in AUC performance across folds ranges from 0.05 to 0.19. Lastly, Fig. 5F shows the classification of TLE vs. FLE based on factor loadings derived from normal interictal epochs. Results indicate that none of the feature sets can differentiate the epileptogenic lobe (i.e., temporal vs. frontal) in focal epilepsy above chance levels (AUCs range between 0.47 and 0.55) based on normal interictal epochs.

Fig. 6
figure 6

Differentiation of drug-resistant and non-lesional temporal lobe epilepsy (TLE) patients using four physiologic pattern loadings (factors 1, 3, 4, and 5). (A) Loadings are compared between non-epileptic controls (CTL), TLE patients that are drug resistant (TLE-resis) and those that are drug responsive (TLE-respon). (B) Binary classifications of drug resistant vs. responsive patients using the same feature sets as Fig. 5. (C-D) Analyses similar to (A) and (B) are conducted for lesional (TLE-les) and non-lesional (TLE-nonles) TLE sub-groups. Loading values in (A) and (C) along y-axes are in arbitrary units. * indicates a significant difference with p < 0.05 and **** indicates a significant difference with p < 1e-4 in the Mann-Whitney-Wilcoxon test with Bonferroni correction.

Full size image

Quantitative loadings of normal interictal EEG exhibit capacity for differentiation in drug-resistant and non-lesional epilepsy

Figure 6A shows differences in loadings of non-epileptic controls (CTL), drug-responsive (TLE-respon), and drug-resistant (TLE-resis) temporal epilepsy patients. Only the PSD loadings for factor 5 show differences between the two sub-groups (p < 0.05), while the others show differences only relative to controls. None of the PC loadings show significant differences between the two sub-groups. PC loadings other than those of factor 1 show no differences between non-epileptic controls and both sub-groups. Figure 6B shows the classification performance of different sets of factor loadings in classifying drug resistance. PSD loadings provided the best average performance (AUC = 0.73) while PC loadings performed marginally better than chance (AUC = 0.58). Variability in model performance ranged from 0.07 to 0.13 AUC points.

Figure 6C shows differences in normal interictal EEG loadings between non-epileptic controls (CTL), non-lesional (TLE-nonles), and lesional (TLE-les) temporal lobe epilepsy. While PSD loadings of factors 1, 3, and 4 show significant differences relative to non-epileptic controls for both groups, only factor 4 shows a significant difference between non-lesional and lesional patients (p < 0.05). Trends seen in factors 1 and 3 are similar between the PSD and PC loadings. However, none of the PC loadings differed significantly between the MRI sub-groups. Figure 6D shows the classification between lesional and non-lesional patients. PSD loadings best differentiate the two groups of patients with an AUC of 0.67. PC loadings, either alone or in addition to PSD loadings, significantly worsened the average classification performance. However, all models exhibited high variability in AUC performance (0.11–0.22 AUC points). Supplementary Figure S4 shows the relative contribution of PSD loadings towards these classifications.

Discussion

The goal of this study was to explore whether normal interictal EEGs of people with focal epilepsy contain subtle signals that could be used to augment epilepsy diagnosis and treatment planning, especially in patients with drug-resistant and MRI normal epilepsy. We proposed a scalable, physiology-informed, and data-driven tensor decomposition approach that extracts spatio-spectral patterns from a large population of normal routine EEGs. Each pattern had a distinct signature in the EEG channel (spatial) and frequency (spectral) dimensions. We obtained patient-specific pattern loadings or “features” that allowed us to study group differences through statistical comparisons and binary classifications. Our findings suggest that quantitative description and analysis of visually reviewed normal routine EEGs has the potential to provide additional value to clinical decision-making in epilepsy.

Tensor decomposition with spectral priors recovers interpretable patterns

This study hypothesized that the information content of normal EEGs can be explained by a parsimonious number of latent patterns. To test this hypothesis, we decomposed the spectral and connectivity contents of a population of normal routine EEGs into several meaningful patterns (i.e., factors) using a canonical polyadic tensor decomposition. In general, determining the appropriate number of factors, i.e., the presumed rank of the population tensor, is challenging and involves trial-and-error63. An entirely computational choice of rank and initialization can lead to dataset-dependent factors and hinder reproducibility. In Supplementary Fig. S2, we inspected the mean-squared reconstruction error for varying ranks as a proxy for variance explained by the corresponding rank-1 factors. We found that there was no optimal decomposition rank value that could be analytically chosen. Prior work has demonstrated that the morphological content of the scalp EEG PSD can be sufficiently explained by six physiological components, namely one aperiodic 1/f pattern and five oscillatory bands53. We used this spectral parameterization model to construct six corresponding frequency priors that, in turn, provided a meaningful initialization as well as an appropriate rank (R = 6) for the decomposition. Supplementary Figure S6 shows the reproducibility of the PSD-tensor factors using a publicly available dataset of healthy subjects54. An analysis of the impact of different rank choices on the classification of focal epilepsy found that rank R = 6, coincidentally, performed the best (see Supplementary Figure S2). Furthermore, we advanced the tensor analysis of resting-state EEG by decomposing connectivity information in the PC-tensor in a manner semantically consistent with power spectral patterns extracted from the PSD-tensor.

Several prior works have explored data-driven or unsupervised recovery of spatial, spectral, or temporal profiles of oscillatory sources and background patterns comprising spontaneous EEG activity38,64,65,66,67. In this study, we presented an approach that quantifies spatio-spectral EEG power and connectivity patterns with the goal of decision support when clinical EEGs are normal on expert visual review. Beyond the use of spectral-prior-based initialization, our approach did not place any assumptions on the statistical nature or morphology of the latent EEG patterns and can be applied without sophisticated artifact removal.

The population patterns (Fig. 3) can be loosely interpreted to reflect dominant and overlapping physiological processes whose linear superposition (summation) yields the original EEG trace. We then interpreted the identified patterns based on clinical domain knowledge. The putative interpretations of these patterns are supported by their sensitivity to patient age and severity of pathology (Fig. 4).

Fig. 7
figure 7

Comparisons highlighting the clinical relevance of the normal interictal EEG-derived PSD/PC factor loadings. (A) ROC curve for the classification of patients with non-lesional TLE (N = 36) against non-epileptic controls using the same feature sets as Fig. 5. (B) Association of Factor 3 PSD loadings with epilepsy duration and patient age in a cohort of patients with drug-resistant TLE (N = 27).

Full size image

Augmenting epilepsy diagnosis and treatment planning

Scalp EEG is an indispensable tool in epilepsy that can non-invasively record brain electrical activity with excellent temporal resolution. Due to this unique resolution, scalp EEG tests can capture transient interictal epileptiform discharges (IEDs) such as epileptiform spikes or sharp waves associated with epilepsy68. In current clinical practice, the expert identification and characterization of IEDs on routine scalp EEG is crucial for epilepsy diagnosis. Routine EEGs are also useful in measuring the efficacy of ongoing ASM trials69. In the case of drug-resistant epilepsy, the distribution of IEDs identified on scalp EEGs can help localize the seizure onset zone, especially in patients with no visible lesion on MRI. Thus, the identification of IEDs is central to the clinical value of scalp EEGs in current practice.

Recent studies have shown significant interest in the automated identification of IEDs to augment expert visual review18,70,71. However, the diagnostic yield of a single routine scalp EEG is limited, with only 29–55% of them capturing epileptiform abnormalities11. Multiple EEGs may increase epileptiform yield up to ~ 75%72,73, but the expected gain sharply drops after the third normal EEG. As such, normal interictal EEGs can cause treatment delays in multiple stages of epilepsy care. Previous studies that explored biomarkers of interictal non-epileptiform EEG support the possibility of augmenting decision support in epilepsy using spectral and connectivity-based EEG features22,23,24,26,27,74,75,76,77. However, most studies focused on epilepsy detection and used healthy controls, thus limiting the translational relevance of their findings. Here, we explored finer and challenging epilepsy classifications using data-driven recovery of normal EEG spectral features and comparisons with non-epileptic neurological patients.

Figure 7 highlights the potential clinical relevance of the data-driven factors/features. In Fig. 7A, we extend the analysis presented in Fig. 5D and differentiate non-lesional TLE from non-epileptic controls. We find that normal interictal EEG-derived PSD/PC loadings can indicate the presence of TLE even when no diagnostic information is available on MRI. Figure 7B shows an analysis with 27 patients with drug-resistant TLE in which we examine associations between their PSD loadings and epilepsy duration. We find a strong association for Factor 3, albeit with a potential age confound (see Supplementary Fig. S7 for remaining results). Further work is needed to control confounding variables (e.g., patient age) and assess correlations with other clinically relevant variables (e.g., seizure frequency).

Our findings in Figs. 5 and 6 suggest that normal interictal EEG activity of focal epilepsy patients contains significant differences in putative physiologic oscillations (factors 3, 4, and 5) as well as aperiodic 1/f(Hz) activity (factor 1). In clinical classifications, PC factors were most effective in detecting epilepsy relative to non-epileptic controls (Fig. 5C-E) while PSD factors helped classify sub-groups within the epilepsy cohort (Fig. 6B and D). The detection of potentially finer connectivity differences within these sub-groups may require higher-density EEGs or connectivity analyses in the source space. Increases in expression of 1/f and theta frequency activity, coupled with a decrease in alpha frequency may represent general intermittent slowing of the EEG background. Although we identified differences in factor 5, the differences in beta frequency rhythm may arise due to the presence of ASMs. The factors exhibited relatively lower performance in detecting FLE (Fig. 5E) and in differentiating FLE vs. TLE (Fig. 5F). We believe that this may be due to either the lower sample size of the FLE cohort compared to the TLE cohort (Fig. 5D) or the global/symmetric nature of the population patterns. Determining the extent to which these symmetric PSD/PC patterns can support spatial characterization of epilepsy requires further investigation (see Supplementary Fig. S5).

Fig. 8
figure 8

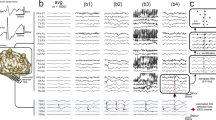
Variability in EEG power and phase characteristics based on factor loading values. (A) Variability in the power spectra of EEGs whose PSD loadings score in the bottom 10-percentile (low), between 40-60-percentile (medium), and top 10-percentile (high). Examples are shown for factors 3, 4, and 5. (B) 8-Hz-filtered EEG traces of the weakest (top) and strongest (bottom) channel pairs for an example EEG that scored in the top 10-percentile for factor 3 (whose spectral power peaks at 8 Hz). Overlapping EEG traces reveal phase relationships, i.e., time lags that maximize correlation within the channel pairs. These lags or phase differences are visualized in polar coordinates (right).

Full size image

Understanding subtle variation in visibly normal EEGs through their quantitative descriptors

Our results (Fig. 5) indicate that factor loadings extracted from normal EEG segments have the potential to classify focal epilepsy above chance levels (best mean AUC = 0.78). We analyzed the changes in actual power spectral and timeseries data corresponding to the changes in factor loadings to further illuminate the factor interpretations.

Figure 8A shows the full power spectra of normal EEG segments whose loadings fall in the bottom 10-percentile (low), between 40-60-percentile (medium) and top 10-percentile (high) of a particular physiologic oscillatory factor. We find that EEGs that score high in factors 3, 4, and 5 have higher power in high-theta/low-alpha, alpha, and beta bands, respectively.

Effects of the phase-lag-based connectivity (i.e., wPLI) at a particular frequency can be observed by leading/lagging relationships in the time-domain EEG signal filtered at that frequency. Figure 8B focuses on factor 3 whose spectral power peaks at 8 Hz, with the weakest edge connecting Fp1 and Fp2, and the strongest edge connecting P4 and P8 (shown in Fig. 3). We visualize the phase relationships using an example EEG segment whose loading value was in the top 10-percentile for factor 3 after filtering its EEG trace around 8-Hz. We find that the strongest channel pair (Fig. 8B, bottom) has a consistent non-zero phase difference, while the weakest channel pair (Fig. 8B, top) has no phase difference. These phase differences can be quantified by the time lag that maximizes timeseries correlation within the channel pair and are visualized in polar coordinates (Fig. 8B, right).

These illustrations highlight that the quantitative loading values provided by this tensor-based framework are interpretable based on physiologically relevant concepts such as signal power and phase and offer sensitivity to subtle changes in the EEG signal. These subtle changes in normal EEGs are likely to be missed during traditional expert visual review, which focuses mostly on transient abnormalities in the time domain.

Fig. 9
figure 9

Repeated CTL vs. TLE classifications using two bootstraps to evaluate bias introduced by the dataset selection process. Strategy A (left) uses either the first or last three of the six EEG epochs from a subset of TLE patients (N = 41). Strategy B (right) uses at most 3 epochs that are randomly chosen but uses all available TLE patients (N = 100).

Full size image

Influence of sample size and selected EEG epochs on study findings

The routine EEG protocol contained diverse patient states (eyes-closed, eyes-open, awake, drowsy, asleep) and provocative maneuvers78 (photic stimulation, hyperventilation, sleep deprivation), making it necessary to select EEG epochs corresponding to a fixed patient state for data analysis. Our preliminary analyses indicated that epochs representing eyes-closed wakefulness were not abundant in our EEG recordings. Nonetheless, six epochs free of excessive artifacts could be reliably extracted from most recordings. A lower epoch count was undesirable as it could bias the average estimate of spectral power and connectivity (average is computed across epochs). Such data selection may introduce bias in our findings since we selected only a maximum of six EEG epochs from each recording for our analyses.

To evaluate whether a bias exists, we repeated the controls vs. TLE classification (result in Fig. 5D) with two bootstrapping strategies, whose results are shown in Fig. 9. In strategy A (Fig. 9A), we considered TLE patients (N = 41) with exactly six normal interictal EEG epochs and showed differences in classification performance depending on which 50% data are used for classification (i.e., first three epochs or last three epochs). Mean performance was higher when the first 3 epochs were used (AUC = 0.65) than last 3 epochs (AUC = 0.59). In strategy B (Fig. 9B), we maintained the sample size of the original TLE cohort (N = 100) but used at most three randomly picked EEG epochs per recording to perform classification. For patients with > 3 epochs available, 3 epochs were randomly chosen and for those patients with < = 3 epochs, all epochs were chosen. Our results did not show any significant differences between those two sampling approaches and the overall performance closely matched that using all available epochs.

These results suggest that: (1) our findings may be sensitive to low cohort size but are less likely to be biased by the algorithmic selection of EEG epochs within a recording, and (2) even as few as three normal interictal EEG epochs (30 s) are sufficient to derive a pretest measure of TLE.

Study limitations

Our goal in this study was to evaluate whether a quantitative analysis of normal EEG segments of epilepsy patients can indicate the possible presence of focal epilepsy. To test this hypothesis, we analyzed non-epileptiform interictal segments identified by a board-certified epileptologist within EEG recordings containing epileptiform abnormalities at other times (i.e., Dysrhythmia grade 3). However, an analysis using entirely normal EEGs of epilepsy patients will be necessary to evaluate the true potential of our results. However, identification of such EEGs requires extensive review of patient records, which we hope to accomplish in a follow-up study. Furthermore, eyes-closed wakefulness was determined by a heuristic algorithm validated in previous studies24,41. Events markers or comments added by EEG technologists79 during the EEG study could help to identify the patient’s behavioral state more reliably. Extension of our analysis to different sleep states will be pursued in future studies.

The estimation of connectivity could benefit from EEG source modeling to avoid volume conduction and active reference effects on the scalp80,81. However, the lower spatial density of clinical EEGs prevented source/inverse modeling efforts, as previous studies have shown that EEG source modeling with fewer than 64 channels is highly error-prone82,83,84. Phase-based connectivity, and wPLI in particular, was chosen to suppress spurious zero-lag correlations and partially alleviate the effects of volume conduction48,85. Due to absence of patient-specific head models, average referencing was chosen to mitigate reference-related effects on connectivity better than alternatives like Cz and linked mastoids80.

Our classification analyses demonstrated a high level of variance between cross-validation folds (Figs. 5 and 6). Such variance could be a result of low sample size and the potential effects of comorbidities86,87 and medications88. The effects of these confounders may be mitigated either by comprehensive patient review to identify a clinically homogeneous set of focal epilepsy patients or with the use of larger epilepsy and matched control cohorts. Given that the EEG background patterns identified in this study are not specific to epilepsy, apparent differences in factor loadings must be interpreted within the appropriate clinical context. Additionally, validations using normal interictal EEGs from an external site are needed to assess the generalizability of the presented findings.

Conclusion

Normal interictal EEGs recorded from epilepsy patients can lead to delays in neurological care, especially in patients with drug-resistant and normal MRI epilepsy. This study explored the value of quantitative analysis of normal interictal EEGs in supporting a focal epilepsy diagnosis. Application of this unsupervised learning approach could benefit treatment planning in the future. We presented a scalable, interpretable, data-driven approach based on canonical polyadic decomposition that recovered physiologically meaningful spectral power and phase-based connectivity patterns from a population-scale dataset of normal EEGs and provided patient-specific loadings for each pattern. These loadings demonstrated value in classifying focal epilepsy and, in temporal lobe epilepsy, drug resistance and absence of lesions. These findings suggest that normal routine EEGs may contain subtle abnormalities that can be captured using a quantitative approach and be potentially used to augment decision-making in clinically challenging scenarios.