A novel meta-heuristic algorithm based on candidate cooperation and competition

Abstract

Traditional meta-heuristic algorithms are often inspired by natural phenomena or biological behaviors, while relatively few are based on human social behavior. Moreover, existing algorithms inspired by human social behavior often suffer from premature convergence and getting trapped in local optima. To address these limitations, we propose a novel metaheuristic algorithm called the Candidates Cooperative Competitive Algorithm (CCCA), which is inspired by distinctive human social behaviors and designed for continuous optimization problems. CCCA consists of two main stages: self-study and mutual influence among candidates. The mutual influence stage includes various cooperative behaviors, such as one-on-one and many-to-one assistance, collaborative discussions among outstanding candidates, and targeted support for average candidates. Additionally, it incorporates competitive mechanisms, including contests among top-performing candidates and elimination strategies. We apply CCCA to solve 23 classical test functions, comparing them with PSO, FA, CSA, HMS, ICA, TLBO, and BSO. The results demonstrate that CCCA outperforms the compared algorithms, achieving optimal solutions in 9 functions. The convergence trends indicate that CCCA has a strong ability to escape local optima in 7 unimodal and multimodal functions. Statistical analysis using the Mann–Whitney U test confirms that CCCA achieves significant performance improvements in over 90% of the test cases. We also compare CCCA with recently developed human-inspired algorithms and obtain similarly competitive results. These findings further underscore the feasibility and robustness of CCCA. Moreover, its successful application to the capacity allocation problem highlights its practical effectiveness and superiority.

Introduction

In recent decades, the complexity of problem-solving in production and daily life has increased due to the technological revolution and advances driven by Artificial Intelligence (AI), causing traditional optimization algorithms to gradually struggle to meet the demand for efficient optimization¹. Therefore, the demand for new optimization techniques is growing across various fields, leading to the emergence of meta-heuristic algorithms. According to their advantages, such as simplicity in principles, strong flexibility, absence of derivation mechanisms, and the ability to escape local optima², meta-heuristic algorithms have demonstrated their superiority in tackling challenging optimization problems across diverse backgrounds³.

Garey and Johnson⁴ initially introduced the concept of meta-heuristic algorithms. The emergence of such algorithms opens up the possibility of efficiently solving mathematical or engineering optimization problems involving complex constraints, high dimensionality, non-linearity, and non-convexity⁵. Currently, over 200 meta-heuristic algorithms with distinct characteristics are known⁶, each suitable for solving optimization problems in different fields, including scheduling problems, pricing optimization, inventory management, traffic simulation, feature selection, and vehicle routing problems^{7,8,9,10,11,12}. Since the proposal of traditional meta-heuristic algorithms like Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO), many problems that were previously unsolvable with conventional optimization methods have now found effective solutions. However, traditional meta-heuristic algorithms have their own shortcomings, such as susceptibility to getting stuck in local optima and slow convergence. To enhance the performance of meta-heuristic algorithms, numerous researchers have dedicated significant efforts to designing new meta-heuristic algorithms with the aim of further improving their accuracy and speed. In recent years, emerging meta-heuristic algorithms like the Wild Horse Optimizer (WHO)¹³, Harris Hawks Optimization (HHO)¹⁴, Manta Ray Foraging Optimization (MRFO)¹⁵, Artificial Rabbits Optimization (ARO)³, and others have shown promising results in practical applications.

Classical sources of inspiration for meta-heuristic algorithms include the habits and inherent characteristics of natural organisms, as well as mathematical, physical, or chemical principles. (1) Algorithms inspired by the habits and inherent characteristics of natural organisms include GA¹⁶, PSO¹⁷, ACO¹⁸, Firefly Algorithm (FA)¹⁹, Artificial Fish Swarm Optimization (AFSA)²⁰, Shuffled Frog Leaping Algorithm (SFLA)²¹, Dragonfly Algorithm (DA)²², Artificial Butterfly Optimization (ABO) algorithm²³, Corona virus optimization (CVO)²⁴, Polar Fox Optimization Algorithm (PFA)²⁵, Artificial Lemming Algorithm (ALA)¹, Snow Geese Algorithm (SGA)²⁶, Puma Optimizer (PO)²⁷. (2) Algorithms inspired by mathematical, physical or chemical principles include Simulated Annealing (SA)²⁸, Gravitational Search Algorithm (GSA)²⁹, Central Force Optimization (CFO)³⁰, Galaxy-based Search Algorithm (GbSA)³¹, Big-Bang Big-Crunch Algorithm (BBBC)³², Charged System Search (CSS)³³, Artificial Chemical Reaction Optimization Algorithm (ACROA)³⁴, Black Hole (BH)³⁵, Water Cycle Algorithm (WCA)³⁶, Elastic Deformation Optimization Algorithm (EDOA)³⁷, Lightning Search Algorithm (LSA)³⁸, Transient search optimization (TSO)³⁹, Wave Search Algorithm (WSA)⁴⁰, Snow Ablation Optimizer⁴¹, Energy Valley Optimizer (EVO)⁴², Sine Cosine algorithm (SCA)⁴³.

Apart from these categories, some meta-heuristic algorithms are inspired by other factors, such as neighborhood search algorithms, iterated local search (ILS), and Tabu Search (TS), which have proven to be highly effective in practical applications of discrete problems^44,45,46.

Although there are many kinds of algorithms available today, they inevitably possess certain drawbacks: they are prone to falling into local optima and may exhibit premature convergence¹. Designing an efficient algorithm capable of escaping local optima and avoiding premature convergence remains an interesting and meaningful area of research. Furthermore, in reference to the No Free Lunch (NFL) theorem⁴⁷, it is essential to acknowledge that not every algorithm performs optimally for all problems. Joyce and Herrmann⁴⁸ studied NFL in-depth and also made the point that no algorithm can effectively and efficiently solve any optimization or instances of the same problem. Based on this theory, multiple studies have progressed in developing meta-heuristics tailored to specific types of problems. Deng and Liu⁴⁹ develop an enhanced social learning swarm optimizer (ESLPSO) to achieve more reliable parameter estimation of photovoltaic (PV) models. Cui et al.⁵⁰ propose an Improved Snow Ablation Optimization Algorithm (MESAO) combined with the Kernel Extreme Learning Machine (KELM) to realize flood prediction. In addition, X-ray image segmentation problems, multiple hydropower reservoir control, etc., are also solved by developing specialized meta-heuristic algorithms^51,52. Thus, no particular algorithm can be considered universally ideal. The NFL theorem encourages us to explore and develop more efficient algorithms, providing researchers and experts in various fields with additional options.

Nevertheless, most traditionally developed meta-heuristic algorithms are inspired by the objective laws of nature or the habits of living organisms, with fewer algorithms being designed based on inspiration from human social behavior. In comparison to meta-heuristic algorithms designed according to the objective laws of nature or the habits of living organisms, those inspired by human social behavior offer several advantages, including: (1) Conform to human thought processes, simulate human behavior more realistically, and are easier for users to understand and accept. (2) Demonstrate superiority in solving social problems and are better suited to solving problems in the humanities and social sciences, such as social networks and the market economy. (3) With better interpretability, it helps users to have a deeper understanding of the decision-making process in real-world applications.

Building on the aforementioned advantages, scholars have gradually explored meta-heuristic algorithms inspired by human social behavior, which have now been introduced as a distinct category^53,54. Consequently, several algorithms have been developed, including Teaching–Learning-Based Optimization (TLBO)⁵⁵, Imperialist Competitive Algorithm (ICA)⁵⁶, Brain Storm Optimization Algorithm (BSO)⁵⁷, and Human Mental Search (HMS) Algorithm⁵⁸.

However, the number of meta-heuristic algorithms inspired by human social behavior remains relatively limited. At the same time, these algorithms inspired by human social behavior all suffer from varying degrees of premature convergence and slow convergence speed. How to avoid premature convergence has become a focus of algorithmic research^59,60. In addition, some meta-heuristic algorithms suffer from inconsistencies between the description and implementation, and degradation of the algorithm’s performance when the standard benchmarks are shifted^61,62,63,64. To truly implement “novel” metaheuristics, appropriate structures and components are the key considerations⁶⁵. Thus, this paper aims to design a novel meta-heuristic algorithm based on the unique human social behavior observed in high school entrance exams and the preparation process (referred to as the “entrance exam”) to address the above problems. This research not only introduces a novel perspective on designing meta-heuristic algorithms but also enriches the theoretical framework of existing meta-heuristic algorithms, aiming to offer more precise solutions to practical problems in production and daily life. The abstract graph of our research is shown in Fig. 1. We first introduce the concept of the “Candidate Cooperative Competitive” and formulate the whole process mathematically. Then, numerous experiments are conducted to confirm the effectiveness of CCCA compared with other meta-heuristic algorithms. Finally, a Capacity Allocation Problem is solved to demonstrate the effectiveness of the CCCA in practical applications. A conclusion is also given to summarize our research.

Fig. 1

Graphical abstract.

The main contributions of this paper are as follows:

(1) We present a detailed mathematical model that abstractly captures the unique human social behaviors observed during entrance exam preparation. This model incorporates the stages of self-study and mutual influence among candidates. (2) Inspired by these behaviors, we propose a novel meta-heuristic algorithm, termed the Candidate Cooperative Competitive Algorithm (CCCA). Rooted in the social behavior model, the CCCA integrates both self-study and influence mechanisms. and encompasses the stages of self-study and influence among candidates. Unlike traditional meta-heuristics, the use of a ranking mechanism and adaptive learning enhances interaction diversity among candidate solutions and enables flexible control over the evolution rate. Moreover, the competition among top-performing candidates functions similarly to a gradient ascent mechanism, helping the algorithm escape local optima. (3) We evaluate the feasibility and effectiveness of CCCA on 23 benchmark test functions. CCCA outperformed all compared algorithms on 16 functions, achieving the theoretical global optimum on 9 of them. Convergence analysis further shows that CCCA achieved significantly faster convergence than other algorithms on 18 functions. For both unimodal and multimodal functions, CCCA exhibited a strong ability to avoid local optima in 7 cases. Additionally, Mann–Whitney U test results confirm statistically significant improvements in over 90% of the experiments. The further validations compared with ESC, ODO, and SBOA obtain similarly competitive results. (4) We further demonstrate the practical applicability of CCCA by applying it to a supply chain capacity allocation problem. Experimental results indicate that CCCA not only surpasses all compared algorithms in performance but also achieves cost reductions over the best existing method. These results underscore both the effectiveness and superiority of CCCA in solving real-world, complex optimization problems.

The rest of the study is structured as follows: section “2Candidates cooperative competition algorithm (CCCA)” describes the inspiration and the mathematical formula of the CCCA. The experiments and analysis for testing the effectiveness of the CCCA are conducted in section “3Experiments and analysis”. In section “4Supply chain network optimization problem”, we validate the effectiveness of the CCCA in the practical problem via the capacity allocation problem in the supply chain network. Section “5Conclusion” summarizes the findings of the study and the directions of future research.

Candidates cooperative competition algorithm (CCCA)

Inspiration

High schools are vital institutions shaping societal elites and professionals, significantly contributing to a nation’s development through high-quality education. The entrance examination system varies globally, with Western countries like the United States relying on exams such as the SAT and ACT, where scores play a crucial role in university admissions⁶⁶. European countries, like the UK, use qualification certificates as a primary evaluation standard, considering academic performance and interviews⁶⁷. In Asia, especially East Asia, countries like China, Japan, and Korea share similar entrance examination systems for higher education institutions, relying on final exams and each institution’s selection criteria.

Despite differing admission systems, students undergo systematic learning and are ranked based on academic performance, forming the basis for higher education assessments. The preparatory period involves continuous learning, improvement, and the pursuit of high scores. So we take students as candidates for high-quality education. Candidates aim for top rankings to secure admission to their preferred institutions. The preparation process includes self-study and influence among candidates stages, each impacting exam scores, leading to fluctuations in candidates’ performance over time. Therefore, the test preparation process can be divided into two main stages: the self-study stage and the influence among peers stage. Each stage involves different modes of operation, cooperation, and competition. After a period of study, each candidate’s exam scores in various subjects will change. The relationship between candidates is shown in Fig. 2. In this work, candidates’ behavior is mathematically modeled in order to design CCCA and perform optimization.

Fig. 2

Schematic of candidates.

Algorithm concept introduction

The proposed CCCA belongs to the category of meta-heuristic algorithms and draws inspiration from the preparation process of candidates. The algorithm incorporates real-world concepts. Therefore, we introduce specific concepts within the algorithm based on the candidate cooperative competitive process.

Candidate scores and weighted assignment

A candidate’s total score is the cumulative sum of their scores in different subjects. Various countries and regions employ distinct methods to compute total scores, involving the weighting of each subject’s scores based on factors like the number of candidates and the selection of subjects. For instance, in China, a candidate’s high school entrance exam score was the sum of the scores from all subjects. In South Korea, with the exception of Korean history and English subjects, candidates’ total scores are determined by the standard deviation of all candidates’ test scores. These scores are converted into standard scores, which are then summed to derive the final score.

Within the algorithm, distinct subject scores undergo weighting and assignment in alignment with the optimization objective of the problem. The scores of each subject for candidates serve as the decision variables of the problem, and the set of scores for each candidate forms feasible solutions for the problem. The total score, obtained by calculating this set using the weighted assignment method, represents the objective value of the problem.

Administrative classes

During exam preparation, candidates commonly engage in collaborative learning at schools. The teaching method in schools typically includes administrative class divisions, where all candidates of the same grade are roughly divided into several classes. Rankings are determined for each class after every exam, and although usually, all candidates in the same grade share a unified ranking, the algorithm considers rankings based on administrative classes.

Within the algorithm, administrative classes represent the set of feasible solutions, where each candidate possesses an attribute of a feasible solution, i.e., an individual solution. Rankings are performed after each exam, and the results are utilized to update each candidate’s learning ability.

Learning ability and improvement space

Each candidate possesses inherent characteristics and unique learning abilities. However, due to external factors, a candidate’s learning ability is not fixed. For instance, as a candidate experiences more exams and the exams draw closer, continuous learning and training can unlock a candidate’s potential, leading to an increase in their learning ability. In our algorithm, learning ability is initialized with a random value for each candidate, symbolizing their potential to acquire knowledge from outstanding individuals. This random value falls within a certain range, and learning ability increases with a rise in the number of exams according to a certain function.

Through continuous exams during the preparation process, historical highest scores will emerge within each class. The candidate with the highest score can be regarded as the best candidate in the class. The difference in total scores between a candidate and the best candidate in the class indicates the candidate’s improvement space. The best candidate in the class is considered the global optimum solution, and the total score they represent is the global optimal value.

Self-study and influence among candidates

In the administrative class, candidates engage in both self-study and peer influence processes. During the self-study process, candidates focus on continuous learning to enhance their scores. Each feasible solution represents an iterative result of refining their current solutions based on insights gained from the optimal solutions available. Conversely, the influence among candidates process encompasses both cooperation and competition among candidates. In the cooperative process, outstanding candidates assist average candidates in improving scores across all subjects, effectively updating worse solutions by leveraging information from superior ones to facilitate their evolution. Additionally, outstanding and average candidates also assist each other in certain subjects within their respective groups. However, in the competitive process, outstanding candidates may experience a slight decrease in their scores due to a disrupted and disturbed study process, which serves to perturb their solutions and broaden the search space. For average candidates, an elimination mechanism is implemented to refresh the administrative class (population), introducing several new candidates to ensure the overall quality of the class.

Exams

During the preparation period, there will be exams of varying sizes to help candidates identify their strengths and weaknesses. In algorithms, each exam represents one iteration of the algorithm, and all operations performed during this iteration constitute the learning process for all candidates.

Candidate redistribution

Due to poor performance and a lack of interest in learning, some candidates may not be able to continue their studies, rendering them unable to participate in exams. In such cases, these candidates are removed from their administrative class, and a certain number of candidates from other classes or schools are introduced to fill the gap in the number of candidates in the administrative class.

In the algorithm, this process serves the purpose of maintaining diversity in the solution set. When some solutions are of poor quality and have not been updated for several iterations or when there is no evident improvement in the solution set after multiple iterations, the algorithm may be trapped in a local optima. In such cases, inferior solutions are removed, and new solutions are introduced following certain rules to preserve the diversity of the solution set and break free from local optima.

Correspondence between problem concepts and algorithm concepts

Based on the previous explanations, the correspondence between problem concepts and algorithm concepts is presented in Table 1.

Table 1 Correspondence between problem concepts and algorithm concepts.

Mathematical model and algorithm

Candidates initialization

As with other meta-heuristic algorithms, we utilize randomized generation of the initial population to create the initial candidates. We assume each candidate has n subjects, represented as n-dimensional decision variables. The structure of each candidate is demonstrated in Eq. (1) and generated according to Eq. (2). Here, X denotes a candidate, where ${x_1}$ represents the score of the first subject, it can be abstracted as the value of the first decision variable. ${X_{lb}}$ represents the lower bound on the decision variable, while ${X_{ub}}$ represents the upper bound, and rand generates a random number within the range [0, 1]. The size of the candidate matrix is ${N_{pop}} \times n$, with ${N_{pop}}$ being the population size of the candidates.

$$\begin{aligned} X = ({x_1},{x_2},...,{x_n}) \end{aligned}$$

(1)

$$\begin{aligned} X = {X_{lb}} + ({X_{ub}} - {X_{lb}}) \cdot rand \end{aligned}$$

(2)

Self-study

For each candidate, the exam results in subject scores. After each exam, candidates engage in self-study, utilizing the best exam result as a reference to update their knowledge and prepare for the next exam. The updated formula for each candidate’s subject scores in the next exam is given by Eq. (3),

$$\begin{aligned} {X}_{i}^{iter+1}={{r}_{1}}{\omega _i^{iter}}{{a}_{i}}({{X}_{best}}-X_{i}^{iter})+X_{i}^{iter} \end{aligned}$$

(3)

where iter is the current iteration number, ${X}_{i}^{iter}$ represents the vector of subject scores for candidate i after the iter-th exam, ${{X}_{best}}$ is the global optimum individual, ${{r}_{1}}$ is a random number in the range [0,1], used to adjust the amount of knowledge the candidate i, $\omega _i^{iter}$ is the learning ability of candidate i in iter. Before the first exam, this is randomly defined to represent the candidate’s inherent learning ability, with $\omega _i^{iter}\in [0,b]$. A number of exam increases will increase the candidate’s learning ability according to Eq. (4).

$$\begin{aligned} \omega _i^{iter+1}=1-\omega _i^{iter}{{{e}}^{-\theta \cdot iter}} \end{aligned}$$

(4)

where $\theta$ is the learning ability increase rate control coefficient.

${{a}_{i}}$ represents the improvement climbing space of candidate i. Candidates aim to learn from the best-performing historical candidates. The calculation of ${{a}_{i}}$ is Eq. (5).

$$\begin{aligned} {{a}_{i}}=\left| \frac{{{F}_{global}}-{{F}_{i}}}{{{F}_{global}}-{{F}_{worth}}} \right| \end{aligned}$$

(5)

where ${{F}_{global}}$ is the optimal objective value representing the global best solution. ${{F}_{i}}$ is the objective value for candidate i. ${{F}_{worth}}$ is the worst objective value representing the global worst solution. The range of the ${{a}_{i}}$ is ${{a}_{i}}\in [0,1]$.

Influence among candidates

Apart from self-study, there is also influence among candidates. As classmates, each candidate has both cooperative and competitive relationships. Therefore, the algorithm designs two solution update mechanisms based on candidate relationships: cooperation and competition.

1. Cooperation

(1) One-on-one assistance

During the learning process within the class, there is often one-on-one guidance where outstanding candidates assist average candidates to improve their exam scores. All candidates in the class are divided into two groups, with m as the number of candidates in the class. Set M represents the set of all candidates. The outstanding 50 percent of candidates are the outstanding candidates, represented by the set of $M_1$, and $M_1=\{1,2,...,\frac{m}{2}\}$. The bottom 50 percent of candidates are the average candidates, represented by the set of $M_2$, and $M_2=\{{\frac{m}{2}}+1,\frac{m}{2}+2,...,m\}$. The updating scores of average candidates are Eq. (6).

$$\begin{aligned} X_{i_2}^{n e w}=r_2 \omega _{i_2} a_{i_2}\left( X_{i_1}-X_{i_2}\right) +X_{i_2}, i_1 \in M_1, i_2 \in M_2 \end{aligned}$$

(6)

where ${X}_{i_2}^{new}$ represents the new solution generated for average candidate $i_2$ after assistance from outstanding candidates, and $i_1=i_2-\frac{m}{2}$. ${{r}_{2}}$ is a random number in the range [0,1], used to adjust the knowledge that average candidates learn from outstanding candidates.

(2) Multiple-to-one assistance

After a certain number of exams, targeted assistance is provided to average candidates who have not shown significant improvement or even regressed in their scores. Assuming every k times of exams requires one time of multiple-to-one assistance, and $iterMax\%k=0$, the criteria for selecting candidates who require multiple-to-one assistance is Eq. (7)

$$\begin{aligned} ran{{k}_{i,iter}}-ran{{k}_{i,iter-k}}<S \end{aligned}$$

(7)

where $ran{{k}_{i,iter}}$ represents the rank of candidate i after the iter-th exams. $ran{{k}_{i,iter-k}}$ represents the rank of candidate i after $iter-k$ exams. S is the threshold for determining whether multiple-to-one assistance is needed.

After selecting R outstanding candidates to assist average candidates $i_2$, the solution that results in the best improvement is retained for the candidate who received assistance. For example, for minimizing the objective value, the update equation for the assisted candidate’s subjects is Eq. (8).

$$\begin{aligned} {X}_{i_2,r}={{r}_{3}}{\omega _{i_2}}{{a}_{i_2}}({{X}_{r}}-{{X}_{i_2}})+{{X}_{i_2}} \end{aligned}$$

(8)

where $r\in R$,${X}_{i_2,r}$ represents the new solution generated for the assisted average candidate $i_2$ by outstanding candidate r.

$$\begin{aligned} {X}_{i_2}^{new} = best({X}_{i_2,r}) \end{aligned}$$

(9)

${X}_{i_2}^{new}$ is the best solution in ${X}_{i_2,r}$. ${{r}_{3}}$ is a random number in the range [0,1], used to adjust the knowledge transfer from outstanding candidates to the assisted candidate.

(3) Outstanding candidates cooperative discussion

Outstanding candidates engage in cooperative discussions during their learning process to integrate knowledge, fill gaps, and progress together. In these situations, random J subjects ($J<n$) are selected, and candidates i and $i+1$ ($i \in M_1$ and $i+1 \in M_1$) compete to select the better result based on the objective. We define our objective function as ${F}({{{X}}_{i}})=\sum _{j=1}^n F\left( x_{i, j}\right)$. For example, if the sub-objective function ${F}({{{x}}_{i,j}})$ is an increasing function within the neighborhood $({{{x}}_{i,j}}-\varepsilon ,{{{x}}_{i,j}}+\varepsilon )$, $\varepsilon$ represents the degree of subject score improvement, and its value can be adjusted according to the problem’s requirements, then the update equation for individual subjects is Eq. (10),

$$\begin{aligned} \left\{ \begin{aligned}&{{x}_{i,j}}=\min ({{x}_{i,j}},{{x}_{i+1,j}})\\&{{x}_{i+1,j}}=\min ({{x}_{i,j}},{{x}_{i+1,j}})\\ \end{aligned} \right. \end{aligned}$$

(10)

where, $j\in J$, ${X}_{i}^{iter}=({{x}_{i,1}},{{x}_{i,2}},...{{x}_{i,j}}...,{{x}_{i,n}})$, ${{x}_{i,j}}$ is the score for subject j of candidate i, and there are n subjects, making it an n-dimensional vector. If ${F}({{{x}}_{i,j}})$ is a decreasing function within the neighborhood $({{{x}}_{i,j}}-\varepsilon ,{{{x}}_{i,j}}+\varepsilon )$, the update equation is Eq. (11).

$$\begin{aligned} \left\{ \begin{aligned}&{{x}_{i,j}}=\max ({{x}_{i,j}},{{x}_{i+1,j}})\\&{{x}_{i+1,j}}=\max ({{x}_{i,j}},{{x}_{i+1,j}}) \\ \end{aligned} \right. \end{aligned}$$

(11)

where ${{x}_{i,j}}$ represents the score of candidate i for subject j.

(4) Specialized assistance for average candidates

Outstanding candidates are often preferred as assistants, but they may not excel in all subjects due to differing talents and interests. Some average candidates, while having lower overall scores, may excel in specific subjects and can also be chosen as assistants. Let candidate i be the one who needs assistance, with a rank of i among the average $\frac{m}{2}$ candidates ($i \in M_2$). Randomly select a candidate with a rank of k ($k<i$ and $k \in M$) to assist candidate i for subject j. The equation for updating the subject score of the candidate receiving assistance is Eq. (12).

$$\begin{aligned} {{x}_{i,j}}={{r}_{4}}{{x}_{i,j}}+{{r}_{5}}{{x}_{k,j}}+{\omega _i}{{\varepsilon }_{i}} \end{aligned}$$

(12)

where ${{r}_{4}}$ and ${{r}_{5}}$ are random values, and ${{r}_{4}}+{{r}_{5}}=1$. ${{\varepsilon }_{i}}\in [-0.1,0.1]$ is the degree of subject score improvement and can be adjusted according to the problem’s requirements.

2. Competition

In addition to cooperation, competition among candidates is prevalent during the preparation process. Especially when there is not much difference in the overall performance of candidates, making the competition more intense. In the algorithm, it can be assumed that the feasible solution set has fallen into a local optima, causing individuals to no longer improve. Therefore, this dissertation introduces a competition mechanism to help the algorithm escape local optima. First, candidate similarity is evaluated using the Manhattan formula to determine whether the feasible solution set has fallen into a local optima.

$$\begin{aligned} & a({{X}_{i}})=\frac{1}{F({{X}_{i}})} \end{aligned}$$

(13)

$$\begin{aligned} & \quad A({{X}_{i}})=\frac{1}{\sqrt{\sum \nolimits _{{{i}'}=1}^{m}{\left| a({{X}_{i}})-a({{X}_{{{i}'}+1}}) \right| }}+1} \end{aligned}$$

(14)

$$\begin{aligned} G({{X}_{i}})=\left\{ \begin{aligned}&1,A({{X}_{i}})\ge \sigma \\&0,A({{X}_{i}})<\sigma \\ \end{aligned} \right. \end{aligned}$$

(15)

$$\begin{aligned} & \quad G=\frac{\sum \nolimits _{i=1}^{m}{G({{X}_{i}})}}{m} \end{aligned}$$

(16)

Equation (13) represents the similarity feature value of individual candidates, expressed as the reciprocal of the objective function value. Equation (14) illustrates how the similarity between candidate individuals is calculated. The higher the similarity between two candidates, the smaller the denominator, resulting in a larger similarity value. Equation (15) determines the degree of similarity, with $\sigma$ being a constant for similarity. When $G({{X}_{i}})=1$, it indicates that candidate ${X}_{i}$ in the class has a high degree of similarity to other candidates. Conversely, if the similarity is low, $G({{X}_{i}})=0$. G represents the similarity density of candidates. Given a constant similarity limit $\eta$, if $G<\eta$, it means that the candidates in the class have a low degree of similarity, suggesting that the algorithm has likely fallen into a local optima and requires adjustment. The adjustment methods mainly consist of two parts: the outstanding candidates competition and the elimination.

(1) Outstanding candidates competition

The outstanding candidates competition can be seen as the reverse operation of the outstanding candidates cooperation and discussion. Candidates with adjacent rankings are facing fierce competition. The candidates with higher rankings hope to maintain their positions, while the candidates with lower rankings hope to surpass the candidates immediately ahead. Outstanding candidates refuse to cooperate with each other, leading to a decline. J subjects ($J<n$) are randomly selected, and the difference between candidate i and candidate $i+1$ ($i \in M_1$ and $i+1 \in M_1$) in subject j is obtained:

$$\begin{aligned} \Delta {{x}_{j}}=\left| {{x}_{i,j}}-{{x}_{i+1,j}} \right| ,j\in J \end{aligned}$$

(17)

The candidates with better scores in this subject will experience a decrease in scores after the competition. Their scores in this subject will be reduced within the range of score difference. For example, for the objective of minimizing the target value, if the sub-objective function ${F}({{{x}}_{i,j}})$ is a decreasing function within the neighborhood $({{{x}}_{i,j}}-\varepsilon ,{{{x}}_{i,j}}+\varepsilon )$, the subject of candidate update equation is Eq. (18). ${\omega _i}$ represents the learning ability of candidate i, where rand is a random number in the range [0, 1]. We control the updating level of the candidate’s subject using the expression ${{e}^{-{\omega _i} \cdot rand}}$.

$$\begin{aligned} \max \left\{ {{x}_{i,j}},\left. {{x}_{i+1,j}} \right\} \right. -\Delta {{x}_{j}} {{e}^{-{\omega _i} \cdot rand}},j\in J \end{aligned}$$

(18)

If the sub objective function ${F}({{{x}}_{i,j}})$ is an increasing function within the neighborhood $({{{x}}_{i,j}}-\varepsilon ,{{{x}}_{i,j}}+\varepsilon )$, the individual subject update formula is:

$$\begin{aligned} \min \left\{ {{x}}_{i,j},\left. {{x}_{i+1,j}} \right\} \right. +\Delta {{x}_{j}} {{e}^{-{\omega _i} \cdot rand}},j\in J \end{aligned}$$

(19)

(2) Elimination

For some individuals who rank at the bottom, they may not participate in the final test for various reasons. Consequently, during the process of learning and exams, a certain number of candidates will be eliminated, while new candidates will continuously join the learning. In the algorithm, we select z of the worst feasible solutions from the latter $\frac{m}{2}$ of the candidates, remove them from the solution set, and then randomly generate an equal number of feasible solutions to add to the set, completing the competitive elimination.

Algorithm steps and process

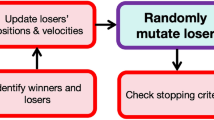
This section describes the CCCA process, and its specific algorithmic flowchart is shown in Fig. 3. The specific steps are as follows:

Fig. 3

Flowchart of CCCA.

Step 1: Construct the objective function, assign values to the parameters involved in the algorithm, generate the initial administrative classes of candidates (initial feasible solution set), and calculate the total score (objective value) for each candidate.

Step 2: Begin the self-study stage, where each feasible solution is updated according to the formula of the self-study stage, calculate the objective value, and update the global optimum value and the best solution.

Step 3: Determine whether the number of iterations satisfies $\operatorname {iterMax}\%k=0$. If true, proceed to Step 4; otherwise, proceed to Step 5.

Step 4: Start the one-on-one assistance mode to update the feasible solution representing the outstanding candidate.

Step 5: Start the multiple-to-one assistance mode to update the feasible solution representing the outstanding candidate.

Step 6: Begin the cooperative discussion for outstanding candidates to update the feasible solution representing the outstanding candidate.

Step 7: Start the special assistance for average candidates to update the feasible solution representing the average candidate, calculate the objective value, and update the global optimum value and the best solution.

Step 8: Calculate the similarity between candidates. If the similarity is greater than $\eta$, implement the competition mechanism; otherwise, proceed to Step 9.

Step 9: Calculate the objective value, update the global optimum value and the best solution. Determine if the algorithm termination conditions are met. If true, proceed to Step 10; if false, update the learning ability and proceed to Step 2.

Step 10: Algorithm termination. Output the optimal value and the best solution found.

The pseudo code of the CCCA algorithm is presented in Algorithm 1.

Algorithm 1

Pseudo-code of CCCA

Computational complexity

The computational complexity of the CCCA algorithm is mainly influenced by three major parts: feasible solution set initialization, the stage of self-study, and the stage of influence among candidates.

The computational complexity associated with initializing the feasible solution set is O(m). Computing the fitness value for each solution in the feasible solution set incurs a complexity of O(mn). During the self-study stage, each solution undergoes an update process, with the complexity of this update process being O(mT). Additionally, the complexity of computing the fitness value for each solution is O(mnT). Sorting the updated feasible solution set has a complexity of $O(m\log m)$.

The stage involving the influence among candidates encompasses two primary mechanisms: cooperation and competition. The cooperation involves one-on-one or multiple-to-one assistance, outstanding candidates cooperative discussion, and specialized assistance for average candidates. Each segment bears a complexity of O(mT), and the complexity of computing the fitness value is O(mnT). The competition includes similarity calculation, outstanding candidates competition, and elimination. The complexity of calculating similarities is $O(m^2nT)$, the complexity of outstanding candidates competition is O(mT), and the complexity of elimination is O(m). The complexity of fitness value calculation is O(mnT), and the complexity of updating the learning ability is O(mT). In summary, the final calculation of the algorithm’s complexity is $O\left( m\left( 2+n+6T+3nT+mnT+\log m\right) \right)$.

Experiments and analysis

This section primarily covers four types of experiments: effectiveness testing of the proposed CCCA algorithm, convergence and box plot validation, and Mann-Whitney U test of CCCA, along with sensitivity analysis experiments for CCCA algorithm parameters. The experimental environment for all experiments includes an Intel(R) Core(TM) i5-8300H CPU @ 2.3GHz, 8GB of RAM, Windows 10 operating system, and MATLAB 2019b software.

Effectiveness testing

To evaluate the effectiveness of the proposed algorithm, 23 optimization functions are selected as test functions based on^22,58. The specific formulas for these functions are provided in Table 2.

Table 2 Test functions.

In Table 2, Dim represents the dimension of the functions, while Range denotes the boundary of the search space. $f_{min}$ indicates the known optimal value of the functions. Functions $F_1(x)$ to $F_6(x)$ are unimodal functions designed to evaluate the algorithm’s local search capabilities. Functions $F_7(x)$ to $F_{13}(x)$ are multimodal functions aimed at assessing the algorithm’s ability to escape local optima and discover global optima. Functions $F_{14}(x)$ to $F_{23}(x)$ are fixed-dimension multimodal test functions, resembling multimodal functions with fixed and low dimensions.

The experimental results are compared with PSO, FA, Crow Search Algorithm (CSA)⁶⁸, HMS, ICA, TLBO, and BSO, which have shown superiority in numerous experiments and applications. The parameters used for comparison algorithms in the experiments are detailed in Table 21 in Appendix A. PSO, FA, and CSA are meta-heuristics inspired by biological behaviors. PSO represents the classical meta-heuristic algorithm, while FA and CSA offer more contemporary approaches. On the other hand, HMS, ICA, TLBO, and BSO are meta-heuristic algorithms influenced by human social behavior. Among them, HMS stands out as a better-performing algorithm developed in recent years, while ICA, TLBO, and BSO are more familiar and widely utilized meta-heuristic algorithms, classically inspired by human social behavior.

Among them, TLBO is another meta-heuristic algorithm inspired by the learning process of students in school. However, it differs significantly from the algorithm proposed in our research. TLBO emphasizes the teaching-learning process, comprising only two phases: the teacher phase and the learning phase. In the teacher phase, the teacher is considered the optimal solution and drives the overall updating process. The learning phase involves only students with better fitness guiding those with poorer fitness through the updating process. From the perspective of this school-based learning behavior, the overall algorithm simplifies but incompletely represents the teaching-learning process. In terms of algorithm design, it lacks certain measures to escape local optima and enhance algorithm performance. In contrast, CCCA proposed in our research is grounded in the entire process of students’ exam preparation. Behaviorally, it introduces a ranking and learning ability parameter, with each individual possessing a distinct learning capacity. This aligns closely with the realistic characteristics of candidates, and the mutual influence considered among students better reflects actual scenarios. This influence encompasses the assistance of outstanding candidates to average candidates. In terms of algorithm design, we optimize the direction and speed of updating each solution through the ranking mechanism and learning ability. We try for the first time to use the updating between decision variables and the gradient ascent idea to update the solution vectors with a very small probability to promote jumping out of the local optima. We also introduce the elimination mechanism. All of these aspects fundamentally distinguish CCCA from TLBO.

Based on the experience with parameter settings in previous meta-heuristic algorithms^69,70,71, the relevant parameters of the proposed CCCA algorithm are shown in Table 3.

Table 3 Parameter settings.

To ensure the accuracy and rigor of the experiments, the same parameters related to each algorithm utilized for comparison are kept consistent: the common parameters include a maximum iteration number ${iterMax = 1000}$ and a population size of ${N = 40}$. To avoid randomness, 10 experiments were tested for each algorithm. The best value (Best) Eq. (20), average value (Ave), standard deviation (Std), the least value (Least), and the average running time (Time) are computed and compared.

$$\begin{aligned}&\min {{{F}}_{i}}(x)=\min \left\{ {{F}_{i}}{{(x)}_{1}},{{F}_{i}}{{(x)}_{2}},...,{{F}_{i}}{{(x)}_{u}} \right\} ,u=20 \end{aligned}$$

(20)

${{{F}}_{i}}(x)$ represents the function value of the i-th function, ${{{F}}_{i}}{{(x)}_{u}}$ represents the function value of the i-th function for the u-th experiment, $\overline{{{{F}}_{i}}(x)}$ is the average function value of the i-th function over q experiments, and Std is the standard deviation of the function values of the i-th function over q experiments.

Results of experiments on functions

Results of experiments on functions are shown in Tables 4 and 5. For unimodal functions, CCCA performs well on F1(x), F2(x), F5(x), and F6(x). Although HMS performs better on F3(x) and F4(x), CCCA solves much faster than HMS, so CCCA will also have advantages in terms of running time. For multimodal functions, CCCA outperforms other algorithms in searching for optimality on ${F_7}(x)$, ${F_8}(x)$, and ${F_{13}}(x)$, whereas HMS performs better in ${F_9}(x)$ to ${F_{12}}(x)$. However, the running time of CCCA is much shorter than that of HMS, and the results of CCCA are better than other algorithms. It can be shown that CCCA and HMS have their advantages in solving multimodal functions. For fixed-dimension multimodal functions, the results indicate that CCCA finds optimal solutions for ${F_{14}}(x)$ and ${F_{16}}(x)$ to ${F_{23}}(x)$, with desirable stability in ${F_{14}}(x)$, ${F_{16}}(x)$, ${F_{17}}(x)$, ${F_{18}}(x)$, and ${F_{19}}(x)$. In contrast, the number of functions for which PSO, FA, CSA, HMS, ICA, TLBO, and BSO can find optimal solutions are 7, 3, 5, 2, 5, 2, and 4, respectively, while CCCA can find 9 optimal solutions, resulting in CCCA having the best search ability.

Table 4 The statistical results of unimodal and multimodal test functions.

Table 5 The statistical results of fixed-dimension multimodal test functions.

In order to visualize how CCCA compares to each of the compared algorithms, we examine the statistics obtained by solving each algorithm individually in Tables 6 and 7. The comparison on ${{{F}}_{1}}(x)$ to ${{{F}}_{6}}(x)$ is shown in Table 6. We utilize “$\times$” to denote the superior statistic of CCCA and “$\checkmark$” to denote the inferior statistic of CCCA when compared to other algorithms. For instance, during the comparison between CCCA and PSO, if CCCA’s “Best” statistic is better than PSO’s, the corresponding cell for PSO’s “Best” statistic is marked with “$\times$”. Conversely, if CCCA’s “Time (s)” statistic is worse than PSO’s, the corresponding cell for PSO’s “Time (s)” statistic is marked with “$\checkmark$”. If the statistics of the two algorithms are the same, the cell is left blank. The overall performance of the algorithm can be assessed by comparing the number of “$\checkmark$” and “$\times$”. According to Table 6, we assess the superiority of CCCA by comparing it to each algorithm individually. For all shown statistics values, the ratio of advantages and disadvantages of CCCA compared to PSO, FA, CSA, HMS, ICA, TLBO, and BSO on unimodal functions are 20:10, 30:0, 22:7, 25:5, 30:0, 24:6, and 30:0. From the comparison results, it can be found that although CCCA lags behind PSO, CSA, and TLBO in terms of solution time, it outperforms them significantly in terms of optimization ability and solution stability. Therefore, CCCA holds an overall advantage in solving unimodal functions.

Table 6 The comparisons between CCCA and other algorithms on unimodal and multimodal test functions.

Table 7 The comparisons between CCCA and other algorithms on fixed-dimension multimodal test functions.

According to Table 6, for multimodal functions, the ratio of advantages and disadvantages of CCCA compared to PSO, FA, CSA, HMS, ICA, TLBO, and BSO are 15:20, 33:2, 24:11, 18:17, 35:0, 28:7, and 33:1. A comprehensive analysis of the CCCA results from the statistics reveals that PSO slightly outperforms CCCA. However, based on the “Best” statistic, CCCA surpasses PSO in ${F_7}(x)$, ${F_8}(x)$, ${F_9}(x)$, and ${F_{11}}(x)$, meanwhile CCCA outperforms the other compared algorithms in multimodal functions, indicating a superiority of CCCA.

Furthermore, we present the comparison of fixed-dimension multimodal functions in Table 7. For all shown statistics values, the ratio of advantages and disadvantages of the CCCA compared to PSO, FA, CSA, HMS, ICA, TLBO, and BSO on fixed-dimension multimodal functions are 17:10, 47:0, 21:10, 47:1, 35:1, 38:10, and 44:1. With the clear advantages of statistical comparisons, CCCA is superior in these functions.

Convergence and box plot validating

Since the final results obtained by the different algorithms vary greatly in magnitude, to illustrate the complete convergence trend of each algorithm in the convergence graph, we take the logarithm of the positive value $F_i(x)$ obtained by solving each algorithm. For negative $F_i(x)$ values, the original values are retained to plot the convergence curves. Since 10 experiments are conducted for each algorithm, the curves depicted are the average convergence curves.

According to Fig. 4, CCCA demonstrates a high convergence rate in most functions. Across various functions, CCCA displays swift initiation of convergence and rapid convergence, notably observed in unimodal function $F_{1}(x)$, multimodal function $F_{8}(x)$, and fixed-dimension multimodal function $F_{20}(x)$. CCCA also presents a notable advantage in escaping local optima. For instance, in functions $F_{1}(x)$, $F_{5}(x)$, and $F_{11}(x)$, the convergence curves of other algorithms are straight line at later stages without finding an optimal value, indicative of falling into local optima. In contrast, CCCA’s convergence curves consistently trend downward, continuously updating toward the optimal solution. This suggests that CCCA either avoids local optima entirely or effectively jumps out of them to pursue the optimal solution further. Thus, it can be inferred that the mechanism designed in CCCA to evade local optima is effective.

Fig. 4

Convergence curves on test functions.

Figure 5 depicts the box plot comparing CCCA with other algorithms on test functions. It is evident from Fig.  5 that CCCA’s experimental results exhibit significant stability across the majority of functions. These findings indicate CCCA’s superiority as an optimizer for most of the test functions.

Fig. 5

Box plot obtained from CCCA and other algorithms on test functions.

Mann–Whitney U test of CCCA

In this section, we examine the notable disparities between the results of CCCA and those of other algorithms. A Mann-Whitney U test with a 5% significance level is conducted, and the corresponding p-values are presented in Table 8. This test helps determine whether the results obtained from CCCA differ significantly from those of other algorithms in a statistical sense. The p-value serves as an indicator of statistical significance for each algorithm. If the p-value associated with a particular algorithm is less than 0.05, it indicates statistical significance for that algorithm. According to the test results, CCCA demonstrates a significant advantage over other algorithms in the vast majority of cases, with CCCA’s experimental results being over 90% effective. This assertion is further corroborated by the p-values presented in Table 8. Hence, it can be concluded that the proposed CCCA exhibits statistically significant differences compared to other competing algorithms.

Table 8 p-values of the Mann-Whitney U test with 5% significance for test functions (p-values $\ge$ 0.05 are shown in boldface).

Further validation for CCCA

To further validate the performance of CCCA, we compare it with the novel meta-heuristic algorithms influenced by human social behavior, which have been validated on the CEC 2022 and demonstrate excellent results, such as Escape Algorithm (ESC)⁷², Offensive Defensive Optimization (ODO)⁷³, and Snooker-Based Optimization Algorithm (SBOA)⁷⁴. The parameter settings for the compared algorithms are the same as in the corresponding literature. The results are shown in Table 9. CCCA has been shown to obtain the best results on 18 functions compared to other algorithms, and most of the results on Ave and Std are outperforming, proving the superiority of CCCA.

Table 9 Results for further validation.

Algorithm parameter sensitivity analysis

To assess the influence of various parameters on the experimental outcomes, we conducted a sensitivity analysis on selected test functions. Given the small dimensionality of fixed-dimension multimodal functions and the attainment of optimal solutions with the current parameters, we focused our experiments on unimodal and multimodal functions. Specifically, we chose ${{{F}}_{1}}(x)$ to ${{{F}}_{11}}(x)$, which have a significant impact on experiments and explored different numerical values for each parameter setting using the controlled variable method in this section. For each set of parameter values, 20 experiments were performed, and the best values were compared. The specific parameters subjected to sensitivity analysis include the maximum number of iterations iterMax (Table 10), the multi-to-one mode assistance interval k (Table 11), the ranking setback threshold S (Table 12), the number of outstanding candidates selected in multi-to-one assistance R (Table 13), the similarity constant $\sigma$ (Table 14), the similarity density judgment $\eta$ (Table 15), the learning ability update parameter $\theta$ (Table 16), the number of candidates for streamlining z (Table 17), and the learning ability range $\omega$ (Table 18).

Table 10 Sensitivity analysis of maximum iteration.

Table 11 Sensitivity analysis of the multiple-to-one assistance interval.

Table 12 Sensitivity analysis of the ranking setback threshold.

Table 13 Sensitivity analysis of the number of outstanding candidates selected in multiple-to-one assistance.

Table 14 Sensitivity analysis of the similarity constant.

Table 15 Sensitivity analysis of the similarity density.

Table 16 Sensitivity analysis of the learning ability update parameter.

Table 17 Sensitivity analysis of the number of candidates for diversion.

Table 18 Sensitivity analysis of the learning ability range.

To visually demonstrate the impact of different parameter settings on each test function, Fig. 6 provides the trends of the best values of each test function under various parameter values.

Fig. 6

Trends of the best values of each test function.

Due to the limitations of the coordinate range, the trends of ${F}_3(x)$, ${F}_4(x)$, ${F}_{11}(x)$ in Fig. 6a , ${F}_{11}(x)$ in Fig. 6f , and ${F}_{11}(x)$ in Fig. 6g are not fully displayed. However, this does not affect the overall trend analysis and the analysis of the algorithm.

From the experimental results and trend charts, it can be seen that the best values of various test functions (${F}_{i}(x),i=1,2,...,11$) under different parameters $par{{a}_{j}}, par{{a}_{j}}\in \left\{ iterMax, k, S, R, \sigma , \eta , \theta , z, \omega \right\}$ can be categorized as follows: (1) Increasing trend, the best value of ${F}_{i}(x)$ increases as $par{{a}_{j}}$ increases, within the given range. Smaller parameter values result in better optimization performance for ${F}_{i}(x)$. For example, the $\sigma$ parameter of ${F}_{11}(x)$ (Fig. 6e ). (2) Decreasing trend, the best value of ${F}_{i}(x)$ decreases as $par{{a}_{j}}$ increases, within the given range. Larger parameter values result in better optimization performance for ${F}_{i}(x)$. For example, the iterMax parameter of all ${F}_i(x)$ (Fig. 6a ). (3) First increasing, then decreasing, within the given parameter range, the best optimization performance for ${F}_{i}(x)$ is achieved when the parameter value is at one end of the interval. For example, the R parameter of ${F}_{3}(x)$ (Fig. 6d ). (4) First decreasing, then increasing, within the given parameter range, the best optimization performance for ${F}_{i}(x)$ is achieved when the parameter value is closer to the middle. For example, the R parameter of ${F}_{7}(x)$ (Fig. 6d ). (5) Fluctuating within a certain range, the parameter value in the given interval has little impact on the algorithm’s optimization capability for ${F}_{i}(x)$, and the fluctuations are likely due to the randomness in the optimization process. For example, the S parameter of ${F}_{6}(x)$ (Fig. 6c ).

Therefore, for different functions or problems, it is necessary to determine the most suitable algorithm parameter values through experiments in order to improve the algorithm’s optimization capability for that function.

Supply chain network optimization problem

To validate the feasibility and effectiveness of the CCCA algorithm proposed in this paper for solving supply chain network optimization problems, this section applies CCCA to solve the capacity allocation problem in the supply chain network. The results are compared with those obtained by PSO, FA, CSA, HMS, ICA, TLBO, and BSO. The algorithm parameters involved in the experiment are as shown in Table 3.

Problem description and mathematical model formulation

Consider a large beverage supplier, company X, which offers an integrated business for the production and distribution of various products. The company has its own production facilities and distribution centers. The problem the company is currently facing is as follows: It has two production factories that need to send 10 different products to five distribution centers. Each distribution center has varying demands for each product, and the transportation costs for sending products from different factories to different distribution centers are also different. The objective is to determine the allocation of products that minimize the total transportation cost for the company.

The set of existing factories is denoted as ${I} = \left\{ 1,2,\ldots ,n \right\}$, the set of distribution centers as $J = \left\{ 1,2,\ldots ,m \right\}$, and the set of product types as $K = \left\{ 1,2,\ldots ,q \right\}$. Other model symbols and variable definitions are presented in Table 19.

Table 19 Model symbols and variable definitions.

Based on the problem description, a mathematical model is formulated as follows:

$$\begin{aligned} & \min \text { Z=}\sum \limits _{i=1}^{n}{\sum \limits _{j=1}^{m}{\sum \limits _{k=1}^{q}{{{c}_{ij}}{{y}_{ijk}}}}} \end{aligned}$$

(21)

$$\begin{aligned} & \quad \sum \limits _{i=1}^{n}{{{y}_{ijk}}}={{d}_{jk}},\forall j\in J,\forall k\in K \end{aligned}$$

(22)

$$\begin{aligned} & \quad {{p}_{ilb}}\le \sum \limits _{j=1}^{m}{\sum \limits _{k=1}^{q}{{{y}_{ijk}}}}\le {{p}_{iub}},\forall i\in I \end{aligned}$$

(23)

Equation (21) represents the objective function, which minimizes the total transportation cost. Equation (22) ensures that the total quantity of product k shipped from factory i to distribution center j meets the demand for product k at distribution center j. Equation (23) enforces that the number of products shipped by factory i must satisfy the upper and lower bounds on daily shipments from the factory.

Solution utilizing CCCA and result analysis

In this section, we apply the proposed CCCA algorithm to address the described problem. We utilize a subset of the available dataset for our experiments, including demand for various products by each distribution center, unit transportation cost from each factory to each distribution center, the upper and lower limits for shipment quantities from each factory, as shown in Tables 22, 23, and 24 in Appendix B.

Where “DC” represents Distribution Center, and “DC1” represents Distribution Center 1; “P” represents Product, and “P1” represents Product 1. The optimal allocation plan achieved by CCCA for each factory to each distribution center across various products is shown in Tables 25 and 26 in Appendix B.

Furthermore, the results obtained by CCCA are compared against those of PSO, FA, CSA, HMS, ICA, TLBO, and BSO, with each algorithm being tested 10 times. The results of the solutions obtained by different algorithms are presented in Table 20.

Table 20 Comparison of results obtained by different algorithms.

From the results in Table 20, it can apparently find that the CCCA algorithm proposed in this paper outperforms other algorithms, thus demonstrating its superiority. Analyzing the average values and standard deviations of the results, ICA exhibits the best average value, but the optimal solution it finds is inferior to that of CCCA. Notably, the standard deviation of CSA is the lowest, indicating greater stability. However, CSA’s optimization-seeking ability is inferior to that of CCCA. In practice, the ability to search for the optimal value and computational efficiency are often more crucial. Even in comparison, the improvement of CCCA algorithm on cost is not significant in this case, a small percentage improvement can result in significant cost savings for enterprises. Overall, when solving practical problems, CCCA outperforms PSO, CSA, TLBO, and BSO. Therefore, from a comprehensive perspective, CCCA holds the advantage.

Ethical approval and informed consent

The authors declare that no experiments involving human participants or animals were performed in the course of this study.

Conclusion

Motivated by the unique human social behavior observed during preparation for higher education entrance exams, this paper introduces a novel meta-heuristic algorithm named the Cooperative Competition Competitive Algorithm (CCCA). Inspired by cooperative and competitive interactions among candidates, the algorithm integrates various behaviors such as self-study, peer assistance, group discussions among outstanding candidates, and targeted support for average candidates. These behaviors, representing both cooperation and competition, are formalized into mathematical components within the algorithm’s intelligent search framework.

As a result, our study contributes to the enrichment of the theoretical framework of meta-heuristic algorithms by designing an algorithm rooted in the specific dynamics of exam preparation behavior. This approach not only expands the theoretical understanding but also offers a promising avenue for addressing practical problem-solving challenges.

The paper conducted performance tests of CCCA using 23 classic test functions and compared the results with those of PSO, FA, CSA, HMS, ICA, TLBO, and BSO. The findings indicated that CCCA consistently outperformed the other algorithms, yielding superior solutions across all tested functions. Specifically, CCCA demonstrated enhanced local search capabilities, effectively navigating away from local optima to identify global optima. Moreover, CCCA exhibited faster convergence rates and greater resilience in escaping local optima compared to its counterparts. Box plots depicted CCCA’s satisfactory stability. Given the involvement of parameter settings in CCCA, a sensitivity analysis was performed to assess the impact of these parameters on algorithm performance across various test functions. Notably, the Mann-Whitney U test revealed CCCA’s significant performance superiority in over 90% of cases.

Finally, the CCCA algorithm was applied to solve the capacity allocation problem in the supply chain network, and the results were compared with PSO, FA, CSA, HMS, ICA, TLBO, and BSO, demonstrating the feasibility and effectiveness of CCCA in practical problem-solving. We also compared CCCA with recently developed human-inspired algorithms and obtained similarly competitive results.

However, the CCCA algorithm is currently limited to solving continuous problems. Future efforts will aim to discretize the algorithm, making it applicable to discrete problems as well. Moreover, as shown in the results, the ability to solve multimodal problems needs to be strengthened, and the optimal solutions haven’t been obtained for some functions. We will develop some operators with stronger search ability to improve the solving of multimodal problems. Additionally, the algorithm presently addresses single-objective problems only. In future research, we intend to integrate specific problems and extend them to multi-objective problems. Furthermore, we will focus on improving and optimizing the algorithm further. This includes enhancing parameters and algorithm flow, as well as improving the algorithm’s optimization ability and runtime. We also make an effort to give the interpretability of the algorithm in terms of mathematical theory. Additionally, we will explore using the algorithm to solve problems in other domains such as electricity price optimization and robot control.