An efficient multiscale simulation framework integrating dynamic heterogeneity for accurate waterflooding prediction

Abstract

Waterflooding is crucial for China’s oil and gas industry, but it induces dynamic heterogeneity in reservoir properties, which commercial simulators fail to model accurately. To address this, we propose a multi-scale simulation method incorporating time-varying absolute permeability (k) and relative permeability (k_r) driven by surface flux. An improved multi-scale finite volume (IMsFV) method solves pressure equations on multi-scale grids, enhancing computational efficiency. SPE10 benchmark validation shows 95.07% reduction in total simulation time and 98.19% in linear solver time versus the fully implicit method, with errors < 5%. Unlike commercial simulators neglecting dynamic heterogeneity, this approach captures opposing mechanisms: dynamic k exacerbates water channeling, reducing recovery, while dynamic k_r enhances fluid mobility and reduces residual oil saturation. Crucially, dynamic k_r’s positive effect dominates during high water-cut stages, ultimately improving recovery. Sensitivity analysis confirms: (1) Dynamic heterogeneity primarily benefits mid-high water-cut stages, reducing water cut and increasing oil production; (2) At 99% water cut, it enhances recovery by 28.88–32.87% across permeabilities (400–2000 md), with greater gains in higher-permeability reservoirs; (3) Under increasing injection rates (50 → 200 m³/day), recovery gains amplify from 18.07 to 45.49%. This approach provides an efficient, accurate tool for predicting remaining oil in high-water-cut reservoirs.

Introduction

In China, waterflooded oil fields constitute approximately 70% of both reserves and production, remaining the predominant development targets¹. However, many of these fields have entered the high-water-cut stage, exhibiting high natural decline rates. Despite substantial cumulative production, the remaining oil saturation still exceeds residual oil saturation, with nearly two-thirds of the original oil in place (OOIP) remaining unrecovered. Consequently, accurately predicting the quantity and distribution of remaining oil is crucial for enhancing recovery efficiency during the late development phase².Numerical simulation represents the most effective technique for characterizing the remaining oil distribution. Yet, during the high-water-cut stage, conventional methods face significant challenges in achieving precise modeling due to computational limitations and methodological constraints. These challenges stem primarily from two factors: (1) Significant reservoir heterogeneity, compounded by dynamic alterations in properties (e.g., permeability) induced by prolonged water injection, leads to increasingly complex flow fields; the continuous evolution of reservoir properties and fluid flow further complicates accurate simulation as development progresses. (2) The highly dispersed nature of remaining oil and complex flow regimes during late-stage waterflooding necessitates fine grid discretization for accurate simulation, imposing substantial demands on computational resources and time. Conventional simulation approaches struggle to address these challenges effectively, highlighting the urgent need for efficient techniques capable of capturing dynamic parameter variations.

Reservoir heterogeneity is paramount for understanding and improving oil recovery, particularly in late development. Prolonged water injection induces dynamic heterogeneity^3,4, characterized by time-varying permeability and flow capacity, which significantly impacts production performance and development efficiency^5,6. While reservoir heterogeneity research originated in the 1970s–1980s and has matured theoretically and technologically, existing studies predominantly focus on static spatial variations of reservoir parameters^7,8,9, By definition, however, heterogeneity inherently encompasses spatiotemporal variations¹⁰. Its study, therefore, necessitates simultaneous consideration of both the spatial distribution and temporal evolution of reservoir parameters. Furthermore, researchers have proposed flow-based heterogeneity metrics (e.g., Lorenz coefficient, flow capacity, sweep efficiency) evaluated over the entire production cycle^11,12. Fundamentally, these assessment indices rely on statistical analysis of post-simulation or flow diagnostic data¹³.

Conventional numerical simulation commonly employs variations in macroscopic parameters like permeability, porosity, and k_r curves to represent heterogeneous changes in reservoir properties. Traditional approaches account for permeability and porosity heterogeneity solely in the spatial dimension via grid cell assignments. Additionally, k_r curves are treated as static functions dependent only on water saturation. Within the classic black-oil model, k is assumed constant, and k_r is determined using initial curves. However, extensive laboratory experiments, pore-scale simulations, and seepage mechanics studies have consistently demonstrated^14,15. That permeability and oil–water k_r undergo dynamic changes during waterflooding, driven by factors including alterations in pore microstructure, fluid–fluid interactions, and displacement conditions. Crucially, the significant influence of flow velocity on k_r cannot be neglected. Therefore, conventional methods for setting k_r curves fail to capture the dynamic flow characteristics of reservoirs adequately.

Traditional simulators generally neglect such dynamic changes, leading to inaccurate history matching in late development stages. Mainstream commercial simulators (e.g., PetrelRE, Intersect, CMG, tNavigator) typically treat reservoir properties as constant, overlooking the temporal variability of key parameters like k and k_r. k_r is modeled solely as a function of water saturation, ignoring dynamic changes induced by factors such as flow velocity¹⁶. Some methods (e.g., tNavigator’s waterflooding multiplier representing reservoir scouring intensity) attempt to simulate time-variant parameters (e.g., permeability, transmissibility, k_r curves) by recalculating properties and adjusting grid conductivities after each timestep. However, such approaches, which externalize physical mechanisms and rely on multipliers to represent temporal variations, yield results sensitive to the grid discretization and often suffer from model instability and convergence issues^16,17.Scholars have developed diverse flux-based indices to quantify water-scouring effects during reservoir waterflooding—including Xu et al.’s injected-water-to-pore-volume ratio¹⁸, Jiang et al.’s surface flux¹⁹, Sun et al.’s pore cross-sectional area flux²⁰, Lin et al.’s effective displacement flux²¹, Zhou et al.’s effective water flux²² , and Wang et al.’s ACE-algorithm-derived k_r endpoint model²³—and subsequently embedded these metrics into numerical simulators through surface-flux-coupled property evolution frameworks¹⁹, pore-flux-integrated black oil models²⁰, core-to-field conversion systems with dynamic k_r²⁴, displacement-flux-based mechanistic models²¹, cumulative-flux formulations, and effective-water-flux-enabled time-variation simulators, with Xu et al²⁵. and Wang et al²³. pioneering solver-enhanced implementations: Xu’s mimetic finite difference (MFD) discretization²⁵ for permeability-degradation models and Wang’s MFD-based dual-dynamic coupling integrating competing k-k_r effects²³. However, critical limitations persist: widely adopted metrics like flushing multiples exhibit pronounced grid-size sensitivity while advanced algorithms (e.g., surface flux coupling) remain excluded from commercial platforms, and external code modifications suffer from narrow applicability, poor interactivity, and computational inefficiency. Consequently, achieving stable, accurate predictions of waterflood-induced reservoir alterations necessitates next-generation simulators featuring intrinsic integration of dynamic parameter physics with enhanced numerical solvers for grid-independent solutions.

Incorporating dynamic heterogeneity substantially increases simulation complexity²⁶, particularly when fine grid discretization is required to resolve these variations^27,28. Practical reservoir simulation faces a dilemma: overly coarse grids fail to represent dynamic changes accurately, while finer discretization leads to exponentially growing computational loads, often causing convergence difficulties and reduced efficiency. Consequently, even advanced simulators achieving higher accuracy often compromise computational efficiency. Moreover, although recent studies incorporate parameter time-dependency to some extent, they predominantly rely on conventional fully implicit or semi-implicit solvers, limiting solution efficiency and often struggling with convergence.

krThis study proposes a novel multiscale simulation approach incorporating dynamic heterogeneity, defined by the spatiotemporal variations in reservoir properties and fluid flow capacity. By integrating time-varying k and k_r, the method enhances simulation efficiency and accuracy. A multiscale grid system and the Improved Multiscale Finite Volume (IMsFV) method are employed to solve the pressure equation, effectively reducing computational errors and accelerating simulations. Results demonstrate that the proposed method significantly improves computational efficiency without sacrificing accuracy, providing a robust tool for predicting remaining oil in high-water-cut reservoirs. This approach not only addresses dynamic heterogeneity but also offers an efficient solution for waterflooding simulation under complex reservoir conditions.

Methods

This study presents a multi-scale reservoir simulation method that incorporates the dynamic heterogeneity of waterflooded oil reservoirs. The research is based on the three-dimensional two-phase numerical simulation model of the MATLAB Reservoir Simulation Toolbox (MRST 2022b)²⁹. Permeability and k_r curves are used to quantitatively characterize reservoir dynamic heterogeneity influenced by changes in surface flux, and the oil–water two-phase black oil model is subsequently modified. The model is then decoupled into pressure and transport equations using a sequential solution approach. The pressure equation is solved iteratively using the IMsFV method with prolongation and restriction operators, while the transport equations are solved through flux reconstruction. The technical approach and methodology are illustrated in Fig. 1.

Fig. 1

Flow chart of the technology roadmap.

Numerical simulation incorporating the dynamic heterogeneity

For immiscible two-phase flow (oil and water) in heterogeneous porous media, and assuming incompressible fluids and rocks, the conservation equations can be written as follows:

$$\frac{{\partial (\phi b_{\alpha } s_{\alpha } )}}{\partial t} = - \nabla \cdot (b_{\alpha } \vec{\nu }_{\alpha } ) + b_{\alpha } q_{\alpha }$$

(1)

where, ϕ is the porosity of the porous medium, $s_{\alpha }$, $b_{\alpha }$ is the saturation and the inverse formation value factor of phase $\alpha$, $q_{w}$ is the injection or production rate per unit volume, respectively.

The phase velocities $\vec{\nu }_{\alpha }$ are described by Darcy’s law:

$$\vec{\nu }_{\alpha } = - \frac{{k_{r\alpha } k}}{{\mu_{\alpha } }}(\nabla p_{\alpha } - \rho_{\alpha } g\nabla z)$$

(2)

where $\mu_{\alpha }$, $p_{\alpha }$, $\rho_{\alpha }$,is the viscosity, the pressure, the density of phase $\alpha$, $g$ is the gravity acceleration, $z$ is the vertical depth, respectively.

The variations in permeability and k are primarily governed by the scouring intensity of injected water. To address the grid dependency associated with water injection multiples, this study employs the surface flux (F) proposed by Jiang et al.¹⁹ for characterizing dynamic heterogeneity. Surface flux (F) is defined as the cumulative volume of the water phase passing through a unit area, expressed as:

$$F = \frac{Q}{S}$$

(3)

In the formula, F represents surface flux, Q is the total volume of water that has passed through the core, and S is the cross-sectional area of the core.

In flow field characterization, this parameter quantifies the cumulative effect of continuous scouring and erosion by the water phase (or oil phase) on the rock, providing a superior representation of cumulative scouring intensity. Zhang et al.³⁰ demonstrated that grid size significantly impacts the calculated displacement multiple value but has minimal impact on the magnitude of the surface flux. Hence, surface flux was selected as the primary parameter for characterizing the reservoir flow field.

For any three-dimensional spatial grid, fluid flow occurs in the x-, y-, and z- directions, with fluid influx or efflux taking place on all faces.

$$F_{x} = \frac{{\left| {Q_{x} } \right|}}{{D_{y} D_{z} }},F_{y} = \frac{{\left| {Q_{y} } \right|}}{{D_{x} D_{z} }},F_{z} = \frac{{\left| {Q_{z} } \right|}}{{D_{x} D_{y} }}$$

(4)

The total surface flux through a grid is equal to the sum of the surface fluxes of water flowing out in the x-, y-, and z- directions.

$$F_{{\text{t}}} = \frac{{\left| {Q_{x} } \right|}}{{D_{y} D_{z} }} + \frac{{\left| {Q_{y} } \right|}}{{D_{x} D_{z} }} + \frac{{\left| {Q_{z} } \right|}}{{D_{x} D_{y} }}$$

(5)

In the formula, $Q_{x}$, $Q_{y}$, and $Q_{z}$ represent the cumulative volume of water flowing out in the three directions, $D_{x}$, $D_{y}$, and $D_{z}$ represent the grid step sizes in the three directions.

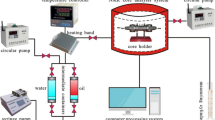
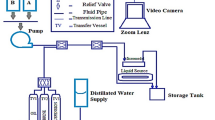
This study utilizes the variations of k and k_r curves with surface flux to quantitatively characterize reservoir dynamic heterogeneity. To quantify permeability evolution, waterflooding scouring experiments were conducted on medium–high permeability core samples, yielding the relationship between permeability variation and surface flux (see Fig. 2). The results demonstrate that core permeability increases progressively with rising surface flux, albeit at a decelerating rate. This trend aligns well with extensive core data and experimental findings reported by previous researchers^4,19,24: In high-permeability reservoirs subjected to long-term waterflooding scouring, formation fines and clay minerals are partially produced with fluids, leading to increased permeability; during the late stages, the quantity of readily detachable fines diminishes, pore structures stabilize, and permeability changes gradually moderate. Conversely, in medium–low permeability reservoirs, deeper waterflooding development tends to cause formation fines to block small pore throats, resulting in decreased permeability. Liu et al.³¹ through statistical analysis of permeability change data from numerous high-rate waterflooding experiments on sandstone cores, established an approximate permeability threshold of 300 mD (millidarcies) delineating the boundary between permeability increase and decrease with cumulative water throughput. The resultant trend reveals the relationship:

$$\Psi_{k} = 0.627\ln F + 1.0593$$

(6)

Fig. 2

Permeability versus surface flux relationship.

Demonstrating enhanced permeability with increasing face flux, validating the method’s physical consistency. Where $\Psi_{k}$ denotes the permeability change factor.

To numerically implement the permeability evolution model based on the correlation between effective displacement flux (F) and permeability multipliers, after calculating saturation and F values at every timestep, the grid transmissibility is recomputed using:

$$T = f(F,K_{base} )$$

(7)

where $K_{base}$ denotes initial permeability.

Then the updated transmissibility values propagate to subsequent timesteps, enabling continuous parameter evolution. The black-oil model is fundamentally enhanced by replacing static permeability with a flux-dependent function:

$$K(t) = K_{0} \cdot \Psi_{k}$$

(8)

where $K_{0}$ and $K(t)$ represent the permeability of different times.

Beyond permeability changes, water injection scouring also induces variations in the k_r of oil and water phases. Following the experimental procedures established by Wang et al.¹⁶, and Fu et al.³², the relationship between k_r curves and surface flux was measured for medium–high permeability reservoir core samples (Fig. 3). The results reveal that with increasing surface flux, irreducible water saturation increases, residual oil saturation decreases, and the water phase permeability at residual oil saturation decreases.

Fig. 3

K_r Curves versus surface flux.

Within the numerical simulations, based on experimentally measured k_r curves and constrained by surface flux (F), the corresponding grid block automatically invokes different k_r curves when the surface flux reaches specific values³³. Specifically, for F ≤ 1.5, the k_r curve corresponding to F = 1.5 is employed, for F ≥ 7.5, the k_r curve corresponding to F = 7.5 is employed, for 1.5 ≤ F ≤ 7.5, a new k_r curve is determined at each saturation point using a weighted average of the two bounding curves (F = 1.5 and F = 7.5).

The modified Darcy’s law incorporating flux-dependent k becomes:

$$\vec{\nu }_{\alpha } (F) = - \frac{{k_{r\alpha } (F)k(F)}}{{\mu_{\alpha } }}(\nabla p_{\alpha } - \rho_{\alpha } g\nabla z)$$

(9)

The auxiliary equations, initial conditions, internal boundary conditions, and external boundary conditions of the new model are the same as those of the traditional black oil model.

Compared to the conventional black-oil model, the novel simulation equations compute, for each timestep and based on the pressure and saturation fields within each grid cell, the water phase flow rate and directional surface flux in every direction along with the total surface flux; subsequently update the permeability and transmissibility fields according to the established permeability evolution relationship with directional surface flux; and select or compute the k_r curve employed for each cell based on its total surface flux value. However, this process incurs substantial computational overhead, making the development of more efficient solution methods imperative.

Multi-scale solution methods

Existing commercial numerical simulators predominantly use fully implicit discretization methods to convert nonlinear systems into linearized systems, which are then solved using Jacobi or Gauss–Seidel iterative methods. Although this method is stable, has weak constraints on time step sizes, and is suitable for solving strongly nonlinear problems, it requires solving a large-scale Jacobian linear algebraic equation system. Moreover, incorporating dynamic heterogeneity substantially increases the complexity of numerical simulations, requiring even higher efficiency for iterative solutions. To achieve higher computational efficiency, Gries et al. proposed replacing direct solvers with iterative solvers using constrained pressure residual preconditioners³⁴. However, Cusini et al. have demonstrated that this method is less effective^35,36. Therefore, after establishing the oil–water two-phase numerical simulation equations that account for dynamic heterogeneity, improving the iterative solution methods and enhancing solution efficiency remain key challenges. This paper adopts a sequential solution method, decomposing the black oil Eqs. (1)–(2) into pressure and transport equations, and fully leverages the parallel advantages of the multi-scale finite volume method. It employs an improved multi-scale method to solve the pressure equation, thereby enhancing model stability and solution efficiency.

Sequential splitting

A sequential solution strategy was employed in the MSFV method, with several such methods available in the literature. These methods vary in terms of primary unknowns, operations, linearization, temporal and spatial discretization, and the sequence in which these operations are applied to derive a set of discrete equations. A classic method is the Implicit Pressure/Explicit Saturation (IMPES) method, which, however, is less effective when solving strongly nonlinear problems. This paper adopts the SFI method proposed by Jenny and De Baun et al.^37,38,39 which decomposes the material balance equation of reservoir fluids into a pressure sub-problem and a transport sub-problem.

In the Sequential Splitting algorithm, each time step is handled by an outer loop that solves the coupled flow and transport problem, and an inner (nonlinear) Newton loop that solves the implicit transport problem given an updated flow field. Figure 4 specifically contrasts the differences between this sequential solution and the fully implicit solution. The FI method in Fig. 4a linearizes and solves all solution variables simultaneously, while the Sequential Splitting method in Fig. 4b decomposes the reservoir dynamics problem at each time step into two sub-problems: one for reservoir pressure and the other for the transport of reservoir fluids.

Fig. 4

Solution workflow: fully implicit (FI) vs. splitting scheme (SS) for black-oil systems⁴⁰.

The pressure sub-problem can be written as the residual pressure equation as follows:

$$\Omega_{\varepsilon } = \left[ {{\mathcal{R}}_{p} ,{\mathcal{R}}_{q,\alpha } ,{\mathcal{R}}_{C} } \right]^{T} = 0$$

(10)

Using phase pressure $p_{\alpha }$ as the primary variable, the Newton–Raphson method is employed to solve for the unknown state quantities $\varepsilon = [p_{\alpha } ,q_{\alpha }^{s} ,p_{bh} ]^{T}$ in the pressure equation.

The pressure equation, which does not depend on saturation and is derived under the condition of satisfaction, is formulated for the oil–water two-phase system.

$${\mathcal{R}}_{p} = \frac{{{\mathcal{R}}_{w} }}{{b_{w}^{n + 1} }} + \frac{{{\mathcal{R}}_{o} }}{{b_{o}^{n + 1} }} = 0$$

(11)

The well model ${\mathcal{R}}_{q,\alpha }$ follows the Peaceman model⁴¹ and can be written as follows:

$$({\mathcal{R}}_{q,\alpha } )_{w} = (q_{\alpha }^{s} )_{w} - \mathop \sum \limits_{{c \in C_{w} }} {\varvec{b}}_{\alpha } [c]{\varvec{q}}_{\alpha } [c] = 0$$

(12)

${\mathcal{R}}_{C}$ represents the well control equation.

$$\left( {{\mathcal{R}}_{C} } \right)_{w} = p_{bh,w} - C_{bh,w} or\left( {{\mathcal{R}}_{C} } \right)_{w} = q_{w}^{s} - C_{q,w}$$

(13)

To derive the transport equations for updating saturation, it is assumed that the pressure state variables, which satisfy the convergence conditions, have already been obtained. Additionally, the relationship between the total flux $\vec{\nu }$ and the phase flux $\vec{\nu }_{\alpha }$ is governed by the following equation:

$$\vec{\nu } = \mathop \sum \limits_{\alpha } \vec{\nu }_{\alpha }$$

(14)

Based on these state variables, the total flux is calculated by summing Darcy’s law for each phase using the pressure equation in Eq. (10) and substituting it into Eq. (15) to determine the phase velocity in the conservation equation.

$$\vec{\nu }_{\alpha } = f_{\alpha } (\vec{\nu } + k\sum\limits_{\nu } {{{\varvec{\uplambda}}}_{\nu } } ({\Delta }\rho g\nabla z + \nabla P_{c} ))$$

(15)

where $f_{\alpha }$ is the partial flow coefficient.

The phase velocity from Eq. (15) is substituted into Eq. (1), thereby solving the saturation of the different phases. In the case of the oil–water two-phase black-oil model, the saturation of the oil and water phases must satisfy the condition that their sum equals one. Therefore, it is only necessary to solve for the oil saturation. Let,

$$\delta = \left[ {s_{o} } \right]^{T}$$

(16)

where $\delta$ represents the column vector composed of the primary variables of the transport equation.

In the pressure subproblem, the fluid pressure equation is solved to balance the total volume of fluid in each cell with the pore volume at the end of each time step. In the transport subproblem, the material balance equation for each fluid in the reservoir is solved on a cell-by-cell basis, where pressure, the total volume of fluid in each cell, and the total volumetric fluxes between cells are held fixed over a time step. After completing the transport nonlinear iteration, it is checked whether the pressure and transport solution variables are sufficiently consistent, and the process can either proceed to the next time step or repeat the pressure and transport steps.

Based on the above iterative solution process, pressure and saturation at each time step are obtained. In this calculation process, pressure is computed by solving the system of discrete equations using the Newton–Raphson method, with the computational cost primarily arising from the construction of the Jacobian matrix and the iterative update of variable increments. Flux calculation is another highly parallelizable operation. The pressure solution typically (if not always) contributes the most to the total computation time; therefore, significant implementation work focuses on optimizing its efficiency.

IMSFV method for flow

Common iterative methods (such as Jacobi and Gauss–Seidel) are used for solving systems of equations on a fixed grid. These methods can quickly eliminate high-frequency errors in the grid but are less effective at removing low-frequency errors, leading to slow convergence. To reduce computational costs, this paper employs an improved multi-scale solution method to solve the pressure equation and incorporates iterative strategies into the solution process^35,40,42.

The core idea of the multi-scale method is to leverage the coarse grid’s ability to reduce the difficulty of converging low-frequency errors and its faster solution speed. It iteratively solves the pressure on the coarse grid and, through grid refinement, extends the pressure solution to the fine scale, thereby increasing the convergence speed of the iterative algorithm and reducing the number of iterations. As a preprocessing step, the multi-scale solution method requires two sets of grids: a fine grid $\{ {\Omega }_{i}^{f} \}_{i = 1}^{{n_{f} }}$ based on the static properties of the reservoir, and a coarse grid $\{ {\Omega }_{j}^{c} \}_{j = 1}^{{n_{c} }}$ formed by dividing the original fine-scale grid into non-overlapping coarse blocks, see Fig. 5. The coarse grid is essentially a collection of fine grids, with each fine grid assigned to one coarse grid. This paper follows the approach outlined by Møyner et al. to establish the grids⁴³. This fine-coarse multi-scale grid is suitable not only for structured grids but also for unstructured grids, making it appropriate for reservoir simulations that account for various geological structures.

Fig. 5

Grid discretization schematic: fine-scale (left) vs. coarse-scale partitioning (right).

In this paper, the coupling between coarse and fine grids is based on the concept of algebraic multigrid, where the interaction between grids is achieved through changes in matrix dimensions.

The primary objective of solving the pressure equation is to determine the pressure increment. To develop a multi-scale solution method for pressure, we first redefine the pressure equation.

$${\varvec{J}}{\Delta }p = r$$

(17)

Since Eq. (17) may involve large coefficient variations and strong coupling between adjacent cells, we aim to avoid solving it directly. Instead, we approximate the pressure through a multi-scale expansion, which allows us to efficiently solve it on a coarser grid system.

Assuming the existence of a restriction operator R and a prolongation operator P which establish transformations from the coarse scale to the fine scale and vice versa, we first establish the relationship between the fine-scale pressure increment approximation $p_{f}$ and the coarse-scale pressure increment $p_{c}$ using the prolongation operator P.

$${\Delta }p \approx {\Delta }p_{f} = P{\Delta }p_{c}$$

(18)

Next, Eq. (18) is substituted into Eq. (17) and both sides are multiplied on the left by the restriction matrix R, transforming the problem of solving the fine-scale pressure increment into solving the coarse-scale pressure increment.

$$(RJP){\Delta }p_{c} = J_{c} {\Delta }p_{c} = Rr = r_{c}$$

(19)

The construction of the prolongation operator P and the restriction operator R is central to implementing the multi-scale solution. This paper follows the approach of Jenny et al.³⁷ in constructing the restriction operator R using the control volume method.

$$\left( {R_{c\nu } } \right)_{ji} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{ if }}x_{i} \in \Omega_{j}^{b} } \hfill \\ {0,} \hfill & {\text{ otherwise}} \hfill \\ \end{array} } \right.$$

(20)

The standard method for constructing prolongation operators P involves sequentially solving a series of local flow problems, all of which are computed numerically^43,44,45,46. For example, in the traditional MSFV method, a dual grid is constructed for the coarse-scale grid, and a series of local flow problems are solved to build the prolongation operator. This method involves complex grid construction, requiring fine, coarse, and dual grids, which also pose storage challenges. Furthermore, this method relies on solving local flow equations to construct the prolongation operator, and the process of constructing basis functions is cumbersome, hindering the creation of high-quality basis functions on unstructured grids.

Unlike the classical MSFV method, this paper adopts the approach of Møyner and Lie^46,47, using an iterative format instead of local flows, and constructs the prolongation operator P based on Restricted-Smoothed Basis Functions. The construction of both the grid and operator is simplified, avoiding the complex setup required for flow problems constrained by different boundary conditions. It is assumed that the iteration matrix has the property of zero row sums, and that the initial prolongation operator has row sums equal to one. Therefore,

$${\varvec{J}} = \frac{1}{2}\{ {\varvec{J}} + {\varvec{J}}^{T} - {\text{diag}}[({\varvec{J}} + {\varvec{J}}^{T} ){\mathbf{1}}]\}$$

(21)

where 1 represents a column vector with elements of 1, and diag is an operator that extends a vector into a diagonal matrix of the same size.

Given the initial condition, the initial basis functions for the coarse grid are set to constant values within the grid and zero elsewhere. That is $P^{0} = R^{T}$, given a suitable matrix J, the prolongation operator can be updated through the following iterative process.

$$P^{n + 1} = P^{n} - {\mathcal{M}}(\omega {\mathbf{D}}_{s}^{ - 1} JP^{n} )$$

(22)

where ${\mathbf{D}}_{s}$ is the smoother constructed as a diagonal matrix, consists of the diagonal elements of matrix J. The smoother is used to find the increment and progressively smooth it. ${\mathcal{M}}$ is a restrictor confines the smoothing of the basis functions within a support region centered on the coarse-scale grid and bounded by the centers of the eight surrounding grid points, thereby ensuring the accuracy of the prolongation.

The convergence criterion for Eq. (22) is governed by two key parameters: the maximum iteration count and the residual threshold. The maximum iteration count is defined as:

$$i_{\max } = 50 \cdot \left( {\frac{{n_{f} }}{{n_{c} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 d}}\right.\kern-0pt} \!\lower0.7ex\hbox{$d$}}}}$$

(23)

where, $n_{f}$ and $n_{c}$ represent the total number of fine-grid and coarse-grid cells, respectively, and d denotes the geometric dimension of the computational domain (d = 2 for 2D, d = 3 for 3D). This formula dynamically adjusts the maximum iteration count using the geometric mean of the ratio of fine-grid to coarse-grid cells, enabling adaptation to problems of varying scale. At higher coarsening ratios, the iteration count increases accordingly, ensuring convergence. Simultaneously, the termination criterion for the iterative process includes a residual threshold of 0.005.

After obtaining the restriction operator R and the prolongation operator P, the multi-scale pressure solution process is established. Since the pressure calculated by the above multi-scale method is usually only an approximation of the fine-scale pressure, this study adopts the method of Wang et al.⁴⁸ and incorporates an ILU(0) smoother to iteratively correct and eliminate the approximation error in the multi-scale pressure solution. We write the defect as:

$$r^{m} = J{\Delta }p^{m}$$

(24)

Assuming

$$s^{m} = U^{ - 1} (L^{ - 1} d^{m} )$$

(25)

And represents the result of applying ILU(0) to the defect, with the initial guess being zero.

$${\Delta }p^{m + 1} = {\Delta }p^{m} + P[J_{c}^{ - 1} R(r^{m} - Js^{m} )] + s^{m}$$

(26)

Therefore, using Eq. (26), only a few multi-scale iterations are applied in each nonlinear iteration step to update the fine-scale pressure increment, without the need to solve the linearized system using the Newton–Raphson method. Once the pressure change satisfies the convergence criteria, the multi-scale solution of the pressure equation is complete, and the flux on the fine-scale grid is reconstructed based on the approximate pressure.

Furthermore, while the multi-scale finite volume method ensures conservation on the coarse-scale grid, mass conservation on the fine-scale grid is challenging to achieve under the approximate pressure field. Therefore, following the method of Olav Møyne⁴⁶, corrections are applied to the flux depending on whether the fine-scale grids connected by grid faces are boundary grids or internal grids of the coarse grid. The correction procedure is outlined as follows:

$$\hat{\user2{\nu }}[f] = \left\{ {\begin{array}{*{20}c} {{\varvec{\nu}}(\varepsilon_{m - 1} ,\nabla \hat{\user2{p}},\delta_{n} ), \, ifB[C_{1} (f)] = B[C_{2} (f)]} \\ {{\varvec{\nu}}(\varepsilon_{m - 1} ,\nabla {\varvec{p}}_{m} ,\delta_{n} ),ifB[C_{1} (f)] \ne B[C_{2} (f)]} \\ \end{array} } \right.$$

(27)

where f represents a grid face, C1 and C2 represent the grids connected by that grid face, and B determines which coarse grid the grid belongs to.

Once the flux field correction is completed, the transport equation can then be solved within the sequential solution process. To solve the transport equation efficiently, the domain decomposition method proposed by Kozlova et al.⁴⁹ can be referenced.

Results and discussion

Building on the methodology outlined in “Methods” section, a multi-scale numerical simulator incorporating dynamic heterogeneity is developed using MRST (2022b).

Validation of multiscale method

The computational accuracy and efficiency of nonlinear pressure equations are evaluated using the SPE10 reservoir benchmark, comparing results obtained from the Multi-scale Method (MS), traditional fine-scale fully implicit method (FI), and the commercial simulator (tNavigator).

The SPE10 reservoir benchmark, introduced in 2000, is the second dataset of the Society of Petroleum Engineers’ (SPE) tenth benchmark problem. It models oil production through water injection in a cuboid domain. The domain is initially fully saturated with oil. Water is injected at a constant rate through a central vertical well, while oil is extracted via four vertical production wells located at the corners, driven by pressure-induced flow. The domain exhibits extreme heterogeneity in permeability, spanning eight orders of magnitude (Fig. 6). Similarly, porosity varies across four orders of magnitude, with some areas even reaching zero. These characteristics make the problem highly ill-conditioned and more challenging to solve than scenarios based on real reservoir data. The model consists of 70,125 active grid cells. In the multi-scale solver, the fine-scale grid with dimensions 15 × 55 × 85 is uniformly coarsened to a coarse grid of size 5 × 11 × 17.

Fig. 6

SPE10 reservoir characterization: well locations (red) & permeability distribution.

The distribution of pressure fields at a simulation time of 5 years is shown in Fig. 7a–c, corresponding to the results obtained using the MS method, the FI method, and the tNavigator, respectively. The pressure field maps from all three approaches exhibit strong agreement, with the results from the MS method closely matching those produced by both the FI method and the commercial simulator. This confirms the computational reliability of the multi-scale approach for solving the nonlinear pressure equation.

Fig. 7

3D pressure field comparisons: FI, MS, and tNavigator solvers (SPE10 benchmark).

The potential errors of the multi-scale pressure solution method developed in this study are quantitatively assessed by plotting the relative error distributions in comparison with both the FI method and tNavigator, as shown in Fig. 8. The results indicate that, regardless of the comparison method, the relative error values of the developed MS method remain minimal. This finding further confirms the reliability of the computational results produced by the method.

Fig. 8

Relative error distribution benchmark: MS vs. FI and tNavigator solvers.

In addition to field maps, production curves for each well were compared across the three methods. Figure 9a–d illustrate the the cumulative oil production curves for production wells P1, P2, P3, and P4, respectively. The results show that the curves for wells from all three methods closely overlap, indicating strong agreement. This further validates the reliability of the proposed MS method.

Fig. 9

Comparative well production performance: Three simulation methodologies.

Additionally, the relative errors between the daily oil production rates at each time step for the production wells, calculated using the MS method presented in this paper, are quantified and compared with those obtained from the commercial simulator and the FI method. Figure 10 shows that the relative errors for the method developed in this study fluctuate significantly during the initial iterations but stabilize over time. Overall, the error values between the proposed method and the two existing methods remain within 5%.

Fig. 10

Temporal evolution of relative errors in daily oil production across production wells.

This section uses the SPE10 model to evaluate the efficiency of the MS method in solving the nonlinear pressure equation. Figure 11a,b compare the linear solution time and total time per time step for the FI method and the MS method, respectively. Two key observations can be mad: First, the FI method spends most of its total time on the linear solution at each iterative time step, indicating the need for a more efficient approach. Second, with the proposed MS method, both the linear solution time and total time decrease exponentially, demonstrating its high computational efficiency. Furthermore, compared to earlier verification results from the EGG model⁵⁰, the efficiency improvement is even more significant in the SPE10 model. This is due to the stronger heterogeneity and larger grid size in the SPE10 model, which enhance the benefits of the multi-scale method in more complex reservoirs.

Fig. 11

Evolution of stepwise CPU time: traditional FI vs. MS solvers using MRST.

Table 1 compares the total computation time and linear solver time between the FI and the MS method for the SPE10 model implemented in MRST. The results demonstrate that the MS method significantly enhances computational efficiency: the total simulation time is reduced from 247.04 min (FI) to 12.17 min (MS), achieving a 95.07% reduction, while the linear solver time decreases from 243.33 to 4.39 min, corresponding to a 98.19% improvement. This comparison highlights the advantages of the MS method in lowering computational costs, particularly in optimizing linear solver performance. The data suggest that the MS method provides an efficient solution framework for large-scale reservoir numerical simulations.

Table 1 Computational efficiency comparison: FI versus MS methods for SPE10 benchmark case (MRST).

Cases and findings of multi-scale dynamic simulator

After validating the accuracy and effectiveness of the proposed multi-scale method, the dynamic multi-scale simulator, which incorporates dynamic heterogeneity, was used to study the impact of dynamic heterogeneity on waterflooding. In the base case, a heterogeneous one-quarter Five-Spot problem was modeled in a 3D reservoir, with the producer and injector placed at opposite diagonal corners. The model dimensions were 250 × 250 m, with a fine-scale grid of 50 × 50 × 9, which was uniformly coarsened to a 10 × 10 × 3 coarse-scale grid, resulting in an upscaling factor of 5 × 3. Additional reservoir parameters are provided in Table 1 (Table 2).

Table 2 Model parameters summary.

This paper characterizes dynamic heterogeneity by examining the temporal changes in k and k_r, with reference to the dynamic variation patterns of these properties shown in Figs. 2 and 3 above.k_r. To investigate how these dynamic changes influence oil–water displacement, residual oil distribution, and waterflooding efficiency, a homogeneous model was initially used. Four scenarios, outlined in Table 3, were set up for typical model simulations. In each scenario, the reservoir is initially saturated with oil, with injection occurring from the lower-left corner and production from the upper-right corner. The water injection rate is maintained at a constant 100 cubic meters per day, with reservoir fluid produced at the same rate under the given conditions.

Table 3 Typical case schemes for homogeneous model.

The impact of dynamic heterogeneity on pressure was quantified by analyzing the bottom hole pressure (BHP) curves for injection and production wells across different cases. Figure 12a shows that incorporating dynamic heterogeneity leads to a more pronounced decline in BHP in the injection well. During the early stages of waterflooding (before water breakthrough (WBT)), dynamic changes in k and k_rresult in relatively small differences in pressure decline. However, when both dynamic changes are considered together, the pressure decline is more significant. In the mid-to-late stages (after WBT), the influence of dynamic changes in k on BHP in the injection well diminishes, while the influence of dynamic changes in k_r becomes more pronounced.

Fig. 12

Multiscale solution: bottom-hole pressure evolution in injector-producer well pairs.

Additionally, when both factors are simultaneously accounted for, a degree of counteraction occurs, resulting in a less pronounced BHP decline than when only the dynamic changes in k_r are considered. Figure 12b illustrates that incorporating dynamic heterogeneity reduces the decline in oil well pressure before WBT. The sharp pressure drop at the moment of WBT is mitigated, particularly when dynamic changes in k_r are included. In this case, the rapid rise following the steep pressure drop is significantly weakened, leading to a more monotonic decrease in BHP at the production wells. As development progresses, the influence of dynamic changes in k on BHP in the production wells diminishes, while the effect of dynamic changes in k_r becomes more pronounced. When dynamic changes in k_r are included, a distinct pressure funnel forms near the production wells.

The saturation field distribution results for Cases 1 to 4 at various times (t = 3 months, 1 year, time of WBT, 1 year after WBT, and 6 years) were calculated separately, as shown in Fig. 13, with consistent color scale limits applied. The results in Fig. 13 highlight differences in the saturation distribution among the four scenarios. In the homogeneous model without dynamic heterogeneity (Fig. 13a), waterflooding progresses relatively uniformly. However, when dynamic changes in k are considered (Fig. 13b), the trend of the oil saturation field remains similar, but the displacement range decreases, and more residual oil accumulates near the boundary at the time of WBT.

Fig. 13

Multiscale solution of oil saturation at different times for homogeneous cases.

Incorporating dynamic changes in k_r (Fig. 13c) alters the shape of the water saturation front and enhances the flow dynamics near the wellbore, leading to a wellbore aggregation effect. Prior to WBT, the impact of dynamic heterogeneity is most noticeable near the injection well, where water saturation values are higher when dynamic k_r is considered. At the time of WBT, the waterflooding front, influenced by dynamic k_r, shows a sharper angle along the diagonal between the injection and production wells, thereby expanding the area unaffected by water injection. After WBT and during the ultra-high water-cut period, the wellbore aggregation effect intensifies, resulting in higher water saturation and steeper gradients near both the injection and production wells. In the region between the wells, water saturation remains lower than near the wellbore ends, creating a “funnel” pattern in the water saturation profile, similar to the observed pressure profile. When both dynamic changes are considered simultaneously (Fig. 13d), the displacement becomes more heterogeneous, with a smaller area affected by water injection. As a result, more residual oil accumulates near the boundaries, both at the time of WBT and during the ultra-high water-cut stage.

To compare the numerical simulator developed in this study, which accounts for dynamic heterogeneity, with conventional numerical simulators that consider only static heterogeneity, the Monte Carlo method was applied to randomly generate models exhibiting spatial heterogeneity in porosity and permeability. Based on the heterogeneous model, numerical experiments were conducted using the four schemes shown in Table 2 again. To distinguish these from the aforementioned homogeneous models, these cases were named as Cases 5 to 8. The saturation field distribution results for Cases 5 to 8 at the same timesteps were calculated separately, as shown in Fig. 14, with consistent color scale limits applied.

Fig. 14

Multiscale solution of oil saturation at different times for heterogeneous media.

In the model without dynamic changes in spatial property heterogeneity (Fig. 14a), which represents the static spatial heterogeneity model commonly used in commercial simulators, a serrated pattern is observed at the waterflooding front. However, the overall non-uniform advancement of saturation is not significant. When dynamic changes in k are considered (Fig. 14b), the distribution trend of the oil saturation field remains similar, but the accumulation of residual oil near the boundary becomes more pronounced. In cases where dynamic changes in k_r are considered (Fig. 14c), the shape of the water saturation front changes, the flooded area decreases further, and a more noticeable non-uniform fingering phenomenon appears between the injection and production wells. Water saturation in the injection and production wells is lower than near the wellbore, creating a “funnel” shape in the saturation profile, similar to the pressure profile. When both dynamic heterogeneity factors are accounted for (Fig. 14d), the displacement becomes more heterogeneous, the area influenced by water injection shrinks, and the “funnel” shape in the water saturation profile forms earlier. More residual oil accumulates near the boundaries at both the time of WBT and during the ultrahigh water-cut period. A comparison between the saturation fields in Fig. 14a, d clearly demonstrates that the influence of dynamic heterogeneity on waterflooding development cannot be overlooked. The remaining oil distribution predicted by conventional commercial simulators, which consider only spatial static heterogeneity, may significantly diverge from actual conditions. This discrepancy becomes especially pronounced during the high water-cut period, where the difference between simulated and actual conditions increases after extended waterflooding.

To further quantify the impact of dynamic heterogeneity on waterflooding development, cumulative oil production and water cut curves in Cases 5–8 were compared, as shown in Fig. 15. The results reveal that, compared to the scenario without dynamic heterogeneity, accounting for dynamic changes in k leads to a reduction in production volume and an earlier WBT. When the dynamic heterogeneity of kr is considered, production volume increases, while the WBT time remains largely unaffected. The most significant differences in the water cut curves are observed during the rapid rise stage. When both dynamic heterogeneities of absolute and k_r are incorporated, production volume is lower than when only k_r heterogeneity is considered. This suggests that dynamic changes in absolute and k_r influence production volume through distinct mechanisms. Specifically, dynamic heterogeneity in k_r improves development outcomes, while changes in k lead to poorer performance. These findings are consistent with the research conducted by by Xu³, Wang¹⁶, and Li et al.¹⁷. The underlying causes of this phenomenon have been investigated. It is widely accepted that the dynamic heterogeneity of permeability arises from the long-term scouring effect of injected water. This effect enhances the permeability of waterflooded regions, particularly along the main flow paths where the highest flow rates occur and permeability changes are most pronounced. However, this scouring effect also exacerbates the fingering phenomenon of injected water, leading to earlier WBT in production wells, reduced utilization of injected water, and ultimately a decline in oil recovery efficiency. Research by Wang¹⁶, and Li et al.¹⁷ suggests that when dynamic heterogeneity in k_r is considered, the oil recovery rate varies with displacement velocity. As k increases, there is a significant rise in oil recovery, indicating that while long-term scouring by injected water intensifies planar heterogeneity and reduces the waterflooding efficiency, it also improves fluid mobility. This increase in mobility enhances waterflood oil displacement efficiency, as the residual oil saturation in areas influenced by injected water gradually decreases. Consequently, oil displacement efficiency increases, leading to more favorable development outcomes.

Fig. 15

Response of water cut and cumulative oil production to dynamic mechanisms in heterogeneous reservoirs.

Table 4 quantitatively reveals the impact mechanisms of dynamic heterogeneity on waterflooding development: Dynamic changes in k significantly reduce oil production (Case 6 shows a 4.21% decrease in cumulative oil production compared to baseline Case 5, down to 5.4868 × 10³ m³), primarily due to exacerbated water channeling impairing development efficiency. Conversely, dynamic changes in k_r enhance development outcomes, with Case 7 achieving a substantial 20.56% production increase over the baseline (reaching 6.9060 × 10³ m³), attributed to enhanced fluid mobility and reduced residual oil saturation. Crucially, during the extra high water-cut stage (f_w > 90%), the positive effect of k_r becomes more pronounced: Case 7’s production gain expands to 27.06% (7.8520 × 10³ m³), while Case 8 (dual dynamic effects) achieves a 28.54% gain later in development (7.9435 × 10³ m³), confirming its sustained improvement of recovery in mid-to-late stages. Although dynamic k exerts negative interference (Case 8 output is 11.07% lower than Case 7), the ultimate oil production under dual dynamic effects remains significantly higher than the baseline (+ 28.54%). This demonstrates the positive contribution of dynamic heterogeneity to long-term ultimate recovery, with dynamic k_r emerging as the dominant driver during later development stages.

Table 4 Cumulative oil production at specific water cut in heterogeneous reservoirs under different dynamic mechanisms.

Sensitivity analysis

To validate the impact of grid size on the computational stability of the software described in this paper, considering time-varying reservoir conditions, two additional conceptual models were established: one with 25 grids in both the x and y directions (planar grid spacing of 10 m), and another with 100 grids in both the x and y directions (planar grid spacing of 2.5 m). All other parameters remained unchanged. These were compared with the baseline model from the previous section, which had 50 grids in both directions and a planar spacing of 5 m. The computational results for the three models are presented in Fig. 16. Statistical analysis of the results shows that the recovery factor errors for the 25 × 25 and 100 × 100 grid models, relative to the 50 × 50 grid model, were 0.110% and 0.290%, respectively. The water cut errors were 0.013% and 0.004%, respectively. This indicates that the influence of grid size on the computational results is minimal and essentially negligible. Consequently, the numerical simulation technique for time-varying reservoirs based on surface flux demonstrates highly stable computational results.

Fig. 16

Water cut and daily oil production behavior: effect of grid resolution incorporating dynamic heterogeneity (homogeneous model).

To investigate the impact of dynamic heterogeneity on production performance in reservoirs with different initial permeabilities, two new medium–high permeability reservoir models were designed based on the homogeneous reservoir model considering dual time variations in k and k_r (Case 4). The initial permeability of the homogeneous reservoir was set to 800 md and 2000 md, respectively, while keeping all other conditions identical to Case 4. Comparative simulations of the three models (initial permeability: 400 md, 800 md, 2000 md) were then performed against corresponding static models (which neglected k and k_r time variations). Figure 17 demonstrates that when dynamic variations are neglected, the initial reservoir permeability exhibits minimal influence on water cut and daily oil production rates; the curves for the three static models essentially overlap. The impact of dynamic heterogeneity on water cut and production primarily manifests during the mid-to-high water-cut stages. Owing to dynamic heterogeneity, the water cut is reduced and the daily oil production rate is increased during these stages. Ultimately, dynamic heterogeneity exerts a positive effect on the production performance of reservoirs in the mid-to-high water-cut stages.

Fig. 17

Water cut and daily oil production rate: with vs. without dynamic heterogeneity in homogeneous models under different initial reservoir permeability.

Cumulative oil production at a water cut of 99% was statistically analyzed for the different initial permeabilities, as presented in Table 5. The results demonstrate that for initial permeabilities of 400 md, 800 md, and 2000 md, the presence of dynamic heterogeneity increases the recovery factor by 28.88%, 29.99%, and 32.87%, respectively. That is, the positive effect of dynamic heterogeneity becomes more pronounced in medium-to-high permeability reservoirs.

Table 5 Cumulative oil production at 99% water cut: with vs. without dynamic heterogeneity under different initial reservoir permeability.

Furthermore, the impact of dynamic heterogeneity on production under different injection rates was investigated. Based on the homogeneous reservoir model considering dual time variations in k and k_r (Case 4), two new medium–high permeability reservoir models were designed. The daily water injection rate was set to 50 m³/day and 200 m³/day, respectively, while maintaining all other conditions identical to Case 4. Simulation results for these three models were compared against corresponding static models (neglecting time variations) at the same injection rates. Figure 18 reveals that with increasing injection rates, WBT occurs earlier and the production plateau period shortens. The influence of dynamic heterogeneity on water cut and production is primarily observed during the mid-to-high water-cut stages following breakthrough. When dynamic variations are neglected, the water cut rises more rapidly, and the decline in daily oil production rate is more pronounced. Consequently, dynamic heterogeneity mitigates the increase in water cut and alleviates the decline in oil production rate to some extent during the mid-to-high water-cut stages of the reservoir.

Fig. 18

Water cut and daily oil production rate: with vs. without dynamic heterogeneity in homogeneous models under different injection rates.

Cumulative oil production at a water cut of 99% was analyzed for the different daily injection rates, as presented in Table 6. The results demonstrate that for injection rates of 50 m³/day, 100 m³/day, and 200 m³/day, dynamic heterogeneity increases the recovery factor by 18.07%, 28.88%, and 45.49%, respectively. That is, the positive effect of dynamic heterogeneity becomes more pronounced under higher injection rates. This amplification stems from intensified scouring under higher injection rates, which enhances the dominance of k_r’s mobility-enhancing effect over k’s channeling detriment.

Table 6 Cumulative oil production at 99% water cut: with versus without dynamic heterogeneity under different injection rates.

Conclusions

This study establishes a multi-scale simulation framework for capturing dynamic heterogeneity in waterflooded reservoirs, and makes three pivotal advances:

• 1. A surface-flux-driven multiscale framework achieving 95% speedup: The proposed framework, combining surface-flux-driven dynamic k models with an improved multiscale finite volume (IMsFV) solver, delivers breakthrough computational performance: 95.07% reduction in total simulation time and 98.19% decrease in linear solver time versus conventional fully implicit methods (SPE10 benchmark). Accuracy remains robust with < 5% relative errors and exceptional grid stability (< 0.3% recovery fluctuation, < 0.02% water-cut deviation across 25 × 25 to 100 × 100 grids).

• 2. Resolution of competing permeability mechanisms where k_r dominates recovery: Dynamic k exacerbates water channeling, reducing the recovery factor by 4.21% (Case 6 vs. baseline Case 5). Conversely, dynamic k_r enhances recovery by 20.56%–27.06% (Case 7) through improved fluid mobility and displacement efficiency. Crucially, during high water-cut stages (> 90%), the positive effect of k_r dominates, enabling the dual-dynamic model (Case 8) to achieve a net 28.54% ultimate recovery gain despite the adverse impact of k degradation (Table 4).

• 3. Sensitivity analysis quantifies critical operational and geological controls: recovery gain at 99% water cut escalates from 28.88% (400 md) to 32.87% (2000 md) (Table 5), confirming greater efficacy in high-permeability reservoirs; amplification surges from 18.07% (50 m³/day) to 45.49% (200 m³/day) under elevated injection rates (Table 6), while peak impact occurs during mid-high water-cut stages with > 10% water-cut reduction (Fig. 17), demonstrating stage-dependent optimization potential.

Despite its contributions, this study has inherent limitations: (1) Omission of thermal/chemical EOR mechanisms; (2) Unmodeled time-dependent fluid viscosity variations; (3) Unvalidated surface-flux-scouring relationships under divergent injection histories (e.g., high-rate/short-term vs. low-rate/long-term flooding). Future research will extend the current two-phase framework to three-phase compositional models with integrated thermal-chemical modules, while establishing quantitative flux-scouring relationships through core-flooding experiments.