Introduction

Pain is an unpleasant, subjective, sensory, and emotional experience associated with actual or potential tissue damage, and it often serves as an intuitive indicator of various underlying medical conditions1. Currently, self-reporting is considered the gold standard for pain assessment. However, older adults often face challenges such as cognitive decline, sensory impairments, and physical disabilities, which can hinder their ability to accurately express their pain. Consequently, healthcare providers may find it difficult to assess pain effectively in this population, leading to inadequate pain management2. Clinical pain assessment in older adults often relies on manual evaluations by medical staff, which is vulnerable to subjective factors, such as professional experience, workload, and emotional state3,4,5. In recent years, advances in science and technology have spurred growing interest in using computers and artificial intelligence to assist in pain assessment. Most existing intelligent pain evaluation methods rely on a single modality, either physiological signals or behavioral indicators, such as facial expressions or cerebral hemodynamic changes. However, because pain is a complex phenomenon and clinical environments pose various challenges, these unimodal approaches have demonstrated limited effectiveness and adaptability in real-world clinical practice6,7,8.

Studies have demonstrated a strong relationship between self-reported pain and facial expressions. However, accurately and automatically assessing pain intensity from facial images or videos remains a challenging task9. This difficulty arises from the subtle visual differences between painful and non-painful facial expressions, as well as the complex external factors that contribute to pain expression10. Sounds often accompany expressions of pain, with vocalizations like groaning and screaming serving as primary acoustic indicators of pain11. Very few studies evaluated adult pain levels based on acoustic features such as loudness and pitch12. While early research in pain phonetics focused on neonates, recent studies have extended this approach to adults13. Recognition of pain expression by multi-information fusion refers to a system of recognition that not only uses information provided by video images, but also combines information provided by other sources, such as physiological signals (heart rate, skin conductivity, etc.), background information, or speech signals for classification and recognition14. Compared to single-signal recognition, multi-information fusion achieves better results. Multi-information fusion improves the accuracy of pain expression recognition, and by identifying the pain state, it can help assess the intensity of pain from facial expressions in videos. The deep learning-based multimodal pain expression and automatic voice classification in older adults can identify pain states by analyzing both visual and audio data from videos. This approach improves the efficiency and accuracy of pain assessment, assists healthcare professionals in updating pain management plans, and provides accurate pain intervention for patients.

Related work

Hamadi proposed a pain assessment method that combines facial expressions and head posture by extracting distance and gradient features from image frames. Using a time-domain window to capture dynamic changes, the method applies a radial basis function support vector machine classifier to differentiate between severe pain and no pain15. Gkikas developed a dual ViT model that processes embeddings extracted from both videos and fNIRS data, achieving 46.76% accuracy in the multilevel pain assessment16. A recent study employed a Vision-MLP combined with a Transformer-based module to analyze both RGB and synthetic thermal videos in unimodal and multimodal settings. Experiments using facial videos from the BioVid database demonstrated the effectiveness of incorporating synthetic thermal videos17. A study introduced PainFormer, a model designed to extract embeddings from multiple input modalities. It utilizes behavioral data, including RGB, synthetic thermal, and estimated depth videos, as well as physiological signals such as ECG, EMG, GSR, and fNIRS. PainFormer was evaluated on two pain datasets, BioVid and AI4Pain, demonstrating promising results18. Another recent study introduced video vision transformers (ViViT) specifically enhanced for pain recognition. These models capture spatiotemporal facial features relevant to binary pain classification, achieving accuracies of 66.96% on the AI4Pain dataset and 79.95% on the BioVid dataset19.

The current approaches for automatic pain assessment have faced some challenges:

  1. 1.

    Pain recognition and classification based on facial expressions remain a primary method in automatic pain detection. Although this approach is relatively well developed, its accuracy is limited by the restricted information available from facial images alone.

  2. 2.

    Pain is a subjective experience influenced by multiple factors, such as the type of pain and previous pain history. Different groups of people exhibit distinct pain characteristics, which significantly impact the accuracy of general pain recognition and classification models.

  3. 3.

    Multimodal pain recognition technology is still in its early stages. Furthermore, acquiring biological signals often requires attaching sensors to patients, which limits its clinical applicability.

  4. 4.

    Currently, most pain databases are composed of experimental data that differ significantly from clinical pain manifestations.

To address these challenges, we developed a multimodal automatic pain recognition and classification system that integrates speech data with a Residual Network 50 (ResNet50)-based facial expression recognition model. The system employs a VGGish network for speech signal recognition and classification. A Softmax classifier is used for multi-class classification, producing probabilities for each pain category.

Methodology

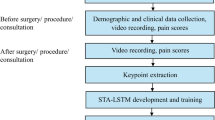
To overcome the limitations of the unimodal deep-learning model in pain recognition, including the complexity of feature extraction and degradation of neural network models, this study proposes an automatic multimodal pain recognition system that integrates facial expression and audio data. The ResNet50 pain recognition model designed in a previous study20, was integrated with an improved VGGish pain recognition model. These two models were integrated at the classification layer to form a multimodal pain recognition model. The optimized model incorporates data pre-processing, a bi-directional long short-term memory (BiLSTM) network, and attention mechanisms. The model flow is illustrated in Fig. 1.

Fig. 1
figure 1

Model flow.

Full size image

Voice data pre-processing

Characteristics of voiceprint information

One-dimensional voice waveform data contains only the time-domain information of the sound source signal. Voiceprint is the frequency spectrum of sound waves carrying speech information displayed using electroacoustic instruments. Voiceprint exhibits specificity and relative stability21. To effectively identify voiceprint, one-dimensional voice waveform data were converted into two-dimensional data in the time and frequency domains, and the network was trained through data balance processing21. During the process, sound data are converted into a sound spectrogram to obtain the time- and frequency-domain information of the sound.

Human perception of the frequency domain (Hz) is non-linear, and the Mayer scale (Mel scale) can effectively describe the relationship between human ear auditory features and frequency units (Hz)22. The relationship between Mel frequency and frequency in Hz is:

$${f_{Mel}}=2595 \times \lg \left( {\frac{f}{{700}}} \right)$$
(1)

In formula (1), f is the original frequency, and fMel represents the mapped Mel spectrum Mel frequency. The log-Mel spectrograms were extracted from the voiceprint signal data23 (Fig. 2).

Fig. 2
figure 2

Log-Mel spectrogram extraction process.

Full size image

Following the pre-aggravation, frame segmentation, and windowing of the Fast Fourier transform (FFT) signal, the transformation results of each frame are superimposed, and a two-dimensional spectrogram is obtained24. The FFT transformation formula is as follows:

$$G\left( k \right)=\sum\limits_{{n=0}}^{{N - 1}} {g\left( n \right){e^{ - j\frac{{2\pi }}{N}nk}}} ,0 \leqslant k \leqslant N$$
(2)

In (2): g(n) is a time-domain signal, G(k) is a frequency-domain signal, N is the length of the signal, and j is the imaginary unit. In (3), N is the FFT points, and they are then converted into the power spectrum25 as follows:

$$E\left( k \right)=\frac{{{{\left| {G\left( k \right)} \right|}^2}}}{N}$$
(3)

To help the model better understand the frequency characteristics of the voiceprint, a mel filter is used to convert the frequency in the frequency domain to the Mel frequency26. The formula for the Mel filter output is:

$$\begin{gathered} {H_{\text{m}}}\left( k \right)=\left\{ \begin{gathered} 0,k<f\left( {m - 1} \right) \hfill \\ \frac{{2\left[ {k - f\left( {m - 1} \right)} \right]}}{{\left[ {f\left( m \right) - f\left( {m - 1} \right)} \right]\left[ {f\left( {m+1} \right) - f\left( {m - 1} \right)} \right]}},f\left( {m - 1} \right) \leqslant k \leqslant f\left( m \right) \hfill \\ \frac{{2\left[ {f\left( {m+1} \right) - k} \right]}}{{\left[ {f\left( m \right) - f\left( {m - 1} \right)} \right]\left[ {f\left( {m+1} \right) - f\left( {m - 1} \right)} \right]}},f\left( m \right) \leqslant k \leqslant f\left( {m+1} \right) \hfill \\ 0,k>f\left( {m+1} \right) \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered}$$
(4)

In (4), the Mel filter bank sets several triangular bandpass filters within the frequency range of human speech, denoted as Hm(k), 0 ≤ m ≤ M, where M is the order of the filters, and the center frequency of the filters is set to f(m). The power spectrum of the voiceprint signal was processed by a filter to obtain the Mayer spectrum27 as follows:

$$S\left( m \right)=\sum\limits_{{k=f\left( {m - 1} \right)}}^{{f\left( {m+1} \right)}} {{H_m}\left( k \right)} \bullet E\left( k \right)$$
(5)

In (5), S(m) represents the Mel power spectrum, and Hm(k) represents the m-th Mel filter. After the calculation, M outputs are obtained, and a logarithmic scale is applied to obtain the log-Mel spectrum, Sm. The filter causes the loss of some dynamic information in the voiceprint signal, which is compensated for by first-order differential deltas28, as follows:

$${{\text{d}}_t}=\frac{{\sum\limits_{{n=1}}^{N} {n\left( {{S_{t+1}} - {S_{t - n}}} \right)} }}{{2\sum\limits_{{n=1}}^{N} {{n^2}} }}$$
(6)

In (6): dt represents the t-th first-order difference; St represents the t-th logarithmic spectral coefficient; N is usually taken as 1 or 2, representing the time difference of the first derivative. The calculation of the first-order difference twice is called the second-order difference, which can also compensate for dynamic information loss. Finally, Sm, the first-order difference, and the second-order difference yield the log-Mel spectrum features of the voiceprint signal, namely, the log-Mel frequency spectrum (MFSC).

The Mayer spectrum inversion coefficient (MFCC), featuring the extraction of voiceprint, requires discrete cosine transformation (DCT) relative to the MFSC. The log-Mel spectrum of Sm. After DCT to obtain the inverted spectrum domain, first- and second-order difference calculations are applied to obtain the Mel frequency inverted spectrum coefficient MFCC29. The formula is:

$${X_{MFCC}}=\sum\limits_{{m=1}}^{{M - 1}} {{s_m}\cos \left( {\frac{{\pi n\left( {m+\frac{1}{2}} \right)}}{M}} \right)} ,0 \leqslant m \leqslant M$$
(7)

The advantage of a spectrogram is that its physical meaning is clear and suitable for use in a deep convolutional neural network for sound recognition tasks. The convolutional neural network is used to extract key feature information from the sound signal.

Sound pressure determination

In acoustics, sound pressure is defined as the difference between the pressure P at a specific point in space and the pressure P in the absence of sound30. The lowest sound pressure audible to people in the air is known as the standard sound pressure, P\(2 \times {10^{ - 5}}N/{m^2}\). If the sound pressure at a given location is Pms, then the sound pressure level is defined as

$${L_p}=20\lg \left( {\frac{{{p_{ms}}}}{{{p_{0ms}}}}} \right)$$
(8)

The relationship between sound intensity and sound pressure is given by

$${L_p}={L_w} - 10\lg \left( {4\pi {r^2}} \right)$$
(9)

In this study, the equivalent continuous, peak, and maximum sound pressure levels were obtained by adjusting the frequency weighting and octave bandwidth settings. The sound intensity over a certain period is called the equivalent continuous sound strength, according to the mean energy or equivalent sound strength31. The maximum sound pressure level is the mean of the total sound pressure level of the steady state that may be generated at each measurement point after commissioning the sound expansion system30. Peak sound pressure is the maximum instantaneous sound pressure in a specific time interval32. The maximum sound pressure level can also be represented by the peak or quasi-peak sound pressure levels.

Researchers at the University of Sussex found acoustic expressions of pain at different pain intensities (mild, moderate, and severe)33: mild pain: high pitch level, non-linear amplitude; moderate pain: longest voice duration, longest period, longest pitch modulation; and severe pain: highest change in pitch. The pitches with different pain intensities were mild pain, 16.6; moderate pain, 44.21; and severe pain: 75.2534. This study draws on the assessment of pain ratings.

Model algorithm

VGGish neural network

VGGish is a variant of the VGG series neural network and is primarily used for audio detection tasks34. VGGish is a neural network used for audio feature extraction, which is adapted based on the VGG network and specifically designed for processing audio data. The primary purpose of VGGish is to convert audio signals into fixed-length vector representations, typically used for tasks such as audio classification, audio retrieval, and speech recognition34. The VGGish network was pre-trained from the AudioSet dataset, which is composed of two million people with 10 s audio signals whose labels are from an ontology of more than 600 audio event classes35. The neural network consists of a two-dimensional convolutional layer, a rectified linear unit activation layer, a maximum pooling layer, and a fully connected layer. A schematic of the VGGish neural network is shown in Fig. 3. The input data format of the VGGish network is a 96 × 64 data matrix, and the output is a high-dimensional depth feature vector of 128 dimensions. The network has the following characteristics: a simple structure, a clear hierarchy, a small convolution kernel, a large number of channels, and wide features.

Fig. 3
figure 3

VGGish Network structure.

Full size image

Model

Bi-LSTM network

As a recurrent neural network (RNN) solves the gradient disappearance problem, it cannot capture long-term dependence information. To solve this problem, Hochreiter et al. proposed an LSTM RNN by adding a storage unit structure. An LSTM network is a special structure that can solve the gradient explosion and disappearance. This structure contains storage units that can save information for a long time36. The LSTM network uses a gating unit to control the previous transmission status and the current input information. The LSTM network has the same structure and parameters at different time lengths. The previous current input and hidden states of the LSTM network at a given time point yield four states: forget gate, input gate, output gate, and memory cell. These four states within the LSTM network can be calculated using the following formulae:

$${q_i}=\alpha \left( {{W_i}{x_t}+{U_i}{h_{t - 1}}+{b_i}} \right)$$
(10)
$${q_f}=\alpha \left( {{W_f}{x_t}+{U_f}{h_{t - 1}}+{b_f}} \right)$$
(11)
$${q_o}=\alpha \left( {{W_o}{x_t}+{U_o}{h_{t - 1}}+{b_o}} \right)$$
(12)
$$q=\tanh \left( {{W_c}{x_t}+{U_c}{h_{t - 1}}+{b_c}} \right)$$
(13)
$${c_t}={q_i} \odot q+{q_f} \odot {c_{t-1}}$$
(14)
$${h_t}={q_o} \odot \tanh \left( {{c_t}} \right)$$
(15)

From (10) to (15), ☉represents the element multiplication, is the sigmoid function. W is the weight matrix of the input gate, [h(t−1), xt] represents the hidden state of the previous moment, h(t−1) is connected to the current input xt, and b is the bias vector of the input gate. The LSTM network can only obtain positive semantic information and ignores backward information. Conversely, the BiLSTM incorporates the forward and reverse LSTMs, which can process sequences in both directions37 (Fig. 4).

$$\overrightarrow {{h_t}} =\overrightarrow {LSTM} \left( {{h_{t - 1}},{W_t},{c_{t - 1}}} \right),t \in \left[ {1,T} \right]$$
(16)
$$\overleftarrow {{h_t}} =\overleftarrow {LSTM} \left( {{h_{t+1}},{W_t},{c_{t+1}}} \right),t \in \left[ {T,1} \right]$$
(17)
$${H_t}=\left[ {\overrightarrow {{h_t}} ,\overleftarrow {{h_t}} } \right]$$
(18)

The pain features extracted from the VGGish model were fed into the BiLSTM layer, and the resulting output was fed to the attention layer.

Fig. 4
figure 4

BiLSTM Network structure.

Full size image

Attention mechanism

In traditional sequence modeling methods, LSTM networks and RNNs often face the problem of gradient disappearance, which limits the ability of the models to handle long-distance dependencies and makes it difficult to capture contextual information in long sequences. Traditional models, such as RNNs, process sequences step-by-step, leading to inefficient models during training and inference. This project introduced attention mechanisms as an additional treatment for the LSTM network. In the speech recognition task, not all time-frequency units in a segment of speech are equally important for the pain recognition results; hence, an attention mechanism is introduced to extract the elements from the audio data that are important for pain38. The specific method is as follows:

$${e_i}={u^T}\tanh \left( {{W_{ai}}+b} \right)$$
(19)
$${a_i}=\frac{{\exp \left( {\lambda {e_i}} \right)}}{{\sum\nolimits_{{K=1}}^{L} {\exp \left( {\lambda {e_i}} \right)} }}$$
(20)
$$c=\sum\limits_{{i=1}}^{L} {{a_i}{a_i}}$$
(21)

As shown in formula (19), a new representation, ei of the input sequence ai, is first obtained through a multi-layer perceptron layer (MLP) with tanh as the nonlinear activation function. Formula (20) normalizes the attention score ei into attention weights ai between 0 and 1 through a Softmax function. Formula (21) uses the obtained attention weights ai to weight the input feature vector ai, and finally obtains the weighted feature representation c.

Experiments

Database Building

Building on existing methods for creating multimodal pain video databases, this project collected video and audio data from older patients with hip fractures experiencing different pain intensities. Video data were recorded during physical examinations and functional exercises of the lower limbs, performed 24 h before and 24 h after surgery. The physical exams included hip lifting, knee flexion, and straight leg elevation, all in the supine position.

A combined approach was used to capture both facial expressions and voice data. Videos were recorded with a 2 K-resolution Dr. Hui Q20 optical camera at 30 frames per second, with 20x lossless zoom to clearly capture facial expressions. Audio was recorded using a 48 V microphone with a Newman MC58 sound card.

Initially, 220 video-audio samples were collected, of which 207 passed screening and were included in the database. Each video lasted approximately 3 to 5 s and was labeled as mild, moderate, or severe pain (Table 1). Individual video frames were treated as separate samples for dataset construction. After shuffling, the data were split into training (80%) and validation (20%) sets, ensuring that samples from the same patient did not appear in both.

To test the model’s robustness and generalizability, the open-source section of the BioVid thermal pain dataset was used for comparison, with permission from the original authors.

The inclusion criteria were as follows: (1) ≥ 65 years, (2) radiographically confirmed diagnosis of hip fracture, and (3) informed consent before data collection. The exclusion criteria were as follows: (1) unconscious states, such as coma or drowsiness; (2) obvious facial trauma, which seriously affected the model’s feature recognition; and (3) difficulty speaking and inability to perform speech recognition.

Table 1 Video dataset.
Full size table

Model evaluation

To measure the performance of the model on the validation dataset, evaluation indicators included accuracy, precision, accuracy of detection of a single target category (average precision, AP), mean average accuracy (mean average precision, mAP), detection speed (frames per second), and intersection of union (IoU) loss function39. Accuracy is the proportion of correctly classified samples in a test dataset. Precision refers to the proportion of positive samples among all the samples tested. Recall is the proportion of the positive samples that are correctly predicted to be positive. IoU represents the ratio of the intersection area to the union area of the predicted and true regions. The mAP represents the area under the precision–recall curve at different IoU thresholds.

Pain intensity classification

The Softmax classifier was used to receive the feature matrix of the fully connected layer and output the probability values of each category corresponding to the input target. Assuming there are N input targets, each target’s label, k, is the type of the model output category (k ≥ 2), and three classifications (1, 2, 3) are performed for pain expressions, with k = 3. For a given input xi, the probability P(y = j/xi) corresponding to category j is estimated using the model’s hypothesis function fθ(xi). The following hypothetical function is used to input and estimate the probability value of the corresponding category40:

$${f_\theta }\left( {{x_i}} \right)=\left[ \begin{gathered} P\left( {{y_i}=1\left| {{x_i};\theta } \right.} \right) \hfill \\ P\left( {{y_i}=2\left| {{x_i};\theta } \right.} \right) \hfill \\ \cdot \hfill \\ \cdot \hfill \\ \cdot \hfill \\ P\left( {{y_i}=k\left| {{x_i};\theta } \right.} \right) \hfill \\ \end{gathered} \right]=\frac{1}{{\sum\limits_{{j - 1}}^{k} {{e^{\theta _{j}^{T}{x_i}}}} }}\left[ \begin{gathered} {e^{\theta _{1}^{T}{x_i}}} \hfill \\ {e^{\theta _{2}^{T}{x_i}}} \hfill \\ \cdot \hfill \\ \cdot \hfill \\ \cdot \hfill \\ {e^{\theta _{k}^{T}{x_i}}} \hfill \\ \end{gathered} \right]$$
(22)

The Softmax Loss function of the classifier is:

$$J\left( {x,y,\theta } \right)= - \frac{1}{N}\left[ {\sum\limits_{{i - 1}}^{N} {\sum\limits_{{j - 1}}^{k} {1\left\{ {{y_i}=j} \right\}{{\log }_2}\left( {\frac{{{e^{\theta _{j}^{T}{x_i}}}}}{{\sum\limits_{{j - 1}}^{k} {{e^{\theta _{j}^{T}{x_i}}}} }}} \right)} } } \right]$$
(23)

The label category with the maximum Softmax output probability was considered to be the pain grade of the pain expression. To avoid misdetection and improve stability, the system determines the pain intensity only after the detected label reaches a stable and continuous frame number. When the output results are satisfactory, a voice prompt can be performed, and data can be recorded.

Multimodal fusion

Due to the differences and complementarity between different modal features in pain recognition, there are many methods for the integration of the decision-making layer, such as the sum rule, the mean rule, the minority rule, the maximum rule, and the voting mechanism41,42,43. The classification results of pain recognition obtained by decision layer fusion consider the relevant rules and the results of each separately identified mode, making the decision layer fusion method advantageous. In this study, the weighted sum method was used to perform decision-layer fusion. However, the weight value was allocated according to the importance of the information from each single mode, making this approach simple, convenient, and effective.

The model was trained on facial expression and speech data of the two modalities. The pain category probability was predicted by the Softmax classifier, and the recognition rate of pain intensity was expressed accordingly. Based on the embedded sound pressure level and the predicted pain intensity category probability, the modal recognition rate is expressed as:

\({P^{face}}=\left( {P_{1}^{{face}},P_{2}^{{face}}} \right),{P^{voice}}=\left( {P_{1}^{{voice}},P_{2}^{{voice}}} \right),{P^{sound}}=\left( {P_{1}^{{sound}},P_{2}^{{sound}}} \right).\)

A weighted matrix of multimodal pain recognition was obtained based on the multimodal pain recognition rate44. The weighted matrix is the weighted matrix corresponding to the facial expression mode, the speech mode, and the acoustic pressure mode.

\({W^{face}}=\left[ {\begin{array}{*{20}{c}} {P_{1}^{{face}}}&0 \\ 0&{P_{2}^{{face}}} \end{array}} \right],{W^{voice}}=\left[ {\begin{array}{*{20}{c}} {P_{1}^{{voice}}}&0 \\ 0&{P_{2}^{{voice}}} \end{array}} \right],{W^{sound}}=\left[ {\begin{array}{*{20}{c}} {P_{1}^{{sound}}}&0 \\ 0&{P_{2}^{{sound}}} \end{array}} \right]\)

\({S^{face}}=\left( {S_{1}^{{face}},S_{2}^{{face}}} \right),{S^{voice}}=\left( {S_{1}^{{voice}},S_{2}^{{voice}}} \right),{S^{sound}}=\left( {S_{1}^{{sound}},S_{2}^{{sound}}} \right)\)

They are the probability distribution results of the sub-classifiers of the facial expression, speech, and acoustic pressure modes. The results of the weighted fusion of each classifier and the weighted matrix formula are as follows:

$$P=\left[ {\begin{array}{*{20}{c}} {P_{1}^{{face}}}&0 \\ 0&{P_{2}^{{face}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {S_{1}^{{face}}} \\ {S_{2}^{{face}}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} {P_{1}^{{voice}}}&0 \\ 0&{P_{2}^{{voice}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {S_{1}^{{voice}}} \\ {S_{2}^{{voice}}} \end{array}} \right]+\left[ {\begin{array}{*{20}{c}} {P_{1}^{{sound}}}&0 \\ 0&{P_{2}^{{sound}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {S_{1}^{{sound}}} \\ {S_{2}^{{sound}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {{P_1}} \\ {{P_2}} \end{array}} \right]$$
(24)

Based on the results calculated using the above steps, the highest pain intensity obtained according to the maximum rule was the final identification result. This final fusion result obtained through the maximum rule reduces the calculation amount, and simplifies the implementation process, thereby compensating for the limitations of unimodal pain intensity identification classification, \(MAX\left( {{P_1},{P_2}} \right)\).

Facial expression image encryption

Since facial expressions involve privacy concerns, such as the portrait rights of the participants, the sequence of images identified by the system was automatically encrypted to protect privacy. In this study, after the model processed the facial images, the system encrypted them using a 3D chaotic logistic mapping to improve the security of image encryption45. The structure of a 3D chaotic logistic map is more complex than that of a low-dimensional chaotic sequence system and produces more random chaotic sequences46. The system uses three initial parameters that serve as initial keys for generating an encrypted chaotic random sequence. As the initial values and parameters increase, the key space generated by the function also significantly increases.

The iterative equation formula for the 3D chaotic logistic map is:

$${x_{i+1}}=\alpha {x_i}\left( {1 - {x_i}} \right)+\beta y_{i}^{2}{x_i}+\gamma z_{i}^{3}$$
(25)
$${y_{i+1}}=\alpha {y_i}\left( {1 - {x_i}} \right)+\beta z_{i}^{2}{y_i}+\gamma x_{i}^{3}$$
(26)
$${z_{i+1}}=\alpha {z_i}\left( {1 - {x_i}} \right)+\beta x_{i}^{2}{z_i}+\gamma y_{i}^{3}$$
(27)

Among \(x,y,z\) is the motion trajectory of the system and \(\alpha ,\beta ,\gamma\)are the control parameters of three-dimensional chaotic logistic mapping. Triple cubic coupling terms \(z_{i}^{3},x_{i}^{3},y_{i}^{3},y_{i}^{2}{x_i},z_{i}^{2}{y_i},x_{i}^{2}{z_i}\)were adopted in the formula, which increased the complexity of the calculation and improved the security of the system (Fig. 5).

Fig. 5
figure 5

Image encryption effect.

Full size image

Model testing

Optimization algorithm

The effects of different optimization algorithms on model training were compared. The effects of the style-guided diffusion model, augmented dynamic adaptive model (Adam), root mean squared propagation, and adaptive gradient optimization algorithms on model training were used for analysis and comparison. The results showed that the Adam optimization algorithm converged the fastest (15 cycles), and the training and verification losses were superior to those of the other optimization algorithms during model training (Table 2).

Table 2 Comparison of the effects of the optimization algorithms on the model training effect.
Full size table

Learning rate strategy

Simultaneously, the effect of the Adam optimizer learning rate strategy was tested on the model training effect. The effects of fixed and segmented learning rates on the training effects of the model were compared. The final training accuracy of the segmented learning rate was 88.7%, and the validation accuracy of 86.5% was superior to that of the fixed learning rate (Table 3). Therefore, the Adam optimizer segment learning rate strategy was used to train the project model on the target database.

Table 3 Comparison of the effects of learning rate strategies on model training effects.
Full size table

Improvement method

Network optimization

The performances of different optimized networks in model training were compared. LSTM, BiLSTM, and gated recurrent unit networks were selected for model training using the speech pain expression database (Table 4). The results showed that the LSTM network had the fastest training completion time (1.8 h); however, it had the lowest accuracy (75.2%). The BiLSTM network had the highest accuracy (80.8%) with a minimum loss value (0.190) and an optimal FI-Score value (78.6%). Based on the results of this comprehensive analysis, the BiLSTM network was selected as the optimized network for the VGGish model.

Table 4 Performance comparison of the optimized network models.
Full size table

Attention mechanism

The results of the first-order attention mechanism (channel attention mechanism), sparse attention mechanism, and model training in an optimized state without the attention mechanism were compared (Table 5). In the optimization state without the attention mechanism, the model training time was the shortest (2.5 h); however, its accuracy was low (76.5%). Comparing the first-order attention mechanism with the sparse attention mechanism, the model training results show that the first-order attention mechanism has a higher loss value (0.370); however, its accuracy and F1-Score value are superior to those of the sparse attention mechanism.

Table 5 Comparison of the attention mechanism and its impact on model performance.
Full size table

Model training parameters

The transfer learning method was used for model training47. The VGGish model parameters were compared with the LSTM model parameters by initializing all layers outside the Softmax layer, and then adding the Softmax layer to process the input results. To ensure that the network weight was not distorted due to the difference in the target dataset, the learning rate was set to be small. This prevented overfitting, eased convergence, improved the model accuracy, and solved the problem of applying deep learning to multimodal pain recognition. The model training parameter configuration is shown in Table 6.

Table 6 Model training parameters.
Full size table

Multimodal pain recognition model training

During the training of the multimodal pain recognition model, the ResNet50 + VGGish model was used to train a self-built pain dataset, which showed severe overfitting. After 500 iterations, the accuracy of the training set approached 100%; however, the accuracy of the validation set was only 80% (Fig. 6). Subsequently, the ResNet50 network + optimized VGGish model was trained on the same dataset, and the results showed that the model did not overfit or underfit. After 500 iterations, the accuracy of the model in the training and validation sets was maintained at 80% (Fig. 7).

Fig. 6
figure 6

Results of the original model training.

Full size image
Fig. 7
figure 7

The optimized model training results.

Full size image

Multimodal pain recognition model test

Data from the BioVid heat pain database were used as the test set. The BioVid heat pain database is a multimodal pain database comprising expression videos and physiological data (skin conductivity, electrocardiograms, myographic signals, and electroencephalogram signals) from 90 volunteers48. After receiving consent from the developer, the project team downloaded the BioVid heat pain database, which used four classifications for pain intensity: Pain 1, the lowest pain value that the subjects could identify; Pain 4, the highest acceptable pain level; and Pain 2 and Pain 3, intermediate intensities, calculated by linear interpolation between Pain 1 and Pain 4. Since the classification model of pain intensity identification designed in this study adopted a three-classification model for older patients with hip fractures and clinical pain symptoms, datasets of the Pain 2, 3, and 4 categories were selected from the BioVid database during model testing. The data for the three categories were shuffled for model training. The results of the confusion matrix test are shown in Table 7; the model achieved 85% accuracy in the Pain 4 category in the BioVid database with the optimal prediction effect.

Table 7 Results of the precision, recall and F1-score tests for the different pain categories.
Full size table

Discussion

The multimodal pain recognition system developed in this study for older patients with hip fractures evaluates pain intensity using two behavioral modalities: facial expressions and speech. It employs a classification-layer fusion mechanism to integrate features from both modalities effectively.

The foundation of facial expression-based pain recognition was established in 1991, when Craig et al. investigated facial responses to acute exacerbations of chronic lower back pain, marking the beginning of research in this area49. Early studies primarily focused on static facial images, which offered advantages such as simplicity, low computational complexity, and ease of use. However, static images provide limited information, making it difficult to achieve high recognition accuracy50. In contrast, video sequences capture the dynamic progression of facial expressions during pain episodes and offer more comprehensive information51. Nevertheless, visual features alone may not be sufficient for accurate pain detection, as pain is a complex interplay of physiological and psychological factors52. To address these limitations, multimodal fusion approaches combine visual data with other sources such as physiological signals, background context, or speech53. The BioVid Heat Pain Database, a widely used resource for pain research, has supported many such efforts. For example, the Hamadi team utilized this database to improve detection accuracy by minimizing feature noise and incorporating physiological signals like electrodermal activity (EDA) and electromyography (EMG). Using a random forest classifier, they achieved a 3–6% increase in accuracy for moderate to severe pain levels (Pain Levels 2–4). However, accuracy for detecting mild pain (Pain Level 1) remained low due to minimal expression and signal variation, making it difficult to differentiate between actual pain and noise54. Studies have shown that skin conductance signals, when combined with video features, outperform other biometric inputs55. As summarized in Table 8, models based on physiological modalities (e.g., EEG, EMG, GSR, fNIRS) generally achieve higher classification accuracy than those based on behavioral modalities (e.g., RGB video, thermal imaging, depth data)56,57,58.

However, collecting physiological data typically requires expensive and specialized equipment, limiting feasibility in clinical settings—particularly in resource-constrained environments.

As a result, research has increasingly focused on behavioral modality-based systems, which are more practical for clinical use. Furthermore, recent studies have demonstrated that transformer architectures and attention mechanisms can enhance the performance of pain recognition models16,17,18,19, yielding promising results for future development.

Table 8 Results of different state-of-the-art pain detection techniques.
Full size table

Current studies on multimodal fusion for pain expression classification systems have primarily focused on integrating video features with biometric signals59. Although physiological signals, such as skin conductivity, electromyograms (EMG), and electrocardiograms (ECG), offer high accuracy and objectivity, their collection poses significant challenges for model development and parameter optimization. These signals typically require specialized equipment, which imposes strict conditions on the data collection environment and the state of the equipment, limiting their applicability in clinical settings60. Additionally, acquiring these signals often involves attaching sensors to the face or body, a process generally feasible only in controlled experimental environments.

Non-contact multimodal fusion methods represent a promising direction for the future of automatic pain recognition systems61. In this study, we employed a multimodal pain recognition and classification approach by integrating facial expressions and speech, using a combined video-audio collection setup. This method requires minimal equipment and is easy for clinical staff to operate. Since elderly patients with hip fractures are typically emergency cases, acute pain may arise during movement and physical examinations. To capture realistic data, video and audio were collected naturally in a clinical lower-limb orthopedics setting.

The model achieved an 80% accuracy rate in training and validation. When tested on an external third-party dataset (BioVid), the recognition accuracy for pain levels 2 to 4 ranged from 82 to 85%, confirming the feasibility of applying a multimodal pain recognition system in clinical environments. Most classification errors occurred with Pain Level 1 (mild pain), where the model’s feature resolution and noise discrimination were less effective, significantly impacting recognition performance.

While this study demonstrates the feasibility of facial expression and speech-based multimodal pain recognition, it has several limitations. First, the system showed low accuracy in classifying mild pain, a common issue among similar models. Second, pain is inherently subjective and influenced by factors such as social context, cause of pain, and prior pain experiences, variables not considered in this study. Lastly, the self-constructed dataset used for training and validation had a limited sample size, which may affect the generalizability of the findings.

Nonetheless, this research marks the first attempt to apply behavioral modalities, specifically facial imagery and speech—for clinical pain recognition and has achieved promising results. It provides valuable insights and directions for future work. Moreover, the study reaffirms that attention mechanisms contribute significantly to classification performance in pain recognition tasks, underlining their potential for broader application in future research.

Conclusion

In this study, we employed facial images and audio features, extracted using ResNet-50 and VGGish respectively, to develop a pain recognition system. To enhance performance, we incorporated an attention mechanism, bidirectional long short-term memory, and Bayesian hyperparameter optimization. The proposed model was evaluated on the BioVid dataset, and the experimental results demonstrated its effectiveness in recognizing pain. For future work, we recommend exploring multimodal approaches that incorporate additional behavioral signals and developing interpretable methods to facilitate integration into clinical practice. .