Genome-wide iterative fine-mapping for non-Gaussian phenotypes

Abstract

Fine-mapping seeks to identify causal variants associated to a phenotype of interest. Fine-mapping searches through genomic regions previously identified by single marker analysis of genome-wide association studies (GWAS) data. This two-stage approach (1) often fails to identify causal variants with smaller effect sizes, and (2) does not properly correct for multiple comparisons. The former problem leads fine-mapping to have low recall of causal genetic variants, and the latter problem leads to high false discovery rate (FDR). To address these issues, we propose a novel Genome-wide Iterative fiNe-mApping method for non-Gaussian data (GINA-X). GINA-X efficiently extracts information from GWAS data by iterating a screening step and a variable selection step. The screening step provides a list of candidate genetic variants and an estimate of the proportion of null genetic variants. After that, the variable selection step selects a more focused list of genetic variants using the estimated null proportion to appropriately control for genome-wide multiplicity. A simulation study shows that, when compared to competing fine-mapping methods, GINA-X reduces FDR and increases recall. Case studies on alcohol use disorder and breast cancer show that GINA-X provides more focused lists of candidate causal genetic variants with better predictive performance.

Introduction

Fine-mapping seeks to identify causal variants associated to a phenotype of interest. Typically, these genomic regions were identified in previous studies using single marker analysis (SMA)^1,2 of genome-wide association studies (GWAS) data. This two-stage approach has two problems: first, SMA often fails to identify causal variants with smaller effect sizes, thus missing important genomic regions; and second, current fine-mapping methods—by not taking into account that SMA was performed in a genome-wide manner—do not properly correct for multiple comparisons. The former problem leads fine-mapping to have low recall of causal genetic variants, and the latter problem leads to high false discovery rate (FDR). To address these issues, here we present GINA-X, a novel Genome-wide Iterative fiNe-mApping method for non-Gaussian data belonging to the eXponential family of distributions. GINA-X iterates in an integrated Bayesian framework two steps: a screening step and a variable selection step. As our results show, when compared to currently used fine-mapping methods, GINA-X reduces the FDR and increases recall of true causal genetic variants.

Here, non-Gaussian data refers to phenotypes such as binary outcomes, time to events, and counts of events. Examples of such phenotypes include an indicator of presence or absence of disease (binary), age of first diagnostic of breast cancer (time to event), and number of alcoholic drinks in the last month (count). Time to event phenotypes not only are asymmetric, which precludes the use of the Gaussian distribution, but also are subject to censoring³. Dealing with censoring is out of the scope of this manuscript; the extension of GINA-X to time to event phenotypes is a potential topic for future research. Currently, GINA-X focuses on binary and counts phenotypes. In our simulation studies, we compare GINA-X with a state-of-art fine-mapping method based on Gaussian regression with summary statistics. In that comparison, GINA-X has favorable performance because, among other reasons, GLMMs are statistically more efficient (smaller standard errors) than Gaussian models to analyze non-Gaussian data. Finally, using the Gaussian approximation may yield nonsensical results such as negative predictions for binary data. This latter problem may occur for example in unbalanced studies with binary data, as often encountered in GWAS.

GINA-X proceeds as follows. GINA-X is initialized with a baseline model with only control covariates. Then, GINA-X’s screening step fits as many generalized linear mixed models (GLMMs) as the number of possible genetic variants, where each model includes the baseline model and one genetic variant. These model fits yield screening posterior probabilities for each genetic variant. After that, GINA-X’s screening step uses Bayesian FDR control^4,5,6,7 to choose a list of candidate genetic variants. Next, the variable selection step performs a search through the space of models defined by all possible GLMMs obtained by combinations of the genetic variants that are either in the list of candidate genetic variants or in the baseline model. This model search is either exhaustive (when the number of candidate genetic variants is small) or done through a genetic algorithm. Then, the model with largest posterior probability found in the model search is declared the best model. If the best model is different from the current baseline model, then the baseline model is updated to be the same as the best model and another iteration of GINA-X starts with a new screening step. On another hand, if the best model is the same as the current baseline model, then GINA-X has converged. In the latter case, GINA-X reports the genetic variants in the best model as the identified genetic variants.

GINA-X usually finds more true causal genetic variants than currently available fine-mapping methods. This is because, while currently available fine-mapping methods⁸ are applied separately from SMA, GINA-X uses an iterative integrated Bayesian approach. Specifically, in SMA as many models as the number of genetic variants are fitted, with each model containing only one genetic variant^1,2. The problem with such an approach is that contributions by causal genetic variants not included in a model inflate the estimate of the error variance. This causes a decrease in statistical power, leading SMA to miss causal genetic variants with smaller effect sizes and their respective regions of interest^9,10. Because currently available fine-mapping methods^11,12 are conditional on the list of genetic variants provided by SMA, they are not able to find those causal genetic variants with smaller effect sizes. In contrast, by iterating the screening and variable selection steps, GINA-X is able to discover causal genetic variants not identified by current fine-mapping methods. In the first iteration, the screening step selects genetic variants which are the most associated with the phenotype under study. However, this step selects not only causal genetic variants but also genetic variants in linkage disequilibrium with them. The variable selection step uses the information about sparsity from the screening step, thus reducing false discovery rate. In consecutive iterations, models in both screening and variable selection steps are based on the detected genetic variants from the last iteration. Conditional on the genetic variants with larger effect sizes in the baseline model, the screening step reconsiders the remainder of genetic variants in the whole genome and finds more regions of interest. These new regions contain genetic variants with smaller effect sizes.

GINA-X is able to handle non-Gaussian phenotypes and related subjects. In contrast, most genetic fine-mapping methods are proposed for Gaussian data from unrelated subjects^13,14. While some of these methods^11,12 are applied to binary traits by using summary data and Gaussian approximation, as shown by a simulation study in section “Simulation studies”, their performance in terms of FDR, recall, and F1 score is much worse than that of GINA-X. To the best of our knowledge, there is no fine-mapping method specifically built for binary or count data. Furthermore, most fine-mapping methods do not consider the correlation among GWAS observations due to population stratification and hidden relatedness^11,15. To allow for binary and count traits as well as related subjects, GINA-X is based on GLMMs with a vector of kinship random effects.

Recent work has shown that fine-mapping may be improved by modeling polygenic infinitesimal effects¹⁶. Similarly to Bayesian sparse linear mixed models (BSLMM)¹⁷ for polygenic modeling, GINA-X considers both infinitesimal polygenic effects (through kinship or relatedness random effects) and Bayesian sparse regression. Specifically, the kinship or relatedness random effect captures the combined infinitesimal polygenic effects of all markers¹⁷. This is in contrast with traditional fine-mapping methods^{11,12,14,15,18,19} that assume linear models with independent observations. Therefore, GINA-X ultimately produces one model with multiple potentially causal genetic variants with medium and large effect sizes while concomitantly accounting for infinitesimal polygenic effects.

We have performed four simulation studies using real genotype data to evaluate the performance of GINA-X when compared to competing fine-mapping methods. Specifically, we compare GINA-X to SuSiE-RSS¹² because: (1) SuSiE-RSS is based on summary statistics and, thus, may be used as an approximate method for the analysis of non-Gaussian phenotypes; (2) SuSiE-RSS performs similarly¹² to its sister method SuSiE¹⁴; and (3) SuSiE has better performance¹⁴ than competing fine-mapping methods DAP-G^18,19, CAVIAR¹⁵, and FINEMAP¹¹. In the first three simulation studies, GINA-X finds more true positives and less false positives than SuSiE-RSS. As a consequence, when compared to SuSiE-RSS, GINA-X has a much smaller FDR. In the fourth case study, the phenotype datasets are simulated from a null model without any causal genetic variants. In this case, GINA-X did not select any genetic variant as causal whereas SuSiE-RSS selected genetic variants as causal in 4% of the datasets. Therefore, these four simulation studies show that, when compared to a state-of-art fine-mapping method, GINA-X has favorable performance.

We further study the usefulness and flexibility of GINA-X with two case studies on alcohol use disorder and breast cancer. The phenotype for alcohol use disorder is the maximum number of alcohol drinks per day, which is count data. While SuSiE-RSS finds 9 genetic variants, GINA-X finds one genetic variant related to alcohol comsumption. The reason for this difference is elicited with a closer look at the results from GINA-X’s screening and variable selection steps. GINA-X’s screening step in the first iteration found the same 9 genetic variants and one more genetic variant. However, in the variable selection step, when controlling for genomewide multiplicity, GINA-X detects only one genetic variant in the best model. In the breast cancer case study, the phenotype is whether the individual has breast cancer or not, which is a binary phenotype. While SuSiE-RSS finds 24 genetic variants, GINA-X finds 16 genetic variants. Of importance, while the genetic variants found by SuSiE-RSS are only from 6 regions of interest, those found by GINA-X are from 16 different regions of interest. Finally, a tenfold cross validation shows that, when compared to SuSiE-RSS, the genetic variants found by GINA-X have better predictive performance.

Results

Overview of the method

We assume the non-Gaussian trait of interest follows a generalized linear mixed model of the form:

$$\begin{aligned} g(E(\pmb {y}|\pmb {\alpha }_1,\pmb {\alpha }_2))= & X_S \pmb {\beta }_S + X_c \pmb {\beta }_c + Z_1 \pmb {\alpha }_1 + Z_2 \pmb {\alpha }_2, \end{aligned}$$

(1)

where $\pmb {y}$ is the vector of n observed phenotypes, $X_S$ is the matrix of candidate genetic variants, and $X_c$ is the matrix of control covariates (e.g., age, gender, and environmental factors). In addition, $\pmb {\alpha }_1$ is the vector of kinship random effects, which follows a multivariate normal distribution $N(\pmb {0}, \kappa _1\Sigma _1)$, where $\kappa _1$ is an unknown scalar and $\Sigma _1$ is a kinship or relatedness matrix. Furthermore, if phenotypes are count data and follow Poisson distribution, we have $\pmb {\alpha }_2$ in the model, which is a vector of overdispersion random effects following $N(\pmb {0}, \kappa _2 I)$. The conditional expectation of phenotypes $E(\pmb {y}|\pmb {\alpha }_1, \pmb {\alpha }_2)$ is linked to the linear predictor $X_S \pmb {\beta }_S + X_c \pmb {\beta }_c + Z_1 \pmb {\alpha }_1 + Z_2 \pmb {\alpha }_2$ by the link function g(.).

GINA-X is a Bayesian iterative two-step fine-mapping method. At the beginning of the algorithm, the baseline model is initialized with only the control covariates and the kinship random effects. Then, the screening step fits as many models as the number of genetic variants where each model is comprised of the baseline model and a single genetic variant. After that, the screening step calculates the posterior probabilities for each genetic variant, and uses Bayesian false discovery rate control to select a set of candidate genetic variants. The second step, variable selection, searches the model space implied by the genetic variants that are either in the baseline model or in the set of candidate genetic variants. Then, the variable selection step selects the genetic variants in the model with the highest posterior probability, which we define as the best model. If the best model is the same as the baseline model from the screening step, then GINA-X has converged. Otherwise, the best model becomes the baseline model for the screening step in the next iteration of GINA-X.

To calculate posterior probabilities for models in both the screening and the variable selection steps, we need the integrated likelihood function. However, the integrated likelihood function $L(\pmb {\beta }_S, \pmb {\beta }_c, \kappa _1, \kappa _2|\pmb {y})$ cannot be computed analytically in GLMMs. To solve this problem, we use a pseudo-likelihood approach, which is an iterative procedure to estimate the parameters $\pmb {\beta }_S$, $\pmb {\beta }_c$, $\kappa _1$, and $\kappa _2$, and the random effects $\pmb {\alpha }_1$ and $\pmb {\alpha }_2$. In addition, the pseudo-likelihood method provides a vector of adjusted observations $\pmb {y}^\star$ which can be approximately modeled by linear mixed models (LMMs). In LMMs, the integrated likelihood function $L(\pmb {\beta }_S, \pmb {\beta }_c, \kappa _1, \kappa _2|\pmb {y}^\star )$ can be computed in closed form.

To speed up computations, GINA-X uses a population parameters previously determined approach (P3D) for GLMMs²⁰. We apply pseudo-likelihood method to the baseline model once in the screening step and the variable selection step. From the baseline model, we obtain the adjusted observations and estimate of variance components for random effects, and assume they are the same for every model in the screening step or in the variable selection step. The general form of the baseline model is

$$\begin{aligned} g(E(\pmb {y}|\pmb {\alpha }_1,\pmb {\alpha }_2))= & X_B \pmb {\beta }_B + Z_1 \pmb {\alpha }_1 + Z_2 \pmb {\alpha }_2, \end{aligned}$$

(2)

where $X_B$ contains covariates in the baseline model. In the screening step of the first GINA-X iteration, the baseline model does not contain any genetic variants and, thus, $X_B$ only contains control covariates and intercept. In the variable selection step of the first GINA-X iteration, the baseline model has the control covariates and all candidate genetic variants from the screening step. Starting in the second iteration, in the screening step $X_B$ contains additionally the genetic variants identified in the previous GINA-X iteration.

Simulation studies

To evaluate the performance of GINA-X when compared to competing fine-mapping methods, we conduct simulation studies that use the real genotypes from the two case studies presented in section “Case studies”. Specifically, we compare GINA-X to the fine-mapping method SuSiE-RSS¹² because: (1) SuSiE-RSS is based on summary statistics and, thus, may be used as an approximate method for the analysis of non-Gaussian phenotypes; (2) SuSiE-RSS performs similarly¹² to its sister method SuSiE¹⁴; and (3) SuSiE has better performance¹⁴ than competing fine-mapping methods DAP-G^18,19, CAVIAR¹⁵, and FINEMAP¹¹. To provide SuSiE-RSS with lists of candidate genetic variants, we first perform single marker analysis with GEMMA²¹. We then define each region of interest as a window of 10,000 base pairs centered around each genetic variant found by GEMMA. Using the summary statistics provided by GEMMA, SuSiE-RSS is then applied separately to each region of interest; the combined set of genetic variants identified by SuSiE-RSS is reported. For context, we also report the performance of GEMMA. Our assessment considers four key criteria: True Positives (TP), False Positives (FP), False Discovery Rate (FDR), and the F1 score. The F1 score is defined as the harmonic mean of precision and recall. Because the objective of fine-mapping is to identify causal genetic variants, we define a false positive as an identified genetic variant that is not causal. This may not be fair to GEMMA, which aims to identify associated –but not necessarily causal– genetic variants. Thus, the reported FPs for GEMMA should be taken with a grain of salt. Additionally, we report the computational time of each method.

We present four simulation studies to evaluate the performance of GINA-X and SuSiE-RSS under different settings. Simulation study 1 evaluates the performance of GINA-X and SuSiE-RSS in the analysis of small datasets with large effect sizes. Meanwhile, simulation studies 2, 3, and 4, evaluate the performance of GINA-X and SuSiE-RSS in the analysis of medium sized datasets. We have designed simulation studies 2 and 3 based on actual analyses of the breast cancer dataset with GINA-X and with SuSiE-RSS. The potentially causal genetic variants selected by each of these two methods have distinct genetic architectures. Specifically, GINA-X tends to select many regions of interest, and one genetic variant per region of interest. Meanwhile, SuSiE-RSS tends to select a smaller number of regions of interest, and many genetic variants per region of interest. Thus, simulation studies 2 and 3 evaluate the performance of, respectively, GINA-X and SuSiE-RSS under each of these two possible genetic architectures. Finally, simulation study 4 evaluates the performance of GINA-X and SuSiE-RSS when the phenotypes are generated with no causal SNPs.

In all presented simulation studies, all datasets are simulated from GLMMs with kinship/relatedness random effects. Similarly to Bayesian sparse mixed linear models for polygenic modeling¹⁷, by including kinship or relatedness random effects we are accounting for the combined contribution of infinitesimal polygenic effects of all genetic variants.

Simulation study 1: Small datasets with large effect sizes

We simulate GWAS phenotype data using real genotypes from the Study of Addiction: Genetics and Environment (SAGE) which is part of the National Human Genome Research Institute’s Gene Environment Association Study Initiative [Database for Genotypes and Phenotypes (dbGaP) study accession phs000092.v1.p1]. We have considered 2772 European Americans from SAGE. In this simulation study, the genetic variants are single nucleotide polymorphisms (SNPs). While the dataset has 846,076 SNPs with minor allele frequency (MAF) larger than 0.01 and missing rate less than 5%, for convenience we considered a subset of 800,000 of these SNPs. From these 800,000 SNPs, we selected 20 evenly spaced SNPs to be the causal genetic variants, where 5 SNPs have relatively large coefficients $\beta _l$ and 15 SNPs have small coefficients $\beta _s$. Likelihood ratio tests indicated that none of the 20 causal genetic variants violate the hypothesis of Hardy-Weinberg equilibrium. We have four parameter settings: (a) $\beta _l=1.2$, $\beta _s = 0.3$; (b) $\beta _l=1.6$, $\beta _s = 0.4$; (c) $\beta _l=2$, $\beta _s = 0.5$; (d) $\beta _l=2.4$, $\beta _s = 0.6$. We set the intercept $\beta _0=-0.5$, and the variance component $\kappa$ of the kinship random effects $\pmb {\alpha }$ equal to 0.15. Thus, the phenotype data are simulated from the Bernoulli GLMM

$$\begin{aligned} logit(p_i)= & \beta _0 + \sum _{j=1}^{5} \beta _l x_{ij} + \sum _{j=6}^{20} \beta _s x_{ij} + \alpha _i, \end{aligned}$$

(3)

$$\begin{aligned} \pmb {\alpha }\sim & N(\pmb {0}, \kappa \Sigma ), \end{aligned}$$

(4)

where $p_i$ is the probability that $y_i$ is equal to 1, and $\Sigma$ is the kinship matrix. The causal SNPs have heritability in the logit scale varying from 0.01 for small effect sizes to 0.17 for large effect sizes. While the number of cases and controls vary among simulated datasets, the average number of cases and controls for each of the four parameter settings is: (a) 1294 cases and 1478 controls; (b) 1344 cases and 1428 controls; (c) 1374 cases and 1398 controls; and (d) 1397 cases and 1375 controls.

Figure 1 shows the number of true positives (TP), number of false positives (FP), false discovery rate (FDR), F1 score (F1), and computational time for GINA-X, GEMMA, and SuSiE-RSS under the four considered parameter settings. For each setting, all reported values of assessment criteria are averages over 100 simulated datasets. With respect to number of true positives, GEMMA and SuSiE-RSS have the same number, thus we can only see the curve for SuSiE-RSS. In addition, under all settings considered, GINA-X finds substantially more true positives than GEMMA and SuSiE-RSS. That is because, on average, GINA-X is able to detect all five genetic variants with large coefficients and, depending on the setting, three to five genetic variants with smaller coefficients. In contrast, GEMMA and SuSiE-RSS have much more difficulty detecting the genetic variants with smaller coefficients. With respect to number of false positives, GINA-X has on average at most only 3 false positives. In contrast, in the settings considered, GEMMA and SuSiE-RSS have on average more than 100 and 30 false positives, respectively. Consequently, when compared to GEMMA and SuSiE-RSS which have FDR of about 0.95 and 0.85 respectively, GINA-X has much lower FDR between 0.18 and 0.25. With respect to F1 score, while GEMMA and SuSiE-RSS have F1 score of about 0.08 and 0.20 respectively, GINA-X has F1 score between 0.55 and 0.64. Therefore, according to F1 score, GINA-X has the best performance detecting genetic variants. Finally, to compare computational time, we note that SuSiE-RSS requires the prior application of an SMA method. Thus, the figure shows the total computational time of SuSiE-RSS and GEMMA, labeled GEMMA+SuSiE-RSS. The total computational time of GEMMA and SuSiE-RSS is more than 30 min per dataset. In contrast, GINA-X is much faster and, in the settings considered, takes only between 10 and 20 min per dataset.

Fig. 1

Comparison of true positives (TP), false positives (FP), false discovery rate (FDR), F1 score (F1), and computational time for GINA-X, GEMMA, and SuSiE-RSS. Four parameter settings: (1) $\beta _l=1.2$, $\beta _s = 0.3$; (2) $\beta _l=1.6$, $\beta _s = 0.4$; (3) $\beta _l=2$, $\beta _s = 0.5$; (4) $\beta _l=2.4$, $\beta _s = 0.6$. For each setting, all reported values of assessment criteria are averages over 100 simulated datasets.

Simulation study 2: Medium sized datasets with genetic variants identified by GINA-X

This simulation study evaluates the performance of GINA-X and SuSiE-RSS when applied to medium sized datasets with causal genetic variants following the genetic architecture identified by GINA-X. In this simulation study, phenotypes are simulated using real genotypes from the DRIVE breast cancer dataset analyzed in the case study in section “Breast cancer”. Considering only genetic variants with MAF larger than 0.01 and missing rate less than 5%, the sample considered has 21,653 individuals with 410,854 genetic variants. Specifically, 50 phenotype datasets are generated from a Bernoulli GLMM with kinship random effects and with causal genetic variants being the 16 genetic variants identified by GINA-X in the analysis of the DRIVE breast cancer dataset. The regression coefficients in the simulation study are the estimates from the breast cancer dataset based on a GLMM fit with kinship random effects and with all 16 genetic variants included in the model. These regression coefficients range from − 0.222 to 0.168. Causal genetic variants have heritability in the logit scale varying from 0.01 for small effect sizes to 0.07 for large effect sizes. While the number of cases and controls vary among simulated datasets, the average number of cases and controls is 9733 cases and 11,920 controls per dataset.

Table 1 presents TP, FP, FDR, and F1 score averaged over 50 simulated datasets. When compared to SuSiE-RSS, GINA-X finds on average 1.19 more true positives and 7.94 less false positives, leading to a much smaller FDR and a much higher F1 score.

Table 1 Simulation study 2 (genetic architecture identified by GINA-X).

Simulation study 3: Medium sized datasets with genetic variants identified by SuSiE-RSS

This simulation study evaluates the performance of GINA-X and SuSiE-RSS when applied to medium sized datasets with causal genetic variants following the genetic architecture identified by SuSiE-RSS. In this simulation study, phenotypes are simulated using real genotypes from the DRIVE breast cancer dataset analyzed in the case study in section “Breast cancer”. Considering only genetic variants with MAF larger than 0.01 and missing rate less than 5%, the sample considered has 21,653 individuals with 410,854 genetic variants. Specifically, 50 phenotype datasets are generated from a Bernoulli GLMM with kinship random effects and with causal genetic variants being the 24 genetic variants identified by SuSiE-RSS. The regression coefficients in the simulation study are the estimates from the breast cancer dataset based on a GLMM fit with all 24 genetic variants included in the model. These regression coefficients range from − 0.633 to 0.604. The magnitudes of the estimated regression coefficients are related to the fact that many of the SNPs identified by SuSiE-RSS are highly positively correlated, and the corresponding estimated coefficients have large absolute magnitudes but with opposite signs. As a result, the total combined heritability of the genetic variants in this simulation study is actually much smaller than the sum of the squares of the regression coefficients. Thus, for this simulation study, it makes more sense to just consider the total heritability of the causal genetic variants (but not the heritability of each causal genetic variant). Here, the total heritability of the causal genetic variants in the logit scale is 0.23. Finally, in this simulation study, there are on average 9725 cases and 11,928 controls per dataset.

Table 2 presents results averaged over 50 simulated datasets. Specifically, when compared to SuSiE-RSS, GINA-X finds on average 0.42 more true positives and 7.04 less false positives, leading to a much smaller FDR and a higher F1 score. Surprisingly, even in this simulation study where the genetic architecture is the same as estimated by SuSiE-RSS for the breast cancer dataset, GINA-X performs better than SuSiE-RSS.

Table 2 Simulation study 3 (genetic architecture identified by SuSiE-RSS).

Simulation study 4: Medium sized datasets without causal genetic variants

This simulation study evaluates the performance of GINA-X and SuSiE-RSS when applied to medium sized datasets without causal genetic variants. In this simulation study, phenotypes are simulated using real genotypes from the DRIVE breast cancer dataset analyzed in the case study in section “Breast cancer”. Considering only genetic variants with MAF larger than 0.01 and missing rate less than 5%, the sample considered has 21,653 individuals with 410,854 genetic variants. Specifically, 50 phenotype datasets are generated from a null Bernoulli GLMM with kinship random effects but with no causal genetic variants. In this simulation study, there are on average 10,817 cases and 10,836 controls per dataset.

For all 50 simulated datasets, GINA-X does not select any genetic variants. Meanwhile, SuSiE-RSS and GEMMA do not select any genetic variants in 48 datasets, but incorrectly select one or two genetic variants as causal in two datasets. Therefore, in this setting with no causal genetic variants, GINA-X also has favorable performance.

Case studies

To illustrate the applicability of GINA-X to non-Gaussian GWAS data, we present here two case studies: alcohol consumption (count data), and breast cancer diagnosis (binary data). In addition, we compare GINA-X with GEMMA and SuSiE-RSS.

Maximum number of alcoholic drinks

The Collaborative Study on the Genetics of Alcoholism (COGA)²² was a large-scale family research project, primarily aiming to pinpoint genes linked to alcohol dependence. Using this dataset, we apply GINA-X to analyze the maximum number of alcoholic drinks consumed within a 24-h span. We focus on single nucleotide polymorphisms (SNPs) as genetic variants in this case study. The COGA dataset was one of the components of the SAGE dataset used in the simulation study in section “Simulation study 1: Small datasets with large effect sizes”. While the part of the SAGE dataset used in section “Simulation study 1: Small datasets with large effect sizes” considered 2772 European Americans, 13 of those did not have information about the maximum number of alcoholic drinks consumed within a 24-h span. Thus, our analysis encompasses data from 2759 European Americans, evaluating 846,076 SNPs with minor allele frequency (MAF) larger than 0.01 and missing rate less than 5%. For this analysis, we employed Poisson GLMMs. Additionally, we incorporated kinship random effects to accommodate the relatedness across the 2759 participants. Finally, we also included overdispersion random effects in the GLMM to account for extra Poisson variability.

GINA-X identified only one SNP residing within the coding region of the PTGER4 gene on chromosome 5. A likelihood ratio test indicated that the identified SNP does not violate the hypothesis of Hardy-Weinberg equilibrium. The PTGER4 gene encodes a receptor for prostaglandin E2 (PGE2), a molecule implicated in the body’s inflammatory response to alcohol intake. Notably, PGE2’s involvement in inflammation is consistent with the observation that tolfenamic acid, a PGE2 inhibitor, significantly mitigates a range of hangover symptoms. Conversely, GEMMA and SuSiE-RSS identify the same 9 SNPs. Importantly, while in the first iteration of GINA-X the screening step identifies a total of 10 SNPs that include the 9 SNPs identified by SuSiE-RSS and GEMMA, the variable selection step reduces that to just 1 identified causal SNP. Finally, GINA-X converges in the second iteration with just that one identified SNP. We have evaluated the predictive performance of the SNPs identified by GINA-X and SuSiE-RSS with a tenfold cross validation. Because the maximum number of alcoholic drinks is a count variable, we compare predictive performance using the mean squared prediction error (MSPE). While the MSPE of SuSiE-RSS based on 9 SNPs is 264.18, the MSPE of GINA-X based on only 1 SNP is 263.97. Therefore, by providing a more focused list of SNPs and avoiding false positives, GINA-X leads to better predictive performance.

Breast cancer

The analysis of GWAS data has played an important role in identifying genetic variants associated with breast cancer. Discovery, Biology, and Risk of Inherited Variants in Breast Cancer (DRIVE) was a project part of the NCI’s Genetic Associations and Mechanisms in Oncology (GAME-ON) initiative (http://epi.grants.cancer.gov/gameon/). The DRIVE dataset has 60,015 breast cancer cases and controls, and is composed by 10 consent groups. Here, we focus on consent group 8, which is the general research use (GRU) group. Considering only genetic variants with MAF larger than 0.01 and missing rate less than 5%, the sample considered has 21,653 subjects with 410,854 genetic variants. For this analysis, we employed Bernoulli GLMMs with kinship random effects to accommodate the relatedness across the 21,653 subjects.

In the analysis of this breast cancer dataset, GINA-X identified a total of 16 genetic variants, 5 of which have not been reported in the breast cancer literature (details in the Supplementary Material). Likelihood ratio tests indicated that none of the identified genetic variants violate the hypothesis of Hardy-Weinberg equilibrium. Meanwhile, GEMMA and SuSiE-RSS found 63 and 24 genetic variants, respectively. Of importance, while the 24 genetic variants found by SuSiE-RSS are located in only 6 regions of interest, the genetic variants found by GINA-X are located in 16 regions of interest. Therefore, GINA-X finds causal genetic variants in 10 additional regions of interest.

Fig. 2

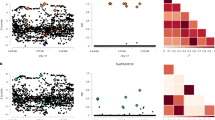
GINA-X analysis of breast cancer data. Posterior probabilities of genetic variants for screening step and variable selection step in the first three iterations. Green dots indicate identified genetic variants at each step. Iteration 4 is not shown because no new SNPs were identified and the results were the same as in Iteration 3. The genetic variants identified at the last iteration of GINA-X belong to 16 distinct regions of interest.

Fig. 3

SuSiE-RSS analysis of breat cancer dataset. Posterior probabilities of genetic variants in the regions of interest. Green dots indicate identified genetic variants. The genetic variants identified by SuSiE-RSS belong to 6 distinct regions of interest, a reduction of 10 regions of interest when compared to GINA-X results.

Figure 2 provides a visual understanding of the progression of GINA-X through the iterations. In this breast cancer case study, GINA-X converged in 4 iterations. Because the fourth iteration is similar to the third iteration, Fig. 2 shows only the first three iterations. For each iteration, Fig. 2 shows the posterior probabilities of the genetic variants given by the screening step and by the variable selection step. In the first iteration, GINA-X’s screening step found 137 candidate genetic variants. Due to linkage disequilibrium, many of the genetic variants are clustered, such as a cluster in chromosome 5. Then, the variable selection step reduces this list of 137 genetic variants to just 13 genetic variants. These 13 variants are included in the baseline model for the second iteration. In the second iteration, the screening step finds 46 additional candidate genetic variants that are reduced by the variable selection step to 2 genetic variants. Then, the number of genetic variants in the baseline model for the third iteration increases to 15. In the third iteration, the screening step finds 44 additional candidate genetic variants, and the variable selection step selects one more genetic variant than those in the second iteration. In the fourth iteration, GINA-X does not find additional candidate genetic variants, and thus, the algorithm converges and reports 16 genetic variants.

For comparison, Fig. 3 shows the posterior probabilities of the 24 genetic variants in the 6 regions of interest considered by SuSiE-RSS. These are the regions of interest initially found by GEMMA. Importantly, GINA-X not only finds these 6 regions, but also finds 10 additional regions of interest.

We have evaluated the predictive ability of the genetic variants identified by GINA-X and SuSiE-RSS with a tenfold cross validation. Because the indicator of breast cancer case is a binary variable, in this study we compare predictive performance with the area under the curve (AUC) of the receiver operating characteristic (ROC) curve. Larger AUC indicates better predictive performance. While the AUC for SuSiE-RSS is 0.5736, GINA-X provides a larger AUC which is equal to 0.5912. Therefore, by providing a more focused list of SNPs, avoiding false positives, and finding more regions of interest, GINA-X leads to better predictive performance.

Discussion

When compared to the competing fine-mapping method SuSiE-RSS, GINA-X has favorable statistical performance. Specifically, a simulation study shows that GINA-X is able to detect more true positives than SuSiE-RSS. In addition, GINA-X has a much lower false discovery rate than SuSiE-RSS. Further, GINA-X is able to detect causal genetic variants in regions not detected by traditional SMA and fine-mapping methods. To validate these simulation study findings, we applied GINA-X and SuSiE-RSS to an alcohol use disorder dataset and a breast cancer dataset. For both datasets, GINA-X provided smaller more focused lists of potentially causal SNPs. In addition, for the breast cancer dataset, the smaller number of SNPs found by GINA-X covered 10 additional regions of interest not identified by SuSiE-RSS. To compare the predictive ability of these fine-mapping methods, we performed tenfold cross validation studies for the two datasets. For both datasets, when compared to SuSiE-RSS, the more focused list of potentially causal SNPs provided by GINA-X has better predictive performance. Therefore, GINA-X has lower FDR, higher recall, and leads to better out-of-sample predictive performance.

GINA-X is designed for the analysis of polygenic traits that exhibit a combination of sparse moderate to strong effect sizes from a relatively small number of genetic variants and infinitesimal contributions from all the other genetic variants. The infinitesimal contributions are modeled by GINA-X through relatedness kinship random effects. Thus, GINA-X will only report a relatively small number of genetic variants with moderate to strong effect sizes. In addition, as our simulation study in the new section “Simulation study 4: Medium sized datasets without causal genetic variants” shows, if the genetic architecture has only infinitesimal contributions from all genetic variants, then GINA-X will usually not report any causal genetic variant. Finally, we note that in cases with genetic architecture with a few genetic variants with moderate to strong effects and infinitesimal contributions from thousands of other genetic variants, there may be scientific, economic, and/or medical value in identifying the genetic variants with moderate to strong effects.

Because of its two-step nature, GINA-X may not be adequate for cases with complex interaction effects among genetic variants. This is because GINA-X screening step fits single-SNP GLMMs, which could overlook interacting genetic variants with weak main effects. In contrast, if the interacting genetic variants have main effects strong enough to be detected by GINA-X screening step, then a modification of GINA-X variable selection step could be able to detect complex interactions among genetic variants. This is a potentially useful future research direction.

Another current limitation of GINA-X is related to scalability. Currently, GINA-X is computationally feasible for datasets with sample sizes of order $10^4$. For example, for the DRIVE breast cancer dataset with sample size $n=21,653$ and $p=410,854$ genetic variants, GINA-X takes about 10 h. In its current implementation, GINA-X computations scale cubicly with sample size. Hence, GINA-X is not computationally feasible for biobank scale data. Therefore, a promising future research direction is to extend GINA-X for the analysis of biobank scale data.

There are many other promising avenues for future research. One highly useful extension is to develop GINA-X for the analysis of survival time data. This may be useful to identify genetic variants that lead to early onset of diseases. Another promising extension of GINA-X is to integrate information about functional annotations in a way similar to that of the recently proposed methods CARMA²³ and Funmap²⁴. Further, connected with its extension for the analysis of larger datasets, an open question is whether GINA-X would produce calibrated FDR in the analysis of biobank scale data. Finally, we anticipate that the application of GINA-X to existing genetic/phenotype datasets may identify many currently undiscovered causal genetic variants.

Methods

Screening step

In the screening step, GINA-X fits a baseline GLMM with covariates $X_B$ to obtain adjusted observations $\pmb {y}^\star$ and estimates $\widehat{\pmb {\beta }}_B$, $\widehat{\kappa }_1$, $\widehat{\kappa }_2$, and $\widehat{V}$. After that, GINA-X fits one GLMM for each genetic variant which is not in the baseline model. To fit these GLMMs. GINA-X takes a pseudo-likelihood approach²⁵ that uses $\pmb {y}^\star$, $\widehat{\pmb {\beta }}_B$, $\widehat{\kappa }_1$, $\widehat{\kappa }_2$, and $\widehat{V}$ obtained from the baseline model. Let $\pmb {x}_s$ be the vector of covariate genetic variant s, and $\beta _s$ be the coefficient of genetic variant s. This pseudo-likelihood approach approximates the GLMM for genetic variant s by the LMM

$$\begin{aligned} \pmb {y}^\star= & X_B \widehat{\pmb {\beta }}_B + \pmb {x}_s \beta _s+ \pmb {\alpha }_1 + \pmb {\alpha }_2 + \widehat{V}^{-1}\pmb {\epsilon }. \end{aligned}$$

(5)

Integrating out the vectors of random effects $\pmb {\alpha }_1$ and $\pmb {\alpha }_2$, the adjusted observations $\pmb {y}^\star$ can be approximately modeled by the multivariate Gaussian distribution $N(X_B \widehat{\pmb {\beta }}_B + \pmb {x}_s \beta _s, \widehat{H})$, where $\widehat{H}= \widehat{\kappa }_1\Sigma + \widehat{\kappa }_2 I+ \widehat{V}^{-1}$.

Consider the spectral decomposition $\widehat{H}=PDP^\top$. Let $\widetilde{\pmb {y}} = P^\top (\pmb {y}^\star -X_B\widehat{\pmb {\beta }}_B)$ and $\widetilde{\pmb {x}}_s = P^\top \pmb {x}_s$. Then, an estimator of $\beta _s$ is $\widehat{\beta }_s = (\widetilde{\pmb {x}}_s^\top D^{-1} \widetilde{\pmb {x}}_s)^{-1} \widetilde{\pmb {x}}_s^\top D^{-1} \widetilde{y}$, which has an approximate distribution $N(\beta _s, \sigma ^2_s)$, where $\sigma ^2_s = var( \widehat{\beta }_s) = (\widetilde{\pmb {x}}_s^\top D^{-1} \widetilde{\pmb {x}}_s)^{-1}.$

Let $\pi _0$ be the probability that genetic variant s is not in the model. We use a mixture prior for $\beta _s$, that is

$$\begin{aligned} p(\beta _s|\pi _0,g)= & \pi _0 \delta (\beta _s = 0) + (1-\pi _0) \pi (\beta _s|g), \end{aligned}$$

(6)

where $\pi (\beta _s|g)$ is the prior density for $\beta _s$ when genetic variant s is in the model. We assume for $\beta _s$ a prior similar to a Zellner g prior given by $\pi (\beta _s|g) = N(\beta _s|0,g \sigma _s^2)$. Then, the marginal density of $\widehat{\beta }_s$ is

$$\begin{aligned} p( \widehat{\beta }_s|\tau ,\pi _0)= & \int p( \widehat{\beta }_s|\beta _s) p(\beta _s|\tau ,\pi _0) \, d\beta _s. \end{aligned}$$

(7)

Assuming that $\widehat{\beta }_1, \ldots , \widehat{\beta }_p$ are conditionally independent given $\pi _0$ and g, the likelihood function of $\pi _0$ and g is

$$\begin{aligned} L(\widehat{\beta }_1, \ldots , \widehat{\beta }_p|\pi _0, g)= & \prod _{s=1}^{p} p( \widehat{\beta }_s|\pi _0, g). \end{aligned}$$

(8)

Let $\pi (\pi _0)$ and $\pi (g)$ be the prior densities of $\pi _0$ and g, respectively. Specifically, we use non-informative flat prior $\pi (\pi _0)\propto 1$ and $\pi (g)\propto 1$. Thus, the joint posterior density of $\pi _0$ and g is

$$\begin{aligned} \pi (\pi _0, g| \widehat{\beta }_1, \ldots , \widehat{\beta }_p)\propto & \pi (\pi _0) \pi (g) L(\widehat{\beta }_1, \ldots , \widehat{\beta }_p|\pi _0, g). \end{aligned}$$

(9)

We use the posterior modes $\widehat{\pi }_0$ and $\widehat{g}$ to estimate $\pi _0$ and g. We then calculate the posterior probability for each regressor genetic variant s in the screening step as

$$\begin{aligned} P(\beta _s \ne 0 | \widehat{\beta }_s, \widehat{\pi }_0, \widehat{g})= & 1 - \frac{\widehat{\pi }_0 N( \widehat{\beta _s}|0,\sigma _s^2)}{p( \widehat{\beta }_s|\widehat{\pi }_0, \widehat{g})}. \end{aligned}$$

(10)

After that, we apply Bayesian FDR control^4,5,6,7 to the posterior probabilities of all genetic variants with nominal FDR at 5% and select a list of candidate genetic variants.

Variable selection step

In the variable selection step, we consider all combinations of candidate genetic variants from the screening step as the candidate models. Assume we obtain k candidate genetic variants from the screening step. The variable selection step considers $S=2^k$ possible models. Let $M_m$ be the $m^{th}$ model with $p_m$ genetic variants, $m=1, \dots , S$.

As mentioned in section “Overview of the method”, we use baseline model to obtain the adjusted observations $\pmb {y}^\star$ and estimates of $\pmb {\beta }_B$, $\kappa _1$ and $\kappa _2$. In the model selecting step, the baseline model is the full model with all k candidate genetic variants. Then, we assume all possible models have the same adjusted observations. Let $X_m$ be the matrix of genetic variants in model $M_m$, and $\pmb {\beta }_m$ be the corresponding vector of regression coefficients. The general model is:

$$\begin{aligned} \pmb {y}^\star= & X_B \widehat{\pmb {\beta }}_B + X_m \pmb {\beta }_m + \pmb {\alpha }_1 + \pmb {\alpha }_2 + \widehat{V}^{-1}\pmb {\epsilon } \end{aligned}$$

(11)

The adjusted observations $\pmb {y}^\star$ can be approximately modeled by a multivariate Gaussian distribution $N(X_B \widehat{\pmb {\beta }}_B + X_m \pmb {\beta }_m, \widehat{H})$, where $\widehat{H}=\widehat{\kappa }_1\Sigma +\widehat{\kappa }_2 I + \widehat{V}^{-1}$. Consider the spectral decomposition $\widehat{H}=PDP^\top$. Let $\widetilde{\pmb {y}}=P^\top (\pmb {y}^\star - X_B\widehat{\pmb {\beta }}_B)$ and $\widetilde{X}_m = P^\top X_m$. Then, conditional on $\pmb {\beta }_m$, the vector of transformed adjusted observations $\widetilde{\pmb {y}}$ is approximately distributed as $N(\widetilde{X}_m \pmb {\beta }_m, D)$. For $\pmb {\beta }_m$ we assign a prior distribution inspired by the well-known Zellner-g prior for linear models^26,27. Specifically, the prior density for $\pmb {\beta }_m$ conditional on model $M_m$ is $\pi (\pmb {\beta }_m|M_m) \sim N(\pmb {\beta }_m|\pmb {0},\hat{g}(\tilde{X}_m^\top D^{-1} \tilde{X}_m)^{-1}),$ where $\hat{g}$ is the estimate from the screening step. Then, by integrating out $\pmb {\beta }_m$ we can obtain the marginal density $m(\widetilde{\pmb {y}}|M_m)$, which is

$$\begin{aligned} m(\tilde{\pmb {y}}|M_m)= & \int N(\tilde{\pmb {y}}|\tilde{X}_m \pmb {\beta }_m,D) N(\pmb {\beta }_m | \pmb {0}, \hat{g}(\tilde{X}_m^\top D^{-1} \tilde{X}_m)^{-1}) \, d \pmb {\beta }_m \nonumber \\= & (2\pi )^{-n/2} (\hat{g}+1)^{-p_m/2} |D|^{-1/2} \nonumber \\ & \exp { \left[ -\frac{1}{2}\tilde{\pmb {y}}^\top D^{-1} \tilde{\pmb {y}}+\frac{1}{2}\tilde{\pmb {y}}^\top D^{-1} \tilde{X}_m (\frac{\hat{g}+1}{\hat{g}} \tilde{X}_m^\top D^{-1} \tilde{X}_m)^{-1} \tilde{X}_m^\top D^{-1} \tilde{\pmb {y}} \right] }. \end{aligned}$$

(12)

The prior probability for model $M_m$ is $P(M_m)=\widehat{\pi }_0^{k -p_m} (1- \widehat{\pi }_0)^{p_m}$, where $\widehat{\pi }_0$ is the estimate from the screening step in the first GINA-X iteration. Then, the posterior probability of model $M_m$ is

$$\begin{aligned} P(M_m|\widetilde{\pmb {y}})\propto & P(M_m) m(\widetilde{\pmb {y}}|M_m). \end{aligned}$$

(13)

GINA-X reports the genetic variants in the model with the highest posterior probability.