Grid tied hybrid PV fuel cell system with energy storage and ANFIS based MPPT for smart EV charging

Abstract

This paper presents the comprehensive design, simulation, and experimental validation of a grid-tied hybrid renewable energy system tailored for electric vehicle (EV) charging applications. The proposed system integrates photovoltaic (PV) panels, a proton-exchange membrane fuel cell, battery storage, and a supercapacitor to ensure reliable and efficient power delivery. An adaptive neuro-fuzzy inference system (ANFIS)-based maximum power point tracking (MPPT) algorithm is employed to enhance PV power extraction under dynamically varying environmental conditions. Simulation results demonstrate effective voltage boosting from 110 V to 150 V and a regulated output of approximately 1100 V at 30 A, with the PV-side current stabilized at 500 A. The fuel cell maintains a steady output of 110 V while its current decreases from 40 A to 25 A, and the battery retains a 60% state-of-charge (SOC) at 120 V output. The hardware prototype, developed using a DSPIC30F4011 microcontroller, achieves an MPPT efficiency of 98.7%, voltage regulation within ± 1.5%, and output power deviation under 2%. Grid voltage and current waveforms exhibit low total harmonic distortion (THD), in compliance with IEEE 519 standards, with measured values of 500 V and 13 A, respectively. The proposed architecture offers enhanced transient response, high energy efficiency, and superior power quality, positioning it as a promising solution for next-generation smart EV charging stations.

Introduction

Energy storage systems (ESS) are crucial for integrating intermittent renewable energy in microgrids. Electric vehicle (EV) batteries serve as storage units when plugged in, as most vehicles remain idle for around 18 h per day. Through grid-to-vehicle (G2V) and vehicle-to-grid (V2G) operations, EVs aid in microgrid energy management by storing surplus power and supplying it back when needed. While V2G in large grids faces challenges like control complexity, EV availability, and slow adoption, its implementation in microgrids is simpler and more feasible.

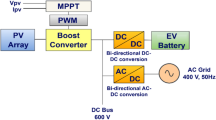
The Society of Automotive Engineers (SAE) defines three charging levels for electric vehicles (EVs). Level 1 uses a standard 120 V household outlet, while Level 2 provides 220 V–240 V at up to 30 A through an EVSE at home or public stations. Level 3 (DC fast charging) delivers up to 90 kW at 200–450 V, cutting charge time to 20–30 min. For vehicle-to-grid (V2G) integration in microgrids, DC fast charging is preferred due to its rapid power transfer capability when using EVs as energy storage units¹.

The global energy demand is rising, necessitating a shift toward renewable energy sources (RES) such as solar PV and fuel cells (FCs) due to their abundance, cost-effectiveness, and environmental benefits. Many rural communities still lack reliable electricity, as traditional grid expansion requires high initial investment. However, DC microgrids powered by PV, fuel cells, and energy storage systems (ESS) offer a cost-effective and efficient solution. Unlike AC grids, DC microgrids eliminate complex frequency and reactive power issues while seamlessly integrating distributed generation using DC-DC converters².

DC microgrids are gaining popularity due to their high energy efficiency, reduced transmission losses, and easier configuration shown in Fig. 1. Since distributed energy resources (DERs) like fuel cells and solar panels generate DC power, the system ensures greater reliability and stability. Additionally, DC microgrids are more power-efficient than AC systems and allow for seamless energy storage integration. This study proposes a hybrid energy storage system combining a supercapacitor and a lithium-ion battery to enhance power capability and system performance³.

This paper addresses voltage stability enhancement in a PV–fuel cell-based DC microgrid by employing various MPPT techniques. Various control methods, including fuzzy logic, neural networks, and particle swarm optimization (PSO), are evaluated for DC-DC boost converters. MPPT is vital for maximizing PV output, but traditional methods struggle under partial shading due to multiple P–V peaks. While PSO offers improved tracking, its slow response limits performance. The hybrid Kalman–PSO approach improves efficiency by over 10% compared to PSO and 30% over P and O, while reducing tracking time by up to 99.998%⁴. Ahessab et al. proposed to maximize the electrical output of solar energy systems by exploring MPPT methods that enhance PV system efficiency. Among various renewable sources, solar power is highlighted for its abundance and cleanliness. A detailed comparison of two widely used MPPT algorithms—Fuzzy Logic and Perturb and Observe (P&O)—is conducted through simulation-based analysis to evaluate their performance in optimizing energy conversion⁵.

Fig. 1

Schematic diagram of DC microgrid.

The adoption of solar energy via PV arrays is rapidly growing due to its cleanliness and sustainability. However, fluctuations in load can shift the operating point away from the maximum power point (MPP), reducing efficiency. To address this, the paper proposes a hybrid MPPT method combining Artificial Neural Networks (ANN) and Fuzzy Logic Control (FLC). ANN estimates the MPP voltage based on varying irradiation and temperature, while FLC refines this value to reduce voltage error. Simulated in MATLAB/Simulink, the ANN-Fuzzy hybrid demonstrates superior tracking under dynamic conditions. Extracted power is stored in lithium-ion batteries and injected into the smart grid via a PID-controlled inverter with an LC filter. A buck-boost converter with PID control manages battery charging and discharging. The study highlights the improved performance of the hybrid ANN-Fuzzy MPPT and the overall efficiency of the integrated power conversion system⁶.

The main objective of this paper is to design and validate a grid-connected hybrid renewable energy system that integrates photovoltaic (PV) panels, a fuel cell, battery storage, and a supercapacitor to support smart EV charging infrastructure. The proposed system aims to enhance energy conversion efficiency, ensure stable voltage and current levels under dynamic load conditions, and maintain compliance with grid standards. To achieve this, an adaptive neuro-fuzzy inference system (ANFIS)-based MPPT controller is implemented to optimize PV power extraction. A Z-source integrated boost converter and bidirectional battery interface are employed for effective power management. The paper includes detailed simulation and experimental validation to assess the system’s performance in terms of MPPT efficiency, power quality, grid synchronization, and overall system stability.

The rest of the paper is structured as follows: Section “Literature review” outlines the literature review and its novel contributions. Section “Configuration of conventional EV charging system” details system configuration. Section “Design and analysis of proposed EV micro-grid system” describes the proposed system block diagram, components modeling, control strategy including the ANFIS-based MPPT and converter design. Section “Results and discussions” presents simulation results under various operating conditions and the hardware prototype and experimental validation. Section “Conclusion” concludes the paper with future research directions.

Literature review

Microgrids (MGs) are widely used in rural and remote areas where connecting to large power grids is costly and environmentally challenging. However, MGs rely on distributed and intermittent renewable energy sources (RESs), requiring effective management for optimal distribution and utilization. One key challenge is frequency control in isolated MGs, especially with the increasing integration of RES-based distributed generation (DG). The emergence of smart grids (SGs) is shifting power systems from centralized to more flexible structures, improving cost efficiency, power quality, and reliability. However, RESs in high-penetration grids have low inertia and damping, posing additional stability concerns.

Yeong Zou et al. proposed an MG load frequency model integrating PV, fuel cells, wind turbines, BESS, and diesel generators. They designed an optimal mixed H2/H ∞ robust controller to minimize frequency fluctuations using hybrid particle swarm optimization and gravitational search (CPSOGSA). Their approach enhances MG control, which is more complex than large grid-connected systems⁷.

Irfan Sami et al. highlight the increasing use of renewable energy in traditional grids to protect the environment. While large hydropower plants face environmental and social challenges, micro-hydro power plants (MHPPs) serve as a viable alternative with mature balancing technology. Pump storage MHPPs use power converters for grid integration and can also operate in standalone mode without grid connection⁸.

Qian Cao et al. addressed distributed frequency control and economic dispatch in microgrids. They formulated an optimal frequency control problem using a nonlinear second-order dynamic model, balancing frequency regulation and cost minimization. To solve this, they proposed a distributed finite-time consensus method for optimal frequency regulation⁹.

Mustafa Al-Tamiami et al. introduced a low-frequency AC (LFAC) transmission network to enhance frequency stability in remote AC grids. Using modular multilevel matrix converters (M3Cs) for instantaneous AC-AC conversion, LFAC serves as an alternative for long-distance power transmission. A key application is connecting large AC grids to isolated grids, which often suffer from frequency fluctuations due to low inertia¹⁰.

Babak Abdolmaleki et al. proposed a droop-based microgrid with distributed switched control to regulate frequency and minimize generation costs, considering generator and line power constraints. Using a consensus algorithm and Lagrange method, they optimize cost based on the equal incremental cost criterion. Additionally, they introduce an online network reconfiguration that bypasses distributed generators when they exceed limits, disconnect, or overload. This reconfiguration is mathematically proven as a distributed online Kron reduction, forming a reduced data network¹¹.

M. A. Rustam et al. highlighted challenges in microgrids due to irregular renewable energy sources like solar and wind, including stochastic power generation, supply-demand mismatches, and frequency fluctuations. To address these, they proposed a distributed secondary control scheme for frequency regulation and economic load dispatch, considering variable operating costs¹².

Bowen Chen et al. developed a synthesizer using an injection-locked frequency tripler (ILFT) cascaded with a fractional-N 9-GHz charge-pump phase-locked loop (CPPLL). The ultra-wideband CPPLL incorporates a charge pump (CP), a voltage-controlled oscillator (VCO) with transformer (TFM) coupling, and a weakly coupled TFM for improved linearity, isolation, and broadband locking range¹³.

Qian Zhang et al. analyzed microgrid frequency stability, which is affected by distributed generators and energy storage systems. They proposed a virtual synchronous generator (VSG)-based self-adapting secondary frequency regulation (FR) scheme for a microgrid integrating electric vehicles, photovoltaic arrays, and wind turbines. Using proportional-integral control, their method enables error-free frequency regulation while improving efficiency and mitigating reserve capacity constraints¹⁴.

Choux Mu et al. addressed microgrid frequency control challenges caused by stochastic power generation and dynamic uncertainties. They proposed an adaptive dynamic programming (ADP)-based intelligent control strategy for frequency stability in PV-integrated microgrids, adjusting the power outputs of micro-turbines and energy storage systems (ESS)¹⁵.

Babak Abdolmaleki et al. developed a frequency and active power-sharing control method for event-triggered communications in inverter-based microgrids. They introduced a proportional-integral consensus-based control that optimizes distributed generator data exchange on a need-based (event-triggered) basis. Their fully distributed communication network architecture reduces data transmission while maintaining system stability, even in Zeno behavior scenarios¹⁶.

Jaime Addin Routen et al. highlighted the growing importance of distributed generation, microgrids, electromobility, and energy storage in reducing greenhouse gas emissions. They discussed challenges in islanded microgrids and weak grids, where voltage and frequency fluctuations occur due to low inertia. To ensure system stability, electrical loads must be resilient to these variations and avoid triggering protection mechanisms¹⁷.

Tarek Hassan Mohamed et al. introduced a modified water cycle algorithm (WCA) with a Balloon Effect for adaptive control. This optimization technique fine-tunes PID controller gains over the internet, improving load frequency control in microgrids and position control in DC motors. Digital simulations confirm the effectiveness, reliability, and cost-efficiency of this flexible controller-based approach¹⁸.

Cheng Huang et al. developed a graphene capacitor integrated with an active frequency selective surface (FSS) loaded with varactors. By modulating bias voltages, they independently controlled the engulf frequency and amplitude, enabling dynamic tunability of reflectivity through graphene resistance adjustments¹⁹.

Aslan Mojela et al. proposed a nonlinear supplementary controller to enhance the transient response of distributed generation (DGs) in microgrids. Using a Port-Controlled Hamiltonian (PCH) model and Interconnection and Damping Assignment Passivity-Based Control (IDA-PBC), their approach ensures smooth transitions between islanded and grid-connected modes within a decentralized DG control scheme²⁰.

Mobin Naderi et al. proposed a low-order, low-frequency small-signal model for large-scale interconnected AC microgrids to facilitate high-level control synthesis and stability analysis. Using a sensitivity-based approach, they identified key inverter-based components, eliminating unnecessary modules to optimize AC microgrid modeling with droop-based and electronically controlled distributed generation units²¹.

Yuan Yu et al. developed a frequency-stabilized optoelectronic oscillator (OEO) using a high-Q silicon microring resonator (MRR). A feedback control loop with threshold detection stabilizes the MRR’s resonant wavelengths, reducing phase noise. They emphasized temperature stabilization and oscillation frequency control to improve performance, with potential for monolithic integration of micro-cavity-based OEOs²².

Jesus Lopez-Gomez et al. developed a firmware-based PWM module and implemented P, PD, and PID controllers on an FPGA-based microprocessor. Their approach achieves performance comparable to commercial servo amplifiers, utilizing PWM duty cycles to regulate torque output and establish a linear relationship in a DC motor control system²³.

Xun Chen et al. proposed a macro-micro combined stage system with dynamic perturbations and interconnections to address the optimal stabilization problem. By reformulating the stabilization challenge as an optimal control problem, they developed a novel cost function, enabling efficient control of interconnected subsystems²⁴.

Zhou et al. presented a comprehensive review of energy management strategies for hybrid renewable energy systems (HRES), emphasizing the integration of fuzzy logic and artificial intelligence (AI) techniques. The paper highlights how intelligent control methods enhance system efficiency, reliability, and adaptability under dynamic conditions, especially in multi-source configurations like PV–wind–battery systems²⁵.

Maharjan, L., et al. introduces an advanced control strategy for a grid-connected hybrid PV–fuel cell system with energy storage. The authors propose a robust hierarchical control framework that ensures stable power flow, improved dynamic response, and enhanced grid compliance. The integration of storage elements further enhances system flexibility and reliability²⁶.

Arif et al. provided a comparative analysis of various AI-based Maximum Power Point Tracking (MPPT) algorithms for photovoltaic (PV) systems. The study evaluates the performance of techniques such as neural networks, fuzzy logic, and ANFIS under different irradiance and temperature profiles, offering valuable insights into their accuracy, convergence speed, and computational efficiency²⁷.

Kaur and Jain developed an ANFIS-based MPPT controller tailored for solar PV systems operating under partial shading conditions. The hybrid intelligence approach effectively mitigates power losses and tracks the global maximum power point with high precision, outperforming traditional MPPT methods in complex shading scenarios²⁸.

Farhadi, M., & Mohamed, Y. A. R. I. investigated the energy management of hybrid systems employing Z-source converters. Farhadi and Mohamed propose control schemes that optimize the performance of these converters in multi-source environments, ensuring efficient power sharing and voltage regulation while enhancing the overall resilience of the hybrid setup²⁹.

Chaudhary et al. introduced a modified Z-source inverter designed for efficient renewable energy integration. The study details improvements in voltage boosting capability and reduced harmonic distortion, making it suitable for interfacing variable renewable sources with the grid or standalone loads³⁰.

Patel et al. presented a review focused on grid integration challenges of renewable energy sources, with special attention to Total Harmonic Distortion (THD) control. The paper discusses existing standards, mitigation techniques, and control strategies to ensure power quality and compliance with regulatory norms in renewable-rich grid scenarios³¹.

The novelty of this work lies in the integrated design and experimental validation of a smart, grid-connected hybrid energy system that combines photovoltaic (PV) panels, a proton exchange membrane fuel cell (PEMFC), battery storage, and supercapacitors, optimized for electric vehicle (EV) charging infrastructure. Key contributions of this paper includes:

• 1. The use of an Adaptive Neuro-Fuzzy Inference System (ANFIS) enables dynamic tuning of membership functions and fuzzy rules, leading to significantly improved MPPT efficiency (98.7%) over traditional PI or perturb-and-observe methods.

• 2. Incorporates a modified Z-source boost stage that enhances voltage gain and stabilizes output with minimal overshoot and ripple—an improvement over classical boost converters.

• 3. The system is successfully implemented on a DSPIC30F4011 controller, bridging the gap between simulation and real-time operation—an aspect often missing in related works.

• 4. Harmonic analysis demonstrates compliance with IEEE 519 standards, achieving a THD of only 2.1%, which is superior to most conventional topologies.

• 5. Unlike prior work that focuses on isolated PV or fuel cell systems, this study enables coordinated energy management between all four sources using AI-based logic, ensuring reliability and extended battery life.

Configuration of conventional EV charging system

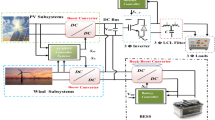
This paper proposes a supervisory control system (SCS) for a microgrid with Z-source converters (ZSCs), ensuring power balance and revenue generation by selling excess energy to the grid. The microgrid integrates a medium voltage DC (MVDC) link, connecting renewable sources, energy storage systems (ESSs), and EV charging stations. It consists of a solar energy system, battery storage, and a hydrogen-based ESS (including a fuel cell, electrolyzer, and hydrogen reservoir), along with a local grid connection and two EV fast chargers.

Under normal conditions, the microgrid operates independently, but the grid steps in only when PV or ESS fails to maintain balance. The system includes two 50 kW fast-charging units, managed by DC/DC ZSC-equipped off-board chargers, with the PV system as the primary energy source, requiring a peak power exceeding the combined fast-charging demand. The complete setup of the optimized MVDC a microgrid for the electric vehicle (EV) charging station is depicted in Fig. 2.

Fig. 2

Configuration of conventional system.

The PV system has a peak power of 186 kW and is supported by two energy storage systems (ESSs): a lead-acid battery (BAT) and a hydrogen-based system. The hydrogen ESS, including a 176 kVA hydrogen production system, six 66 kW fuel cell (FC) modules, and a 450 kg hydrogen tank, provides additional energy when PV and BAT cannot meet demand.

The system is integrated using Z-source converters (ZSCs), where an impedance network connects the PV system, BAT, and the grid. The grid links to the AC side, PV to the DC side, and BAT to the impedance network in parallel. The impedance network also serves as the MVDC (≈ 1800 V) link for other ZSCs, offering voltage regulation and reducing the need for extra power converters. In the MVDC microgrid, the PV system operates at its maximum power point, but its output rarely matches the EV load demand. To maintain power balance, the ESS (BAT or hydrogen system) compensates for this difference, represented as net power (P_net).

Design and analysis of proposed EV micro-grid system

EV charging stations provide electricity for charging electric vehicles (EVs), reducing pollution and fossil fuel dependence. However, increased power demand strains the grid, necessitating renewable energy sources (RESs) for sustainable energy production. Photovoltaic (PV) technology is the most cost-effective and reliable RES, but its intermittent nature poses challenges like power fluctuations and microgrid stability. Battery backup systems play a crucial role in ensuring grid reliability, resilience, and continuous power supply.

A three-phase grid-connected PV system using a high-gain single-switch DC-DC Z Source Integrated Boost converter is proposed for EV charging shown in Fig. 3. MPPT (ANFIS algorithm) ensures maximum power extraction, addressing voltage fluctuations. The Z Source converter offers advantages over conventional DC-DC converters, while PWM generators control the inverter and converter. The system’s steady-state and transient response are analyzed, demonstrating its efficient operation. Additionally, a PI-controlled Z Source Boost converter enhances fuel cell voltage.

PV system

Photovoltaic (PV) systems convert solar energy into electricity using the photovoltaic effect. Their efficiency depends on the material and arrangement of solar cells, with gallium arsenide (29%) being more efficient than silicon (12–14%). Performance is affected by temperature and load conditions, requiring Maximum Power Point Tracking (MPPT) for optimal energy extraction.

Fig. 3

Block Diagram of Proposed System.

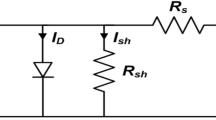
The following is a description of the PV cell’s electrical equivalent diode model shown in Fig. 4. The electrical equivalent model of a PV cell consists of a diode, shunt resistance (R_sh), series resistance (R_s), and a current source. The shunt resistance (R_sh) represents leakage at the cell’s edges, while the overall current (I) is derived from the light-generated current (I_Ph), shunt resistance (R_sh), and diode current (I_d)².

Fig. 4

Equivalent Circuit of PV Cell.

$$\:I={I}_{ph}-{I}_{d}-{I}_{sh}$$

(1)

Equations (2) and (3) show the Diode current I_d and Shunt Resistance current I_sh

$$\:{I}_{d}={I}_{0}\left\{\text{exp}\left[\frac{q}{{mkT}_{c}}\left(V+I{R}_{s}\right)\right]-1\right\}$$

(2)

$$\:{I}_{sh}=\frac{V+{IR}_{s}}{{R}_{sh}}$$

(3)

$\:{I}_{0}$ = Cell reverse saturation current

K = Boltzmann constant.

M = Idealizing factor.

V = Potential across cell.

q = Charge of electron.

$\:{T}_{c}$ = Absolute temperature of cell

Equations are used to show the following

$$\:I={I}_{G}-{I}_{0}\left\{exp\left[\frac{q}{mk{T}_{c}}\left(V+I{R}_{s}\right)\right]-1\right\}-\frac{V+I{R}_{s}}{{R}_{sh}}$$

(4)

Most often shunt PV cells have strong $\:{R}_{sh}$ resistance, which results in the elimination of$\:\:\:\frac{V+I{R}_{s}}{{R}_{sh}}$. Hence,

$$\:I={I}_{G}-{I}_{0}\left\{exp\left[\frac{V+I{R}_{s}}{A}\right]-1\right\}$$

(5)

A is a parameter for fitting curves.

$$\:A=\frac{mk{T}_{c}}{q}$$

(6)

The phase current $\:{I}_{ph}$ is calculated. Under normal test settings, the output current to be

$$\:I={I}_{ph}-{I}_{0}\left[exp\left(\frac{V}{a}\right)-1\right]$$

(7)

When a PV cell gets short circuited

$$\:{I}_{sc}={I}_{ph}-{I}_{0}\left[exp\left(\frac{0}{a}\right)-1\right]={I}_{ph}$$

(8)

Equation (8) is only accurate in the ideal scenario. The equality is therefore untrue. The notation for Eq. (9) is

$$\:{I}_{ph}\approx\:{I}_{sc}$$

(9)

Irradiance & temperature equally affect the photocurrent

$$\:{I}_{ph}=\frac{G}{{G}_{ref}}\left({I}_{ph}+{\mu\:}_{sc}.\varDelta\:T\right)$$

(10)

$\:{G}_{ref}$= irradiance at standard testing conditions

G = irradiance.

The following equation is represented as the voltage ($\:{V}_{mp}$) and current ($\:{I}_{mp}$) at maximum power,

$$\:{I}_{sc}={I}_{ph}-{I}_{0}\left[exp\left(\frac{{I}_{sc}.{R}_{s}}{A}\right)-1\right]$$

(11)

$$\:O={I}_{ph}-{I}_{0}\left[exp\left(\frac{{V}_{oc}}{A}\right)-1\right]$$

(12)

$$\:{I}_{pm}={I}_{ph}-{I}_{0}\left[exp\left(\frac{{V}_{pm}+{I}_{pm}{R}_{s}}{A}\right)-1\right]$$

(13)

Since term (-1) is so little in comparison to exponential term, it is deleted. Equation (5) is amended by replacing ($\:{I}_{ph}$) in Eq. (13)

$$\:0\approx\:{I}_{sc}-{I}_{0}exp\left(\frac{{V}_{0}}{A}\right)$$

(14)

Hence,

$$\:{I}_{0}={I}_{sc}\:exp\left(\frac{-{V}_{0c}}{A}\right)$$

(15)

Figures 5 and 6 typically represent the Current-Voltage (I-V) and Power-Voltage (P-V) characteristic curves of a single solar cell under different levels of irradiance (solar radiation intensity). As irradiance increases, both current and power output increase significantly. Voltage increases slightly but does not change as dramatically as current. The shape of the curves remains similar, but the magnitude of power and current scales with irradiance.

Fig. 5

Single Solar Module I-V Curve.

Fig. 6

Single Solar Module P-V Curve.

Z-Source integrated boost converter

A Z-Source Integrated Boost Converter (ZSIBC) with reduced voltage stress and high step-up capability is proposed and its circuit diagram is shown in Fig. 7. The design includes a Z-source network and a switched capacitor cell, ensuring a common ground for input and output for better application compatibility. The converter features two synchronously controlled switches, an input diode, an output diode, and a capacitor.

Fig. 7

Circuit diagram.

Operating modes of converter

The operating philosophies of Continuous Conduction Mode (CCM) and Discontinuous Conduction Mode (DCM) are contrasted and compared in this section. The analysis that follows is based on the following assumptions. Every capacitor has a suitable size. Consequently, the voltage of the capacitors is assumed to be constant during the switching period^32,33.

The CCM operating modes are explained as follows:

Fig. 8

Mode 1 Functionality.

Fig. 9

Mode 2 Functionality.

Mode 1: [t_o – t₁] the output diode Do and switches S₁, S₂ are all in the ON state. The diodes D_o, D₁ and D₂ are reverse biased using V₀ – V₁ and V_c1. Figure 8 shows the flow of current. Capacitors C_z1 and C₁ are used to charge the inductor L₂, while capacitors C_z2 and C₂ are used to charge the other inductor L₂. Meanwhile, C_z1, C_z2 and C₁ are connected in series to power loads R and C_o. Kirchhoff Voltage Law (KVL) is applied to obtain Eqs. (16) and (17).

$$\left\{ \begin{gathered} {V_{L1}}={V_{C1}}+{V_{CZ1}} \hfill \\ {V_{L2}}={V_{C1}}+{V_{CZ2}} \hfill \\ \end{gathered} \right.$$

(16)

$${V_0}={V_{C1}}+{V_{CZ1}}+{V_{CZ2}}$$

(17)

Mode2: [t₂ – t₁] Switches have been switched OFF and diodes D_o, D₁ and D₂ are turned ON. There is a reverse bias on the output diode. Figure 9 shows the path of the current flow. The converter’s capacitorV_cz1 is charged with V₁ and V_cz2 and using V₁ and L₁. Inductors L₁, L₂ and V₁ provide an additional charge to the capacitor C₁. C_o is in charge of keeping the output voltage constant. KVL says that these connections are made.

$$\left\{ \begin{gathered} {V_{L1}}={V_i} - {V_{CZ2}} \hfill \\ {V_{L2}}={V_i} - {V_{CZ1}} \hfill \\ \end{gathered} \right.$$

(18)

$${V_{C1}}={V_{CZ1}}+{V_{CZ2}} - {V_i}$$

(19)

The DCM operating modes are consists of 3 modes and is explained as follows:

Mode 1: [t₀ – t₁] the circuit layout remains the same as in continuous conduction mode (CCM), and this stage, Eqs. (16) and (17) remain applicable. Taking into account the inductor current fluctuation during this interval, it can be approximated as follows:

$$\left\{ {\Delta {i_{L1}}=\frac{{\left( {{V_{CZ1}}+{V_{C1}}} \right)}}{{{L_{}}}}} \right.D{T_S}$$

(20)

$$\left\{ {\Delta {i_{L2}}=\frac{{\left( {{V_{CZ2}}+{V_{C2}}} \right)}}{{{L_{}}}}} \right.D{T_S}$$

(21)

Mode 2: [t₁ – t₂] the current flow remains in the same direction as in continuous conduction mode (CCM). Accordingly, Eqs. (18) and (19) from the CCM operation remain valid. Mode 2 ends when the inductor current drops to zero at any moment during the operation.

Mode 3: [t₂ – t₃] in this stage, the output voltage is maintained while all switches and diodes remain in the OFF state. The corresponding equivalent circuit topology for this mode is illustrated in Fig. 10. Mode 3 ends when the switches turn ON, marking the beginning of the next switching period.

Fig. 10

Mode 3 Functionality.

ANFIS based MPPT controller

An ANFIS-based MPPT method is proposed to optimize solar panel output under varying weather conditions. It uses PV voltage (V_PV), current (I_PV), and temperature (T_PV) as input variables, with the duty cycle as the output to control a DC-DC switched boost Landsman converter for maximum power tracking. Unlike conventional fuzzy logic controllers (FLCs), ANFIS learns optimal membership functions and rules from trained data. The training process involves:

• Simulating MPPT algorithms under different solar conditions.

• Using MATLAB to process and refine the collected data.

• Filtering data to extract distinct values for training.

Fig. 11

ANFIS Model Structure.

The ANFIS model processes V_PV, I_PV, and T_PV as input data in a five-layer network, using bell-shaped membership functions (low, medium, high). The overall proposed architecture of the ANFIS model, a five-layer network, is shown in Fig. 11. The PV voltage (V_PV) membership function produced by ANFIS is shown in Fig. 12. The created membership functions for PV current (I_PV) are shown in Fig. 13, and those for PV cell temperature (T_PV) are shown in Fig. 14. It compares the duty cycle with a sawtooth signal to generate trigger pulses for the switched boost Landsman converter. PV voltage, current, and temperature fluctuate with environmental changes, requiring dynamic adjustments in the ANFIS controller. With sufficient training epochs, ANFIS optimizes MPPT performance by refining fuzzy rules and minimizing errors, making it ready for real-time control applications.

Fig. 12

Membership Function of the Input Variable ($\:{V}_{pv}$)

Fig. 13

Membership Function of the Input Variable ($\:{I}_{pv}$)

Fig. 14

Membership Function of the Input Variable ($\:{T}_{pv}$)

Three phase voltage source inverter

This study examines inverter-side control in two-stage rectifier-fed inverter systems, emphasizing voltage management (input, internal, and output). A three-phase VSI (Fig. 15) uses a single DC source and n-channel IGBTs for medium-power applications. A DC link capacitor (CDC) stabilizes voltage and minimizes stray inductance. Proper bus line arrangement reduces inductance, while fast-switching IGBTs (Q1, Q2, Q3, etc.) are paired with anti-parallel fast recovery diodes (D1, D2, D3, etc.). The AC load connects via terminals A, B, and C, with single-phase inverters having one load pair and three-phase inverters having three load-phase terminals³⁴.

Fig. 15

Topology of a 3-Phase VSI.

Bidirectional battery converter

The bidirectional battery converter allows power to flow between the battery and the load or grid in either way, depending on the needs of the system is shown in Fig. 16. Bi-Directional Battery Converter During high demand, the battery discharges via the DC/AC inverter to supply power, while during low demand, excess grid power charges the battery through an AC/DC rectifier^35,36.

The BDC, during charging mode, operates in buck mode owing to the fact that the dc-link serves as its input, while the ESS functions as its load. The capacitor and inductor values during buck mode is estimated as,

$$\:{L}_{buck}=\frac{({V}_{DC}-{V}_{ESS}){D}_{buck}}{{\varDelta\:I}_{L}f}$$

(22)

$$\:{C}_{buck}=\frac{(1-{D}_{buck}){V}_{ESS}}{8{L}_{buck}\varDelta\:{V}_{ESS}{f}^{2}}$$

(23)

Fig. 16

Bi-Directional Battery Converter.

Where, the ripple current and switching frequency are specified using the terms$\:{\:\varDelta\:I}_{L}$ and$\:\:f,$ respectively, while the duty ratio is specified by the term$\:\:D$. In the case of the discharging mode, the conditions are reversed as the BDC is in boost mode, while the ESS operates as the input this time and the dc-link serves as the load. The capacitor and inductor values in this mode are estimated as,

$$\:{L}_{boost}=\frac{{V}_{ESS}{D}_{boost}}{{\varDelta\:I}_{L}f}$$

(24)

$$\:{C}_{boost}=\frac{{V}_{DC}{D}_{boost}}{8{R}_{0}\varDelta\:{V}_{Dc}f}$$

(25)

Where, output resistance and ripple voltage are referred as$\:{\:R}_{0}$ and$\:\:\varDelta\:{V}_{DC}$ respectively.

LC filter

To reduce current harmonics in the inverter, an L-filter is commonly used, but it requires high inductance and increases cost. To improve dynamic response, LC or LCL filters are preferred, as they use smaller inductors and capacitors while effectively filtering harmonics.

Results and discussions

This section presents simulation results, hardware validation, and analysis of the proposed Grid-tied Hybrid PV-Fuel Cell with Energy Storage System (ESS) for EV charging.

Simulation results

Initially, the overall proposed system is validated through MATLAB/Simulink 2021a /Simulink for showing the significance of converter and optimized PI controller based VSI driven EV charger. MATLAB/Simulink 2021a serves as a simulation platform is used to validate the system performance and its overall matlab simulation is shown in Fig. 17.

The Grid-tied Hybrid PV-Fuel Cell with Energy Storage System (ESS) for EV charging is simulated in MATLAB 2021a/Simulink to evaluate its performance under varying conditions. The simulation results highlight power flow management, voltage/current regulation, and efficiency improvements.

Fig. 17

Overall Matlab Simulation.

Figure 18 shows a voltage-time graph, where voltage starts at 110 V at 0.2s and rises afterward, indicating an increasing voltage trend in the system over time. After t = 0.2 s, the voltage shows a step-wise rise and then stabilizes, rather than a continuous increase. This behavior reflects the response of the converter’s control system, which adjusts the output voltage in response to the load and MPPT operation. Figure 19 illustrates the current waveform of a solar panel over time. Initially, at 0s, the current peaks at 1500 A, likely due to a startup surge from sunlight exposure or load connection. Over time, the current decreases significantly, possibly due to MPPT adjustments, shading effects, or load variations. Eventually, the current stabilizes at 400 A, indicating system regulation and normalization.

Fig. 18

Solar Panel Voltage Waveform.

Fig. 19

Solar Panel Current Waveform.

Figure 20 shows the output voltage response of the Z-source integrated boost converter. The voltage smoothly rises in two stages before stabilizing at ~ 1100 V around 0.35s, meeting EV fast charging requirements. The minimal oscillations indicate high power quality and efficient regulation. Compared to traditional boost converters, the Z-source design achieves higher voltage gain, improved stability, and lower ripple, enhancing MPPT tracking and power conversion efficiency. Figure 21 depicts the output current response of the Z-source integrated boost converter. The current rapidly rises and then stabilizes at ~ 30 A after 0.35s, demonstrating effective current regulation with minimal oscillations. The smooth transient response indicates a fast reaction to load demands, low overshoot, and reduced harmonic distortion, improving power quality. Unlike traditional boost converters, the Z-source topology minimizes inrush currents and enhances stability, while the ANFIS-based MPPT ensures optimal power extraction and fast settling time.

Fig. 20

Converter Output Voltage Waveform.

Fig. 21

Converter Output Current Waveform.

Figure 22 illustrates the fuel cell’s output voltage waveform. Before 0.3s, the voltage fluctuates due to startup transients, reaction stabilization, or fuel flow adjustments. After 0.3s, the voltage stabilizes at 130 V, indicating steady-state operation with a balanced fuel supply and load demand. This suggests the control system effectively regulates the output, ensuring reliable performance.

Figure 23 shows the fuel cell’s output current waveform. Initially, the current rises due to load demand and fuel reaction dynamics. After 0.3s, the current decreases, likely due to power regulation, load adjustment, or fuel optimization. It then stabilizes at 25 A, indicating that the fuel cell has reached steady-state operation, efficiently supplying consistent power to the load.

Figure 24 shows the Battery SOC (State of Charge) waveform, which remains constant at 60%. This indicates that the battery is neither charging nor discharging, meaning energy input and output are balanced. The power demand is being met by other sources (fuel cell, solar, or grid), so the battery remains idle in the system.

Fig. 22

Fuel Cell Output Voltage Waveform.

Fig. 23

Fuel Cell Output Current Waveform.

Fig. 24

Battery State of Charge Waveform.

Figure 25 shows the battery voltage waveform, which remains constant at 120 V throughout the observation period. This indicates that the battery is in a steady-state condition, meaning it is not actively charging or discharging. The load demand and charging input are balanced, keeping the voltage unchanged. In a hybrid system (solar, fuel cell, etc.), this suggests the battery is not the primary energy source. In an EV or grid system, it could indicate standby mode or minimal power draw. Figure 26 shows the battery current waveform, which remains constant at 2 A throughout the observation period. This indicates that the battery is either slowly discharging or charging at a steady rate. The system is maintaining a low and constant power flow, possibly for supporting a small load or trickle charging. If the battery is receiving a small charging current, it might be in a maintenance or float charging phase. A Battery Management System (BMS) could be regulating the current to prevent overcharging or deep discharge.

Fig. 25

Battery Volatge Waveform.

Fig. 26

Battery Current Waveform.

The Grid Current and Voltage waveform is shown in Fig. 27. The grid current has a value of 13 A, and the grid voltage is 500 V. These values indicate the electrical parameters of the power supplied to or from the grid.

Stable Grid Parameters (13 A, 500 V): The grid voltage at 500 V suggests a high-voltage power system, likely for efficient power transmission. The grid current at 13 A indicates the amount of current being drawn or supplied by the system.

If this system includes renewable energy sources (solar, fuel cell, battery, etc.), the waveform might indicate: Power injection into the grid (if it’s an inverter-based system). Power consumption from the grid (if the system is drawing power to charge batteries or support loads). The constant values suggest a steady-state operation without major fluctuations in load or supply.

Fig. 27

Grid Current and Voltage Waveform.

Hardware implementation results

The hardware validation in this paper is conducted on a lab-scale prototype, demonstrating the feasibility of the proposed Grid-tied Hybrid PV-Fuel Cell with Energy Storage System (ESS) for EV charging systems. The hardware prototype is designed using a DSPIC30F4011 microcontroller and operates under controlled laboratory conditions. The hardware prototype model are shown in Fig. 28 and its key parameters are given in Table 1. This figure illustrates the DC bus voltage and current waveform, highlighting the system’s ability to maintain voltage stability and regulate power flow under varying load and generation conditions. It reflects the effectiveness of the proposed control scheme in ensuring a steady and balanced DC link for reliable inverter operation and grid interfacing.

Fig. 28

Hardware Prototype.

MPQI-CI Network: Likely refers to a Modified Perturb and Observe with Intelligent Control Integration (MPQI-CI) technique. This method enhances power optimization and control, improving the efficiency of the energy conversion system.

DSPIC30F4011 Microcontroller: A 16-bit microcontroller from Microchip, commonly used in power electronics and real-time control applications. It handles PWM control, data acquisition, and decision-making for efficient system performance.

ANFIS-Based MPPT (Adaptive Neuro-Fuzzy Inference System - Maximum Power Point Tracking): ANFIS is an AI-based intelligent control method that combines fuzzy logic and neural networks for decision-making. Used for Maximum Power Point Tracking (MPPT), ensuring optimal power extraction from renewable sources (like solar or fuel cells). Compared to traditional MPPT methods, ANFIS can handle dynamic environmental changes more effectively.

Table 1 Key parameters of the prototype.

Prototype Implementation and Testing: The hardware model is constructed to validate the simulation results. The control mechanism using DSPIC30F4011 is tested with the ANFIS-based MPPT. Performance is evaluated under real-time conditions, ensuring the system effectively tracks and delivers maximum power.

Successful transition from simulation to hardware implementation using DSPIC30F4011, bridges the gap between simulation and real-world implementation, Validates system efficiency, control accuracy, and response under real operating conditions and Demonstrates the feasibility of using AI-based MPPT for advanced power management in renewable energy systems. Figure 29. Digitally captured oscilloscope waveforms showing phase voltage and current delivered to the grid. The results confirm clean sinusoidal characteristics, stable power delivery, and effective synchronization.

Fig. 29

Phase Voltage and Current Waveform to Grid.

The hardware section will be enhanced by including more detailed performance analysis, comparisons with simulation results, and efficiency evaluation. The hardware prototype testing involved measuring the output voltage and current of various components under open-loop (50% duty cycle) and closed-loop (15% duty cycle) conditions. These measurements validate the system’s efficiency, power regulation, and control effectiveness in a real-world implementation.

Solar panel output analysis

In open-loop mode, the duty cycle remains fixed at 50%, leading to a higher current output (8.9 A). In closed-loop mode, the duty cycle is reduced to 15%, resulting in a lower voltage (11.08 V) and current (5.9 A). This variation indicates that closed-loop MPPT control optimizes the power extraction based on real-time environmental conditions (irradiance, temperature).

Fuel cell output analysis

Fuel cells require time to stabilize their output due to the electrochemical reaction. Higher duty cycle (50%) allows greater power draw (37.6 V, 14 A), but this can reduce fuel efficiency over time. Lower duty cycle (15%) optimizes power extraction (28.9 V, 9.23 A), ensuring better fuel utilization and stability. The closed-loop control dynamically adjusts the power extraction to avoid excessive fuel consumption and maintain steady output.

Z-source integrated boost converter output analysis

The Z-source boost converter increases voltage using an impedance network, enabling high-voltage gain. In open-loop mode, the high duty cycle (50%) results in higher voltage output (52.3 V) but with low current (0.24 A), indicating inefficient power conversion. Under closed-loop control, the system regulates the voltage to 16 V and increases current (0.8 A), improving overall power efficiency.

Bi-directional converter output analysis

The bi-directional converter enables power transfer between the battery and the grid/load. Under open-loop mode, it provides higher voltage (11.4 V) and current (7.2 A), which may cause excess power flow or losses. Closed-loop operation ensures regulated power flow (9.7 V, 4.9 A), preventing overcharging/discharging of the battery and enhancing system reliability.

Battery output analysis

In open-loop mode, the battery discharges more power (11 V, 6.3 A) without regulation, potentially leading to unnecessary power losses. Closed-loop control optimizes power transfer to match demand, keeping the battery stable (9.7 V, 4.9 A), which extends battery life.

Voltage source inverter (VSI) output analysis

The VSI converts DC power to AC for grid or load connection. Under open-loop operation, higher voltage (230 V) and current (15.33 A) can lead to power fluctuations and higher losses. Closed-loop regulation stabilizes voltage (220 V) and current (12.8 A), ensuring efficient power delivery with lower losses and improved system performance.

Comparison of results

The performance of the proposed hybrid energy system was evaluated through both simulations and hardware implementation. While the simulation results demonstrated idealized system behavior, the experimental validation highlighted real-world constraints affecting performance. A detailed comparison of key parameters is presented in Table 2, which includes observed deviations and their underlying causes.

Table 2 Detailed comparison of key parameters.

While the hardware prototype aligns well with simulation trends, minor discrepancies arise due to real-world factors and is mentioned in below:

Switching Losses & Power Dissipation: Practical MOSFETs and IGBTs experience conduction and switching losses, reducing power conversion efficiency and slightly lowering MPPT efficiency (98.7% vs. 99.5%).

Environmental & Thermal Factors: Temperature variations affect semiconductor performance, while passive components behave differently under thermal stress, causing minor voltage deviations.

Sensor & Measurement Inaccuracies: Noise and calibration offsets in voltage/current sensors and the DSPIC30F4011 microcontroller lead to small reading variations, impacting MPPT accuracy.

Load Transients & Dynamic Response: Real-world load fluctuations introduce transient variations in voltage and current, causing slightly higher power output fluctuations than those observed in simulations.

To further validate the proposed Grid-tied Hybrid PV-Fuel Cell with Energy Storage System (ESS) for EV charging, a detailed quantitative comparison between the simulation and hardware experimental results was conducted. This analysis focuses on transient response times, power conversion efficiency, and power quality through Total Harmonic Distortion (THD) measurements, providing a comprehensive assessment of system performance and reliability.

Transient response time

The transient response time measures how quickly the system stabilizes following a change in load or generation condition. In the hardware prototype, the transient response time was observed at approximately 0.34 s, closely matching the simulation prediction of 0.35 s. This minimal deviation (~ 2.9%) confirms that the real-time control implemented on the DSPIC30F4011 effectively replicates the simulated dynamic behavior, ensuring fast and stable power regulation suitable for EV charging applications.

Power conversion efficiency

Power losses arise primarily due to switching events, conduction losses in power devices, and control signal processing overhead. The hardware prototype demonstrated an overall system efficiency of approximately 98.7%, compared to 99.5% in simulation. This 0.8% efficiency difference is attributed to non-idealities such as MOSFET switching losses, parasitic resistances, and sensor inaccuracies. These results validate the effectiveness of the optimized PI controller and ANFIS-based MPPT in minimizing power losses and maintaining high system efficiency under real operating conditions.

Total harmonic distortion (THD) and power quality

Despite these real-world constraints, the proposed system maintains stable power conversion, grid voltage regulation within ± 1.5%, and steady-state power output fluctuation below 2%, confirming its feasibility for practical applications. To evaluate the power quality and ensure grid compliance, a harmonic analysis was conducted on the inverter output. The Total Harmonic Distortion (THD) of the output current and voltage was measured under steady-state conditions using FFT tools in both simulation and hardware experiments shown in Fig. 30 and given in Table 3.

• Power quality is critical for grid-tied renewable systems to ensure compliance with standards and prevent equipment damage. The inverter output voltage and current THD were measured using FFT analysis:

• These THD values confirm that the hardware implementation complies with IEEE 519 standards, ensuring that the grid is not adversely affected by harmonic pollution. The use of an LCL filter at the inverter output effectively reduces high-frequency harmonics and improves waveform quality.

• This enhanced quantitative analysis strengthens the argument for the practical feasibility and reliability of the proposed system by explicitly showing how hardware results correlate with simulations and meet industry standards.

Table 3 Total harmonic distortion (THD) of the output current and voltage.

Fig. 30

Harmonic Analysis both Simulation and Hardware.

These results indicate that the proposed system operates well within the IEEE 519 standard, which mandates voltage THD below 5% for systems below 69 kV. The use of an LCL filter at the inverter output significantly reduces high-frequency harmonics and improves waveform quality.

To validate the performance of the proposed hybrid PV–Fuel Cell–Battery–Supercapacitor system with ANFIS-based MPPT, a comparative analysis is conducted with conventional configurations. The key metrics compared are MPPT efficiency, voltage regulation, harmonic distortion, and dynamic response are given in Table 4.

Table 4 Key metrics comparison with similar topologies.

The proposed ANFIS-based hybrid PV–Fuel Cell–Battery system with Z-source converter demonstrates superior performance over conventional systems. It achieves higher MPPT efficiency (98.7%), faster dynamic response, and lower voltage and current ripple, ensuring stable operation under varying conditions. Compared to PI and fuzzy MPPT methods, ANFIS offers better adaptability and tracking accuracy.

The Z-source converter enables higher voltage gain and improved reliability compared to traditional boost converters. The system achieves THD < 3%, ensuring IEEE 519 compliance and high power quality. Unlike many existing works, this study includes hardware validation using DSPIC30F4011, confirming real-time feasibility. Additionally, effective bidirectional power flow control supports stable EV charging and enhances energy management, making the system ideal for smart grid applications.

Clarification of contribution and novelty

The core novelty of the proposed system lies in the integration of an Adaptive Neuro-Fuzzy Inference System (ANFIS) based MPPT controller, which is validated both in simulation and hardware. This hybrid intelligent controller combines the learning capabilities of Artificial Neural Networks (ANN) with the rule-based logic of Fuzzy Inference Systems (FIS) to improve convergence speed, steady-state accuracy, and adaptability under dynamic conditions such as partial shading or fast-changing solar irradiance.

To highlight the effectiveness of the proposed ANFIS-based MPPT strategy, Table 5 summarizes a comparative analysis between ANFIS, conventional Fuzzy Logic Controller (FLC), and standalone ANN-based MPPT methods under identical test conditions.

Table 5 Summarization of a various MPPT methods.

Key benefits of ANFIS in real-time implementation

• Fast Adaptation and Learning: Unlike static fuzzy systems, ANFIS can adjust its membership functions and rules using real-time data, enhancing its accuracy during dynamic solar conditions.

• Reduced Power Ripple: The hybrid logic in ANFIS effectively minimizes output oscillations, ensuring smoother power delivery to the DC link and downstream converter stages.

• Improved Convergence Speed: ANFIS achieves maximum power point faster than standalone FLC or ANN, improving energy harvesting, especially under fast-changing irradiance levels.

• Hardware Suitability: Despite its hybrid complexity, ANFIS was successfully implemented in real-time on a DSPIC30F4011 platform with optimized rule sets and compact neural architecture, confirming its practical feasibility.

Conclusion

This study successfully demonstrates the design, simulation, and experimental validation of a grid-tied hybrid energy system integrating photovoltaic panels, a fuel cell, battery storage, and a supercapacitor for electric vehicle charging applications. The implementation of the ANFIS-based MPPT algorithm ensures optimal PV power extraction under varying environmental conditions, resulting in high energy conversion efficiency of 98.7%. The system maintains DC link stability, regulating voltage from 110 V to 150 V, and outputting 1100 V at 30 A, with minimal fluctuations. The battery remains at 60% SOC, contributing 120 V with stable performance. Grid voltage and current are sustained at 500 V and 13 A, respectively, and the inverter output exhibits low THD, complying with IEEE 519 standards. Experimental results validate a voltage regulation margin of ± 1.5% and power fluctuation under 2% during steady-state operation.

Compared to traditional systems, the proposed architecture offers faster dynamic response, superior efficiency, and cleaner power output, proving its suitability for next-generation EV charging infrastructure. Future research will focus on scaling the system to higher power levels and integrating predictive control techniques for real-time optimization and adaptive energy management.