Introduction

Multi-label sentiment classification (MLSC) is a critical task for understanding the nuanced and often complex emotions expressed in text, with applications ranging from market research to public opinion analysis1,2,3,4. Unlike single-label tasks, MLSC acknowledges that a single text can convey multiple sentiments simultaneously5. However, this task is impeded by two persistent challenges: severe class imbalance, where minority emotions are poorly learned6, and the flawed label independence assumption inherent in standard fine-tuning approaches. Pre-trained models like BERT7, despite their power, often inherit this limitation by using loss functions like Binary Cross-Entropy (BCE), which by design treats each label as a separate binary problem, thus failing to model the rich interdependencies between them5,8.

This failure to model label relationships is not merely a statistical issue; it represents a fundamental misunderstanding of sentiment. Emotions are not independent events but exist in a structured, dynamic relationship9. For instance, an increase in ’joy’ often corresponds to a decrease in ’sadness’10, and the co-occurrence of ’joy’ and ’surprise’ has a different proportional intensity than ’anger’ and ’disgust’. To overcome these limitations, we argue for a paradigm shift: from predicting independent label probabilities to modeling a structured label distribution11. Our core hypothesis is that by supervising not only the presence of labels but also their relative proportions and their rates of change (differences), a model can learn the underlying structure of the label space without requiring external knowledge graphs or complex architectural changes12,13.

To operationalize this paradigm shift, we propose the Weighted Difference Loss (WDL) framework. This paper makes the following primary contributions:

  • We introduce a novel ratio-to-difference mechanism that normalizes label values into a distribution of relative proportions and then computes higher-order differences to explicitly model the dynamic trends and interdependencies between labels.

  • We design a learnable weighting scheme that allows the model to adaptively balance the supervisory signals from the base classification loss, the ratio-matching loss, and the multi-order difference losses, thereby optimizing the learning process.

  • We incorporate a label-shuffling augmentation strategy during training, which forces the model to learn intrinsic, order-invariant relationships between emotions, significantly enhancing its robustness and generalization capabilities.

  • We empirically demonstrate through extensive experiments on four public benchmarks that our WDL framework achieves state-of-the-art performance and, most critically, substantially improves the recognition of minority classes, evidenced by a 0.90 absolute F1-score gain for the ’grief’ category on the GoEmotions dataset.

The remainder of this paper is organized as follows: Section "Related work" reviews related work. Section "The WDL framework" details the proposed WDL framework. Section "Experimental analysis" presents the experimental setup and results. Section "Ablation study and discussion" provides ablation studies and discussion. Finally, Section "Conclusion" concludes the paper.

Related work

Sentiment analysis aims to automatically extract subjective information from text14,15. Multi-label sentiment classification (MLSC), a subfield, addresses the realistic scenario where a text expresses multiple, intertwined emotions16,17. The evolution of MLSC methods reflects a continuous effort to better capture textual context and label relationships.

Evolution and persistent challenges in MLSC

Early approaches relied on traditional feature engineering (e.g., N-grams, TF-IDF), which required significant manual effort and lacked deep contextual understanding18,19. The advent of deep learning models like CNNs and RNNs automated feature extraction but often struggled with long-range dependencies and implicitly assumed label independence20,21.

The introduction of Transformer-based Pre-trained Language Models (PLMs), particularly BERT7, revolutionized the field with powerful contextual representations22. However, even when fine-tuned, PLMs still face two core MLSC challenges: (1) Class Imbalance, where models become biased towards frequent emotions23, and (2) the Label Independence Assumption, where standard loss functions like BCE neglect the rich, natural correlations between emotions24.

Modern strategies for enhanced MLSC

Contemporary research has explored various strategies to overcome these limitations, as summarized in Table 1. Our work primarily contributes to the “Loss Function Modification” category, but its prompt-based input formulation also connects it to “Advanced Representation” techniques.

Table 1 High-level overview of modern approaches in multi-label sentiment classification.
Full size table

Innovations in loss functions directly steer model training. Focal Loss25 and ASL26 address class imbalance by re-weighting examples. LDL27 learns a probability distribution over labels, implicitly modeling relationships. While effective, these methods may not fully capture the relative proportional strength or dynamic shifts between co-occurring emotions.

Explicit modeling of label dependencies directly represents label relationships. GNNs31 are a dominant paradigm, constructing a label graph (from co-occurrence statistics or external knowledge) and propagating information to learn correlation-aware predictions. While powerful, GNN-based methods introduce significant overheads: they require the pre-construction of a label graph, which may be suboptimal or unavailable, and add notable computational complexity35. To circumvent these issues, we propose an alternative, loss-driven approach. Instead of encoding label relationships into a fixed graph structure, our method forces the model to learn these relationships dynamically from the data itself, guided purely by the loss function.

Advanced representation learning techniques, such as contrastive learning33 and prompt-based learning34, aim to improve the underlying features. Contrastive methods learn more discriminative embeddings by pushing dissimilar samples apart in the feature space. Prompting reformulates the task to better align with the PLM’s pre-training objectives. Our work incorporates a prompt-inspired input formulation but focuses its core innovation on the loss function, making it complementary to these representation-focused methods.

Motivation for weighted difference loss

Existing approaches often specialize in either class imbalance or label dependency, introduce significant architectural complexity, or fail to model the nuanced, relative proportional strengths of emotions. Our proposed WDL offers a unified, lightweight solution that operates directly on the model’s output distribution. By focusing on the learnable, weighted differences in normalized label proportions, WDL provides a computationally tractable method to simultaneously mitigate class imbalance and model label interdependencies, aiming to improve performance, particularly for minority classes.

The WDL framework

Framework overview

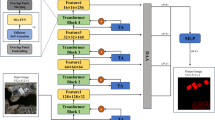
The WDL framework enhances a standard BERT model by introducing a multi-component loss function that supervises the model on label presence, relative proportions, and inter-label trends. Figure 1 illustrates the overall workflow. Given an input text and a set of labels, the framework proceeds in three steps: 1. Prediction: A prompt-based BERT model with a feature refinement module generates predicted logits \(\hat{\textbf{y}}_l\) for each label. 2. Transformation: Both predicted logits and true labels \(\textbf{y}\) are transformed into normalized ratio vectors, \(\hat{\textbf{r}}\) and \(\textbf{r}\), respectively. Higher-order differences (\(\Delta ^d\hat{\textbf{r}}, \Delta ^d\textbf{r}\)) are then computed from these ratio vectors. 3. Weighted Loss Calculation: A final loss, \(\mathcal {L}_{\text {WDL}}\), is computed as a dynamically weighted sum of the binary classification loss, the ratio-matching loss, and the difference losses.

The complete loss function is defined as:

$$\begin{aligned} \mathcal {L}_{\text {WDL}} = w_l \cdot \text {BCE}(\hat{\textbf{y}}_l, \textbf{y}_{\text {bin}}) + \sum _{d=0}^D w_d \cdot \text {MSE}(\Delta ^d \hat{\textbf{r}}, \Delta ^d \textbf{r}) \end{aligned}$$
(1)

where \(\textbf{w} = [w_l, w_0, \dots , w_D]\) are learnable weights, \(\hat{\textbf{y}}_l\) are the predicted logits, \(\textbf{y}_{\text {bin}}\) are the true binary labels, and \(\Delta ^d\hat{\textbf{r}}\) and \(\Delta ^d\textbf{r}\) are the d-th order differences of the predicted and true ratios, respectively.

Fig. 1
figure 1

The Bert-WDL architecture. An input text is prepended with emotion-guided [MASK] prompts. BERT generates representations, which are refined by a Self-Attention Network (SAN) module. The final logits are supervised by the multi-component WDL, which includes losses on labels, ratios, and their differences (2nd-order shown).

Full size image

Prompt-based input and feature refinement

Inspired by prompt-based learning36, we construct inputs by prepending emotion labels with [MASK] tokens to the text: "\(e_1\)[MASK]…\(e_M\)[MASK]. ti". After extracting the final-layer representations for each [MASK] token from BERT, we hypothesize that these initial representations can be further refined to be more discriminative. To this end, we employ a Self-Attention Network (SAN) module to act as a feature refiner. Each [MASK] token’s representation is independently processed by the SAN to enhance its contextual features before being passed to the classifiers. As our ablation study confirms (Section Component effectiveness analysis), this refinement step creates a higher-quality substrate for the WDL and is crucial for overall performance.

Ratio and difference formulation

From a theoretical standpoint, we posit that the set of co-occurring emotions in a text can be viewed as a discrete signal over the label space. The value at each point corresponds to the intensity of an emotion. The first-order difference (\(\Delta ^1\)) of this signal approximates its derivative-the rate of change in intensity from one emotion to the next. The second-order difference (\(\Delta ^2\)) approximates the second derivative, or the “acceleration” of this change. By supervising these derivatives, we compel the model to learn not just the static presence of emotions (the “position” of the signal), but also their dynamic relationships and trends (the “velocity” and “acceleration”).

To operationalize this, we first transform both true labels and predicted logits into ratio vectors. For a given instance with a multi-hot true label vector \(\textbf{y}_{\text {bin}} \in \{0, 1\}^M\), the true ratio vector \(\textbf{r}\) is computed by L1 normalization:

$$\begin{aligned} \textbf{r} = \frac{\textbf{y}_{\text {bin}}}{||\textbf{y}_{\text {bin}}||_1} \end{aligned}$$
(2)

If an instance has no positive labels (\(||\textbf{y}_{\text {bin}}||_1 = 0\)), \(\textbf{r}\) is a zero vector. The predicted logits \(\hat{\textbf{y}}_l\) are passed through a softmax activation to produce a probability distribution \(\hat{\textbf{r}}\), ensuring it is also L1-normalized.

To explicitly model label dependencies, we then compute the d-th order forward difference \(\Delta ^d \textbf{r}\) recursively:

$$\begin{aligned} \Delta ^d \textbf{r}[i] = \Delta ^{d-1} \textbf{r}[i+1] - \Delta ^{d-1} \textbf{r}[i] \end{aligned}$$
(3)

where \(\Delta ^0 \textbf{r} \triangleq \textbf{r}\). The 1st-order difference captures intensity transitions between adjacent labels, while higher orders encode more complex, non-local dependencies.

Order-invariant learning via label shuffling

Since the difference calculation is sensitive to label order, we introduce a crucial augmentation step. During each training iteration, the original batch is expanded by creating K random permutations of the emotion label sequence for each sample. The input prompts, true labels, and true ratios are re-constructed according to these permutations, forming an augmented batch of size \(K \times \text {batch}\_\text {size}\). The WDL loss is computed over this entire augmented batch in a single forward and backward pass. This procedure forces the model to learn true semantic correlations between emotions (e.g., ’joy’ and ’excitement’) rather than spurious positional artifacts (e.g., ’the 5th label is always higher than the 4th’), thereby improving model robustness and generalization. During inference, predictions from shuffled sequences are re-ordered back to their original label sequence before evaluation.

Learnable multi-component loss

The final WDL (Eq. 1) combines the losses from the binary classification task (BCE) and \(D+1\) orders of ratio/difference matching (MSE). The weights \(\textbf{w}\) are not fixed hyperparameters but are learned dynamically. They are parameterized by a vector of logits \(\textbf{u} \in \mathbb {R}^{D+2}\), such that \(\textbf{w} = \text {softmax}(\textbf{u})\). Both the model parameters \(\theta\) and the weight logits \(\textbf{u}\) are updated via gradient descent, allowing the framework to adaptively determine the importance of each loss component. The complete training process is detailed in Algorithm 1.

Algorithm 1
figure a

Training the WDL framework.

Full size image

Implementation details

Our framework was implemented in PyTorch 2.0.0 and run on an Ubuntu 20.04 system with a 48GB vGPU. We fine-tuned bert-base-uncased and bert-base-chinese models from Hugging Face. The architecture includes a single-layer SAN for feature refinement and employs a dedicated SGD optimizer for the loss weight logits. All experiments were conducted using the comprehensive set of hyperparameters detailed in Table 2, with early stopping based on validation loss to prevent overfitting.

Table 2 Training hyperparameters.
Full size table

Experimental analysis

Datasets

We evaluated our method on four public multi-label emotion datasets: two Chinese (NLPCC 2018 Task 1 with 5 emotion labels and Ren-CECPs with 8 labels) and two English (GoEmotions with 28 labels and SemEval 2018 Task 1, E-c with 11 labels). For NLPCC, GoEmotions, and SemEval, we used the official train/validation/test splits. For datasets lacking official splits, such as Ren-CECPs, we randomly partitioned the data into training (70%), validation (15%), and test (15%) sets. To ensure reproducibility, all random partitioning was performed using a fixed random seed (42).

Evaluation metrics

We use a comprehensive suite of metrics: Macro-F1 (MF1) and Micro-F1 (mF1) to assess classification performance, with MF1 being particularly sensitive to minority class performance. We also report Average Precision (AP), Hamming Loss (HL), Coverage Error (CE), and Ranking Loss (RL). Arrows (\(\uparrow /\downarrow\)) indicate the desired direction for each metric.

Baseline methods

We compare Bert-WDL against state-of-the-art models including prompt-based (PC-MTED37), capsule network (CapsLDM38), neural architecture (MEDA-FS39, LEM40, EduEmo41), and hybrid methods (Hybrid HEF-DLF42, Seq2Emo43). All baseline results are sourced from their original publications. In the following tables, a dash (-) indicates that a specific metric was not provided in the source paper.

Experimental results

Cross-dataset performance

Table 3 and Table 4 show that the WDL framework consistently delivers top-tier performance across all four datasets, demonstrating its robustness and generalizability. Unlike baseline methods that excel on one dataset but falter on another, WDL variants consistently rank among the top performers. For example, WDL2 achieves the best MF1 and mF1 on NLPCC, while WDL1 is highly competitive on Ren-CECPs and SemEval, and secures the best MF1 and mF1 on GoEmotions. This stability highlights the effectiveness of modeling label dynamics as a general principle.

Table 3 Performance comparison across various difference orders.
Full size table
Table 4 Performance comparison with 1st-order difference model.
Full size table

Effectiveness on minority classes

The primary strength of WDL lies in its ability to mitigate class imbalance. The heatmap in Fig. 2 provides a clear visual proof of this effect on the 28-category GoEmotions dataset. In the figure, emotions are sorted by their training sample count, from the least frequent at the top to the most frequent at the bottom. This arrangement vividly illustrates that the most significant performance gains, indicated in green, occur on minority classes.

The exceptional performance on ’grief’ (F1-score of 0.91 vs. a baseline of 0.01), despite only 6 training samples, strongly validates our core hypothesis. A standard BCE loss struggles with such extreme sparsity. However, WDL forces the model to consider ’grief’ in relation to other emotions. By learning the difference patterns-how the presence of ’grief’ alters the proportions of ’sadness’ or ’disappointment’-the model can effectively infer its presence even from minimal direct evidence. This pattern of significant gains is consistent across most low-to-mid frequency emotions. While some high-frequency emotions like ’gratitude’ and ’remorse’ show a trade-off, indicated in red, the overall 17.4% improvement in MF1 (0.46-0.54) confirms a more balanced and robust predictive capability across the entire emotion spectrum. This is further detailed in Table 5.

Fig. 2
figure 2

Heatmap illustrating the F1-score gain of Bert-WDL1 over the baseline on the GoEmotions dataset. Emotions are sorted by their training sample count (from lowest to highest) to visualize the strong performance gains on minority classes (green) and the trade-offs on some majority classes (red).

Full size image
Table 5 Performance comparison of Bert-WDL1 and baseline on different emotions (GoEmotions Dataset). The table showcases results for a selection of emotions, focusing on the least frequent categories to highlight improvements on minority classes.
Full size table

Comparison of loss functions

To isolate the effect of our loss design, we compared WDL1 against standard multi-label loss functions on GoEmotions, keeping the model architecture fixed. As shown in Table 6 and the conceptual gain plot in Fig. 3, WDL1 consistently outperforms BCE, ASL, and Focal Loss in terms of both MF1 and mF1. While ASL achieves higher recall and Focal Loss higher precision, WDL1 provides the best balance, validating that explicitly modeling label dynamics is more effective than only re-weighting for class imbalance. Wasserstein loss performed poorly, suggesting it is ill-suited for this classification task without significant tuning.

Fig. 3
figure 3

Bar chart showing the relative percentage improvement in Macro-F1 score of WDL1 compared to other loss functions (BCE, ASL, Focal) on the GoEmotions dataset.

Full size image
Table 6 Performance comparison of different loss functions on emotion recognition (GoEmotions dataset).
Full size table

Computational cost analysis

To assess the practical viability of our framework, we analyze its computational cost relative to a standard BERT baseline on the GoEmotions dataset (Table 7). Our Bert-WDL model introduces a modest increase in parameters (from 110M to 112.4M) due to the SAN module. The primary overhead comes from the label shuffling strategy (\(K=3\)), which triples the number of forward passes per batch. This results in a reduction in training throughput (from 158.4 to 53.1 samples/sec) and a corresponding increase in training time per epoch. However, this is a direct and worthwhile trade-off for the substantial gains in minority class recognition and overall robustness. In contrast, the inference cost remains comparable to a standard BERT model, as shuffling is not required during evaluation. The theoretical complexity is dominated by the Transformer’s \(O(NL^2D)\), with the WDL component adding a negligible \(O(NKD_{diff})\) term.

Table 7 Computational cost analysis.
Full size table

Ablation study and discussion

Component effectiveness analysis

We conducted extensive ablation studies on the GoEmotions dataset to dissect the WDL framework and validate the contribution of each component. The results, detailed in Table 8, systematically compare variants by removing or altering key elements: the SAN for feature refinement, the learnable weights (WDL vs. D series), and the difference order. The base ‘Bert‘ model (BERT-base with a simple classifier) serves as the fundamental baseline.

The results reveal a clear synergistic effect. First, comparing the learnable weight models (e.g., ‘WDL1‘) against their unweighted counterparts (‘D1‘) shows that the adaptive weighting is critical. ‘WDL1‘ (MF1=52.18%) outperforms ‘D1‘ (MF1=50.27%) by 1.91 absolute points, demonstrating that allowing the model to balance loss components is superior to a fixed combination.

Second, the SAN module for feature refinement provides a significant boost. ‘SAN + WDL1‘ (MF1=53.55%) outperforms ‘WDL1‘ without the SAN (MF1=52.18%) by 1.37 absolute MF1 points. This supports our hypothesis that the SAN creates richer, more discriminative emotion representations, which in turn provides a higher-quality substrate for the WDL to operate on. Without well-defined features, calculating differences might be noisy; the SAN sharpens these features, allowing the difference loss to capture meaningful trends more effectively. The full model (‘SAN + WDL1‘) achieves the best Macro F1, showcasing the importance of both feature refinement and learnable difference loss.

Table 8 Ablation study on GoEmotions dataset.
Full size table

Impact of backbone model scale

To assess the scalability of our WDL framework and understand its interaction with more powerful encoders, we conducted an additional set of experiments replacing the bert-base-uncased backbone with its larger counterpart, bert-large-uncased. The results, presented in Fig. 4, reveal a nuanced relationship between model scale and performance, rather than a simple monotonic improvement.

Fig. 4
figure 4

Performance comparison of Bert-WDL using BERT-Base (orange line) and BERT-Large (blue line) backbones. The plots show mF1 and MF1 scores across different WDL difference orders (0 to 3 on the x-axis) for the GoEmotions (top row) and SemEval (bottom row) datasets.

Full size image

As shown in Fig. 4, employing BERT-Large can lead to a higher peak performance. For instance, on the SemEval dataset, the BERT-Large model achieves a significantly higher peak MF1 score (approx. 59.1%) compared to the relatively flat performance of the BERT-Base model. This suggests that a larger model has the capacity to better leverage the WDL framework to capture more complex label dynamics under certain configurations.

However, the performance gains are not consistent. On the SemEval mF1 metric, the BERT-Base model consistently outperforms BERT-Large in three out of four configurations. Similarly, on the GoEmotions MF1 metric, the performance of BERT-Large is more volatile and is surpassed by BERT-Base at one of the configuration points. This indicates that simply increasing the model size does not guarantee superior performance and may even introduce instability, possibly due to overfitting or a more challenging optimization landscape.

This analysis underscores an important trade-off: while a larger backbone offers the potential for higher peak performance, it comes at a significant computational cost and without a guarantee of consistent improvement across all metrics and datasets. The choice of backbone model should therefore be considered in the context of the specific application’s requirements for both performance and efficiency. This finding suggests that the primary benefits observed in our study stem from the WDL framework itself, which proves effective on both base and large model scales, rather than from simply using a larger model.

Weight dynamics and order effects

Figure 5 visualizes the learned weight distributions, revealing two key patterns. First, the weight for the ’label’ component remains remarkably stable across all configurations, acting as a prediction anchor. Second, our weight parameterization scheme is designed to impose a structural prior where weights for higher-order differences decay monotonically. This design choice reflects the hypothesis that lower-order differences (e.g., ’d1’) contain the most valuable signal for capturing label dynamics, while complex, higher-order interactions are progressively down-weighted to prevent the amplification of noise. As Fig. 5 confirms, the first-order difference (’d1’) in the WDL1 model consequently receives a significant weight, which correlates with its strong performance on several benchmarks.

Fig. 5
figure 5

Weight distribution across difference orders.

Full size image

Analysis of performance trade-offs and limitations

Despite its strong performance, particularly on minority classes, our analysis reveals an important performance trade-off. As seen in Table 5, while WDL significantly boosts F1 scores for rare emotions like ’grief’, it can lead to a performance decrease for some high-frequency, semantically distinct emotions like ’gratitude’ and ’remorse’. We posit that this is a consequence of WDL’s implicit attention re-allocation. By forcing the model to learn the relationships and relative proportions across all labels, WDL effectively redistributes the model’s capacity from “over-learned” majority classes to under-represented minority classes. This is beneficial for overall balanced accuracy (MF1) but can come at the cost of peak performance on specific, well-represented labels. This trade-off highlights a key challenge for future work: developing more dynamic weighting schemes that can adapt at an instance level.

Furthermore, our experiments indicate a performance plateau or even degradation with higher-order differences (\(D>2\)). We hypothesize this is due to two factors: 1) a noise amplification effect, where higher-order derivatives become overly sensitive to small perturbations in the predicted ratios, and 2) semantic sparsity, where meaningful third-order or higher emotional dependencies are rare in natural language and thus difficult to learn from limited data. This suggests that simply increasing the order is not a viable path for improvement. Future research could explore adaptive order selection mechanisms or apply regularization techniques to stabilize the learning of higher-order differences.

Extensibility and future work

The WDL framework is designed as a model-agnostic loss function. Although this paper implements it on BERT, its principles can be extended to other architectures. For instance, in a GNN-based model, WDL could be applied to the final node-level predictions to further refine label relationships beyond what is captured by the graph structure. However, extending WDL to new domains requires careful consideration.

In Extreme Multi-Label Classification (XMLC), where the number of labels can be in the thousands, the direct application of WDL with prompt-based inputs becomes computationally infeasible. A potential solution is a two-stage approach: first, use a candidate-sampling model to retrieve a smaller, relevant subset of labels, then apply WDL to this subset for fine-grained ranking and classification. This would leverage WDL’s strength in modeling local dependencies without incurring prohibitive costs.

In Hierarchical Multi-Label Classification (HMLC), the difference calculation could be adapted to respect the hierarchy. For example, differences could be computed primarily among sibling nodes at each level, and perhaps between parent-child nodes, rather than across a flat list. This would allow WDL to model dependencies that are consistent with the predefined label structure. These adaptations, while promising, require substantial future work to validate and implement effectively.

Conclusion

This research introduces the WDL, a novel framework that fundamentally reframes the multi-label classification task from predicting independent probabilities to modeling a dynamic label distribution. By supervising not only label presence but also their relative proportions and rates of change, WDL effectively captures inter-label dependencies without requiring complex architectural modifications or external knowledge graphs.

Our extensive experiments across four diverse datasets demonstrate three key advantages of the WDL framework:

  1. 1.

    Dynamic Relationship Modeling: WDL successfully captures the nuanced, dynamic trends between emotion labels, leading to more robust and accurate predictions, especially in complex scenarios.

  2. 2.

    Implicit Minority Class Boosting: The focus on relative proportions naturally re-allocates model attention to under-represented classes, yielding substantial improvements in minority class F1-scores and overall balanced accuracy.

  3. 3.

    Architecture-Agnostic Simplicity: As a loss-driven innovation, WDL is a lightweight, plug-and-play module that can be easily integrated with various pre-trained models to enhance their performance with minimal overhead.

Our analysis also shows that while the WDL framework can leverage larger backbone models like BERT-Large for potential peak performance gains, this does not guarantee consistent improvement, highlighting that the core benefits stem from the loss design itself. Despite these strengths, our work also highlights areas for future research, including the development of instance-level adaptive weighting to manage performance trade-offs on high-frequency classes and exploring regularization techniques for stable high-order difference learning. The promising results presented here establish WDL as a potent and flexible tool for a wide range of multi-label classification tasks, paving the way for future explorations into more sophisticated dynamic label modeling.