An enhanced fusion of transfer learning models with optimization based clinical diagnosis of lung and colon cancer using biomedical imaging

Abstract

Lung and colon cancers (LCC) are among the foremost reasons for human death and disease. Early analysis of this disorder contains various tests, namely ultrasound (US), magnetic resonance imaging (MRI), and computed tomography (CT). Despite analytical imaging, histopathology is one of the effective methods that delivers cell-level imaging of tissue under inspection. These are mainly due to a restricted number of patients receiving final analysis and early healing. Furthermore, there are probabilities of inter-observer faults. Clinical informatics is an interdisciplinary field that integrates healthcare, information technology, and data analytics to improve patient care, clinical decision-making, and medical research. Recently, deep learning (DL) proved to be effective in the medical sector, and cancer diagnosis can be made automatically by utilizing the capabilities of artificial intelligence (AI), enabling faster analysis of more cases cost-effectively. On the other hand, with extensive technical developments, DL has arisen as an effective device in medical settings, mainly in medical imaging. This study presents an Enhanced Fusion of Transfer Learning Models and Optimization-Based Clinical Biomedical Imaging for Accurate Lung and Colon Cancer Diagnosis (FTLMO-BILCCD) model. The main objective of the FTLMO-BILCCD technique is to develop an efficient method for LCC detection using clinical biomedical imaging. Initially, the image pre-processing stage applies the median filter (MF) model to eliminate the unwanted noise from the input image data. Furthermore, fusion models such as CapsNet, EffcientNetV2, and MobileNet-V3 Large are employed for the feature extraction. The FTLMO-BILCCD technique implements a hybrid of temporal pattern attention and bidirectional gated recurrent unit (TPA-BiGRU) for classification. Finally, the beluga whale optimization (BWO) technique alters the hyperparameter range of the TPA‐BiGRU model optimally and results in greater classification performance. The FTLMO-BILCCD approach is experimented with under the LCC-HI dataset. The performance validation of the FTLMO-BILCCD approach portrayed a superior accuracy value of 99.16% over existing models.

Introduction

Cancer relates to illnesses where abnormal cells grow within the human body due to random mutations¹. Specific tumour types can be highly fatal and are the second leading cause of death after cardiovascular diseases². Approximately 17% of cases are associated with lung cancer. Moreover, there is a significant possibility of tumour cells spreading among the dual organs without an earlier analysis³. Inspecting either kind of cancer in patients and identifying it earlier is essential. Symptoms may offer a timely cancer identification, but are not direct signs of a tumour. Typical symptoms like cough, muscle pain, fatigue, and more happen together with various illnesses⁴. Radiographic imaging models like US, MRI, histopathological image (HI), CT, positron emission tomography (PET), and mammography are often employed for recognizing cancer⁵. In particular, HI contains phenotypic data crucial for assessing and analyzing clinical tumours. The non-invasive models for identification comprise CT colonoscopy for colon cancer and CT image and radiography for tractable sigmoidoscopy and lung cancer. Furthermore, the physical grading of HI is tiresome to pathologists⁶. In addition, precise grading of the LCC subdivision needs trained pathologists, and physical grading is error-prone. Thus, automated image processing models for LCC subdivision screening are acceptable to reduce the inconvenience for pathologists⁷. With advancements in machine learning (ML) and big data analytics, clinical informatics continues to revolutionize modern healthcare systems. ML is a sub-region of AI that enables machines to learn a particular task from data, without clear programming⁸. DL models are advanced to allow machines to control large-dimension data, namely, multi-dimensional anatomical videos and images⁹. DL is a sub-region of ML models in layers for creating an artificial neural network (ANN), depending on the function and structure of the human brain. Clinical data are typically radiographic images; consequently, the convolutional neural network (CNN) is an eminent framework of DL generally leveraged for examining clinical images¹⁰. Pre-trained or pre-designed CNN methodologies have been recently preferred due to their convenience and higher performance.

This study presents an Enhanced Fusion of Transfer Learning Models and Optimization-Based Clinical Biomedical Imaging for Accurate Lung and Colon Cancer Diagnosis (FTLMO-BILCCD) model. The main objective of the FTLMO-BILCCD technique is to develop an efficient method for LCC detection using clinical biomedical imaging. Initially, the image pre-processing stage applies the median filter (MF) model to eliminate the unwanted noise from the input image data. Furthermore, fusion models such as CapsNet, EffcientNetV2, and MobileNet-V3 Large are employed for the feature extraction. The FTLMO-BILCCD technique implements a hybrid of temporal pattern attention and bidirectional gated recurrent unit (TPA-BiGRU) for classification. Finally, the beluga whale optimization (BWO) technique alters the hyperparameter range of the TPA‐BiGRU model optimally and results in greater classification performance. The FTLMO-BILCCD approach is experimented with under the LCC-HI dataset. The key contribution of the FTLMO-BILCCD approach is listed below.

• The FTLMO-BILCCD model employs ML techniques to mitigate noise while preserving crucial edges and textures, enhancing image clarity. This step improves the efficiency of downstream feature extraction by maintaining vital structural details. It also contributes to better classification accuracy by ensuring higher-quality input data.

• The FTLMO-BILCCD approach integrates CapsNet, EfficientNetV2, and MobileNet-V3 large models to extract complementary spatial features from input images, improving representation diversity. This fusion employs the unique strengths of each architecture to capture fine-grained and global patterns effectively. It enhances robustness and generalization across heterogeneous image data.

• The FTLMO-BILCCD methodology implements the hybrid TPA-BiGRU framework, which captures complex spatial dependencies and temporal patterns from the extracted features. This dual modelling approach strengthens the network’s capability to interpret sequential and contextual cues in complex image data. It improves classification precision while giving deeper insight into the decision process.

• The FTLMO-BILCCD method uses the BWO technique to dynamically fine-tune critical hyperparameters, improving the overall model’s training efficiency and stability. This strategic optimization results in faster convergence and more accurate predictions, reinforcing the classification system’s adaptability and performance.

• The integration of multi-source CNN feature fusion with a temporal attention-driven Bigru classifier, optimized using BWO, constructs a novel and streamlined framework for precise remote sensing image classification. This model uniquely employs spatial diversity and temporal relevance. Its novelty is in harmonizing spatial-temporal learning with adaptive hyperparameter tuning. The result is a highly effective model that surpasses conventional single-stream classifiers.

The article’s structure is as follows: Sect. 2 reviews the literature, Sect. 3 describes the proposed method, Sect. 4 presents the evaluation of results, and Sect. 5 offers the study’s conclusions.

Review of literature

Alotaibi et al.¹¹ introduced an innovative Colorectal Cancer Diagnosis utilizing the Optimum Deep Feature Fusion on Biomedical Images (CCD-ODFFBI) model. The projected method, the MF model, is primarily employed for removing noise. It employs a fusion of 3 DL methodologies, Squeeze-Net, SE-ResNet, and MobileNet, for extracting features. Furthermore, the DL hyperparameter choice method is accomplished using the Osprey Optimiser Algorithm (OOA). Lastly, the DBN is used to classify CRC. The author¹² develops a refined DL technique that combines feature fusion for the multi-classification of LCC. The projected method integrates 3 DL frameworks: EfficientNet-B0, ResNet-101-V2, and NASNetMobile. Mix the pre-trained individual vector features from EfficientNet-B0, NASNetMobile, and ResNet-101-V2 into a single vector feature and then adjust it. Li et al.¹³ introduce dual results attained over the application of an enhanced YOLOv5 model with annotated microscopy images of medical cases and publicly accessible polyp image data: (I) Improvement of the C3 module with several layers to C3SE through the attention mechanism squeeze-and-excitation (SE). (II) Fusion of high-level features employing the Bi-FPN. Mim et al.¹⁴ offer a novel structure named Explainable AI for cancer categorization (EAI4CC) employing FL. In this paper, EAI4CC employed CNNs like DenseNet121, VGG19, VGG16, ResNet50, and Vision Transformer for inspecting HI from lung and colon tissue. In addition, advanced XAI presentation models are employed. Especially, GradCAM integrated with EAI4CC to clarify the process of decision-making. Maqsood et al.¹⁵ presented the Efficient Enhanced Feature Framework (EFF-Net), a deep neural network structure intended for RCC grading by employing the identification of HI. EFF-Net merges strong feature extractors from convolution layers with effective Separable convolutional layers, intending to speed up model inference, mitigate overfitting, elevate RCC grading precision, and reduce trainable parameters. In¹⁶, an effective Deep Attention module and a Residual block (RB)-based LCC classification Network (DARNet) are proposed. RBs are employed to improve the capability of DARNet for learning and acquiring residual data that enables DARNet to perceive intricate patterns and enhance precision. The attention module (AM) improves feature extraction and acquires valuable data from the input data. Eventually, Bayesian optimization (BO) is utilized to adjust the DARNet’s hyperparameters. In¹⁷, a pathological knowledge-inspired multi-scale transformer net (PKMT-Net) is presented. The multi-scale soft segmentation module primarily replicated the pathologist’s reading of HI at multiple scales, acquiring microscopic or macroscopic features.

In¹⁸, a miRNA-Disease association prediction (TP-MDA) depends upon a tree path global feature extractor, and a fully connected ANN (FANN) with an MHSA mechanism is projected. The presented technique employs an association structure of a tree to depict the data relations, MHSA for removing vector features, and FANN with a 5-fold CV for the training model. Rawashdeh et al.¹⁹ proposed an efficient computer-aided diagnosis system for lung cancer classification by utilizing DL models, comprising CNN + VGG19, AlexNet, and multi-scale feature fusion CNN (MFF-CNN), applied to histopathological image analysis. Gowthamy and Ramesh²⁰ developed an accurate and fast lung cancer diagnosis methodology by integrating pre-trained DL techniques, namely ResNet-50, Inceptionv3, DenseNet, with kernel extreme learning machine (KELM) and optimized with mutation boosted dwarf mongoose optimization algorithm (MB-DMOA) model. Șerbănescu et al.²¹ aimed to improve lung cancer diagnosis by integrating pCLE and histological imaging using dual transfer learning for accurate, less invasive detection. Musthafa et al.²² developed an advanced ML approach for lung cancer stage classification using CT scan images, CNN, pre-processing techniques, SMOTE for class imbalance, and computing performance through various metrics. Kumar et al.²³ proposed a model for diagnosing colon diseases from endoscopic images utilizing a fused DL methodology integrating EfficientNetB0, MobileNetV2, and ResNet50V2 with auxiliary fusion and residual blocks. Alabdulqader et al.²⁴ developed a resource-efficient EfficientNetB4 model integrated with local binary pattern features for accurate cancer detection. Khan et al.²⁵ classified and localized gastrointestinal diseases from wireless capsule endoscopy images using a DL technique with Sparse Convolutional DenseNet201 with Self-Attention (SC-DSAN), CNN-GRU, and optimization techniques. Amirthayogam et al.²⁶ developed a robust DL approach utilizing EfficientNetB3 to accurately classify lung and colon cancer histopathology images. Diao et al.²⁷ compared hand-crafted features and DL-based methods for lung cancer detection, evaluating their efficiency using GLCM features and a Bi-LSTM network. Shivwanshi and Nirala²⁸ proposed a methodology by applying feature extraction using Vision Transformer (FexViT) for feature extraction and Quantum Computing-based Quadratic unconstrained binary optimization (QC-FSelQUBO) for feature selection, attaining superior performance compared to existing techniques.

Despite the extensive application of DL models across various cancer diagnosis tasks, existing studies still encounter critical challenges. Several models rely on a single structure, lacking robust generalization across diverse image modalities and disease types. Feature redundancy and irrelevant data significantly impact classification accuracy, particularly in high-dimensional medical datasets. Diverse techniques do not integrate effective fusion or selection models, resulting in overfitting and computational overhead. Moreover, limited integration of optimization algorithms with the DL approach highlights a research gap in dynamic tuning and interpretability. The lack of unified benchmarks across existing studies complicates comparative evaluation and scalability.

The proposed method

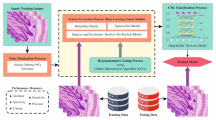
This paper introduces an enhanced FTLMO-BILCCD technique. The main objective of the technique is to develop an efficient method for LCC detection using clinical biomedical imaging. It comprises four stages: image pre-processing, fusion of transfer learning, hybrid classification, and parameter optimization. Figure 1 represents the general flow of the FTLMO-BILCCD model.

Fig. 1

Overall flow of the FTLMO-BILCCD model.

Image pre-processing using MF model

Initially, the image pre-processing stage applies the MF model to eliminate the unwanted noise from input image data²⁹. This model was chosen for its robust capability of removing noise while conserving crucial structural details, which is significant for accurate feature extraction. This technique effectively handles salt-and-pepper noise, maintaining the image’s edge and important texture data. This makes it particularly effective for medical and remote sensing images, where clarity and edge preservation are vital. Other noise-reduction techniques, such as Gaussian or bilateral filters, may blur edges or lose fine details, which could compromise the accuracy of subsequent classification models. This technique presents a balanced approach, enhancing the quality of input data and improving model performance. Additionally, it operates efficiently with minimal computational overhead, making it appropriate for real-time processing tasks. Figure 2 illustrates the working flow of the MF methodology.

Fig. 2

Workflow of the MF technique.

MF is a nonlinear model for smoothing images, substituting all pixels with the median value of their neighbours. The smoothing degree is established in the size of the kernel; more specifically, small kernels have additional details, whereas larger kernels present a smoother image.

During the process of MF, the middle pixel in the $\:P\text{x}P$ window was substituted by the median value of the pixels of the windows. This procedure was described as shown:

$$\:f\left(x,\:y\right)=median\:\left\{g\left(m,\:n\right)\right\},\:where\:\left(m,\:n\right)\in\:{S}_{xy}$$

(1)

Whereas, the MF describes the value of the median grey for all pixels inside a rectangular sub-image window positioned at $\:(x,\:y)$ pixels. Then, the provided pixel is positioned at coordinates $\:(x,\:y)$, and the filter inspects a rectangular window near the pixel. The dimensions of these windows are outlined via the kernel, usually signified as $\:P\text{x}P$. In this window, the median value of every pixel is calculated. The pixel at the middle of these windows $\:(m,\:n)$ is thus substituted by this median value.

Fusion of transfer learning

Besides, fusion models such as CapsNet, EfficientNetV2, and MobileNet-V3 Large are employed in the feature extraction process. This fusion model is highly efficient for image analysis tasks. CapsNet outperforms in capturing spatial hierarchies and relationships between features, improving the model’s capability to handle discrepancies in image orientations and perspectives. EfficientNetV2 balances accuracy and computational cost, presenting high performance while maintaining lower resource usage. MobileNet-V3 Large, prevalent for its lightweight architecture, ensures fast processing without compromising feature extraction capabilities. By incorporating these models, the fusion approach employs the unique strengths of each, resulting in a more robust and accurate feature extraction process than a single architecture. This approach is advantageous for handling diverse and complex image patterns found in complex datasets, ensuring high classification accuracy across varying image types.

CapsNet

CapsNet is an ANN model that can be applied to mimic hierarchical connections more effectively³⁰. The various capsules’ output was also applied to create additional constant images for bigger capsules, which include the pose and the probability of the observations. This method recommends particular advantages, such as overcoming the “Picasso problem” in identifying images, whereas the images have completely accurate components. However, they never occur in proper 3D relationships. The proposed system applied the viewpoint that modifications have nonlinear impacts on the pixel level; still, it contains linear effects on the level of an object, similar to reversing the component method by various percentages.

The $\:{\widehat{u}}_{j|i}$ presents the predicting vector calculation, which was performed once the $\:{x}_{i}$ were exemplified as the vector input to the capsule $\:i$ inside the lower layer and after the $\:{w}_{ij}$ was represented as the weight matrix, which joined the capsule $\:i$ to the lower layer of the capsule $\:j$ inside the higher layer.

$$\:{\widehat{u}}_{j|i}={w}_{ij}{x}_{i}$$

(2)

The output vector was represented by $\:{k}_{i}$, a combination that made its capsule $\:j$ inside the high layer of the predicting vectors through the dynamic routing model. It includes an iterative process in that all coupling coefficients $\:{c}_{ij}$ were updated. The present coefficients exemplify that the quantity capsule $\:i$ needs to be connected to the capsule $\:j$. The Softmax function was applied to calculate the coupling coefficients that are measured in the following way:

$$\:{c}_{ij}=\frac{\:\text{e}\text{x}\text{p}\:\left({b}_{ij}\right)}{{\sum\:}_{k}\text{e}\text{x}\text{p}\left({b}_{\iota\:k}\right)}$$

(3)

The first preceding logarithmic scale was established by $\:{b}_{ij}$ and exemplifies the probability of directing the capsule output $\:i$ to the capsule output $\:j$. The$\:\:\text{l}\text{o}\text{g}$ priors were initially established to be $\:zero$; previously, they were modified consistently through the agreement between the predicting and output vectors. The present agreement is measured by utilizing the scalar product presented by $\:{a}_{ij}$, acquired by calculating the dot product of the vectors $\:{v}_{i}$ and $\:\widehat{u}$.

$$\:{b}_{ij}\leftarrow\:{b}_{ij}+{a}_{ij}$$

(4)

The output vector is measured by adding each predicting vector by reviewing weights and utilizing the squashing function with the target, limiting the length of the output vector in the interval of $\:(0$,1).

$$\:{s}_{j}={\sum\:}_{i}{c}_{ij}{\widehat{u}}_{j|i}$$

(5)

$$\:{v}_{j}=\frac{\Vert\:{s}_{j}{\Vert\:}^{2}}{1+\Vert\:{s}_{j}{\Vert\:}^{2}}\frac{{s}_{j}}{\Vert\:{s}_{j}\Vert\:}$$

(6)

The squashing functions can maintain the vector’s orientation, representing the object’s posture.

Margin loss acts as a function of loss applied inside CapsNets to help with optimization. Its objective is to guarantee that the difference among the different types inside the capsule area is higher compared to particular margins. The present model can help achieve an improved division of classes. The margin loss is measured through the addition of the positive and negative margins in the following manner:

$$\:{L}_{margin}={T}_{c}^{*}max(0,{m}_{pIus}-\left|\left|{v}_{c}\right|\right|{)}^{2}+{\lambda\:}^{*}{\left(1-{T}_{c}\right)}^{*}\text{m}\text{a}\text{x}(0,\:\left|\left|{v}_{c}\right|\right|-{m}_{minus}{)}^{2}$$

(7)

Whereas $\:{T}_{c}$ exemplified the object indication parameter of class $\:c$. $\:{v}_{c}$ presented the length of the output vector inside the capsule related to class $\:c$. The weighting component is established by $\:\lambda\:,$ and the positive and negative margins are signified by $\:{m}_{\:\text{m}\text{i}\text{n}us}$ and $\:{m}_{plus}$, which act as constants.

EffcientNetV2

EfficientNet-V2, the following version of EfficientNet-V1, is a new family of deep CNNs concentrated on two crucial features: improving the parameter efficacy and training speed³¹. The fast training is attained using either MB Conv or Fused-MB Conv layers. Now, layers of MB Conv represent fundamental elementary components of MobileNet-V2 made from the inverted RB. The initial dual blocks (depth‐wise $\:3\text{x}3$ convolution and the extension $\:1\text{x}1$ convolution blocks) of MB Conv were substituted by the fixed $\:3\text{x}3$ convolutional block to get the fused-MB Conv layer. Then, an SE block in either the fused-MB Conv or MB Conv layers was utilized to weigh various channels adaptively. Lastly, a $\:1\text{x}1$ squeeze layer was deposited to lessen the channel counts equivalent to the networks provided in the input of both MB Conv and Fused‐MB Conv layers.

This proposed study considers EfficientNet-V2-L, M, and S methods, which use Fused-MB Conv blocks in the first layers. The final layers have a $\:1\text{x}1$ pooling and convolution, and are completed by the fully connected (FC) layer. The EfficientNet-V2-S method was also extended using a compound scaling approach to obtain EfficientNet-V2-M and ‐L methods. The concept behind compound scaling is in balancing the sizes of width ($\:w$), input image resolution ($\:r)$, and depth ($\:d$) by scaling them to a constant ratio.

SE block $\:C,H,W$: channel counts, image height, and width.

$$\:d={\alpha\:}^{\phi\:},\:w={\beta\:}^{\phi\:},\:r={\gamma\:}^{\phi\:}$$

like

$$\:\alpha\:.{\beta\:}^{2}.{\gamma\:}^{2}=2$$

(8)

$\:\alpha\:,\beta\:$, and $\:\gamma\:$ values are continuously higher than or equivalent to 1 and are established by grid searching. Intuitively, $\:\phi\:$ establishes the additional computational efficiency needed for user-described model scaling. Practically, the convolutional processes control the computing cost in CNNs.

MobileNet-V3 large

MobileNetV3 Large is a progression of an earlier version, MobileNetV2, and is particularly enhanced for applications on edge and mobile gadgets, while performance and efficacy are dominant³². MobileNetV3 incorporates advances from neural architecture search (NAS) with characteristics, namely hard-swish activator algorithms and SE modules, to improve precision while guaranteeing lower latency and energy economy. This model protects the depth-separable convolution from MobileNetV1. However, it improves by combining bottleneck layers and expanded layers of SE, increasing feature representations but reducing computational expenses. MobileNetV3 Large is optimized for semantic segmentation and image classification, making it suitable for real-world mobile apps without giving up speed. MobileNetV3 Large considerably improves precision according to MobileNetV2, whereas preserving a lightweight model appropriate for distribution on resource-restricted smartphones. Using the SE modules allows the method to underline important features by rearranging channel-wise information, leading to improved feature extraction. This structure is widely used in numerous regions, including healthcare. The incorporation of accuracy and efficiency reduces MobileNetV3 Large as an incomparable opportunity for tasks requiring greater computational cost and robust results. Figure 3 exemplifies the framework of MobileNetV3.

Fig. 3

Architecture of MobileNetV3.

Hybrid classification model

In addition, the FTLMO-BILCCD methodology employs a hybrid of the TPA-BiGRU methodology for the classification process³³. This technique was chosen because of its ability to effectively capture both temporal and spatial dependencies in data, which is crucial for tasks that involve sequential or time-dependent information. The TPA model improves the capability of the technique to concentrate on essential time-related features, enhancing the model’s performance in dynamic environments. The BiGRU component allows the model to process data from past and future contexts, making it more robust in comprehending the temporal relationships in data. Compared to conventional methods, this hybrid model is more effective in handling complex sequences, giving better accuracy and interpretability. It outperforms single-direction recurrent networks by integrating forward and backwards context, making it ideal for comprehensive sequence modelling applications. The TPA-BiGRU model is specifically advantageous when handling long-range dependencies, a limitation in many simpler models. Figure 4 specifies the flow of the TPA-BiGRU model.

Fig. 4

Architecture of TPA-BiGRU technique.

The presented model initially utilizes the deep BiGRU model for processing. Previously, the temporal relationships of all feature quantities were removed and handled for long-range memory. Furthermore, it uses the TPA mechanism to strengthen the method’s memory function, emphasizing the significance of the local information and guaranteeing stability.

GRU substitutes the input and forgetting gates in LSTM using an update gate. Therefore, the GRU method has smaller parameters and a more direct framework, and the performance of the dual is comparable. The particular computations are as demonstrated:

$$\:{r}_{t}=\sigma\:\left({W}_{r}\cdot\:\left[{h}_{t-1},{x}_{t}\right]\right)$$

(9)

$$\:{z}_{t}=\sigma\:\left({W}_{z}\cdot\:\left[{h}_{t-1},{x}_{t}\right]\right)$$

(10)

$$\:{\stackrel{\sim}{h}}_{t}=\text{t}\text{a}\text{n}\text{h}\left(\left({W}_{h}\right)\cdot\:\left[{r}_{t}\cdot\:{h}_{t-1},x\right]\right)$$

(11)

$$\:{h}_{t}=\left(1-{z}_{t}\right)\cdot\:{h}_{t-1}+{z}_{t}\cdot\:{\stackrel{\sim}{h}}_{t}$$

(12)

Whereas, $\:\sigma\:$ characterizes the activation function of sigmoid $\:\sigma\:\left(z\right)=\frac{1}{1+{e}^{-z}}$; $\:{x}_{t}$ refers to present data; $\:{h}_{t-1}$ stands for the upper hidden layer (HL) output; $\:{z}_{t}$ and $\:{r}_{t}$ represents the update door and reset door, correspondingly; $\:{\stackrel{\sim}{h}}_{t}$ symbolize candidate HL gate; $\:{W}_{r},$ $\:{W}_{z}$, and $\:{W}_{h}$ symbolize networking parameter matrices; $\:\left[\:\right]$ means vector splicing; and$\:\cdot\:$ denote matrices multiplication by components.

This study selects the Bi-GRU model to analyze the relationships between the input data in a bidirectional time series to better map their relationships. The Bi-GRU model output has either historical or upcoming information on the input data, which can prevent the absence of information and enhance the prediction precision after addressing rolling enhanced data.

In this study, TPA is presented to strengthen the algorithm’s memory of long-range time-series information while strengthening the main features of local short‐range details, emphasizing the main factors influencing the output, and enhancing the prediction of the effect model. The intended TPA is measured as shown:

$$\:{H}_{i,j}^{c}={\sum\:}_{l=1}^{w}{H}_{i,(t-w-1+l)}\times\:{C}_{j,T-w+l}$$

(13)

$$f({H}_{i}^{C},{h}_{t}) = ({H}_{i}^{C})^{T}{W}_{a}{h}_{t}$$

(14)

$$\:{\alpha\:}_{i}=sigmoid\left(f\left({H}_{i}^{C}\cdot\:{h}_{t}\right)\right)$$

(15)

$$\:{c}_{t}={\sum\:}_{i=1}^{n}{\alpha\:}_{i}{H}_{i}^{C}$$

(16)

$$\:{h}_{t}^{A}={W}_{h}\left[{c}_{t};{h}_{t}\right]$$

(17)

Here, $\:H=\left[{h}_{t-w+1},{h}_{t-w+2},\dots\:,{h}_{t-1}\right]$ denote hidden layer matrix of the unique time-series comprising numerous moments of information afterward processing Bi-GRU, and the length of the time window is $\:w,$ $\:C$ refers to convolution kernel of length $\:T$, generally considered as the window length; $\:{H}_{i,j}^{c}$ refers to convolution value in row $\:i$ and column $\:j,$ $\:{H}^{C}$ signifies the temporal pattern matrix; $\:{h}_{t}$ embodies the hidden layer information removed by the NN from the input data feature matrix at the present moment; $\:{W}_{a}$ and $\:{W}_{h}$ represents weighted parameter matrices; $\:{\alpha\:}_{i}$ represents attention-weighted vector that symbolizes the significance of the HL information at all moments in the state matrix, and length $\:w,$ $\:{c}_{t}$ denote feature vector symbolizes the temporal relationship after weighting; and $\:{h}_{t}^{A}$ refers to splicing of the feature vector and the present moment state information, and it is furthermore the last output outcome of TPA.

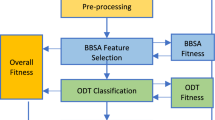
Parameter selection using BWO model

Finally, the BWO technique alters the hyperparameter range of the TPA-BiGRU model optimally and results in greater performance of classification³⁴. This model was chosen for its ability to effectively explore and exploit abilities, which is significant for fine-tuning hyperparameters in intrinsic DL models. Unlike conventional optimization techniques, BWO replicates the adaptive foraging behaviour of beluga whales, giving a robust mechanism for navigating the search space and avoiding local optima. This characteristic makes it highly appropriate for optimizing models with large, high-dimensional hyperparameter spaces. The capability of the BWO model in balancing exploration and exploitation enhances convergence speed and ensures better global solutions, resulting in an improved classification performance. Furthermore, its flexibility and computational efficiency make it an ideal choice over other optimization methods, such as grid or random search, which are often computationally expensive and less effective. By using BWO, the model benefits from improved accuracy and faster convergence, contributing to better performance in real-world applications. Figure 5 depicts the flow of the BWO methodology.

Fig. 5

Working flow of the BWO approach.

The BWO model is a bio-inspired meta-heuristic optimizer model. The design of this approach is stimulated by the beluga whale’s natural behavioural patterns within their environment, particularly their qualities in group cooperation, environmental adaptation, and predation. As highly social aquatic mammals, BW communities typically travel and search for cooperative behaviours like mirror swimming and synchronized swimming. These behaviours establish their group cooperation capability and enhance the efficacy of discovering food sources in general habitats. In the searching procedure, BWs utilize extremely flexible strategic searching techniques, allowing the community to surround prey and improve the capture rate of success cooperatively. This quality presents details for the global searching stage in BWO, permitting the model to perform a wide-ranging search in the composite search area and prevent being stuck in local bests. The phenomenon of whale falls, where a whale corpse arrives at the ocean floor after death, giving food to deep-sea environments, stimulated the BWO model. Whale falls not only disclose the recycling and regeneration mechanisms of environmental resources but also establish the system’s capability to attain self‐repair over random changes after facing challenges, as shown by information distribution and location upgrades after individual deaths. During BWO, this mechanism is replicated as a random perturbation approach, permitting the model to present moderate randomness in the searching procedure to improve global convergence and prevent falling into local bests.

1) Population Initialization and Stage Transition Approach: At the start of the model, randomly initialize the first location matrix of BWs. This matrix was demonstrated as:

$$\:X=lb+rand\left(n,nd\right)\times\:\left(ub-lb\right)$$

(18)

Whereas, $\:X$ characterizes the first location matrix of BWs. $\:lb$ and $\:ub$ denote the minimal and maximal value of all dimensions in the searching region, i.e., the lower and upper limit of the variables. $\:n$ denoted the BW’s population size. $\:nd$ refers to the variable’s dimension. $\:rand$ $\:(n,\:nd)$ creates a matrix of dimensions $\:n$x$\:nd$ with components uniformly distributed among $\:(0$,1).

In the optimization procedure, it is essential to split the model into exploitation and exploration phases according to the balance feature, as demonstrated:

$$\:{B}_{f}=b{0}_{i}\times\:\left(1-\frac{t}{2}\times\:{t}_{\text{m}\text{a}\text{x}}\right),b{0}_{i}\in\:\left(\text{0,1}\right)$$

(19)

Whereas $\:b{0}_{i}$ refers to arbitrarily generated numbers in the interval of ($\:\text{0,1}),$ $\:t$ means the present iteration number, and $\:{t}_{\text{m}\text{a}\text{x}}$ is the maximal iteration count. Once the balance factor $\:{B}_{f}$ is superior to 0.5, the model enters the exploration phase; after the value of $\:{B}_{f}$ is lower than or equal to 0.5, the model enters the exploitation phase.

Exploration phase

If the $\:{B}_{f}$value exceeds 0.5, the model goes into the exploration phase. The equation to update the BW’s location in the exploration phase is as demonstrated:

$$\:{X}_{i,j}^{t+1}={X}_{i,{p}_{f}}^{t}+({X}_{r,{p}_{j}}^{t}.-{X}_{i,{p}_{f}}^{t})(1+{r}_{1})\:\text{s}\text{i}\text{n}\left(2\pi\:{r}_{2}\right),j=even$$

$$\:{X}_{i,j}^{t+1}={X}_{i,{p}_{j}}^{t}+\left({X}_{r,pi}^{t}-{X}_{i,{p}_{j}}^{t}\right)\left(1+{r}_{1}\right)\text{c}\text{o}\text{s}\left(2\pi\:{r}_{2}\right),j=odd\:$$

(20)

Whereas $\:{X}_{{i}_{J}}^{t+.1}$ refers to updated location of the $\:j$ beluga whale in dimension $\:j$, $\:{p}_{j}(j=\text{1,2},\dots\:d)$ characterizes a randomly formed integer in dimension $\:d$ is the location of the BW in dimension $\:j$ $\:{X}_{r,{p}_{1}}^{t}$ and $\:{X}_{i,{p}_{j}}^{t}$ characterize the present locations of the $\:j$ and $\:r$ beluga whales, correspondingly. $\:{r}_{1}$ and $\:{r}_{2}$ specify randomly generated numbers in the interval (0,1). $\:\text{s}\text{i}\text{n}\left(2\pi\:{r}_{2}\right)$ and $\:\text{c}\text{o}\text{s}\left(2\pi\:{r}_{2}\right)$ identify whether the BW fins are in front of the water surface, and according to the comparability of the dimension, establish the exploration equation to utilize.

Exploitation phase

In the exploitation phase, the population of BW diverts their location information to help with foraging behaviour. The Levy flight (LF) approach is used in the model to catch prey, and the particular equation is as shown:

$$\:{X}_{i}^{t+1}={r}_{3}{X}_{best}^{t}-{r}_{4}{X}_{i}^{t}+{C}_{1}\times\:{L}_{F}\times\:\left({X}_{r}^{t}-{X}_{i}^{t}\right)$$

(21)

$$\:{C}_{1}=2{r}_{4}(1-t/{t}_{\text{m}\text{a}\text{x}})$$

(22)

Here, $\:{X}_{i}^{t+1}$ characterizes the updated location of the $\:jth$ beluga whale, and $\:{X}_{best}^{t}$ denotes the optimal location of the BW population. $\:{X}_{r}^{t}$ and $\:{X}_{i}^{t}$ characterize the present locations of the $\:r$ and $\:i$ beluga whales. $\:{r}_{3}$ and $\:{r}_{4}$ signify randomly generated numbers in the interval $\:\left(\text{0,1}\right)$. $\:{C}_{1}$ refers to the parameter that determines the random jumping intensity in the LF approach. $\:{L}_{F}$ characterizes the function of LF.

Whale fall stage

During this whale fall stage, the location of the BW population is upgraded according to their positions and step sizes. The equation for the whale fall is as demonstrated:

$$\:{X}_{i}^{t+1}={r}_{5}{X}_{i}^{t}-{r}_{6}{X}_{r}^{t}+{r}_{7}{X}_{step}$$

(23)

Whereas $\:{\gamma\:}_{5}$ and $\:{\gamma\:}_{6}$ signify randomly generated numbers in the interval $\:\left(\text{0,1}\right)$, $\:{X}_{step}$ characterizes the step size of the whale fall, as demonstrated.

The BWO methodology originates from a fitness function (FF) for attaining an enhanced classification performance. It describes a positive numeral to denote the better outcomes of the candidate solution. The classification rate of error reduction is measured as FF, as specified in Eq. (24).

$$\:fitness\left({x}_{i}\right)=ClassifierErrorRate\left({x}_{i}\right)$$

$$\:=\frac{No.\:of\:misclassified\:instances}{Total\:no.\:of\:instances}\times\:100$$

(24)

Result analysis

The performance analysis of the FTLMO-BILCCD technique is investigated under the LCC-HI dataset³⁵. The method is simulated using Python 3.6.5 on a PC with an i5-8600k, 250GB SSD, GeForce 1050Ti 4GB, 16GB RAM, and 1 TB HDD. Parameters include a learning rate 0.01, ReLU activation, 50 epochs, 0.5 dropout, and a batch size of 5. This dataset contains 25,000 images below five classes as depicted in Table 1. Figure 6 illustrates the sample image and LCC.

Table 1 Details of the dataset.

Fig. 6

Sample images (a) colon cancer and (b) lung cancer.

Figure 7 states the confusion matrix designed by the FTLMO-BILCCD methodology across diverse epochs. The performances indicate that the FTLMO-BILCCD approach specifically has an efficacious identification and detection of all class labels.

Fig. 7

Confusion matrix of FTLMO-BILCCD method (a-f), Epochs 500–3000.

The LCC detection of the FTLMO-BILCCD technique is determined under 500–3000 epochs in Table 2; Fig. 8. The values of the table specify that the FTLMO-BILCCD technique is suitably renowned for all the samples. Based on 500 epochs, the FTLMO-BILCCD technique presents an average $\:acc{u}_{y}$ of 97.43%, $\:pre{c}_{n}$ of 93.60%, $\:rec{a}_{l}$ of 93.58%, $\:{F1}_{score}$ of 93.58%, and MCC of 91.98%. Moreover, based on 1000 epochs, the FTLMO-BILCCD method provides an average $\:acc{u}_{y}$ of 98.24%, $\:pre{c}_{n}$ of 95.60%, $\:rec{a}_{l}$ of 95.59%, $\:{F1}_{score}$ of 95.59%, and MCC of 94.49%. Also, on 2000 epochs, the FTLMO-BILCCD method provides an $\:acc{u}_{y}$ of 98.63%, $\:pre{c}_{n}$ of 96.57%, $\:rec{a}_{l}$ of 96.56%, $\:{F1}_{score}$ of 96.56%, and MCC of 95.71%. Besides, on 3000 epochs, the FTLMO-BILCCD method provides an $\:acc{u}_{y}$ of 99.16%, $\:pre{c}_{n}$ of 97.89%, $\:rec{a}_{l}$ of 97.89%, $\:{F1}_{score}$ of 97.89%, and MCC of 97.36%.

Table 2 LCC detection of the FTLMO-BILCCD model under different epochs.

Fig. 8

Average of the FTLMO-BILCCD model under distinct epochs.

In Fig. 9, the training (TRAN) and validation (VALN) $\:acc{u}_{y}$ performances of the FTLMO-BILCCD methodology below Epoch 3000 are exemplified. The $\:acc{u}_{y}$ values are computed through an interval of 0–25 epochs. The figure underscored that both values of $\:acc{u}_{y}$ express a cumulative propensity, indicating the proficiency of the FTLMO-BILCCD method using enhanced outcomes through multiple repetitions. Moreover, both $\:acc{u}_{}$-ruins approaches through the epochs, notifying diminished overfitting and expressing superior outcomes of the FTLMO-BILCCD method, guaranteeing reliable calculation on unseen instances.

Figure 10 illustrates the TRA loss (TRANLOS) and VAL loss (VALNLOS) graph of the FTLMO-BILCCD approach. The loss values are calculated through an interval of 0–25 epochs. Both values illustrate a diminishing propensity, indicating the competency of the FTLMO-BILCCD model in corresponding to an equilibrium between generalization and data fitting. The succeeding dilution in values of loss and securities increases the outcome of the FTLMO-BILCCD model and tunes the calculation results over time.

Fig. 9

$\:Acc{u}_{y}$ curve of the FTLMO-BILCCD model under Epoch 3000

Fig. 10

Loss curve of the FTLMO-BILCCD model under Epoch 3000.

In Fig. 11, the PR curve of the FTLMO-BILCCD at epoch 3000 delivers elucidation into its results by scheming Precision against Recall for 5 class labels. The outcome demonstrates that the FTLMO-BILCCD continually attains maximum PR outcomes through distinct class labels, indicating its competency to sustain a noteworthy portion of true positive predictions among every positive prediction (precision) and securing a large proportion of actual positives (recall). The fixed growth in PR analysis among the five classes describes the efficacy of the FTLMO-BILCCD in the classification technique.

Fig. 11

PR curve of FTLMO-BILCCD at Epoch 3000.

In Fig. 12, the ROC of the FTLMO-BILCCD technique is examined. The performances indicate that the FTLMO-BILCCD technique below epoch 3000 gains maximal ROC performances across each class label, representing substantial ability to discern the class labels. This steady propensity of higher ROC values through multiple classes shows the skilful solutions of the FTLMO-BILCCD approach in calculating each class, underscoring the strong environment below the classification process.

Fig. 12

ROC curve of the FTLMO-BILCCD model under Epoch 3000.

Table 3; Fig. 13 inspect the comparison analysis of the FTLMO-BILCCD method with existing methodologies^19,36,37. The performances underscored that the PortNet, ResNet, Xception, MobileNetV2, CancerDetecNN V5, LCGANT, KPCA-CNN, CNN + VGG19, AlexNet, and MFF-CNN techniques illustrated poorer performance. Furthermore, the FTLMO-BILCCD technique indicated superior performance with an increased $\:acc{u}_{y},$ $\:pre{c}_{n}$, $\:rec{a}_{l},\:$and $\:{F1}_{score}$ of 99.16%, 97.89%, 97.89%, and 97.89%, correspondingly.

Table 3 Comparative outcome of the FTLMO-BILCCD technique with existing models^{19,36]– [37}.

Fig. 13

Comparative outcome of the FTLMO-BILCCD technique with existing models.

Table 4; Fig. 14 illustrate the computational time (CT) performances of the FTLMO-BILCCD technique with other models. According to CT, the FTLMO-BILCCD method presents a minimal CT of 9.08 s. At the same time, the PortNet, ResNet, Xception, MobileNetV2, CancerDetecNN V5, LCGANT, KPCA-CNN, CNN + VGG19, AlexNet, and MFF-CNN methodologies attained improved CT values of 18.64 s, 23.67 s, 21.96 s, 23.19 s, 20.70 s, 14.36 s, 12.08 s, 13.90 s, 11.78 s, and 20.00 s, respectively.

Table 4 CT analysis of FTLMO-BILCCD approach with existing methods^19,36,37].

Fig. 14

CT analysis of FTLMO-BILCCD approach with existing methods.

Table 5; Fig. 15 demonstrate the ablation study of the FTLMO-BILCCD technique across diverse DL methods. The CapsNet model with an $\:{F1}_{score}$ of 94.57%, shows steady improvements in $\:acc{u}_{y},$ $\:pre{c}_{n}$, $\:rec{a}_{l},\:$and $\:{F1}_{score}$ with each subsequent approach. MobileNet-V3 and BWO portrays higher results, while TPA-BiGRU additionally enhances performance with an $\:{F1}_{score}$ of 97.17. The FTLMO-BILCCD technique outperforms all other methods, attaining the highest scores across all metrics including an $\:{F1}_{score}$ of 97.89%, demonstrating its superior capability in capturing complex patterns and ensuring reliable predictions.

Table 5 Result analysis of the ablation study of the FTLMO-BILCCD methodology.

Fig. 15

Result analysis of the ablation study of the FTLMO-BILCCD methodology.

Conclusion

In this paper, an enhanced FTLMO-BILCCD technique is presented. The main objective of the FTLMO-BILCCD technique is to develop an efficient method for LCC detection using clinical biomedical imaging. Initially, the image pre-processing stage applies the FTLMO-BILCCD model to eliminate the unwanted noise from the input image data. Furthermore, fusion models such as CapsNet, EffcientNetV2, and MobileNet-V3 Large are employed for the feature extraction. For the classification process, the FTLMO-BILCCD model implements a hybrid of the TPA-BiGRU technique. Finally, the BWO model alters the hyperparameter range of the TPA‐BiGRU technique optimally and results in greater classification performance. The FTLMO-BILCCD approach is experimented with under the LCC-HI dataset. The performance validation of the FTLMO-BILCCD approach portrayed a superior accuracy value of 99.16% over existing models. The FTLMO-BILCCD approach’s limitations include reliance on a specific dataset, which may restrict the model’s generalization to other remote sensing images or diverse geographical areas. Additionally, while the model illustrates high accuracy, its performance could degrade when applied to noisy or low-quality images not sufficiently represented in the training data. The model also needs computational resources for training, which might restrict its practicality for real-time applications in resource-constrained environments. Moreover, the interpretability of the model could be improved, as DL techniques often function as black boxes, making it challenging to comprehend the reasoning behind specific classifications. Future work may expand the dataset to enhance the technique’s robustness across diverse image types and optimize it for real-time processing in practical applications. Additionally, enhancing model interpretability through explainable AI techniques would increase its reliability for deployment in sensitive areas like healthcare or environmental monitoring.