Spatio-temporal transformer and graph convolutional networks based traffic flow prediction

Abstract

Traffic flow prediction is a core component of intelligent transportation systems, providing accurate decision support for traffic management and urban planning. Traffic flow data exhibits highly complex spatiotemporal characteristics due to the intricate spatial correlations between nodes and the significant temporal dependencies across different time intervals. Despite substantial progress in this field, several challenges still remain. Firstly, most current methods rely on Graph Convolutional Networks (GCNs) to extract spatial correlations, typically using predefined adjacency matrices. However, these matrices are inadequate for dynamically capturing the complex and evolving spatial correlations within traffic networks. Secondly, traditional prediction methods predominantly focus on short-term forecasting, which is insufficient for long-term prediction needs. Additionally, many approaches fail to fully consider the local trend information in traffic flow data which reflects short-term temporal variations. To address these issues, a novel deep learning-based traffic flow prediction model, TDMGCN, is proposed. It integrates the Transformer and a multi-graph GCN to tackle the limitations of long-term prediction and the challenges of using the predefined adjacency matrices for spatial correlation extraction. Specifically, in the temporal dimension, a convolution-based multi-head self-attention module is designed. It can not only capture long-term temporal dependencies but also extract local trend information. In the spatial dimension, the model incorporates a spatial embedding module and a multi-graph convolutional module. The former is designed to learn traffic characteristics of different nodes, and the latter is used to extract spatial correlations effectively from multiple graphs. Additionally, the model integrates the periodic features of traffic flow data to further enhance prediction accuracy. Experimental results on five real-world traffic datasets demonstrate that TDMGCN outperforms the current most advanced baseline models.

Introduction

With the acceleration of urbanization and the continuous growth of the national economy, the number of motor vehicles has been increasing, leading to more severe traffic congestion and a higher frequency of traffic accidents. As a critical component of smart cities, Intelligent Transportation Systems (ITS) play a pivotal role in traffic management and urban traffic optimization¹. One of the core functionalities of ITS is accurate traffic flow prediction, which not only supports various traffic applications such as route planning and vehicle scheduling², but also provides scientific decision-making bases for traffic management departments. This enables the optimization of traffic resource allocation and the improvement of urban traffic conditions. Therefore, enhancing the accuracy of traffic flow prediction holds significant importance.

Traffic flow is a core metric used to describe the operational status of road traffic, typically defined as the number of vehicles passing through a specific section or node in the road network within a given time interval. Depending on the research objectives, traffic flow can be categorized into inflow/outflow and origin-destination (OD) flow. Inflow refers to the number of vehicles entering a specific road segment or node per unit time, while outflow denotes the number of vehicles exiting from it. These metrics are the most commonly used objects for modeling in current traffic flow prediction tasks. On the other hand, OD flow represents the number of vehicles traveling from a specific origin to a destination within a specified period. This paper focuses primarily on predicting inflow and outflow.

Traffic flow prediction methods can be broadly categorized into three main types: statistical methods, machine learning methods, and deep learning methods. Early statistical approaches were based on linear assumptions, which constrained the expressive power of the models and made it difficult to capture the complex variations in traffic flow. The later machine learning methods saw significant development; however, their performance heavily relies on feature engineering, and they are generally ineffective at extracting and modeling spatiotemporal correlations³. With the rapid advancement of deep learning, Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs) have been widely applied to traffic flow prediction. However, since traffic networks inherently exhibit graph-structured characteristics, these methods are not well-suited for processing such data, resulting in relatively lower prediction accuracy⁴.

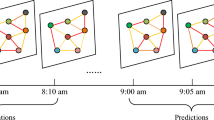
Considering the remarkable effectiveness of GCNs (Graph Convolutional Neural Networks) in processing graph structure data, many scholars have attempted to combine GCNs with RNNs to solve the complex prediction problem of traffic flow. Although the results of such methods are better than those based on CNNs, most of the adjacency matrices used are based on static assumptions. In reality, traffic networks exist within a continuous space, where positions and time points are not independent but are dynamically correlated in both space and time⁵. As shown in Fig. 1, where A, B, and C represent road nodes, while $\:t$, $\:{t}_{1}$, and $\:{t}_{2}$ represent three consecutive moments on the time axis. The solid lines represent spatial correlations, while the dashed lines represent temporal correlations. Spatial correlation refers to the mutual influence between different nodes at each time step, which varies over time, with darker colors in the figure indicating stronger influence. For example, the spatial correlation between nodes C and B at time $\:t$ is stronger than that at time $\:{t}_{1}$. Temporal correlation refers to the fact that a node’s traffic state at a certain moment is not only closely related to its own state at previous moments but also influenced by the states of other nodes at those previous moments. For instance, the temporal correlation of node B at time $\:{t}_{2}$ is not only related to node B at time $\:{t}_{1}$ but also to nodes A and B at time $\:t$.

Fig. 1

Schematic diagram of spatial and temporal correlation. This figure shows the spatiotemporal correlation where A, B, and C represent road nodes, while $\:t,$ $\:{t}_{1}$, and $\:{t}_{2}$ represent three consecutive moments on the time axis. The solid lines represent spatial correlations, while the dashed lines represent temporal correlations. Spatial correlation refers to the mutual influence between different nodes at each time step, which varies over time, with darker colors in the figure indicating stronger influence. Temporal correlation refers to the fact that a node’s traffic state at a certain moment is not only closely related to its own state at previous moments but also influenced by the states of other nodes at those previous moments.

However, static adjacency matrices cannot effectively capture dynamic spatial correlations, thus limiting the accuracy of those prediction models. Existing RNN-based methods, although capable of capturing temporal correlations, tend to suffer from gradient vanishing in long-term prediction tasks, making it difficult to perform such prediction tasks. CNN-based approaches, on the other hand, can handle long sequential data by stacking multiple convolutional layers; however, this leads to higher computational complexity, which negatively impacts training efficiency. Therefore, long-term traffic flow prediction remains a challenging problem.

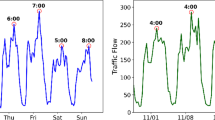
Furthermore, influenced by people’s travel habits and life patterns, traffic data also has prominent periodicity characteristics. Figure 2 shows the traffic flow data from the PEMS04 dataset in California, USA, over a two-week period. The left plot presents the traffic flow from January 1, 2018, to January 7, 2018, while the right plot shows the flow from January 8, 2018, to January 14, 2018. Figure 3 displays the traffic flow for two consecutive days from the same dataset: the left plot shows the flow on February 2, 2018, and the right plot shows the flow on February 3, 2018.

By comparing the left and right plots in both Figs. 2 and 3, it can be observed that the traffic flow data exhibits similarities across different weeks and days. This indicates that traffic flow data possesses clear periodic patterns across weeks and days. Several studies have shown that modeling such periodicity can improve prediction accuracy^6,7. Therefore, accurately capturing and modeling the periodic characteristics in traffic flow is crucial for enhancing the prediction performance.

Fig. 2

Schematic diagram of weekly cycle characteristics. This figure illustrates two weeks of traffic for the California PEMS04 dataset, where (left) illustrates traffic for January 1, 2018 through January 7, 2018 and (right) illustrates traffic for January 8, 2018 through January 14, 2018.

Fig. 3

Schematic diagram of diurnal cycle characteristics. This figure demonstrates the traffic flow for two days for the PEMS04 dataset in California, USA, where (left) demonstrates the traffic flow for January 2, 2018, and (right) demonstrates the traffic flow for January 3, 2018.

In addition, influenced by factors such as geographical locations and surrounding facilities, different areas of the transportation network often have different traffic characteristics, which is known as spatial heterogeneity. Meanwhile, nodes located in different geographical locations may also exhibit similar characteristics. As shown in Fig. 4, where nodes A and B are both located near a school, thus exhibiting similar traffic characteristics. Given the dynamic changes in traffic conditions over time and space, and the complex spatial-temporal characteristics of traffic data, effectively extracting the above features is key to improving prediction accuracy.

Fig. 4

Functional similarity schematic. This figure is a schematic diagram of similar functions, where A and B are road nodes located near schools, indicating that nodes A and B have similar traffic patterns throughout the day.

In order to solve the above problems, researchers have started to introduce Transformer model for traffic flow prediction in recent years, and achieved better results⁸. Transformer was originally used for natural language processing, and its core mechanism, Self-Attention, has a good parallelism and global modeling ability, and can effectively capture long-range dependencies. Compared with traditional RNN, Transformer avoids the problem of information decay and gradient disappearance brought by recursive structure; and compared with convolutional neural network (CNN), which needs to stack multiple convolutional layers to expand the sensory field, Transformer can directly model the dependency relationship between any time steps through the attention mechanism, which can significantly improve the modeling efficiency and reduce the computational complexity. Additionally, the self-attention mechanism in Transformers can dynamically allocate weights based on differences in the input data, allowing it to effectively extract spatiotemporal correlations in traffic flow data over time, thereby improving the model’s prediction accuracy.

However, most self-attention-based methods compute attention weights between queries and keys point-wise across time dimensions^3,9,10,11, neglecting the inherent local trend information in traffic flow data—specifically, the patterns of change within a certain time window around each time step. For example, at a given time step A, a traffic accident may cause congestion and a sudden drop in traffic flow. Another time step B may have a similar traffic flow value to A, but occurs in the early morning, when traffic is naturally light. Clearly, these two time steps are not meaningfully related. Yet, traditional self-attention mechanisms might incorrectly associate them based solely on their numerical similarity, even though their local trend patterns are quite different. As the accident at time A clears up, the local trend around A is fluctuating, whereas the trend around B, which occurs during the early morning hours, is stable and smooth.

Therefore, directly applying the traditional self-attention mechanism to traffic flow segments that exhibit similar values but differ in local trend patterns may result in incorrect weight assignments, ultimately affecting the model’s prediction accuracy.

For this reason, this paper proposes a Transformer-based long-term traffic flow prediction model called TDMGCN (Transformer-based and Dynamic Multi-Graph Convolutional Networks). The main contributions of this paper are as follows:

• (1) Transformer based long-term traffic flow prediction model: A Transformer based traffic flow prediction model is constructed, which can not only effectively extract the dynamic spatiotemporal correlation of the traffic data but also provides high-precision long-term prediction results.

• (2) Local trend-aware self-attention: To fully extract the temporal correlation, a local trend-aware self-attention is designed, so that the model can assign the attention weights more accurately according to the local trend information in the traffic flow data, thus improving the prediction accuracy.

• (3) Multi-graphs based adaptive graph convolution: A multiple graphs based dynamic graph convolution module is proposed, which can extract spatial correlations in traffic data more comprehensively and deeply.

• (4) Spatial location embedding and periodic modeling: A spatial location embedding module, combined with periodic modeling, has been constructed, enabling the learning of both the periodic characteristics of traffic data and the traffic flow characteristics at different nodes, thereby further enhancing its prediction performance.

• (5) Experimental validation and comparison: Experiments are carried out on five accurate traffic data from two categories. The experimental results demonstrate that the proposed model significantly outperforms other advanced traffic flow methods.

Related work

Traffic flow prediction is a classic problem in intelligent transportation systems¹². Early research mainly focused on statistical methods, which used mathematical methods such as mathematical statistics and calculus to process historical road information. It used Historical Average(HA)¹³, Auto-Regressive Integrated Moving Average(ARIMA)^14,15,16, Kalman Filter(KF)¹⁷, Vector Auto-Regressive(VAR)¹⁸, and other models to predict traffic flow at a particular time in the future. Although these methods are simple and computationally convenient and can deal with the linear features of traffic flow, the prediction accuracy of such models is limited due to the nonlinear and uncertain characteristics of traffic flow.

Machine learning methods such as Support Vector Regression(SVR)¹⁹, K-Nearest Neighbor(KNN)^20,21, and Random Forest(RF)²² overcome the limitations of statistical methods. However, they cannot deal with more complex spatial-temporal dependencies in traffic data, such as extracting the topological relationship of road networks, so it is not easy to improve the accuracy of such models further. It requires an artificial selection of features, which will consume much time.

With the widespread deployment of road sensors and rapid development of deep learning techniques, an increasing number of scholars have focused on applying deep learning to traffic prediction research. Deep learning modeling is broadly divided into two aspects: one is to model temporal and spatial separately, and the other is to model spatial and temporal simultaneously. The latter commonly uses graph convolution instead of matrix multiplication in RNNs^23,24.

For spatial modeling, the traffic network is initially divided into grids, and CNN is used to extract spatial correlation^7,25,26. However, the traffic network belongs to the graph structure, and CNN will destroy this structure, so more and more scholars have begun to use GCN to extract spatial correlation^{23,27,28,29,30}, and achieved significant results. However, the above literature uses a local graph convolution method based on static graphs. However, nodes are affected by neighboring nodes and other more distant nodes, so the spatial correlation may be non-local⁴. For this reason, literature [31–33] used an adaptive adjacency matrix to extract the hidden spatial correlation, but the weights of the edges are fixed in the above literature. Since the spatial correlation changes over time in the real world, the static graph cannot reflect the dynamic spatial correlation. In order to further improve the ability of spatial modeling, many studies use the attention mechanism to dynamically allocate the weights of edges so that the model can extract the spatial correlation of dynamic changes. Literature [5] extracted dynamic spatial correlations using the spatial attention mechanism³⁴, and literature [3] and [35] extracted dynamic spatial correlations using the scaled dot product attention mechanism³⁶.

For temporal modeling, the existing methods are divided into three main categories: RNNs-based, CNN-based, and attention mechanism-based. LSTM (Long Short Term Memory)³⁷ and GRU (Gate Recurrent Unit)³⁸, as commonly used RNN methods, have achieved remarkable results in short-term temporal modeling. Due to the GRU method’s simplicity and fast training speed³⁹, thus GRU is currently used for temporal modeling^23,32,39. However, due to the problems of gradient vanishing and gradient explosion⁴⁰, RNNs are less efficient in extracting long-term temporal correlation⁴¹. CNN-based methods can improve the efficiency of processing long sequence data by processing different time steps in parallel. Literature [31] and [42] achieve the extraction of long-term temporal correlations by stacking dilated 1D convolutions⁴³that exponentially increase the receptive domain. However, as the convolutional layers increase, information loss and ambiguity increase, leading to difficulties in efficiently extracting long sequence relationships. In contrast, methods based on attention mechanisms^3,4,5,44,45can focus on the location of each time step in parallel when dealing with long sequence data, thus enabling the model to extract long-term temporal correlations better.

As an excellent model in natural language processing, the Transformer has shown excellent performance in long sequence processing³⁶. The Transformer model utilizes multi-head attention³⁶to learn the correlations of different subspaces, making modeling more flexible. Literature[46] was the first to apply the Transformer to time series prediction, utilizing causal convolution to generate queries and keys, leads to better integration of local context into the attention mechanism. In literature [9], an time embedding method is proposed specifically for the temporal aspects of traffic flow data. Additionally, the original Transformer encoder-decoder architecture is modified into a global encoder and a global-local decoder to mitigate the common error accumulation problem found in seq2seq frameworks. Literature^1,10 employ a spatial self-attention mechanism, combined with a mask matrix, to extract spatial correlations between nodes.

Given the advantages of Graph Convolutional Networks (GCNs) in handling graph-structured data, numerous studies in recent years have attempted to integrate GCNs with Transformers. The aim is to simultaneously model both temporal and spatial dependencies in traffic flow data. For instance, literature⁴⁵ utilizes a temporal Transformer to extract long-term temporal dependencies and employs a spatial Transformer to capture dynamic spatial correlations. Literature³ replaces the feed-forward neural networks in the Transformer with GCN and integrates an attention mechanism to extract dynamic spatial features. Additionally, it introduces a time trend-aware multi-head self-attention mechanism to enhance the modeling of temporal dependencies. This approach has achieved promising prediction results. Literature⁴⁷ models both long-term and short-term temporal dependencies by integrating the Transformer with GRU, and extracts dynamic spatial correlations through an adaptive spatial GCN. Literature⁴⁸ utilizes a temporal Transformer to capture long-term temporal dependencies, employs a convolutional attention mechanism to highlight key features, and combines graph diffusion convolution to enhance spatial representation capabilities. Literature⁴⁹ also adopts a Transformer to model long-term temporal characteristics and uses a Graph Neural Network (GNN) combined with an adaptive adjacency matrix to explore dynamic spatial correlations.

Despite the significant advancements in prediction accuracy achieved by the integration of Transformers and GCNs, these methods generally rely on a pre-defined adjacency matrix, making it challenging to effectively uncover spatial correlations between nodes. Additionally, the self-attention mechanism employed in these models does not fully consider the inherent local trend characteristics of traffic flow data, thereby limiting the models’ predictive accuracy to some extent.

Preliminaries

This section begins with a description of the traffic flow prediction problem, outlining the attention mechanism as prerequisite knowledge for understanding the methodology of this paper.

Description of the problem

Definition 1

(Traffic network) The traffic network is defined as a directed graph $\:G=(V,E,A)$. Here, $\:V=({v}_{1},{v}_{2},\dots\:,{v}_{n})$ denotes the set of $\:N$ nodes of the traffic network, and $\:E$ denotes the set of edges, and $\:A$ denotes the adjacency matrix. Given a threshold value $\:k$, $\:A$ can be described by formula (1):

$$\:\begin{array}{c}{A}_{dist}=\left\{\begin{array}{c}\text{exp}\left(-\frac{dist{\left({v}_{i},{v}_{j}\right)}^{2}}{{\sigma\:}^{2}}\right)\:\:\:\:if\:dist\left({v}_{i},{v}_{j}\right)\le\:k\\\:\:\:\:\:\:\:\:\:\:\:\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\:\:\end{array}\right.\end{array}$$

(1)

$$\:s.t\:i,j\in\:N.$$

Definition 2

(Traffic flow) Let the traffic flow observed by node $\:i$ at time $\:t$ be represented as $\:{x}_{t}^{i}\in\:{R}^{C}$, where $\:C$ is the number of features. The traffic flow observed by all nodes at time $\:t$ is denoted as $\:\:{X}_{t}=\:\left[{x}_{t}^{1},{x}_{t}^{2},\dots\:,{x}_{t}^{N}\right]\in\:{R}^{N\times\:C}$.

Problem Statement: Given historical traffic flow data for the past $\:P$ intervals of historical traffic flow data $\:x=\:\left[{x}_{t-P},{x}_{t-P+1},{\dots\:,x}_{t-1}\right]\in\:{R}^{P\times\:N\times\:C}$, the target is to predict the traffic flow $\:y=\:\left[{x}_{t},{x}_{t+1},{\dots\:,x}_{t+Q-1}\right]\in\:{R}^{Q\times\:N\times\:C}$ for the next time interval $\:Q$.

Attention mechanism

The Attention Mechanism⁵⁰is an approach that mimics the human visual and cognitive system by focusing on the important parts of the input. By introducing Attention Mechanism, neural networks can automatically learn and selectively focus on the important information in the input, thereby improving the performance and generalization of the model.

The Scaled Dot-Product Attention³⁶is a form of attention mechanism. By introducing a scaling factor, it can alleviate the problem of numerical instability that may result from dot-product operations when the dimensions are large. The detailed formulation is provided in formula (2):

$$\:\begin{array}{c}Attention\left(Q,K,V\right)=softmax\left(\frac{Q{K}^{T}}{\sqrt{{d}_{model}}}\right)V\end{array}$$

(2)

Where$\:Q,K,V\:\text{a}\text{n}\text{d}\:{d}_{model}$ represent queries, keys, values and their dimensions, respectively.

The Multi-Head Attention³⁶, as an extension of the attention mechanism, allows the model to focus on different parts of the input sequence. Each head is responsible for focusing on a different subspace, which can improve the ability to model complex relationships. The detailed formulation is provided in formula (3):

$$\:\begin{array}{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:MultiHead\left(Q,K,V\right)=Concat\left(hea{d}_{1},hea{d}_{2},\dots\:hea{d}_{i}\dots\:,hea{d}_{N}\right){W}^{O}\\\:hea{d}_{i}=Attention\left(Q{W}_{i}^{Q},K{W}_{i}^{K},V{W}_{i}^{V}\right)\end{array}$$

(3)

Where$\:N$ denotes the number of heads, and$\:{W}^{O}\in\:{R}^{N{d}_{v}\times\:{d}_{model}}\:,{W}_{i}^{Q}\in\:{R}^{{d}_{model\times\:{d}_{Q}}},{W}_{i}^{K}\in\:{R}^{{d}_{model\times\:{d}_{K}}},{W}_{i}^{V}\in\:{R}^{{d}_{model\times\:{d}_{V}}}$ is the learnable parameter, and $\:{d}_{Q}={d}_{K}={d}_{V}={d}_{model}/N$ .

Methods

In order to solve the long-term traffic flow prediction problem, this section introduces a Transformer based Dynamic Multi-Graph GCN (TDMGCN) model.

Fig. 5

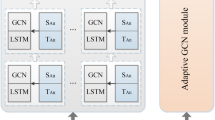
Schematic of the model. This figure shows the TDMGCN model diagram, which is mainly composed of spatiotemporal embedding layers and L identical encoders and decoders. The function of the spatiotemporal embedding layer is to enable the model to learn spatiotemporal information. The encoder and decoder are composed of a local trend-aware self-attention mechanism and an adaptive graph convolution based on multiple graphs. The model generates prediction results through autoregression, using the data generated in the previous steps as additional input when predicting the next value.

As shown in Fig. 5, the proposed TDMGCN model is based on the encoder-decoder architecture. Both the encoder and decoder are constructed from L same sublayers. Each sub-layer in the encoder consists of a local trend-aware self-attention mechanism and an adaptive graph convolution based on multiple graphs. In the decoder, each sub-layer includes two local trend-aware self-attentions and one adaptive graph convolution based on multiple graphs. Additionally, to accelerate model convergence and enhance generalization, residual connections and normalization are employed within each sub-layer. The specific flow of this model is as follows:

• 1. Convert the original data $\:x\in\:{R}^{P\times\:N\times\:C\:}$ to a higher-dimensional representation $\:{x}^{\left(0\right)}\in\:{R}^{P\times\:N\times\:{d}_{model}}$​ by linear projection, where $\:{d}_{model}$>$\:C$. The purpose is to increase the richness and expressive power of the features, thus better capturing complex patterns and structures in the data.

• 2. Let $\:{x}^{\left(0\right)}=\left({x}_{t-p+1}^{\left(0\right)},{x}_{t-p+2}^{\left(0\right)}\:,\dots\:,{x}_{t}^{\left(0\right)}\right)\in\:{R}^{P\times\:N\times\:{d}_{model}}$​ pass through a spatiotemporal embedding layer before entering the encoder. After passing through $\:L$ layers of the encoder, the output $\:{x}^{\left(L\right)}=\left({x}_{t-p+1}^{\left(L\right)},{x}_{t-p+2}^{\left(L\right)},\dots\:,{x}_{t}^{\left(L\right)}\right)\in\:{R}^{P\times\:N\times\:{d}_{model}}$ is obtained. After ′ layers, the decoder generates the output sequence $\:{\widehat{y}}^{\left({L}^{{\prime\:}}\right)}=\left({x}_{t+1}^{{(L}^{{\prime\:}})},{x}_{t+2}^{{(L}^{{\prime\:}})},\dots\:,{x}_{t+q}^{{(L}^{{\prime\:}})}\right)\in\:{R}^{Q\times\:N\times\:{d}_{model}}$​.

• 3. Obtain the prediction result $\:\widehat{y}$ by adopting linear projection to$\:{\widehat{y}}^{\left({L}^{{\prime\:}}\right)}$. The process of generating the output sequence is autoregressive, meaning that to generate $\:{\widehat{y}}_{i}^{\left({L}^{{\prime\:}}\right)}$​​, the decoder uses the encoder’s output $\:{x}^{\left(L\right)}$ together with all previous decoder outputs $\:{\widehat{y}}_{1:i-1}^{\left({L}^{{\prime\:}}\right)}$, where $\:i\in\:(\text{1,2},\dots\:,Q)$​.

The components of the proposed TDMGCN will be introduced later.

Periodic modeling

Let $\:{X}_{hour}$ represent hourly traffic flow data, $\:{X}_{day}$ represent daily periodic traffic flow data, and $\:{X}_{week}$ represent weekly periodic traffic flow data. In this paper, $\:{X}_{hour}$, $\:{X}_{day}$ and $\:{X}_{week}$ are jointly used as model inputs, to explicitly model the periodicity characteristics of traffic flow at different time scales. The composition of $\:{X}_{hour}$, $\:{X}_{day}$, and $\:{X}_{week}$ can be expressed by formula (4) to formula(6):

$$\:\begin{array}{c}{X}_{hour}=\left({x}_{t-{T}_{h}+1},{x}_{t-{T}_{h}+2},\dots\:,{x}_{t}\right)\in\:{R}^{{T}_{h}\times\:N\times\:C}\end{array}$$

(4)

$$\:\begin{array}{c}{X}_{day}=\left(\begin{array}{c}{x}_{t-\left(\frac{{T}_{d}}{{T}_{p}}\right)*q+1},{x}_{t-\left(\frac{{T}_{d}}{{T}_{p}}\right)*q+{T}_{p}},\dots\:,{x}_{t-\left(\frac{{T}_{d}}{{T}_{p}}-1\right)*q+1},\\\:\dots\:{x}_{t-\left(\frac{{T}_{d}}{{T}_{p}}-1\right)*q+{T}_{p}},\dots\:,{x}_{t-q+1},\dots\:{x}_{t-q+{T}_{p}}\end{array}\right)\in\:{R}^{{T}_{d}\times\:N\times\:C}\end{array}$$

(5)

$$\:\begin{array}{c}{X}_{week}=\left(\begin{array}{c}{x}_{t-7*\left(\frac{{T}_{w}}{{T}_{p}}\right)*q+1},{x}_{t-7*\left(\frac{{T}_{w}}{{T}_{p}}\right)*q+{T}_{p}},\dots\:,{x}_{t-7*\left(\frac{{T}_{w}}{{T}_{p}}-1\right)*q+1},\\\:\dots\:{x}_{t-7*\left(\frac{{T}_{w}}{{T}_{p}}-1\right)*q+{T}_{p}},\dots\:,{x}_{t-7*q+1},\dots\:{x}_{t-7*q+{T}_{p}}\end{array}\right)\in\:{R}^{{T}_{w}\times\:N\times\:C}\end{array}$$

(6)

where $\:q$ represents the sampling frequency within a day, $\:t$ denotes the current time step, $\:{T}_{p}$ represents the prediction window size, and $\:{T}_{h},{T}_{d}$, and $\:{T}_{w}$ represent the time series segment lengths for hours, days, and weeks, respectively.

Temporal location embedding

Unlike the sequential processing of inputs in RNNs, the attention mechanism allows for the computation of dependencies between elements in parallel. As a result, the attention mechanism is agnostic to the temporal order in traffic flow data³. However, in time series prediction tasks, analyzing the temporal relationships between data points is crucial. For example, when predicting traffic flow at 5:00 on a certain road segment, the traffic flow data at 4:30 is more important than the data at 3:00. Therefore, this paper adopts the method of positional embedding according to literature³⁶. The detailed formulation is provided in formula (7):

$$\:\begin{array}{c}P{E}_{\left(pos,2i\right)}=\text{sin}(pos/{10000}^{\frac{2i}{{d}_{model}}})\\\:P{E}_{\left(pos,2i+1\right)}=\text{cos}(pos/{10000}^{\frac{2i}{{d}_{model}}})\end{array}$$

(7)

where $\:pos\:$represents the time index within the input traffic flow segment, $\:{d}_{model}\:$denotes the encoding dimension, and $\:i$ is the dimension index ($\:0\le\:i\le\:{d}_{model}-1$).

Spatial location embedding

In addition to temporal positional relationships, each node is also influenced by spatial positions, including the local topological structure of the nodes and the types of roads. Different road types may exhibit distinct traffic characteristics; for example, urban arterials, highways, and suburban roads have varying traffic features. Introducing spatial heterogeneity can provide richer spatial information for traffic flow prediction, thereby enhancing prediction accuracy.

In this paper, a learnable spatial location embedding layer is used to learn the spatial embedding of nodes. Let $\:{E}^{spa}\in\:{R}^{N\times\:N}$ denote the learned spatial location embedding matrix, which is initialized as the distance based adjacency matrix $\:{A}_{dist}$ to account for connectivity and proximity between nodes. Subsequently, $\:{E}^{spa}$ is extended and added to the input data $\:X$, resulting in an enhanced feature representation that enables the model to better capture spatial positional relationships.

Encoder

The encoder consists of $\:L$ identical sub-layers, each comprising two parts: a local trend-aware self-attention module and an adaptive graph convolution based on multi-graph construction module. The former is responsible for modeling dynamic temporal correlations, while the latter is for modeling complex dynamic spatial correlations. These two modules will introduced separately.

Local trend-aware self-attention

Compared to RNN or CNN-based methods, the attention mechanism enables global dependency modeling by computing and weighting the features of any two-time steps in the traffic flow sequence, thereby efficiently extracting long-term temporal correlations.

However, the traditional multi-head self-attention mechanism was originally designed to process independent elements and does not consider the inherent local trend information in sequential data. For example, the curve in Fig. 6 shows traffic flow sequence data collected by road sensors, where A, B, and C represent traffic flow values at different time steps. Since A and B have similar values, the traditional self-attention mechanism would assign a high attention weight between them, indicating a strong correlation. However, from the perspective of local trends, A is in a stable period while B is at the peak of a fluctuation period, and their local trends are clearly different. Therefore, directly applying the traditional attention mechanism to traffic flow data may result in matching errors that rely solely on numerical similarity while ignoring local trend similarity, which can negatively impact the model’s prediction accuracy.

Fig. 6

Traditional self-attentive processing of traffic flow data. This figure demonstrates that the traditional self-attention mechanism assigns attention weights based on the similarity of traffic flow values. The local trend information inherent in the traffic flow data is not considered.

In contrast, CNNs are capable of effectively extracting patterns and relationships between adjacent data points in time series data through convolution operations, thereby improving the accuracy of feature extraction. Therefore, to address the limitation of traditional self-attention mechanisms in capturing local trend information within traffic flow data, a local trend-aware self-attention mechanism has been designed, as illustrated in Fig. 7.

Specifically, this approach replaces the linear mappings of Q (queries) and K (keys) in the traditional self-attention mechanism with 1D convolutions. The detailed formulation is shown in formula (8).

$$\:\begin{array}{*{20}c} {MHCSelfAttention\left( {Q,K,V} \right) = \oplus \:\left( {Chead_{1} , \ldots \:,Chead_{h} } \right)W^{O} } \\ {\:Chead_{j} = Attention(\theta \:_{j}^{Q} { \star }Q,\theta \:_{j}^{K} { \star }K,VW_{j}^{V} )} \\ \end{array}$$

(8)

Where $\:Q,K,V$ represent queries, keys, values, respectively, $\:{\theta\:}_{j}^{Q}$ represents the convolution kernel parameters, and${ \star }$ represents the convolution operation.

Fig. 7

Local trend‑aware self‑attention architecture diagram. This figure demonstrates the structure of the local trend-aware self-attention mechanism.

The local trend-aware self-attention mechanism can allocate attention weights more accurately based on the local trend information in traffic flow data. As shown in Fig. 8, even though B and C have significant numerical differences, they exhibit similar local trends, both being at peak positions during fluctuation periods. Therefore, the local trend-aware self-attention mechanism identifies a strong correlation between B and C and assigns higher attention weights to them accordingly.

Fig. 8

Local trend-aware self-attentive processing of traffic flow data. This figure demonstrates the local trend-aware self-attention assigning attention weights based on the local trend information of the data points.

Multi-graph based dynamic graph Convolution

One of the key issue of traffic flow prediction is how to capture complex spatial correlations. Since urban roads are essentially graphs and GCN generalizes the convolution operation to graphs, this paper will use GCN to extract dynamic spatial correlations.

The main idea of GCN is to update the representation of each node by aggregating the features of their neighboring nodes. The detailed formulation is provided in formula (9):

$$\:\begin{array}{c}GCN\left({H}^{\left(l-1\right)}\right)=\sigma\:\left({\stackrel{\sim}{D}}^{-\frac{1}{2}}\stackrel{\sim}{A}{\stackrel{\sim}{D}}^{-\frac{1}{2}}{H}^{\left(l-1\right)}{W}^{\left(l\right)}\right)\end{array}$$

(9)

Where$\:\stackrel{\sim}{A}=A+{I}_{N}$ represents the adjacency matrix, $\:{I}_{N}$ represents the identity matrix, $\:\stackrel{\sim}{D}$ represents the degree matrix,$\:\stackrel{\sim}{D}={\sum\:}_{j}{\stackrel{\sim}{A}}_{ij}$, $\:{H}^{\left(l-1\right)}$ represents the input of GCN, $\:{W}^{\left(l\right)}$ represents the weight matrix, and$\:\sigma\:$ represents the activation function, which aims to introduce a nonlinear transformation.

In traditional GCNs, the adjacency matrix A is typically a binary matrix, where 0 indicates non-adjacency between nodes and 1 indicates adjacency. However, in traffic flow prediction, the distance between nodes can reflect their correlation; nodes that are farther apart generally exhibit weaker correlations, while nodes that are closer together tend to show stronger correlations. Therefore, a distance-based adjacency matrix can better capture the structural features of the traffic network, thereby aiding the model in understanding the network’s topology.

Furthermore, functional similarity is also a significant factor that can affect spatial correlation. For instance, certain disconnected nodes may exhibit similar traffic characteristics due to their locations within the same commercial or residential areas. Hence, in addition to the distance-based adjacency matrix, a similarity matrix should be introduced to reflect functional similarities between nodes, thereby allowing the model to more comprehensively capture the spatial relationships of traffic flow. The detailed formulation is provided in formula (10):

$$\:\begin{array}{*{20}c} {A_{{sim\left( {i,j} \right)}} = {\text{exp}}\left( {\left\{ { - \frac{{\left\| {x_{{hist}}^{i} - x_{{hist}}^{j} } \right\|^{2} }}{{{\text{min}}\left( {\left\| {x_{{hist}}^{i} } \right\|^{2} ,\left\| {x_{{hist}}^{j} } \right\|^{2} } \right)}}} \right\}} \right)} \\ \end{array}$$

(10)

Where$\:sim(i,j)$ represents the similarity value between node$\:{v}_{i}$ and $\:{v}_{j}$, $\:{x}_{hist}^{i}$ represents the historical data of node $\:{v}_{i}$. By selecting edges with a similarity value greater than a threshold, a similarity matrix $\:{A}_{sim}\:$can be constructed.

In order to enable the model to better learn the feature representations and enhance its ability to model the spatial correlations, this paper combines the distance matrix and the similarity matrix to form a matrix $\:{A}_{fusion}$ through adaptive convolution. The detailed formulation is provided in formula (11):

$$\:\begin{array}{c}{A}_{fusion}=Conv\left(\right({W}_{dist}{A}_{dist}\left)\right||\left({W}_{sim}{A}_{sim}\right)\end{array}$$

(11)

Where$\:Conv(\bullet\:)$ represents the convolution operation, $\:{A}_{dist}$ and$\:{A}_{sim}$ represent the distance matrix and similarity matrix, respectively. $\:{W}_{dist}$ and$\:{W}_{sim}$ represent the weight matrix, respectively, and || represents the concatenation operation.

Furthermore, considering that the spatial correlations are constantly changing in reality, both $\:{A}_{dist}$ and$\:{A}_{sim}$ are static matrices, which means that they cannot capture this dynamic nature. For this reason, this paper utilizes the attention mechanism to dynamically compute the correlation between nodes. The process can be described as formula (12):

$$\:\begin{array}{c}{S}_{t}^{\left(l-1\right)}=softmax\left(\frac{{H}_{t}^{\left(l-1\right)}{{H}_{t}^{\left(l-1\right)}}^{T}\:}{\sqrt{{d}_{model}}}\right)\end{array}$$

(12)

Where$\:{S}_{t}^{\left(l-1\right)}$ represents the strength of the association between nodes, with larger values indicating stronger associations. $\:{H}_{t}^{\left(l-1\right)}$ represents the output of the $\:l-1$ layer at time $\:t$.

The dynamic spatial correlations will be extracted by utilizing the node correlation matrix $\:{S}_{t}^{\left(l-1\right)}$, with adjustment to the static matrix. However, since the correlation matrix is constructed by fusing the distance matrix and the similarity matrix, directly performing the Hadamard product with the adjacency matrix $\:{S}_{t}\:$ may alter the original distance or similarity information, thereby disrupting the inherent topological relationships. Therefore, this paper will apply the Hadamard product between the correlation matrix $\:{S}_{t}^{\left(l-1\right)}$ and a traditional 0–1 matrix. This approach can maintain the structural integrity of the spatial adjacency matrix during the dynamic adjustment process. The detailed formulation is provided in formula (13):

$$\:\begin{array}{c}{A}_{\text{0,1}}=\{\begin{array}{cc}1,&\:\:if\:{v}_{i}\:and\:{v}_{j}\:areconnected\:\\\:0,&\:\:ifnot.\:\end{array}\\\:{A}_{dya}={S}_{t}{\text{A}}_{0-1}\:\end{array}$$

(13)

Where$\:{A}_{\text{0,1}}$ represents the 0–1 adjacency matrix, $\:{S}_{t}$ represents the correlation matrix, $\odot$ represents the Hadamard product, and$\:{A}_{dya}$ represents the dynamic adjacency matrix.

Furthermore, both the spatial adjacency matrix $\:{A}_{fusion}$ and the dynamic adjacency matrix $\:{A}_{dya}$ are predefined adjacency matrices. Relying solely on these predefined matrices cannot fully capture the spatial dependencies between nodes³¹. For instance, the traffic conditions of certain nodes may impact some distant nodes; purely using these predefined adjacency matrices may fail to capture such hidden spatial correlations accurately. So an adaptive adjacency matrix $\:{A}_{adp}$will be introduced, which can learn through gradient descent without requiring any prior knowledge. The adaptive adjacency matrix $\:{A}_{adp}$ can be obtained by randomly initializing two learnable embedding dictionaries, $\:{E}_{1}$ and$\:{E}_{2}$. The detailed formulation is provided in formula (14):

$$\:\begin{array}{c}{A}_{adp}=softmax\left(Relu\left({E}_{1}{E}_{2}^{T}\right)\right)\:\end{array}$$

(14)

Through the product of $\:{E}_{1}$ and $\:{E}_{2}^{T}$, the spatial dependency weights between nodes will be obtained. Here $\:{E}_{1},{E}_{2}\in\:{R}^{N\times\:dim}$, where $\:dim$ represents the dimensionality of the node embeddings. The $\:ReLU$ function is applied to sparsify the matrix, and the $\:softmax$ function is used to normalize it.

By combining the predefined adjacency matrix and the adaptive adjacency matrix, a multi-graph dynamic convolutional layer is proposed. The detailed formulation is provided in formula (15):

$$\:\begin{array}{c}{H}^{\left(l\right)}=DMGCN\left({H}^{\left(l-1\right)}\right)=\sigma\:\left({A}_{set}{H}^{\left(l-1\right)}{W}^{\left(l\right)}\right)\end{array}$$

(15)

Here, $\:{A}_{set}=[{A}_{fusion},{A}_{dya},{A}_{adp}]$ represents the set of adjacency matrices, where $\:{A}_{fusion}$ is the spatial adjacency matrix, $\:{A}_{dya}$ is the dynamic adjacency matrix, and $\:{A}_{adp}$ is the adaptive adjacency matrix.

Decoder

Since the decoder generates the output sequence in an autoregressive manner, a masking mechanism is used to prevent the use of information from future time steps. The decoder consists of $\:L{\prime\:}$ identical sublayers, each comprising two local trend-aware self-attention modules and an adaptive graph convolution based on multi-graph construction module.

Specifically, the first local trend-aware self-attention module is used to extract correlations between input sequences of the decoder. Considering that each output element of the causal convolution depends only on its previous elements and not on future elements, it can maintain temporal causality. Therefore, the causal convolution⁵¹will be used instead of traditional 1D convolution to mask future information.

The second local trend-aware self-attention model is employed to extract correlations between the output sequence $\:{H}^{\left(l-1\right)}$ (key) of the encoder and the sequence (query) of the decoder, with causal convolution used for the query and 1D convolution for the key. The multi-graph based adaptive graph convolution module is identical to that of the encoder and is designed to extract the dynamic spatial correlations.

Experiments

To assess the predictive performance of the proposed TDMGCN model, this section conducts extensive experiments on real datasets and compares it with a variety of baseline models. And then, the key components in the TDMGCN model are analyzed through ablation experiments. TDMGCN is implemented based on the PyTorch 1.10.1 framework. The code execution environment is a server equipped with Intel Core i9-13900 K + RTX4090 (24G).

Datasets

The model is evaluated on two types of datasets. The first is a freeway traffic flow dataset⁵²collected by the California Department of Transportation’s PEMS (Performance Measurement System) at 30-second intervals and aggregated at 5-minute intervals. In this study, three areas—PEMS04, PEMS07, and PEMS08—are utilized. The second type is a metro crowd flow dataset⁵³, which is summarized at 15-minute intervals. The details of these datasets are provided in Table 1.

Table 1 Description of the data set.

Experimental settings

The purpose of this paper is to predict the future 1 h data. The dataset is divided into training set, validation set and test set, and the division ratio is shown in Table 2. The Max-Min normalization method is used to improve the stability and convergence speed of the model. The input dimension of the California freeway dataset is 1, i.e.$\:C=1$ and the input dimension of the metro crowd flow dataset is 2, i.e.$\:C=2$.

In the training phase, historical data is first fed into the encoder. Based on the true values and the output of the encoder, the decoder generates predictions. In the testing phase, predictions are performed autoregressively; that is, the output of the decoder is used as input for the next step.

To evaluate the performance of the model, the predicted values are denormalized and then compared with the true values. The mean absolute error (MAE), root mean square error (RMSE) and mean absolute percentage error (MAPE) are used as evaluation metrics. The evaluation indicators are shown in formula (16–18). Where $\:\text{Y}=({\text{y}}_{1},{\text{y}}_{2}\dots\:{\text{y}}_{\text{i}},\dots\:{\text{y}}_{\text{N}})$ represents the true value, $\:\widehat{Y}=({\widehat{y}}_{1},{\widehat{y}}_{2},\dots\:{\widehat{y}}_{i},\dots\:{\widehat{y}}_{N})$ represents the predicted value, and $\:N$ represents the number of samples.

$$\:\begin{array}{c}MAE=\frac{1}{\text{n}}\sum\:_{i=1}^{n}|{y}_{i}-{\widehat{y}}_{i}|\:\end{array}$$

(16)

$$\:\begin{array}{c}RMSE=\sqrt{\frac{1}{\text{n}}{\sum\:}_{\text{i}=1}^{\text{n}}{\left(\widehat{{\text{y}}_{\text{i}}}-{\text{y}}_{\text{i}}\right)}^{2}}\end{array}$$

(17)

$$\:\begin{array}{c}MAPE=\frac{100\%}{n}{\sum\:}_{i=1}^{n}\left|\frac{\widehat{{y}_{i}}-{y}_{i}}{{y}_{i}}\right|\end{array}$$

(18)

The Mean Absolute Error is selected as the loss function, and Adam is chosen as the optimizer. Hyperparameters and the optimal model parameters are determined based on performance metrics evaluated on the validation set. The similarity threshold is 0.1, the model dimension $\:{d}_{model}$ is 64, the number of attention heads $\:h$ is 8, learning rate$\:lr$ is 0.001. The traffic flow data incorporates periodic features, with the daily and weekly periods both set to 1, meaning that data from the previous day and the corresponding day of the previous week are selected for modeling. Further detailed settings and configurations are provided in Table 2.

Table 2 Dataset settings.

Baseline methods

To thoroughly assess the performance of the proposed TDMGCN model, 14 baseline models are selected for comparison. The first 6 of these are classical traffic flow prediction models, while the remaining 8 are more recent models that share similarities with the proposed TDMGCN model. These models are described as follows:

LSTM³⁷: The Long Short-Term Memory network, which is a variant of the recurrent neural network. It is commonly used to process sequential data and performs well in processing time series, text data, and speech recognition.

DCRNN²³: The Diffusion Convolutional Recurrent Neural Network, which models the traffic flow as diffusion of directed graphs and replaces the matrix multiplication in the seq2seq-based GRU with a diffusion convolution operation.

Graph Wave Net³¹: The Graph WaveNet networks, which use stacked 1D convolution and self-adaptive adjacency matrices to extract spatio-temporal features.

AGCRN³²: The Adaptive graph convolutional recurrent network, which learns node-specific patterns and interdependencies between sequences through two adaptive modules.

ASTGCN⁵: The Attention-based spatio-temporal graph convolutional networks, which use graph convolution and standard convolution to extract spatio-temporal features respectively.

STGCN³⁰: The Spatiotemporal graph convolutional network, which is composed of multiple spatiotemporal convolution blocks. It employs graph convolution and temporal gated convolution to extract spatial-temporal correlations respectively.

ASTGNN³: The Attention-based spatial-temporal graph neural network, which employs a local contextual self-attention mechanism in the temporal dimension and a dynamic graph convolution module in the spatial dimension.

PDFormer¹⁰: The Propagation Delay-aware dynamic long-range transformer, which uses a self-attention mechanism to extract the spatio-temporal correlation and incorporate a traffic delay-aware module. This design enables the model to account for the temporal delays in information propagation between nodes.

STWave⁵⁴: The disentangle-fusion framework, which decomposes traffic data into long-term trend and short-term events, by means of Discrete Wavelet Transform (DWT). And a two-channel spatio-temporal network is used to model the spatio-temporal features.

ST-ABC⁵⁵: The Spatio-temporal attention-based convolutional network, which extracts spatio-temporal correlations through local attention graph convolution with dilation convolution based on the attention mechanism, and enables each node to fuse and utilize contextual information on a global scale through a global attention layer.

ASTTN⁴⁷: The Adaptive Spatial–Temporal Transformer network, which extract temporal correlations via a multi-view temporal attention module and dynamic spatial correlations via an adaptive spatial map convolutional network.

TSGDC⁴⁸: Transformer-based spatiotemporal graph diffusion convolution network, which utilizes graph diffusion convolutional network with Transformer to extract spatio-temporal correlations of complex dynamics.

IEEAformer¹: Implicit-information Embedding and Enhanced Spatial-Temporal Multi-Head Attention Transformer, which employs an environment-aware temporal self-attention mechanism to extract temporal correlations. A parallel spatial self-attention combined with a graph mask matrix is also employed to extract spatial correlations.

TSTGNN⁴⁹: Deep Transformer-based heterogeneous spatiotemporal graph learning model, which extracts long-term temporal correlations through temporal Transformer module and capture dynamic spatial correlations using an adaptive graph structure.

Experimental results and analysis

This paper aims to predict traffic flow for the next hour. Table 3 presents the results of the 15 methods for the next hour on the freeway dataset, and Table 4 shows the results of the 8 methods for the next hour on the metro crowd flow dataset. All results are averaged over all time steps. The best performance are highlighted in bold, and the underlined data indicate sub-optimal results.

Table 3 Comparison of different models on the highway traffic flow dataset.

Table 4 Comparison of different models on the metro crowd flow dataset.

The results summarized in Tables 3 and 4 demonstrate the effectiveness of the proposed TDMGCN model in traffic flow prediction. Specifically:

• (1) PEMS07 and HZMetro Datasets.

  The TDMGCN model achieves the best results across all three metrics: MAE, RMSE, and MAPE.

  On the PEMS07 dataset, improvements over the second-best results are as follows:

  MAE: Improved by 2.4%.

  RMSE: Improved by 0.75%.

  MAPE: Improved by 0.25%.

  On the HZMetro dataset, the improvements are even more pronounced:

  MAE: Improved by 0.71%.

  RMSE: Improved by 6.72%.

  MAPE: Improved by 10.82%.

• (2) PEMS08 and SHMetro Datasets.

  Despite not achieving the best results for the MAPE metric, the TDMGCN model outperforms all baseline models in terms of MAE and RMSE. This indicates strong performance in capturing the overall trends and patterns in these datasets.

• (3) PEMS04 Dataset.

  For the PEMS04 dataset, the TDMGCN model achieves the optimal MAE. While it does not lead in RMSE and MAPE, the differences from the second-best results are minimal. Notably, for the MAPE metric, the IEEAformer model, which ranks second, is only 0.25% higher than the TDMGCN model.

These findings underscore the robustness and versatility of the TDMGCN model across various traffic datasets, demonstrating its capability to effectively capture both spatial and temporal dependencies in traffic flow data.

To provide a more intuitive illustration of the TDMGCN model’s performance, Fig. 9 shows the predictive performance over time for 10 methods including DCRNN, GWN, ASTGNN, and others on both highway traffic and metro crowd flow datasets. Generally, as the prediction horizon increases, the prediction accuracy tends to decrease. However, the proposed TDMGCN model exhibits the smallest decline in accuracy in most cases, indicating its strong effectiveness in long-term predictions.

The reasons for the above results can be mainly attributed to the following aspects:

LSTM only considers temporal features and ignores spatial features, resulting in the worst prediction performance. DCRNN is a typical RNN-based spatio-temporal forecasting method; compared to LSTM, DCRNN uses a bidirectional random walk matrix and GRU to extract spatiotemporal features. However, it fails to effectively capture dynamic spatial characteristics, and RNN methods suffer from gradient explosion in long-term forecasting, leading to poor performance.

GWN, ASTGCN, STGCN, and ST-ABC are typical methods that use convolution to extract temporal dependencies. Among them, STGCN and ASTGCN employ 1D convolution to extract temporal correlations, while GWN and ST-ABC utilize dilated TCNs to expand the receptive field for capturing long-term temporal features. However, compared to attention mechanisms, TCNs require multiple convolutional layers to connect arbitrary positions in the sequence, resulting in similarly unsatisfactory prediction performance.

ASTGCN, PDFormer, ASTTN, and TSGDC all adopt traditional attention mechanisms to extract dynamic temporal dependencies. However, this mechanism fails to allocate attention weights based on local trend information, thereby limiting its effectiveness in extracting temporal correlations. In contrast, ASTGNN and IEEAformer also use attention mechanisms that can allocate attention weights according to local trend information, achieving higher prediction accuracy.

Regarding spatial correlation extraction, ASTGCN, ASTGNN, and ASTTN employ attention mechanisms combined with GCN to capture dynamic spatial dependencies. TSGDC utilizes graph diffusion convolution for spatial dependency extraction. However, these models rely on predefined adjacency matrices, which have limitations in capturing spatial correlations effectively. PDFormer and IEEAformer both utilize two parallel spatial self-attention modules to extract spatial dependencies but do not consider hidden spatial correlations between nodes, leading to suboptimal predictive performance. ST-Wave uses a global GAT (Graph Attention Network) to extract spatial correlations among all nodes and achieves good prediction results, yet it may overlook correlations between weakly connected nodes.

Given that predefined graphs cannot fully capture spatial dependencies, AGCRN and GWN adopt adaptive adjacency matrices to extract hidden spatial correlations. Results show that using adaptive adjacency matrices yields better outcomes than predefined ones. TSTGNN also employs multiple graphs to extract spatial dependencies and relies on traditional attention mechanisms for the temporal dimension, resulting in inferior performance compared to the proposed model TDMGCN. By contrast, TDMGCN models spatiotemporal dependencies through local trend-aware self-attention and multi-graph convolution, achieving superior predictive performance.

Fig. 9

Results of different methods for multi-step prediction on each dataset. This figure mainly shows the prediction results at each time step on 5 datasets. As the prediction interval increases, the prediction accuracy will decrease to some extent, but the TDMGCN model proposed in this paper has the smallest decrease.

Ablation study

In order to further analyze the impact of the key components in the TDMGCN, this section conducts ablation experiments on the highway dataset and analyzes the results. The variants of the model are as follows:

w/o TE: The temporal position embedding was removed as a way to investigate the importance of considering sequential information for the model.

w/o Conv: The 1-dimensional convolution and causal convolution are replaced by using a traditional linear mapping as a way to study the importance of extracting local trend information for the model.

w/o SE: Remove the spatial position embedding to investigate the importance of incorporating spatial location information into the model.

w/o P: Disregarding periodic features of traffic flow data to study the importance of considering periodic features into the model.

w/o d-a indicates that only the predefined adjacency matrix is retained; w/o f-a indicates that only the dynamic adjacency matrix is retained; w/o f-d indicates that only the adaptive adjacency matrix is retained. These setups are used to investigate the importance of multi-graph modeling in capturing spatial correlations within the model.

Table 5 presents the one-hour-ahead prediction results of TDMGCN and its variants.

• (1) Regarding the temporal dimension:

  Compared with the w/o TE setting, the temporal position embedding in TDMGCN helps the model learn the sequential order of time steps.

  Compared with the w/o Conv setting, the results demonstrate that TDMGCN can allocate attention weights based on local trend information in traffic flow data, thereby improving prediction accuracy. On the PEMS04 dataset, MAE, RMSE, and MAPE improved by 7.76%, 6.20%, and 10.48%, respectively.

  Compared with the w/o P setting, the results indicate that TDMGCN benefits from incorporating periodic features, enabling the model to fully exploit temporal regularities in traffic flow data and thus enhance prediction performance.

• (2) Regarding the spatial dimension:

  Compared with the w/o SE setting, the spatial position embedding in TDMGCN helps the model capture spatial heterogeneity in traffic flow data.

  Compared with the w/o d-a, w/o f-a, and w/o f-d settings, the results show that TDMGCN effectively captures spatial correlations among nodes through multi-graph convolution. Among these, the w/o f-d setting performs best, indicating that the adaptive adjacency matrix has a significant advantage in capturing hidden spatial correlations. In contrast, w/o d-a performs worst, suggesting that relying solely on the predefined adjacency matrix is insufficient for extracting comprehensive spatial dependencies between nodes.

  Table 5 Comparison of prediction results between variant model and TDMGCN in highway dataset.

Figure 10 illustrates the multi-step prediction performance of TDMGCN and its variants on the highway dataset. As shown in the figure, TDMGCN consistently outperforms its variants at all time steps, and the decline in prediction performance is smallest as the time step increases.

In general, it can be observed that w/o TE performs poorly across all four datasets, indicating that temporal position embedding plays a crucial role in time series forecasting. Similarly, w/o d-a also shows unsatisfactory results on all datasets, suggesting that predefined adjacency matrices are not sufficient for capturing the complex dependencies between nodes. The w/o Conv variant performs notably worse on the PEMS04 dataset, demonstrating that local trend-aware self-attention is better suited to time series forecasting than traditional self-attention mechanisms. Furthermore, w/o P leads to the most significant performance drop on the PEMS07 and PEMS08 datasets, which indicates that incorporating daily and weekly periodicities enables the model to effectively exploit the inherent repetitive patterns in traffic flow data and thus improve prediction accuracy.

Fig. 10

Comparison of multi-step prediction performance between TDMGCN and its variants on the highway dataset. This figure demonstrates the comparison of multi-step prediction performance between the variant model and TDMGCN on the highway dataset.

Effect of different hyperparameters

In this section, the PEMS08 dataset was selected to test the influence of different hyperparameters on the prediction accuracy of the proposed model. The hyperparameters are mainly divided into the number of attention heads (heads), the feature dimension ($\:{d}_{model}$), the number of network layers (L), the similarity threshold $\:\epsilon\:$, the incorporation of residual connections ($\:Rc$), and the application of layer normalization ($\:Ln$), and the rest of the settings are the same as those in Sect. 5.2.

Figure 11 illustrates the results of different hyperparameters on the PEMS08 dataset. It can be seen that although the results vary with different hyperparameters, their overall impact on the performance of the model is not significant.

Fig. 11

Results for different hyperparameters in the PEMS08 dataset. This figure shows the prediction results of the model under different hyperparameters on the PEMS08 dataset.

From Fig. 11, it can be concluded that the optimal prediction performance is achieved when the number of attention heads is 8, the feature dimension $\:{d}_{model}$ is 64, the number of layers L is 4, the similarity threshold $\:\epsilon\:$ is 0.1, and the model includes residual connections and layer normalization. Increasing the number of attention heads, feature dimensions, and layers appropriately can improve prediction accuracy. For example, using 8 attention heads results in better performance compared to 4 attention heads. This is because different attention heads can learn in parallel within different subspaces, enabling the extraction of more features. Similarly, a feature dimension of 64 performs better than 32 because a higher $\:{d}_{model}$ provides more dimensions for learning and representing the characteristics of the input data, thus enhancing the model’s expressive power.

However, hyperparameters are not always better when set to larger values. For instance, the results with 8 attention heads outperform those with 16 attention heads. This is because too many attention heads result in each head having a smaller dimension, making it difficult to fully learn the features from traffic flow data. Additionally, an excessive number of attention heads introduces more parameters and noise, leading to overfitting issues. The model performs worst with 6 network layers. This may be due to overly deep networks causing overfitting, which reduces the model’s generalization ability on the test set and consequently impacts prediction performance. Moreover, deeper networks have higher computational complexity, resulting in longer training times and difficulties in convergence. Residual connections help mitigate gradient issues in deep networks, while layer normalization enhances training stability. Removing residual connections and layer normalization can lead to training difficulties, preventing the model from converging effectively during the training process.

The size of the similarity threshold $\:\epsilon\:$ also affects the prediction accuracy of the model. Figure 12 shows the similarity matrices under different threshold values. It can be seen that the larger the threshold $\:\epsilon\:,$ the sparser the similarity matrix becomes. As a result, the model learns less information, leading to poorer prediction performance.

Fig. 12

Visualization of similarity matrices under different thresholds. This figure demonstrates the sparsity of the similarity matrix under different thresholds $\:\epsilon\:$.

Conclusion

In this paper, a transformer architecture based traffic flow prediction model TDMGCN is proposed. The model simultaneously considers the temporal and spatial correlations within traffic flow data. Since traffic flow prediction is a typical temporal-sequence prediction, a temporal position embedding module is designed to enable the model to learn the time-sequence information. Considering that different nodes may have different spatial characteristics, a spatial location embedding layer is designed to learn the spatial embedding of nodes.

For temporal correlations, the proposed TDMGCN model adopts a local trend-aware self-attention, which can not only capture long-term temporal correlations, but also capture the local trends of traffic sequences. For spatial correlations, an adaptive graph convolution based on multi-graph construction module is designed. This module considers the physical connectivity and similarity between nodes simultaneously, enabling it to dynamically adjust the association strength between nodes through input data and capture the hidden spatial correlations through adaptive adjacency matrices. By testing on two practical traffic datasets, the proposed TDMGCN model outperforms the baseline model in most of the indexes, proving its high feasibility and effectiveness.