Enhanced multi objective graph learning approach for optimizing traffic speed prediction on spatial and temporal features

Abstract

Traffic Speed Prediction (TSP) is decisive factor for Intelligent Transportation Systems (ITS), targeting to estimate the traffic speed depending on real-time data. It enables efficient traffic management, congestion reduction, and improved urban mobility in ITS. However, some of the challenges of TSP are dynamic nature of temporal and spatial factors, less generalization, unstable and increased prediction horizon. Among these challenges, the traffic speed prediction is highly challenged due to complicated spatiotemporal dependencies in road networks. In this research, a novel approach called Multi Objective Graph Learning (MOGL) includes the Adaptive Graph Sampling with Spatio Temporal Graph Neural Network (AGS-STGNN), Pareto Efficient Global Optimization (ParEGO) as multi objective Bayesian optimization in adaptive graph sampling and enhanced Attention Gated Recurrent Units (EAGRU). The proposed MOGL approach is composed of three phases. The first phase is an AGS-STGNN for selecting the optimal samples of both spatial and temporal. Second phase has a ParEGO-based adaptive graph sampling is employed to extract spatial features that are refined through GNN layers by selecting temporal features. Third phase is an EAGRU module to enhance feature representation and prediction reliability by incorporating the feature fusion stage to dynamically prioritizing the critical road segments and time intervals, allowing the model to focus on the most influential factors affecting traffic speed variations in prediction. The supremacy of the proposed model is validated using the two available benchmark traffic datasets METR-LA and PeMS-BAY. The experimental results of the proposed MOGL approach is evaluated in terms accuracy, Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Mean Absolute Error (MAE) to predict and estimate the traffic speed. It ensures the proposed approach offers a better real-time and large-scale traffic speed prediction compared to existing approaches with the values 2.09 and 2.15 for MAE, 3.29 and 3.22 for RMSE and 3.17 and 3.21 for MAPE in both datasets. The proposed approach showed higher performance, notably on the METR-LA dataset, with a significant RMSE reduction of up to 28.9% compared to DSTMAN, outperforming other models like STGCN variants.

Introduction

Intelligent Transportation Systems (ITS) are advanced applications that integrate communication, computing, and sensing technologies to enhance transportation efficiency, safety, and sustainability. It uses real-time data collection, analytics, and decision-making tools to optimize traffic flow, reduce congestion, and improve road safety¹. ITS plays a critical role in modern traffic management by facilitating data-driven decision-making for urban planners, traffic authorities, and commuters. Real-time traffic speed prediction is a core function of ITS, enabling proactive management of road networks². It helps in traffic congestion reduction, enhanced navigation and routing, accident prevention and safety improvement, public transportation efficiency, and smart city integration³. Currently, some of the incidents happened worldwide due to the high traffic speed are on 15 march 2025, the old man was died owing to high speed (110 km) in vehicle on busy roads and in USA⁴, three colleges students were died in road accident, as they were drunk and high speed (120 km) during traffic in car⁵. Similarly, more incidents are happening in busy road networks all over the world.

To prevent accident and sudden death, its necessary for ITS to enable traffic speed prediction method in all traffic signals. Traffic speed prediction improves urban mobility, congestion management, and transportation efficiency by enabling smoother travel times, reducing uncertainty for commuters, detecting and mitigating congestion hotspots, and enhancing transportation efficiency⁶. Traffic speed prediction uses data from sensors, GPS, and cameras to predict future traffic conditions, enhancing road safety and congestion management⁷. In earlier time the statistical models are mostly used, then the machine and deep learning models are used to analyse the speed variations, enabling dynamic traffic control, adaptive speed limits, accident risk detection, and optimized emergency services and autonomous vehicles⁸. However, the common challenging factors in traffic speed predictions are spatial and temporal dependencies, lack of interpretability and reduced generalization⁹.

Recently, predicting the traffic speed based on spatial and temporal dependencies are highly complicated task due to dynamic and interconnected nature of road networks¹⁰. The various Deep Learning (DL) models have been used to predict the traffic speed to improve the accuracy of predictions, leading to smarter and more efficient transportation systems. Though the traditional DL models have some limitations are less spatial awareness and difficulty in capturing long-term dependencies that leads to inaccurate traffic speed prediction^11,12. Existing deep learning models for traffic speed prediction, such as CNNs, RNNs, LSTMs, GRUs, and GNNs, often struggle to capture the complex spatio-temporal dependencies in dynamic road networks. These models typically face limitations, including: (i) inability to adapt to evolving graph structures, (ii) overlooking multi-objective optimization in feature selection, and (iii) ineffective balance between spatial and temporal feature interactions. Hybrid models like GCN-LSTM, STGCN, and GMAN have shown progress but are often constrained by fixed graph structures or static temporal windows, limiting their generalizability. To overcome the aforementioned challenges, a novel, unified, and adaptive pipeline that combines structural optimization (AGS), sample efficiency (ParEGO-AGS), and selective temporal attention (EAGRU) within a spatio-temporal graph neural network framework. To our knowledge, no prior work has integrated these components holistically in a single traffic prediction system, offering a significant advancement in the field. This approach enables more accurate and efficient traffic prediction, particularly under complex traffic conditions. The main contributions of MOGL approach in predicting the traffic speed in dynamic traffic conditions are,

• (i) An Adaptive Graph Sampling with Spatio Temporal Graph Neural Network (AGS-STGNN) is used for optimal selection of both spatial and temporal features dynamically in graph structure. It ensures the graph structure would retain the essential nodes with timestamps, so it automatically reducing the computationally overhead whereas conserving the effective spatio-temporal dependencies.

• (ii) Pareto efficient global optimization (ParEGO) based Multi Objective Bayesian Optimization for Adaptive Graph Sampling (ParEGO-AGS) is employed to extract the samples of spatial features which are the essential for learning objective. It assures the stable trade-off among spatial attention and depictive efficiency by identifying the selective node subsets with timestamps which successfully reduces the dimensionality without disturbing the underlying structure of data.

• (iii) Enhanced Attention Gated Recurrent Unit (EAGRU) is used for feature fusion process to dynamically prioritize critical road segments and time intervals in spatio-temporal data to predicts the traffic speeds. The combination of attention with self-mechanism in GRU architecture successfully fuse the informative samples of both spatial and temporal features. It allows the model to capture the dynamic traffic forms and increase the performance of the model while predicting the traffic speed.

• (iv) The proposed MOGL approach is implemented in two publically available road network datasets are METR-LA and PeMS-BAY. The effectiveness of the proposed approach is evaluated in terms of accuracy, Root Mean Square Error (RMSE), Mean Square Error (MSE) and Mean Absolute Error (MAE). The experimental results ensure the efficacy of the proposed approach to simplify transversely varied traffic situations and road environments that insights the strength and consistency for traffic speed prediction tasks.

The structure of the paper is summarizing the following sections in detail, beginning with a literature review to contextualize our approach in Section “Literature review”, introduces the proposed MOGL approach in Section “Materials and methods”, presents experiments and results in Section “Proposed methodology”, and concludes and suggests future improvements in Section “Experimentation and discussion”, such as real-time sensor feedback and scalability for large-scale ITS deployment.

Literature review

This section delivers a detailed review on works that concentrates on spatial and temporal features of real time traffic data and prediction of traffic speed using the machine learning (ML), deep learning (DL) and neural network models. Ali et al.¹³ introduces a neural network framework that integrates attention mechanisms with spatial-temporal elements to enhance traffic flow prediction. Despite exhibiting performance enhancements compared to baseline models, significant limitations encompass dependence on static spatial correlations that may fail to account for dynamic alterations in road networks, restricted scalability for extensive urban networks due to computational intricacies, and the potential oversimplification of external variables such as weather or events that affect traffic patterns. The model’s interpretability is limited by its complex hybrid architecture, and its assessment on certain datasets prompts concerns regarding its applicability to a range of traffic situations with differing periodicities or anomaly occurrences. Ali et al.¹⁴ presents a dynamic framework that enhances energy efficiency by strategically allocating traffic prediction tasks between edge devices and cloud servers, contingent upon data complexity and resource availability. Although it achieves a balance between energy efficiency and predictive accuracy, significant limitations encompass scalability issues in extensive deployments due to computational burdens from edge-cloud coordination, possible accuracy compromises amid real-time traffic variations, and dependence on idealized assumptions regarding network stability and uniformity of edge-node capabilities. The model’s assessment in controlled settings may fail to consider real-world variability in IoT infrastructure or unexpected hardware malfunctions, and its energy optimization approach neglects dynamic external influences (e.g., weather, accidents) that could interfere with traffic patterns and computational processes. Lin et al.¹⁵ discussed a study explores the relationship between traffic factors, meteorological conditions, and air pollutants in Taipei City. Researchers used a Bayesian network probability model and a Long Short-Term Memory (LSTM) neural network to analyze causal relationships and predict airborne pollutants. The model achieved high performance, with correlation coefficients exceeding 0.9 for primary pollutants and 0.8 for secondary pollutants. However, traditional statistical methods for data pre-processing may not capture short-term variations, requiring advanced techniques. Chan RK et al.¹⁶ designed a Cluster Augmented LSTM (CAL), a novel approach for long-term traffic forecasting using time-series segmentation, data clustering, and CNN-based classification. The clustering step refines traffic data, reducing outliers and providing additional features. The model is evaluated using Mean Absolute Percentage Error (MAPE) and Root Mean Squared Error (RMSE), showing improvements of 1.42–1.76% in MAPE and 0.25–0.41 in RMSE over competing models. However, the study only uses a single feature (traffic speed) for prediction, limiting its generalizability across different locations and scenarios. Ali et al.¹⁷ propose a multi-graph neural network (MGNN) framework to optimize traffic prediction in edge computing environments by modelling dynamic spatial dependencies and resource constraints across distributed nodes. Prioritizing computational tasks on resource-rich edge servers improves prediction accuracy and reduces latency, but managing multi-graph structures is complex, increasing training overhead and hindering real-time adaptability for rapidly changing traffic scenarios. In environments with occasional network disruptions or diverse technology, the framework’s reliance on stable edge node connectivity and uniform resource availability may fail. Due to exponential graph-based computing growth, scaling to mega-city networks is difficult, and the model’s-controlled evaluation ignores sensor noise, data sparsity, and adversarial edge-node failures. Without integration with external elements like emergencies and weather that interrupt traffic patterns, the resource allocation technique is vulnerable in unpredictable circumstances. Shen et al.¹⁸ proposed a decentralized federated learning-based spatial–temporal transformer network model (DeFedSTTN) for forecasting freight traffic speed in urban areas. In place of a conventional graph convolutional network, the model incorporates a spatial-temporal transformer network, improving local personalized learning that involved in requirement of a centralized cloud server. A real-world dataset from the Nanjing Metropolitan Area was used to validate the model, which offers higher forecasting accuracy than conventional GCN-based models. However, in urban settings with limited resources, its practical application may be limited by computational and communication overhead. Ounoughi et al.¹⁹ suggested the “Grizzly” model, a hybrid method that makes use of an enhanced Sequence-to-Sequence Bi-directional Long Short-Term Memory (Bi-LSTM) neural network. In terms of Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE), the model performs better than deep learning graph-based models and conventional time series models. The Sequence-to-Sequence Bi-LSTM architecture integration, strong data preparation, and comprehensive performance evaluation are some of the model’s strong points. Nonetheless, the model’s constraint is its incapacity to identify outliers or abrupt trend occurrences in traffic patterns. This may result in incorrect forecasts under atypical traffic circumstances and heightened susceptibility to erratic data. Awan et al.²⁰ suggested a deep stacking-based ensemble model for short-term traffic speed forecasting in urban transportation networks. The model uses eXtreme Gradient Boosting, Random Forest, and Extra Tree as base learners and a Multi-Layer Perceptron as a meta-learner. Tested on real-world Floating Cars Data, it showed significant improvements in accuracy and performance compared to traditional models. However, the model lacks consideration for external factors like weather conditions, road incidents, and public events, which could limit its adaptability to sudden traffic changes. Vijayalakshmi B et al.²¹ developed an SLSTM_AE-BiLSTM model is a multivariate short-term traffic congestion prediction model that uses a Stacked Long Short-Term Memory Autoencoder to encode weather features, a Bidirectional Long Short-Term Memory network to capture traffic data, and a Convolutional Neural Network to predict congestion status. The model achieved a congestion prediction accuracy of 92.74% using the Caltrans PEMS dataset. However, its reliance on a single source may limit its applicability to diverse urban environments. Ma et al.²² designed a hybrid deep-learning model (STFSA-CNN-GRU) for short-term traffic speed prediction, combining spatial-temporal feature selection (STFSA), Convolutional Neural Network (CNN), and Gated Recurrent Unit (GRU). The model uses CNN to extract deep features and GRUs to capture long-range dependencies. However, it does not consider road occupancy, traffic density, special dates, or emergencies, which could limit its applicability to real-world traffic scenarios. The model’s effectiveness may decrease in unexpected traffic conditions. Hu X et al.²³ introduces AB-ConvLSTM, a hybrid deep-learning model for large-scale traffic speed prediction. It combines Convolutional Long Short-Term Memory, an attention mechanism, and Bidirectional LSTMs. The model outperforms existing models in predicting urban traffic speed, demonstrating high accuracy and efficiency. However, its accuracy is compromised during special scenarios like holidays and extreme weather conditions. Future work should expand the dataset and refine the model to improve its adaptability in unpredictable conditions. Qu L et al.²⁴ proposed a “Features Injected Recurrent Neural Networks for Short-term Traffic Speed Prediction” introduces a novel approach that combines sequential time data with contextual factors to improve traffic speed forecasting accuracy. The model uses a stacked Recurrent Neural Network and a sparse Autoencoder to predict future traffic speeds. However, its performance diminishes in the presence of missing data, requiring robust data imputation techniques. Wang et al.²⁵ presents FDLTCP, a traffic congestion prediction model that uses fuzzy logic, stochastic estimation, and deep stacked LSTM networks to predict traffic congestion. The model extracts traffic data from route planners’ websites, enabling congestion level detection at intersections. The deep stacked LSTM network and online training improve prediction accuracy compared to traditional methods. Experimental evaluations show FDLTCP outperforms baseline models in terms of RMSE and performance metrics. However, the study’s limitations include reliance on web-scraped traffic images and the need for manual tuning. Ahmad et al.²⁶ proposed a GCN-DHSTNet model that combines CNN, LSTM, and Graph Convolutional Networks to predict crowd flow patterns, improving accuracy by 27.2% in RMSE. However, it relies on a static graph structure and predefined temporal segments, limiting adaptability. The model’s complexity affects scalability and real-time performance. Accuracy also depends on external data quality, like weather and POIs. Riaz et al.²⁷ proposed a VMR algorithm optimizes VM placement in cloud data centers to reduce energy consumption while maintaining QoS by reallocating VMs and powering down idle servers. It achieves significant energy savings (2× to 4×) compared to First-Fit and Random algorithms. However, the approach’s assumption of static workloads limits its adaptability in real-time environments with dynamic or unpredictable task patterns.

A comprehensive survey on the existing traffic speed prediction approaches contends the requirement for developing an essential neural network models for prediction of traffic speed to avoid the road accidents and protect the environment from averting crashes and serious injuries. However, predicting the traffic speed based on spatial and temporal features are complex. To address this problem, the researchers proposed an Multi Objective Graph learning approach that include the AGS-STGNN to select the optimal spatial and temporal features; MOBO-AGS for extracting the samples of spatial features and distinguish the samples of spatial from temporal and the EAGRU employed to the process of feature fusion which dynamically depicts the dangerous road segments depending on times to predict the traffic speed.

Materials and methods

Adaptive graph sampling with Spatio Temporal graph neural network (AGS-STGNN)

Adaptive graph sampling with spatio temporal graph neural network (AGS-STGNN) is graph based dynamic neural network architecture which includes spatial and temporal features. It selects the adaptive and relevant features based on entities according to the connected entities, formation of groups with its time which produce the essential information present in the data. The importance of AGS-STGNN is scalability, flexibility, isolated capture of spatial and temporal patterns and fast. It achieves, the improved performance with reduced computational cost. The structure of AGS-STGNN includes spatial and temporal convolutional module, adaptive graph sampling (hybrid sampling (Node + Edge + Regions), spatial aware sampling and temporal aware adaptive sampling with its corresponding score functions, joint spatial-temporal adaptive sampling and joint spatial temporal embedding and finally prediction²⁸. The steps of AGS-STCNN are follows as.

Step 1 Construct spatial graph convolutional is given in Eq. (1)

$${S}^{(q+1)}=\:\theta\:(\widehat{{A}_{m}}{S}^{\left(q\right)}{Wgh}^{q}.$$

(1)

Where $\widehat{{A}_{m}}$ is normalized adjacency matrix; ${S}^{\left(q\right)}$indicates the presence of nodes with features at qth layer; ${Wgh}^{q}$ is the weight of qth layer with non-linear activation.

Step 2 Construct temporal convolution module is given in Eq. (2)

$${O}_{t}=Conv1D\:\left({X}_{:,t-m:t,:}\right)\in\:\:{\mathbb{p}}^{G*\:{C}_{out}}.$$

(2)

Where $\left({X}_{:,t-m:t,:}\right)$ is time slice with convolution output ${C}_{out}$ for the output features in time ${O}_{t}$.

Step 3 Determine the Adaptive Sampling based on hybrid, temporal and spatial.

• (a) Hybrid Sampling: Construct the graph where the node represents features and the edge represent the node connecting line which defines the relationship between the nodes. The hybrid sampling is combination of three methods are node, edge and regions. The node sampling computes the importance score and top-k nodes sample selection. Then, determine edge sampling based on attention weights between the nodes. Finally, integrate node and edge sampling by using region sampling. In region sampling, formation group is depending on the features²⁹.

  Node based score sampling ${N}_{s}=\:{f}_{scr}\:\left({Y}_{m}^{t},[{Y}_{n}^{t}\right|\:n\:\in\:N\left(m\right)\left]\:\right)$ where ${N}_{s}$ is node score ; ${f}_{scr}$ is attention layer’s learnable function and ${Y}_{m}^{t}$ is the feature node at time t. Then apply, tok-selection for selecting the hard sample selection ${F}_{sam}^{t}=Top\:G\:\left(\right\{{scr}_{m}^{t}{\}}_{m=1}^{t},g$ where ${scr}_{m}^{t}$ is the essential node score at time t is determined by its features and nearby feature. $\{{scr}_{m}^{t}{\}}_{m=1}^{t}$denotes the score of all nodes in graph and Top G denotes the selecting higher score nodes for the set of samples ${F}_{sam}^{t}$

  Edge based Attention weight sampling -Selecting the edges effectively by applying dynamic pattern depending on attention weights of each edge present between to nodes is given in equ.

  $${\varvec{E}\varvec{d}}_{\varvec{m}\varvec{n}}^{\varvec{t}}=\varvec{l}\varvec{e}\varvec{a}\varvec{k}\varvec{y}\varvec{R}\varvec{e}\varvec{L}\varvec{U}\:\left({\varvec{a}}^{\varvec{T}}\right[\varvec{W}\varvec{g}\varvec{h}{\varvec{X}}_{\varvec{m}}^{\varvec{t}}\left|\left|\varvec{W}\varvec{g}\varvec{h}{\varvec{X}}_{\varvec{m}}^{\varvec{t}}\right]\right)$$

  Where wgh is the attention weight. ${X}_{m}^{t}$ is the node’s vector at time t, ${a}^{T}$ gives importance score from linear to scalar. Then the SoftMax normalization with Attention in Eq. (3).

  $${\alpha\:}_{mn}^{t}=\:\frac{\text{e}\text{x}\text{p}\left({e}_{mn}^{i}\right)}{{\sum\:}_{k\in\:N\left(m\right)}\text{e}\text{x}\text{p}\left({e}_{mk}^{t}\right)}.$$

  (3)

Where the final attention weight from node (n to m) for ${\alpha\:}_{mn}^{t}$. N(m) is set of nearby nodes. Then group the graph depending on the features including centroids in Eq. (4)

(4)

Step 3 Temporal-aware adaptive sampling ${e}_{i}^{t}=\:{f}_{tem}\left({Y}_{m}^{t-n:t}\right)$.The adaptive sampling was presented with temporal based features.

Step 4 Spatial -aware adaptive sampling ${S}_{i}=\:{f}_{strt}(B,y)$.The spatial sampling was presented with spatial based features.

Step 5 Joint spatial-temporal based AGS ${\stackrel{\sim}{e}}_{i}^{t}=\:\alpha\:\:{e}_{i}^{t}+\left(1-\alpha\:\right){s}_{i}$.It fuse the two features and form the embedded as combination of spatial and temporal based AGS.

Step 6 Joint spatial-temporal Embedding after applying sampling is given in Eq. (5)

$${S}^{(q+1)}=GCN(\:{\stackrel{\sim}{A}}_{m}^{t},\:{X}_{s}^{t})\:\text{a}\text{n}\text{d}\:{O}_{t}=TCN\:\left({A}_{s}^{t-k;t}\right).$$

(5)

Thus, the fused spatial temporal features of STGNN with adaptive sampling is illustrated clearly with definition and explanation³⁰.

Pareto efficient global optimization based adaptive graph sampling (ParEGO-AGS)

ParEGO is multi-objective Bayesian optimization technique is developed to essential estimation of the pareto front for the black box functions in various inconsistent objectives. The main aim of parEGO is to evaluate the function while training the model when it has high computational cost or more time consumption. The simultaneous optimization of multiple objectives efficient in reducing the computation cost with improved performance with releases of new set of pareto optimal solutions³¹. The parent optimal solution is a solution arises when no objective can be increased without disturbing or deteriorating the other one. The following are the steps to be practiced for parEGO,

Step 1 Construct graph with vertices and edges with multiple objectives that derive the objective factor, $f\left(x\right)=\{{f}_{1}\left(x\right),{f}_{2}\left(x\right),{f}_{3}\left(x\right),\dots\:\dots\:,{f}_{m}\left(x\right)\}$, where $x\:\in\:N$ denoted the set of nodes which represent the samples.

Step 2 Initialize the samples by selecting the initial subset from nodes randomly ${x}_{0}\:\in\:N$.Then compute the objective values for the $f\left(x\right)$ and align the values with dataset.

Step 3 Deploy the pareto global optimization as scalar function by transforming the multi-objective function into scalar function by using the Tchebycheff method is given in Eq. (6)

$$sf\left(x,\:\lambda\:\right)=\text{max}{\lambda\:}_{i}|\:{f}_{i}\left(x\right)-\:{y}_{i}^{*}|.$$

(6)

Where $\lambda\:=[{\lambda\:}_{1},\dots\:\dots\:,\:{\lambda\:}_{m}]$ defines the samples weight vector which taken randomly and the ${y}_{i}^{*}$ shows the ideal objective vector for every objective which modifies the multi-objective sampling into scalar objective problem.

Step 4 Then, train the surrogate model using gaussian process regression (GPR) which takes the input as encoded samples nodes and output as predicted scalar function based objective values.

Step 6 Present the acquisition function to optimize and select the adjacent node set that balances the exploration and exploitation for the graphs.

Step 7 Representing the selected adjacent node to point the new sample nodes, compute the entire objective functions for the selected adjacent nodes and add all to the dataset which defines the process fit to the graph with trade-offs.

Step 8 To achieve convergence then iterate the steps of scalar function to deployment adaptive sampling because for each iteration improves the performance of surrogate model and the diversified scalar function from parEGO approximate the pareto front of graph sampling strategies.

Step 9 The approximated parent front indicates its correspondence to its sampled graph with various trade-off between objectives. Then select the final subgraph depending on the dataset constraints³².

Thus, the ParEGO in AGS sampling enriched by transformation of multi to single using scalar function. Then, the scalar function contributed to all the objectives. The benefits of the ParEGO are effective sampling is achieved, the indication multiple objectives with trade off emphasizes the balancing of accuracy, cost and data. It highly supports for high dimensional and heterogenous graph³³.

Enhanced attention gated recurrent unit (EAGRU)

The Enhanced Attention Gated Recurrent Unit is a hybrid neural network models that hybridizes the temporal characteristics of GRU with the context of self-attention mechanism. The aim of EAGRU is to fuse the consecutive samples depending on context relationships in the input which predict and classify the according to the data and application used. The EAGRU is composed of input layer, GRU layer, self- attention layer, fusion layer and output layer. The major benefits of EAGRU are effectively collects both short- and long-term series, the presence of self-attention in GRU, collects the contextual relationship between the series of both short and long³⁴. The presence of attention weights encloses the important sequential samples alone which decreases the data loss and high flexible while working with high dimensional data and achieves enhanced performance. The step of EAGRU is follow as,

Step 1 The input data is given in Eq. (7) is aligned in format of temporal sequence by presenting the sliding time window

$${A}_{i}^{t}=\left\{\:{a}_{i}^{t-s},\dots\:\dots\:\dots\:,\:{a}_{i}^{t}\right\}\:where\:{a}_{i}^{t}\:\in\:\:{\mathbb{p}}^{d}.$$

(7)

Step 2 Employ the self-attention depending on temporal features to collect the importance of each sequential time series is given in Eqs. (8) and (9)

$$L,M,N,\:=\:{Wgh}_{l}A,\:\:{Wgh}_{m}A,\:\:{Wgh}_{n}A$$

(8)

$$Att\left(V\right)=softmax\:\left(\frac{{LM}^{t}}{\sqrt{{d}_{m}}}\right)N.$$

(9)

Where $V\:\in\:\:{\mathbb{p}}^{wgh*d}$ is sliding time window of the node which defines the temporal embedded features.

Step 3 Then temporal sequenced attention weighted series in Eq. (10) is feed towards the gated recurrent unit to experience the temporal dynamics in the data³⁵.

$${Hi}_{t}=GRU\left(\widehat{V}\right)=GRU\:(\:\stackrel{\sim}{{v}^{t-w}},\dots\:\dots\:\dots\:\:\stackrel{\sim}{{v}^{t}}).$$

(10)

Where ${Hi}_{t}$ includes overall fused temporal features which includes the non-linear sequence dynamics.

Step 4 Then, concatenate all the fused temporal features at feature fusion layer which include the GRU hidden state ${Hi}_{t}$, node embedding ${st}_{t}$ and its spatial features from AGS shows the node embedding ${g}_{t\:}$in Eq. (11).

$${u}_{t}=fusion\left(\left[{Hi}_{t}\:\left|\right|{st}_{t}\left|\right|,{g}_{t\:}\right]\right).$$

(11)

Step 5 The fully connected output layer is presented for the purpose of prediction to be performed in Eq. (12).

$${\stackrel{\sim}{f}}_{i}^{t}=\:{Wgh}_{out}\odot\:{u}_{t}+b.$$

(12)

Thus, the EAGRU assures the enhancement in patterns and dependencies in long range time series data. In prediction, the EAGRU mainly captures both the local and global dependencies which concentrate to have improved accuracy in prediction. It decreases the noise and enhances the critical time while prediction with stable performance³⁶.

Proposed methodology

The proposed Multi Objective Graph Learning (MOGL) approach used to predict the traffic speed based on spatial and temporal features. The MOGL approach is composed of three phases are (i) Adaptive Graph Sampling with Spatio Temporal Graph Neural Network (AGS-STGNN) for optimal selection of spatial and temporal features, (ii) Pareto efficient global optimization (ParEGO) based Multi Objective Bayesian Optimization for Adaptive Graph Sampling (ParEGO-AGS) for extracting the spatial samples distinguished from temporal samples and (iii) Enhanced Attention Gated Recurrent Unit (EAGRU) for feature fusion to predict the traffic speed dynamically. The architecture of proposed MOGL approach is shown in Fig. 1.

Fig. 1

Architecture of proposed MOGL approach.

Data collection

The real-time spatiotemporal traffic data can be collected using loop detectors, GPS sensors or other monitoring devices in metropolitan environments. This data generally comprises speed, volume, and occupancy metrics gathered at consistent time intervals from various sensor sites throughout a transportation network. The dataset is organized as a spatiotemporal graph, with nodes symbolizing traffic sensors or monitoring locations, and edges delineating road connectivity. It is important for comprehending traffic patterns, recognizing congestion points, and forecasting future roadway conditions. This data is extensively utilized in traffic management, urban planning, and intelligent transportation systems to enhance mobility and mitigate congestion.

Data preprocessing

Data pre-processing is inevitable to improve the performance of the learning model. The dataset considered for the evaluation is imputed with sensors which arises sensor failures and transmission errors. Also, there exists so many missing values in the location-based features of both META-LR³⁷ and PeMS-BAY³⁸ datasets. Hence, the above said missing values are handled using K- nearest Neighbour (K-NN). It leverages the spatial and temporal relationship for the effective reconstruction of these values. The proposed model includes the graphical construction where the samples have high dimensional data points and are normalised using Min-Max normalization. Apart from this feature fusion is performed with integrating the traffic parameters such as speed, congestion levels, road topology to form a unified representation. Once the data is pre-processed, a graphical construction is implemented where the nodes represent the sensor locations road connectivity and traffic flow strength based on the adjacency matrix values. This graph-based structure enables the AGSTGNN model to effectively model road network relationships and time-based variations.

Phase 1: Adaptive graph sampling with Spatio Temporal graph neural network (AGS-STGNN)

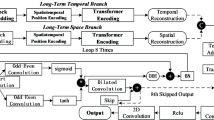
Adaptive Graph Sampling with Spatio -Temporal Graph Neural Network (AGS-STGNN) is a dynamic neural network framework designed for intricate data, such as traffic speed forecasting, where spatial and temporal characteristics are essential. In these circumstances, AGS-STGNN utilises spatial interdependence (e.g., road network architecture) and temporal dynamics (e.g., historical traffic speed patterns) to improve prediction accuracy while minimising processing cost³⁹. The model initiates the creation of a spatial graph, whereby each node signifies a road segment or sensor site, and the edges denote the physical or functional links among these segments. Attributes at each node, like speed or occupancy, are subsequently disseminated using spatial graph convolution, which identifies localised spatial patterns.

A temporal convolutional module is employed to process series of traffic data over time intervals. This component captures temporal trends for each node, allowing the model to comprehend the evolution of traffic throughout the network over time. The AGS-STGNN subsequently does adaptive graph sampling, an essential process that continuously identifies foremost significant segments of the data graph for effective learning⁴⁰. It is hybrid and encompasses node, edge, and region-level sampling. In node sampling, attention mechanisms evaluate values to identify the nodes that possess the greatest number of important attributes at a specific moment. Edge sampling emphasises the identification of especially pertinent connections between nodes, utilising attention weights to capture critical interactions throughout the network. The selected nodes and edges are subsequently categorised into areas according to their feature similarity, so creating representative clusters of the graph structure.

Furthermore, enrichment is attained using temporal-aware adaptive sampling, which assesses the significance of nodes according to their recent temporal feature patterns. It allows the model to concentrate on temporal intervals that significantly influence future forecasts. Simultaneously, spatial-aware adaptive sampling selects samples according to their spatial location and structural impact throughout the graph, to make sure different and significant spatial contexts are taken into account. The results from both spatial and temporal samplings are subsequently integrated into a unified spatial-temporal adaptive score, which equilibrates spatial and temporal contributions via a learnable parameter⁴¹.

Subsequent to adaptive sampling, AGS-STGNN produces a unified spatial-temporal embedding for each node. The resulting integration integrates localised spatial patterns and dynamic temporal trends, enhanced by the adaptive sampling process. The embedded structures are ultimately input into spatial graph convolution and temporal convolution layers to derive advanced representations utilised for forecasting potential traffic speeds. AGS-STGNN facilitates effective. versatile, and precise traffic speed prediction with a structured, however adaptable pipeline, dynamically responding to variations in spatial and temporal patterns within traffic datasets⁴².

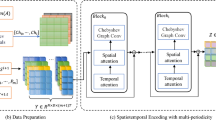
Figure 2 describes the structure of the AGS-STGNN, where the graph structure is formed initially depending on STGNN, then it’s divided into three types of sampling carried within the STGNN framework itself, type 1 is hybrid sampling is deployed by combination of node-based score sampling, edge-based attention weight sampling and region-based sampling. Type 2 of spatial aware sampling taken to capture the spatial features and the type 3 is about to capture the temporal features of the data. Then, the joint spatial-temporal adaptive sampling is formed by combine the type 2 and type 3. Finally, the graph based adaptive sampling based on temporal and spatial features are taken and its forwarded towards the GNN with the embedded features of spatial and temporal.

Fig. 2

The structure of AGS-STGNN.

Phase 2: Pareto efficient global optimization for adaptive graph sampling (ParEGO-AGS)

Pareto Efficient Global Optimization-based Adaptive Graph Sampling (ParEGO-AGS) is a sophisticated multi-objective optimisation approach incorporated into the Adaptive Graph Sampling framework of Spatio-Temporal Graph Neural Networks (STGNNs). In traffic speed prediction, ParEGO-AGS effectively identifies excellent quality, distinct spatial and temporal data that provide unique and independent learning objectives, enhancing the model’s capacity to generalise across intricate urban traffic data⁴³.

In this scenario, traffic data inherently demonstrates double heterogeneity: spatially across road networks and temporally across time intervals. Traditional adaptive graph sampling methods may address spatial and temporal significance with a unified goal, resulting in inferior feature selection due to redundancy or overlapping learnt tendencies. ParEGO-AGS tackles this issue by implementing multi-objective determination of samples, aiming primarily to enhance sampling knowledge but to optimise different although independent objectives—one designed for spatial learning and another for temporal dynamics.

ParEGO-AGS fundamentally employs scalarization methods derived from Pareto optimisation, encoding multiple objectives—such as minimising spatial feature reliability, maximising topological variance, and capturing temporally significant trends—into a scalar surrogate model using Gaussian Process. In the optimisation process, ParEGO stochastically samples weight vectors from a uniformly distributed simplex to scalarize the objectives. This results in a varied selection of spatial and temporal node subsets, each contributing uniquely to the learning process and so preventing the predominance of one feature space over another.

In traffic speed prediction, spatial sampling seeks to emphasise essential road segments (e.g., intersections, bottlenecks) that exhibit significant fluctuation in traffic movement or overcrowding dissemination. Simultaneously, temporal sampling delineates time segments to encapsulate busy behaviours, abrupt variations resulting from events or anomalies, or consistent regularities⁴⁴. ParEGO-AGS guarantees that the two sample sets—spatial and temporal—are optimised under separate though interrelated obstacles, resulting in a more balanced and expressive feature embedding when input into the AGS-STGNN architecture. This optimisation approach enhances flexibility and effectiveness by employing well-structured acquisition procedures that minimise the necessity for exhaustive sampling or brute-force selection.This renders it appropriate for extensive traffic patterns characterised by substantial sensor data volumes. ParEGO-AGS cultivates a sophisticated and distinct learning approach that separates spatial and temporal factors influencing traffic dynamics, hence enhancing the predicted precision and interpretability of the STGNN model in practical applications. Figure 3 describe the working of ParEGO in AGS for the process extracting the samples of spatial features.

Fig. 3

Working flow of ParEGO.

Phase 3: enhanced attention gated recurrent unit (EAGRU)

The combination of self-attention processes into Gated Recurrent Units (GRU) marks a notable progression in the prediction of traffic speed, effectively capturing both short-term and long-term dependencies in temporal traffic data. Conventional GRU models are engineered to process sequential input via gated memory techniques, enabling them to retain or discard information at each time step. Nonetheless, GRUs sometimes have difficulties when managing intricate and extremely volatile sequences, such as those present in metropolitan traffic systems, particularly when the impact of prior events is dispersed throughout temporal compared to localised. Self-attention-enhanced GRU architectures demonstrate notable efficacy in these circumstances⁴⁵.

Self-attention in GRU layers facilitates the selective emphasis on pertinent time steps in the input sequence, irrespective of their temporal proximity. Rather than depending solely on the continuous flow of data via hidden states, self-attention allows the model to generate weighted contextual representations by directly comparing all time steps with one another¹⁷. This indicates that the GRU can prioritise traffic patterns or anomalies from a matter of minutes or hours prior if they are pertinent to the current prediction. For instance, if a traffic deceleration at 8 AM is typically succeeded by congestion at 9 AM due to work-hour patterns, the self-attention method enables the model to deliberately acquire this temporal link, rather than depending implicitly on the GRU’s memory state²⁶.

Within the architecture of the self-attention-based GRU, subsequent to encoding the traffic speed sequences via the GRU’s hidden states, a self-attention layer is implemented on these hidden representations. Every concealed state is converted into a collection of query, key, and value vectors²⁷. These vectors are employed to calculate attention weights that assess the significance of each preceding time step in relation to the current forecast. The outcome is a context vector that encapsulates globally pertinent temporal relationships, which is subsequently integrated with the GRU’s output to produce the final prediction. This hybrid methodology enables the model to utilise the temporal gating of GRUs while simultaneously harnessing the adaptable, global reasoning capabilities of self-attention⁴⁶.

This connection provides multiple benefits for traffic speed prediction activities. Firstly, it augments the model’s ability to comprehend periodicity and irregular patterns, such weekend traffic behaviour, special events, or weather-related abnormalities, by including non-local factors. Furthermore, it enhances predictive accuracy and resilience, particularly in extended sequences, by alleviating the vanishing gradient and information degradation problems typically associated with conventional RNNs. Finally, the implementation of self-attention enhances interpretability, since the derived attention weights might indicate which historical time points most strongly impacted the prediction—essential for comprehending traffic causation and dynamics⁴⁶. The incorporation of self-attention in GRUs significantly enhances temporal feature learning, rendering the model more attuned to subtle traffic patterns and thereby markedly improving the accuracy and adaptability of traffic speed prediction systems in data-rich, real-world contexts.

Experimentation and discussion

Experimental setup

The system specifications for this experiment include a hardware configuration of Intel Core i7-9700 K or AMD Ryzen 9 5900X processor, 64 GB DDR4 RAM or higher, 1 TB SSD storage or higher, and NVIDIA GeForce RTX 3080 or AMD Radeon RX 6800 XT graphics card. The software requirements include Windows 11 Operating system, virtual environment with conda, Python 3.8, tensorflow and Deep Graph Library (DGL) for graph construction package manager.

Dataset description

The performance of the proposed model is evaluated using two real-world traffic datasets METR-LA³⁷ and PeMS-BAY³⁸. METR-LA dataset consists of traffic data collected from 207 loop sensors across Los Angeles over the period of 4 months (March to June 2012) with 5 min of interval. It contains 1.5 million individual data points, covering speed, traffic volume, congestion levels, and timestamps. A crucial component of this dataset is the adjacency matrix (W_metrla.csv), a 207 × 207 weighted matrix representing connectivity between sensors. Each value in the matrix indicates a traffic-related metric, such as distance, congestion, or traffic flow strength, between sensor nodes. This matrix is vital for constructing the graph representation in the AGSTGNN model, capturing spatial dependencies among sensors. Their lies the unique sensor ID for each traffic sensor with the traffic congestion level categorised into low, high and medium. Also, the traffic data is observed in both the latitude and longitude time. The PeMS-BAY dataset contains 325 sensor stations considered for the period of 6 months with the features such as traffic speed, flow, and occupancy levels. Additionally, the dataset includes a metadata file (PEMS-BAY-META.csv), which provides details about freeway IDs, lane counts, location coordinates, and segment lengths. These features improve the proposed model’s generalization across diverse urban and highway environments.

Results and discussion

Evaluation metrics

The performance of the proposed model is evaluated using four metrics such as MAPE, MSE, MAE, RMSE, R² score are given in Eqs. (13)–(17). The following tables [Table] presents the equation for calculation, ${Y}_{i}$ – True samples, ${Y}^{v}$ – predicted values, ${Y}^{{v}_{i}}$ – mean value of $Y$.

$$MAPE\: \left(Mean\:Absolute\:Percentage\:Error\:=\frac{1}{n}(\frac{Actual\:values-forecasted\:values\:}{Actual\:Values}\right)$$

(13)

$$MSE\:\left(Mean\:Squared\:Error\right)=\frac{1}{n}(\sum\:\frac{n}{{i}_{1}=1}{\left({Y}_{i}-{Y}^{\nu\:}\right)}^{2}$$

(14)

$$MAE\:(Mean\:Absokute\:Error=\:\frac{1}{n}(\sum\:\frac{n}{{i}_{1}=1}|{Y}_{i}-{Y}^{\nu\:}|$$

(15)

$$RMSE\:\left(Root\:Mean\:Squared\:Error\right)=\:\sqrt{MSE}$$

(16)

$$RMSE\:\left(Root\:Mean\:Squared\:Error\right)=\:\sqrt{MSE}$$

(17)

Model training and validation

Learning parameter setup

Adam Optimizer is utilised to tune the parameters such as learning rates, momentum and RMSprop for faster convergence in spatio temporal data. The model is trained with 100 epochs and data is split with the ratios 70:15:15. 70% samples are considered for training and 15% data is for testing. Similarly, 15% data is used for validation. The hyper parameter optimization using Bayesian optimization of pareto efficient global optimization was carried out at validation set, and the results are captured in the unseen test set. The following Table 1 captures the parameters utilised for the experimentation which ensures the model generalizes well and avoids overfitting issues.

Table 1 Parameters of the learning model.

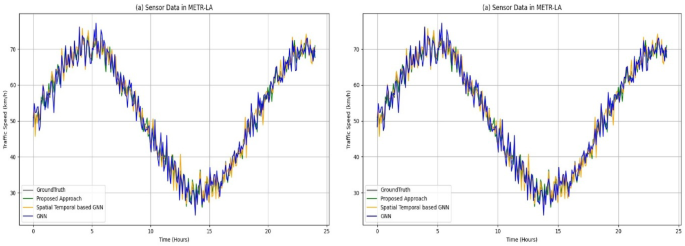
The performance of the proposed model is evaluated with other baseline models by considering the two datasets in terms of RMSE, MAE and MAPE. Figure 4 represents the time-series plot of displaying the traffic speed in km/h for a period of 24 h. The cyclic pattern is followed for the traffic speed, it is observed that the traffic speed is increased for the 6–7 h, then it gets deteriorations considerably from 12 to 15 h. Finally, it rises to its peak at the end of the day. The grey line exposes the ground truth value, green line expresses the proposed model, orange and blue line represents the baseline models. It is observed that the proposed model tracks the ground truth value more closely whereas the baseline models exhibit fluctuations at peak hours. Also, it is observed that the proposed model performs better than the other models capturing the traffic speed dynamics with the spatial and temporal feature extraction patterns.

Fig. 4

Time-Series Analysis on METR-LA and PeMS-BAY dataset using proposed vs. baseline methods.

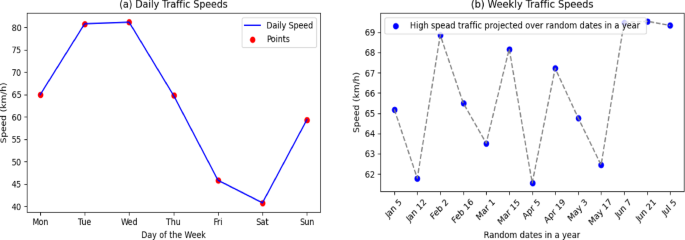
From the below Fig. 5 it is observed that the proposed model captures the spatial and temporal patterns from the META-LR data efficiently. As left side diagram indicates that the traffic speed observed on Tuesday and Wednesday is little higher stating that the traffic is less on those days. In Saturday the vehicle speed is observed at 40 km/hr indicating that the traffic is higher than usual and again rises to 60 km/hr on Sundays which is indicates that reduced congestion in the traffic. The right-side diagrams specifies that the more fluctuations in the traffic speed from the time period of Jan till July, might relies on changes in the nature of the transportation. Adaptive graph sampling captures these fluctuations in the traffic speed by prioritizing the traffic time intervals in order to reflect the real time traffic/dynamic traffic patterns. Optimised MOBO approach ensured that the model is robust in traffic predictions. Also, the proposed model alleviates congestion traffic in this time. (a) Daily traffic speeds – The average vehicle speed is recorded in km/hr which is represented in blue line. The diagram is for each day of the week and the high-speed traffic observations are captured in red points. 4(b) Weekly Traffic Speeds - The blue markers indicate high-speed traffic observations on random dates between January and July, with a grey dashed line connecting them to highlight fluctuations. Our adaptive graph sampling (AGS) mechanism effectively captures these patterns, which are then optimized by MOBO to accurately reflect dynamic traffic trends.

Fig. 5

Spatial and temporal stamps of daily and weekly traffic speed.

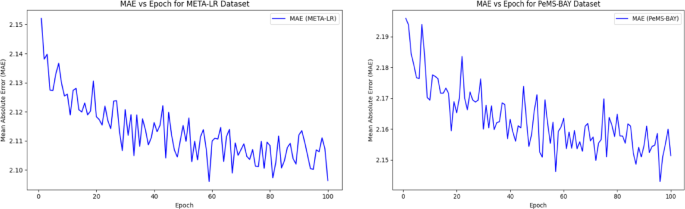
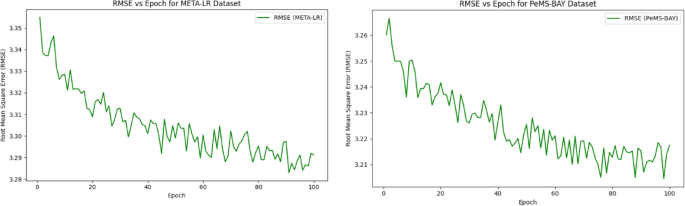
Figures 6 and 7 illustrate the performance of the proposed model on META-LR and PeMS-BAY datasets, showcasing MAE and RMSE scores over 100 epochs. The MAE plot (Fig. 6) demonstrates a steady decrease in error, indicating improved prediction accuracy with training data, converging to ~ 2.10 and ~ 2.15 for META-LR and PeMS-BAY datasets, respectively. The RMSE plot (Fig. 7) also exhibits a decreasing trend, converging at ~ 3.29 for META-LR and ~ 3.21 for PeMS-BAY, highlighting the model’s robustness and generalizability. Both figures show minor fluctuations due to batch-level noise or learning rate dynamics, but no evidence of overfitting is observed, as the training curves converge smoothly without a “U-turn” pattern. The consistent decreasing trend in MAE and RMSE scores across epochs indicates continual learning and optimization of the model’s parameters, demonstrating its effectiveness in predicting traffic patterns.

Fig. 6

MAE of META-LR Dataset and PeMs-BAY.

Fig. 7

RMSE of META-LR and PeMS-BAY.

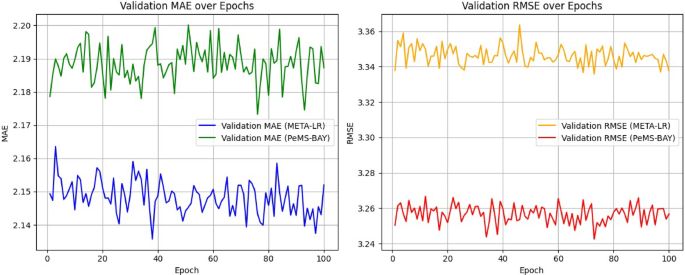
Figure 8 illustrate the validation performance of model on META-LR and PeMS-BAY datasets, showcasing MAE and RMSE over 100 training epochs. In Fig. 8, both datasets exhibit a downward trend with minor fluctuations, indicating steady improvement in prediction accuracy without sudden divergence. Similarly, Fig. 8, shows a slight decline followed by stabilization, suggesting effective learning and convergence. The performance trends indicate rapid decreases in MAE and RMSE during initial epochs, followed by stabilization after ~ 40–50 epochs, confirming convergence. Both validation MAE and RMSE remain stable, confirming retained generalization and posed a well-regularized training process. Overall, these plots demonstrate consistent performance improvement and no overfitting across both datasets.

Fig. 8

Validation of MAE and RMSE for META-LR and PeMS-BAY Datasets.

To ensure robust evaluation and prevent overfitting, we implemented a three-way data split strategy, dividing each dataset into 70% training, 15% validation, and 15% testing subsets. The training subset was used for learning model parameters, while the validation subset was exclusively used for hyperparameter tuning and early stopping. The testing subset was held out for final model performance evaluation, ensuring no data leakage. We conducted hyperparameter optimization using a Multi-Objective Bayesian Optimization (MOBO) framework.Table 2 captures the parametric values for the proposed model with the range explored and considered for training, validation Table 2.

Table 2 Parameters of proposed MOBO approach during training and testing.

To prevent overfitting, we used early stopping based on validation loss with a patience threshold, ensuring the model retains optimal generalization ability. This approach, combined with our rigorous training and evaluation pipeline, ensures reported performance metrics accurately reflect the model’s predictive capabilities on unseen data.

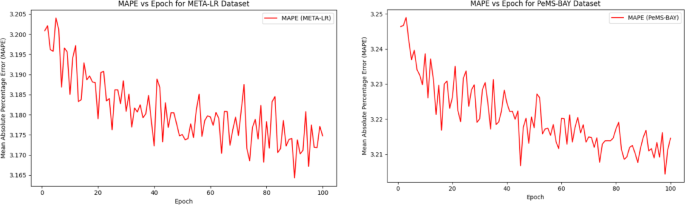
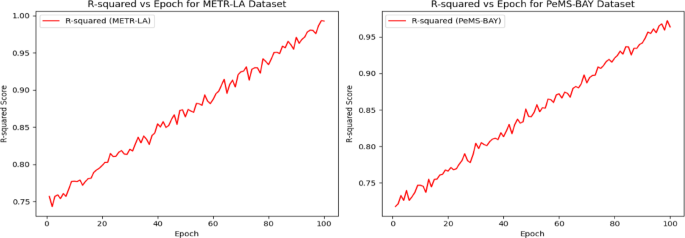
Figure 9 captures the MAPE comparison for the proposed model in the training data with two different datasets. MAPE values reduced from 3.20 to 3.17 over 100 epochs for training data, which increases the enhanced prediction percentage errors. For META-LR its has 3.17 value and for PeMS-BAY it achieved 3.21. Figure 10 captures the ${R}^{2}Score$ where it increase progressively from 0.75 to 1.00 epochs which echoes the strongest fitness between the actual values and the predicted values for the training data. Likewise, the values of ${R}^{2}Score$ increases from 0.75 to 0.95 for PeMS-BAY dataset indicates that the model exhibits the improved performance in Fig. 10.

Fig. 9

MAPE for META-LR and PeMS-BAY.

Fig. 10

R squared score for METR-LA and PeMS-BAY.

Discussion

Table 3 Comparing the proposed MOGL approach with existing techniques.

From the Table 3 it is inferred that the proposed model outperforms well on both the META-LR and PeMS-BAY dataset with lowest MAE (2.09), RMSE (3.29) and MAPE (3.17), similarly on PeMS-BAY dataset it has lowest values of MAE (2.15), RMSE (3.22) and MAPE (3.21). The existing DSTMAN³³ model on META-LR and PeMS-BAY had achieved MAE (2.94), RMSE (5.95) and MAPE(7.98) and the STGCN (Cheb)³⁴ have implemented in PeMSD7(M) and PeMSD7(L) which achieved MAE (2.25), RMSE(4.04) and MAPE(5.26) in PeMSD7(M) and the another dataset PEMSD(L) have MAE(2.37), RMSE(4.32) and MAPE(5.56).The STGCN³⁴ in PeMSD7(M) and PeMSD (L) have reached two different values, for PeMSD(M) had MAE (2.26), RMSE (4.07) and MAPE (5.24) and the PeMSD(L) have MAE(2.40), RMSE(4.38) and MAPE(5.63).Then, the GMAN³⁵ model in PeMS and Xiamen datasets have reached the MAE (1.86),RMSE(4.32) and MAPE(4.31) for PeMS dataset and the Xiamen dataset had achieved MAE(11.50), RMSE(12.02) and MAPE(12.79) and the final existing model BiGRU for the china peak MAE(22.08),RMSE(48.47),MAPE(9.67)and china low peak datasets have reached MAE(31.12),RMSE(10.19) and MAPE(24.61). Amongst all, Bi-GRU method shows higher errors when compared with all the methods. Apart from these observations, STGCN and GMAN methods exhibits better performance on the smaller datasets however, it is unknown about its performance on larger data. While proposed model shows better performance in all aspects, fortifying the robustness across different data ranges.

Comparison of MOGL approach with baseline models

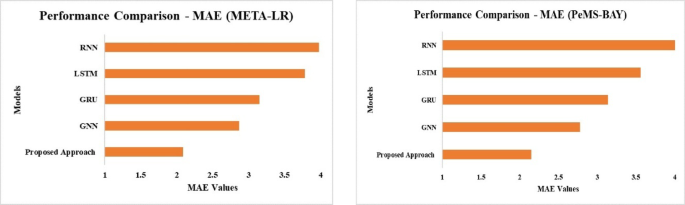
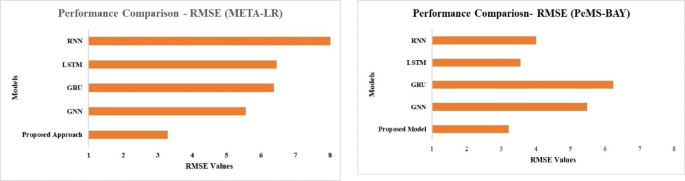
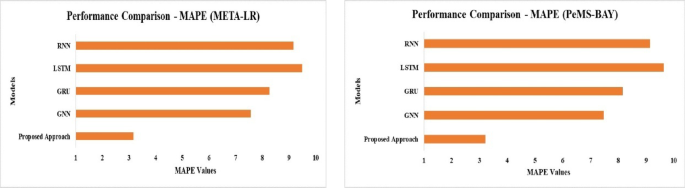
The following Figs. 11 and 12 shows that by minimising prediction errors (MAE, RMSE) while decreasing percentage errors (MAPE), the proposed MOGL approach outperforms baseline models (GNN, GRU, LSTM, RNN) on both datasets. This demonstrates how well it works to solve issues like dynamic spatiotemporal interdependence and enhancing the precision of traffic speed predictions.

Figure 11 represents the MAE values for various models on META-LR and PeMS-BAY datasets. Amongst all models, the proposed model achieves the lowest MAE signposts its supremacy in prediction accuracy. RNN model exhibits highest MAE values for both the dataset indicating the poor performance over all the other models. LSTM, GRU and GMM performs better performance whereas not as better than the proposed model. The overall inference from this shows that the proposed model is effective in reducing the prediction errors by increasing the robustness of the model.

Fig. 11

Comparison of MAE values for METR-LA and PeMS-BAY with existing DL models.

The Root Mean Square Error (RMSE) for each model on the META-LR and PeMS-BAY datasets is displayed in the Fig. 10. With the lowest RMSE (~ 3.29 for META-LR and ~ 3.22 for PeMS-BAY), the suggested model shows a smaller error magnitude. RNN has a large prediction deviation with the greatest RMSE (~ 7 for META-LR and ~ 5.5 for PeMS-BAY). Although GNN outperforms RNN, the Proposed Model still outperforms is show in Fig. 12. These outcomes demonstrate how well the Proposed Model reduces overall prediction errors.

Fig. 12

Comparison of RMSE values for META-LR and PeMS-BAY with existing DL models.

The Mean Absolute Percentage Error (MAPE) of various models on the two datasets is shown in Fig. 13. With the lowest MAPE (~ 3.17 for META-LR and ~ 3.21 for PeMS-BAY), the Proposed Model exhibits the best percentage-based prediction accuracy. For both datasets, RNN has the highest MAPE (~ 9), indicating subpar relative error reduction performance. The Proposed Model outperforms LSTM, GRU, and GNN, which have modest performance. This attests to the Proposed Model’s dependability in lowering percentage mistakes.

Fig. 13

Comparison of MAPE values of METR-LA and PeMs-BAY with existing DL models.

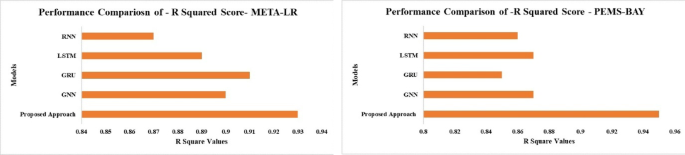
The ${R}^{2}\:Score$ for each model and dataset is shown in Fig. 14, which gives information about how well predictions match actual data. With the greatest ${R}^{2}\:Score$of almost 0.92 for the METR-LA and PeMS-BAY datasets, the proposed model demonstrates a strong correlation between expected and actual results. On the other hand, the RNN model shows poor prediction dependability with a relatively low R2 Score of about 0.8. Although LSTM, GRU, and GNN models perform better than RNN, they are still not as accurate as the Proposed Model. The better performance of the proposed approach shows that it can produce forecasts that are more reliable and accurate. In applications where predicted accuracy is essential, this is especially important. The strong ${R}^{2}\:Score$ of the suggested model indicates that it can successfully identify the underlying relationships and patterns in the data. The other models’ lower ${R}^{2}\:Score$, in contrast, show a poorer relationship between expected and actual values. All things considered, the Proposed Model’s outstanding performance highlights its potential for practical uses.

Fig. 14

Comparison of R squared score of METR-LA and PeMS-BAY with existing DL models.

The key findings from the above discussed subsections are the proposed model achieves lowest MAE value with 2.09 for METR-LA and 2.15 for PeMS-BAY model. This indicates that the efficiency of the proposed model with minimised prediction errors. This exceptional performance shows that the suggested model has effectively streamlined the learning procedure, producing precise predictions under a range of circumstances. Additionally, the performance of the model has been greatly improved by the use of multi-objective Bayesian optimization. The model has successfully navigated the intricate search space by utilizing this optimization strategy to find the ideal hyperparameters that reduce prediction errors. The result of this synergy between multi-objective Bayesian optimization and the suggested model is a strong and trustworthy forecasting framework. These results have significant ramifications, indicating that the suggested methodology can be successfully applied to real-world situations where precise forecasting is essential, such traffic flow prediction. The model’s potential for broad acceptance and use is shown by its strong generalization across various datasets and situations.

Comparison of imputation method

Table 4 Comparison of imputation Method.

From the Table 4 it is observed that KNN achieved the lowest MSE and RMSE in both imputation and prediction which indicates that KNN suits well in all aspects. GRU-D suits for temporal gaps, slightly it underperformed which is possibly due to the limited number of data or overfitting in low level missing scenarios. Whereas, Linear Interpolation model was less effective in analysing the temporal patterns in complex data.

Ablation study

Table 5 Ablation study to ensure the importance of feature selection.

In Table 5, the baseline model was considered as gate recurrent unit (GRU ) without the feature selection process was implemented in two different dataset have greater values of MAE(25.4), RMSE(37.2) and MAPE(21.1). Then the graph-based pooling of STGNN with AGS was taken as feature selection technique have reached MAE(23.5), RMSE(34.2) and MAPE(18.9) better compared to simple GRU predict the traffic speed. Then, the Bayesian optimization based AGS is deployed as centrality-based sampling process have achieved MAE (21.5), RMSE (32.2) and MAPE (17.2). and the final is proposed approach MOGL have achieved (2.09) MAE, (3.29) RMSE and (3.17) MAPE has achieved stable performance with limited time complexity.

Comparison of proposed MOGL approach with statistical test

Table 6 Comparison of proposed MOGL approach with statistical test.

To validate the proposed MOGL approach robustness through 5 independent runs on META-LR and PeMS-BAY datasets, reporting mean and standard deviation for MAE, RMSE, MAPE, and R² Score in Table 6. The proposed model outperformed baselines with lower errors and higher R² scores. Paired t-tests confirmed statistically significant improvements (p < 0.05), demonstrating the model’s reliability for traffic speed forecasting under varying conditions.

Conclusion

The rapid increase in accidents and high traffic congestion leads to predict the traffic speed level in ITS. Predicting the traffic speed is challenges due to dynamic nature of road network, spatio temporal features and computational efficiency. Among these challenges, the most complicated one is spatio temporal features. In this research work, the proposed MOGL approach is majorly concentrated on spatial and temporal sample to predict the traffic speed. The MOGL approach has three distinct model are AGS-STGNN for optimal selection spatial and temporal features; MOBO-AGS for extraction of spatial samples by differentiating temporal samples through sampling layers; EAGRU for fusing the samples of spatial and temporal feature to manage the traffic congestion and predict the traffic speed. The performance of the proposed approach is ensured by evaluating in terms of MAPE, RMSE, MSE and R² score. Thus, the proposed approach was implemented in real time road traffic dataset which achieves high scalability, low computational cost and robust prediction. However, due to the dynamic factor of road network traffic, the models defend complexity. In future work, the proposed approach can be implemented in more complicated dynamic road network traffic to avoid accidents.