Introduction

With global climate warming, extreme rainfall events have become more frequent1,2. Rainfall plays a critical role in destabilizing slopes through infiltration, thereby greatly increasing the likelihood of rainfall-induced landslides3,4. Rainfall-induced landslides often occur suddenly and without warning, causing extensive damage to both property and human lives5. For example, the Manipur landslide on June 30, 2022, resulted in 61 casualties and buried approximately 435 m of railway line under debris6. Similarly, the cluster landslides in Jiangwan Township, Shaoguan, Guangdong on April 20, 2024, triggered by extreme rainfall, led to substantial economic losses7. Landslide early warning systems (LEWSs) are essential for mitigating the impact of rainfall-induced landslides5,8. Rainfall thresholds are crucial components of LEWSs and are often used to predict the probability of landslide initiation in a given study area. When rainfall conditions reach or exceed rainfall thresholds, the stability of a slope is significantly compromised, increasing the risk of landslides9,10,11.

Rainfall thresholds can be determined using physical models or empirical statistical approaches12,13. Physical models simulate the process of rainfall infiltration leading to landslide initiation by integrating hydrological and slope stability models14,15,16. However, the applicability of physical models is limited due to the extensive and detailed data requirements concerning surface and subsurface environments, which are challenging to obtain at a regional scale13,17. Empirical statistical rainfall thresholds are employed to define the relationship between past rainfall events and landslides. Owing to their reduced data requirements, empirical rainfall thresholds are widely used to determine early warning thresholds for rainfall-induced landslides12,18. Various empirical rainfall thresholds, such as the rainfall intensity duration (I–D) threshold5,19,20, the rainfall event duration (E–D) threshold21,22,23, and the rainfall event intensity (E–I) threshold24, have been proposed based on the relationships between different rainfall parameters and landslides. Additionally, some researchers suggest that cumulative effective antecedent rainfall can serve as a useful indicator for threshold models, as it accounts for rainfall losses due to runoff and evaporation2,10. However, there is an ongoing debate about the appropriate period for calculating antecedent rainfall in specific study areas.

Accurate rainfall data and a comprehensive landslide database are crucial for establishing empirical thresholds, with their reliability closely linked to the quality of the input rainfall data25. Previous studies have predominantly utilized rain gauge measurements to identify rainfall events that induce landslides26,27. However, the application of rain gauge measurements presents two main challenges. First, the limitations of rain gauges in capturing spatial variations in rainfall make it difficult to accurately reflect the true amount of rainfall in landslides. This shortcoming is significant, especially in mountainous areas prone to landslides28,29. To address this issue, researchers rely on interpolation models to predict the rainfall distribution30. However, the selection and application of these models introduce uncertainty, which can further affect the reliability of rainfall thresholds31. Additionally, the high installation and maintenance costs of rain gauges result in sparse network coverage in mountainous areas, leading to data gaps that hinder research on rainfall thresholds32,33. Compared with unreliable rain gauge networks, radar-derived rainfall offers a solution to address the limitations of rain gauges, providing high spatial- and temporal-resolution observations that are particularly beneficial for landslide studies34,35. Nonetheless, the traditional empirical relationship between radar echo reflectivity (Z) and rainfall intensity (R), known as the Z-R relation, has limitations in capturing the dynamic evolution of rainfall processes, and its universal applicability is poor, resulting in significant differences between the retrieved rainfall conditions and the actual ground conditions36. With the rapid development of deep learning, it has provided an effective means to process radar data for more accurate estimation of ground rainfall37,38,39.

This study aimed to establish reliable I-D thresholds for rainfall-induced landslides applicable to LEWSs, utilizing data from 217 historic landslides in the Sichuan Basin and radar-derived rainfall data processed through deep learning. Additionally, it examined the impact of antecedent rainfall on the initiation of landslides. The advantages of developing rainfall thresholds based on radar rainfall data are discussed, in comparison to global, national, and regional thresholds derived from international studies. The study also addresses potential uncertainties and proposes a multilevel warning model to enhance the accuracy of LEWSs. These findings provide valuable insights into rainfall-induced landslides in regions with limited rainfall data and have potential applicability in other geographical areas.

Study area and data

Study area

The study area is located in the northeastern part of the Sichuan Basin, and encompasses the cities of Nanchong and Bazhong (105.44°–107.76° E, 30.46°–32.74° N). The terrain is complex, with altitudes ranging from 154 to 2458 m (Fig. 1a). The southern region is primarily hilly, whereas the rest of the region is mountainous. The area experiences a subtropical humid monsoon climate, with an annual average rainfall of 1100 mm. Geologically, the area is characterized by lacustrine and fluvial sedimentary rocks from the Jurassic and Cretaceous periods. The lithology mainly consists of soft rocks (mudstone and conglomerate) and hard rocks (siltstone and sandstone), which are often interbedded in rhythmic patterns40. The rocks are rich in hematite, giving them a distinctive red color, and are commonly referred to as “red beds”41. These formations are characterized by poor cementation, low strength, and a high susceptibility to deformation and weathering. The overlying soil layer consists of Quaternary weathered materials, primarily composed of clay minerals and clastic components, exhibiting strong hydrophilicity and rheological behavior. Experimental results have shown that the natural soil in this area has an internal friction angle of 17° and cohesion of 15 kPa, while the internal friction angle at saturation is 10°, with a cohesion of 8 kPa. The soil exhibits low permeability, with a saturated hydraulic conductivity ranging between 2 × 10−⁷ and 1.4 × 10−⁶ m/s, indicating that infiltration through the surface layer alone is typically insufficient to trigger landslides42. However, due to long-term cycles of wetting and drying, the surface soil has become highly loosened and contains numerous irregular cracks. These fissures facilitate preferential flow paths for rainfall infiltration, allowing water to penetrate more rapidly into the subsurface. Therefore, the study area is highly prone to rainfall-induced landslides43.

Fig. 1
figure 1

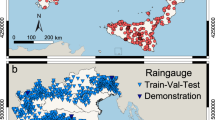
(a) Distribution of rainfall-induced landslides, rain gauges, and radar station. The map was created using the software ArcGis 10.8 (URL: https://desktop.arcgis.com). (b) Average monthly rainfall and rainfall-induced landslides from 2018 to 2021. (c) Slope angle distribution of rainfall-induced landslides. Both plots (b) and (c) were generated using Origin 2021 (URL: https://www.originlab.com).

Full size image

Landslide data

The landslide database used in this study was sourced from the Department of Natural Resources of Sichuan Province (DNRSP) and the State Key Laboratory of Geohazard Prevention and Geo-environment Protection (SKLGP). This dataset includes 244 landslide events recorded between 2018 and 2021, with detailed information on each event’s location, initiation time, type, triggering factors, and associated property damage. To improve the accuracy of rainfall threshold estimation, 17 events that occurred on days without recorded rainfall and with no observed seismic or meteorological triggers were excluded, as they were likely caused by human activities. The spatial distribution of the remaining 227 natural rainfall-induced landslides is illustrated in Fig. 1a. These events were divided into two subsets using an 8:2 ratio: 181 landslides for threshold model construction and 46 for validation. The landslides occurred primarily between June and September, coinciding with the regional rainy season, which indicates a strong association between landslide occurrence and rainfall patterns (Fig. 1b). These events are predominantly shallow failures characterized by relatively simple internal structures and sliding surfaces that are mostly parallel to the ground surface. The slope angles range from 3° to 53°, with most cases concentrated between 10° and 20° (Fig. 1c), which aligns with the typical slope-foot range (7° to 32°) of shallow soil layers in red-bed regions43,44.

Rainfall data

Rainfall data were collected from Colorful Clouds Technology Co., Ltd. (caiyunapp.com/). These data are generated through a deep learning-based fusion process that integrates radar echo images with rain gauge measurements during model training, resulting in radar-derived rainfall data. Figure 2 illustrates this process, which involves the following key steps. First, a radar noise reduction dataset was constructed using knowledge of radar signals and noise to effectively differentiate rainfall echoes from noise. Three time-continuous radar echo images (from t-2 to t) were fused into a 3-channel RGB image as input. The denoised radar echo image at time t (manually corrected) served as output. Then, cross-entropy was employed as the loss function to train the modified U-Net network classification method on the basis of these input and output data. The modified network, known as SE-ResUNet, combines U-Net, ResNet, and squeeze-and-excitation networks37. After denoising, every 10 consecutive radar echo images were stacked into one input tensor, representing the rainfall history of the past hour. Finally, the SE-ResUNet model corrects radar-derived rainfall data by aligning each rain gauge’s location with its corresponding position in the radar echo image. The model uses 1-h radar echo images as inputs and 1-h rain gauge measurements as outputs for this correction process.

Fig. 2
figure 2

Schematic diagram of the process of obtaining radar-derived rainfall data.

Full size image

The rainfall data used for threshold analysis were obtained from the Nanchong radar station (Fig. 1a) and processed via the integrated approach. These continuous radar-derived rainfall data, combining radar’s spatial resolution with gauge accuracy, provide specific rainfall information for each landslide location, facilitating the study of rainfall thresholds that trigger landslides.

Comparison of radar-derived rainfall data with independent rain gauges

The purpose of this section is to independently evaluate the accuracy of the radar-derived rainfall data (processed via deep learning as described in Section “Rainfall data”) by comparing it with independent ground-based rain gauge measurements that were not used in model training. Radar-derived rainfall data are typically subject to uncertainties from beam blockage and topography36, while rain gauge measurements serve as ground truth for calibration38. Here, we assume rain gauge measurements are error-free (despite potential incompleteness due to installation time or power issues). A total of 175 gauges from DNRSP (installed post-2018) were used. The radar-derived rainfall data at rain gauge coordinates were evaluated using four statistical parameters: correlation coefficient (CC), root mean square error (RMSE), bias (B), and relative bias (RB)45.

Figure 3 illustrates the results of the correlation analysis between the radar-derived rainfall data and the rain gauge measurements, which include both daily and monthly rainfall data. The correlation between the radar-derived rainfall and rain gauge measurements for the daily rainfall at all the stations is notably strong, with a mean CC of 0.822 and an RMSE of 2.97 mm. Similarly, the correlation is even greater for monthly rainfall, with a mean CC of 0.905 and an RMSE of 24.64 mm. Compared with the rain gauge measurements in the study area, the CC for the daily values of radar-derived rainfall (0.822) is greater than that of the Integrated Multi-satellite Retrievals for Global Precipitation Measurement Mission (IMERG) rainfall data (0.65), as reported by Yang46. The radar-derived rainfall data can reasonably approximate ground-level rainfall patterns. Notably, radar-derived rainfall data generally underestimate both daily and monthly rainfall, with an average relative bias of -10.79%, which is likely attributed to the radar’s difficulty in capturing the full spectrum of rainfall types47. However, the data do not affect the performance of rainfall thresholds constructed based on radar-derived rainfall data in predicting rainfall-induced landslides. This is because the same underestimated rainfall products, with consistent temporal and spatial resolutions, are used in both phases of the rainfall threshold and landslide forecasting. The phenomenon of underestimating observed rainfall data is also common in satellite rainfall products28,48. Consequently, radar-derived rainfall data show promise for establishing reliable rainfall thresholds.

Fig. 3
figure 3

Correlation parameters between radar-derived rainfall and rain gauge measurements. (a) Root mean square error, RMSE. (b) Correlation coefficient, CC. (c) Relative bias, RB. (d) Bias, B.

Full size image

Methods

Rainfall events and antecedent rainfall

Rainfall thresholds in LEWSs are subject to various uncertainties49. One specific approach for addressing this issue is to establish clear criteria for delineating rainfall events34. However, there has been a lack of consistency in the criteria employed in the literature50. To enhance consistency in our study, we adopted a commonly utilized criterion for defining rainfall events in some regions with similar climatic conditions and rainfall patterns to those in our study area51,52. Specifically, this criterion delineates the separation between two rainfall events as a period of at least 24 consecutive hours without rainfall, allowing for the clear determination of the start and end of each rainfall event (Fig. 4). By incorporating the times of landslide initiation, rainfall events can be further classified into those that trigger landslides (T-LEs) and those that do not (NT-LEs). In the cases of T-LEs, if a landslide occurs before the end of the rainfall event, the end time of the rainfall event (Te) is considered to coincide with the time of landslide initiation. Otherwise, the Te of the rainfall event remains unchanged and independent of landslide initiation. Additionally, the criterion for dividing the daily rainfall data based on landslide initiation and the antecedent rainfall prior to the landslide is defined (Fig. 4). The rainfall parameters of these events, including duration D (h), mean intensity I (mm/h), and cumulative effective antecedent rainfall (CER), are then determined.

Fig. 4
figure 4

Definitions of rainfall events and antecedent rainfall.

Full size image

The amount and duration of rainfall occurring prior to a landslide, which control the soil water content and pore water pressure of the slope, are crucial factors influencing both the initiation and triggering of landslides53. However, not all rainfall has a significant effect on landslide initiation. When assessing the impact of rainfall on landslide risk, it is essential to consider the effects of runoff and evaporation during rainfall40, as well as the combined effects of other relevant factors such as terrain, soil type, and vegetation cover. To more intuitively reflect the impact of antecedent rainfall on landslide initiation, we employ the concept of cumulative effective antecedent rainfall as proposed by Crozier54, which is defined as follows:

$$CER = \sum\limits_{i = 1}^{n} {R_{i} (K)^{i} }$$
(1)

The cumulative effective antecedent rainfall for n days before landslide initiation is denoted as the CER. For example, the cumulative effective rainfall for 3 days prior to the landslide is expressed as CER-3. Ri represents the daily rainfall for the i-th day (1 ≤ i ≤ n) before landslide initiation. K is a dimensionless coefficient ranging from 0.7 to 0.9. This coefficient depends on various factors specific to the study area, including the soil porosity, depth, evaporation rates, and drainage rates55,56,57. Previous studies have typically assumed that landslide initiation is predominantly influenced by rainfall occurring in the 10 days leading up to an event, resulting in the establishment of an attenuation coefficient K = 0.8458. However, the specific duration of antecedent rainfall that significantly impacts landslide initiation in the study area remains uncertain. Therefore, in this study, the impact of cumulative effective antecedent rainfall over varying periods (ranging from 3 to 20 days) on landslide initiation is explored. Furthermore, considering that the prevailing K values in the literature are within the 0.8–0.9 range51,59,60,61, we specifically investigate the effects of incremental changes in K on cumulative effective antecedent rainfall within this range at intervals of 0.01.

Rainfall threshold analysis

The I–D rainfall threshold is widely used worldwide. Therefore, we combined the rainfall conditions associated with each rainfall event and constructed an I–D rainfall threshold using frequency theory and Bayesian probability analysis method.

Frequency theory

The I–D rainfall threshold is determined using the frequency theory proposed by Brunetti9, which defines a power function relating the average rainfall intensity (I) to the rainfall duration (D), as expressed in Eq. (2):

$$I = \left( {\alpha \pm \Delta \alpha } \right)D^{{ - \left( {\beta \pm \Delta \beta } \right)}}$$
(2)

where α and β are constants and the latter is the shape parameter that determines the slope of the power curve. ∆α and ∆β are the standard deviations of α and β, respectively, representing the uncertainties of α and β.

A frequency analysis of T-LEs is carried out to determine the I-D thresholds corresponding to various exceedance probabilities, utilizing the frequency theory outlined in Brunetti9. The process involves transforming I and D into logarithmic forms, fitting the best-fit line (T50) (Fig. 5a), calculating the difference (δ) between the fitting result and actual parameters for each event, using a kernel density function to establish the probability density function (PDF), and fitting it with a Gaussian distribution curve (Fig. 5b). Rainfall thresholds for various exceedance probabilities are then identified on the basis of this Gaussian model. Specifically, the α value for the exceedance probability (T5) rainfall threshold is obtained by subtracting the α value of the T50 threshold from δ5, while β remains the same. This allows for the construction of the T5 rainfall threshold curve. Assuming the completeness and representativeness of the rainfall data in the study, the likelihood of landslide initiation is minimal when the rainfall intensity is below the T5 threshold.

Fig. 5
figure 5

Schematic diagram of the frequency theory. (a) The 181 T-LEs within the study area from 2018 to 2021, with known values of rainfall duration D and the mean rainfall intensity I. The black line is the best fit (least squares method) of the empirical rainfall conditions (D, I). (b) Kernel density estimation of the differences δ (blue dotted line) fitted with a Gaussian function (black) for the distribution of the empirical data points (D, I); the red line represents the threshold corresponding to the 5% exceedance probability (T5).

Full size image

Bayesian probability analysis

Bayesian probability analysis is a statistical method used to determine the posterior probability of an event occurring under known conditions. The method can be used to effectively calculate the conditional probability of rainfall-induced landslides12,62,63. This method combines data from NT-LEs, enhancing the dataset of rainfall events. In this research, the probability of landslide initiation is based on two factors: rainfall intensity (I) and duration (D). The relationship is expressed as follows:

$$P\left( {L|I,D} \right) = \frac{P(I,D|L) * P(A)}{{P(I,D)}}$$
(3)
$$P(L) \approx \frac{{N_{L} }}{{N_{R} }}$$
(4)
$$P(I,D) \approx \frac{{N_{I,D} }}{{N_{R} }}$$
(5)
$$P(I,D|L) \approx \frac{{N_{(I,D|L)} }}{{N_{L} }}$$
(6)

where L represents the event of landslide; I represents the rainfall intensity of the event; D represents the duration of rainfall; P(L) represents the prior probability of a landslide occurring; P(I, D) refers to the marginal probability of specific I and D rainfall conditions occurring, which is independent of whether a landslide occurs or not; P(I, D|L) is the likelihood probability of a landslide occurring, which is the probability of specific I and D rainfall conditions occurring given that a landslide has occurred; and P(L|I, D) represents the posterior probability of a landslide occurring under specific I and D rainfall conditions.

Method for evaluating the rainfall threshold

The evaluation of rainfall thresholds is typically performed using a contingency table, skill scores, and receiver operating characteristic (ROC) analysis60,64,65. A contingency table (Fig. 6a) functions as a binary classifier model with four potential outcomes: true positive (TP), false positive (FP), true negative (TN), and false negative (FN). From these outcomes, two skill scores are derived: the probability of detection (POD) and the probability of false detection (POFD).

$$POD = \frac{TP}{{TP + FN}}$$
(7)
$$POFD = \frac{FP}{{TN + FP}}$$
(8)
Fig. 6
figure 6

(a) Contingency tables. (b) ROC space, with hypothetical model results.

Full size image

Both the POD and POFD values are within the range of 0 to 1, with the POD indicating the proportion of actual positives correctly identified and the POFD indicating the proportion of negatives incorrectly identified as positives.

ROC analysis was employed to assess the predictive ability of rainfall thresholds for different exceedance probabilities (Fig. 6b). The ROC curve consists of points representing different prediction performances of rainfall thresholds, with each triangle indicating a specific threshold. The area under the curve (AUC) measures the accuracy of the I-D threshold, where a higher AUC value signifies greater accuracy. The black point on the ROC curve represents a perfect classification point, where the POD is 1 and the POFD is 0.

Results

Rainfall threshold

Frequency rainfall thresholds

Various exceedance probabilities for rainfall thresholds were determined using frequency theory based on the database of threshold construction comprising 181 T-LEs. Figure 7a illustrates the double logarithmic coordinate distributions of the combination of I and D for these T-LEs, shown as red dots. Kernel-smoothed density distribution curves for I and D are also plotted separately to better characterize their distributions. Among these events, D values range from 3.17 to 473.5 h, and I values range from 0.42 to 49.21 mm/h. On the basis of frequency theory, rainfall thresholds with various exceedance probabilities (5%, 25%, 50%, and 75%) are plotted in the graphs and labeled T5, T25, T50, and T75, respectively. The 5% threshold, T5, can be expressed as I = (28.07 ± 1.01)D-(0.77±0.05); the T25 threshold can be expressed as I = (48.71 ± 1.07)D- (0.77±0.05); the T50 threshold can be expressed as I = (71.46 ± 1.16)D- (0.77±0.05); and the T75 threshold can be expressed as I = (104.83 ± 1.29)D- (0.77±0.05). These thresholds indicate the probability of landslide initiation under different rainfall conditions. Notably, 6 out of 181 T-LEs are below the T5 threshold, which is consistent with the methodological assumption proposed by Brunetti9.

Fig. 7
figure 7

(a) I–D empirical rainfall thresholds with various exceedance probabilities. (b) Logarithmic two-dimensional Bayesian probability plot of rainfall intensity versus duration. The T5, T25, T50, and T75 thresholds were calculated via the frequency approach.

Full size image

Table 1 presents the parameters and relative uncertainties of different types of rainfall thresholds. The relative uncertainties of the rainfall thresholds clearly decrease as the exceedance probability increases. The relative uncertainties of the rainfall thresholds defined in this study are significantly smaller than those thresholds proposed by Zhao48 and Jiang63. This improvement is attributed to the use of more accurate radar-derived rainfall data, which reduces the uncertainty in obtaining T-LEs, leading to a more uniform distribution of empirical data66,67.

Table 1 Parameters of the rainfall thresholds and relative uncertainties.
Full size table

Bayesian probability

The dataset for constructing the rainfall threshold comprises a total of 1112 rainfall events (NR = 1112), of which 181 resulted in landslides (NL = 181). This yields an a priori probability of landslide initiation of P(L) = 0.16. Using Bayesian probability analysis, we calculated the posterior probability of landslides for different combinations of I and D under specific rainfall conditions. This probability was then mapped onto graphs with 100 × 100 grids, generating probability curves representing landslide initiation probabilities of 0.05, 0.25, 0.50, and 0.75 (Fig. 7b).

The cluster of probability distribution curves reveals that the likelihood of inducing landslides increases with increasing intensity and duration of rainfall events. Additionally, the T5, T25, T50, and T75 thresholds were superimposed on the I-D probability curves, showing alignment with the probability curves for certain durations within the studied range (outside the purple polygonal region). Bayesian probability curves theoretically better match the actual rainfall thresholds because they provide more detailed information about rainfall events. However, overfitting may occur because of sparse T-LE sample points in certain regions, causing some probability curves to deviate from the actual situation. For instance, when the duration exceeds 2.5 (316 h), the probability of landslide initiation on the probability distribution graph surpasses 0.75, and the impact of rainfall intensity on landslide probability diminishes.

Verification of the rainfall threshold

The proposed rainfall thresholds were evaluated using validation data to assess the reliability of the warning model. The validation dataset comprises 46 T-LEs and 241 corresponding NT-LEs preceding landslides. Figure 8a illustrates the rainfall events, along with various rainfall threshold curves and the kernel-smoothed density distribution curves of I and D of the NT-LEs. The durations are concentrated in the 10–100 h range, with rainfall intensities focused within 0.2–5 mm/h. Figure 8b depicts the performance of the rainfall thresholds through the ROC curves, where each point represents a specific threshold. These findings indicate that a higher probability threshold for landslide initiation can reduce the false alarm rate, but it may also decrease the hit rate of the threshold. In comparing the frequency threshold with the Bayesian probability threshold, our study revealed that the frequency threshold exhibits relatively better predictive performance in this study area, as evidenced by its higher AUC value (0.939) than the AUC value of the Bayesian probability threshold (0.724). This discrepancy is attributed to the limited sample points in certain areas, resulting in the Bayesian probability curve not accurately reflecting the real-world scenario. Therefore, the frequency threshold appears more suitable for early warning models in this study area.

Fig. 8
figure 8

Evaluation of rainfall thresholds with various probabilities using different approaches on the basis of the validation datasets. (a) The dashed and solid lines represent the rainfall thresholds of various exceedance probabilities calculated via frequency theory and Bayesian probability analysis, respectively. (b) The red and blue lines represent the ROC curves calculated via the frequency theory and Bayesian probability methods, respectively.

Full size image

Effect of antecedent rainfall on landslide initiation

Figure 9 illustrates the proportion (RD>CER-i) of the daily rainfall associated with landslide initiation that exceeds the CER, across various antecedent periods and different reduction coefficient K values. This reveals a consistent trend: this proportion progressively decreases as the antecedent rainfall period increases, stabilizing at 15 and 20 days. Notably, this trend is independent of the K value.

Fig. 9
figure 9

Proportion (RD>CER-i) of the daily rainfall associated with landslide initiation exceeding the CER for different periods preceding failure across various K values.

Full size image

To visually compare the relationship between daily rainfall associated with landslide initiation and CER over different periods, we employed a reduction coefficient K = 0.9, which is a well-researched and validated constant for calculating antecedent rainfall up to 20 days51,69. Our analysis encompassed all 227 T-LEs to examine daily rainfall and CER over various periods (3, 5, 7, 10, 15, and 20 days), as depicted in Figs. 10a–f. The diagonal line in the graph separates it into two halves, distinguishing the influence of daily rainfall (y-axis) versus CER (x-axis) for landslide initiation. Notably, most of the points plot below the line, indicating the prevailing influence of antecedent rainfall. Specifically, in Fig. 10a, 18.1% of the landslide events (i.e., 41 landslides) are biased toward daily rainfall, whereas the remaining 81.9% (i.e., 186 landslides) are biased toward CER-3. Similarly, Figs. 10b–f illustrate that more landslide events are biased toward CER, ranging from 91.9% to 96.9%, as the period of calculation of antecedent rainfall increases. The largest bias of 96.9% is observed for a period of calculation of 15 days before landslide initiation, which remains consistent at 20 days. Consequently, selecting the cumulative effective rainfall for 15 days prior to a landslide in the study area as another threshold is well founded. This conclusion aligns with the findings of Zhang4, who examined landslides in geological and lithological settings similar to those in this study and emphasized that 15-day antecedent rainfall has a significant influence on landslide stability. Importantly, applying the same reduction coefficient K = 0.9 for threshold construction and landslide prediction requires at least 133 mm and does not affect the early warning results.

Fig. 10
figure 10

Daily rainfall during landslide initiation compared with the various periods of antecedent rainfall prior to landslide initiation: (a) 3 days, (b) 5 days, (c) 7 days, (d) 10 days, (e) 15 days, and (f) 20 days.

Full size image

Discussion

Comparison of different rainfall thresholds

Previous studies have established different rainfall thresholds at global, national, and regional scales, as shown in Fig. 11 and Table 2. While these thresholds were determined using different approaches, they generally reflect the lowest critical rainfall conditions that induced landslides, allowing for direct comparisons. Figure 11 shows that the T5 threshold identified in this study is higher than most other global and national rainfall thresholds. However, the T5 threshold is lower than the global threshold proposed by Caine19 and the national threshold for China proposed by Li20. Moreover, the T5 threshold is lower than the regional-scale rainfall threshold in coastal areas of China (Fig. 11, orange and blue lines). These differences can be explained by several factors: (i) data size: the size of the disaster database influences rainfall thresholds. Compared with smaller datasets, large datasets tend to produce smaller thresholds. For example, the global threshold based on a smaller set of 97 landslide events19 is greater than the threshold based on a larger set of 2626 events40. (ii) Methodology: different methods for rainfall threshold analysis lead to variations. For example, the rainfall threshold proposed by Li20 (solid line 6) was obtained via visual empirical methods. Brunetti9 also reported differences between thresholds obtained through Bayesian and frequency methods. (iii) Rainfall sources: for example, the rainfall thresholds obtained from satellite rainfall products are mostly lower than those obtained from rain gauges27. (iv) Climate and terrain conditions: for example, coastal regions of China often experience typhoons and heavy rainstorms, resulting in higher average annual rainfall and, consequently, higher rainfall thresholds (Fig. 11, orange and blue lines). (v) Criteria for defining rainfall events: for example, Fig. 11 shows four different purple threshold curves obtained using the same data and analytical methods but with varying rain-free intervals (6 h, 12 h, 18 h, 24 h) that represent rainfall events. Owing to these factors, fully explaining the differences in I-D thresholds between different regions is challenging.

Fig. 11
figure 11

Comparison between the I–D thresholds from this study (red line) and those of previous studies.

Full size image
Table 2 Different scales of I–D rainfall thresholds.
Full size table

To evaluate the effectiveness of the rainfall threshold calculated with radar-derived rainfall data, we extracted 107 independent rainfall-induced landslide events that occurred in or near the study area (Qin-Ba Mountain, Fig. 1a) on the basis of the results of Wang70. These events are not included in the original dataset of this study. The methodology for determining threshold 13 aligns with the procedures detailed in our research. However, rainfall data were derived from ERA5-Land data from the European Centre for Medium-Range Weather Forecasts (ECMWF), with a spatial resolution of 9 kms. This finding reveals that threshold 13 is greater than the T5 threshold proposed in this study because of the coarse spatial resolution of the ECMWF data and its limited representation of rainfall patterns. Consequently, the use of threshold 13 as an early warning model may lead to false negatives in landslide prediction. For instance, among the 107 events, the use of threshold 13 led to 96 predicted landslides, indicating a greater chance of missed events. In contrast, threshold T5 did not produce any false negatives, indicating a significantly higher level of predictive accuracy. Furthermore, as noted by Guzzetti71 the values of the β curve of rainfall thresholds defined for midlatitude climates range between -0.70 and -0.81. The thresholds proposed for the study area, which is also located in a midlatitude region, are similarly within this range. These two aspects suggest the rationality of extracting rainfall thresholds via radar-derived rainfall data obtained through deep learning.

Uncertainties

While improvements have been made in establishing reliable rainfall thresholds on the basis of radar rainfall data, uncertainties still persist in our research. The identified T-LEs may overestimate the actual rainfall events that trigger landslides. This overestimation is primarily due to the inability to accurately determine the onset time of the landslide event73. This study highlights the significant impact of CER-15 on landslide initiation in the study area, with a significant threshold of at least 133 mm. However, it does not precisely reflect the soil moisture content before the landslide, and this threshold value depends on the size of K and requires further analysis in conjunction with detailed hydrological and evapotranspiration conditions specific to the study area. Furthermore, to evaluate the performance of landslide prediction for various rainfall thresholds, we utilized contingency table analysis and ROC curves, both of which rely on the assumption of a comprehensive and accurate landslide inventory. However, in practice, ensuring the completeness of landslide inventories can be challenging. For example, as depicted in Fig. 7b, data scarcity leads to overfitting in the Bayesian two-dimensional plane. This overfitting may result in TNs being misclassified as FNs and FPs being erroneously counted as TPs. Therefore, future efforts should strive to increase the completeness of landslide inventories to the greatest extent possible. Moreover, the variability of rainfall thresholds is influenced not only by uncertainties in rainfall estimation but also by the diverse characteristics of landslides, including their scale and geo-mechanical properties44. For instance, larger-scale landslides scale generally require more extreme rainfall conditions to trigger a critical failure. Additionally, different material compositions affect rainfall thresholds: argillaceous clastic landslides tend to have higher thresholds compared to shale landslides of similar volume due to differences in permeability and shear strength74. While our dataset lacks systematic volumetric and geotechnical measurements to quantify these effects. Nevertheless, the inherent variability in landslide types and scales likely contributes to the observed dispersion in rainfall thresholds.

Potential application of the rainfall threshold for slope-scale landslide early warning systems

This section presents the integration of the proposed rainfall thresholds into an existing LEWS and explores their application at the slope scale. The I-D rainfall threshold is established as a pivotal criterion for identifying rainfall-induced landslides, with the probability of initiation increasing significantly when this threshold is exceeded. However, as shown in Fig. 8 (blue dots), not all rainfall events above the threshold resulted in landslides, highlighting the potential for false alarms if rainfall thresholds are used in isolation. Additionally, factors such as micro geomorphic and hydrogeological conditions significantly impact landslide initiation alongside rainfall. Improving the reliability of LEWSs requires the integration of other monitoring parameters such as groundwater level, soil moisture, and pore water pressure. In the study area, GNSS units and crack gauges have been extensively deployed in susceptible zones to detect deformation prior to failure. Nonetheless, exclusive reliance on deformation monitoring can lead to false alarms or missed events due to sensor malfunctions or environmental interference75. A multilevel early warning model is therefore developed by integrating the proposed rainfall thresholds with a deformation-based alert system76,77,78. In this model, the rainfall threshold forms the first level, reflecting its role as the primary trigger for changes in pore pressure and soil strength. The first-level warning model involves real-time assessments of rainfall intensity (It) and the CER-15. If the threshold is exceeded, the model incorporates deformation data to refine the warning level. This integrated approach enhances the reliability of warnings and reduces false alarms associated with single-parameter systems. Figure 12 shows a schematic diagram of the multilevel early warning model and the corresponding early warning matrix.

Fig. 12
figure 12

Schematic diagram of a multilevel early warning model for rainfall-induced landslides.

Full size image

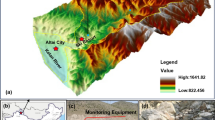
The continuously monitored Houjia landslide (Fig. 1a, Houjia) was selected to validate the reliability of the proposed multilevel early warning model. It is classified as a muddy landslide, with a typical sliding surface developed along the interface between Quaternary slope wash deposits and the underlying Jurassic bedrock. Monitoring equipment, including a crack gauge and a rain gauge, was installed at the crest and toe of the slope, respectively (Fig. 13a), to capture deformation and hydrological triggers. According to the longitudinal profile (Fig. 13b), the sliding mass is composed of silty clay from the slope wash layer, underlain by interbedded brownish-red sandstone and mudstone.

Fig. 13
figure 13

(a) Layout of monitoring equipment in Houjia. (b) Longitudinal profile taken along line 1–1′.

Full size image

The long-term displacement and rainfall data of the Houjia landslide from April to August 2021 are shown in Fig. 14a. The critical rainfall event began on August 21, 2021, at 14:00. The evolution of real-time rainfall intensity during this event is illustrated in Fig. 14b. At 6:00 on August 22, the rainfall intensity exceeded the T75 threshold, and the 15-day cumulative effective rainfall (CER-15) reached 155.8 mm. Consequently, the LEWS issued a red warning message to field personnel to enhance site inspection. At 11:45 on the same day, the crack gauge triggered red-level (alarm) warnings (Fig. 14c), while the rainfall threshold remained at the red warning level at that moment. The actual slope failure occurred 11 h later, at 21:41 on August 22, validating the effectiveness of the integrated early warning approach.

Fig. 14
figure 14

Monitoring data and warning levels of the Houjia landslide. (a) Cumulative displacement and rainfall over time. (b) Real-time rainfall intensity in the I–D space with warning thresholds. (c) Crack gauge displacement and associated warning levels.

Full size image

Furthermore, the rainfall conditions prior to the Houjia landslide were systematically analyzed, and 32 distinct rainfall events were identified according to the criteria described in Section “Rainfall events and antecedent rainfall”. A detailed overview of each event—including duration, total precipitation, and peak hourly intensity—is provided in the supplementary material (Section “Introduction”, Table S1). Had a single-rainfall threshold model been used, the LEWSs would have issued four false alarms (Section “Introduction”, Figure S1). Similarly, if only displacement monitoring data had been relied upon, a false alarm would have been triggered on July 26, even though no actual slope failure occurred. Relevant displacement records and warning outputs are shown in the supplementary material (Section “Study area and data”, Figure S2). These results highlight the benefits of the proposed multilevel warning model. By integrating cumulative antecedent rainfall with intensity–duration (I–D) rainfall thresholds, the system improves the identification of non-triggering rainfall events. It also helps reduce false alarms caused by short-term fluctuations or sensor noise. Overall, the model enhances the reliability of LEWSs and offers valuable support for landslide risk mitigation.

Nevertheless, there is still room for improvement. Future work should explore integrating real-time radar-based rainfall forecasting with machine learning models to improve the timeliness and accuracy of warnings. For example, Yan Zhao73 employed TSfresh and machine learning techniques to extract rainfall features from time-series data, demonstrating improved accuracy in early warning models. Additionally, resulting in more accurate early warning performance. Additionally, developing adaptive rainfall thresholds that account for seasonal variation and soil moisture dynamics remains an important direction. These advancements will support the long-term goal of creating intelligent, scalable, and location-specific early warning systems for rainfall-induced landslides.

Conclusions

In this study, a landslide database was developed containing over 227 rainfall-induced landslides during 2018–2021 in the Sichuan Basin. Based on this database, the study integrates radar-derived rainfall data, frequency theory, Bayesian probability analysis, and ROC curve validation to establish reliable I-D thresholds for LEWSs. A key advantage of this study is the use of 1 km resolution radar-derived rainfall data processed by deep learning, which objectively facilitates the determination and comparison of I-D thresholds.

The results demonstrate a high degree of consistency between the radar-derived rainfall data and rain gauge measurements, with mean correlation coefficients of 0.822 and 0.905 for daily and monthly rainfall, respectively. Importantly, based on the radar-derived rainfall data, the relative uncertainties associated with the rainfall thresholds derived from frequency theory are substantially lower than those of existing thresholds48,63. Moreover, the frequency rainfall thresholds exhibit superior predictive performance, as validated by ROC curve analysis (AUC = 0.939), outperforming Bayesian probability-based rainfall thresholds (AUC = 0.724). Furthermore, the study delved into the influence of CER on landslide initiation, particularly the high correlation (exceeding 96.9%) between CER-15 and landslide initiation, providing crucial insights for selecting antecedent rainfall thresholds in landslide warning systems. Recognizing the diverse hydrological factors influencing landslide initiation, we have innovatively developed a multilevel early warning model that seamlessly integrates rainfall thresholds with a ‘deformation monitoring’ model of the landslide body, thereby significantly enhancing the reliability and timeliness of warnings. This study offers important insights into improving the accuracy and reliability of rainfall thresholds for LEWSs in mountainous regions with sparse rain gauge networks.