Introduction

The deposition of abundant collagen fibers near the wound or scars leads to Keloids. This may also occur on pathological scars during plastic surgery when the change occurs after tissue injury heals. It causes extreme discomfort, swelling, itching, characterized by pain when the skin surface is thicker than the regular skin. Keloids frequently occur on the chest, upper arms, earlobe, belly, shoulder, back and the joints, while it can occur anywhere on the body. They are aggressive exophytic growth that expands into the surrounding skin with high chances of recurrence post therapy. For keloid research, there is a lack in the number of studies on human skin and animals, making it a challenging issue. Lab-based (in vitro) culture studies focusing on keloid derived fibroblasts have been very useful compared to studying keloids in live animals. A major challenge is that these patient-derived fibroblasts are often scarce as they are repeatedly grown and divided in the lab which loses its original characteristics due to ageing. This makes it difficult to conduct long-term studies1. Certain sample keloid scars are displayed in Fig. 1.

Fig. 1
figure 1

Sample keloid scars.

Full size image

Due to its unpredictable nature, keloid formation is a clinical challenge, and it has high rate of recurrence even after the treatment. Significant disparities are found in epidemiological studies of keloid prevalence which suggests a strong genetic influence. It reveals from the studies that people with darker skin tones are at higher risk, especially in African and Asian countries. It is evident from the studies that the prevalence rate in black populations is 2.4%, 1.1% in Asians while 0.4% in Caucasians. This percentage varies drastically from UK at 0.09% to Congo at 16%. Another factor is also age, as it is commonly seen in the people between 10 and 30 years. In China, the family members of affected individuals have shown high incidence of keloids based on first, second and third degree relatives. Also, it is more common in females, although the reasons are still unclear. There are other factors that are linked to keloid which includes hypertension, Vitamin D deficiency, and atopic dermatitis. Treatment for keloid includes radiation therapy, laser therapy, cryotherapy, and several intralesional injections apart from topical corticosteroids and silicone dressings. Although, they reduce symptoms and scar size but has potential side effects2.

Skin could heal wounds that take four main stages namely haemostasis, inflammation, proliferation, and extracellular matrix (ECM) remodeling. The most significant role in the wound healing process is played by dermal fibroblasts in which collagens are produced by the cells to regulate the ECM remodeling. Hypertrophic scars are formed when there is an excess collection of collagens while healing of wound. Unlike keloids, hypertrophic scars are confined to the wound and the scars left would be smaller and show wavy or spiral pattern in a specific direction. Over time, hypertrophic scars become smaller and reduce while keloids are different which grows or remains for longer time. Sometimes, keloids are classified as benign fibro-proliferative skin tumors3. In Korean and Taiwan population, it is found that keloid is associated with atopic dermatitis (AD). Studies reveal that keloid forms by excessive scarring with eczema which strongly shows that keloids are strongly associated with AD4. Inflammation, irritation of the skin and redness are the symptoms of AD that has maximum probability of relapsing. It is considered as type 2 immune response as it is connected to increased skin cellular infiltration, increased levels of Immunoglobulin E and eosinophilia.

Impact of drugs in the treatment of different diseases

Substances that alter the physiology or psychology of an organism upon consumption are referred to as drugs. Some people use drugs for medicinal reasons, while others do it for fun. It is possible to treat multiple diseases with a single drug. Several authors studied about drugs and its uses. Yeo et al.5 considered betamethasone for which they developed a multifunctional, double-network hydrogel, with cerium oxide nanoparticles (CeNPs). Said et al.6 reviewed 12-h dosage regimen of betamethasone for NICU admissions. Barbosa et al.7 aimed to develop and characterize hybrid hydrogels for treating AD having high skin retention which is composed of gel-forming polymers. Payamifar et al.8 studied about CD-based nanocarrier systems as a transformative approach in cancer therapy for delivering doxorubicin (DOX). You et al.9 studied doxorubicin and its effectiveness in the immunogenicity of glioblastoma (GBM). Kelly et al.10 carried out an elaborate study on doxorubicin, anthracycline, and Carfilzomib, and focused on finding differential and common mechanism(s) linked with Doxorubicin and Carfilzomib-induced cardiac dysfunction. Imantay et al.11 reviewed the mechanisms associated with types of nanoparticles of doxorubicin. Yang et al.12 reviewed plant foods along with the uses of 5-Flurourcil in the treatment of colon cancer.

Bogari et al.13 examined the efficacy of 5-Flurourcil in facial plastic surgery for a variety of conditions, including scar modulation, because it inhibits the proliferation of fibroblasts and the synthesis of collagen. Sprung et al.14 studied the impact of hydrocortisone and it is found that hydrocortisone accelerated shock reversal in patients whose shock was reversed. Confalonieri et al.15 worked on the hypothesis that patients with severe community-acquired pneumonia would have faster resolution of symptoms and fewer sepsis-related complications if they receive hydrocortisone infusions, which reduce systemic inflammation. Dockrell et al.16 examined the impact of imiquimod in immunocompetent individuals. Chen et al.17 investigated that Condyloma and Cervical Intraepithelial Neoplasia (CIN) are two examples of lesions caused by the Human Papillomavirus (HPV) that can be treated with imiquimod. Li et al.18 revealed the efficacy of mitomycin in the treatment of scar inhabitation after the surgery. Parker et al.19 reviewed that several hallmarks of heart failure are influenced by impaired ATRA signaling, along with important aspects of retinoid metabolism and signaling. Nijnatten et al.20 investigated that adjuvant therapy for estrogen-positive breast cancer includes the use of tamoxifen, an ER antagonist. Liu et al.21 determined the effective delivery methods of Triamcinolone Acetonide for treating macular edema. Matsumura et al.22 indicated that tranilast can effectively prevent cardiac function deterioration. Cao et al.23 investigated that Verapamil has promising clinical translational potential for the treatment of postmenopausal osteoporosis. Levenfors et al.24 examined that zidovudine plays a major role in fighting with antibiotic-resistant infections.

The present study considered the above 12 drugs in the treatment of keloid scars.

Significance of MCDM

MCDM techniques have proven useful in many fields, including drug design, materials science, molecular structure optimization, and evaluation. It is crucial in the evaluation and selection of the best option among alternatives involving multiple criteria. Several researchers actively worked on various drugs using MCDM techniques mostly (TOPSIS, SAW, QSPR) in the prediction of best drug for different diseases like multiple sclerosis, anti-psychotic, and eye disorder etc., listed few25,26,27.

Significance of AHP

To structure complex decisions, Multi-Criteria Decision-Making (MCDM) technique, Analytic Hierarchy Process (AHP) is used. AHP helps in providing a systematic and logical approach to breakdown a complex decision problem using criteria and alternatives. It permits the decision makers to consider both tangible and intangible criteria in the decision-making process. It is as flexible as it can be applied in different fields like engineering, healthcare, management and many more. AHP allows assigning weights based on the importance of the criteria which helps in reducing bias in the process of decision making. Consistency check ratio helps in measuring consistency of judgements ensuring the decision being valid. Finally, it provides ranks for alternative to make it easier for justifying the best choice. Dominico et al.28 applied AHP in finding the balanced global priorities. Pinheiro et al.29 used AHP and identified the efficacy of energy utilization of commercial building air conditioning equipment. Hu et al.30 assessed the road network resilience by combining AHP method with coefficient of variation method. Silva et al.31 addressed the biosecurity risk in Brazil using AHP. Wenrui et al.32 determined the best route for medication delivery using AHP and Kruskal algorithm. Ciceri et al.33 utilized the analytic hierarchy process to prioritize risks distressing the pharmaceutical source, considering both the individual’s perspective and the complete source. Liu et al.34 applied AHP to prevent and control Infections with Salmonella in chicken farms. Xiao et al.35 used AHP for calculating the weights in the expert allocation process. Farook et al.36 applied AHP technique in the ranking process of HIV drugs. Overall, AHP is used to select and optimize the medication. Motivated by the works of Farook et al., the present work used the similar approach on the drugs of treating keloid.

Procedure to calculate the rank using analytic hierarchy process

Analytic Hierarchy Process is a methodological framework for decision-making by organizing intricate issues, quantifying subjective assessments, and maintaining consistency.

The step-by-step procedure is listed here:

  1. (1)

    Articulate the purpose of the decision unequivocally.

  2. (2)

    Ascertain the elements that will affect the decision-making process.

  3. (3)

    Determine the options that are accessible.

  4. (4)

    Evaluate each criterion in relation to others utilizing Saaty’s scale37 (ranging from 1 to 9).

  5. (5)

    Assess the relative significance of each criterion.

  6. (6)

    Evaluate alternatives according to the specified criteria.

  7. (7)

    Consolidate the findings to identify the optimal alternative.

  8. (8)

    Guarantee the comparisons are uniform.

The step-by-step process is illustrated in Fig. 2.

Fig. 2
figure 2

Step by step process in analytic hierarchy process.

Full size image

There are various studies that are carried out on QSPR approach on several ailments. This article focuses on the drugs used in the treatment of Keloid using Analytic Hierarchy Process (AHP), making it a novel study as there are no articles on keloid using this approach till date. Twelve keloid drugs are explored to rank the most predictive drug, through three physical chemical properties such as non-hydrogen atom count (heavy atom count), molecular weight, and complexity.

Material’s approach

The combination of mathematics and chemistry gives rise to a branch of science called chemical graph theory. In line with the concepts of graph theory, atoms are depicted as nodes and chemical bonds as edges in the representation of molecular structures. In the present study, the structure of a drug for keloid is considered as a graph, J = (V(J), E(J)) where V(J), the vertex set, represents an atom and E(J), the edge set represents the chemical bond between atoms(vertices). All graphs considered are simple and connected. The degree of a (atom) vertex is defined by the number of (bonds) edges that connect it38. The degree of vertices \(\upsilon\) and \(\mu\) are represented by \(T\left( \upsilon \right),\,T(\mu )\) respectively. The topological indices considered in the present study for a chemical graph J are defined as follows:

Definition 1

Milan Randic’39 proposed an index named Randic’ index which is defined by the following formula:

$$R\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\frac{1}{{\sqrt {T\left( \upsilon \right) \times T\left( \mu \right)} }}}$$
(1)

Definition 2

The Harmonic index introduced by Fajtlowicz40 which is defined as follows:

$$H\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\frac{2}{T\left( \upsilon \right) + T\left( \mu \right)}} .$$
(2)

Definition 3

The Atom-bond connectivity index, \(ABC\left( J \right)\) proposed by Estrada et al.41 and it is proposed as:

$$ABC\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\frac{{\sqrt {T\left( \upsilon \right) + T\left( \mu \right) - 2} }}{T\left( \upsilon \right) \times T\left( \mu \right)}} .$$
(3)

Definition 4

Gutman and Trinajstic42,43,44 introduced the first and second Zagreb indices namely, \(M_{1} \left( J \right),\) \(M_{2} \left( J \right),\) respectively as follows:

$$M_{1} \left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\left( {T\left( \upsilon \right) + T\left( \mu \right)} \right)}$$
(4)
$$M_{2} \left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\left( {T\left( \upsilon \right) \times T\left( \mu \right)} \right)}$$
(5)

Definition 5

Vukicevic et al.45 introduced the index named Geometric Arithmetic (\(GA\left( J \right)\)) Index defined as follows:

$$GA\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\frac{{2\sqrt {T\left( \upsilon \right) \times T\left( \mu \right)} }}{T\left( \upsilon \right) + T\left( \mu \right)}} .$$
(6)

Definition 6

The Sum-Connectivity Index is introduced by Zhou et al.46, and is expressed by the following formula:

$$SCI\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\frac{1}{{\sqrt {T\left( \upsilon \right) + T\left( \mu \right)} }}} .$$
(7)

Definition 7

Shirdel et al.47 proposed an index named the Hyper Zagreb index (\(HM\left( J \right)\)) which is defined as:

$$HM\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\left( {T\left( \upsilon \right) \times T\left( \mu \right)} \right)}^{2}$$
(8)

Definition 8

The forgotten Zagreb index introduced by Furtula et al.48

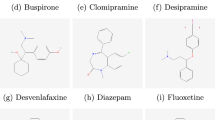
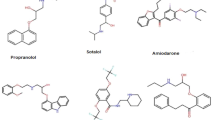
$$F\left( J \right) = \sum\limits_{\upsilon ,\mu \in E\left( J \right)} {\left( {\left( {T\left( \upsilon \right)} \right)^{2} + \left( {T\left( \mu \right)} \right)^{2} } \right)}$$
(9)

Molecular structures of all the considered 12 drugs are as shown in Fig. 3 and Fig. 4 respectively. Figure 5 shows the sample molecular graph of the drug Tamoxifen. Figure 6 explores the Tamoxifen complexity metrics as sample.

Fig. 3
figure 3

3D representation of molecular structures of keloid drugs49.

Full size image
Fig. 4
figure 4

2D representation of molecular structures of keloid drugs49.

Full size image
Fig. 5
figure 5

Molecular graph of tamoxifen.

Full size image
Fig. 6
figure 6

Tamoxifen complexity metrics.

Full size image

Results and discussion

In the present study, the goal is finding the optimal drug for keloid among the considered drugs namely Betamethasone, Doxorubicin, Fluorouracil, Hydrocortisone, Imiquimod, Mitomycin, Retinoic Acid, Tamoxifen, Triamcinolone Acetonide, Tranilast, Verapamil and Zidovudine. Molecular structures, physicochemical properties of the drugs are identified using PubChem and ChemSrc. The number of atoms in a molecule that are not hydrogen atoms is referred as Non-Hydrogen Atom Count or Heavy Atom Count. This property is used in drug discovery and ligand efficiency calculations; it is used to describe the size of a molecule. The process of calculating mass of a substance is important in chemistry which is referred to as molecular weight. Complexity is assessed by considering the number of different atoms and the types of bonds present, as well as the presence of rings, branches, and functional groups. It is a property or calculation of a chemical compound has been determined using the Cactvs 3.4.8.18 software. This software is part of the PubChem49 database, which was released on 2025.04.14. The formula used to calculate complexity is \(C = \ln ( {\prod\limits_{j = 1}^{n} {\omega_{j} } d_{j} !} )\) where \(\omega_{j}\) the atomic weight factor is based on valence, element type, aromaticity, hybridization, charge, etc., \(d_{j}\) is the number of non-hydrogen atom neighbors. The present study deals with these three physicochemical properties, non-hydrogen atom count (heavy atom count), molecular weight, and complexity. The molecular structures are treated as graphs with atoms as vertices and bonds as edges and computed the topological indices using the definitions 1–8 and shown in Table 1. Correlation between the physical chemical properties and topological indices are computed and tabulated in Table 4.

Table 1 Values of topological indices for Keloid drug candidates.
Full size table

Based on the scaling principles shown in Table 2. the judgement matrices (P) are formed for all the three properties namely non-hydrogen atom count (heavy atom count), Molecular Weight, and Complexity. In the judgement matrix, the value in the (i,j)th position is considered as \(\delta_{ij}\). Along with the scaling rules, the following rules also added.

Table 2 Scaling principles.
Full size table

\(\delta_{ij} \ge 0\) for all i and j.

\(\delta_{ij} > 0\), for i < j.

\(\delta_{ij} = 1,\) for i = j.

\(\delta_{ji} = \frac{1}{{\delta_{ij} }},\) for i > j.

  • Let the sum of all the elements in each column be CTk, where k is the column number. Then the scaled decision matrix is identified using the formula \(Q = \left[ {\begin{array}{*{20}c} {\frac{{\delta_{11} }}{{CT_{1} }}} & {\frac{{\delta_{12} }}{{CT_{2} }}} & \ldots & {\frac{{\delta_{91} }}{{CT_{9} }}} \\ {\frac{{\delta_{21} }}{{CT_{1} }}} & {\frac{{\delta_{22} }}{{CT_{2} }}} & \ldots & {\frac{{\delta_{92} }}{{CT_{9} }}} \\ \vdots & \vdots & \vdots & \vdots \\ {\frac{{\delta_{91} }}{{CT_{1} }}} & {\frac{{\delta_{92} }}{{CT_{2} }}} & \ldots & {\frac{{\delta_{99} }}{{CT_{9} }}} \\ \end{array} } \right]\).

  • Calculate the average of each row in \(Q\) called Weights and is represented as a column matrix \(U = \left[ {\begin{array}{*{20}c} {\tau_{11} } \\ {\tau_{21} } \\ \vdots \\ {\tau_{91} } \\ \end{array} } \right]\). Compute \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda } = PU\). Identify the maximum value of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }\) and is represented as \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{\max } .\)

  • Consistency Index is C.I. = \(\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\lambda }_{\max } - 1}}{n},\) where \(^{\prime}n^{\prime}\) is the number of criteria.

  • Consistency Ratio is C.R. = \(\frac{C.I.}{{Random\,\,Index}},\) where the \(Random\,\,Index\) (shown in Table 3) is considered from Satty50.

  • If the Consistency Ratio is < 0.1, then the evaluations are deemed significant, the matrix P is consistent.

  • After the consistency check the next step is finding the rank column by using Rank column RC = Scaled decision matrix * Weights.

Table 3 The values of \(Random\,\,Index\).
Full size table

Finally, the rank will be decided based on the value of RC.

Evaluation of rank through AHP for non-hydrogen atom count (heavy atom count) qspr extractions

Quantitative structure–property relationship (QSPR) analysis is a tool for predicting molecular characteristics from their chemical structures in the fields of chemistry and materials science. It entails developing mathematical models that relate physical, chemical, or biological properties to molecular descriptors like size, shape, electrical characteristics, and functional groups. The impact of molecular descriptors on the predicted property of interest is referred to as the beneficiary and non-beneficiary criteria in QSPR (Quantitative Structure–Property Relationship) analysis. Beneficiary Criteria are characteristics that have a positive effect on the target attribute. Based on this concept, the high correlation is identified (shown in Table 4) between topological indices and non-hydrogen atom count (heavy atom count) and chosen the non-hydrogen atom count (heavy atom count) is beneficiary criteria for the present study. Based on the dependency order of each topological index with the non-hydrogen atom count (heavy atom count) criteria, the judgement matrix P is formed and is displayed in Table 5. The judgement matrix will be scaled via beneficial criteria and technique of AHP, and the scaled decision matrix is revealed in Table 6. Ranks of Keloid drugs for non-hydrogen atom count (heavy atom count) case are explored in Table 7. For better understanding, the weights are illustrated in the graph shown in Fig. 7.

Table 4 Physico-chemical properties V/S coefficient of correlation of topological indices.
Full size table
Table 5 Judgement matrix P for the property non-hydrogen atom count (heavy atom count).
Full size table
Table 6 Scaled decision matrix \(Q\) for the property non-hydrogen atom count (heavy atom count).
Full size table
Table 7 Ranks of keloid drugs for the property non-hydrogen atom count (heavy atom count).
Full size table
Fig. 7
figure 7

Chart of weights for the property non-hydrogen atom count (heavy atom count criteria).

Full size image

Evaluation of rank through AHP for molecular weight QSPR extractions

The higher correlation value is identified between topological indices and molecular weight, considered as the second beneficiary criteria. Based on the relationship between topological indices and molecular weight, the Judgement matrix in Table 8 is formed. The scaled decision matrix for the molecular weight case is found as per AHP methodology and displayed in Table 9. The rank column is identified by summing up the product of scaled matrix values and weights. The rank for the molecular weight case is shown in Table 10. For better understanding, the weights are illustrated in the graph shown in Fig. 8.

Table 8 Judgement matrix P for the property molecular weight.
Full size table
Table 9 Scaled decision matrix \(Q\) for the property molecular weight.
Full size table
Table 10 Ranks of keloid drugs for the property molecular weight.
Full size table
Fig. 8
figure 8

Chart of weights for the property molecular weight.

Full size image

Evaluation of rank through AHP for complexity

The higher correlation value is identified between topological indices and Complexity, considered as the third beneficiary criteria. Based on the dependency between topological indices and complexity the Judgement matrix in Table 11 is formed. The scaled decision matrix for the complexity case is originated as per AHP approach and posed in Table 12. The rank column is identified by summing up the product of scaled matrix values and weights. The rank for the complexity case is indicated in Table 13 and Fig. 9 illustrated the chart for criteria weights in the case of complexity. Rank comparison chart is displayed in Fig. 10.

Table 11 Judgement matrix P for the property complexity.
Full size table
Table 12 Scaled decision matrix \(Q\) for the property complexity.
Full size table
Table 13 Ranks of keloid drugs for the property complexity.
Full size table
Fig. 9
figure 9

Chart of weights for the property complexity.

Full size image
Fig. 10
figure 10

Rank comparison chart.

Full size image

Conclusion

This study explores the impact of the physicochemical properties of keloid drugs through topological indices. The 12 drugs targeted for keloid treatment were selected using the highly effective MCDM method known as AHP. The evaluations performed using QSPR modeling, which considered properties such as non-hydrogen atom count (heavy atom count), molecular weight, and complexity, play a crucial role in shaping the background for AHP. Pharmacological studies based on this approach reveal that these three variables significantly influence the drug dosages. The correlation coefficients, which reflect the relationship between the selected degree-based topological indices and the physicochemical properties of each drug, were analyzed to identify the most relevant properties, such as non-hydrogen atom count (heavy atom count), molecular weight, and complexity, based on the highest correlation values. The 12 keloid drugs were ranked using the AHP technique based on these three properties. The AHP results show that Doxorubicin is the optimal drug for all three properties, while 5-Fluorouracil is ranked as the least optimal. However, the rankings for the three properties remain consistent, with the exception of complexity, where the 4th and 5th positions are swapped.

Limitations

The limitations of this study arise when a drug used for a specific ailment is upgraded to a more effective version. Such advancements enhance the drug’s performance, necessitating fresh investigations and performance evaluations of the improved formulation. This study focuses on the currently available drugs for Keloid treatment and provides a ranking based on their properties. Among the analyzed drugs, Doxorubicin ranks the highest, while 5-Fluorouracil ranks the lowest within the selected group.