Introduction

Water hyacinth (Eichhornia crassipes) is an invasive aquatic plant known for its rapid propagation and free-floating nature on water surfaces such as lakes and rivers1. Its exceptional growth rate allows it to cover extensive areas of water bodies within a short period, leading to severe ecological and economic consequences. The dense mats formed by water hyacinth negatively affect aquatic ecosystems by blocking sunlight, depleting oxygen, and altering habitats, thereby threatening both flora and fauna. Additionally, the plant significantly contributes to water loss through evapotranspiration2.

This plant, originally from the Amazon Basin, has spread far and wide across Latin America. It’s truly a nightmare for aquatic environments, as it’s the most invasive and destructive aquatic plant, causing significant harm wherever it goes1. Initially, the presence of water hyacinth was recorded in the year 1965 in South-Central Ethiopia in the area of Lake Koka and the Awash River. It has gone on to colonize many waterbodies in the country from the very initial foothold. Most affected areas include the Awash River Basin (the Koka Dam, the Lake Koka), the Abb ay River Basin (the Lake Tana, the Blue Nile), the Baro-Akobo River Basin (the Baro, the Sobat, the Pibor, and the Gilo rivers), and the Rift Valley Basin System (the Lake Abaya, the Lake Elltoke). The invasive nature has resulted in serious problems, greatly limiting the utilization of such waterbodies as essential resources3. The expansion of the plant has been recorded further in the Gambela Region, along the Blue Nile from slightly below the Lake Tana into the Sudan, and in the Lake Ellen near the location of AlemTena4.

Potable water is essential for the survival and daily activities of all living beings. Even though over three-quarters of our planet is covered in water, very little of it is actually available for us to use in farming, at home, or in factories. Groundwater often contains dissolved solids, including toxic heavy metals, which can make it hazardous to health. Surface water, which is more commonly used, is frequently contaminated by both anthropogenic and natural activities5. Among various pollutants, heavy metals such as chromium (VI), lead (II), and arsenic (V) pose particularly severe risks due to their non-biodegradable nature and long-term persistence in the environment. Chromium (VI), for instance, can alter genetic material, cause cancer, and adversely affect aquatic ecosystems by binding to sediments and becoming immobile, with only a small portion dissolving in the water6. While it does not typically bioaccumulate in fish, high concentrations near disposal sites can damage fish gills. In animals, chromium exposure has been linked to respiratory problems, weakened immune systems, birth defects, infertility, and tumor development. Despite these known dangers, only a limited number of industries implement proper treatment technologies to remove heavy metal contaminants, while most untreated waste continues to pollute surface and groundwater. Thus, a primary goal of wastewater treatment is to reduce heavy metal concentrations to levels that pose no harm to aquatic life or human health. Heavy metals are generally defined as elements with an atomic mass greater than that of iron (55.8 g/mol) or a density exceeding 5 g/cm³7.

Numerous research efforts have explored the potential of water hyacinth waste and other bio-based materials as biosorbents for eliminating chromium from wastewater. Biosorption offers a straightforward, non-metabolic process where metal ions (biosorbates) attach to the surface of a biologically derived material (a biosorbent)8,9. This category of biological removal methods encompasses the use of microorganisms, plant-derived substances like water hyacinth, agricultural or industrial byproducts, and biopolymers, among others. This quick and reversible process involves ions binding to functional groups on the biosorbent’s surface in water through various interactions, rather than through metabolic oxidation.

Biosorption presents several benefits, including ease of operation, no requirement for added nutrients, minimal sludge production, low operating expenses, high effectiveness, the possibility of biosorbent reuse, and no increase in the water’s chemical oxygen demand (COD), which are significant drawbacks of many traditional methods. Biosorption is effective even at low concentrations of contaminants and is particularly relevant for the removal of heavy metals, which can be toxic at parts per billion (ppb) levels10,11.

Over the past few years, tremendous effort has gone into creating affordable, efficient technologies. The aim is to cut down on wastewater discharge and clean it up before it enters the environment. Established methods for eliminating toxic metals from wastewater, including ion exchange, chemical precipitation, flotation, and adsorption, have been extensively researched12. A significant area of focus has been the development of cost-efficient adsorbents. Among the various materials studied, iron oxides, particularly magnetite, have demonstrated high effectiveness in removing heavy metals13,14,15.

Iron oxides are naturally occurring minerals within the Earth’s crust, recognized for their highly active surfaces. These reactive sites, combined with their large surface area, allow iron oxides to adsorb both positively and negatively charged ions16,17. Employing iron oxides in wastewater treatment shows particular promise when their size is reduced to the nanoscale. As nanoparticles, iron oxides provide high efficiency, rapid reaction speeds, and enhanced reactivity towards individual ions due to their extremely small size and large surface area. Moreover, these nanoparticles exhibit magnetic properties, a distinct advantage in water and wastewater treatment systems. This magnetism allows for simple separation of the nanoparticles from the water after the adsorption process using a small magnetic field18.A particularly straightforward and cost-effective way to create magnetite nanoparticles is through chemical co-precipitation. This process involves simultaneously causing iron(II) and iron(III) salts to form a solid by adding a base19.

This research investigated a cost effective and sustainable method for removing hexavalent chromium (Cr(VI)) from water. It used a novel magnetite-infused water hyacinth nanocomposite, leveraging the plant’s abundance and the nanoparticles’ high reactivity and magnetic separation properties. The study optimized removal efficiency by examining the impact of chromium concentration, contact time, and adsorbent dosage.

Materials and methods

Materials

Materials and equipment used for Preparation and analysis

The preparation of nano-sized magnetite particles and chromium analysis involved various chemicals and equipment. Iron (III) chloride, ammonia solution, iron sulphate, and distilled water were used to synthesize magnetite nanoparticles, while diphenyl carbazide (DPC) and acetone were used for chromium detection via the carbazide method. Potassium dichromate served in preparing chromium stock solutions, and NaOH and HCl were used for pH adjustments. Key equipment included a UV spectrophotometer for chromium concentration measurement, a zeta size analyzer for particle size distribution, and FTIR for identifying functional groups on the magnetic water hyacinth biosorbent. Conical flasks facilitated batch adsorption, while a beaker, pH meter, digital balance, and heating oven supported the co-precipitation reaction. Additionally, an oven and furnace were employed to determine the moisture, ash content, and volatile matter in the water hyacinth samples.

Methods

Collection and preparation of the water hyacinth sample

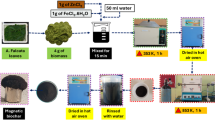
Water hyacinth samples were gathered from Lake Koka using clean bags (Fig. 1). Once collected, the shoots of the water hyacinth weed were separated and taken to the laboratory. Lake Koka is located in central Ethiopia, within the Awash River Basin, approximately 90–100 km southeast of Addis Ababa. The lake lies in the northern part of the Main Ethiopian Rift Valley and is geographically positioned at approximately Latitude 8°26’ N and Longitude 39°02’ E, with an elevation of 1600 m above sea level. It has a surface area of about 200 km² and a storage capacity of 1650 Mm³.Water hyacinth (Eichhornia crassipes) plant material used in the referenced study has been taxonomically identified by Mr. Abiyu Enyew Molla, a qualified botanist affiliated with the Department of Biology, University of Gondar, Gondar, Ethiopia. a voucher specimen of the identified plant has been deposited in the University of Gondar Herbarium, a publicly accessible collection managed by our department. The identification was conducted following standard taxonomic procedures.The deposition number assigned to this voucher specimen is 003/ATM/2022.

There, the plant material underwent a thorough washing process, rinsed multiple times with distilled water to eliminate any dust and soluble impurities. Following the washing, the samples were cut into smaller pieces and left to dry under sunlight for approximately 72 h. After this initial drying phase, the smaller pieces of shoot were placed in an oven at 105 °C for 24 h to ensure complete dryness. Subsequently, the dried shoots were ground using a mortar. The resulting particles were then passed through a sieve to obtain a uniform size of 63 μm and stored in a plastic bottle, ready for subsequent use.

Fig. 1
figure 1

Water hyacinth samples were gathered from Lake Koka, Ethiopia.

Full size image

Proximate analysis of water hyacinth grinded powder

A) Moisture content: The moisture content was found by measuring the weight lost during drying. A crucible holding 5 g of water hyacinth powder was placed in an electric hot air oven set at 100 °C. The sample’s weight was recorded every hour. Once the weight remained consistent over successive measurements, the moisture content was determined by Eq. 1:

$$\:Moisture\, content (\%) = \frac{\left(W2-W1\right)-(\:W3-W1)}{\left(W2-W1\right)}\times100$$
(1)

Where, W1 = Crucible weight, W2 = sample initial weight and crucible, W3 = Sample final weight and crucible.

B) Ash content: The ash content, the non-combustible inorganic matter, was calculated after heating the sample. For the determination of ash content, 10 g of the water hyacinth powder was placed in a crucible, which was then transferred into a 650 °C muffle furnace. The crucible was then transferred after heating to a desiccator for cooling down to room temperature, and its weight was recorded. The process was performed several times until the weight became stable. The percentage ash content (dry basis) was determined via Eq. 2, subsequent to the weight remaining stable.

$$\:Ash\, content = \frac{W3-W1}{W2-W1}\times\:100$$
(2)

Where, W1 = Crucible weight, W2 = weight of the sample before igniting and crucible, W3 = weight of the sample after igniting and crucible.

C) Volatile matter content: To determine the volatile matter was present, 10 g of the powdered water hyacinth sample went into a crucible. That crucible then spent 10 min in a furnace, heated to 550 °C. Once the heating was done, the crucible was removed from the furnace and allowed to cool down in a desiccator. The percentage of volatile matter in the sample was then determined by Eq. 3.

$$\:\:\:\%volatile\, matter (VM) = (\frac{W2-W1)-(\:W3-W1)}{W2-W1}$$
(3)

Where, W1 = Crucible weight, W2 = weight of sample and crucible, W3 = weight of crucible and sample after incineration for the given time.

D) Fixed carbon content: The percentage of fixed carbon was determined by subtracting the total ash and volatile matter percentages from 100%, representing the combustible substance left after their extraction (Eq. 4).

$$Fixed\, carbon (\%) = 100 - (ash \% + volatile\, matter \%)$$
(4)

E) Bulk density: To determine the bulk density, ten grams of ground water hyacinth powder were carefully placed into a 100 mL graduated cylinder. The volume occupied by the solid sample was then recorded. This measurement was repeated a second time, and the average of the two readings was used for the calculation. The bulk density was calculated using the using Eq. 5:

$$\:Bulk\, density\,(g/cm^3) =\frac{\text{w}\text{e}\text{i}\text{g}\text{h}\text{t}\:\text{o}\text{f}\:\text{d}\text{r}\text{y}\:\text{s}\text{a}\text{m}\text{p}\text{l}\text{e}}{\text{v}\text{o}\text{l}\text{u}\text{m}\text{e}\:\text{o}\text{f}\:\text{p}\text{a}\text{c}\text{k}\text{e}\text{d}\:\text{s}\text{a}\text{m}\text{p}\text{l}\text{e}}$$
(5)

F) Particle density: The particle density of the water hyacinth powder was measured with the help of a pycnometer. Initially, the dry pycnometer’s weight was recorded. Then, it was filled with distilled water and weighed again. Then, the pycnometer was filled halfway with water hyacinth powder, and its weight was recorded. Finally, the balance was made up with distilled water, and its weight was recorded. The particle density was calculated with the help of Eq. 6.

$$\:Particle\, density = \frac{\text{m}\text{a}\text{s}\text{s}\:\text{o}\text{f}\:\text{s}\text{a}\text{m}\text{p}\text{l}\text{e}}{\text{V}\text{p}-\text{V}\text{w}\text{a}}$$
(6)

Where, Vp = volume of Pycnometer; Vwa = volume of water added.

G) Porosity: Porosity is the fraction of the total powder volume taken up by pores, was determined for the water hyacinth powder. This was done by using both the particle density and bulk density, as shown in Eq. 7.

$$\:Porosity = 1-\frac{\left(\text{B}\text{u}\text{l}\text{k}\:\text{d}\text{e}\text{n}\text{s}\text{i}\text{t}\text{y}\right)}{\text{P}\text{a}\text{r}\text{t}\text{i}\text{c}\text{l}\text{e}\:\text{d}\text{e}\text{n}\text{s}\text{i}\text{t}\text{y}}$$
(7)

Synthesis of iron oxide impregnated water hyacinth nano composite

In the synthesis of iron oxide-impregnated water hyacinth nanocomposite, a co-precipitation reaction was used for the formation of iron oxide/water hyacinth nanocomposites. In this process, approximately 5 g of water hyacinth powder and 20 mL of ammonia solution (25%) were added to a 50 mL mixed solution containing 2.78 g of ferrous sulfate and 5.4 g of ferric chloride (with a molar ratio of Fe³⁺ to Fe²⁺ of 2:1). The temperature was raised and maintained at 100 °C for 4 h. After that, the Fe₃O₄/water hyacinth composite, which turned black in color, was decanted. After removing the supernatant liquid, the black solid residue was washed repeatedly with deionized water. The material was then collected and dried in a vacuum oven at 50 °C for 24 h.

Characterization of iron oxide impregnated water hyacinth nano composite

  1. A)

    PH of zero charge determination of iron oxide impregnated water hyacinth Nano composite.

For the determination of the adsorbent point of zero charge (pHₚzc), the solid addition method was adopted. Fifty milliliters of 0.1 M KNO₃ was transferred into multiple 100 mL conical flasks. The initial pH value for each solution was measured carefully from 2 to 12 by adding 0.1 M HCl or 0.1 M NaOH. Then, 1.5 g of the sorbent powder was transferred into each flask, and the flask was sealed at once. The flasks were then shaken in the constant-temperature shaker for 24 h in order for the solid and the solution to reach equilibrium state. The pH value of the supernatant liquid was measured after 24 h. The initial and final pH (ΔpH) value differences on the y-axis were plotted against the initial pH value on the x-axis. The x-axis point of intersection for the resulting curve provided the pHₚzc20.

  1. B)

    Specific surface area of iron oxide impregnated water hyacinth Nano composite.

To determine the specific surface area of the iron oxide-impregnated water hyacinth nanocomposite, the method described by Egesa et al., 2018 21was followed. This involved combining one gram of the adsorbent with 100 mL of distilled water and 20 g of NaCl. After stirring the solution for five minutes, the pH was adjusted to 4 using 0.1 M HCl. Next, the mixture was titrated with 0.1 M NaOH to raise the pH from 4 to 9. The volume of 0.1 M NaOH used, recorded in milliliters, was measured across multiple trials and averaged. This average value was then used to calculate the surface area using the Sears method, with the final surface area determined by applying Eq. 8.

$$S = 32 x V-25$$
(8)
  1. C)

    FTIR analysis.

Functional groups in the iron oxide-impregnated water hyacinth before and after the adsorption of chromium (VI) were determined using an FTIR IS50 ABX machine. The FT-IR spectra of the iron oxide-impregnated water hyacinth nanocomposite adsorbent, both before and after the adsorption of Cr (VI), were obtained to identify the major functional groups in the adsorbent within the wavelength range of 4000–400 cm⁻¹.

  1. D)

    Size analysis.

The size distribution by intensity of the iron oxide-impregnated water hyacinth nanocomposite was determined using a zeta size analyzer. Before determining the size distribution, the nanocomposite adsorbent particles were uniformly distributed using a homogenizer for about 25 min.

Equilibrium adsorption studies

Batch adsorption experiments were performed by shaking 50 mL synthetic waste solutions with varying initial concentrations of Cr (VI) (25, 50, 75 mg/L) in 250 mL conical flasks, with suitable adsorbent weights (1, 3.5, 6 g) and varying shaking times (60 min, 90 min, 120 min) at room temperature using an agitator at 150 rpm. Chromium (VI) concentration was analyzed using the Diphenyl Carbazide (DPC) method, in which 0.25 g of powder form of DPC was dissolved in 50 mL acetone and 50 mL distilled water. The prepared Diphenyl Carbazide (DPC) was stored in amber or dark-colored bottles since it is light-sensitive. For the estimation of the concentration of chromium (VI), 0.2 mL sulfuric acid was added to the well-known concentration sample, and the pH was neutralized with 0.1 M hydrochloric acid and 0.1 M sodium hydroxide. 0.2 mL Diphenyl Carbazide (DPC) solution was added after it was mixed together, after which the mixture was thoroughly mixed. After complete color development, the supernate was filtered through Whatman filter paper and analyzed spectrometrically at 540 nm using the UV spectrophotometer. The influences of the principal experimental parameters (chromium (VI) concentration, dosage, and shaking time) on the removal capacity of the adsorption process for the elimination of Cr (VI) were analyzed, whereas the concentrations of the chromium (VI) were analyzed using the UV spectrophotometer having a calibration curve.

Adsorption isotherm

Adsorption isotherms were used to figure out how much solute the biosorbent could hold. These isotherms show how much solute sticks to the adsorbent. Essentially, an adsorption isotherm paints a picture of how much solute gets adsorbed per unit of adsorbent, depending on the concentration of the adsorbate left in the solution once everything has settled. It reveals how the solute spreads out between the solid and liquid parts at different equilibrium concentrations. The Freundlich and Langmuir isotherms are the models most frequently employed for this purpose. The Langmuir adsorption isotherm applies to solid/liquid systems and represents monolayer adsorption on a surface with a limited number of adsorption sites, where each site can hold only one molecular or atomic component. It presupposes uniform surface sites with no inter-coverage between adsorates and no lateral movement on the surface. The Freundlich adsorption isotherm, in contrast, models adsorption on heterogeneous surfaces and considers multilayer adsorption with inter-coverage between adsorbed molecules. The suitability of the isotherm models was compared through the comparison of their coefficients for determination (R²). In the present work, Langmuir and Freundlich isotherm were implemented for the determination of the adsorption intensity of the adsorbent towards the adsorbat.

The linearized Langmuir isotherm equation is:

$$\:\frac{1}{q_e}\frac{1}{{q}_{0}\:}\frac{1}{b\:{q}_{0}\:{C}_{e}\:}$$
(9)

Where qe = amount of adsorbate adsorbed at equilibrium (mg/g), Ce = adsorbate equilibrium concentration (mg/l), qo = maximum sorption uptake (mg/g), and b = Langmuir constant (l/mg), and depends on the strength with which the binding sites interact with the adsorbate. Values of b and qo could be found by using the slope and y-intercept of the 1/qe versus 1/Ce plot.

To describe the key features of the Langmuir isotherm, a dimensionless separation factor RL is used, defined as:

$$\:R_L=\frac{1}{1+b{C}_{0}}$$
(10)

Where b = Langmuir constant, and C0 = initial chromium (VI) concentration.

RL shows whether the Langmuir isotherm is unfavorable (RL > 1), follows a straight line (when RL = 1), is irreversible when RL = 0 or is favorable if 0 < RL < 1. Also, an RL value close to zero points to very positive adsorption22.

The Freundlich isotherm is represented by the equation:

$$q_e = K_fC_e^{1/n}$$
(11)

Where Ce = equilibrium concentration (mg/l), qe = adsorbed amount (mg/g) and Kf and n are Freundlich constants corresponding to the capacity of multiple layers and the difference in surface texture, respectively. Data on sorption was explored with the Freundlich adsorption isotherm in a linear form as.

$$ln q_e = lnK_f + \frac{1}{n}lnC_e$$
(12)

The equilibrium was obtained from experimental results of batch adsorption. The amount of chromium (VI) adsorbed (qe) was found using the Eq. 13:

$${q_e}=({C_0}-{C_e}){V/W}$$
(13)

Where Co= Initial Concentration and Ce = equilibrium concentration (mg/l) of Cr (VI) respectively. V = volume (L) of the sample solution and W = weight (g) of the dry sorbent. The Cr (VI) removal percentage by the water hyacinth/magnetite nanocomposite was similarly calculated with this equation:

$$\% \,adsorbent = ( C_0-C_e)/C_0*100\,\%.$$
(14)

Adsorption kinetics

The adsorption mechanism is being studied using adsorption kinetics. The adsorption process is influenced by both adsorbent properties and mass transfer pathways. By applying the pseudo first and second order models, we investigated the kinetics of adsorption and learned about rates, adsorption capacity and the mechanism involved. In this study, we investigated the pseudo-first-order and second-order models in the Eqs. 15 and 16.

The pseudo-first-order equation as follows:

$$ln({q_e} - {q_t})= \ln ({q_e}){k_1}t$$
(15)

The slope and intercept of the ln(qe−qt) versus t plots allowed to determine k1 and qe.

$$\frac{t}{q^t}= \frac{1}{k_2q_e^2} + \frac{t}{q_e}$$
(16)

The pseudo-second-order equation, which describes the adsorption rate based on the amount of adsorbate that can be adsorbed, is expressed as:

where k2 is the rate constant (g/mg min). From the slope and intercept of the t versus t/qt plot, qe and k2 were determined.

Design of experiments by using central composite (CCD)

To find the best conditions for removing chromium(VI) from water using the iron oxide-impregnated water hyacinth nanocomposite, a central composite design (CCD) was employed for optimization (Table 1). This statistical approach involved conducting 20 carefully planned experiments to understand how different process variables interact and affect the removal efficiency.

\(N = 2k + 2k + n0 = 23+ 2(3) + 6 = 20\).

Where N = total number of experiments; K = number of factors; n = number of replications.

Table 1 Experimental factors and levels used in CCD.
Full size table

Results and discussion

Proximate analysis of water hyacinth

Proximate analysis of water hyacinth is essential as it provides important information about the material’s composition, including the percentages of volatile components, fixed carbon, and inorganic waste material (ash). This analysis is crucial before undergoing the co-precipitation reaction between hydrated ferrous sulfate and ferric chloride. The primary reason for conducting proximate analysis on water hyacinth is to evaluate the percentage of unburned material. This is necessary because, during the co-precipitation reaction, some components of water hyacinth may be lost. Therefore, understanding the composition of the water hyacinth before the reaction is essential to predict how much of it will be lost. As shown in Table 2, the values for moisture, ash, and volatile matter contents were found to be nearly consistent with previous literature reports.

Table 2 Proximate analysis of water hyacinth.
Full size table

characterization of magnetite impregnated water hyacinth nano composite

Physical properties of iron oxide impregnated water hyacinth

Table 3 Physical properties of iron oxide impregnated water hyacinth.
Full size table

As shown in Table 3, the iron oxide-impregnated water hyacinth exhibited a porosity of 68%. This significant porosity suggests that the material possesses a substantial surface area along with a multitude of internal pore spaces. These characteristics are highly advantageous for biosorption processes. A higher porosity generally translates to a greater ability of the material to capture hexavalent chromium (Cr(VI)). This finding indicates that this particular biosorbent is exceptionally well-suited for the task of removing chromium(VI) from water-based solutions.

(FT-IR) spectrum analyses of iron oxide impregnated water hyacinth nano composite

Fig. 2
figure 2

FT-IR analyses of the adsorbent before (a) and after adsorption (b).

Full size image

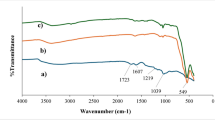
The functional groups present in the iron oxide-impregnated water hyacinth, both before and after it adsorbed chromium, are illustrated in Figs. 2(a) and 2(b). Water hyacinth, being a cellulosic material, primarily consists of cellulose, hemicellulose, and lignin. To observe any changes in the vibration frequencies of these functional groups upon chromium(VI) adsorption, the FT-IR spectra of the iron oxide-impregnated water hyacinth were obtained both before and after the process. This analysis was conducted across the infrared region with wavelengths ranging from 4000 to 400 cm⁻¹. The FT-IR spectrum of the iron oxide-impregnated water hyacinth showed several major intense bands around 3124.23, 3034.95, 1631.30, 1399.92, 1077.28, 556.76, and 431.05 cm−1 before adsorption. After adsorption, the major peaks shifted to 3267.11, 1636.27, and 944.56 cm−127. The changes indicate specific functional groups are involved in Cr(VI) adsorption.

Figure 2(a) shows bands at 3124.23 cm⁻¹ and 3034.95 cm⁻¹, which correspond to the stretching vibrations of OH groups, likely due to water adsorbed on the material. This could also be due to the presence of alcohol, carboxylic acid, or phenol functional groups in the adsorbent. The band appearing at 1631.3 cm⁻¹ suggests the presence of a carbon-oxygen double bond (C = O), which is typically found in functional groups such as esters or carboxylic acids. The band at 1399.92 cm⁻¹ represents the C–H functional group, attributed to hydrocarbons, particularly alkanes. The band at 1077.28 cm⁻¹ indicates the presence of a C–O stretch, which is associated with ethers. The peaks at 556.76 cm⁻¹ and 431.05 cm⁻¹ correspond to the Fe–O stretch, which is consistent with the presence of magnetite (Fe₃O₄), as previously reported by Nyamunda et al.

After the adsorption of chromium, the band at 3124.23 cm⁻¹ shifts to 3267.11 cm⁻¹. This could indicate that some of the hydrogen ions in the OH group were replaced by chromium (VI) ions during the adsorption process. Similarly, the broad band at 1631.3 cm⁻¹ shifts to 1636.27 cm⁻¹, which could be a result of the replacement of some oxygen ions in the C = O functional group with chromium (VI) ions. These shifts in the functional groups suggest that chromium (VI) has been successfully adsorbed onto the iron oxide-impregnated water hyacinth composite.

Size analysis of iron oxide impregnated water hyacinth nano composite

Fig. 3
figure 3

Iron oxide impregnated water hyacinth size analysis.

Full size image

The Fig. 3 shows the size distribution of iron oxide-impregnated water hyacinth particles by intensity. The average size of the particles was found to be 21.04 nm for peak 1 and 304.2 nm for peak 2, which is in close agreement with the previous literature report by Wei et al. This size distribution falls within the nanoscale range, making the particles highly suitable for the adsorption of hexavalent chromium. The nanoscale size contributes to their significantly higher specific surface area, providing a large number of binding sites that are available for adsorbing chromium, thereby enhancing their effectiveness as a biosorbent.

Point of zero charge value

The point of zero charge (pHzpc) is a key characteristic of an adsorbent. It’s simply the pH where the adsorbent’s surface has no net electrical charge. If the surrounding solution’s pH drops below this pHzpc, the adsorbent’s surface takes on a positive charge. On the other hand, if the pH rises above the pHzpc, the surface becomes negatively charged.

This surface charge significantly influences how well the adsorbent can attract and hold different types of ions. For instance, positively charged ions (cations) are more likely to be adsorbed when the pH is higher than the pHzpc, as the adsorbent surface will be negatively charged. On the other hand, negatively charged ions (anions), such as dichromate ions (such as Cr₂O₇²⁻) are more effectively adsorbed when the pH is lower than the pHzpc, because the adsorbent surface will be positively charged.

In the case of the iron oxide-impregnated water hyacinth nanocomposite, the experimentally determined pHzpc was found to be 5.3, as illustrated in the Fig. 4. This finding aligns with a previous study reported by Romero-Guzmán et al. in 2013. Consequently, to achieve the highest possible adsorption of chromium(VI), it is advisable to keep the pH of the solution below 5.3. In these acidic conditions, the negatively charged Cr₂O₇²⁻ ions are drawn to the positively charged adsorbent biomass through electrostatic attraction, resulting in improved chromium(VI) removal from the solution.

Fig. 4
figure 4

Zero Point charge of iron oxide impregnated water hyacinth Nano composite.

Full size image

Determination of specific surface area

To find out the surface area available for adsorption, the Sears method (Eq. 3.8) was used for both plain water hyacinth and water hyacinth treated with iron oxide. The amount of sodium hydroxide needed to change the pH of the test solution from 4 to 9 was measured: 7.2 mL for the regular water hyacinth and 8.2 mL for the magnetite-treated version. This resulted in specific surface areas of 205.4 square meters per gram (m²/g) for the untreated material and 237.81 m²/g for the treated one28. The fact that the surface area increased after adding magnetite suggests that the treated water hyacinth can adsorb more effectively, making it better at capturing hexavalent chromium compared to water hyacinth on its own.

Study and optimize the effect of the selected process variable

Effect of contact time

Fig. 5
figure 5

Effect of Contact time on Cr (VI) adsorption.

Full size image

Removal efficiency of chromium was mostly determined by the amount of contact between iron oxide-treated water hyacinth and the water containing chromium. Here, the parameters studied were kept the same during adsorption: 6 g of adsorbent, pH 2, a starting chromium concentration of 25 mg/L and 150 rpm agitation. Figure 5 shows the rapid increase in germination efficiency of chromium (VI) from 55.2 to 77.9% when the exposure time was increased from 60 min to 90 min. The maximum efficiency of 87.2% was reached at about 120 min. This trend was found to be similar to the report by (kumar, et at., 2019)29. As indicated in the graph, the removal efficiency of chromium (VI) initially increased rapidly. However, beyond 90 min, the increase in removal efficiency became very slight. This is because, during the initial period of stirring, the binding sites for adsorption were more abundant, but as the contact time increased, almost all the active sites became occupied by chromium (VI). Consequently, the biosorbent reached its maximum biosorption capacity under the defined conditions, and further increases in contact time did not lead to a significant improvement in adsorption.

Effect of adsorbent dose on adsorption efficiency

Fig. 6
figure 6

Effect of dosage of magnetite water hyacinth on Cr (VI) adsorption.

Full size image

Figure 6 shows how the amount of magnetite-impregnated water hyacinth used affected chromium adsorption. As the amount of adsorbent was increased, the efficiency of chromium removal also went up. This is because more adsorbent provides a larger surface area for contact. When more adsorbent particles were present, there were also more active sites available, making it easier for chromium ions to find and bind to these sites. The removal of chromium(VI) improved noticeably from 68.48 to 78.28% when the amount of biosorbent was increased from 1 gram to 3.5 g. The highest removal efficiency, reaching 80.5%, was achieved when 6 g of the adsorbent were used. However, beyond 3.5 g, the rate of increase in removal efficiency slowed considerably. This can be attributed to the limited initial chromium concentration; at lower adsorbent dosages, the ratio of chromium ions to adsorbent mass was higher, resulting in greater uptake per unit mass. As the adsorbent dose increased further, the number of chromium ions became insufficient to fully utilize the available active sites, reducing the uptake per unit mass. Therefore, increasing the adsorbent dose beyond 6 g yielded minimal improvements, making 6 g the optimal dosage for efficient and economical removal of chromium (VI).

Effect of adsorbate (chromium (VI)) concentration on adsorption efficiency

Fig. 7
figure 7

Effects of initial chromium concentration on adsorption efficiency.

Full size image

The initial amount of chromium(VI) in the water was a key factor influencing how effectively it could be removed. To study this, experiments were run with different initial chromium concentrations (25, 50, and 75 mg/L) while keeping other conditions optimal: a contact time of 120 min, an adsorbent amount of 6 g, a mixing speed of 150 rpm, and a pH of 2. Figure 7 illustrates a decline in the percentage of chromium(VI) removed as the initial chromium concentration rose. The best removal, 85.81%, occurred when the starting concentration was lowest (25 mg/L)30. This happens because when there’s less chromium to begin with, there are enough adsorption sites available on the material to capture it effectively. However, when the initial concentration is higher, there are more chromium(VI) ions than available binding sites. This leads to the sites becoming full, and the removal efficiency drops. The main reason for the reduced removal efficiency at higher initial concentrations is simply that the adsorbent has a fixed, limited number of spots for chromium ions to attach.

Evaluation of the adsorption isotherm models

Various isotherm models exist to help understand how adsorbates attach to adsorbents based on experimental data. Among these, the Freundlich and Langmuir models are most often used, and this study focused on just these two. The Freundlich model explains adsorption on surfaces that aren’t uniform and can involve multiple layers of the adsorbate building up. In contrast, the Langmuir model describes adsorption forming a single layer on a uniform surface with a limited number of identical binding spots. The findings here indicated that the Langmuir model described the experimental data more accurately, showing a strong fit with a high coefficient of determination (R² = 0.9963), as illustrated in Figs. 8 and 9. This suggests that the adsorption of hexavalent chromium onto iron oxide-impregnated water hyacinth primarily follows a monolayer adsorption process on a uniform surface, where adsorption at one site does not influence neighboring sites, indicating no lateral interaction or transmigration of chromium ions. The Freundlich isotherm, which illustrates the connection between the amount of chromium held by a specific weight of the adsorbent and the concentration of chromium remaining in the solution at equilibrium, also provided a fairly good description of the data, showing an R² value of 0.977. A Freundlich constant value of n = 2.083 indicates favorable adsorption, as values of n greater than 1 are associated with beneficial adsorption characteristics (Table 4).

Table 4 Equilibrium parameter value of cr with different isotherm model.
Full size table
Fig. 8
figure 8

Freundlich plot.

Full size image
Fig. 9
figure 9

Langmuir plot.

Full size image

Kinetic studies

The kinetics of model uptake by the carbonate system take place using both pseudo-1st -order and 2nd -order approaches. Analyzing the linear plots allowed for the determination of the kinetic rate constants, adsorption capacities, and correlation coefficients. When comparing the two models, the pseudo-first-order model matched the experimental data slightly better because it gave a higher R². Thus, it indicating that the rate of adsorption of solute is linked directly to the difference in concentration between the time and the volume absorbed. At the start of adsorption, this model suggests that boundary layer diffusion may be the factor that determines the rate. In contrast, when the pseudo-second-order model is assumed, the slowest stage is thought to be chemical adsorption, during which electrons are traded or shared between the chromium ions and the surface of the adsorbent. R2 increased from 0.9775 to 0.9805 (Table 5) for the pseudo-first-order model, compared to 0.9775 for the pseudo-second-order model showen in Figs. 10 and 11. Based on this better fit, the observations by Rani et al., 201728 indicate that chromium adsorption here is influenced mostly by how it travel in the boundary area of the adsorbent.

Table 5 Pseudo first & second order parameters for chromium sorption.
Full size table
Fig. 10
figure 10

Pseudo -first-order kinetic model plot.

Full size image
Fig. 11
figure 11

Pseudo -second-order kinetic model plot.

Full size image

ANOVA for the design model

Design-Expert Software (version 12) played a crucial role in planning and optimizing the experimental data, which had been arranged randomly. To develop a model and pinpoint the ideal settings for various process variables – specifically, the initial chromium concentration, the amount of adsorbent used, and the contact time in relation to how effectively chromium(VI) was removed, Response Surface Methodology (RSM) was employed. An Analysis of Variance (ANOVA) was then carried out to confirm the statistical significance and dependability of the generated model. The ANOVA results, presented in Table 6, show the multiple linear regression analysis for the second-order response surface model.

Table 6 ANOVA results for percentage removal.
Full size table

The importance of each part of the model is judged by its F-value and p-value. A higher F-value and a p-value below 0.05 usually mean that the model term is statistically important. In this study, the model produced a very high F-value and a p-value below 0.0001, showing that the regression model is statistically significant. The p-values for the individual components of the model – A (contact time), B (adsorbent dosage), C (initial chromium concentration), AB, A², and B² – are all less than 0.05, indicating that they significantly influence the chromium removal efficiency. Because the overall model also has a p-value below 0.05, it can be considered statistically sound.

To see how well the model fits the data, the coefficient of determination (R²) was used. This value tells us what percentage of the changes in the response (chromium removal efficiency) can be explained by the model. Here, the R² value was 0.9964, meaning the model can explain 99.64% of the variability in chromium removal. Additionally, the adjusted R² value was 0.9932, which also supports the high reliability and strength of the model.

The final regression equation in terms of coded factors is:

$$Efficiency = 78.26 + 16.02A + 6.01B -8.48C -4.95AB -0.6AC -0.75BC -7.14A^2 - 3.79B_2 -0.9445C_2$$
(17)

Where A = Contact time, B = Adsorbent dosage, C = initial chromium concentration.

The equation shows the linear and quadratic effects of each variable, along with their interactions, on chromium adsorption. Positive coefficients (e.g., for A and B) indicate a positive influence on the removal efficiency, whereas negative coefficients (e.g., for C, AB, A²) suggest that increasing these variables reduces the adsorption efficiency. For instance, increasing contact time and adsorbent dosage improves Cr(VI) removal, while increasing initial chromium concentration lowers it.The comparison between actual and predicted values of Cr(VI) removal, as shown in Fig. 12, demonstrates that the predicted values align closely with the actual experimental data. This close alignment confirms the adequacy and predictive accuracy of the developed RSM model.

Fig. 12
figure 12

Predicted vs. actual plot of response values.

Full size image

Optimization of chromium (VI) removal efficiency

The key process variables were optimized to ensure the most effective removal of chromium(VI) from the water. This involved adjusting the initial chromium concentration, the amount of biosorbent used, and the stirring contact time of the solution. This optimization was carried out using Design-Expert 12 software.

Response (Cr (VI) removal efficiency) surfaces design plots of factor interaction

Fig. 13
figure 13

3D plot showing the combined effect of contact time & dosage.

Full size image

Figure 13 visually demonstrates how adjusting both the adsorbent dosage and contact time simultaneously influences chromium(VI) removal. This illustration holds the initial chromium(VI) concentration steady at 50 mg/L. The graph clearly indicates that as both the contact time and the amount of adsorbent increase, more chromium(VI) is removed. For instance, the removal efficiency notably rose from 40.14 to 78% when the adsorbent amount was increased from 1 gram to 3.5 g and the contact time extended from 60 min to 90 min. This positive trend continued, albeit at a somewhat slower rate, eventually reaching 84% when the dosage was further boosted to 6 g and the contact time to 120 min.

Initially the removal of chromium(VI) jumped dramatically. This happened because the adsorbent material had an abundance of active spots ready to bind with the chromium. As time passed, however, that removal rate slowed down; more and more of those binding sites were getting filled up with chromium(VI) ions. A similar pattern emerged when increasing the amount of adsorbent. The efficiency of chromium(VI) removal quickly climbed as the dose went from 1 gram to 3.5 g. But when the dose was further boosted, from 3.5 g to 6 g, the improvement in removal wasn’t as significant. This indicates that at those higher adsorbent amounts, the limited number of chromium(VI) ions left in the solution became the bottleneck, as there were simply more binding sites than ions to capture. As indicated by the coded equation for the response variable, the combined effect of adsorbent dosage and contact time (A, B) negatively impacted the removal efficiency, with a coefficient of −4.95 (Eq. 4.1). This interaction had a statistically significant effect, as evidenced by the p-value of 0.0001, indicating that both factors together significantly influenced chromium (VI) removal efficiency.

Fig. 14
figure 14

3D plot for effect of contact time & chromium (VI) concentration.

Full size image

Figure 14 illustrates that longer contact times generally lead to better chromium(VI) removal. However, the effectiveness of removal decreases as the initial concentration of chromium(VI) in the water increases. For example, the highest chromium removal efficiency, 85.81%, was achieved with a 90 min contact time when the starting chromium concentration was 50 mg/L.

The reason for the reduced removal at higher initial chromium concentrations likely lies in the saturation of the adsorbent’s binding sites. When the chromium concentration is low, the metal ions can more readily find and attach to the available binding sites on the adsorbent, leading to greater removal. This is because at lower concentrations, there’s a larger ratio of available surface area on the adsorbent compared to the number of chromium ions present. As the concentration of chromium increases, there are more chromium ions than available binding sites, causing these sites to become full and consequently reducing the overall efficiency of adsorption.

Fig. 15
figure 15

3D plot for effect of dosage & chromium (VI) concentration.

Full size image

As depicted in Fig. 15, increasing the amount of adsorbent caused the removal efficiency to jump from 70 to 80%. On the other hand, a rise in chromium starting concentration from 25 mg/L to 45 mg/L reduced the efficiency of chromium removal by 10%. When 6 g of the adsorbent were used with a 50 mg/L Cr (VI) concentration, the removal efficiency was 80.5%. Setting the initial chromium concentration at 50 mg/L and the dosage at 3.5 g resulted in a 78.28% removal efficiency.

Conclusion

This study demonstrates the effective use of nano-sized iron oxide-modified water hyacinth, sourced from Lake Koka in Ethiopia, as a low-cost and efficient adsorbent for the removal of hexavalent chromium [Cr(VI)] from synthetic wastewater. The adsorption process was systematically optimized by adjusting key parameters such as adsorbent dosage, contact time, and initial Cr(VI) concentration. The experimental design and statistical modeling were conducted using Design Expert software to achieve optimal conditions. Comprehensive physicochemical analyses, including Fourier-transform infrared (FTIR) spectroscopy, revealed the presence of critical functional groups—such as hydroxyl, carbonyl, carboxylic, and aliphatic alkane—and a relatively large surface area, with particle sizes ranging between 21.04 and 304.2 nm, indicating abundant active binding sites. Batch adsorption trials indicated that Cr(VI) removal efficiency improved with increased contact time and adsorbent quantity, while higher initial concentrations of Cr(VI) led to reduced removal rates. The Central Composite Design (CCD) approach effectively optimized the process variables for maximum removal efficiency. The adsorption data were best described by the Langmuir isotherm model (R² = 0.9963), implying monolayer adsorption on a homogeneous surface. According to this model, the maximum sorption capacity (q0) was determined to be 12.5 mg/g, and the rate constant (k₂) from the pseudo-second-order kinetic model was calculated as 0.00106 (mg·min)/g.