A novel dual-student reverse knowledge distillation method for magnetic tile defect detection

Abstract

Magnetic tiles surface defect detection is crucial in industrial production. However, it is difficult to effectively detect and locate defective areas in magnetic tiles due to the following problems: (1) The defect texture of the magnetic tile material is highly similar to the background texture; (2) The image contrast between the normal and defective areas of the magnetic tile is low; (3) The size and morphology of the defects of the magnetic tile vary greatly. To address the above problems, this study proposes a novel dual-student reverse knowledge distillation framework based on reverse distillation called binary struct and detail reverse distillation (BSDRD). In this framework, a pre-trained teacher network that uses a deep learning model to learn multi-scale and multi-level feature representations serves as the feature extractor. The obtained features are processed by two student networks with different responsibilities. Specifically, the struct student dynamically fuses and compresses multi-scale features. The detail student applies wavelet transform to decompose high-level features into low-frequency and high-frequency components, and this decomposition not only retains global structural information of the high-level features but also enhances the detection ability for complex textures, gradients, and irregular defects. In addition, this paper introduces a multi-dimensional feature gated fusion loss (MD-GFLoss) to improve the model’s selectivity for key features and sensitivity to abnormal areas. Experiments on the magnetic tile defect detection dataset show that the proposed BSDRD is particularly effective in handling complex textures and small defects. It outperforms existing methods in both pixel-level and sample-level anomaly detection tasks.

Introduction

In modern industrial manufacturing, permanent magnet motors have become key driving components in fields^1,2,3,4 such as electric vehicles , wind power generation, industrial automation, and household appliances. As a core component of the motor, the quality of the magnet tiles directly affects the motor’s performance and lifespan. Both large-area continuous defects and small surface defects can undermine the safety and functionality of the equipment^5,6. Traditional methods for detecting magnet tile defects mainly include manual monitoring^7,8,9, ultrasonic testing, and electromagnetic testing. Manual monitoring often struggles to ensure accuracy due to potential inspector fatigue and the lack of standardized evaluation criteria. Ultrasonic testing^10,11,12 is suitable for identifying internal defects. However, it has limited adaptability to complex shapes, which restricts its use in high-precision applications. Electromagnetic testing^13,14 faces issues with insufficient sensitivity in identifying tiny cracks and material inhomogeneity.

To overcome the limitations of these traditional methods, various image detection methods have been proposed for surface defects of magnetic tiles. These methods are mainly divided into two categories: traditional machine learning methods and deep learning methods. In traditional machine learning methods, Xie et al.¹⁵ developed a surface defect detection algorithm for magnetic tiles based on shearlet transform. This method enhanced image contrast during preprocessing and then extracted defects through thresholding, using multi-scale geometric analysis for more effective defect identification. Liu et al.¹⁶ introduced a surface defect recognition method for aluminum strips using non-subsampled shearlet transform combined with kernel local preserving projections. This method optimizes feature extraction by reducing redundant features and interference. Liu et al.¹⁷ proposed a self-referential image decomposition algorithm for detecting surface defects in steel strips. It generates a self-referential template based on the statistical features of defect-free images, guiding the decomposition of the image into structural and textural components to improve defect detection. However, these methods based on traditional machine learning have the following drawbacks. First, they are susceptible to noise interference when processing images with complex backgrounds, low contrast, or subtle defects. This noise can significantly affect the accuracy of defect detection, particularly in scenarios where the visual quality of the image is compromised. Second, many approaches rely on specific assumptions or mathematical models¹⁸, which are typically grounded in an idealized understanding of image features. However, real-world images often deviate from these ideal conditions. When the actual image diverges from the assumptions, the performance of the model can be significantly reduced, limiting its effectiveness in practical applications.

Deep learning has gained attention in surface defect detection due to its powerful feature extraction ability. Fu et al.¹⁹ proposed a region-based fully convolutional network enhanced with deformable convolutions and attention mechanisms, which allow the network to focus on relevant image areas and adapt to various deformations in defects. However, the model’s performance may be affected by preprocessing steps and the complexity of real-time defect detection. Lu et al.²⁰ developed a multimodal fusion convolutional neural network that uses a cross-attention mechanism to integrate information from multiple imaging modalities for better detection of internal defects in tiles. However, it needs high-quality multimodal data, which may not always be easily available in industrial environments. Liang et al.²¹ proposed a deep neural network named ELCNN for detecting small object defects on tiles. It focuses on advanced neural network architectures tailored for small-scale defect detection. But this method still faces challenges related to highly variable image quality and lighting conditions. These factors may affect its generalization ability across different datasets. Cao et al.²² proposed an unsupervised defect segmentation method using attention-enhanced flexible U-Net, focusing on segmenting defects in tile images without requiring large amounts of labeled data. But this method struggles to handle high-texture backgrounds that may confuse the segmentation process and requires further improvement.

Although deep learning methods show great promise in defect detection, they still face challenges when handling poor image quality, lighting variations, and background noise interference. These issues can impact the performance of deep learning models, especially when the defects are small or the background is complex. To address these challenges, recent research has started to focus on utilizing intermediate features from pre-trained deep models for defect detection. Intermediate features can capture fine-grained information and multi-scale representations, which help address common issues like noise interference, illumination changes, and occlusions. Knowledge distillation is an effective approach that utilizes intermediate layer features. In this method, teacher model is usually pre-trained on large-scale datasets such as ImageNet²³, making it with the capability to extract and propagate multi-level intermediate features. The student model learns by mimicking the intermediate outputs of the teacher model, thereby improving its performance in defect detection tasks. In knowledge distillation-based anomaly detection methods²⁴, the teacher model acts as a powerful feature extractor to learn representative feature embeddings from normal samples. These feature embeddings capture the distribution of normal samples. The student model is trained only using normal samples and imitates the response of the teacher model to normal features. During the inference phase, the anomaly score is obtained by measuring the difference between the student features and teacher features. Since anomalies may appear at different scales and abstraction levels, the multi-layer features of the teacher model help the student model more comprehensively identify various anomalies. Although the method based on knowledge distillation has shown significant advantages in improving defect detection performance, particularly in processing multi-scale features. However, it still faces challenges. First, there is a high similarity between the defect of the magnetic tile and the background textures. Second, the image contrast between the normal and defective areas is low. Finally, the size and morphology of the defects vary greatly. Specifically, cracks usually appear as complex long, thin lines or network-like structures with irregular boundaries and textures similar to the surrounding areas. Fractures generally present linear or fragmented structures with obvious directionality and high semantic complexity. And unevenness usually appears as gradient or dot patterns with hidden morphology. Therefore, a model is needed that can effectively deal with overall structural defects while properly handling complex textures, gradients, and irregular defects.

To address the above problems, this paper proposes a dual-student reverse knowledge distillation framework based on the concept of reverse distillation²⁵. Unlike traditional ensemble methods^26,27, the structural student focuses on reconstructing the teacher model’s low-level features, concentrating on overall structural anomalies. The detail student uses wavelet transform to decompose the image features into low and high-frequency parts, capturing both the overall structural information of the teacher’s high-level feature maps and the detailed defect information. By differentially processing and combining the low and high-frequency parts, the detail student not only suppresses redundant information but also effectively captures long-range feature dependencies, improving the recognition of complex textures and fine defects. Moreover, this paper introduces a multi-dimensional feature gated fusion loss to comprehensively enhance the defect-capturing ability of the detail student. This approach improves the model’s selectivity for key features and increases its sensitivity to anomalous regions.

The contributions of the proposed BSDRD are highlighted as follows:

• 1. A novel dual-student reverse knowledge distillation framework with two student models is proposed: the struct student focuses on identifying overall structural anomalies, while the detail student specializes in capturing complex textures and subtle defects. This framework enhances the model’s defect detection capability in low-contrast and high-texture backgrounds.

• 2. A new multi-dimensional feature gated fusion loss is introduced to further improve the model’s ability to capture defect areas. It can effectively promoted the deep mining and processing of detail information, leading to an improvement in the model’s performance in complex scenarios.

• 3. Extensive experiments conducted on the public magnetic tile dataset show that the proposed BSDRD method achieves superiority performances in both pixel-level and image-level indicators.

Related work

This section provides a brief overview of recent typical methods and advancements in unsupervised anomaly detection. Recent works in AD can be categorized into three main approaches: reconstruction-based methods, embedding-based methods, and synthesis-based methods.

Reconstruction-based methods

Reconstruction-based methods have shown good application in anomaly detection tasks. These models aim to learn feature representations of input data and then reconstruct normal samples from the encoded feature space. Anomalies are detected by analyzing the residual images before and after reconstruction. Autoencoders (AE)²⁸ and Variational Autoencoders (VAE) are classic methods in this field. AE compresses the input data into a low-dimensional latent representation using an encoder, and then reconstructs the input data from this representation using a decoder. Its goal is to minimize the difference between the original input data and the reconstructed data. VAE introduces the concept of probabilistic modeling, using the probability distribution of latent variables to generate data. However, they have limitations when dealing with complex structures and nonlinear data. Additionally, AE and VAE struggle to effectively capture textures and long-range dependencies. To address these issues, Gangloff et al.²⁹ introduced Gaussian Random Fields as a prior in the latent space, enabling the model to better capture local dependencies and global structures in the data. Nguyen et al.³⁰ combined the self-attention mechanism of Vision Transformer³¹ for better image modeling in the latent space and uses ViT’s advantages to extract more complex image features. In practical industrial inspection, although these models perform well in some scenarios, they still face challenges when handling changes in object position, complex textured backgrounds, and diverse anomaly types. Fang et al.³² adopted an adversarial learning strategy, using a small amount of coarse-labeled anomaly data to optimize the model through adversarial training³³, improving the localization ability of anomaly regions. Deng et al.³⁴ introduced noise into the image and combines it with a reconstruction network, making it difficult for the model to reconstruct the anomaly regions. This method improves anomaly detection accuracy, especially when dealing with noisy and complex industrial data. Yao et al.³⁵ proposed a framework called FOcus-the-Discrepancy (FOD). This framework learned the correlations both within and between images to improve anomaly detection. By using the self-attention mechanism of Transformer³⁶, FOD enhanced the detection of various anomaly types, especially logical and global anomalies. Wang et al.³⁷ proposed a semi-supervised learning framework based on diffusion probabilistic models^38,39 named SDDiff. This framework aims to reduce the dependence on large amounts of labeled data. It combines unsupervised learning for broad data understanding with supervised learning for precise pattern recognition. This combination improves the accuracy of surface defect detection. Wang et al.⁴⁰ proposed an anomaly detection method that focuses on improving detection accuracy through a multi-scale architecture. The method uses multi-scale diffusion model branches to enhance coverage of anomalies at different scales. It further introduces a partial Markov chain strategy to improve noise handling during the diffusion process. This strategy helps preserve more useful information during reconstruction. However, these reconstruction-based methods still face challenges in effectively handling complex anomalies, data distribution changes, and avoiding over-reconstruction or mis-reconstruction of anomaly regions.

Synthesis-based methods

Synthetic methods view the generation of abnormal samples as a data augmentation technique and incorporate it into a reconstruction-based framework. In most of these methods, the abnormal samples are synthesized at the image level, using a self-supervised approach to assist in model training. Li et al.⁴¹ introduced a self-supervised data augmentation strategy by cutting and pasting image regions to create rough abnormal data. This strategy enhanced the model’s sensitivity to anomalies. To make the synthetic anomalies more realistic, Hu et al.⁴² incorporated strong prior knowledge from diffusion models⁴³. By utilizing spatial anomaly embedding and an adaptive attention re-weighting mechanism, it generated more realistic and accurately aligned anomaly data with only a small amount of real anomaly data. However, industrial anomaly detection often faces challenges such as small-scale training data and anomalies that are close to the normal data distribution. Zavrtanik et al.⁴⁴ introduced a dual decoder architecture that directly generates anomalies in the quantized feature space. It significantly improved the detection performance when anomalies are close to the normal distribution. Chen et al.⁴⁵ learned a robust Gaussian descriptor through adversarial interpolation, effectively mitigating overfitting issues when abnormal data is polluted or when the data scale is small. Chen et al.⁴⁶ treated anomaly synthesis as a normal data augmentation technique. It generated abnormal features adaptively along predefined spherical boundary directions in the feature space, making anomaly synthesis more diverse and effective. Xiao et al.⁴⁷ proposed a surface defect detection method named WFF-Net. The method introduces a trainable weight feature fusion module. This module reduces information redundancy and semantic differences during multi-scale feature fusion. It also enhances feature representation through an attention mechanism. In addition, a dual-decoding module is introduced. This module further reduces feature loss during the upsampling process. Additionally, Liu et al.⁴⁸ simplified the anomaly detection framework by combining feature adaptation and the simple strategy of adding Gaussian noise in the feature space. It established an easy-to-train and efficient detector, which is highly applicable in industrial environments. Although the above synthesis-based methods can effectively generate abnormal data, considering that anomalies in industrial environments are extremely small and complex⁴⁹. Therefore, how to generate anomalies at a high semantic level remains a challenging task.

Embedding-based methods

In recent years, embedding-based anomaly detection and localization methods have gained widespread application and achieved excellent performance. These methods extract features using pretrained networks and map the normal sample features to a compact space, making it easy to distinguish anomalies from normal samples in the feature space. The core idea is to detect anomalies by calculating the distance of features between test images and the normal sample cluster. Knowledge distillation structures utilize this idea, where the teacher and student networks judge anomalies by calculating the differences between them. To capture the contextual similarity between features, Cao et al.⁵⁰ introduces a contextual similarity loss into the teacher-student structure. This loss not only constrains the point-to-point feature regression from the student network to the teacher network, but also employs Adaptive Hard Sample Mining. This method helps highlight the differences between anomaly and normal samples. Yu et al.⁵¹ uses 2D normalizing flows to model the distribution of normal image features. By mapping the features from their original distribution to a standard normal distribution, this method is able to better capture both local and global feature dependencies. Salehi et al.⁵² adopts a multi-resolution knowledge distillation paradigm, using the pretrained teacher network’s feature outputs at multiple layers and scales to guide the student network. This allows it to adapt well to both local texture and global structure differences, handling anomalies of different sizes. In contrast, Deng et al.²⁵ makes bold changes to the network structure, using a “teacher encoder - student decoder” reverse distillation framework with a trainable low-dimensional bottleneck embedding module between the two. This setup makes it difficult for the student to fully replicate the high-level features extracted by the teacher, amplifying the significant differences in anomaly samples. To further improve inference speed, Batzner⁵³ achieves efficient anomaly detection through a lightweight feature extraction network and a student-teacher framework. It also has low latency and high throughput, making it suitable for industrial real-time detection applications. Although embedding-based methods can better capture multi-scale features and avoid the issue of anomaly generation at high semantic levels, they still exhibit certain limitations in handling defects with diverse feature distributions, shapes, and varying degrees of semantic complexity.

Proposed method

The method proposed in this article is a dual student knowledge distillation framework based on reverse distillation called BSDRD, which is different from the paired distillation method⁵⁴, which uniformly processes all features. Our method is more effective in dealing with defects in industrial datasets with different feature distributions, shapes, and semantic complexities. BSDRD is proposed for the localization and detection of defects on magnetic tile surfaces. It consists of two important components: the struct student and the detail student. These components are shown in Fig. 1 and the model is described as follows.

Overview of the dual-student framework

In most existing knowledge distillation frameworks, using a single-branch student model to compress multi-scale features into a compact space via a low-dimensional bottleneck embedding can lead to the loss of high-frequency texture variations and subtle perturbations. Moreover, the decoding process in such models usually emphasizes the recovery of global structures, rather than fine-grained textures. Since the student model mainly focuses on reconstructing normal patterns, it is less sensitive to minor local anomalies, such as crack or blowhole. Consequently, these small defective regions are often mistaken for normal features and ignored. To address these issues, a novel dual-student reverse knowledge distillation approach has been proposed. The key idea is to divide the student model into two distinct branches: a struct student and a detail student. Each branch has a specific learning objective—one captures global structural information, while the other preserves fine-grained local details. This dual-branch design effectively enhances the framework’s ability to detect defects. As illustrated in Fig. 1, our BSDRD model is composed of five modules. The first is a deep neural network pre-trained on ImageNet, serving as a fixed teacher network T. The second is a single-class multi-scale bottleneck embedding module $\text {OCBE}_{\text {str}}$ designed specifically for the student model. The third is a struct student decoder $\text {S}_{\text {str}}$. The fourth is a detail feature fusion network $\text {WSFFN}_{\text {dt}}$ specifically designed for processing high-level semantic features. Finally, the fifth is a detailed student decoder $\text {S}_{\text {dt}}$.

Fig. 1

Overview of the dual-student reverse knowledge distillation framework: Our model leverages a pre-trained teacher encoder as a feature extractor. The struct student focuses on the efficient integration and reconstruction of multi-level features, while the detail student enhances the handling of fine-grained, gradient, and irregular texture variations.

The teacher network T is capable of effectively extracting both normal and abnormal feature representations from input samples. The student model has a network architecture similar to that of the teacher model, including comparable configurations in network layers, convolutional structures, and activation functions. In this approach, the teacher model acts as an “encoder” of features, while the student model serves as a “decoder,” aiming to reconstruct low-level, input-like feature representations from the high-level features provided by the teacher model. The struct student focuses on learning structural features, especially structural anomalies such as break and fray. It is designed to emphasize the reconstruction of low-level features, aiming to enable the model to accurately identify these types of structural anomalies. In contrast, the detail student specializes in capturing textures and fine-grained variations. These kinds of anomalies are influenced by factors such as low background contrast and significant variation in defect morphology, requiring the model to have strong capabilities in capturing detailed information. Specifically, the multi-level feature maps obtained from the teacher network T are processed through four distinct modules. The primary goal of the $\text {OCBE}_{\text {str}}$ module is to dynamically adjust the spatial weighting of feature maps from different scales to achieve efficient integration and reconstruction of multi-level features. The struct student first fuses the multi-level features obtained from the teacher model using the ASFF module, and then compresses them through the OCE module. This enables the effective extraction and utilization of the multi-layered feature representations in the teacher network. Subsequently, these features are decoded by the struct student decoder $\text {S}_{\text {str}}$ to achieve precise reconstruction of low-semantic features. To further enhance the handling of fine-grained details and address issues such as gradual or irregular texture deviations, a $\text {WSFFN}_{\text {dt}}$ module is designed to extract and enhance the key details from the high-semantic features obtained from the teacher network. In this module, the high-level semantic features extracted by the teacher model are first decomposed into two parts—a low-frequency component and a high-frequency component—through wavelet transform. The low-frequency component is processed by a module called Dynamic Frequency Channel Selection (DFCS), which integrates relevant information to enhance feature representation. Meanwhile, the high-frequency component is fed into multi-branch analysis and fusion (MBF-Enhance) to capture local detail and texture features. The results from both branches are dynamically fused through a gated fusion network, which adaptively adjusts the weights of each branch during integration. Finally, the output of this module is then passed to the detail student decoder $\text {S}_{\text {dt}}$, allowing the effective reconstruction and restoration of detailed features under complex conditions.

Structural knowledge distillation

Unlike traditional discriminative paradigms, reverse distillation enables the student network to reconstruct the features extracted by the teacher network through a generative approach. Specifically, the student decoder receives the encoded features from the collection and progressively decodes them into lower-level semantics. During the inference phase, the aggregated feature space may inadvertently overlook subtle abnormal features, resulting in a greater difference in abnormal feature intervals. We adopt the reverse distillation and combine it with an adaptive spatial feature fusion (ASFF) strategy to achieve more accurate feature reconstruction, and the specific implementation details of $\text {OCBE}_{\text {str}}$ framework are shown in Fig. 2. Unlike traditional adaptive fusion methods, which typically rely on static fusion weights or simpler mechanisms, ASFF introduces a more sophisticated spatial weight adjustment strategy. By dynamically adjusting the weight distribution across different feature levels, ASFF improves the ability to capture subtle abnormal features that other methods might overlook. Additionally, while many fusion techniques focus on individual feature-level importance, ASFF adapts the fusion at multiple levels simultaneously, which allows for better integration of hierarchical features from the teacher network into the student network. This multi-level adaptive adjustment contributes significantly to enhancing defect detection, making ASFF particularly effective in contexts where fine-grained details matter, such as anomaly detection in complex images. For a given image I , the pretrained teacher net extracts intermediate features $F_{\text {T}}^i \in \mathbb {R}^{h_i \times w_i \times c_i}$, where $i \in \{1, 2, 3\}$. These features are encoded into the embedding space $\Phi _{\text {str}}$ through the $\text {OCBE}_{\text {str}}$ framework. The student network $\text {S}_{\text {str}}$ then maps obtained features in $\Phi _{\text {str}}$ to generate the corresponding feature projection $F_{\text {S}_{\text {str}}}^{i}$. To enhance multi-level feature fusion, the ASFF module dynamically adjusts the spatial weights of features from different levels, enabling adaptive multi-level feature fusion. Specifically, the intermediate features extracted by the teacher network T are compressed using 1 $\times$ 1 convolutions to obtain feature maps. Then, the feature maps are upsampled to ensure uniform size, and then their attention weights are calculated. These obtained weights are concatenated to obtain weight cat and normalized using softmax to get the final weights weight fused. Then, the feature maps are weighted and fused, and the fused features are obtained through $\text {OCE}$ based on the weighted fusion results. Unlike static feature fusion methods, the adaptive spatial feature fusion module fully leverages multi-layer feature representations from the teacher network, effectively filtering redundant information and highlighting key features. The vector cosine distance is used as the loss function to constrain the student network during training. By evaluating on a per-layer scale, a two-dimensional anomaly score map can be generated

$$\begin{aligned} F_{\text {str}}^{i} = 1 - \frac{{F}_{\text {T}}^{i} \cdot {F}_{\text {S}_{\text {str}}}^{i}}{\Vert {F}_{\text {T}}^{i}\Vert \Vert {F}_{\text {S}_{\text {str}}}^{i}\Vert } \end{aligned}$$

(1)

Here, $\Vert \mathbf {\cdot } \Vert$ represents the norm of the feature map.

The final loss of structural students is

$$\begin{aligned} \mathcal {L}_{\text {str}} = \sum _{i=1}^{3} \left\{ \frac{1}{h_i \cdot w_i} \sum _{i=1}^{h_i \cdot w_i} F_{\text {str}}^{i} \right\} \end{aligned}$$

(2)

Among them, $h_i$ represents the height of the i-th layer feature map, $w_i$ represents the weight of the i-th layer feature map.

Fig. 2

Implementation details of $\text {OCBE}_{\text {str}}$ module.

Fig. 3

A detail compression block named $\text {WSFFN}_{\text {dt}}$ designs to enhance the handling of fine-grained, gradient, or irregular texture variations.

Detail knowledge distillation

The encoder-decoder structure can retain a large amount of critical information, and multi-scale feature extraction frameworks are capable of efficiently processing both low-level and high-level information. However, student models still struggle to effectively learn detailed features when encountering irregular or subtle patterns. Moreover, after receiving the fused and compressed hierarchical semantic information through $\text {OCBE}_{\text {str}}$ , the student model is assisted in recursively reconstructing and compressing features. Therefore, this process weakens the model’s ability to capture subtle details and irregularities when embedding the final features into $\Phi _{\text {str}}$. To address the above issues, this paper proposes a detailed feature fusion network named $\text {WSFFN}_{\text {dt}}$ that aims to enhance the retention of the most critical detailed information at a high efficiency while suppressing redundant features. $\text {WSFFN}_{\text {dt}}$ improves the student model’s ability to learn at various levels of granularity, as shown in Fig. 3.

Fig. 4

Visualizations of features before and after wavelet decomposition. (A) The magnetic tile image. (B) The high-level semantic feature $F_{T}^{3}$ through the teacher network. (C) The low-frequency component of the $F_{T}^{3}$ through wavelet transform. (D) The high-frequency component of the $F_{T}^{3}$ through wavelet transform.

The core mechanism of the detail feature fusion network is based on frequency decomposition, dynamic channel selection, and gate fusion strategies, which aim to extract and enhance key details from the high-level semantic feature $F_{T}^{3}$. As shown in Fig. 4, for the magnetic tile image (A), BSDRD extracts the high-level semantic feature $F_{T}^{3}$ through the teacher network, as illustrated in figure (B). However, these features may still be insufficient to fully capture subtle details such as fine cracks, small spots, or surface irregularities. To address this issue, BSDRD apply wavelet transform to obtain both low-frequency component map (C) and high-frequency component map (D). As seen in figure (C), the low-frequency component presents a smoother structure with less regional variation, resulting in an overall blurred and simplified appearance. This is because the low-frequency part of the wavelet transform mainly retains the global structural information while suppressing detailed and high-frequency components. In contrast, figure (D) highlights the detailed features in the feature map, showing clearer and more localized characteristics. Figure (D) is a merged high-frequency tensor obtained by concatenating three high-frequency components in the channel dimension, so it appears wider. After wavelet decomposition, noise in the high-frequency components can be effectively reduced. The remaining high-frequency information becomes more refined and concentrated on key details. By analyzing these high-frequency features across multiple scales and directions, subtle texture variations in the image can be more effectively captured. Meanwhile, such decomposition minimizes the interference between low-frequency and high-frequency features, providing a more independent representation for subsequent processing. Specifically, for the low-frequency components, this paper designs a DFCS module. This module selects the most relevant channels by integrating spatial information. Additionally, the network dynamically generates channel attention weights to enhance the global representation capability of the features, and improving the representation effectiveness of $F_{T}^{3}$. For the high-frequency components, a feature enhancement module based on MBF-Enhance is employed. This module fully utilizes the relationship among the three high-frequency feature maps, which are independently decomposed from horizontal, vertical, and diagonal directions, respectively. These three maps are associated with different aspects of high-frequency features, such as edge, texture, and fine-grained changes. Each map contains detailed information specific to a particular spatial granularity and has varying degrees of relevance during changes in local spatial positions. To effectively model the collaborative relationships among these tensors, we perform $1 \times 1$ convolution operations on the high-frequency components to achieve channel dimensionality reduction and extract their local features. Subsequently, depth-wise $3 \times 3$ convolutions are utilized to further capture the internal local correlations within the high-frequency components, enhancing their fine-grained feature representation capabilities. On this basis, a mutual interaction matrix is constructed through dot-product operations, representing the dependencies among the high-frequency components. This matrix explicitly captures their complementarity and overlap in spatial structures and semantic features. The joint modeling module further combines the interaction matrix of the high-frequency components with their own features, generating a unified high-frequency representation through normalization and weighted integration. This joint processing method for high-frequency feature maps captures unique local detail information within the high-frequency components. It also enhances the global semantic consistency and discriminative ability of high-frequency features through collaborative interactions between tensors. The weights in gated fusion networks will be introduced in next section.

Multi-dimensional feature gated fusion loss function

To support the operation of the detail compression block and optimize the model’s fine-grained feature representation capability, this paper also designs a multi-dimensional feature gated fusion loss, which optimizes the model training process from the image pixel level, channel level, and frequency domain level. To optimize the ability of the detail student model to capture both local details and global features of $F_{T}^{3}$, this paper adopts a reconstruction loss based on the input feature to guide model training. Consistent with the loss format of the struct student model, the reconstruction loss of the detail student model also employs Euclidean distance, which calculates the similarity between the decoded features and the input features. This balances the detail student network’s ability to reconstruct features and measures the two-dimensional abnormal score generated for each feature scale

$$\begin{aligned} F_\text {dt}^i = 1 - \frac{F_{T}^i \cdot F_{S_\text {dt}}^i}{\Vert F_{T}^i \Vert \Vert F_{S_\text {dt}}^i \Vert } \end{aligned}$$

(3)

The specific form of the reconstruction loss is given as follows

$$\begin{aligned} \mathcal {L}_{\text {dt}_{\text {rec}}} = \sum _{i=1}^{3} \left\{ \frac{1}{h_i \cdot w_i} \sum _{i=1}^{h_i \cdot w_i} F_\text {dt}^i \right\} \end{aligned}$$

(4)

To further enhance the detail student’s ability to effectively model high-frequency and low-frequency features, this paper introduces an innovative frequency-domain cross-correlation loss. This loss constrains the fusion features and the high-frequency and low-frequency components from the perspective of frequency-domain correlation, ensuring that the model faithfully captures the important information in the frequency domain. Specifically, the fusion features $F_{\text {fu}}$, low-frequency features $F_{\text {l}}$, and high-frequency features $F_{\text {h}}$ are projected onto the frequency domain through the fast Fourier transform , respectively. The corresponding frequency-domain feature representations are given by

$$\begin{aligned} \mathcal {F}_{\text {fu}}, \mathcal {F}_{\text {l}}, \mathcal {F}_{\text {h}} = FFT(F_{\text {fu}}, F_{\text {l}}, F_{\text {h}}) \end{aligned}$$

(5)

Subsequently, the frequency domain cosine similarity of the weighted combination of the fused features with the low-frequency and high-frequency components is calculated

$$\begin{aligned} FreqCC(\mathcal {F}_\text {fu}, \mathcal {F}_\text {l}, \mathcal {F}_\text {h}) = \frac{\sum \text {Re}(\mathcal {F}_\text {fu} \cdot \overline{(\mathcal {F}_\text {l} + \mathcal {F}_\text {h})})}{\sqrt{\sum |\mathcal {F}_\text {fu}|^2} \cdot \sqrt{\sum |\mathcal {F}_\text {l} + \mathcal {F}_\text {h}|^2 + \epsilon }} \end{aligned}$$

(6)

Among them, $\textrm{Re}(\cdot )$ denotes the real part operation; $\overline{(\cdot )}$ represents the complex conjugate operation; $\epsilon$ is a very small value to avoid division by zero. The frequency domain cross-correlation loss is defined as

$$\begin{aligned} \mathcal {L}_{\text {dt}_{\text {FreqCC}}} = -\frac{1}{N} \sum _{n=1}^{N} \text {FreqCC}_{n} \end{aligned}$$

(7)

In the detail student network, the gating mechanism is introduced for dynamically selecting and weighting high-frequency and low-frequency component features to achieve adaptive feature fusion. However, during the weight generation process of the gating network, the lack of constraints on the distribution of feature weights may lead to redundant weight distribution. Therefore, we employ the gating selection loss to regularize the distribution of gating weights, ensuring that the network focuses on learning critical features. The weights $g \in \mathbb {R}^{batch \times 1 \times h_{F_{\text {fu}}} \times w_{F_{\text {fu}}}}$ generated by the gating network serve as an adaptive feature selection mask, which is used to weight and fuse high-frequency and low-frequency features. To constrain the distribution of the weights, we suppress redundant information by limiting the entropy of the weight distribution. The definition of the gating selection loss is as follows

$$\begin{aligned} \mathcal {L}_{\text {dt}_{\text {gate}}} = -\frac{1}{N} \sum _{n=1}^{N} \sum _{i=1}^{h_{\mathcal {F}_{\text {fu}}} \cdot w_{\mathcal {F}_{\text {fu}}}} g_n^i \cdot \log (g_n^i + \varepsilon ) \end{aligned}$$

(8)

Among them, $g_n^i$ represents the gating weight at position i in the n-th sample, $\epsilon$ is a small positive number used to prevent instability in numerical computations, $h_{\mathcal {F}_{\text {fu}}}$ is the height of the fusion features, and $w_{\mathcal {F}_{\text {fu}}}$ is the width of the fusion features. Therefore, the final loss of the detail student is expressed as

$$\begin{aligned} \mathcal {L}_\text {dt} = \lambda _1 \mathcal {L}_{\text {dt}_{rec}} + \lambda _2 \mathcal {L}_{\text {dt}_{FreqCC}} + \lambda _3 \mathcal {L}_{\text {dt}_{gate}} \end{aligned}$$

(9)

Pixel and image anomaly scoring

According to Equation (1) and Equation (3), the model can obtain anomaly score maps $M_{\text {str}}^{i}$ and $M_{\text {dt}}^{i}$ from the i-th layer of the structural student and the detail student. Each element represents the discrepancy in structural or detailed feature characteristics of the image at that location. To accurately accomplish the detection and localization of missing anomalies, each score map is first up-sampled to the resolution of the input image and the structural student and detail student scores are then combined element-wise. Therefore, for an input image I, its final anomaly score map is the normalized combination of the results from the two types of students

$$\begin{aligned} M(I) = \frac{M_{\text {str}} - \mu _{\text {str}}}{\sigma _{\text {str}}} + \frac{M_{\text {dt}} - \mu _{\text {dt}}}{\sigma _{\text {dt}}} \end{aligned}$$

(10)

where

$$\begin{aligned} M_{\text {str}} = \sum _{i=1}^3 \Psi (M_{\text {str}}^i), \!\!\!\!\quad M_{\text {dt}} = \sum _{i=1}^3 \Psi (M_{\text {dt}}^i) \end{aligned}$$

(11)

Here, $\mu$ and $\sigma$ represent the mean and standard deviation values, respectively, which are computed on the validation set, $\Psi$ denotes bilinear up-sampling operations.

Experiments and results analysis

Dataset description

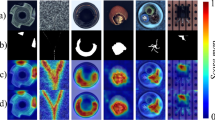
To evaluate the performance of BSDRD in magnetic tile surface defect localization and detection, extensive experiments were carried out in the magnetic tile dataset⁵⁵. This dataset, as shown in Fig. 5, released by the Institute of Automation, Chinese Academy of Sciences, includes six categories of magnetic tile surface defects: free (no defect), blowhole, break, crack, fray, and uneven. Among the five types of anomalies, the most challenging categories are blowhole, fray, and uneven, as shown in Fig. 6. For blowhole, the anomalies are typically small and irregular in shape, making them difficult to distinguish from other regions in a complex background. In some images, the pore area closely resembles the normal region. Fray typically appears as surface wear in localized areas, often showing irregular grayscale changes and lacking clear boundaries. As for uneven, it refers to areas with inconsistent texture or gloss, which may manifest as uneven brightness, uneven color distribution, etc. Some areas inside uneven may appear very similar to the normal image, affecting detection accuracy. The number of images in each category is 952, 115, 85, 57, 32, and 103, respectively, as shown in Table 1. The dataset exhibits a significant imbalance between defect and non-defect images, with a total of 392 defect images and 952 non-defect images.

Fig. 5

Magnetic tile surface defects types and pixel-level ground truth annotation examples. GT refers to a reference label that accurately marks the position and shape of abnormal areas in an image.

Fig. 6

Challenging image examples of surface defects in Magnetic tiles. We have made simple annotations on these examples. These defect areas are not only difficult to distinguish, but also very similar to some areas of normal images.

Table 1 The number of normal images and various types of defect images in the dataset used.

Fig. 7

Dataset segmentation of magnetic tiles defect images..

In this study, we adopted an unsupervised learning approach, where the training set contains only defect-free images, while the validation and test sets include both defect-free images and images with five different types of defects. Since the teacher network T is pre-trained on a large-scale natural image dataset, the proposed model demonstrates robust performance in handling small sample sizes and imbalanced datasets. We did not apply any data augmentation to either defect-free or defective images but instead performed a random split of the dataset, with the splitting results shown in Fig. 7. Furthermore, to enhance the robustness and reliability of the experimental results, we employed the Monte Carlo sampling method to randomly split the dataset three times. This strategy helps mitigate the bias introduced by a single split, ensuring the stability and statistical significance of the model’s performance evaluation.

Implementation details

Experimental Training Setup. The hardware environment for this study consists of a Windows 11 operating system, an AMD Ryzen 7 5800H with Radeon Graphics processor, and an NVIDIA GeForce RTX 3060 GPU. The network was built using Python 3.8.19, PyTorch framework 2.0.0, and CUDA 11.8. The training parameters of the network model are as follows: the learning rate was set to 0.001, following the default value of Aadm, with 200 epochs of training, and a batch size of 8 images per iteration. For the parameters in formula (9), we set $\lambda _1$ to 1.1, $\lambda _2$ to 0.6, and $\lambda _3$ to 0.8. The experimental parameter configuration is shown in Table 2 below.

Table 2 Experimental environment and parameters.

Evaluation Metrics: We use Image AUROC, Pixel AUROC, Pixel AUPRO, Image F1 and Image ACC to evaluate the performance of image anomaly detection and localization.

Image AUROC: Image-level AUROC⁵⁶ assesses the model’s performance in detecting anomalies at the overall image level by determining whether each sample is correctly classified as normal or anomalous. Unlike pixel-level AUROC, which evaluates the model’s classification capability for each pixel in the image, image-level AUROC focuses on distinguishing normal and anomalous categories at the image level.

Pixel AUROC: Unlike image-level AUROC, pixel-level AUROC focuses on analyzing the model’s performance at the pixel level. Pixel-level AUROC evaluates the model’s detection performance in local image regions by examining whether each pixel is correctly classified as normal or anomalous. Compared to image-level AUROC, pixel-level AUROC provides a more detailed performance evaluation, accurately reflecting the model’s performance in different regions of the image. This fine-grained evaluation method has significant application value in tasks that require high precision in locating anomalous positions.

Pixel AUPRO: Unlike Pixel AUROC, Pixel AUPRO focuses on analyzing the model’s performance at the region level. Pixel AUPRO evaluates the model’s localization effect in local image regions by examining the overlap between the predicted anomalous regions and the ground truth annotated anomalous regions. With this metric, the model can be more accurately evaluated for its ability to precisely identify the location and extent of anomalous regions, even in complex backgrounds.

Image F1: Image F1 is an important indicator for measuring image-level classification performance. It is the harmonic mean of precision and recall. The higher the F1 value, the better the balance of the model in identifying positive and negative categories in the image. This indicator is very suitable for evaluating the classification effect of the model when dealing with unbalanced data sets, especially when the positive and negative samples are unbalanced.

Image ACC: Image ACC is a commonly used indicator to measure the performance of image classification models. It indicates the proportion of images that are correctly classified by the model. ACC calculates the ratio of the number of samples that the model predicts correctly to the total number of samples. Image ACC provides an intuitive way to measure the overall classification performance of the model, reflecting the model’s ability to correctly classify all categories.

Fig. 8

Qualitative examples for each category. Abnormalities from top to bottom: Blowhole, Fray, Crack, Break, Uneven, and Free. We presented the detection results of seven advanced methods for three prototypes of AD work recently.

Results on magnetic tile dataset

In this study, we compare the proposed architecture with state-of-the-art models in the anomaly detection (AD) field, covering three recent prototypes: reconstruction-based methods, embedding-based methods, and synthesis-based methods. We randomly select predictions from the proposed anomaly detection model in the test set and compare them with advanced models such as PBAS, CKAAD, and RD4AD, as shown in Fig. 8. From the figure, it is clear that our proposed model performs better than other unsupervised anomaly detection models in predicting defect areas. The boundaries of the areas predicted by our model are closer to the actual anomaly boundaries. While most models cannot accurately and continuously predict the anomaly areas, the proposed detection network still satisfies the prediction requirements. Although our model did not completely detect all areas of fray and uneven, it managed to more accurately capture the boundaries of the anomaly regions. Moreover, our model is able to more accurately capture subtle defects, rather than just capturing the rough outlines of minor imperfections.

Table 3 Abnormal detection and localization results on magnetic tiles.

As shown in Table 3, the detection network proposed in this paper performs excellently in most evaluation metrics, especially in Pixel Aupro and Image F1. Specifically, in the Image Auroc metric, the proposed method achieves a score of 0.974, significantly higher than other methods, demonstrating its superior performance in image-level anomaly detection. In the Pixel Auroc and Pixel Aupro metrics, the proposed method scores 0.802 and 0.793, respectively, both of which are at a high level, indicating stable performance in pixel-level anomaly detection and localization. In the Image F1 and Image ACC metrics, which are related to image-level classification, the proposed method scores 0.972 and 0.957, further verifying its outstanding performance in overall image anomaly detection. Compared to other methods, the proposed detection network stands out in multiple key metrics, particularly in handling complex backgrounds and subtle defects, demonstrating its strong anomaly detection and localization ability. In terms of computational complexity, the BSDRD requires 133.23 GFLOPs. This is lower than some existing methods, indicating a balanced trade-off between accuracy and efficiency. The model contains 101.08 M parameters, which ensures sufficient representational capacity to capture complex defect patterns while maintaining a reasonable model size.

Fig. 9

The results examples for the ablation studies of the proposed modules on magnetic tile dataset.

Table 4 Evaluation metrics comparison.

Ablation studies and discussion

To demonstrate the capability of the proposed dual-student architecture and multi-level frequency-domain gated fusion loss function in capturing fine-grained, gradient, or irregular textures in complex environments, we used the trainable One-Class Bottleneck Embedding module proposed by Deng et al.²⁵ as the baseline, and validated the effectiveness of ASFF, $\text {WSFFN}_{\text {dt}}$, and the multi-dimensional feature gated fusion loss function, with numerical results reported in Table 4. Our trainable dual-student architecture strikes a balance between global and subtle defects, enabling the extraction, fusion, and compression of rich features for more accurate defect detection and localization.

As shown in Fig. 9 and Table 4, the visual results of the ablation study indicate that using only the detail student as the student model tends to emphasize the contour of defects while missing larger structural anomalies such as break and uneven. Although detail student aims to enhance the extracy of specific high-frequency features, it may not effectively reconstruct broader and more structured characteristics within the image, especially in complex backgrounds. Replacing the ASFF method in the baseline network did not lead to significant improvements in detection performance. From figures (D) to (H), we conducted ablation studies on the modules within the detail student. Since the detail student applies wavelet transform to high-frequency feature maps, processes them through various modules, and finally combines the results via a gating fusion network, five experiments from (D) to (H) retained loss functions $\mathcal {L}_{\text {dt}_{\text {rec}}}$ and $\mathcal {L}_{\text {dt}_{\text {gate}}}$. Significant improvements are observed in Figures (F) and (H), along with their corresponding metrics. One reason for this improvement is the MBF-Enhance module, which performs multi-branch analysis and enhancement on high-frequency features. This helps the detail student better capture fine-grained and irregular texture features. In images with complex background textures, defects often resemble the background and can be easily overlooked. The MBF-Enhance module analyzes and fuses high-frequency features from multiple directions, extracting and strengthening important high-frequency information, thereby enabling the identification of abnormal regions even in complex backgrounds. Additionally, as shown in (H) of Fig. 9, the introduction of the $\mathcal {L}_{\text {dt}_{\text {FreqCC}}}$ further enhances the model’s ability to capture frequency characteristics. By analyzing and comparing low-frequency and high-frequency components in the frequency domain, this loss ensures the extraction of critical features across different frequency levels. As a result, the model can more accurately distinguish between these hierarchical features, reducing interference between low-frequency and high-frequency information. The BSDRD framework benefits from the complementary strengths of each model: the struct student handles global structural anomalies, while the detail student excels at detecting fine textures and subtle irregularities. This dual-strategy approach ensures effective detection of both types of anomalies. With the integration of the $\text {WSFFN}_{\text {dt}}$ and the MD-GFLoss, our method achieves improved edge detection of defects and precise localization of regions that are highly similar to the background texture.

Table 5 Quantitative comparison with different backbones.

Fig. 10

The impact of different backbone networks on model performance.

Table 5 and Fig. 10 provide a qualitative comparison of various backbone networks employed as teacher models. In our model, WResNet50 is employed as the backbone. While deeper networks, such as ResNet101, generally offer stronger representation capabilities due to their increased depth and complexity, they also demand more computational resources—such as memory and processing power—leading to higher training and inference costs. Moreover, deeper networks are more prone to overfitting, especially when the available training data is limited in size or diversity. On the other hand, shallower backbones like ResNet18 suffer from limited depth and capacity, resulting in smaller receptive fields and an inability to learn sufficiently abstract high-level semantic features. This often leads to underfitting when dealing with complex images. In contrast, WResNet50 maintains a more balanced architecture. By widening the channel dimensions of the intermediate convolutions within each Bottleneck block, it significantly enhances both model capacity and receptive field, allowing for more effective capture of structural and detailed information. It is worth noting that regardless of whether a more compact or a deeper backbone is used, our BSDRD framework consistently achieves commendable performance.

Fig. 11

AITEX dataset sampling images and mask diagrams. (A) NODefect images. (B) Defect images. The fabric defects are marked with red boxes.

Comparison of experiments on different datasets

To evaluate the generalization capability of the proposed method, BSDRD conducted experiments on the publicly available AITEX⁵⁷ dataset. This dataset comprises 245 images with a resolution of $4096 \times 256$ pixels. It is composed of two main subsets: a set of 140 defect-free reference images and a set of 105 images containing common textile defects encountered in industrial settings. The defect-free subset includes seven distinct fabric textures, with 20 images provided for each texture type. The defective image set captures a variety of typical fabric imperfections, reflecting real-world scenarios in the textile industry. Importantly, the AITEX dataset provides pixel-level segmentation masks for all defective images, where white pixels indicate defective regions and black pixels correspond to normal areas. These ground-truth annotations facilitate accurate evaluation of detection and localization performance. An illustrative example is shown in Fig. 11.

The AITEX dataset also presents characteristics of a small sample size and imbalance between classes. In our experiments, no data augmentation techniques were applied to either defect-free or defective images. The dataset was randomly divided as follows: 100 defect-free images for training; 20 defect-free images in both the validation and test sets; and 52 defective images in the validation set versus 53 in the test set. During training, consistent with experiments on the magnetic tile dataset, images were resized to $256 \times 256$ pixels. The learning rate was set at 0.001, with the number of epochs fixed at 200. A batch size of 8 images was used. Despite the AITEX dataset’s emphasis on subtle defects and complex backgrounds—contrary to the magnetic tile dataset, which focuses on defects similar to their background—our experimental results shown in Fig. 12 and Table 6 indicate strong performance of BSDRD on the AITEX dataset. These findings highlight the model’s capability in identifying minor defects and demonstrate its generalization ability across different contexts.

Fig. 12

Visualization of detection results. GT and BSDRD denote the ground truth and the result predicted by BSDRD, respectively. Defects in GT and visualization results are marked with red boxes..

Table 6 Abnormal detection and localization results on magnetic tiles.

Conclusion

This paper explores a novel dual-student reverse knowledge distillation framework based on reverse distillation and a multi-dimensional feature gated fusion loss. The model for defect detection of magnetic tile images and has a strong ability to capture complex textures, gradients, and irregular defects. The goal of the structural student is to reconstruct low-level features and capture overall structural defects. The detail student is more sensitive to details and texture differences. The proposed multi-dimensional feature gated fusion loss further improves the model’s selectivity for key features and sensitivity to abnormal areas. Experiments show that the method proposed in this paper has achieved significant improvements in both image-level and pixel-level indicators in the task of surface defect detection and positioning of magnetic tiles.

Although our method has achieved remarkable results in unsupervised magnet tiles surface defect detection and localization, model training still requires a large amount of data samples. However, in industrial applications, obtaining samples and annotating information is a big challenge. Therefore, it is of great practical significance to study how to improve the generalization ability of the model with limited samples. In the next phase of our research, we intend to utilize advanced generative techniques to augment the training dataset, thereby improving the model’s performance in anomaly detection tasks under small-sample conditions.