ALDP-FL for adaptive local differential privacy in federated learning

Abstract

Federated learning, as an emerging distributed learning framework, enables model training without compromising user data privacy. However, malicious attackers may still infer sensitive user information by analyzing model updates during the federated learning process. To address this, this paper proposes an Adaptive Localized Differential Privacy Federated Learning (ALDP-FL) method. This approach dynamically sets the clipping threshold for each network layer's updates based on the historical moving average of their $L_2$-norm, thereby injecting adaptive noise into each layer. Additionally, a bounded perturbation mechanism is designed to minimize the impact of the added noise on model accuracy. A privacy analysis of the method is provided. Finally, experiments on the MNIST, Fashion MNIST, and CIFAR-10 datasets demonstrate the effectiveness and practicality of the proposed method. Specifically, ALDP-FL achieves an average improvement of over 10% across all evaluation metrics: Accuracy increases by 10.57%, Precision by 10.64%, Recall by 10.52%, and F1 Score by 10.64%. Regarding the reconstructed images under the iDLG attack, the average improvement rates in MSE and SSIM reach 391.2% and –85.4%, respectively, significantly outperforming all other comparison methods.

Introduction

In today's data-driven era, the tension between privacy protection and data sharing becomes increasingly prominent¹. Many traditional machine learning approaches² rely on centralized data storage and processing, which can enhance model performance³. However, in sensitive fields such as healthcare, finance, and the Internet of Things, data often exhibits data silos due to privacy regulations or commercial confidentiality, making cross-institutional sharing difficult⁴. Consequently, how to leverage massive datasets for model training while safeguarding user privacy has become a significant research challenge.⁵

Federated Learning (FL)⁶, as an emerging distributed machine learning framework, enables model training across multiple user devices without centralizing data, effectively protecting user privacy^7,8,9. Nonetheless, studies show that despite FL providing a layer of privacy protection¹⁰, it still faces threats such as model inversion attacks, membership inference attacks, and gradient leakage. Attackers can analyze intermediate parameters to infer sensitive information from original training data, making privacy preservation a critical bottleneck for deploying FL systems^11,12. Yin¹³ et al. categorize potential privacy leakage risks into five fundamental aspects: attacker, attack method, attack timing, attack location, and attack motivation. Gupta¹⁴ et al. proposed a data poisoning attack, which reverses the benign model's loss function to degrade the global model's performance. Gu¹⁵ et al. introduced CS-MIA, a novel membership inference attack based on prediction confidence sequences, posing serious privacy threats to FL. Zhu¹⁶ et al. demonstrated that private data could be obtained from publicly shared gradients, referring to this type of privacy breach as gradient deep leakage.

Currently, privacy enhancement techniques for FL primarily fall into three categories: Differential Privacy¹⁷ (DP), Homomorphic Encryption, and Secure Multi-Party Computation¹⁸. Differential privacy adds random noise to data or model outputs to hide individual information¹⁹. However, its noise injection often slows convergence and reduces accuracy, especially under non-i.i.d. data distributions²⁰, making it challenging to balance privacy budgets and model utility. Homomorphic encryption and secure multi-party computation provide strong cryptographic guarantees but incur high computational and communication overhead, limiting their applicability to large-scale deep neural network training²¹.

This paper mainly investigates the application of differential privacy to address privacy and security issues in federated learning. Existing research includes McMahan²² et al., who first applied differential privacy in FL by adding Gaussian noise to the aggregated model at the central server after weighted parameter aggregation. However, they did not consider whether the central server is honest or trustworthy. Yang²³ et al. proposed GFL-ALDPA, a gradient-compressed federated learning framework based on adaptive local differential privacy budget allocation. They developed a novel adaptive privacy budget allocation scheme based on communication rounds to reduce privacy budget wastage and model noise. By allocating different privacy budgets to distinct communication rounds during training, this approach maximizes the utilization of limited privacy budgets while enhancing model accuracy. Moreover, they introduced a dimension reduction-based gradient compression mechanism that simultaneously reduces communication costs, overall noise magnitude, and total privacy budget consumption of the model, thereby ensuring accuracy under specified privacy protection guarantees. Truex²⁴ et al. developed the LDP-Fed local differential privacy method, which introduces privacy protection during local training by perturbing gradients, achieving localized differential privacy. They employed fixed gradient clipping and fixed noise addition. Yang²⁵ et al. introduced Fed-DPA, which uses a layer-wise Fisher information-based dynamic personalized strategy to achieve flexible personalization while reducing noise impact. Most current research focuses on static defenses against single attack scenarios, lacking systematic protection against multi-layer attack chains in dynamic adversarial environments. This fragmentation results in existing solutions facing dilemmas of either over-protection leading to performance loss or incomplete defenses leaving vulnerabilities in actual deployment.

To address the aforementioned challenges, this paper proposes a novel adaptive local differential privacy federated learning method. This method innovatively employs a sliding window mechanism to introduce adaptive noise for clients. The incorporation of the sliding window mechanism not only maintains model training accuracy but also integrates adaptive differential privacy protection into the data, effectively addressing the limitations of existing approaches.

Furthermore, to mitigate the impact of differential privacy on model performance, this study designs a bounded perturbation mechanism. A bounded perturbation function $B(\sigma , \epsilon , \eta )$, composed of the variance of added noise, the privacy budget of differential privacy, and a bounding factor, is utilized to constrain the range of noise injected into the data. This function organically combines these parameters to enhance the efficiency of differential privacy protection.We conducted three sets of experiments on the MNIST and Fashion MNIST datasets to validate the effectiveness and practicality of the ALDP-FL method.

In summary, this paper makes the following contributions:

• (1) Proposes an Adaptive Local Differential Privacy Federated Learning (ALDP-FL) method, which dynamically sets the clipping threshold for each network layer based on the historical moving average of the $L_2$ norms of layer updates, adding adaptive noise accordingly.

• (2) Designs a bounded perturbation mechanism that constrains the noise range to reduce the accuracy loss of the federated model caused by local differential privacy.

• (3) Through extensive experiments on MNIST, Fashion MNIST and CIFAR-10 datasets, we demonstrate the effectiveness, scalability, and practicality of our method. Results show significant improvements in privacy-utility trade-offs compared to state-of-the-art baselines.

Related work

Federated learning acts as a distributed machine learning framework, where models are trained locally and only model parameters are uploaded to the server, significantly reducing the risks of data transmission and leakage. However, despite this, federated learning still faces various privacy and security challenges, such as model inversion, membership inference, and data poisoning²⁶. Li²⁷ et al. categorized existing research on model inversion attacks in FL into two types: update-based attacks, which utilize one or more historical versions of the target model to infer membership information; and trend-based attacks, which analyze the trajectory of specific metrics to determine membership status. Zhao²⁸ et al. discovered that sharing gradients indeed leaks the true labels, and they proposed a simple yet reliable method to extract accurate data from the gradients. Their method can reliably extract the true labels, and they named it the improved DLG (iDLG). Their method is applicable to any differentiable model trained with cross-entropy loss on one-hot labels. They mathematically explained how their method extracts the true labels from gradients and demonstrated its advantages over DLG through experiments. Khraisat²⁹ et al. investigated targeted data poisoning attacks in FL systems, where a small fraction of malicious participants compromise the global model through updates with mislabeled data. Their findings reveal that even a limited number of malicious participants significantly degrades classification accuracy and recall, particularly when attacks concentrate on specific classes. They also examined both the duration and timing of these attacks during early and late training rounds, highlighting the impact of malicious participant availability on attack effectiveness.

The above studies demonstrate that federated learning has many security issues. Researchers have proposed some corresponding solutions. Depending on different attack types, they suggest techniques³⁰ such as encryption, differential privacy, and anomaly detection to safeguard the security of federated learning. Tripathy³¹ et al. proposed the HalfFedLearn framework, which uses homomorphic encryption and local horizontal data partitioning to address challenges such as slow convergence, high computational and communication costs, and the security of parameter sharing. They leveraged the inherent distribution of the dataset, employed horizontal data partitioning based on data sensitivity, and implemented selective privacy protection for private data samples using homomorphic encryption. While homomorphic encryption provides robust protection for data privacy, it also consumes significant computational resources when performing operations on encrypted data³². The volume of encrypted data expands substantially, leading to increased bandwidth requirements for transmission and higher storage costs³³. This challenge is particularly pronounced in federated learning scenarios, which require frequent exchanges of gradients or model updates³⁴. Furthermore, in multi-party settings, strict security mechanisms are essential for key generation, distribution, updating, and revocation³⁵. If keys are compromised, the security of all encrypted data would be jeopardized, posing additional challenges to federated learning systems.

The use of differential privacy (DP) technology to protect privacy in federated learning³⁶ addresses a series of issues caused by homomorphic encryption (HE). By adding controlled noise (e.g., Laplace noise, Gaussian noise)³⁷ during the local training or parameter aggregation phase, differential privacy prevents attackers from inferring individual data through gradient analysis. Xie³⁸ et al. proposed a new privacy-preserving federated learning framework, enhanced by adaptive differential privacy, to achieve secure medical data collaboration. They introduced a dual-layer privacy protection mechanism combining local and central differential privacy, dynamically adjusting the allocation of privacy budgets based on training progress and data sensitivity. The framework implements a hierarchical architecture where edge servers perform preliminary aggregation to reduce communication overhead and enhance privacy protection. A novel adaptive privacy budget allocation strategy was developed to optimize the privacy-utility trade-off throughout the training process.

While differential privacy enhances data privacy in federated learning by adding noise, this approach introduces bias, particularly when data is sparse or the privacy budget is small³⁹. Such bias can slow down model convergence or significantly degrade final accuracy. Additionally, to prevent noise amplification, gradient norm clipping⁴⁰ must be applied. However, selecting appropriate clipping thresholds requires repeated experimentation and may introduce clipping bias⁴¹. Furthermore, in multi-round training, the privacy budget must be dynamically allocated for each round to avoid exceeding cumulative privacy leakage thresholds⁴². These challenges highlight the complexity of jointly optimizing and tuning parameters such as⁴³ privacy budgets, noise distributions, and clipping thresholds, which often leads to prohibitive debugging costs in practical implementations.Wang⁴⁴ et al. proposed a novel adaptive differential privacy method with feedback regulation, called FedFR-ADP. First, they employed Earth Mover's Distance (EMD) to measure the data heterogeneity of each client and adaptively applied Gaussian noise based on the degree of heterogeneity, making the noise addition more targeted and effective. Second, they introduced a feedback regulation mechanism to dynamically adjust the privacy budget based on the error feedback of the global model, further enhancing the model's performance. Talaei⁴⁵ et al. proposed injecting adaptive noise into FL based on the relative importance of data features. They first introduced two effective methods for prioritizing features in deep neural network models and then perturbed the model weights based on this information. Specifically, they explored whether the idea of adding more noise to less important parameters and less noise to more important parameters could effectively preserve model accuracy while protecting privacy. Their experiments confirmed this claim under certain conditions. The amount of noise injected, the proportion of parameters involved, and the number of global iterations can significantly alter the output. While carefully selecting parameters by considering dataset attributes can enhance privacy without severely compromising accuracy, incorrect choices may degrade model performance.

Despite significant advancements in existing research addressing privacy and security challenges in federated learning, current frameworks still exhibit notable limitations. For instance, homomorphic encryption-based approaches suffer from computational resource inefficiency, excessive communication overhead, and risks of key leakage. Meanwhile, differential privacy-based methods face challenges in balancing privacy budget allocation, setting appropriate clipping thresholds, and optimizing noise distributions. This study aims to enhance privacy protection in federated learning through differential privacy techniques. Specifically, we propose an adaptive clipping threshold mechanism to dynamically adjust noise injection, thereby minimizing the adverse impact of noise on model performance while ensuring robust data privacy safeguards.

Overview of federated learning

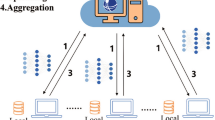
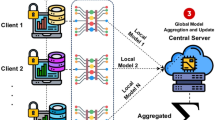
Federated learning is a privacy-preserving distributed collaborative learning framework⁴⁶, primarily aimed at achieving joint model training across multiple participants without sharing raw data, as shown in Fig. 1 of its framework.

Fig. 1

Federated learning framework.

This approach employs decentralized local computation and parameter aggregation mechanisms to effectively mitigate data silo issues while ensuring privacy compliance⁴⁷. Assuming the system involves $K$ participants, with the $k$-th participant possessing a private dataset $D_k$ of size $n_k$, and the total global sample size being $N = \sum _{k=1}^K n_k$. The optimization objective of federated learning⁴⁸ is to minimize the weighted global empirical risk:

$$\begin{aligned} \min F(\theta )=E_{k \ P}\left[ F_k(\theta )\right] =\sum _{k=1}^K \frac{n_k}{N} F_k(\theta ) \end{aligned}$$

(1)

Among them, $F_{i}(\theta ) = \frac{1}{n_{k}} \sum _{(x_{i,j}; y_{i,j}) \in D_{k}} \ell (x_{i,j}; y_{i,j}; \theta )$ represents the empirical risk function for the $k$-th local dataset, where $\ell (x_{i,j}; y_{i,j}; \theta )$ denotes the local loss function for data point $(x_{i,j}, y_{i,j})$, the P subset involves participant data with weighted contributions.

The federated learning process can be divided into three phases. Local model updates⁴⁹: Each participant performs model updates based on their local private data, starting from the current global model, and executes gradient descent steps. Parameter aggregation: After the participants' updates are uploaded to the server, the server executes the model aggregation algorithm, merging the updates from each participant into a global model update. This process yields a new global model. Model synchronization and iteration: After updating, the global model parameters are broadcast back to all participants. This process repeats until convergence criteria are met, such as reaching a predefined number of communication rounds or achieving desired accuracy.

Local differential privacy

Local Differential Privacy⁵⁰ (LDP) is a distributed privacy-preserving model that fundamentally involves users directly perturbing sensitive data on their local devices before submitting it to a server for statistical analysis or model training. Unlike centralized differential privacy, where data is collected first and then anonymized, LDP ensures that the privacy of individual data points is protected even before data transmission. It is particularly suitable for IoT, federated learning, and various distributed scenarios.

The Gaussian Mechanism⁵¹, as an example of an LDP method, adds Gaussian noise to continuous data to achieve privacy guarantees while maintaining data utility. This mechanism supports an ($\epsilon , \delta$)-differential privacy definition, ensuring that for all neighboring datasets $v, v'$ differing in one element, and for all possible output sets $S \subseteq Y$, the following holds:

$$\begin{aligned} \operatorname {Pr}[M(v) \in S] \le e^{\varepsilon } \operatorname {Pr}\left[ M\left( v^{\prime }\right) \in S\right] +\delta \end{aligned}$$

(2)

Among them, $M$ represents the perturbation mechanism, $\epsilon$ is the privacy budget, and $\delta$ is the relaxation parameter. For a user with local data $v \in \mathbb {R}^d$, the released output after perturbation is modeled as $Y = v + N(0, \sigma _{I}^2 I_{d})$, where $N(0, \sigma _{I}^2 I_{d})$ is a multivariate Gaussian noise with mean zero and covariance matrix $\sigma _{I}^2 I_{d}$. The noise scale $\sigma$ is typically determined based on the privacy parameters $\epsilon , \delta$ and the sensitivity $f$, which is set to satisfy the $\sigma \ge \frac{\Delta f}{\epsilon } \sqrt{2 \ln \left( \frac{1.25}{\delta } \right) }$, where $\Delta f = \max _{v, v'} \Vert v - v'\Vert _2$ is the $d$-dimensional $L_2$ sensitivity, and $f$ is the sensitivity of the function under consideration.

Methods

The overall workflow of the ALDP-FL framework

Federated learning, as a distributed machine learning framework, achieves privacy protection through client-side local training and parameter aggregation. However, privacy security issues still persist. The locally updated parameters inherently encode features of the raw data, and attackers can potentially reconstruct users' training samples by analyzing gradient update information. Traditional federated learning architectures assume the central server is honest and trustworthy, but if the central server is curious, clients may inadvertently leak their private data during collaboration.

Algorithm 1

ALDP-FL

To address these issues, this paper proposes an adaptive local differential privacy-based federated learning method. This approach ensures that clients can safely and effectively participate in federated model training with an honest-but-curious central server. Even if an attacker intercepts the transmitted model parameters, the privacy of local data can still be preserved.

The ALDP-FL algorithm is shown as Algorithm 1, The relevant symbols and parameters⁵² involved in this paper are as shown in Table 1. And its workflow is as follows: First, initialize the global model parameters as $\omega _0$, then perform T rounds of iterative training. In each round, the server selects K clients from N clients as participants for that round and distributes the current global model $\omega _t$ to these participants. After local training, each participant returns its model update $\Delta \omega _{t}^{k}$ to the server. The server aggregates all participants' updates by computing the arithmetic mean $\Delta \omega _{t} \leftarrow \frac{1}{K} \sum _{k=1}^{K} \Delta \omega _{t}^{k}$ to obtain the global model update for this round, and correspondingly updates the global model as $\omega _{t+1} \leftarrow \omega _{t} + \Delta \omega _{t}$. This process repeats until T rounds are completed.

The ALDP-FL method framework primarily consists of two parts: the server-side algorithm and the client-side algorithm, with the specific workflow illustrated in Fig. 2. The server-side algorithm is similar to traditional federated learning server algorithms, responsible for initializing model parameters, aggregating data from participating clients, and updating the global model. The client-side algorithm employs an adaptive local differential privacy mechanism designed to ensure the privacy and security of client data.

Fig. 2

ALDP-FL framework process.

The core concept of the adaptive local differential privacy algorithm revolves around adaptivity and localization. Localization refers to performing all differential privacy-related processes locally on the client side, while adaptivity means that the noise perturbation introduced in differential privacy is dynamically adjusted based on the current state of the model. Pruning is a critical technique in differential privacy; choosing the appropriate pruning threshold for protected data is particularly important. Fixed pruning thresholds may lead to excessive information loss and impair model accuracy if set too low, or insufficient privacy guarantees if set too high. The adaptive local differential privacy mechanism dynamically adjusts pruning thresholds for different neural network layers during each iteration, thereby addressing the limitations of fixed thresholds.

Table 1 Relevant symbols and parameters.

To select the pruning threshold for each neural network layer at each iteration, a temporal moving average approach is employed, leveraging the temporal similarity principle. This principle states that system behavior at nearby time points tends to be similar. By using the average change in previous rounds as the current threshold, the method effectively reduces information loss caused by pruning and enables the threshold to be adaptively updated. After determining the pruning threshold, Gaussian noise is added to the updates by incorporating bounded perturbation mechanisms, providing differential privacy guarantees. This not only significantly enhances data privacy but also helps maintain model accuracy.

ALDP-FL client-side algorithm

The client-side algorithm is shown in Algorithm 2, and the flowchart is depicted in Fig. 3. After receiving the model $\omega _t$ sent from the central server, the client initializes the local model $\omega _e \leftarrow \omega _t$, copying the global model parameters $\omega _t$ into the local model $\omega _e$. It then performs E rounds of local training loops, where each round represents a complete local training iteration. In each iteration, gradient descent updates are first applied to each batch d from the local dataset D as follows:$\omega _e' \leftarrow \omega _e - \alpha \nabla L(\omega _e; d)$ where $\alpha$ is the learning rate and $\nabla L$ is the gradient of the loss function L with respect to the model parameters $\omega _e$. Based on the gradient descent update, the parameter update for the current iteration is computed as $\Delta \omega _e = \omega _e' - \omega _e$. The $L_2$ norm of $\Delta \omega _e$ for the current iteration is then calculated and stored in a sliding window H.

The update for each model layer, $\Delta \omega _e$, is clipped using $\text {Clip}_e$ to obtain the clipped update $\Delta \omega _e'$. $\text {Clip}_e$ is a dynamic value, which is calculated based on the average $L_2$ norm of the most recent k updates (where k is the sliding window size), as shown in Fig. 4. When $||\Delta \omega _e||_2 \le \text {Clip}_e$, the update $\Delta \omega _e$ remains unchanged. Otherwise, $\Delta \omega _e$ is clipped to $\text {Clip}_e$.

Algorithm 2

Client-side

Fig. 3

Flowchart of the ADP-FL method client-side process.

Fig. 4

The process of calculating $Clipe_e$.

Based on the local differential privacy definition, in order to ensure that the participants satisfy $(\delta ,\varepsilon )$-differential privacy during local training, Gaussian noise must be added to the clipped update $\Delta \omega _e'$. The standard deviation of the noise is:$\sigma = \frac{\Delta f \sqrt{2 \ln (1.25 / \delta )}}{\varepsilon }$where $\delta$ is the slack parameter of differential privacy and $\varepsilon$ is the privacy budget. Based on the noise standard deviation and the bounded perturbation function B, the differential privacy-protected update is obtained by adding noise to the clipped update $\Delta \omega _e'$ as follows:$\Delta \tilde{\omega }_e \leftarrow \Delta \omega _e^{\prime }+B\left( \sigma , \varepsilon , \eta \right)$ Finally, the model update for the current round is computed as:$\omega _e \leftarrow \omega _e + \Delta \tilde{\omega }_e$. This process repeats for E rounds to complete the local model training. After completing E rounds of local training, the participant's update is calculated as:$\Delta \omega ^k = \omega _e - \omega _t$and this value is returned to the server.

Regarding the $\sigma$ value proposed above, a mathematical proof demonstrating that this value ensures $\Delta \omega ^k$ satisfies $(\delta ,\varepsilon )$-differential privacy will be provided in the following sections. Additionally, the bounded perturbation mechanism B mentioned earlier will be concretely designed and analyzed in subsequent content.

Bounded perturbation mechanisms

The ALDP-FL method proposed in this paper selects the Gaussian distribution as the source of noise for differential privacy. The probability density function of the Gaussian distribution is a symmetric bell-shaped curve. The curve is unimodal, reaching its highest point at the mean and is perfectly symmetric about the mean, meaning the distribution shapes on the left and right sides of the mean are identical. When the mean of the Gaussian distribution is set to 0, zero-mean noise can be added, avoiding systematic bias. However, since the Gaussian distribution has infinite support, its long-tail effect may potentially harm the model's performance. This paper designs a bounded perturbation mechanism to eliminate the possible impact of the long-tail effect of the Gaussian distribution. The added noise is constrained within the bounds of [–b, b].

$$\begin{aligned} b = \frac{e^{\epsilon } - \eta }{e^{\epsilon } + \eta } \end{aligned}$$

(3)

Among them, $\epsilon$ is the privacy-preserving privacy budget, $\eta$ is a superparameter, and $\eta \in (-1, 1)$.

$$\begin{aligned} f(x; \sigma ) = \frac{1}{\sigma \sqrt{2\pi }} e^{-\frac{x^2}{2\sigma ^2}} \end{aligned}$$

(4)

The function $f(x; \sigma )$ represents a high-dimensional probability density function with a mean value of 0 and a standard deviation $\sigma$. Since we are limited to the range of the high-dimensional noise values, we need to normalize the high-dimensional distribution. The normalized high-dimensional probability density function after normalization is defined as $f_b(x; \sigma )$. Here, $Z$ is a normalization constant.

$$\begin{aligned} f_b(x; \sigma ) = {\left\{ \begin{array}{ll} \frac{1}{Z\sigma \sqrt{2\pi }} e^{-\frac{x^2}{2\sigma ^2}}, & -b< x < b \\ 0, & \text {other} \end{array}\right. } \end{aligned}$$

(5)

$$\begin{aligned} Z = \int _{-b}^{b} \frac{1}{\sigma \sqrt{2\pi }} e^{-\frac{x^2}{2\sigma ^2}} dx \end{aligned}$$

(6)

The cumulative distribution function of the standard normal distribution is introduced into the normalization constant.

$$\begin{aligned} Z = \Phi \left( \frac{a}{\sigma }\right) - \Phi \left( -\frac{a}{\sigma }\right) = 2\Phi \left( \frac{a}{\sigma }\right) - 1 \end{aligned}$$

(7)

The standard deviation $\sigma _b^2$ of the truncated normal distribution can be used to estimate the standard deviation $\sigma _b$.

$$\begin{aligned} \sigma _b^2 = \int _{-b}^b x^2 f_b(x) dx = \frac{1}{Z} \int _{-b}^b x^2 e^{-\frac{x^2}{2\sigma ^2}} dx = \frac{\sigma ^2}{Z} \int _{-b}^b \frac{u^2}{\sigma ^2} e^{-\frac{u^2}{2\sigma ^2}} du = \sigma ^2 \left[ 1 - \frac{2 \frac{b}{\sigma } \phi \left( \frac{b}{\sigma } \right) }{2 \Phi \left( \frac{b}{\sigma } \right) - 1} \right] \end{aligned}$$

(8)

According to the standard deviation of the normal distribution, we can use the Hoeffding inequality⁵³ to calculate the deviation of the empirical mean from the true mean of the distribution. Hoeffding inequality is a type of concentration inequality that does not require the assumption of independence and identical distribution of random variables. It estimates the probability that the sample mean deviates from the true mean by a certain amount. Suppose $X_1, X_2, \dots , X_n$ are independent random variables bounded between $a$ and $b$, and their sample mean is $\bar{X} = \frac{1}{n} \sum _{i=1}^n X_i$. Then, for any $\epsilon > 0$, Hoeffding's inequality can be expressed as:

$$\begin{aligned} P(|\overline{X} - E[X]| \ge \epsilon ) \le 2e^{-\frac{2n\epsilon ^{2}}{(d-c)^{2}}} \end{aligned}$$

(9)

Here, $E[X]$ is the expectation of the random variable $X$, and $\epsilon$ is the error bound for the mean estimation.

Since the mean of the truncated Gaussian distribution is zero, $E[X] = 0$. Substituting the range of the truncated Gaussian distribution (-b, b) into Hoeffding's inequality, we obtain:

$$\begin{aligned} P(|\overline{X}| \ge \epsilon ) \le 2e^{-\frac{2n\epsilon ^2}{(2b)^2}} = 2e^{-\frac{n\epsilon ^2}{2b^2}} \end{aligned}$$

(10)

This inequality indicates that, with a fixed probability $\delta$, the sample mean $\bar{X}$ deviates from the true mean 0 with a probability not exceeding $2e^{-\frac{n \varepsilon ^2}{2b^2}}$. For convenience, we can set the confidence level to $\delta$, and solve for the corresponding $\varepsilon$.

$$\begin{aligned} \varepsilon = b \sqrt{\frac{2}{n} \ln \frac{2}{\delta }} \end{aligned}$$

(11)

From the above analysis, it can be concluded that the noise processed by the boundary perturbation mechanism satisfies the high-dimensional Gaussian distribution $(0, \sigma _b^2)$.Moreover, with at least a probability of $1 - \delta$, the average noise value $\bar{X}$ falls within the interval $(-b \sqrt{\frac{2}{n} \ln \frac{1}{\delta }}, b \sqrt{\frac{2}{n} \ln \frac{1}{\delta }})$. Although this method improves the accuracy of the model, it reduces the precision of noise sampling.

Privacy-security analysis

To ensure that the ADP-FL presented in this paper satisfies $(\varepsilon _i, \delta _i)$-privacy, we need to demonstrate that for the corresponding datasets $D$ and $D'$, as well as any output set $S \subseteq R$, the following condition holds:

$$\begin{aligned} \Pr [M(D) \in S] \le e^{\varepsilon _i} \Pr [M(D') \in S] + \delta _i \end{aligned}$$

(12)

Suppose $f(D)$ and $f(D')$ are the outputs of the function $f$ on neighboring datasets $D$ and $D'$. As can be seen from the above text, the sensitivity $\Delta f = |f(D) - f(D')| = \frac{2c}{d}$. The output of the Gaussian mechanism is:

$$\begin{aligned} M(D) = f(D) + Z \end{aligned}$$

(13)

$$\begin{aligned} M(D') = f(D') + Z \end{aligned}$$

(14)

where $Z \sim N(0, \sigma _i^2)$ is a random variable drawn from a Gaussian distribution with mean zero and variance $\sigma _i^2$. Therefore, we need to prove that:

$$\begin{aligned} \int _{S}\frac{1}{\sqrt{2\pi \sigma _{i}^{2}}} \exp \left( -\frac{(x - f(D))^{2}}{2\sigma _{i}^{2}} \right) dx \le e^{\varepsilon _{i}} \int _{S} \frac{1}{\sqrt{2\pi \sigma _{i}^{2}}} \exp \left( -\frac{(x - f(D'))^{2}}{2\sigma _{i}^{2}} \right) dx + \delta _{i} \end{aligned}$$

(15)

Calculate the ratio of probabilities of $M(D)$ and $M(D')$:

$$\begin{aligned} \frac{P_M(x|D)}{P_M(x|D')} = e^{\frac{(f(D)-f(D'))}{\sigma _i^2}\left( x-\frac{f(D)+f(D')}{2}\right) } \end{aligned}$$

(16)

For any chosen $x$, assuming $x$ lies within the interval $(f(D) - \Delta f, f(D) + \Delta f)$, perform boundary analysis on $x = f(D) + \Delta f$.

$$\begin{aligned} \frac{p_M(f(D) - \Delta f | D')}{p_M(f(D) + \Delta f | D)} \approx e^{\frac{\Delta f^2}{2 \sigma _i^2}} \end{aligned}$$

(17)

According to the definition of differential privacy, we need to satisfy:

$$\begin{aligned} \frac{p_M(x | D)}{p_M(x | D')} \le e^{\varepsilon _i} \end{aligned}$$

(18)

Certainly:

$$\begin{aligned} \sigma \ge \frac{\Delta f}{\sqrt{2 \varepsilon _i}} \end{aligned}$$

(19)

To consider the impact of $\delta _i$, we need to use the properties of the Gaussian mechanism:

$$\begin{aligned} Pr\left[ | M(D) - M(D') | > \delta _i \right] \le 2e^{-\frac{\delta _i^2}{2\sigma _i^2}} \end{aligned}$$

(20)

Finally, the lower bound of $\sigma$ is:

$$\begin{aligned} \sigma _i \ge \frac{\Delta f \sqrt{2 \ln (1.25 / \delta _i)}}{\varepsilon _j} \end{aligned}$$

(21)

Therefore, in each addition of Gaussian noise, choose $\sigma _i = \frac{\Delta f \sqrt{2 \ln (1.25 / \delta _i)}}{\varepsilon _i}$, so that the participant's local training process satisfies the differential privacy $(\varepsilon _i, \delta _i)$.

Experiment

Experimental setup

We employed two convolutional neural network models, LeNet and ResNet-18, to test the ALDP-FL method. LeNet consists of a total of 7 layers, including 2 convolutional layers, 2 pooling layers, and 3 fully connected layers. It is a lightweight and simple model, making it suitable for relatively straightforward tasks such as basic image classification. ResNet-18 consists of 18 layers, including 17 convolutional layers and 1 fully connected layer. It is commonly used for more complex image classification tasks due to its deep architecture and ability to handle more intricate patterns.

We utilized three datasets: MNIST, Fashion MNIST, and CIFAR-10. The MNIST dataset contains 70,000 grayscale images of handwritten digits, each 28x28 pixels, with 60,000 images for training and 10,000 for testing. The labels range from 0 to 9, each corresponding to a handwritten digit. The Fashion MNIST dataset also consists of 70,000 grayscale images with the same dimensions as MNIST, with 60,000 for training and 10,000 for testing. However, these images represent 10 different clothing categories, such as T-shirt, Trouser, and Pullover, making it more complex than MNIST. The CIFAR-10 dataset consists of 60,000 color images, each 32x32 pixels with 3 color channels, of which 50,000 are used for training and 10,000 for testing. These images belong to 10 common object categories, such as Airplane, Automobile, and Bird, making the CIFAR-10 dataset more challenging for method evaluation. The hardware platform and environmental parameters used during the experimental training process are shown in Table 2.

Table 2 The hardware platform and environmental parameters.

In our experiments, we set the total number of FL clients, $N = 40$, and the number of participants per global iteration, $K = 10$. We set the total number of global iterations, $T = 80$, and the number of local iterations per participant, $E = 10$. The batch size was set to 128, and the learning rate $\alpha$ was 0.001. For the optimization algorithm, we employed the Adam optimizer, known for its adaptive learning rate capabilities. For the incorporated differential privacy, we set the privacy budget per client, $\epsilon = 4$, and the slack variable $\delta = 1 \times 10^{-7}$.

To verify the effectiveness of the proposed ALDP-FL method, we compared it with existing methods: FedAvg (without differential privacy protection), Fed-DPA, GFL-ALDPA, and LDP-Fed. We designed three sets of experiments:

• (1) Using different models and datasets to validate the impact of the sliding window on performance.

• (2) Comparing the performance of ALDP-FL with state-of-the-art methods across different models and datasets.

• (3) Testing the privacy protection capabilities of different methods through model inversion attacks.

Evaluation metrics

To conduct a quantitative evaluation of ALDP-FL's comprehensive performance, we employed four widely adopted metrics: Accuracy, the most intuitive metric, represents the proportion of correct predictions; Precision measures the accuracy of positive predictions, Recall evaluates the ability to identify positive samples, and F1-score balances both precision and recall.

For evaluating ALDP-FL's privacy-preserving capabilities, we used four established metrics: Mean Squared Error (MSE) calculates the average squared difference between pixel values, with lower values indicating superior reconstruction quality; Peak Signal-to-Noise Ratio (PSNR) measures the ratio of signal to distortion power, being sensitive to uniform distortions but less so to structural ones; Mean Absolute Error (MAE) computes the average absolute difference between pixels, providing an intuitive interpretation of per-pixel error; and Structural Similarity Index (SSIM) assesses luminance, contrast, and structural similarity on a [0,1] scale, with higher values denoting greater similarity and better alignment with human visual perception.

Experimental validation of the impact of sliding window on ALDP-FL performance

This set of experiments aims to explore the optimal sliding window size k for the ALDP-FL method when the local iteration rounds E is 10, under different models and datasets, to achieve the best performance of the global model. We set the range of the sliding window k to [2,5].

The experimental process is illustrated in Fig. 5, where the first row presents the results obtained using the LeNet-5 architecture, and the second row corresponds to ResNet-18. On the MNIST dataset, all configurations converge rapidly within the initial training epochs, achieving accuracies exceeding 90%. As shown in Fig. 5a (top row), LeNet-5 achieves optimal performance when the sliding window size is $k=3$, marginally outperforming other settings. A larger window size ($k=5$) results in a slight decline in accuracy, likely due to the simplicity of the dataset, where excessive contextual information may introduce redundancy rather than benefit learning. In the case of ResNet-18 (Fig. 5a, bottom row), the performance gap across different k values is minimal, though $k=3$ and $k=4$ still yield marginally higher final accuracies, suggesting that moderate window sizes contribute positively even in deeper models.

Fig. 5

Comparison test of different sliding windows.

For the Fashion MNIST dataset (Fig. 5b), which presents greater intra-class variability and visual complexity than MNIST, the influence of window size becomes more pronounced. With LeNet-5, increasing k from 2 to 3 leads to a noticeable improvement in performance; however, further enlargement to $k=4$ or $k=5$ does not result in continued gains and even causes a minor accuracy drop, especially at early stages of training. Notably, $k=5$ produces the lowest accuracy during the initial epochs. This observation suggests that excessive window size may introduce noise and hinder generalization in shallow networks. ResNet-18 demonstrates improved robustness across varying window sizes due to its enhanced representational capacity and residual connections, though $k=3$ remains the most effective setting.

The CIFAR-10 dataset, characterized by complex spatial features and significant inter-class variation, further amplifies the impact of network depth and window configuration (Fig. 5c). LeNet-5 exhibits limited performance, failing to exceed 70% accuracy under any configuration, and the differences between sliding window sizes become more evident. Configurations with $k=3$ and $k=4$ consistently outperform those with $k=2$ and $k=5$. For ResNet-18, all settings surpass 80% accuracy after 80 epochs, with $k=3$ again delivering the best performance. It is worth noting that the performance gap between $k=3$ and $k=5$ is most evident during the initial training phase, indicating that overly large sliding windows may inject high-variance information that negatively affects convergence speed and stability in complex tasks.

In summary, these results demonstrate that the sliding window size is a critical hyperparameter affecting model convergence and generalization, particularly for shallow architectures and complex datasets. Across all datasets and model configurations, a window size of $k=3$ consistently achieves superior or near-optimal results. Smaller window sizes ($k=2$) may lead to insufficient contextual encoding, while larger windows ($k=5$) risk incorporating irrelevant information and increasing overfitting potential. These findings offer empirical evidence to inform the selection of sliding window parameters in context-aware learning scenarios, especially those involving temporal or spatial dependencies.

To further evaluate the impact of sliding window size on model performance, Table 3 reports four key evaluation metrics—Accuracy, Precision, Recall, and F1-score—under different window lengths $k = 2, 3, 4, 5$. As observed from Table 3, both LeNet-5 and ResNet-18 achieve strong performance across all metrics on the MNIST dataset, reflecting the simplicity of this task. LeNet-5 achieves optimal results at $k = 3$, with Accuracy (0.9721), Precision (0.9701), Recall (0.9714), and F1-score (0.9707) all reaching their highest values. As k increases to 5, performance slightly declines. A similar trend is observed in ResNet-18, which performs best at $k = 3$ (Accuracy = 0.9805, F1 = 0.9774), with a slight decrease in all metrics occurring at $k = 5$. These results suggest that for MNIST, a moderate sliding window size like $k = 3$ is most suitable, while overly large windows may introduce redundant spatial information, causing marginal performance degradation.

Table 3 Comparison test of different sliding windows.

On the more complex Fashion MNIST dataset, model sensitivity to window size becomes more pronounced. LeNet-5 achieves its best performance at $k = 3$, with the F1-score increasing from 0.8038 at $k = 2$ to 0.8283 at $k = 3$, showing only a slight improvement at $k = 4$ (0.8333) and a clear decline at $k = 5$ (0.7923), particularly during early training stages. This suggests that an overly large sliding window may introduce noise or irrelevant features, impairing the generalization ability of shallow networks. ResNet-18 also achieves optimal results at $k = 3$ on this dataset (Accuracy = 0.9129, F1 = 0.9111). Although performance at $k = 2$ and $k = 5$ is slightly lower, the model demonstrates greater stability overall while still benefiting from an appropriate window size.

CIFAR-10 is the most challenging of the three datasets due to its greater category diversity and structural complexity. On this task, LeNet-5 performs significantly worse than on the other datasets, with accuracy ranging from 0.5658 to 0.6083, and the best performance again observed at $k = 3$. In contrast, ResNet-18 exhibits substantially better results, achieving an accuracy of 0.8495 and F1-score of 0.8486 at $k = 3$. Although there is a slight performance drop at $k = 4$ and $k = 5$, the overall metrics remain stable. This demonstrates that deep networks are more tolerant to changes in window size, yet $k = 3$ still yields the best results under complex task conditions.

Overall, the results in Table 3 clearly indicate that sliding window size k is a crucial hyperparameter affecting model performance. Across all datasets and model architectures, $k = 3$ consistently achieves optimal or near-optimal performance. Shallow models (e.g., LeNet-5) are more sensitive to changes in window size, while deeper models (e.g., ResNet-18) show greater robustness but still benefit from well-chosen window sizes. A too-small window (e.g., $k = 2$) may lead to insufficient contextual information, while a too-large window (e.g., $k = 5$) may introduce redundancy or noise, increasing the risk of overfitting and slowing convergence.

Performance comparison experiment between ALDP-FL and state-of-the-art methods

In this set of experiments, comparative tests were conducted on the ALDP-FL method against FedAvg, Fed-DPA, GFL-ALDPA, and LDP-Fed methods using different network models and datasets. Based on the previous set of experiments, the sliding window parameter k in the ALDP-FL method was set to 3.

As illustrated in Fig. 6, five methods—Fed-DPA, FedAvg, LDP-Fed, GFL-ALDPA, and ALDP-FL—are compared in terms of test accuracy across three benchmark datasets: MNIST, Fashion MNIST, and CIFAR-10. Two backbone models are employed: LeNet-5 (top row) and ResNet-18 (bottom row).On the MNIST dataset, all methods converge rapidly within the first 20 global epochs, and the accuracy stabilizes quickly. The baseline method FedAvg achieves the best performance in both LeNet-5 and ResNet-18 models, with accuracy consistently exceeding 95%. Among the privacy-preserving approaches, ALDP-FL achieves the best results, followed by GFL-ALDPA, while Fed-DPA remains the weakest. Notably, ALDP-FL significantly narrows the performance gap with FedAvg, especially when using the deeper ResNet-18 model. These results suggest that ALDP-FL achieves a favorable balance between privacy protection and model utility in relatively simple tasks.

Fig. 6

Comparison test of different methods.

The Fashion MNIST dataset poses greater complexity and class similarity. In this case, FedAvg still attains the highest accuracy; however, its advantage over privacy-enhanced methods becomes smaller. ALDP-FL outperforms all other privacy-preserving methods, further closing the gap with FedAvg. GFL-ALDPA ranks second, while Fed-DPA still performs the worst. With ResNet-18, the overall performance improves substantially, and ALDP-FL benefits more significantly from the deep model, yielding faster convergence and higher accuracy. These findings demonstrate that ALDP-FL is more robust to data complexity and scales well with deeper architectures.

CIFAR-10 represents the most challenging task in this study due to its high visual complexity and ambiguous semantic boundaries. The performance differences between methods become more pronounced. FedAvg still achieves the highest accuracy in both models. Among privacy-preserving approaches, ALDP-FL clearly performs best, achieving nearly 85% accuracy under ResNet-18. In contrast, Fed-DPA performs the worst, with accuracy failing to surpass 73% even under the deep model. These results indicate that ALDP-FL maintains strong performance in complex scenarios, making it more applicable to real-world deployments with privacy constraints.

Table 4 further presents the quantitative results of four key evaluation metrics—Accuracy, Precision, Recall, and F1 Score—across the five methods. The experimental results clearly demonstrate that ALDP-FL exhibits significant advantages across multiple performance indicators, with particularly strong performance in complex tasks and deep model architectures. To provide a more intuitive understanding of this advantage, we conducted a comparative analysis of the four core metrics and calculated the average performance improvement of ALDP-FL over other privacy-preserving methods.

Statistical analysis shows that ALDP-FL achieves an average improvement of over 10% in all metrics: Accuracy increases by 10.57%, Precision by 10.64%, Recall by 10.52%, and F1 Score by 10.64%. Notably, in the most challenging dataset—CIFAR-10—ALDP-FL demonstrates a substantial F1 Score improvement of 9.60% over LDP-Fed when using the ResNet18 model. This highlights its effectiveness in handling fine-grained classification tasks and ambiguous object boundaries.

These findings suggest that ALDP-FL not only offers robust privacy protection but also effectively mitigates the performance degradation typically associated with conventional privacy-preserving techniques in image recognition tasks. In contrast, although Fed-DPA implements a basic differential privacy mechanism, it severely compromises model performance, with an average performance drop exceeding 17%. While GFL-ALDPA and LDP-Fed partially alleviate this issue, they still show noticeable deficits in terms of Accuracy and F1 Score.

Table 4 Comparison test of different methods.

In conclusion, ALDP-FL significantly outperforms existing privacy-preserving methods in terms of overall performance while maintaining strong privacy guarantees, making it a promising solution for privacy-sensitive federated learning scenarios.

Privacy protection capability testing experiment based on model inversion attacks

To evaluate the effectiveness of different privacy-preserving methods against reconstruction attacks, this study employs the improved Deep Leakage from Gradients (iDLG) algorithm to perform gradient leakage attacks on ResNet models trained on three benchmark datasets: MNIST, FashionMNIST, and CIFAR-10. The reconstructed images are visualized for comparative analysis. The experimental results are shown in Fig. 7.

Fig. 7

Visual results of the iDLG attack on the three datasets.

From the visualizations, the following observations can be made:In the MNIST dataset, the original images exhibit clearly recognizable digits with sharp edges. Under the FedAvg method, which does not incorporate any privacy protection, the attacker is able to almost perfectly reconstruct the original images, indicating that the model gradients contain a significant amount of recoverable sensitive information. In contrast, when privacy-preserving mechanisms such as Fed-DPA, GLF-ALDPA, LDP-Fed, and ALDP-FL are applied, the quality of the reconstructed images deteriorates significantly. The boundaries become blurred, and in many cases, the digits become unrecognizable. Particularly, ALDP-FL produces the most distorted reconstructions with no discernible digit structure, demonstrating its strong resistance to iDLG attacks.

In the FashionMNIST dataset, the images are more complex than MNIST, containing finer texture information. Similar to MNIST, the reconstructions under FedAvg still retain a relatively high degree of fidelity, with identifiable clothing contours. However, the other privacy methods introduce substantial interference to the reconstruction. Notably, GLF-ALDPA and ALDP-FL severely distort the reconstructed images across many samples, rendering them almost completely noisy and effectively suppressing information leakage.

For the CIFAR-10 dataset, which consists of color images with semantically complex content, a higher robustness against reconstruction is required. The original images clearly depict natural objects such as airplanes, horses, and ships. While FedAvg is still able to partially recover the global color structure of the images, the reconstructions are blurry and lack detail. The privacy-preserving methods, particularly ALDP-FL, demonstrate more effective protection in this scenario. The reconstructed images under ALDP-FL are nearly fully covered by color noise and are visually unrecognizable, exhibiting excellent leakage prevention capabilities.

Overall, the privacy-preserving methods show consistent trends across datasets: for grayscale datasets like MNIST and FashionMNIST, the methods strongly disrupt structural information; for color datasets like CIFAR-10, the defensive effect remains robust. Among these, ALDP-FL consistently achieves the best performance across all three datasets, maximally impairing the reconstructability under iDLG attacks and proving to be an effective approach for safeguarding image privacy.

To further quantify the protective effects of the methods, Table 5 presents four evaluation metrics of reconstructed image quality under iDLG attacks: Mean Squared Error (MSE), Peak Signal-to-Noise Ratio (PSNR), Mean Absolute Error (MAE), and Structural Similarity Index (SSIM). Using FedAvg as the baseline, we calculate the percentage change in performance for ALDP-FL across all metrics:On the MNIST dataset, ALDP-FL increases the MSE to 0.2226 (a 237.6% increase over FedAvg) and reduces the SSIM from 0.5368 to 0.0525 (a 90.% decrease), indicating that the reconstructed images have nearly lost all structural resemblance to the originals.On FashionMNIST, ALDP-FL increases the MSE from 0.0341 to 0.1852 (an increase of 443.7%) and decreases SSIM by 82.6%, further confirming its strong resistance to reconstruction in grayscale image scenarios.For the CIFAR-10 color image dataset, ALDP-FL achieves an MSE of 0.1836 (a 492.3% increase) and reduces SSIM to 0.0808 (an 83.5% decrease). Although MAE decreases, this does not significantly affect the overall structural disruption.These results demonstrate that ALDP-FL effectively increases the unrecognizability of reconstructed images across all three datasets. Specifically, its average improvement in MSE and SSIM reaches 391.2% and -85.4%, respectively, substantially outperforming all other compared methods.

Table 5 Privacy evaluation metrics between original and reconstructed images under the iDLG attack.

In summary, ALDP-FL exhibits the most robust and comprehensive defense performance against gradient-based reconstruction attacks. It significantly increase reconstruction error while destroying structural similarity, making it a highly effective and generally applicable solution for enhancing privacy protection in federated learning.

Conclusion

This paper addresses privacy leakage issues in federated learning by proposing ALDP-FL, a federated learning method based on adaptive local differential privacy. The algorithm is designed to mitigate privacy risks caused by malicious interception of sensitive data by central servers, real-time distributed attackers, or other adversaries. Additionally, a bounded noise mechanism is introduced to reduce the impact of noise on the accuracy of the global model. A series of experiments validate the effectiveness and practicality of ALDP-FL.

Future work will explore rational allocation of privacy budgets to enhance global model accuracy while preserving participant privacy, as well as extending differentially private federated learning methods to more real-world applications.