Introduction

Renewable energies have become as one of the most valuable solutions to the modern energy problem. Some advantages are to protect the environment, inexpensive, renewable, available everywhere, and cannot be depleted. From here came the idea of compulsory exploitation of these energies as much as possible.

The hybrid system refers to the use of more than one source of energy at the same time. Solar and wind energy are two of the most popular green energies, and to fully utilize them, we must use storage units to store excess energy and use it when demand exceeds production. Energy storage is necessary for solving challenges in power generation such as intermittent and demand fluctuations. Various technologies have been developed for efficient energy storage. Lead-acid batteries are highly durable and cost-effective, widely used in vehicles and continuous power supplies1. Hydrogen storage systems collect and store hydrogen for later conversion into electricity through fuel cells2. Supercapacitors, or ultra-capacitors, are excellent at rapidly storing and releasing energy due to their electrostatic operation. They offer high power density and prolonged cycle life, making them ideal for applications demanding rapid energy peaks3. Superconducting Magnetic Energy Storage (SMES), based on superconductivity principles, stores energy in a magnetic field for swift release, making it ideal for applications requiring rapid response times and high-power quality4. Together, these technologies showcase a dynamic range of options in energy storage, each addressing specific needs in the evolving energy ecosystem.

The configuration of a multi-source power system can vary widely, and its structure often depends heavily on the specific situation in which it is applied. For instance, some configurations are integrated with the grid, as discussed in references5,6,7,8,9, while others are designed to function in isolation, as detailed in references10,11,12. The fact that these systems can be configured in a variety of ways demonstrates their flexibility and the broad range of applications they can serve. To further understand and optimize these systems, various hybrid system architectures are explored and analysed in the references13,14. These studies provide valuable insights into the advantages and challenges of multi-source power systems, paving the way for future advancements in this exciting field of research. To capture the maximum power energy from the wind turbine and solar panels, many algorithms allow raising the efficiency of these sources called Maximum Power Point Tracking (MPPT) strategies. For example, some of the MPPT techniques in wind energy are the TSR (Tip Speed Ratio) technique15, Optimal Torque Control (OTC) technique 16, and Power Signal Feedback (PSF) MPPT17. Some techniques for extracting maximum energy from solar panels are P&O MPPT18, Incremental conductance method19,20, and many others. The hybridization between solar and wind energy is due to its abundance in nature in many studies, including21,22,23, as well as the addition of storage systems, batteries, capacitors, hydrogen, etc. In24,25,26. And as we know, clean energies are unpredictable, and production changes with weather change. This makes it harder to control the system and the flow of energy and maintain between storage and energy use. We must use effective control techniques to get a robust and stable hybrid system. All control methods used in the system, such as Machine-Side-Control (MSC), Grid-Side-Control (GSC), MPPT control, Battery control, and Supercapacitor control, contain PI controllers, and they must find the best parameters of controllers to achieve our goal. In the following studies27,28,29,30, many optimization algorithms were used to obtain this controller gain. After obtaining the gains, each system has its energy management strategy, which was considered in5,27,28,29,30,31,32.

Many studies of renewable energy systems exist, but they are dispersed, and organizing them into one system has become necessary for researchers. For that, we collected these studies and built a hybrid PV-wind system with a storage system connected to the grid. After that, it simulates a scenario closer to reality with a variable load and develops a management strategy that controls energy flow. This is the best way to exploit clean energies that are considered the future of energy sources. A detailed literature review and comparison is given in Table 1.

The article analyses and simulates a hybrid power system that includes a wind turbine, solar panels, a Battery Energy Storage System (BESS), and a supercapacitor. Most works typically use a simple PI controller to control the system, but our paper does not follow this approach. In this paper, we propose a PI-PID cascade controller and utilize the COOT optimization algorithm to determine the optimal controller parameters, a task that is challenging to achieve through guesswork. All of these efforts are aimed at achieving a more stable and reliable system compared to using a simple PI controller.

To test our system, we created a more realistic study incorporating a variable DC load. For this purpose, a management strategy must be developed to control the energy storage units (BESS-Supercapacitor). It requires storing surplus energy and utilizing it when needed, with limits on the maximum power-sharing of the batteries. The grid is essential in providing the necessary power and absorbing the surplus when the batteries reach their limits.Additionally, the supercapacitor controls the voltage to enhance the system’s stability during sudden load changes. And we used optimization methods with the objective function ISE employed to determine the optimal settings of this control.

Finally, we summarize the most important goals of this paper.

  1. 1.

    To simulate a grid-connected hybrid power system PV-Wind energy system.

  2. 2.

    To evaluate the effectiveness of the COOT bird algorithm’s optimization method in determining the optimal controller parameter compared with the GA algorithm.

  3. 3.

    To compare the proposed PI-PID controller with the simple PI controller in obtaining a stable system.

  4. 4.

    To validate the supercapacitor’s role in achieving stable voltage and system reliability during a step load perturbation and real-life scenario.

  5. 5.

    To confirm the role of BESS in exploiting as much energy as possible from renewable energies.

  6. 6.

    To demonstrate the efficiency of our energy management strategy by creating a realistic scenario that includes variable load, variable solar irradiation, variable wind speed, and battery system limits.

Table 1 Literature review and comparison.
Full size table

The article was separated into the following sections: Sect. 2 presents the power system under study, Sect. 3 describes the architecture of the system, Sect. 4 explains the control approaches, Sect. 5 introduces the optimization algorithm, Sect. 6 proposes the energy management strategy, Sect. 7 discusses the obtained results, and Sect. 8 explains the conclusion of the work..

Power system under study

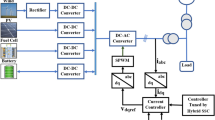
In hybrid power systems, there are two types of bus coupling: AC-coupled and DC-coupled. Each has advantages discussed in11,33,34,35,36, but we chose the DC-coupled method for its flexibility and ease of configuration. Our system is made up of the following components: on the DC side, Solar panels with an incremental conductance MPPT-controlled DC-DC boost converter, a Wind turbine based on a Permanent Magnet Synchronous Generator PMSG with Machine-Side-Converter MSC controlled by Rotor Field Oriented RFO and TSR MPPT, a Supercapacitor with a bidirectional converter to control the voltage, Battery energy storage system BESS using bidirectional DC-DC converter to control the energy of the system, Variable DC load, and bidirectional inverter with Grid Side Control GSC for converting the DC energy to AC and the inverse, Fig. 1 explains in detail the structure of our hybrid power system.

Fig. 1
figure 1

Architectural diagram of a hybrid PV/wind system connected to the grid with BESS, Supercapacitor, and variable DC load.

Full size image

Modeling the main components of the hybrid power system

PV system model

Figure 2 shows the overall equivalent circuit of a single-diode PV cell model that describes the fundamental function of the PV cell. This model comprises many silicon cells that function as a current source. PV panels are created by connecting these cells into a large unit and grouping them into arrays. In general, the number of cells in a specific parallel or series configuration controls the produced PV current or changes the number of cells on every panel3..

Fig. 2
figure 2

PV cell equivalent circuit.

Full size image
$$\:{I}_{PV}={I}_{g}-{I}_{D}-{I}_{sh}\:$$
(1)

The value \(\:{I}_{g}\) represents the illumination current, \(\:{I}_{sh}\) represents the shunt resistance current, and \(\:{I}_{D}\) represents the diode current.

$$\:{I}_{PV}={n}_{p}{I}_{g}-{n}_{p}{I}_{o}\left[exp\left(\frac{q\left({V}_{PV}+\frac{{I}_{PV}{r}_{s}{n}_{s}}{{n}_{p}}\right)}{{n}_{s}{n}_{c}AkT}-1\right)\right]-\frac{{V}_{PV}+\frac{{I}_{PV}{r}_{s}{n}_{s}}{{n}_{p}}}{\frac{{r}_{sh}{n}_{s}}{{n}_{p}}}$$
(2)

where \(\:{V}_{PV}\) represents the PV array’s output voltage, \(\:q\) has been the electron charge, \(\:T\) is the solar panel’s temperature, \(\:{n}_{p\:}\)is the total number of PV panels in parallel, \(\:{n}_{s}\)is the number of PV arrays in series, \(\:{n}_{c}\)is the number of series-positioned PV cells, \(\:k\)symbolizes the Boltzmann constant, \(\:A\) is the diode’s ideality factor, \(\:{r}_{sh}\)and \(\:{r}_{s}\) are the seriesandshunt resistance.

Figure 3 shows the obtained I-V characteristics and P-V characteristics of the solar cell module SPR-305E-WHT-D for various levels of illumination with a temperature equal to 25 degrees Celsius. The electrical power of an array of solar cells is a nonlinear function of operating voltage and contains a maximum power point (MPP).

Fig. 3
figure 3

(a) I-V and (b) P-V properties of a solar cell at various levels of irradiance and constant temperature (25°).

Full size image

Wind system model

The wind turbine is utilized to transform wind movement energy into electrical power, which can be expressed as follows:

$$\:{P}_{wind}=\frac{1}{2}\rho\:\pi\:{R}^{2}{{V}_{w}}^{3}$$
(3)

Where \(\:{V}_{w}\) represents the wind speed, \(\:R\) blade radius in meters, \(\:\rho\:\) air density in kg/m3.

The mechanical energy\(\:{P}_{m}\) received by the wind turbine is just a small part of the total available energy. The power coefficient \(\:{C}_{p}\)measures the effectiveness of the first exchange from wind speed to mechanical energy. This coefficient is influenced by wind speed and rotor speed, and has a maximum value of 59.3% determined by the Betz limit37. Equation (4) then presents the extracted mechanical power:

$$\:{P}_{m}={C}_{p}\left(\lambda\:,\beta\:\right){P}_{wind}$$
(4)

The wind turbine’s efficiency coefficient is represented by \(\:{C}_{p}\). It is dependent on both the blade pitch angle \(\:\left(\beta\:\right)\) and tip speed ratio \(\:\left(\lambda\:\right)\). Equation (5) defines the tip speed ratio as follows:

$$\:\lambda\:=\frac{\varOmega\:R}{{V}_{w}}$$
(5)

where \(\:R\) is the rotor radius, \(\:\varOmega\:\) is the generator’s rotor speed.

The power coefficient Cp, which characterizes turbine performance, is intricately influenced by two key parameters: the tip speed ratio λ and the blade pitch angle β. Existing research5,15,16,38,39 has proposed the following equations to approximate the power coefficient Cp:

$$\:{C}_{p}\left(\lambda\:,\beta\:\right)={c}_{1}\left(\frac{{c}_{2}}{{{\uplambda\:}}_{i}}-{c}_{3}\beta\:-{c}_{4}\right){exp}^{(-\frac{{c}_{5}}{{{\uplambda\:}}_{i}})}+{c}_{6}{\uplambda\:}$$
(6)
$$\:{{\uplambda\:}}_{i}={(\frac{1}{{\uplambda\:}+0.08\beta\:}-\frac{0.035}{{\beta\:}^{3}+1})}^{-1}$$
(7)

The variables \(\:{c}_{1}\) through \(\:{c}_{6}\) in this context denote the coefficients describing wind turbine attributes (\(\:{c}_{1}\) = 0.5176, \(\:{c}_{2}\) = 116, \(\:{c}_{3}\) = 0.4, \(\:{c}_{4}\) = 5,\(\:{c}_{5}\)= 21, \(\:{c}_{6}\) = 0.0068), and represent the blade pitch angle measured in degrees.

Figure 4 illustrates that there exists an optimum tip speed ratio \(\:{\lambda\:}_{opt}\) at which the power coefficient \(\:{C}_{p}\) achieves its highest value \(\:{Cp}_{max}\). In the wind system, where the wind turbine operates under normal conditions with a blade pitch angle \(\:\beta\:\:\)equal 0 degrees, the optimal tip speed ratio is determined to be \(\:{\lambda\:}_{opt}\) = 8.1 where the \(\:{Cp}_{max}\) is equal to 0.48.

Fig. 4
figure 4

The curves of the power coefficient \(\:{C}_{p}\) with various tip speed ratio values \(\:\lambda\:\) and a blade pitch angle β15.

Full size image

The PMSG wind turbine modeling is described in the rotating reference frame \(\:d-q\), and is founded on the next formulas28,38:

$$\:{v}_{sd}={-R}_{s}{i}_{sd}-{L}_{d}\frac{{di}_{sd}}{dt}+{\omega\:}_{e}{\psi\:}_{sq}$$
(8)
$$\:{v}_{sq}={-R}_{s}{i}_{sq}-{L}_{q}\frac{{di}_{sq}}{dt}-{\omega\:}_{e}{\psi\:}_{sd}$$
(9)
$$\:{\omega\:}_{e}={N}_{p}{\omega\:}_{m}\:$$
(10)

The following equations give the stator flux vector’s \(\:dq\) components:

$$\:{\psi\:}_{sd}={L}_{d}{i}_{sd}-{\psi\:}_{PM}$$
(11)
$$\:{\psi\:}_{sq}={L}_{q}{i}_{sq}$$
(12)

where: \(\:{v}_{sd}\), \(\:{v}_{sq}\) is the\(\:\:dq\) components of the stator voltage vector,\(\:Rs\) is the stator phase resistance, \(\:{i}_{sd}\), \(\:{i}_{sq}\) represents\(\:dq\) components of the stator current vector,\(\:{L}_{d}\), \(\:{L}_{q}\) describes the direct and quadrature stator inductances, \(\:{\omega\:}_{m}\), \(\:{\omega\:}_{e}\) represents the mechanical and electrical angular speed of the PMSG rotor,\(\:{N}_{p}\) is the number of pole pairs of PMSG, \(\:{\psi\:}_{sd}\), \(\:{\psi\:}_{sq}\) describes \(\:dq\) components of the stator flux vector, \(\:{\psi\:}_{PM}\) define the flux generated by the permanent magnets.

The following equation represents the electromagnetic torque:

$$\:{T}_{e}=\frac{3}{2}{N}_{p}\left({\psi\:}_{sd}{i}_{sq}-{\psi\:}_{sq}{i}_{sd}\right)$$
(13)

Furthermore, electromagnetic wind turbine torque and mechanical torque are interconnected by the swing Eq. (14):

$$\:{T}_{m}-{T}_{e}=J\frac{d{\omega\:}_{m}}{dt}+D{\omega\:}_{m}$$
(14)

In this model, the inertia is \(\:J\) and \(\:D\) representsthedamping friction coefficient.

Battery energy storage system model

The battery mathematical model utilized in this work builds upon the basic battery model, which incorporates the State of Charge (SoC), As seen in the following Equations, the battery is defined as a controlled voltage source with specific resistance 04,40,41.

$$\:E={E}_{0}-\frac{{P}_{v}{C}_{BESS}}{{C}_{BESS}-{\int\:}_{0}^{t}idt}+Aexp\left(-B\underset{0}{\overset{t}{\int\:}}{i}_{BESS}dt\right)$$
(15)
$$\:{V}_{BESS}=E-{R}_{i}{i}_{BESS}$$
(16)

Where \(\:E\) describe the battery open-circuit voltage, \(\:{E}_{0}\) define the no load voltage of the battery, \(\:{P}_{v}\) represent the polarization voltage, \(\:{C}_{BESS}\) is the battery capacity, \(\:{\int\:}_{0}^{t}idt\) illustrate the charge drawn and supplied by the battery, \(\:A\)meaning the exponential zone amplitude, \(\:B\) define the exponential zone time constant inverse, \(\:{i}_{BESS}\) symbolize the battery current, \(\:{V}_{BESS}\) describe the battery voltage, and \(\:{R}_{i}\) is the internal resistance.

Supercapacitor system model

The supercapacitor is the name of the Energy Storage System (ESS). Supercapacitors are made up of two electrodes with ionic holes that enable ions to travel freely across the area between them. This ESS type is crucial since it works to establish energy balance within a system, which makes it a type that helps control power fluctuations under challenging conditions. Even while it performs comparable tasks to other energy storage devices, it has a number of benefits over them. These include a long lifespan, less maintenance, a small size, quick charging and discharging abilities, a large amount of energy storage, and very simple integration into power systems3,42. Because of their ability to store greater power, supercapacitors are ideal for high-power engineering applications. The following equations can be used to compute the storage energy of this supercapacitor\(\:{W}_{ESS}\) .

$$\:{W}_{ESS}=\int\:{P}_{Sc}dt={P}_{sc}t$$
(17)

where \(\:{P}_{Sc\:}\)represents the storage energy in the supercapacitor at the time \(\:t\). The capacity size of a supercapacitor is depicted below43.

$$\:{W}_{ESS}=\frac{1}{2}{C}_{Sc}{V}_{Sc}^{2}$$
(18)
$$\:{C}_{Sc}=\frac{{2P}_{Sc}t}{{V}_{Sc}^{2}}$$
(19)

where \(\:{V}_{Sc}\) indicates the voltage of the supercapacitor and \(\:{C}_{Sc}\) equals its capacity size.

Control approaches

Control of the PV system

Maximum Power Point Tracking (MPPT) algorithms must be used to optimize the power output of a photovoltaic system shown in Fig. 5. These algorithms may be implemented using various techniques, including electrical circuits, coded algorithms, and MATLAB Simulink simulations. The method selected is determined by the system’s complexity and the time necessary to track the maximum power point. The Incremental Conductance (IC) technique44,45 is the suggested strategy in this study for attaining maximum power tracking from the PV system and is shown in Fig. 6.

Fig. 5
figure 5

The control of PV system.

Full size image
Fig. 6
figure 6

Flowchart for the incremental conductance MPPT.

Full size image

To execute this algorithm, voltage, and current detectors must be used to measure the output voltage and current of the photovoltaic (PV) array. The optimal operating point, where the maximum power is obtained, occurs when the slope of the power-voltage (P-V) curve reaches zero21,22. explains this:

$$\:{\left(\frac{dP}{dV}\right)}_{MPP}=d\left(VI\right)/dV$$
(20)
$$\:0=I+V{\left(\frac{dI}{dv}\right)}_{MPP}or\:{\left(\frac{dI}{dv}\right)}_{MPP}=-\frac{I}{V}$$
(21)

Control of the wind system

MPPT of the wind turbine

This strategy tries to maximize the turbine’s power production by achieving the best Tip Speed Ratio (TSR). Figure 7 demonstrates this process. An ideal reference speed for the rotor (\(\:{\omega\:}_{opt}\) ) is derived by computing the rotor and wind speeds. The TSR approach determines the best power extraction while accounting for system factors. The TSR MPPT algorithm has many benefits, including simplicity and quick response. As a result, it is used to effectively control the rotor speed in the face of changing environmental circumstances17,46.

Fig. 7
figure 7

Tip speed ratio (TSR) MPPT technique with COOT bird optimization algorithm.

Full size image

To obtain a dependable and stable system, we employed an optimization method called COOT bird with an objective function \(\:ISE\) to determine the best settings for the proposed controller of the Tip Speed Ratio (TSR) technique; Sect. 5 explains in detail that.

Machine side control of PMSG

The system’s Machine Side Control (MSC) uses a two-level voltage inverter in a three-phase AC/DC converter as in traditional designs. The Permanent Magnet Synchronous Generator (PMSG) with MSC’s control strategy is based on vector control, especially Rotor Field Oriented Control (RFOC) method [5], as detailed in Fig. 8.

Fig. 8
figure 8

Schematic of rotor field orientated control for MSC in a permanent magnet synchronous generator (PMSG) with COOT bird optimization algorithm.

Full size image

Figure 8 depicts the Rotor Field Oriented Control method. However, in the strategy, we must look for the gains of the proposed controllers. To find these parameters, we propose the ISE objective function and the COOT bird optimization technique for finding these parameters.

Control of the battery system

To control the BESS, we need two-way energy flow (charging and discharging), which requires a Bidirectional DC/DC Converter in the circuit, as shown in Fig. 9.

Fig. 9
figure 9

Control of switching signals for bidirectional DC/DC converter of the battery system.

Full size image

Figure 9 displays the control strategy for the switches of the bidirectional DC/DC converter used in the BES system. The constructed control loop is responsible for managing the operation of the switches. The desired battery power reference value, \(\:{P}_{batt}^{*}\), is computed by subtracting the load power demand, \(\:{P}_{load}\), from the total of renewable energy generated power (solar power \(\:{P}_{PV}\), wind power \(\:{P}_{wind}\)). The \(\:{P}_{batt}^{*}\) is then divided by the battery voltage \(\:{V}_{batt}\), to get the reference battery current,\(\:{I}_{batt}^{*}\).

The measured battery current, \(\:{I}_{batt}\), is compared to the reference battery current, \(\:{I}_{batt}^{*}\). The error signal produced goes into a proposed controller. The proposed controller output serves as the reference signal for the duty cycle D, of the bidirectional DC/DC converter.

A saturation block is integrated into the installed control system to protect the battery from excessive power flow over the maximum permissible limit\(\:\left({P}_{batt\:max}\right)\). This block limits the amount of power flowing into the battery, preventing it from exceeding the specified boundary.

The gains of the proposed controllers must be determined. For determining these parameters, we propose the \(\:ISE\) objective function and the COOT bird optimisation algorithm. In addition, enhancing battery life includes a supplemental algorithm for battery safety from excessive overcharging and deep discharging47.

Grid side converter control

The Grid Side Converter (GSC) is a kind of two-level voltage inverter that uses a three-phase DC/AC converter architecture. The dq axis theory has been used to regulate the GSC. The GSC’s main goal is to manage system control operations. These duties include monitoring the instantaneous supply of active and reactive power to the AC grid as well as controlling the DC link voltage of the GSC, the gains of the proposed controllers in the loops control have been achieved using the ISE objective function and the COOT bird optimization technique. Figure 1048,49 shows the detailed strategy for controlling the system..

Fig. 10
figure 10

Grid side converter control using d-q axis theory.

Full size image

Control of the supercapacitor system

The bidirectional DC/DC converter and its control loops are essential to the Supercapacitor system. As shown in Fig. 11, the main function of the bidirectional converter, which uses a PI controller, is to detect and determine the Supercapacitor system’s operational state. The three operating modes of the Supercapacitor are charging, discharging, and standby mode3.

Fig. 11
figure 11

The supercapacitor control system.

Full size image

The charging mode is started when the voltage of the DC bus \(\:{V}_{dc\:}\) changes positively. To reduce this variation, the Supercapacitor stores the energy surpluses. And the discharge mode is exactly the opposite. If the DC bus voltage decreases, the Supercapacitor rapidly gives power to the system to correct this error. In standby mode, the variation in tension (error) is almost equal to 0, so no energy is transferred between the Supercapacitor and the system..

This control method is implemented using a dual PI controller setup, as shown in Fig. 11. The first PI controller aims to minimize the error in the DC voltage. Its output is a reference for the second PI controller, which controls the Supercapacitor current. We suggest the COOT bird optimization algorithm with the use of the objective function ISE to determine the values of the controller constants \(\:Kp,\:Ki\) .

PI-PID cascade controller structure

The traditional PI controller produced acceptable results; however, it is critical for us as researchers to develop more effective control approaches. After many attempts, we achieved promising results using the PI-PID cascade controller, whose parameter values were determined using the COOT control algorithm is shown in Fig. 12. Our findings will demonstrate the superiority of the cascade controller over the PI controller. The figure below illustrates the design of this controller.

Fig. 12
figure 12

Structure of PI-PID cascade controller.

Full size image

Where \(\:Err\) represents the signal of error and \(\:{S}_{c}\) is the signal of control.

Optimization technique

Objective function

To increase the performance of our control of the system, we have to determine the optimal gains of each controller used in the subsystems (MPPT of the wind system, Machine-side-converter control of the PMSG, BESS control, and Grid-side-converter control). To do this, we must use an objective function, such as Integral Square Error (\(\:ISE\)), for computing the errors or the difference between the actuals value and the reference values, as described in the following equation:

$$\begin{gathered} Objective~function \hfill \\ = ~\sum ISE = \mathop \smallint \limits_{0}^{{t_{{sim}} }} \left[ \begin{gathered} w_{1} \left( {\omega _{m} - \omega _{{opt}}^{*} } \right)^{2} + w_{2} \left( {i_{{sd}} - i_{{sd}}^{*} } \right)^{2} + w_{3} \left( {i_{{sq}} - i_{{sq}}^{*} } \right)^{2} \hfill \\ + w_{4} \left( {I_{{batt}} - I_{{batt}}^{*} } \right)^{2} + w_{5} \left( {V_{{dc}} - V_{{dc}}^{*} } \right)^{2} + w_{6} \left( {I_{{gd}} - I_{{gd}}^{*} } \right)^{2} \hfill \\ + w_{7} \left( {I_{{gq}} - I_{{gq}}^{*} } \right)^{2} \hfill \\ \end{gathered} \right]dt \hfill \\ \end{gathered}$$
(22)

Where \(\:{t}_{sim}\)is the simulation time, The weights \(\:{w}_{1},{w}_{2},\dots\:{w}_{7}\) is used to balance between the errors ( \(\:{e}_{1},{e}_{2}\dots\:{e}_{7}\)) in the objective function \(\:ISE\), \(\:{\omega\:}_{m}\) is the rotor speed of wind turbine, \(\:{i}_{sq}\) and \(\:{i}_{sd}\)represent the stator current vector components \(\:,\:{I}_{batt}\) define the current of the battery, \(\:{V}_{dc}\) is the DC bus voltage, \(\:{I}_{gq}\) and \(\:{I}_{gd}\) express the grid current vector components .

To establish the weights in the objective function, we run the GA optimization method with 100 iterations and a population size of 10 with all weights equal to 1, and we record the best values for each error in Table 2. Then we select the weights that will balance all of the errors.

Table 2 Values of the weights used.
Full size table

Problem constraints

We can use the COOT bird optimization technique to identify the optimal values of the gains, but we know that each system has limitations. The optimization problem could be described in this way:

Minimize \(\:Objective\:function\) subject to:

$$\:\left\{\begin{array}{c}{Kp}_{j}^{min}\le\:{Kp}_{j}\le\:{Kp}_{j}^{max}\\\:{Ki}_{j}^{min}\le\:{Ki}_{j}\le\:{Ki}_{j}^{max}\\\:{Kd}_{j}^{min}\le\:{Kd}_{j}\le\:{Kd}_{j}^{max}\end{array}\right.$$
(23)

Given that the value of ‘j’ varies from 1 to the number of controllers, we chose the limits of \(\:{Kp}_{j}\) and \(\:{Ki}_{j}\) [0-100], and \(\:{Kd}_{j}\) between [0-0.01].

Equation 23 illustrates the gains limitations. So, the min and max denote the minimum and maximum limitations, and the limits of all gains were set based on the following sources3,27,28,38,50.

COOT bird optimization algorithm

The COOT Bird Optimization algorithm, a new swarm-based meta-heuristic algorithm, we chose it for its novelty, innovative nature, relatively high accuracy, and stable results across multiple runs, as verified by the research paper51. It exhibits specific behaviours during the search for food, which can be divided into four stages: random motion, chain motion, coot position enhancement by following the leaders, and leader movement towards the optimum zone where food exists. An initial population is chosen randomly to begin the algorithm. The objective function iteratively evaluates this population until an optimal value is reached. The evaluation of a randomly generated population can be expressed as follows:

$$coot\,position\left( i \right) = Rand\left( {1,\dim } \right) \times \left( {UB - LB} \right) + LB$$
(24)
$$\:LB={LB}_{1},{LB}_{2},{LB}_{3},\dots\:,{LB}_{dim}$$
(25)
$$\:UB={UB}_{1},{UB}_{2},{UB}_{3},\dots\:,{UB}_{dim}$$
(26)

Following the initial population and placement of the coots, an objective function is used to determine each coot’s fitness. The objective function needs to be optimized by the COOT Bird Optimization algorithm, as shown in the Eqs. 20,21.

The random movement of a coot is critical to the algorithm’s capability to explore various parts of the search space and eventually converge on the optimal global solution. Equation (27) depicts this process, while Eq. (28) estimates the COOT’s new position.

$$\:Q = Rand\left( {1,dim} \right)\: \times \:\left( {UB - LB} \right) + LB$$
(27)
$$\:coot\:position\left( i \right) = coot\:position\left( i \right) + A \times \:R_{1} \times \:(Q - coot\:position\left( i \right))$$
(28)

Where R1 represents a random number in [0,1] and A is calculated as follows:

$$\:A=1-\frac{Iter}{Iteration}$$
(29)

The maximum number of iterations is indicated in this context by “\(\:Iteration\),” whereas the current iteration is represented by “\(\:Iter\)”.

The next phase, known as chain movement, is done by determining the average position of two coots as follows:

$$\:coot\:position\left(i\right)=0.5\times\:(coot\:position\left(i-1\right)+coot\:position\left(i\right))$$
(30)

where \(\:coot\:position(i-1)\) is the location of the second coot..

Leader tracing can be used to enhance coot positions by randomly selecting a small sample of leaders and estimating their average position. The locations of ten coots are then adjusted based on the median leader position. The criteria for selecting leaders are described in Eq. (31), and the updated coot positions, considering leader position, are computed using Eq. (32).

$$\:K=1+\left(iMODLD\right)$$
(31)
$$\:coot\:position\left( i \right) = LDP\left( K \right) + 2 \times \:R_{2} \times \:{\text{cos}}\left( {2R\pi \:} \right) \times \:(LDP\left( K \right) - coot\:position\left( i \right))$$
(32)

In this case, \(\:K\:\)represents the index number of the chosen leader, \(\:LD\) indicates the total number of leaders, \(\:{R}_{2}\) is a random number distributed in the range [0,1], \(\:R\) is a random number distributed in the range [-1,1], and \(\:LDP\left(K\right)\) represents the position of the chosen leader. To find a new optimal point near the best location found, the positions of the leaders are adjusted using the following expression:

$$\:LDP\left(i\right)=\left\{\begin{array}{c}B\times\:{R}_{3}\times\:cos\left(2R\pi\:\right)\times\:\left(GB-LDP\left(i\right)\right)+GB,\:\:\:\:{R}_{4}<0.5\\\:B\times\:{R}_{3}\times\:cos\left(2R\pi\:\right)\times\:\left(GB-LDP\left(i\right)\right)-GB,\:\:\:\:{R}_{4}\ge\:0.5\end{array}\right.$$
(33)

Here, \(\:{R}_{3}\) and \(\:{R}_{4}\) are random numbers in [0,1]. \(\:GB\) represents the best location found so far, and \(\:B\) is determined by the following calculation:

$$\:B=2-\frac{Iter}{Iteration}$$
(34)

The term “B×R3” allows for larger random movements to prevent the COOT bird algorithm from becoming stuck in a local optimum and to maintain a balance between exploration and exploitation. This enables the COOT bird algorithm to conduct a more thorough search of the search space. Furthermore, using \(\:"cos\left(2R\pi\:\right)"\:\)aids in locating positions close to the best-found position, varying the radii for better exploration. The flowchart in Fig. 13 depicts the sequence of steps involved in the COOT bird algorithm.

Fig. 13
figure 13

Flowchart of COOT bird optimization algorithm.

Full size image

Energy management approaches

The objective of the energy management strategies is to fully utilize the energy received from renewable sources, such as solar and wind energy and minimize the energy imported from the grid as much as possible. For that, MPPT algorithms were implemented in the two sources, and using batteries to ensure that the energy of renewable sources is not lost due to an imbalance between generation and load. Finally, to make the study more realistic, maximum power charging and discharging limits of the batteries \(\:{P}_{batt\:max}\) have been added, as well as State of Charge (\(\:SoC\)) limits between 30% and 90% to increase the battery life cycle. To apply the power balance equation equal (generation = demand) we used the following equation:

$$\:{P}_{PV}\left(t\right)+{P}_{WT}\left(t\right)\pm\:{P}_{Sc}\left(t\right)\pm\:{P}_{batt}\left(t\right)\pm\:{P}_{grid}\left(t\right)-{P}_{load}\left(t\right)=0$$
(35)

where: \(\:{P}_{PV}\) is the power generated by the PV system, \(\:{P}_{WT}\) represents the energy produced by the wind system, \(\:{P}_{Sc}\) is the energy charged or discharged by the supercapacitor, \(\:{P}_{batt}\) defined as the energy of batteries, \(\:{P}_{grid\:}\) is the power exchanged between the system and the grid, \(\:{P}_{load\:}\) represent the power consumption of the load ; The equation was developed with the presumption that the system experiences negligible power losses and is in steady-state operation.

The supercapacitor power \(\:{P}_{Sc}\) sign depends on the derivative of the DC bus voltage \(\:d{V}_{dc}\). If the \(\:d{V}_{dc}\) is positive, the supercapacitor stores energy (\(\:{P}_{Sc}\) take the same sign of the load); if it is negative, it discharges energy (\(\:{P}_{Sc}\) take the opposite sign of the load), all of that to improve the voltage stability.

If the sum of the power produced by the photovoltaic \(\:{P}_{PV}\) and wind turbine \(\:{P}_{WT}\) systems is higher than the load demand \(\:{P}_{load}\), any extra electricity (\(\:{P}_{sur}={P}_{PV}+{P}_{WT}-{P}_{load}\pm\:{P}_{Sc}\)) is given preference for battery charging (\(\:{P}_{batt}\)). if the excess energy \(\:{P}_{sur\:}\)is greater than its maximum charging capacity (\(\:{P}_{batt\:max}\)), the remaining surplus energy will be sent back to the grid (\(\:{P}_{grid}=\:{P}_{sur}-{P}_{batt\:max}\)). However, the battery can be charged until it reaches 90% of the capacity. When the battery is charged, the entire surplus power can be delivered to the grid (\(\:{P}_{grid}={P}_{sur}\)).

If the sum of the power produced by the photovoltaic \(\:{P}_{PV}\) and wind turbine \(\:{P}_{WT}\) systems is lower than the load demand \(\:{P}_{load}\), any deficit energy (\(\:{P}_{def}={{P}_{load}-P}_{PV}-{P}_{WT}\pm\:{P}_{Sc}\)) is given by the battery discharging \(\:{P}_{batt}\). if the deficit energy \(\:{P}_{def}\) is greater than its maximum discharging capacity \(\:{P}_{batt\:max}\), the remaining deficit energy will be imported from the grid (\(\:{P}_{grid}=\:{P}_{def}-{P}_{batt\:max}\)). However, the battery can be discharged until it reaches 30% of the capacity. When the battery is discharged, the entire deficit power can be imported from the grid (\(\:{P}_{grid}={P}_{def}\)).

Figure 14 summarizes the energy management strategy of the hybrid power system PV-wind with hybrid storage BESS-Supercapacitor connected to the grid.

Fig. 14
figure 14

The scheme of the energy management strategy.

Full size image

Simulation results and discussion

The data and parameters used in the simulation studies are presented in the following part:

  • The PV array’s specifications are as follows52: Module SPR-305E-WHT-D, rated power is \(\:{P}_{PV}=\:\)6.1 kW, number of series panels \(\:{n}_{s}=\)5, number of parallel lines \(\:{n}_{p}=\)4, open circuit voltage \(\:{V}_{oc}=\:\)64.2 V, and short circuit current \(\:{I}_{sc}=\:\)5.96 A.

  • The wind turbine system and PMSG parameters53: Rated power \(\:{P}_{WT}=\)12 kW, rotor radius \(\:R\:=\)2.75 m, rated wind speed \(\:{v}_{w}=\:\)12 m/s, the air density \(\:A=\)1.225 kg/m2, number of pair poles \(\:{N}_{p}=\)5, stator inductance \(\:{L}_{s}=\)15 mH, PMSG moment of inertia \(\:\varTheta\:=\)0.01 kg.m2, permanent magnet flux \(\:{\psi\:}_{PM}=\:\)0.85 Vs, DC capacitor \(\:{C}_{dc}=\:\)15mF.

  • Parameters of BESS and Supercapacitor [03,05]: Rated capacity \(\:{C}_{batt}=\:\)5 Ah, single battery voltage \(\:{V}_{batt}=\)24 V, number of batteries in series \(\:{N}_{batt}=\:\)20, rated power of battery \(\:{P}_{batt\:max}=\:\)2 kW, Series resistance \(\:{R}_{s}=30\:m\varOmega\:\)capacitance of supercapacitor \(\:{C}_{Sc}=\:\)1000 F.

  • Other parameters: AC voltage \(\:{V}_{ac}=\)380 V, Frequency \(\:f\:=\)50 Hz, Filter inductance \(\:{L}_{f}=\)10 mH, Filter resistance \(\:{R}_{f}=\)20 mΩ, DC-link voltage \(\:{V}_{dc}=\)700 V, Sampling time \(\:{T}_{s}=\)10 µs.

We have two primary goals in our work. The first goal is to evaluate the proposed controller PI-PIDwiththe supercapacitor’s performance on the system by using COOT bird optimization. The second purpose is to develop an energy management plan that will improve energy flow in the system, making it more stable and economical. To achieve these goals, we have identified the following two scenarios:

Scenario 1:To begin, it is essential to evaluate the COOT optimization algorithm in comparison to the base optimization method, which is the Genetic Algorithm (GA). This evaluation will provide insights into the performance of the COOT optimization algorithm. After that, we will assess the performance of two control methods: the basic Proportional-Integral (PI) controller and the PI-PID cascade controller. Subsequently, we introduce a supercapacitor with voltage control to compare the system’s performance with and without this control. The comparison is based on the Peak Undershoot (\(\:{U}_{s}\)), Peak Overshoot (\(\:{O}_{s}\)), and settling time (\(\:{T}_{st}\)) of the active power generated \(\:{P}_{g}\) and the DC voltage (\(\:{V}_{dc}\)), where \(\:{(P}_{g}=\:{P}_{PV}+{P}_{WT}\pm\:{P}_{batt}\pm\:{P}_{Sc}\pm\:{P}_{grid}).\).

To apply this, we simulate the hybrid power system PV-wind with BESS connected to the grid, including its control systems such as MPPT for PV and wind system, Machine-Side Converter control for the PMSG, BESS control, and Grid-Side Converter control. The system starts in an initial stable state as defined in scenario (2) by changing the load to step load perturbation (SLP) (\(\:\pm\:\)10 kW). The simulation time \(\:{t}_{sim\:}\)is of 0.6 s. \(\:The\:objective\:function\)is used to calculate errors in the system, Ga and COOT optimization algorithms aims to minimize these errors as much as possible. The optimization methods used 42 search agents and 100 iterations. After the optimization process, we obtained the results in the following Table 3:

Table 3 The optimum parameters of the PI controllers used in the system control.
Full size table
Table 4 The optimum parameters of the PI-PID controllers used in the system control.
Full size table
Table 5 The optimum parameters of the PI controllers used in the supercapacitor control.
Full size table
Table 6 The integral square error of all errors in the system control.
Full size table
Table 7 Results of \(\:{T}_{st}\) ( of ± 0.25 V,±00 W), \(\:{\varDelta\:U}_{s}\), \(\:\varDelta\:{O}_{s}\) of the \(\:{V}_{dc}\) and \(\:{P}_{g}\), with the objective function ISE for the system at \(\:\varDelta\:{P}_{load\:}\left(SLP\right)\) = \(\:+\)10 kW with and without supercapacitor.
Full size table
Table 8 THD of all proposed control techniques.
Full size table

Many results can be extracted from the previous tables and figures. Table 3 represents the parametersof PI controllers obtained by the COOT and GA optimization methods; we can conclude from Table 3 that the algorithms have successfully obtained the optimal parameters necessary to achieve system stability. Table 4 shows that the COOT optimization algorithm completed the difficult challenge of finding 35 parameters of the seven proposed controllers PI-PID in the system control, also in Table 5, the optimization algorithm successfully obtained the optimal control parameters for the supercapacitor voltage control system.

From Table 6, we observe that the errors are balanced, and this helps the optimization algorithm understand the optimization problem and try to reach the optimal settings that arefair to all control loops, after comparing GA-PI with the proposed method COOT-PI-PID + SC based on the total errors multiplied by the weights, which equals ∑ISE, and represents the objective function, we notice an improvement of 89%.

Table 7 represents the numerical results extracted from Figs. 15 and 16, comparing the system performance (GA-PI with COOT-PI-PID + SC). From Table 7, we can see the DC voltage Peak Undershoot Us was reduced by 66%, Peak Overshoot minimized by 64%, the settling time \(\:{T}_{st}\) decreased by 96%, Although the active power generated \(\:{P}_{g}\)results of the proposed COOT-PI-PID + SC method do not match the performance of the GA algorithm in terms of Peak Undershoot, Peak Overshoot, and settling time, we have asignificant improvement in \(\:THDi\) and \(\:THDv\), with improvement percentages of 39% and 82%, respectively, all of this indicated in Table 8 and explained in Figs. 17 and 18. Figure 19 shows the convergence curves of the optimization prosses of each control method, and we notice a remarkable superiority of the proposed control technique COOT-PI-PID + SC as shown in Fig. 20.

Fig. 15
figure 15

Results of the comparisonof\(\:{V}_{dc}\) for the system with \(\:SLP\).

Full size image
Fig. 16
figure 16

Results the comparison of \(\:{P}_{g}\) for the system with \(\:SLP\).

Full size image
Fig. 17
figure 17

\(\:THDi\%\) Comparison between GA-PI and COOT-PI-PID + SC.

Full size image
Fig. 18
figure 18

\(\:THDv\%\) Comparison between GA-PI and COOT-PI-PID + SC.

Full size image
Fig. 19
figure 19

Convergence curvesof the \(\:\sum\:ISE\).

Full size image
Fig. 20
figure 20

Comparison between the \(\:\sum\:ISE\)values.

Full size image

In Fig. 21, we observe that when the load suddenly increases to a value of SLP = + 10 kW, the supercapacitor discharges abruptly to maintain voltage stability. Conversely, when the load decreases, the supercapacitor stores energy to ensure system stability. Once the system stabilizes, it returns to isolated mode.

Fig. 21
figure 21

The power of supercapacitor when applied SLP \(\:\pm\:10\:\)kW.

Full size image

All of the above can be summarized as follows: The COOT algorithm outperformed GA, and the cascade controller PI-PID outperformed the simple PI, but produced peaks, here comes the role of the supercapacitor to eliminate these peaks.

Scenario 2

The objective is to create a power system thatsimulatesreality based on real-world scenarios. Getting started, the PV system utilizes Maximum Power Point Tracking (MPPT) technology to extract the most energyfrom the solar panels available and to enhance the study’s realism; we employ a variable solar irradiation profile that closely mimics real-world conditions. Secondly, the wind turbine system employs the MPPT technique to extract maximum power while adapting to changing wind speeds. Next, we establish battery charge and discharge limits \(\:{P}_{batt\:max}\) and state of charge SOC boundaries (30%-90%) for a longer battery life cycle. Subsequently, we introduce a variable load that mirrors real load fluctuations over a 24-hour period. Finally, the addition of a supercapacitor ensures the system’s stability.

In order to operate this system, you need a powerful and stable control system, which we covered in the first scenario using the cascade controller PI-PID with the COOT bird optimization algorithm and supercapacitorcontrol. In addition, you need an effective power management approach, which we also addressed in Sect. 6. In the following figures, we show the results obtained:

Figure 22 shows the changes in solar radiation values during the simulation period. Figure 23 illustrates the fluctuations in wind speed throughout the simulation time, which exhibit random variability, mirroring natural conditions. Figure 24 displays the changes in \(\:{i}_{sd\:}\)and \(\:{i}_{sq}\). It is notable that \(\:{i}_{sd\:}\) of COOT-PI-PID + SC control remains close to zero when compared to GA-PI, which aligns with the requirements of the control loop. On the other hand, \(\:{i}_{sq}\)varies with the wind speed, influencing the electromagnetic torque of the PMSG generator, The proposed technique exhibits less fluctuation when compared to GA-PI, which helps reduce total harmonic distortion (THD). In Fig. 25, we can observe the actual angular speed \(\:{\omega\:}_{m}\) of the turbine in COOT-PI-PID + SC control equals the optimum value \(\:{\omega\:}_{opt}^{*}\) as required by the TSR technique, but in the GA-PI method, it deviates a little bit from the reference. Furthermore, Fig. 26 demonstrates that the electromagnetic torque is equal to the opposite of the mechanical torqueof the wind generator, as expected. Additionally, Fig. 27 shows the constant value of \(\:{C}_{p}\) for the proposed technique, providing evidence that the MPPT control loop successfully achieves its intended purpose, this achievement enables the extraction of the maximum possible energy from the wind generator by reaching the highest \(\:{C}_{p}\)value during operation.

Fig. 22
figure 22

Variations of the solar irradiance over time.

Full size image
Fig. 23
figure 23

Wind speed fluctuates throughout time.

Full size image
Fig. 24
figure 24

The PMSG’s stator current vector’s \(\:{i}_{sd}\) and \(\:{i}_{sq}\) component curvesof GA-PI and COOT-PI-PID + SC technique.

Full size image
Fig. 25
figure 25

The curves of the actual angular speed \(\:{\omega\:}_{m}\:,\:\)with the reference speed \(\:{\omega\:}_{opt}^{*}\) of the wind turbine system of GA-PI and COOT-PI-PID + SC methods.

Full size image
Fig. 26
figure 26

The PMSG’s electromagnetic torque \(\:{T}_{e}\) and mechanical torque \(\:{T}_{m}\)(with inverse sign) curves of COOT-PI-PID + SC control.

Full size image
Fig. 27
figure 27

The curve of power coefficient \(\:{C}_{p\:}\)of wind turbine of GA-PI and COOT-PI-PID + SC control.

Full size image

Figure 28 displays the tip speed ratio values for both COOT-PI-PID + SC and GA-PI methods. We observe that the proposed method, COOT-PI-PID + SC, outperformed GA-PI and was closer to the reference, which helps in achieving higher values for Cp, In Fig. 29, we observe the changes in battery current values along with its reference value curve. We note that the battery current is equal to the reference value curve until it reaches a certain point, which represents the maximum value for battery current. The maximum battery current value can be calculated as \(\:{I}_{batt\:max}={P}_{batt\:max}/{V}_{batt}\). Moving on to Fig. 30, we observe the variations in the values of the grid current components\(\:{I}_{gd\:}\) and\(\:{\:I}_{gq}\) in relation to \(\:{I}_{gd}\), which is almost equal to zero. This achievement reflects the control loop objective. Regarding \(\:{I}_{gq}\), its values fluctuate based on changes in load and saturation of the battery. If \(\:{I}_{gq}\)is less than 0, the surplus energy that the battery couldn’t store is absorbed by the grid. Conversely, if \(\:{I}_{gq}\)is greater than 0, the grid compensates for the remaining energy that the battery couldn’t provide. If \(\:{I}_{gq}\)is equal to zero, the system does not exchange any energy with the grid, this is made possible by the batterywhich either charges the surplus energy or discharges it to make up for the deficiency of energy, after we compare the curves of the COOT-PI-PID+SC method with GA-PI, we find that the fluctuations are much lower, and this helps in obtaining lower THD values.

Fig. 28
figure 28

The tip speed ratio of GA-PI and COOT-PI-PID + SC control.

Full size image
Fig. 29
figure 29

A comparison between the reference current and the actual current of battery values \(\:{I}_{batt}^{*}\), \(\:{I}_{batt}\)of COOT-PI-PID + SC control.

Full size image
Fig. 30
figure 30

The values of the grid current vector’s components \(\:{I}_{gd}\) and \(\:{I}_{gq}\) of GA-PI and COOT-PI-PID + SC technique.

Full size image

In Fig. 31, the DC bus voltage \(\:{V}_{dc\:}\)changes, and GA-PI control it is noticeable that it tracks its reference value of 700 V. Moreover, we observe that as the load increases, the voltage value decreases, and conversely, as the load decreases, the voltage value increases. This is where the COOT-PI-PID control plus supercapacitor unit plays a crucial role in maintaining voltage stability. It achieves this by either storing surplus energy or supplying energy to the system when needed, as shown in the figure, there is a constant and stable voltage. Moving on to Fig. 32, we notice that the curve of the active generated power\(\:{P}_{g}\), aligns with the load \(\:{P}_{load\:}\), providing clear evidence of the system’s efficient and stable operation.

Fig. 31
figure 31

The DC bus voltage \(\:{V}_{dc}\) variations of GA-PI and COOT-PI-PID + SC control.

Full size image
Fig. 32
figure 32

The curves of the load fluctuations \(\:{P}_{load}\) with produced active power \(\:{P}_{g}\)of COOT-PI-PID + SC control.

Full size image

As shown in Fig. 33, the system goes through several stages. In phase [0–1 s], we notice that (\(\:{P}_{PV}+\:{P}_{WT\:}<{P}_{load}\)), where the remaining energy is compensated by the battery through discharge.During the [1–2 s] phase, we observe that at 1s, there is a step load perturbation (SLP) with a value of +6 kW. In response, the supercapacitor performs its role, which is to discharge lots of energy in order to maintain the stability of the voltage and the system. Conversely, at the 2s, there is a load reduction of 6 kW, during which the supercapacitor stores energy as needed to maintain system stability, this demonstratesthe proposed energy management strategy: discharge, when \(\:d{V}_{dc}<\:0\), and charge, when \(\:d{V}_{dc}>\:0\), all of the previous because of step load perturbations, when the voltage stabilizes \(\:d{V}_{dc}\:\approx\:\:0\), the supercapacitor returns to the isolated mode.As in the first phase [0–1 s], a similar result is observed in phase [2–6 s]. In phase [6–9 s], there is a significant increase in the load value, resulting in (\(\:{P}_{PV}+\:{P}_{WT}+\:{P\:}_{batt\:max}<{P}_{load}\)). This is where the grid plays a role in compensating for the energy deficiency. From [9–14 s], there is a significant increase in renewable energy production, resulting in the equation (\(\:{P}_{PV}\:+\:{P}_{WT}>{P}_{load}\)). Renewable energies fulfill the load’s requirements, and the surplus energy is stored in the battery. Moving to [14–17.5 s], we note that the battery reaches its maximum charging limit (\(\:{P}_{batt\:max}\)), and the equation becomes (\(\:{P}_{PV}+\:{P}_{WT}+\:{P}_{batt\:max}>{P}_{load}\)). In this case, the grid is utilized to transfer the excess energy. From [17.5–19 s], we observe the battery switching from charging to discharging due to a significant decrease in solar energy production (sunset), resulting in the equation (\(\:{P}_{PV}\:+\:{P}_{WT}<{P}_{load}\)), and the battery compensates for the remaining energy. From [19–24 s], we notice that the battery reaches its maximum discharge limit (\(\:{P}_{batt\:max}\)), leading to the equation (\(\:{P}_{PV}\:+\:{P}_{WT}\:+\:{P}_{batt\:max}<{P}_{load}\)). At this point, the system imports the remaining energy from the grid.

Fig. 33
figure 33

The curves of PV system Power \(\:{P}_{PV},\:\)wind turbine active power \(\:{P}_{WT}\), power of battery system \(\:{P}_{batt}\), Power of Supercapacitor \(\:{P}_{Sc}\), active power of grid \(\:{P}_{grid}\), and load curve \(\:{P}_{load}\).

Full size image

The strategy recommended in Sect. 6 has been implemented, and based on the previous results, our system operates effectively under the second scenario. Any extra energy is stored in the battery by effectively utilizing solar and wind power. We can use the grid to transmit extra energy in case the battery runs out of capacity. We can use the energy stored in the batteries if renewable energy sources are unavailable. Additionally, we have the choice to import energy from the grid if the battery reaches its capacity limits. The supercapacitor is essential for maintaining the overall system’s voltage by supplying or storing energy in case ofstep load perturbation.

Conclusion

The study investigated a hybrid power system connected to the grid, integrating wind and photovoltaic (PV) energy sources with a hybrid storage system using batteries and a supercapacitor. The research focused on evaluating the stability of control mechanisms and the efficiency of the energy management strategy. The study applied the Incremental Conductance MPPT algorithm for PV systems and TSR-based MPPT technology for the wind turbine to ensure maximum energy extraction. Furthermore, storage units (batteries) store excess energy when there is a surplus in renewable energy production, and supply it when there is a deficit. The system includes various control loops for wind turbine MPPT, MSC control, BESS control, supercapacitor control, and GSC control. This is where our contribution comes in: we improve these control loops by proposing a PI–PID cascade controller plus a supercapacitor system to control the DC bus voltage. All of the parameters of these control loops were optimized by the COOT bird optimization algorithm with the help of the objective function ISE. The results of the proposed approach, COOT–PI–PID + SC, surpassed the simple PI controller optimized by the genetic algorithm by providing a settling time 96% faster, with lower oscillations in current and voltage. This led to reductions in \(\:{THD}_{i\:}\)and \(\:{THD}_{v\:}\)by 30% and 81%, respectively, and eliminated the peaks produced by the PI–PID controller. The DC voltage peak undershoot (Us) was reduced by 66%, and the peak overshoot was minimized by 64%, confirming the capability of our proposed method. In the second scenario, we performed a more realistic simulation to evaluate the efficiency of the proposed energy management strategy. The results confirmed the optimal utilization of renewable energy sources and storage units, ensuring system stability.

In the future work section, we recommend exploring new optimization algorithms with different objective functions (e.g., ITSE, IAE, ITAE, etc.) due to the promising results achieved with the proposed approach. Additionally, there is potential to enhance the control loops by incorporating alternative controllers, such as a fuzzy controller, cascade controller, or an ANN-Controller, incorporating adaptive or intelligent energy management strategies—such as neural networks, or reinforcement learning—could significantly improve the system’s decision-making and adaptability under dynamic conditions.