Introduction

The generalized linear model (GLM) framework provides statisticians with a powerful and adaptable approach to modeling different data types beyond the limitations of the traditional linear regression model (LRM). By incorporating different probability distributions and link functions, GLMs can handle binary outcomes, count data, and continuous positive variables41,42. Among its most Useful specializations is the Poisson regression model (PRM), specifically designed for analyzing event counts (discrete occurrences) such as patient admissions, mechanical failures, or traffic accidents recorded over fixed intervals. This modeling approach proves necessary across multiple fields, from public health (where it might track disease outbreaks) to industrial engineering (where it could predict equipment malfunctions). The PRM’s analytical strength is its ability to relate predictor variables to event frequencies through a log-linear relationship while accounting for the inherent randomness in count processes. When researchers encounter data representing rare events or frequent occurrences, whether studying crime patterns, insurance claims, or epidemiological trends, PRM provides the required mathematical accuracy and practical accessibility for significant inference.

Usually, the parameters are estimated in an LRM and a GLM using maximum likelihood estimation (MLE), but when the explanatory variables are strongly correlated, this issue is known as multicollinearity, which violates the assumptions of linear regression models, leading to unstable estimates and may produce unreliable estimates with unexpected signs, inflated variance, increased mean squared error (MSE), and reduced overall reliability of the regression model. As a result of this issue, many researchers have introduced some biased estimation techniques to solve this problem in LRM and GLM, such as Hoerl and Kennard21 proposed the ridge regression estimator, Liu27 presented the Liu estimator, Özkale and Kaciranlar44 developed a new two parameter estimator, Liu31 suggested a Liu-type estimator, Kibria and Lukman29 defined the Kibria-Lukman estimator, Khan et al.28 presented two-parameter ridge estimators, and Lukman et al.35 developed a modified ridge-type estimator. Recently, numerous biased estimators have been specifically developed for PRM, such as Månsson and Shukur40, Månsson et al.39, Alkhateeb and Algamal4, Akay and Ertan3, Ertan and Akay16, Amin et al.9, Abdelwahab et al.1, Lukman et al.32, Asar Genç12, Alrweili7, and others. These studies have played an important role in addressing multicollinearity in PRM, as they have proven their efficiency and reliability in estimating parameters in various real-world applications compared to MLE.

On the other hand, there is another issue faced in data analysis in LRM and GLM, called outliers. This results in a disproportionate influence on regression coefficients, reduced predictive accuracy, misleading hypothesis testing results, and a negative impact on the quality of statistical measures (such as R2 and MSE)10. Several studies have developed robust estimators to address the impact of outliers in LRM, for example, Gervini and Yohai19, Huber22,23, Ruckstuhl49, Tsou52, Almetwally and Almongy5, and others. Building upon these works, Researchers have recently turned to introducing robust biased estimators to address both the outliers and multicollinearity problems in LRM. Among them, Pfaffenberger and Dielman45, Ertaş17, Majid et al.38, Ibrahim and Yahya24, Yasmin and Kibria55, Ahmad et al.2, and Lawrence30. Following Rana et al.48, Idriss and Cheng25, Otto et al.43, the issue of outliers is particularly significant in the PRM, which inherently assumes equidispersion and is also sensitive to multicollinearity. To address these challenges, Lukman et al.34 proposed a ridge regression estimator incorporating a robust transformed M-estimator (MT) to effectively handle both outliers and multicollinearity. Building on this, Lukman et al.37 suggested an enhanced ridge-type estimator that also employs the robust MT estimator to further improve resistance to outliers and multicollinearity. Additionally, Arum et al.11 developed a modified jackknife ridge estimator integrated with the robust MT estimator to mitigate the influence of outliers and address multicollinearity.

Lukman et al.34 and Lukman et al.37 made valuable contributions in dealing with multicollinearity and outliers in statistical models. Although their methods, such as ridge and modified ridge-type estimators, have shown good results, the continuous development in statistical research calls for new approaches. Recently, the improved ridge estimator has gained attention for its better performance compared to the traditional ridge estimator, both in linear models and in GLM and PRM. This progress encourages the development of new estimators that can more effectively handle multicollinearity and outliers while improving model accuracy. Introducing a new estimator could offer a more advanced solution to these challenges in PRM. Therefore, our main objective in this study is to present a new effective robust bias estimator assuming that it is based on two biasing parameters in order to handle the outliers and multicollinearity problems in PRM.

The structure of this paper is organized as follows. Section 2 provides a comprehensive review of MLE along with existing regularized estimators and robust biased estimators for PRM. In Section 3, we introduce a new robust biasing estimator and provide a detailed theoretical comparison with several well-known estimators in the literature, including a discussion on the selection of biasing parameters. Section 4 presents the results of a Monte Carlo simulation study designed to evaluate the performance of the proposed method. Section 5 demonstrates the practical application of the estimator using a real-world dataset. Finally, Section 6 summarizes the key findings and outlines potential directions for future research.

Literature review

In this section, we present the MLE for the PRM with regularized estimators, which can also be called biased estimators, that handle only multicollinearity. In addition, we present a transformed M-estimator to handle outliers, as well as existing robust biased estimators to handle multicollinearity and outliers.

Regularized estimators

Consider a random variable \(Y_i\) following a Poisson distribution (PD) with probability mass function:

$$\begin{aligned} P(Y_i = y_i) = \mu _i^{y_i} \frac{e^{-\mu _i}}{y_i!}, \quad y_i \in {\mathbb {N}}_0, \end{aligned}$$
(1)

where \({\mathbb {N}}_0\) represents the set of non-negative integers and \(\mu _i> 0\) is the rate parameter. The mean and variance of PD are \(\text {E}(Y_i) = \text {Var}(Y_i) = \mu _i\).

The relationship between the mean response and the linear predictor is established through a link function \(g(\mu _i) = {\textbf{X}}_i^\prime \beta\), where \({\textbf{X}}_i\) is the vector of covariates and \(\beta\) represents the regression coefficients. The log-link function, \(g(\mu _i) = \ln (\mu _i)\), is particularly advantageous as it ensures \(\mu _i> 0\). The corresponding log-likelihood function for PRM is given by:

$$\begin{aligned} \ell ({\beta }) = \sum _{i=1}^n \left( y_i{\textbf{x}}_i^\prime \beta - \exp ({\textbf{x}}_i^\prime \beta ) - \ln (y_i!)\right) . \end{aligned}$$
(2)

The Poisson maximum likelihood estimate (PMLE) is obtained by solving the score equation derived from the first derivative of the log-likelihood function:

$$\begin{aligned} S(\beta ) = \sum _{i=1}^n \left[ y_i - \exp ({\textbf{x}}_i^\prime \beta )\right] {\textbf{x}}_i = 0, \end{aligned}$$
(3)

where we assume the model includes an intercept term. Due to the nonlinearity in (3), the iteratively reweighted least squares (IRLS) algorithm is employed to compute the PMLE. The final estimator takes the form:

$$\begin{aligned} {\hat{\beta }}_{\text {PMLE}} = D^{-1} X^\prime {\hat{U}} {\hat{z}}, \end{aligned}$$
(4)

where \(D=(X^\prime {\hat{U}} X)\), \({\hat{z}}\) is a transformation of the response variable \({\hat{z}}_i = \log ({\hat{\mu }}_i) + \frac{y_i - {\hat{\mu }}_i}{{\hat{\mu }}_i}\), and \({\hat{D}} = \text {diag}({\hat{\mu }}_i)\). Let F and \(\omega _j\) represent the eigenvectors and eigenvalues of D respectively, where \(D=F^\prime \Omega F\) with \(\Omega = \text {diag}(\omega _j)\) and r represents the covariates including intercept. The mean squared error matrix (MSEM) and MSE of the PMLE are as follows:

$$\begin{aligned}&\text {MSEM}({\hat{\beta }}_{\text {PMLE}}) = D^{-1}, \end{aligned}$$
(5)
$$\begin{aligned}&\text {SMSE}({\hat{\beta }}_{\text {PMLE}}) = \text {tr}(F^\prime \Omega F) = \sum _{j=1}^{r} \frac{1}{\omega _j}. \end{aligned}$$
(6)

Although MLE is the standard approach for PRM, it suffers from significant instability under multicollinearity, where near-linear dependencies among predictors inflate parameter variances and compromise the accuracy of estimation15,50. This problem mirrors the well-known issues in PRM, motivating the development of biased alternatives that trade a slight bias for substantial variance reduction1,7. Among these, the Poisson ridge regression estimator (PRRE) defined by Månsson and Shukur40 as follows:

$$\begin{aligned} {\hat{\beta }}_{\text {PRRE}} =(D+kI_r)^{-1}D{\hat{\beta }}_{\text {PMLE}}, \quad k> 0, \end{aligned}$$
(7)

where \(k\) is the regularization ridge parameter, and \(I_r\) is the \((r \times r)\) identity matrix. For \(k = 0\), the \({\hat{\beta }}_{\text {PRRE}}\) reduces to the \({\hat{\beta }}_{\text {PMLE}}\). The MSEM and MSE of the PRRE are given by:

$$\begin{aligned}&\text {MSEM}( {\hat{\beta }}_{\text {PRRE}}) = F\Omega _k^{-1}\Omega \Omega _k^{-1} F^\prime + k^2 F\Omega _k^{-1}\alpha \alpha ^\prime \Omega _k^{-1}F^\prime , \end{aligned}$$
(8)
$$\begin{aligned}&\text {MSE}({\hat{\beta }}_{\text {PRRE}}) = \sum _{j=1}^{r} \frac{\omega _j}{(\omega _j+k)^2} + k^2 \sum _{j=1}^{r} \frac{\alpha _j^2}{(\omega _j+k)^2}. \end{aligned}$$
(9)

Lukman et al.33 introduced the Poisson modified ridge-type estimator (PMRTE) with an additional regularization parameter, showing superior performance to conventional PRRE. The PMRTE is given by:

$$\begin{aligned} {\hat{\beta }}_{\text {PMRTE}}=(D+k(1+d)I_r)^{-1} D {\hat{\beta }}_{\text {PMLE}},\qquad 0<d<1, ~k>0, \end{aligned}$$
(10)

where \(d\) and \(k\) are two regularization parameters. If \(k=0\), where setting \(k = 0\) recovers the standard PMLE and \(d = 0\) yields the PRRE, demonstrating its flexible structure. The MSEM and the MSE expressions for PMRTE are:

$$\begin{aligned}&\text {MSEM}({\hat{\beta }}_{\text {PMRTE}}) = F \Omega _{kd}^{-1} \Omega \Omega _{kd}^{-1}F^\prime + k^2(d+1)^2 F \Omega _{kd}^{-1} \alpha \alpha ^\prime \Omega _{kd}^{-1} F^\prime , \end{aligned}$$
(11)
$$\begin{aligned}&\text {MSE}({\hat{\beta }}_{\text {PMRTE}}) = \sum _{j=1}^{r} \frac{\omega _j}{(\omega _j+k(d+1))^2} + k^2(d+1)^2 \sum _{j=1}^{r} \frac{\alpha _j^2}{(\omega _j+k(d+1))^2}. \end{aligned}$$
(12)

where \(\alpha =F^\prime \beta _{\text {PMLE}}\), \(\Omega _k=\text {diag}(\omega _1 + k, \omega _2 + k, \ldots , \omega _r + k)\), \(\Omega _{kd} = \text {diag}({\omega }_1+k(1+d), {\omega }_2+k(1+d),..., {\omega }_{r}+k(1+d))\), \(\Omega _{1} = \text {diag}({\omega }_1+1, {\omega }_2+1,..., {\omega }_{r}+1)\), and \(\Omega _{d} = \text {diag}({\omega }_1+d, {\omega }_2+d,..., {\omega }_{r}+d)\).

Robust Poisson regression

The GLM framework establishes the relationship between a response variable \(y\) and explanatory variables through \(\mu =E(y) = g^{-1}({\textbf{X}}\beta )\), where \(g\) is a known, strictly increasing link function, \(y\) follows an exponential family distribution (discrete or continuous) with parameter space \(\Theta\), \(\phi\) denotes the dispersion parameter, The response domain \((a,b)\) may have finite or infinite bounds. The link function satisfies \(g'(a)> 0\) and \(g'(b) < \infty\), ensuring model validity14,53.

To handle heteroscedasticity, we introduce a bounded, continuous \(\rho\) function with a unique minimum at zero. This yields the transformation \(\psi (t) = \frac{\rho '(t)}{\rho (t)}\), where \(\psi\) is continuous and well-defined everywhere. For observed data \((y_1,\ldots ,y_n)\), the MT estimator solves:

$$\begin{aligned} {\hat{\beta }}_{MT} = \arg \min _{\beta } \sum _{i=1}^n \rho \left( \frac{y_i-\mu _i}{\sqrt{V(\mu _i)}}\right) , \end{aligned}$$

where \(\mu _i = g^{-1}({\textbf{x}}_i^\prime \beta )\) are fitted values, \(V(\mu _i)\) is the variance function assumes approximate variance homogeneity.

For the PRM with a log link function \(g(\mu ) = \log (\mu )\), the variance-stabilizing transformation is given by \(\rho (t) = \sqrt{\mu }\). The MT estimator for PRM is efficiently implemented in the robustbase package in R, which provides a practical and robust tool for analyzing count data11,34,37.

To address the challenges of multicollinearity and outliers commonly encountered in PRM, researchers have focused on developing robust biased estimators by integrating biased estimation techniques with MT-estimation methods. The estimator \({\hat{\beta }}_{\text {PMT}}\) represents the MT estimation of \(\beta\) in the PRM, obtained through the MT approach, which is specifically designed to minimize the influence of outliers while effectively managing multicollinearity within the dataset. The MSEM of this estimator is denoted as \(\text {MSEM}({\hat{\beta }}_{\text {PMT}}) = \Psi\), and its MSE is given by \(\text {MSE}({\hat{\beta }}_{\text {PMT}}) = \sum _{j=1}^{r} \psi _{jj}\), and the term \(\alpha _{_{\text {MT}}} = F^\prime \beta _{\text {MT}}\).

Lukman et al.34 introduced the robust ridge MT estimator (PMT-RRE) for PRM. This estimator is defined as:

$$\begin{aligned} {\hat{\beta }}_{\text {PMT-RRE}} = \left( D + k I_r \right) ^{-1} D {\hat{\beta }}_{\text {PMT}}, \qquad k>0. \end{aligned}$$
(13)

The expressions for the MSEM and the MSE of the PMT-MRTE are given by:

$$\begin{aligned}&\begin{aligned} \text {MSEM}( {\hat{\beta }}_{\text {PMT-RRE}})=F\Omega _k^{-1}\Omega \Psi \Omega \Omega _k^{-1} F^\prime +k^2 F\Omega _k^{-1}\alpha _{_{\text {MT}}}\alpha _{_{\text {MT}}}^\prime \Omega _k^{-1}F^\prime , \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned}&\text {MSE}({\hat{\beta }}_{\text {PMT-RRE}})=\sum _{j=1}^{r}\frac{\omega _j^2\psi _{jj}}{(\omega _j+k)^2}+k^2\sum _{j=1}^{r}\frac{{\alpha }_{_{\text {MT}_j}}^2}{(\omega _j+k)^2}. \end{aligned}$$
(15)

The robust modified ridge-type MT estimator (PMT-MRTE) proposed by Lukman et al.37 combines the modified ridge-type method with the MT estimator to improve parameter estimation under multicollinearity and outliers as follows:

$$\begin{aligned} {\hat{\beta }}_{\text {PMT-MRTE}} = \left( D + k(1 + d) I_r \right) ^{-1}D {\hat{\beta }}_{\text {PMT}}, \qquad 0<d<1, ~k>0. \end{aligned}$$
(16)

The expressions for the MSEM and the MSE of the PMT-MRTE are given by:

$$\begin{aligned} \text {MSEM}({\hat{\beta }}_{\text {PMT-MRTE}})=F \Omega _{kd}^{-1} \Omega \Psi \Omega \Omega _{kd}^{-1}F^\prime + k^2(d+1)^2 F \Omega _{kd}^{-1} \alpha _{_{\text {MT}}} \alpha _{_{\text {MT}}}^\prime \Omega _{kd}^{-1} F^\prime , \end{aligned}$$
(17)
$$\begin{aligned} \begin{aligned} \text {MSE}({\hat{\beta }}_{\text {PMT-MRTE}})= \sum _{j=1}^{r} \frac{\omega _j^2\psi _{jj}}{(\omega _j+k(d+1))^2}+ k^2(d+1)^2\sum _{j=1}^{r} \frac{ {\alpha }_{{_{\text {MT}}}_j}^2}{(\omega _j+k(d+1))^2}. \end{aligned} \end{aligned}$$
(18)

Proposed robust estimator

One of the most popular biased estimators for handling multicollinearity recently is the two-parameter estimator, which Yang and Chang introduced54 and has been applied to many GLMs. Following Yang and Chang54, the Poisson two-parameter estimator (PTPE) is used to address severe multicollinearity. It is defined as:

$$\begin{aligned} {\hat{\beta }}_{\text {PTPE}}=(D+I_r)^{-1} (D+dI_r) (D+kI_r)^{-1} D{\hat{\beta }}_{\text {PMLE}}, \quad 0<d<1,~k>0 \end{aligned}$$
(19)

where \(d\) and \(k\) are the regularized parameters. If \(d=0\) and \(k=0\), then \({\hat{\beta }}_{\text {PTPE}}={\hat{\beta }}_{\text {PMLE}}\). The expressions for the MSEM and the MSE of the PTPE are given by:

$$\begin{aligned} & \begin{aligned} \text {MSEM}({\hat{\beta }}_{\text {PTPE}}) =&F \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}F^\prime + (d\Omega -k\Omega -k-\Omega )^2 F \Omega _k^{-1} \Omega _1^{-1} \\ &\times \alpha \alpha ^\prime \Omega _k^{-1} \Omega _1^{-1} F^\prime , \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned} & \begin{aligned} \text {MSE}({\hat{\beta }}_{\text {PTPE}})&= \sum _{j=1}^{r} \frac{\omega _j{(\omega }_j+d)^2}{(\omega _j+k)^2(\omega _j+1)^2}+ \sum _{j=1}^{r} \frac{ (d\omega _j-k\omega _j-k-\omega _j)^2{\alpha }_{_j}^2}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned} \end{aligned}$$
(21)

Building upon the robust methodologies developed by Lukman et al.34,37, this paper proposes a novel robust two-parameter MT estimator for PRM (PMT-TPE). By integrating the multicollinearity-handling capabilities of Yang and Chang’s two-parameter estimator54 with the outlier-resistant properties of MT estimation, our approach simultaneously addresses two major challenges in PRM. The resulting hybrid estimator demonstrates enhanced stability in parameter estimation, improved reliability in the presence of contaminated data, and superior performance in terms of MSE reduction compared to existing methods. The PMT-TPE is defined as follows:

$$\begin{aligned} {\hat{\beta }}_{\text {PMT-TPE}}=(D+I_r)^{-1} (D+dI_r) (D+kI_r)^{-1} D{\hat{\beta }}_{\text {PMT}}, \end{aligned}$$
(22)

where \(k~ (k>0)\) and \(d ~(0<d<1)\) are the robust shrinkage parameter. If we set \(d = 1\) in Equation (22), we get \({\hat{\beta }}_{\text {PMT-TPE}} = {\hat{\beta }}_{\text {PMT-RRE}}\) and if we set \(d = 1,~ k=0\) in Equation (22), we get \({\hat{\beta }}_{\text {PMT-TPE}} = {\hat{\beta }}_{\text {PMT}}\).

The expected value, bias, and variance-covariance matrix of the PMT-TPE \({\hat{\beta }}_{\text {PMT-TPE}}\) are given by:

$$\begin{aligned} & \text {E}({\hat{\beta }}_{\text {PMT-TPE}})=(D+k(1+d)I)^{-1} (D-k(1+d)I) \beta , \end{aligned}$$
(23)
$$\begin{aligned} & \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})=E({\hat{\beta }}_{\text {PMT-TPE}})-\beta =(d\Omega -k\Omega -k-\Omega ) \phi \Omega _k^{-1} \Omega _1^{-1} \alpha _{_{\text {MT}}}, \end{aligned}$$
(24)
$$\begin{aligned} & \begin{aligned} \text {Var-Cov}({\hat{\beta }}_{\text {PMT-TPE}})=&E\left( \left[ {\hat{\beta }}_{\text {PMT-TPE}}-E({\hat{\beta }}_{\text {PMT-TPE}}) \right] \left[ {\hat{\beta }}_{\text {PMT-TPE}}-E({\hat{\beta }}_{\text {PMT-TPE}}) \right] ^\prime \right) \\ =&F \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}F^\prime . \end{aligned} \end{aligned}$$
(25)

Using the variance-covariance matrix and the bias, the SMSE and the MMSE of the PMT-TPE are derived as follows:

$$\begin{aligned}\text {MMSE}({\hat{\beta }}_{\text {PMT-TPE}})&=\text {Var-Cov}({\hat{\beta }}_{\text {PMT-TPE}})+\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime \\&=\phi \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\phi ^\prime + (d\Omega -k\Omega -k-\Omega )^2 \phi \Omega _k^{-1} \Omega _1^{-1} \\ &\quad\times \alpha _{_{\text {MT}}} \alpha _{_{\text {MT}}}^\prime \Omega _k^{-1} \Omega _1^{-1} \phi ^\prime , \end{aligned}$$
(26)
$$\begin{aligned}&\begin{aligned} \text {SMSE}({\hat{\beta }}_{\text {PMT-TPE}})&=\text {tr}\left( \text {MMSE}({\hat{\beta }}_{\text {PMT-TPE}})\right) \\&= \sum _{j=1}^{r} \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}+ \sum _{j=1}^{r} \frac{ (d\omega _j-k\omega _j-k-\omega _j)^2{\alpha }_{{_{\text {MT}}}_j}^2}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned} \end{aligned}$$
(27)

Superiority of proposed estimators

We investigate the superiority of the proposed estimator over existing estimators theoretically using the following Lemmas

Lemma 1

For any positive definite matrix \(\zeta\), nonzero constant vector \(\nu\), and positive scalar \(a\), the matrix inequality \(a\zeta - \nu \nu ^{\prime }> 0\) holds if and only if the quadratic form \(\nu ^{\prime }\zeta \nu < a\) is satisfied18.

Lemma 2

Consider two estimators \({\hat{\tau }}_1\) and \({\hat{\tau }}_2\) of a parameter \(\tau\). The estimator \({\hat{\tau }}_1\) is superior to \({\hat{\tau }}_2\) under the MSEM criterion if and only if their MSEM difference \(\Delta ({\hat{\tau }}_1, {\hat{\tau }}_2) = \text {MSEM}({\hat{\tau }}_1) - \text {MSEM}({\hat{\tau }}_2)\) is positive definite37.

Lemma 3

Let \({\hat{\tau }}_1 = Z_1 y\) and \({\hat{\tau }}_2 = Z_2 y\) be two linear estimators of \(\tau\). If the difference in their covariance matrices \(\Delta = \text {Cov}({\hat{\tau }}_1) - \text {Cov}({\hat{\tau }}_2)\) is positive definite. Then, the difference in their MSEM is \(\delta ({\hat{\tau }}_1, {\hat{\tau }}_2) = \Delta + z_1z_1′ - z_2z_2′.\) The estimator \({\hat{\tau }}_1\) dominates \({\hat{\tau }}_2\) in the MSEM sense (i.e., \(\delta ({\hat{\tau }}_1, {\hat{\tau }}_2)> 0\)) if and only if \(z_2′(\Delta + z_1z_1′)z_2 < 1,\) where \(z_1\) and \(z_2\) are the bias vectors of \({\hat{\tau }}_1\) and \({\hat{\tau }}_2\), respectively18,51.

Theorem 1

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PMLE}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PMLE}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [\Omega ^{-1} - \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} ]\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PMLE}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _1=\text {Cov}({\hat{\beta }}_{\text {PMLE}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) = \Omega ^{-1} - \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} . \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _1 = \sum _{j=1}^{r}\frac{1}{\omega _{j}} - \sum _{j=1}^{r} \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^{\prime }\) is nonnegative definite, the difference matrix \(\Omega ^{-1} - \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _1> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Omega ^{-1} - \Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PMLE}}\). \(\square\)

Theorem 2

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PRRE}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PRRE}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [\Omega _k^{-1}\Omega \Omega _k^{-1}-\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}&+\text {Bias}({\hat{\beta }}_{\text {PRRE}})\text {Bias}({\hat{\beta }}_{\text {PRRE}})^\prime ]\\ &\times \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned} \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PRRE}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _2=\text {Cov}({\hat{\beta }}_{\text {PRRE}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) = \Omega _k^{-1}\Omega \Omega _k^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}. \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _2=\sum _{j=1}^{r}\frac{\omega _j}{(\omega _j+k)^2} - \sum _{j=1}^{r} \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime\) and \(\text {Bias}({\hat{\beta }}_{\text {PRRE}})\text {Bias}({\hat{\beta }}_{\text {PRRE}})^\prime\) is nonnegative definite, the difference matrix \(\Omega _k^{-1}\Omega \Omega _k^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _2> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Omega _k^{-1}\Omega \Omega _k^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PRRE}}\). \(\square\)

Theorem 3

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PMRTE}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PMRTE}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [ \Omega _{kd}^{-1} \Omega \Omega _{kd}^{-1}-\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}&+\text {Bias}({\hat{\beta }}_{\text {PMRTE}})\text {Bias}({\hat{\beta }}_{\text {PMRTE}})^\prime ]\\ &\times \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned} \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PMRTE}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _3=\text {Cov}({\hat{\beta }}_{\text {PMRTE}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) = \Omega _{kd}^{-1} \Omega \Omega _{kd}^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} . \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _3 = \sum _{j=1}^r \frac{\omega _j}{(\omega _j+k(d+1))^2} - \sum _{j=1}^{r} \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime\) and \(\text {Bias}({\hat{\beta }}_{\text {PMRTE}})\text {Bias}({\hat{\beta }}_{\text {PMRTE}})^\prime\) is nonnegative definite, the difference matrix \(\Omega _{kd}^{-1} \Omega \Omega _{kd}^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _3> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Omega _{kd}^{-1} \Omega \Omega _{kd}^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PMRTE}}\). \(\square\)

Theorem 4

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PTPE}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PTPE}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [ \Omega _k^{-1} \Omega _1^{-1}\Omega _d \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}-\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}&+\text {Bias}({\hat{\beta }}_{\text {PTPE}})\text {Bias}({\hat{\beta }}_{\text {PTPE}})^\prime ]\\ &\times \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned} \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PTPE}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _4=\text {Cov}({\hat{\beta }}_{\text {PTPE}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) = \Omega _k^{-1} \Omega _1^{-1}\Omega _d \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} . \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _4 = \sum _{j=1}^r \frac{\omega _j{(\omega }_j+d)^2}{(\omega _j+k)^2(\omega _j+1)^2} - \sum _{j=1}^{r} \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime\) and \(\text {Bias}({\hat{\beta }}_{\text {PTPE}})\text {Bias}({\hat{\beta }}_{\text {PTPE}})^\prime\) is nonnegative definite, the difference matrix \(\Omega _k^{-1} \Omega _1^{-1}\Omega _d \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _4> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Omega _k^{-1} \Omega _1^{-1}\Omega _d \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PTPE}}\). \(\square\)

Theorem 5

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PMT}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PMT}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [\Psi -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} ]\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PMT}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _5=\text {Cov}({\hat{\beta }}_{\text {PMT}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) =\Psi -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} . \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _5 = \sum _{j=1}^{r}\psi _{jj} - \sum _{j=1}^{r} \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime\) is nonnegative definite, the difference matrix

\(\Psi -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _5> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Psi -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PMT}}\). \(\square\)

Theorem 6

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PMT-RRE}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PMT-RRE}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [\Omega _k^{-1}\Omega \Psi \Omega \Omega _k^{-1}-\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}&+\text {Bias}({\hat{\beta }}_{\text {PMT-RRE}})\text {Bias}({\hat{\beta }}_{\text {PMT-RRE}})^\prime ]\\ &\times \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned} \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PMT-RRE}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _6=\text {Cov}({\hat{\beta }}_{\text {PMT-RRE}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) = \Omega _k^{-1}\Omega \Psi \Omega \Omega _k^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}. \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _6= \sum _{j=1}^r\frac{\omega _j^2\psi _{jj}}{(\omega _j+k)^2} - \sum _{j=1}^r \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime\) and \(\text {Bias}({\hat{\beta }}_{\text {PMT-RRE}})\text {Bias}({\hat{\beta }}_{\text {PMT-RRE}})^\prime\) is nonnegative definite, the difference matrix \(\Omega _k^{-1}\Omega \Psi \Omega \Omega _k^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _6> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Omega _k^{-1}\Omega \Psi \Omega \Omega _k^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PMT-RRE}}\). \(\square\)

Theorem 7

In PRM, the estimator \({\hat{\beta }}_{\text {PMT-TPE}}\) is superior to the \({\hat{\beta }}_{\text {PMT-MRTE}}\) in the MSEM criterion, i.e. \(\text {MSEM}({\hat{\beta }}_{\text {PMT-MRTE}}) - \text {MSEM}({\hat{\beta }}_{\text {PMT-TPE}})>0\) iff:

$$\begin{aligned} \begin{aligned} \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime [ \Omega _{kd}^{-1} \Omega \Psi \Omega \Omega _{kd}^{-1}-\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}&+\text {Bias}({\hat{\beta }}_{\text {PMT-MRTE}})\text {Bias}({\hat{\beta }}_{\text {PMT-MRTE}})^\prime ]\\ &\times \text {Bias}({\hat{\beta }}_{\text {PMT-TPE}}) < 1. \end{aligned} \end{aligned}$$

Proof

The covariance matrices of the \({\hat{\beta }}_{\text {PMT-MRTE}}\) and \({\hat{\beta }}_{\text {PMT-TPE}}\) differ according to the following relationship:

$$\begin{aligned} \Delta _7=\text {Cov}({\hat{\beta }}_{\text {PMT-MRTE}}) - \text {Cov}({\hat{\beta }}_{\text {PMT-TPE}}) = \Omega _{kd}^{-1} \Omega \Psi \Omega \Omega _{kd}^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1} . \end{aligned}$$

The expression for this difference is:

$$\begin{aligned} \Delta _7= \sum _{j=1}^r \frac{\omega _j^2\psi _{jj}}{(\omega _j+k(d+1))^2} - \sum _{j=1}^r \frac{\omega _j^2{(\omega }_j+d)^2\psi _{jj}}{(\omega _j+k)^2(\omega _j+1)^2}. \end{aligned}$$

Since \(\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})\text {Bias}({\hat{\beta }}_{\text {PMT-TPE}})^\prime\) and \(\text {Bias}({\hat{\beta }}_{\text {PMT-MRTE}})\text {Bias}({\hat{\beta }}_{\text {PMT-MRTE}})^\prime\) is nonnegative definite, the difference matrix \(\Omega _{kd}^{-1} \Omega \Psi \Omega \Omega _{kd}^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite iff \(\Delta _7> 0\) for \(0< d < 1\) and \(k>0\). This implies that \(\Omega _{kd}^{-1} \Omega \Psi \Omega \Omega _{kd}^{-1} -\Omega _k^{-1} \Omega _1^{-1}\Omega _d\Omega \Psi \Omega \Omega _d\Omega _k^{-1} \Omega _1^{-1}\) is positive definite, confirming that \({\hat{\beta }}_{\text {PMT-TPE}}\) is better than \({\hat{\beta }}_{\text {PMT-MRTE}}\). \(\square\)

The theoretical conditions established in Theorems 1 to 7 are empirically verified through a comprehensive analysis of real-world data presented in Section 5.

Selection of biasing parameters

The selection of biasing parameters (k, d) plays a crucial role in balancing bias and variance in biased estimators. Based on both theoretical and empirical considerations, k is often determined by minimizing the MSE, as shown by Hoerl and Kennard21, while d is typically restricted to the interval (0, 1) to maintain proper shrinkage27. Practical approaches commonly follow using geometric mean-based estimators derived from predictor eigenvalues. This strategy, supported by studies such as Månsson and Shukur40, demonstrates superior bias-variance trade-offs, especially in high-dimensional or multicollinear contexts. These techniques, theoretically grounded and empirically validated, provide robust solutions for optimal parameter selection in biased estimation frameworks.

  • Following Månsson and Shukur40, Hoerl and Kennard21, Alqasem et al.6, Abdelwahab et al.1, and Lukman et al.34,37, the recommended biasing parameter \({\hat{k}}\) for PRM is derived as:

    $$\begin{aligned} {\hat{k}}_1=\frac{1}{\sum _{j=1}^{r}{\hat{\alpha }}_j^2}, \qquad {\hat{k}}_2=\min \left( \frac{1}{{\hat{\alpha }}_j^2}\right) . \end{aligned}$$
    (28)

  • Building upon the work of Lukman et al.33,35 and Alrweili8, the recommended biasing parameter \({\hat{k}}\) for PMRTE is derived as:

    $$\begin{aligned} {\hat{k}}_1=\min \left( \frac{1}{(1+{\hat{d}}){\hat{\alpha }}_j^2}\right) , \qquad {\hat{k}}_2=\min \left( \frac{1}{(r+{\hat{d}}){\hat{\alpha }}_j^2}\right) ^\frac{1}{2}, \end{aligned}$$
    (29)

    with biasing parameter \({\hat{d}}\) equal \({\hat{d}}= \min \left( \frac{{\hat{\alpha }}_j^2}{{\hat{\alpha }}_j^2+\frac{\sigma ^2}{\omega _j}}\right)\)

According to the work of Chang estimator54 and Awwad et al.13, we use the following parameters for PTPE.

$$\begin{aligned} {\hat{d}} = \frac{ \sum _{j=1}^{r} \left( \frac{((k + 1)\omega _j + k)\omega _j {\hat{\alpha }}_{j}^2 - \omega _j^2}{(\omega _j + 1)^2 (\omega _j + k)^2} \right) }{ \sum _{j=1}^{r} \left( \frac{(1 + \omega _j {\hat{\alpha }}_{j}^2)\omega _j}{(\omega _j + 1)^2 (\omega _j + k)^2} \right) , } \end{aligned}$$
(30)

where the initial \(k={\hat{k}}_2\) as in PRRE to compute the value of \({\hat{d}}\), then using \({\hat{d}}\) to compute the value of parameter \({\hat{k}}\) as follows:

$$\begin{aligned} {\hat{k}}_1 = \min \left( \frac{(\omega _j + d) - (1 - d)\omega _j {\hat{\alpha }}_{min}^2}{\max (\omega _j + 1){\hat{\alpha }}_{j}^2} \right) , \qquad {\hat{k}}_2 = \frac{1}{p+1}\min \left( \frac{(\omega _j + d) - (1 - d)\omega _j {\hat{\alpha }}_{min}^2}{(\omega _j + 1){\hat{\alpha }}_{j}^2} \right) . \end{aligned}$$
(31)

The biasing parameters of robust estimators such as PMT-RRE and PMT-MRTE are the same as in regularized estimators, but with \({\hat{\alpha }}_j^2\) is replaced by its robust analogue \({\hat{\alpha }}_{{_{\text {MT}}}_j}\).

Monte Carlo simulation study

This section employs a Monte Carlo simulation to evaluate robust and non-robust estimator performance under different scenarios. The response variable is generated from a PD, \(y_i \sim \text {Po}(\mu _i)\), where the rate parameter \(\mu _i = \exp (x_i^\prime \beta )\) depends on a linear predictor incorporating the design matrix \({\textbf{X}}\) and coefficient vector \(\beta\)1,8.

To systematically examine the impact of predictor correlation, explanatory variables are generated using a modified data-generating process36,37. Each covariate \(x_{ij}\) is constructed as a linear combination of standard normal variates, \(x_{ij} = (1 - \theta ^2)^{\frac{1}{2}} \, \Gamma _{ij} + \theta \, \Gamma _{i,j+1}\), where where \(\theta\) controls the level of multicollinearity, and \(\Gamma _{ij}\) is derived from a standard normal distribution. The simulation considers four correlation levels (\(\theta = 0.85, 0.90, 0.95, 0.99\)) to represent varying degrees of multicollinearity, ranging from moderate to severe.

The simulation evaluates three explanatory variables (\(p = 3, 8\)) to assess dimensionality. The intercept term assumes values of \(-1\), \(0\), or \(1\) to examine varying intercept in the PRM. Regression coefficients are standardized such that \(\sum _{j=1}^{r} \beta _j^2 = 1\), with equal weights assigned to each predictor to ensure balanced contributions11,37. Sample sizes span \(n = 30, 75, 100, 200, 300, 400\) to capture small-to-large data scenarios.

Robustness is evaluated by introducing artificial outliers to the response variable. A contamination mechanism replaces a subset of observations (\(10\%\) or \(20\%\)) with values \(y_i = 10 \max (y) + y_i\), where the multiplier \(10\) ensures extreme deviations from the majority of the data36,37.

Estimator accuracy is quantified via MSE, computed over \(1000\) Monte Carlo replications for stability:

$$\begin{aligned} \text {MSE}({\hat{\beta }}) = \frac{1}{1000} \sum _{j=1}^{1000} ({\hat{\beta }}_*^{(j)} - \beta )^\prime ({\hat{\beta }}_*^{(j)} - \beta ) \end{aligned}$$

where \(({\hat{\beta }}_*^{(j)} - \beta )\) is the difference between the estimated parameter and the true value. This metric aggregates both bias and variance components, providing a comprehensive assessment of estimation quality20. The large number of replications ensures reliable inference about estimator properties.

Algorithm 1
figure a

Simulation Procedure for Evaluating Robust and Non-Robust Biased Estimators in PRM

Full size image
Table 1 Estimated MSE for robust and non-robust estimators at 10% outliers, \(p=4\), and \(\beta _0=1\).
Full size table
Table 2 Estimated MSE for robust and non-robust estimators at 10% outliers, \(p=4\), and \(\beta _0=0\).
Full size table
Table 3 Estimated MSE for robust and non-robust estimators at 10% outliers, \(p=4\), and \(\beta _0=-1\).
Full size table
Table 4 Estimated MSE for robust and non-robust estimators at 20% outliers, \(p=4\), and \(\beta _0=1\).
Full size table
Table 5 Estimated MSE for robust and non-robust estimators at 20% outliers, \(p=4\), and \(\beta _0=0\).
Full size table
Table 6 Estimated MSE for robust and non-robust estimators at 20% outliers, \(p=4\), and \(\beta _0=-1\).
Full size table
Table 7 Estimated MSE for robust and non-robust estimators at 10% outliers, \(p=8\), and \(\beta _0=1\).
Full size table
Table 8 Estimated MSE for robust and non-robust estimators at 10% outliers, \(p=8\), and \(\beta _0=0\).
Full size table
Table 9 Estimated MSE for robust and non-robust estimators at 10% outliers, \(p=8\), and \(\beta _0=-1\).
Full size table
Table 10 Estimated MSE for robust and non-robust estimators at 20% outliers, \(p=8\), and \(\beta _0=1\).
Full size table
Table 11 Estimated MSE for robust and non-robust estimators at 20% outliers, \(p=8\), and \(\beta _0=0\).
Full size table
Table 12 Estimated MSE for robust and non-robust estimators at 20% outliers, \(p=8\), and \(\beta _0=-1\).
Full size table

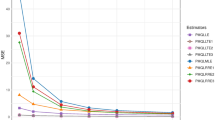
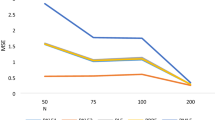
The performance of various estimators is compared in Tables 1-12 under different scenarios, including variations in the number of predictors (\(p\)), intercept (\(\beta _0\)), outlier proportion, and multicollinearity levels. The analysis includes both non-robust estimators (designed only for multicollinearity) and robust estimators (which address multicollinearity and outliers). Overall, robust estimators outperform non-robust ones in the presence of outliers. The main observations are:

  • Impact of Outliers: Non-robust estimators are highly sensitive to outliers, resulting in larger MSE values, particularly as outliers increase from 10% to 20%. In contrast, robust estimators remain stable, delivering consistently lower MSE values.

  • Effect of Sample Size: While larger samples improve estimation accuracy for both estimator types, robust estimators show greater improvement, especially with higher outlier contamination.

  • Dimensionality Influence: Models with more predictors (\(p=8\)) exhibit higher MSE values than those with fewer predictors (\(p=4\)), indicating increased estimation complexity. Nevertheless, robust estimators retain their superiority, particularly when outliers are present.

  • Role of the Intercept (\(\beta _0\)): Although the intercept affects estimation accuracy, its impact is less pronounced than that of outliers and sample size. However, when \(\beta _0 = -1\), robust estimators demonstrate a clear advantage.

  • Multicollinearity Effects: Non-robust estimators (e.g., PMLE, PRRE) are notably vulnerable to multicollinearity, leading to higher variance in estimates and elevated MSE values.

  • Comparative Performance: Non-robust methods (PMLE, PRRE, PMRTE) yield higher MSE values, particularly with small samples and high outlier percentages. Conversely, robust estimators (PMT, PMT-RRE, PMT-MRTE) consistently produce lower MSE values, confirming their robustness against outliers. The PMT-TPE estimator performs best, especially with large samples and high outlier rates. Additionally, robust estimators maintain better accuracy in higher dimensions (\(p = 8\)), where outliers have a more substantial effect.

These results underscore the superiority of robust estimators in datasets affected by outliers and multicollinearity. They provide more reliable estimates and sustain accuracy with increasing sample sizes, making them preferable in real-world applications. Among robust methods, PMT-TPE stands out as the most effective choice for complex data scenarios.

Fig. 1
figure 1

Estimated MSE for different estimators across different sample sizes and outlier percentages.

Full size image
Fig. 2
figure 2

Estimated MSE for different estimators under different multicollinearity levels and outlier percentages.

Full size image
Fig. 3
figure 3

Estimated MSE for different estimators considering different intercept values and outlier percentages.

Full size image
Fig. 4
figure 4

Estimated MSE for different estimators with different numbers of explanatory variables and outlier percentages.

Full size image

Figures 1-4 provide a comprehensive summary of the performance of various estimators under different experimental conditions. The graphical results compare both robust and non-robust methods across scenarios that vary in multicollinearity levels, sample size, the number of predictors, and intercept values, with outlier contamination levels of 10% and 20%.

Robust estimators consistently show better performance, especially in the presence of outliers and multicollinearity, as indicated by their consistently lower MSE values. In contrast, non-robust methods show a marked decline in performance when dealing with three major challenges: outlier contamination, correlated predictors, and high-dimensional data. Robust estimators, however, maintain stable and reliable performance despite these difficulties.

Among all the evaluated methods, PMT-TPE stands out as the most effective, consistently delivering the best results across all tested scenarios. These findings strongly advocate for the use of robust estimation techniques, particularly PMT-TPE, in regression analyses that involve complex datasets prone to outliers and multicollinearity.

Applications

We demonstrate the PMT-TPE estimator’s effectiveness using data from Sweden’s top football league (Allsvenskan) for 2025. This dataset, previously examined by Jadhav26 and Qasim et al.46,47, contains 98 match records with home team goals as the outcome variable (y). Nine betting market indicators serve as predictors, including: full time result (1=Home Win, 2=Draw, 3=Away Win)(\(x_1\)), pinnacle odds for home win (\(x_2\)), draw (\(x_3\)), and away win (\(x_4\)); market maximum odds for home win (\(x_5\)), draw (\(x_6\)), and away win (\(x_7\)); and market average odds for home win (\(x_8\)), draw (\(x_9\)), and away win (\(x_{10}\)); Betfair Exchange odds for home win (\(x_{11}\)), draw (\(x_{12}\)), away (\(x_{13}\)).

Three standard diagnostic tools were employed to evaluate multicollinearity among the predictor variables. First, the correlation matrix (Figure 5) revealed exceptionally strong linear relationships between variable pairs. Second, the condition number, calculated as the square root of the maximum to minimum eigenvalue ratio of matrix \(D\), produced a value of 586.998, well above the threshold indicating severe multicollinearity. Third, variance inflation factors are 1.21, 506.33, 374.37, 785.51, 270.79, 101.94, 531.02, 769.41, 338.06, 1296.31, 188.82, 162.43, and 422.49 for all predictors, with most values exceeding 10. These consistent findings from multiple metrics confirm the presence of substantial multicollinearity in the dataset.

Figures (6, 7, and 8) identified several data anomalies. The residual analysis showed three key patterns: non-linear trends in fitted values, non-normal error distribution, and heteroscedasticity. Leverage plots pinpointed influential observations capable of distorting model parameters. Boxplot visualization confirmed multiple outliers across variables, while half-normal plots revealed residuals deviating significantly from expected patterns. These collective findings demonstrate that the dataset contains both outliers and influential points that could compromise estimation accuracy, necessitating robust analytical approaches to mitigate potential bias.

Fig. 5
figure 5

Correlation matrix for explanatory variables in the Allsvenskan dataset.

Full size image
Fig. 6
figure 6

Diagnostic plot of the Allsvenskan dataset.

Full size image
Fig. 7
figure 7

Boxplots of variables in the Allsvenskan dataset.

Full size image
Fig. 8
figure 8

Analysis of residuals for the Allsvenskan dataset.

Full size image
Table 13 MSE and Coefficients for robust and non-robust estimators in Allsvenskan dataset.
Full size table

The MSE values and coefficient estimates for different estimators based on the Swedish football dataset are provided in Table 13. The comparative performance of robust and non-robust estimators reveals several key findings: the strongest negative effects appear for \(\beta _3\) (max away win odds), ranging from −3.73 (PMLE) to −0.27 (PMT-TPE), suggesting bookmakers heavily adjust odds for likely away wins. \(\beta _{2}\) (draw odds) shows particularly large variation (−2.01 to −0.18), indicating this is the most sensitive market indicator. \(\beta _{9}\) (market max home win odds) has the strongest positive effect (2.79-0.33), reflecting how extreme home win odds may overestimate scoring potential. \(\beta _6\) and \(\beta _{11}\) maintain consistent positive signs across methods, suggesting certain market indicators reliably predict goal outcomes.

PMT-TPE shows the smallest coefficient variations (e.g., \(\beta _{1}\) = −0.5931±40.0000 vs PMLE’s −0.7227±40.0778). Non-robust methods exhibit wider fluctuations, particularly for \(\beta _3\) (range of 3.40) and \(\beta _{9}\) (range of 2.46). PMT-TPE achieves 55.9% lower MSE than PMLE (18.66 vs 41.74). Robust methods collectively show 20-45% better prediction accuracy than non-robust alternatives. The consistent predictive power of \(\beta _{7}\)-\(\beta _{9}\) (market averages) suggests these aggregate measures contain valuable information. Large coefficient variations for extreme odds (\(\beta _3\), \(\beta _{9}\)) may indicate market overreactions. PMT-TPE’s optimal performance (MSE = 18.66) supports its use for football prediction models. The method’s stable coefficients (e.g., \(\beta _{12}\) = −0.077±40.001) provide a more reliable interpretation. Robust estimators particularly improve predictions for: high-variance outcomes (\(\beta _{8}\) improvement from −0.39 to −0.08) and market extreme values (\(\beta _{9}\) stabilization from 2.79 to 0.39).

This analysis demonstrates that while all estimators capture fundamental market relationships, robust methods provide both statistical and practical advantages for sports betting applications through superior accuracy and more stable parameter estimates. The results particularly highlight PMT-TPE as the most reliable approach for this dataset.

Table 14 Validation theorem conditions using the Allsvenskan dataset.
Full size table

Table 14 provides the results of validation testing of the theories using Allsvenskan data. The results confirm that all proposed bias coefficient estimators fully meet the required criteria.

Conclusion

In this paper, we proposed a new robust PMT-PTE designed to simultaneously address the problems of outliers and multicollinearity in PRM. The PMLE, while widely used, is highly sensitive to both issues, leading to biased coefficient estimates, inflated variances, and increased MSE. While several robust and biased estimators have been introduced separately to mitigate these challenges, there has been limited work on combining robustness and multicollinearity correction into a single framework. Our proposed PMT-PTE integrates the MT with the two-parameter estimator, offering a novel solution that effectively handles outliers while reducing the adverse effects of multicollinearity. Theoretical comparisons and extensive Monte Carlo simulations demonstrated the superiority of the PMT-PTE over existing estimators, particularly in scenarios where both outliers and multicollinearity are present. The simulation results consistently showed that the proposed estimator outperformed alternatives in terms of MSE minimization. Furthermore, the application of the PMT-PTE to a real-world dataset confirmed its practical utility, reinforcing the findings from the theoretical and simulation analyses. This study not only provides a robust and efficient alternative to traditional Poisson regression estimators but also opens new avenues for future research in robust regularized regression models. Overall, the PMT-PTE represents a significant advancement in Poisson regression analysis, offering researchers and practitioners a reliable tool for handling datasets affected by both outliers and multicollinearity. Although the PMT-PTE showed strong performance in this study, there are some limitations to consider. First, our work focused only on the Poisson regression model. It would be useful in the future to apply the PMT-PTE to other models, like negative binomial or zero-inflated models, especially when the data have overdispersion or many zeros. Second, our simulation covered certain situations with specific types of outliers and multicollinearity. Future studies could test the PMT-PTE on larger datasets, more complex data patterns, and different levels of data variability to better understand its performance. Future research could also explore using PMT-PTE with high-dimensional data and in machine learning models to handle more complex problems, or applying this estimator with other regression models.