Introduction

In the current period, recycling waste and reducing environmental pollution are the main goals of sustainable development. For this purpose, many researchers are working on new techniques in the field of concrete technology by evaluating the waste material in concrete and considering innovation1,2,3. Human hair (HH) is one of these utilized waste materials. Due to its non-biodegradable nature, the most cost-effective option to dispose of hair is to recycle it in an environmentally friendly manner. As a result, it was observed that various studies have been carried out to recycle these waste materials in an environmentally safe manner. In the literature, it has been realized that HH fibers can be used in concrete.

Bheel et al.4 conducted a study to observe the influence of HH as fiber on the fresh, physical, and mechanical belongings of concrete up to 4% HH by volume of cement. CS was improved by 8.15% at 1% of HH. STS and FS were enhanced by 21.83% and 12.71% at 2% of HH after 28 days, correspondingly. Jain and Kothari5 performed another investigation to observe the influence of HH on the mechanical properties of concrete. For this purpose, tests were performed on concrete samples with different ratios of HH fiber up to 3% by the weight of the cement. At the end of this study, an increase in the mechanical properties of concrete was reported. Meghwar et al.6 investigated using HH for the construction industry and to decrease the environmental influence of HH waste. For this purpose, HH waste was consumed in concrete as fiber with ratios of 1%, 2%, and 3% by the weight of the cement. At the end of this study, it was found an increase in CS of about 26.8%, 8.2%, and 9.1% at 1%, 2%, and 3%. HH, respectively.

In another study7, HH fibers were selected in 0.4, 0.8, and 1.2 weight percentages and the length of the fibers in each case mixed among 15 and 60 mm, and the examples were prepared of lengths of 40 × 40 × 160 mm. At the end of this investigation, it was observed that for more than 0.4 weight percentage hair, a hair length of 60 mm was more effective than hair with a length of 15 mm. The strength and durability of conventional concrete with additions of 0%, 0.5%, 1%, 1.5%, and 2% HH by weight of cement were compared in this study by Manaf et al.8. The optimum results were obtained with the use of 1% HH. CS and FS were increased by 12% and 22% when 1% HH was utilized. Nila et al.9 carried out CS and FS tests using waste HH. Experiments were performed on concrete cubes and various percentages of waste HH i.e. 0%, 1.5%, and 2% by weight of cement. At the end of the experiment, it was observed that waste HH additives for concrete improved the mechanical properties of concrete. Kameran et al.10 performed mechanical tests using HH of 0%, 2% and 2.5%. The highest results were obtained at 2.5%; however, it was indicated that increasing this amount may lead to workability problems. Akbar et al.11 utilized HH fiber as a fiber up to 5% with length of 30–40 mm and diameter of 70 µm into the concrete where partial replacement of silica fume was used as a cement replacement. Optimum results were obtained with the use of 2% HH. The workability problem was reported at higher dosages due to amalgamation. Manjunatha et al.12 used chopped HH up to 3% by weight of cement into concrete to investigate the effects on both mechanical and durability properties. Optimum results were obtained at 2–2.5 and reduction was observed at 3%. Adedokun et al.13 examined the impact of adding synthetic hair up 6% with increments of 2% on CS, STS, and density of concrete. Based on the results, 2% of synthetic hair by weight of cement was recommended. Small dosage of HH up to 1% was studied by14. HH increased CS by 17.8%, 12.9%, and 3.6% by 0.25%, 0.5%, and 0.75%, respectively. However, CS decreased by 5.2% at 1%. STS was increased by 27%, 31%, 32% and 17% for the use of 0.25%, 0.5% and 0.75% and 1.0% HH, respectively.

Ullah et al.15 performed another investigation. This research investigates the use of chopped HH, which is non-biodegradable. Different percentages of HH with 1%, 1.5%, 2%, 2.5%, and 3% by weight of cement were added to concrete. The optimum results of 2.5% HH increased CS, STS, and FS by 18%, 24%, and 31%. Nasreddine et al.16 conducted a study using HH up to 8% to examine the effects of HH on the mechanical capacity, durability, and thermal conductivity of mortar. At the end of this study, it was found that beyond 4% HH by cement weight enhances mortar toughness and ductility. On the contrary to other studies, CS and FS decreased as HH ratio increased in this study16.

Response Surface Methodology (RSM) emerged as a useful statistical method for optimizing composite mix designs, particularly when numerous factors influence the desired responses simultaneously17. RSM combines mathematical and statistical tools to model and evaluate problems where several independent variables influence a response variable, enabling researchers to find optimal operating conditions with limited experimental runs 18. In concrete manufacturing, RSM has been effective for comprehending intricate interactions between constituent ingredients and their impact on fresh, mechanical, and durability properties19. Recent high-impact studies have evidenced the efficacy of RSM in concrete optimization, with Alani et al.20 utilizing RSM alongside Central Composite Design to enhance ultra-high-performance concrete, attaining satisfactory correlation value (R2) of 98.11, 96.08, and 98.21 for compressive, flexural, and splitting tensile strength at 28 days, respectively. And, Onyelowe et al.21 demonstrated exceptional prediction accuracy with the Kstar model achieving R2 of 0.995, showing RSM’s reliability in multi-objective optimization scenarios. The application of RSM in fiber-reinforced concrete has shown particular promise, with studies by Awolusi et al.22 and Sridhar et al.23 revealing that RSM could successfully model the complex interactions between fiber content, matrix composition, and resulting mechanical properties, enabling the identification of optimal fiber dosages that maximize strength while maintaining workability. These experiments collectively illustrate RSM’s capacity to regulate the non-linear correlations inherent in fiber-concrete composites. Furthermore, comprehensive reviews confirm the applicability of machine learning methods—including adaptive and ensemble-based algorithms—throughout the construction lifecycle for prediction, optimization, and automation tasks, especially in areas involving fiber-reinforced and bio-based concrete systems24.

ANOVA helps researchers to separate the overall variation in experimental data into components owing to different sources, so identifying which factors significantly influence the response variables25 in concrete technology, ANOVA has become indispensable for confirming experimental results and ensuring the statistical significance of observed effects. In addition, a study by Ahmad and Alghamdi26 proved that ANOVA could efficiently identify significant factors influencing concrete strength with p-values less than 0.05, recent literature has extensively used ANOVA for concrete optimization studies, so providing confidence levels exceeding 95% for factor significance. The study also showed that ANOVA’s ability to detect interaction effects between multiple variables makes it particularly valuable for complex concrete systems where synergistic effects may occur. The integration of ANOVA with RSM has proven especially powerful for concrete research, as illustrated by Benyarar et al.27 who showed how ANOVA tables could validate RSM models by confirming the statistical significance of model terms, with F-values and p-values providing quantitative measures of factor importance. This combined approach enables researchers to not only optimize concrete properties but also understand the underlying mechanisms governing these improvements.

Artificial neural networks (ANN) for property prediction and optimization emerged from the complexity of concrete behavior, especially when including special elements28,29. Using conventional statistical approaches, ANNs show in capturing non-linear correlations and complex interactions that could prove challenging to characterize30. Recent advances in ANN implementations for concrete research have demonstrated remarkable mechanical parameter prediction accuracy. Using relatively large datasets, research by Aziz et al.31 developed ANN models achieving R2 values exceeding 0.96 for compressive strength prediction, so proving that ANN models could outperform conventional regression approaches, especially for complex concrete systems with many variables. Research by Ganasen et al.32 shows that this combined approach could achieve prediction accuracies exceeding 99% while providing statistical validation via ANOVA and optimization capacities through RSM, so forming as a comprehensive framework for concrete optimization from RMS, ANOVA, and ANN approaches. This multifarious approach helps scientists to not only precisely forecast specific properties but also grasp the statistical relevance of influencing elements and methodically improve mix designs.

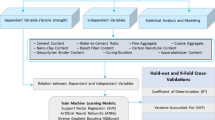
Considering numerous studies validating the efficacy of human hair (HH) fibers in improving concrete properties, significant research gaps exist. Previous research has primarily concentrated on empirical observations, neglecting the application of advanced modeling techniques. The application of advanced analytical techniques, including Artificial Neural Networks (ANN) and Analysis of Variance (ANOVA), to model and optimize the impacts of HH in concrete is still insufficiently investigated. This study systematically assesses the influence of HH at 1%, 2%, 3%, 4%, and 5% by weight of cement on the fresh, physical, and mechanical characteristics of concrete. This study performs experimental evaluations of compressive strength (CS), splitting tensile strength (STS), and flexural strength (FS), while also constructing predictive artificial neural network (ANN) models and utilizing response surface methodology (RSM) and analysis of variance (ANOVA) to identify statistically significant variables and improve performance. The originality of this work lies in its integration of experimental methods and machine learning techniques to enhance the design and understanding of HH fiber-reinforced concrete, thereby offering a comprehensive framework for sustainable material use and performance prediction.

Material processes and method

The scope of the study includes examining the microstructure of concrete, thoroughly assessing the impact of human hair on mechanical behavior, and combining mechanical property testing with ANOVA analysis. Therefore, the use of waste HH as a material that strengthens concrete has been found to lead to considerable improvements in a variety of concrete qualities, as shown by the different investigations described above. For this investigation, concrete samples that were generated by including waste HH at percentages of 1%, 2%, 3%, 4%, and 5% of the total weight of the cement were subjected to strength tests. Conventional reference concrete was produced by mixing water (W), cement (C), fine (FA), and coarse (CA) materials, without any HH additives. The fine aggregate has a range of 0–4 mm, the coarse aggregate has a range of 5–12 mm, the water used in the combination has a pH value that falls between 6.0 and 8.0, the cement is of the CEM 1 32.5 (32.5 MPa) class33. The experimental process resulted in the formation of a total of five distinct groupings. The specifics of this classification were shown in Table 1. According to the mixing ratios, reference and fibrous concretes were produced in each of the groups. The sum of the fine (FA) and coarse (CA) aggregates present in the mixture was represented by the letter A in the symbol. Some concretes have W/C ratios as high as 0.7 and as low as 0.234, however they are not recommended for good quality concrete34. The capillary porosity rises with the W/C ratio and has a significant impact on the concrete’s strength and permeability. Thus, it was decided that the W/C ratio for each group would be either 0.33 or 0.40. Additionally, the ratio of W + C/A was decided to be 0.40, 0.50, or 0.60.

Table 1 Mixing ratios required for 1 m3 of concrete.
Full size table

The physical and chemical properties of HHs have a significant effect on the durability and strength of the concrete. The diameter of the fibers has a direct relationship with certain mechanical properties35. The keratin found in the cortex is responsible for this property, and its long chains are compacted to produce a regular structure that, in addition to being firm, is also flexible36,37. Hair is characterized by its ability to resist stretching, elasticity, and hydrophilic power, which are all physical properties. It is estimated that around 65–95 percent of HH is composed of proteins, with the percentage of proteins ranging from 65 to 95%37. The widths of the hairs range from 50 to 100 µm, and their bumps are nanoscale38. Through the use of hair cords, these bumps assist in locking cement mortar7. Depending on the kind of hair, the size and quantity of these bumps might vary.

The SEM images of HH used in concrete production are presented in Fig. 1. The SEM photos illustrate the textured surface of the hair samples (Fig. 1a), which is crucial for assessing their adhesion within the concrete matrix. Edge detection illustrates fiber smoothness and keratin configuration, which could affect mechanical interlocking within the composite material (Fig. 1b). The roughness of the surface indicates that hair fibers might promote mechanical interlocking when incorporated with concrete. Using image processing techniques, the maximum simulated swelling effect percentages varied between 0.04% and 0.13%, showing minimal swelling. HHs can absorb water but do not expand significantly. The results indicate that HHs are unlikely to induce considerable micro-cracking in concrete due to swelling, which is advantageous for long-term durability. Similar observations were made in biochar-cement systems, where microstructural stability and limited expansion were linked to enhanced interfacial bonding and long-term matrix integrity39.

Fig. 1
figure 1

HH samples: (a) diameter, (b) broken strand.

Full size image

X-ray diffraction (XRD) analysis results are given in Fig. 2. The XRD pattern reveals a large peak at approximately 2θ = 20°, indicative of amorphous keratin in HH. The peak width and intensity indicate restricted crystalline domains, aligning with the semi-crystalline characteristics of keratin fibers. The amorphous keratin structure suggests low inherent rigidity, indicating that hair strands could serve as flexible reinforcements in concrete.

Fig. 2
figure 2

XRD results.

Full size image

The results of the energy-dispersive X-ray spectroscopy (EDX) analysis of HH are presented in Fig. 3. Calcium (Ca) and phosphorous (P) may engage with cement phases, thereby enhancing the adhesion between hair fibers and the concrete matrix. The oxygen peak corresponds with moisture content, indicating that HH can contribute internal curing effects in concrete.

Fig. 3
figure 3

EDX results.

Full size image

XRD and EDX studies were essential for complete characterization of the fiber-matrix system even if human hair functions primarily as a physical fiber reinforcement rather than a pozzolanic component40. In addition, comparable outcomes were also reported in composites utilizing waste steel fiber and fly ash, where the reinforcing contribution was primarily physical, while pozzolanic synergy was achieved through secondary components like fly ash41. By means of elemental composition of hair fibers (C: 45.2%, N: 16.8%, O: 23.1%, S: 14.9%), EDX analysis confirmed the absence of mineral contaminants, so producing baseline data corresponding with improvements in mechanical performance42. The studies mostly revealed amorphous keratin properties with no crystalline phases, so verifying fiber structural integrity in the alkaline concrete environment and proving that mechanical reinforcement rather than chemical processes produce the desired properties43,44. According to the characterization, hair fibers show stable, non-reactive reinforcing properties over the lifetime of the concrete since the observed increases in tensile strength and crack resistance directly correspond with this4. By providing necessary baseline data for reproducibility and allowing significant comparisons with past natural fiber studies, the results confirm the suitability of hair as a simply mechanical reinforcing element rather than a chemically active pozzolanic material45.

The simple tensile test setup is shown in Fig. 4. The tensile stress–strain plot of HH used is presented in Fig. 5. In the graph drawn by taking the average of the test results of 9 HH samples, the maximum tensile stress was obtained as 216.74 MPa. Stress values were obtained by Eq. (1), as follows:

$$\sigma = \frac{F}{di}$$
(1)

where F and di denote the maximum force and the radius of HH before deformation, respectively. The di value was taken 60 µm based on SEM analysis.

Fig. 4
figure 4

Simple tensile stress measurement system.

Full size image
Fig. 5
figure 5

Tensile stress vs. tensile stress diagram of utilized HH.

Full size image

Standardization of HH and optimization of the quantity required is important. The distribution of the length of HH was presented in Fig. 6. HH is collected from the authors (located in Türkiye) of this study. The HHs were meticulously kept in polypropylene bags to preserve their integrity after being collected. A superplasticizer was not used in the design combination. In Fig. 7, photographs of strength and slump tests are shown. Table 1 contains the mixture design information. The nomenclature used in Table 1, namely W/C0.33_WC/A0.4_FA/CA1.5_0%, refers to the following ratios: a water-to-cement ratio of 0.33, a water plus cement-to-aggregate ratio of 0.4, a fine aggregate-to-coarse aggregate ratio of 1.5, and a waste hair ratio of 0%. Likewise, specific terminologies are assigned to each respective category. The slump test was carried out by the requirements of standard TS EN206-1/2004.

Fig. 6
figure 6

Distribution of length of human hair.

Full size image
Fig. 7
figure 7

Testing: (a) Slump test, (b) test specimen, (c) ST test, (d) FS test instances.

Full size image

Artificial neural network (ANN) and analysis of variance (ANOVA)

The application of the ANN approach in this study was carried out using a commercial neural computing software. The proposed technique employed is visually represented in Fig. 8. The optimization algorithm employed in this study was the quasi-Newton approach. The Brent technique was employed to compute the learning rate tolerance, and a value of 0.001 was chosen as the learning rate tolerance. These methods were implemented for their ability to reliably estimate parameters and rapidly navigate the multi-dimensional response surface model, especially on cementitious based composites. The quasi-Newton approach is a popular iterative method for optimizing complex non-linear functions when computing full second-order derivative information is impractical or difficult46. It improved the mechanical properties of the response surface model combination, making it ideal for our study. The quasi-Newton method accelerated convergence to optimal solutions while using fewer resources due to the non-linear and sometimes noisy nature of concrete mixing experimental data47. As mentioned above, a tolerance of 0.001 was selected to attain a balance between accuracy and computing efficiency. This method allows systematic modifications to enhance the performance of the model without any significant computational expense. The selected tolerance level improved the accuracy of concrete optimization while ensuring applicability and preventing premature conclusions. The Brent strategy assisted in the identification of a suitable learning rate tolerance by reducing the error function linked to the response surface methodology and artificial neural network model. The Brent approach relies exclusively on function evaluations, distinguishing it from other techniques that necessitate derivative information, therefore making it suitable for scenarios where derivative calculations are impractical or resource-intensive48.

Fig. 8
figure 8

The proposed ANN structure.

Full size image

The artificial neural network (ANN) architecture employed in this study utilized a multi-layer perceptron structure with feed-forward propagation49. The hidden layer output was calculated using the following equation (Eq. 2):

$$h = f\left( {W_{1} x + b_{1} { }} \right)$$
(2)

where \(W_{1}\) represents the weight matrix connecting input to hidden layers, x denotes the input vector containing concrete mixture parameters (W/C, (W + C)/A, FA/CA, HH), b₁ is the bias vector for the hidden layer, and f represents the sigmoid activation function defined in Eq. 350:

$$f\left( z \right) = \frac{1}{{1 + e^{ - z} }}$$
(3)

The final output layer prediction was computed with Eq. (4). To minimize prediction errors for compressive strength, splitting tensile strength, and flexural strength responses, the network was trained using the quasi-Newton optimization method with backpropagation 51.

$$y = f\left( {W_{2} h + b_{2} } \right)$$
(4)

The accuracy of the created models was evaluated using mean absolute error (MAE), root mean square error (RMSE), and mean absolute percentage error (MAPE). ANOVA was conducted to assess the statistical significance of the inputs (W/C, W+C/A, FA/CA, HH). MAE assesses the mean differences between the predicted and actual values by avoiding excessive penalization of greater errors. Furthermore, it provides a balanced perspective on error distribution in contrast to RMSE (I). RMSE measures the magnitude of error in the same unit as actual data. RMSE improves the understanding of model performance relative to the observed data(K). Finally, MAPE is a crucial indicator that evaluates prediction accuracy as a percentage by averaging the absolute percentage difference between actual and predicted data. It provides advantages as it normalizes errors in relation to the observed values, facilitating interpretation across various scales and situations (L, M). Selected performance indicators are presented as following equations (Eqs. 5–7):

$${\text{RMSE }} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {t - y} \right)^{2} }$$
(5)
$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {t - y} \right)$$
(6)
$${\text{MAPE }} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {t - y} \right|$$
(7)

A response surface model with main effects, interaction effects, and quadratic terms for concrete mixture components including HH, cement content, and water-to-cement ratio was created to start the ANOVA process. These elements were chosen for their possible impact on concrete mechanical qualities. ANOVA was then used to partition the observed data’s total variance into factors and interaction terms for a full investigation of the model’s predictive components. This partitioning procedure calculated the sum of squares for each factor to measure its variation relative to the total variance. Interpreting the ANOVA findings required identifying factors and interactions with significant p-values that affected concrete mechanical parameters52,53.

Investigational test results and discussions

The objective of this experimental research is to investigate the usage of different combinations of cement and aggregate, where fine aggregate and cement are mixed with waste HH in specific proportions. The impact of the discarded HH was also assessed. As stated previously, to accomplish this goal, the percentage of used HH in the concrete mixture was varied as follows: 0%, 1%, 2%, 3%, 4%, and 5%.

The slump values of the concrete samples, which were determined by considering the mixing ratios specified in each group as shown in Table 1, are depicted in Fig. 9 for various proportions of waste hair. The determination of five distinct consistency classes (S1, S2, S3, S4, and S5) is outlined in TS EN206-1/200454 using the Slump test. The slump value of concrete can be categorized into different consistency levels based on the range of measurements. When the slump value falls within the range of 1–4 cm, it is classified as S1, indicating a dry consistency. A slump value between 5 and 9 cm corresponds to S2, representing a plastic consistency. Similarly, a slump value ranging from 10 to 15 cm is categorized as S3, indicating a fluid consistency. When the slump value falls within the range of 16–21 cm, it is classified as S4, signifying a very fluid consistency. If the slump value is greater than 22 cm, it is classified as S5 (slimy consistency). In the samples that do not include waste hair, as shown in Fig. 9, the slump value ranges between 14 and 17 cm, or at the S3 consistency level. In the concrete samples containing a waste hair ratio of 1%, the slump value is measured to be between 12 and 15 cm, indicating a consistency level classified as S2. In a similar, when considering a waste hair rate of 2%, the hair length falls within the range of 11–14 cm, denoted as S3. Likewise, with a waste hair rate of 3%, the hair length ranges from 9 to 12 cm, also classified as S3. Furthermore, a waste hair rate of 4% corresponds to a hair length range of 7–11 cm, categorized as S2-S3. Lastly, a waste hair rate of 5% corresponds to a hair length of 6–6 cm. The resulting values for slump, namely 10 cm, which corresponds to S1 consistency, were recorded. The results mentioned above indicate a negative correlation between the waste hair fiber ratio and both workability and slump value. Hence, it is evident that the inclusion of waste fiber in concrete should be limited to a certain proportion. The slump test findings indicate a transition in the consistency of the samples from S3 to S1 with an increase in the quantity of waste hair in the concrete. This reduction in workability may be related to the fact that there is less water available, specifically since hair requires some water to coat its surface. As a result of a shortage of freely accessible water, which might impart workability, the result is a decrease55.

Fig. 9
figure 9

Slump test results for different groups.

Full size image

Detailed analysis of CS effect

This test’s primary goal is to evaluate a sample’s fracture strength under axial force. The CS tests required for all test specimens were performed according to ASTM C3956 procedures. The cube test samples’ dimensions of 150 mm × 150 mm × 150 mm were used for this purpose. These samples were tested under axial load and failure loads were determined. In this way, the specimens could be compared. As given in Fig. 10, the CS test values were obtained after 28-day curing. Based on the findings presented in Fig. 10, the CSs of cubes are shown for five distinct groupings. When the 1st Group trials (W/C0.33_WC/A0.4_FA/CA1.5) are analyzed, the CSs of the samples containing 1%, 2%, 3%, 4%, and 5% HH improved CS by 4%, 6%, 14%, 4%, and 4% respectively, compared to the samples that do not include HH. Group 2 research studies (W/C0.4_WC/A0.6_FA/CA1.5) showed a change in CS of 2.6%, −2.6%, −4.6%, and −4.5% when compared to the reference sample devoid of HH (W/C0.4_WC/A0.6_FA/CA1.5_0%).

Fig. 10
figure 10

CS the results for the various groups.

Full size image

In the Group 3 trials, the samples (W/C0.33_WC/A0.6_FA/CA1.5) were compared to the reference sample (W/C0.33_WC/A0.6_FA/CA1.5_0%). The observed differences in the corresponding percentages were 0.7%, 0.4%, 7.1%, and 9.3%. A decrease of −0.58% was noticed.

In the tests conducted in Group 4 (W/C0.4_WC/A0.5_FA/CA1.5), the observed values for the variables were compared to those of the reference sample (W/C0.4_WC/A0.5_FA/CA1.5_0%). The results showed a difference of 17.5%, 20.5%, and 2.5% for the three respective variables. A positive growth rate of 10.4% and a negative decline rate of 24.0% were observed.

In the Group 5 experiments (W/C0.33_WC/A0.5_FA/CA1.0), the observed values for the variables were 6.1%, 10.5%, and 10.7% when compared to the reference sample (W/C0.33_WC/A0.5_FA/CA1.0_0%). A reduction of 12.3% and 14.9% was noted.

Last but not least, 6.1%, 10.5%, and 10.7%, respectively, were found in the trials performed by Group 5 (W/C0.33_WC/A0.5_FA/CA1.0) in comparison to the reference sample (W/C0.33_WC/A0.5_FA/CA1.0_0%). A reduction of 12.3% and 14.9% was noted. A decline in the CS of concrete was seen across all discarded HH ratios within Group 5. In the concrete mixture containing 5% used human hair, the biggest decrease, 14.9%, was recorded. This instance demonstrates the need to accurately determine the proportions of water, cement, fine, and coarse material used to produce concrete. Based on the observed enhancement in CS, it was determined that the optimal mixing ratio was found within the fourth group, namely in the sample containing 2% waste HH addition (W/C0.4_WC/A0.5_FA/CA1.5_2%).

Comparing Group 1 and Group 2, it could be noted that the resulting concrete had a greater CS than the first group. It is important to acknowledge that the present rate may be susceptible to prospective increments of up to 30%. According to research results, it has been shown that the effectiveness of a mixture might decrease when the fraction of HH residue exceeds 3% for both experimental groups. Comparing Group 1 and Group 3, the investigation revealed a decrease in the CSs of the combination by 0.32%, 3.86%, 5.87%, 6.06%, 4.80%, and 5.08%. This phenomenon took place under the condition where the water-to-cement ratio (W/C) was maintained at a constant value of 0.33, but the ratio of water plus cement to aggregate ((W + C)/A) was raised from 0.40 to 0.60. Comparing Group 2 and Group 4, in contrast, when the water-to-cement ratio (W/C) is consistently set at 0.4 and the ratio of water plus cement to aggregate ((W + C)/A) is reduced from 0.6 to 0.50, it has been observed that the addition of waste HH in concrete at levels of 0%, 1%, 2%, and 3% results in reductions in CS. Specifically, the CSs of the concrete mixture decreased by 30%, 17.3%, 17.8%, 26.3%, 34.3%, and 44.3% respectively. Based on the data, it has been shown that the use of waste HH at a concentration of 2% in conjunction with a water-to-cement ratio of 0.4 may provide the most favorable CS value for concrete additives. When the ratio of W/CT is altered from 0.4 to 0.33 while keeping the ratio of (W + C)/A fixed at 0.60 (Comparing Group 2 and Group 3), the corresponding percentage decreases are determined to be 23.4%, 22.5%, 25.1%, 15.7%, 12.2%, and 20.2% accordingly. This is the case when the ratio of (W + C)/A is held constant. The chemical and physical structure of concrete, which includes waste human hair, can help to explain this situation.

An in-depth analysis of impact of splitting tensile tests (STS)

Each concrete sample underwent STS, which was completed in compliance with ASTM C49657 regulations. The results of STS often follow a pattern that is parallel to that which is seen in the CS test. This is shown in Fig. 11. The tensile strength of concrete is increased as HH at concentrations increased up to 3%. Except for 5th group, after that point, however, there is a noticeable and steady decline in strength. In addition to the CS of concrete, which is indicative of its ability to sustain applied loads, there exists an analogous relationship between the two. According to the findings shown in Fig. 11, adding a tiny quantity of waste HH to the concrete mix resulted in greater STS values in the finished concrete than ordinary concrete mixes without waste HH. Kindly note that observations have shown that exceeding a certain limit of 3% in the quantity of waste HH may result in a reduction in STS. When Fig. 11 is inspected, it can be noted that STS has increased in the first four groups by up to 3% and in the fifth group by up to 4%. The observed increases in comparison to the reference sample for HH ratios of 1%, 2%, and 3% were 21.6%, 27.13%, and 35.73%, respectively, for the first group; 16.27%, 18.20%, and 16.49% for the second group; 9.87%, 21.48%, and 30.23% for the third group; and 4.78%, 10.65%, and 23.71% for the fourth group. Within Group 5, the observed increments were 6.02%, 17.71%, 27.71%, and 54.70%, respectively. The sample in Group 5 that exhibited the most substantial rise was the W/C0.33_WC/A0.5_FA/CA1.0_4% sample. The sample W/C0.33_WC/A0.4_FA/CA1.5_3% in Group 1 had the highest rise among the first four groups.

Fig. 11
figure 11

Comparison of STS outcomes across categories.

Full size image

In Group 1, for 4% and 5% of the mixture was swapped out for a smaller size, it was found that the STSs of the concrete admixture dropped by 4.3% for 4% and 16% for 5%. The most favorable STS value for incorporating concrete with W/C0.33_WC/A0.5_FA/CA1.0 may be achieved by using waste HH at a concentration of 4%, alongside a water-to-cement ratio of 0.4.

Comprehensive investigation of influence of flexural performance tests

According to ASTM C7858 criteria, the FS test was performed on each concrete sample. The FS examination was based on a beam example with a length of 100 × 100 × 400 mm. The FS of concrete was improved when used with HH in proportions of up to 3%. After that point, however, there is a noticeable weakening of the effect. According to the data shown in Fig. 12, including waste HH into the concrete mixture up to 3% led to the strength of concrete with higher FS values when compared to reference concrete. The FS of a combination will decrease if the amount of HH waste in the combination is more than 3%, except for the W/C0.33_WC/A0.5_FA/CA1.0_4% sample in Group 5. The observed increase in Group 5, namely in the sample with a waste HH rate of 4% (W/C0.33_WC/A0.5_FA/CA1.0_4%), exhibits a significant 54.82% rise in the FS compared to the reference sample (W/C0.33_WC/A0.5_FA/CA1.0_0%). Based on the obtained findings, it can be said that the FS of the samples exhibits a consistent rise to 3% for the first four groups, and up to 4% for the fifth group. However, the introduction of waste HH beyond these thresholds results in a reduction in the capacity. According to the findings of the research, the highest increase in FS value for concrete with W/C0.33_WC/A0.5_FA/CA_1% may be accomplished by using 4% HH.

Fig. 12
figure 12

Findings from FS for many categories.

Full size image

ANN and ANOVA results

The predictive efficacy of the developed ANN model was assessed by comparing the model’s anticipated values with the experimentally obtained strengths. The strong connection between the anticipated and actual data is demonstrated by the optimal linear relationships, which may be expressed as follows Eqs. (8–10):

$$\begin{gathered} {\text{CSpredicted}}\left( {{\text{MPa}}} \right) = {5}.{1}0 + {12}.{32}\left( {{\text{W}}/{\text{C}}} \right) + {2}.0{1}\left( {\left( {{\text{W}} + {\text{C}}} \right)/{\text{A}}} \right) \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + {7}.{24}\left( {{\text{FA}}/{\text{CA}}} \right) + 0.{6}\left( {{\text{HH}}^{{2}} } \right) + {3}.{\text{5HH}} \hfill \\ \end{gathered}$$
(8)
$$\begin{gathered} {\text{STSpredicted}}\left( {{\text{MPa}}} \right) = 0.{5}0 + 0.{84}\left( {{\text{W}}/{\text{C}}} \right) + 0.{3}0\left( {{\text{W}} + {\text{C}}} \right)/{\text{A}}) \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 0.{9}0\left( {{\text{FA}}/{\text{CA}}} \right) + 0.00{8}\left( {{\text{HH}}^{{2}} } \right) + 0.{\text{6HH}} \hfill \\ \end{gathered}$$
(9)
$$\begin{gathered} {\text{FSpredicted}}\left( {{\text{MPa}}} \right) = {3}.00 + 0.{12}\left( {{\text{W}}/{\text{C}}} \right) + 0.0{5}\left( {\left( {{\text{W}} + {\text{C}}} \right)/{\text{A}}} \right) \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + 0.0{7}\left( {{\text{FA}}/{\text{CA}}} \right) + 0.{4}\left( {{\text{HH}}^{{2}} } \right) + {1}.{\text{7HH}} \hfill \\ \end{gathered}$$
(10)

The equations exhibit slopes around one and minimal interceptions, signifying that the ANN-based forecasts align closely with the measured intensities. Figure 13 displays the correlation coefficients acquired using ANN technique for CS (a), STS (b), and FS (c), respectively. R2 coefficients were calculated as 0.9621, 0.9563, and 0.9472 as seen in Fig. 13. A correlation coefficient of R greater than 0.90 indicates that the model is appropriate for predicting the outcome. In addition, RMSEs were determined between 1.39 and 1.53, MAPEs varied between 0.030 and 0.034, and the maximum MAE of 1.137 was obtained.

Fig. 13
figure 13

Correlation coefficient of (a) CS, (b) STS, (c) FS for ANN.

Full size image

ANOVA outcomes for CS, STS, and FS are presented in Tables 2, 3, and 4, respectively. ANOVA was utilized to determine the statistical significance of the models and their individual input terms at a 95% confidence level. In this context, a p-value less than 0.05 indicates statistical significance of a given factor on the response variable.

Table 2 ANOVA results for CS at 28 days.
Full size table
Table 3 ANOVA results for STS at 28 days.
Full size table
Table 4 ANOVA results for FS at 28 days.
Full size table

Table 2 illustrates that all mix design ratios—specifically the water-to-cement (W/CT), water and cement-to-aggregate (W + CT/A), and fine-to-coarse aggregate (FA/CA) ratios—exhibited highly significant effects on compressive strength (CS) (p = 0.000). The incorporation of HH fibers did not yield a statistically significant effect (p = 0.159), suggesting that although HH may facilitate enhancements, the primary impact on CS is derived from the essential mix proportions. This corresponds with literature findings indicating that mixed ratios primarily dictate compressive strength.

Table 3 presents results for splitting tensile strength (STS) that exhibit a comparable trend. The ratios W/CT (p = 0.014), W + CT/A (p = 0.001), and FA/CA (p = 0.000) were statistically significant, while HH fiber content was not (p = 0.087). This indicates that tensile strength is more responsive to aggregate and binder ratios than to fiber content within the examined range.

On the other hand, Table 4 shows a distinct trend in flexural strength (FS). The HH addition exhibited a highly significant effect (p = 0.0027), surpassing all other input variables, which had p values markedly greater than 0.05. This result underscores the essential function of HH fibers in augmenting tensile strength under bending stresses, consistent with anticipated outcomes for fibrous reinforcement. Consequently, although HH may assume a subordinate role in compressive and splitting strengths, it remains an essential factor in flexural performance59.

Figures 14, 15, 16 depict the outcomes of the Response Surface Methodology (RSM) analysis for compressive strength (CS), splitting tensile strength (STS), and flexural strength (FS). These plots illustrate the interaction effects of the input parameters—water-to-cement ratio (W/C), combined water and cement to aggregate ratio ((W + C)/A), fine to coarse aggregate ratio (FA/CA), and human hair (HH) fiber content—on the target strength responses.

Fig. 14
figure 14

Response surfaces of CS (created by using python 3.10. https://www.python.org/).

Full size image
Fig. 15
figure 15

Response surfaces of STS (created by using python 3.10. https://www.python.org/).

Full size image
Fig. 16
figure 16

Response surfaces of FS (created by using python 3.10. https://www.python.org/).

Full size image

The RSM analysis results of CS were plotted in Fig. 14. Figure 14 shows that there is an interaction between (W + C)/A, W/C and HH, F/CE in terms of CS. Decreasing W/C contributed to the non-linear increase in CS. When (W + C)/A is close to 0.50, CS decreases gradually. With the decrease in F/CE, CS increased linearly. These analysis results are in line with the related previous studies4,10. Moreover, the compressive strength (CS) increases with a decrease in the fine aggregate to coarse aggregate ratio (FA/CA), indicating that coarse aggregates improve load-bearing capacity. HH’s influence seems moderate, yielding positive contributions up to an optimal threshold. The ideal parameter configuration for attaining a compressive strength of 48.50 MPa at 28 days comprises: W/C = 0.393, (W + C)/A = 0.42, FA/CA = 1.05, and HH = 0.5%. Validation tests produced an average compressive strength of 47.14 MPa, indicating a slight deviation (≈3%) within permissible engineering limits 60,61.

Figure 15 illustrates that the RSM model for STS exhibits steeper slopes for the (W + C)/A and HH variables, signifying their predominant influence on tensile resistance. Based on the analysis performed via RSM, the optimal values for the parameter’s W/C, (W + C)/A, FA/CA, and HH are determined to be 0.338, 0.402, 1.025, and 4.97, respectively. These values are found to be associated with a goal splitting strength of 2.81 MPa at a curing period of 28 days. The incline of the (W + C)/A and HH is steeper in comparison to the W/C and FA/CA. This suggests that the STS of concrete is notably affected by (W + C)/A and HH. The mean STS of the validation samples were obtained as 2.74 MPa indicating that margin of error in the limits57,62.

Figure 16 illustrates the three-dimensional surface for FS. The interaction analysis indicates that FS is primarily affected by (W + C)/A and HH content, as demonstrated by the steeper slopes. This substantiates the idea that flexural capacity is augmented by improved matrix-fiber cohesion and optimal paste volume. The optimal parameters for achieving a compressive strength of 19.46 MPa at 28 days are W/C = 0.399, (W + C)/A = 0.459, FA/CA = 1.01, and HH = 1.91%. The mean FS from three validation samples was 19.03 MPa, with an error margin of 2.2%, conforming to ASTM C78/C78M-22 standards58.

The predictive accuracy and reliability of the RSM models were further evaluated by examining the correlation between predicted and experimental values for each strength parameter. As illustrated in Fig. 17, scatter plots comparing actual versus predicted values for CS, STS, and FS indicate strong alignment, reinforcing the validity of the regression models developed. The correlation coefficients (R2 values) were 0.9434 for CS, 0.9311 for STS, and 0.9365 for FS, indicating an exceptional model fit and negligible divergence between the observed and predicted results. The elevated coefficients indicate the efficacy of the RSM methodology accurately representing the nonlinear characteristics of concrete response variables affected by various interacting factors. The results confirm that the equations derived from RSM can be consistently used for predictive and optimization objectives in fiber-reinforced concrete systems, so supporting a data-driven approach for performance improvement and resource efficiency in sustainable mix design.

Fig. 17
figure 17

Predicted and actual value of CS, STS and FS.

Full size image

Conclusions

With HH at 0%, 1%, 2%, 3%, 4%, and 5% of the cement weight, concrete was made to test different waste HH ratios. The W/C ratio was 0.33 or 0.40 for each group. The (W + C)/A ratio was 0.40, 0.50, and 0.60. According to this study, the following may be concluded. As waste HH increases in concrete sample, slump test results decline. This decrease in workability may be due to that hair needs some water to coat its surface63. Another reason for the reduction in the workability can be accumulation of HH, which tends to cluster together as fibers, hindering the flow of the mixture. Concrete samples with up to 3% HH had greater mechanical properties than reference samples. With waste HH exceeds 3%, the mixture may lose capacity. The literature reports similar capacity losses at a specific amount of HHs4,11,12,14,55,64. This decline in strength might result from concrete’s density decreasing as the proportion of HH increases55,64. Besides, the presence of a significant quantity of HH also results in the existence of space inside the mixture during the pouring process64. The another reason can be due to agglomeration of HHs at higher dosage, which results in reductions of bonding strength of cement11. Similar reason was explained by 1 that at high dosage HHs form spherical clusters, making separation difficult which leads to amalgamation in concrete. This interlocking effect leads to fiber balls that resemble voids in the concrete, which can negatively impact its overall strength1. SEM analyses at the microstructural level revealed that HH fibers exhibit a textured, somewhat rough surface, thereby improving mechanical interlocking with the cement matrix. XRD validated the semi-crystalline keratin structure, indicating flexibility and low rigidity, whereas EDX results revealed minimal mineral contaminants and implied internal curing potential via oxygen and phosphorus content. These microstructural observations corroborate the assertion that HH serves as a durable, physical reinforcement over time without undermining matrix integrity. ANN model showed strong correlation coefficients: R2 = 0.9621 for compressive strength, R2 = 0.9563 for splitting tensile strength, and R2 = 0.9472 for flexural strength. This confirms the substantial correlation between estimated and experimental results. Additionally, the research indicated that the W/C, (W + C)/A, FA/CA, and HH components in CS interact strongly. The ideal W/C, (W + C)/A, FA/CA, and HH values for a target CS of 48.50 MPa at 28 days are 0.393, 0.42, 1.05, and 0.5, according to RSM analysis predicts W/CT, W + CT/A, F/CE, and HH of 0.338, 0.402, 1.025, and 4.97 for the 28-day objective STS of 2.81 MPa. RSM gives the optimum W/C, (W + C)/A, FA/CA, and HH values of 0.399, 0.459, 1.01, and 1.91 for 28-day FS of 19.46 MPa. Experiments revealed HH increases mechanical characteristics. Future study might investigate the load-bearing capacity, durability, and long-term performance of concrete containing HH in beams, columns, and slabs.