Introduction

One of the most serious types of diseases is cancer, which is caused by uncontrolled cell divisions and aberrant cell growths in tissues or organs1. Owing to its severe consequences, cancer ranks among the top global public health priorities and is a leading cause of mortality worldwide. According to the International Agency for Research on Cancer (IARC), approximately 20 million new cancer cases and 9.7 million cancer-related deaths occurred in 2022, accounting for 1 in 6 deaths globally (IARC, GLOBOCAN 2022)2,3. However, if detected early, the condition can often be effectively treated with radiation therapy, surgery, or chemotherapy4. Different nanoformulations with superior pharmacokinetic qualities such as enhanced tumor accumulation, prolonged systemic circulation, reduced off-target toxicity, and stimuli-responsive drug release and biocompatibility hold significant promise for the delivery of innovative anti-cancer medications as nanomedicine becomes more widely used5,6,7,8,9. The issues of unfavorable side effects and low water solubility during the therapeutic medication delivery agents are resolved by these nanocarriers. Additionally, these nanocarriers facilitate their use for tumor therapies and lengthen the therapeutic circulation period in blood for increased therapeutic and delivery efficacy10,11,12. Through the encapsulation of certain therapeutic chemicals, nanomedicines can be produced in nanocarriers to effectively target tumors through the effect-mediated passive targeting approach13.

Among different anti-cancerous drugs, the Flutamide (FLT), Gemcitabine (GB), (Fig. 1) are widely used14. Flutamide (FLT) is a unique antiandrogenic medication without a steroidal composition. Flutamide is a popular nonsteroidal antiandrogen medication used to treat prostate cancer, yet there have been isolated reports of hepatotoxicity in patients taking it. Its toxicity is thought to result from the bioactivation of FLT and its subsequent covalent attachment to cellular proteins. It is being utilized more frequently as a neoadjuvant treatment prior to radical prostatectomy and as part of total androgen ablation therapy15. Advanced prostate cancer is treated with flutamide, a drug that has no hormone agonist action16. DFT studies have also examined its interactions with several nanocarriers, which unveiled principal binding mechanisms and stability. For instance, a study on the complexation of flutamide with cucurbit[n]uril showed exothermic binding and spontaneous inclusion complex formation due to electrostatic interactions and hydrogen bonding17 .Another study explored the interaction of flutamide with COOH- and COCl-functionalized carbon nanotubes and found that COOH-functionalized nanotubes provided more desirable binding energies18. Graphitic carbon nitride (g-C3N4) was also examined as a flutamide carrier, with DFT verifying stable drug-nanocarrier interaction19. Zinc oxide nanosheets (ZnONS) also exhibited good adsorption behavior for flutamide, as verified by DFT calculations20.

A pyrimidine nucleoside antimetabolite, gemcitabine is one of the cytotoxic medications. Breast, pancreatic, bladder, and large cell lung cancer can all be treated with gemcitabine21,22,23. It is effective against ovarian cancer, according to recent studies. Nowadays, clinical trials are conducted to assess the role of gemcitabine in conjunction with novel targeted treatments24. Certain theoretical studies have also been evaluated their binding with different nanocarriers, including carbon nanotubes and fullerenes. Pd-doped carbon nanotubes have strong interaction with gemcitabine, indicating potential for effective drug delivery25. Further, interactions between gemcitabine and Mg@B40 or Ca@B40 fullerenes were shown to have strong adsorption energies, reflecting partial covalent interactions improving drug stability26. Another research identified pure B40 fullerene as a potential carrier for gemcitabine and concluded that DFT and QTAIM calculations were helpful in establishing its effectiveness27.

Even though these medications have therapeutic benefits, if taken in excess, they might harm healthy cells as well. Melanotic cells are destroyed along with healthy cells by standard chemotherapeutic, non-targeted approaches28,29. Therefore, it is necessary to regulate the plasma concentration of these anti-cancer medications using a targeted drug delivery system and to adjust the dosage based on the patient’s tolerance level and the severity of the disease30,31. Thus, new, and effective drug delivery systems with superior therapeutic characteristics are inevitable.

Recent years have seen a sharp advancement in nanotechnology, opening up a plethora of fascinating concepts and opportunities for the detection and management of disease32,33,34,35. As a result, nanocarriers’ focused assault on malignant cells has drawn a lot of interest. While protecting healthy cells, the medication delivery via nanocarriers in cancer treatment has demonstrated encouraging outcomes. Additionally, the use of nanoparticle-based drug delivery systems can address the problem of reduced absorption, demonstrating the remarkable potential of nanoparticle-based DDS in the treatment of cancer29. Examples of such nanocarriers that have been used for encapsulation and effective drug delivery including, micelles, nanoparticles, polymeric conjugates, dendrimers, liposomes, carbon nanotubes capsules and hydrogel28,30. When used as anticancer medication vehicles, these nanocarriers have demonstrated effective performance in reducing side effects36.

Literature reveals many structures which have been used as carriers such as, amphiphilic copolymers can be used to create nano self-assembled structures that function as effective delivery systems for anticancer medications like doxorubicin37.Moreover, a variety of near-IR light-responsive drug delivery vehicles have been effectively synthesized and described. When it comes to treating cancer cells, these drug delivery vehicles have remarkable outcomes. P. N. Samanta et al. described the use of fullerene (C60) nanocages as a drug delivery system for the transportation of temozolomide and carmustine38.They found that the increase in polarity of the C60 nanocage following adsorption of carmustine and temozolomide aids in the off-loading of these medications into biological systems. Additionally, it has been revealed that graphene and graphene oxide (GO) can also be used as nanostructured drug delivery vehicles. Because of their efficient loading, focused drug delivery, and regulated release, both have the potential as excellent options for the delivery of different medications39. To achieve considerable therapeutic efficacy and quick response, high sensitivity, selectivity, and minimal adverse effects, additional research must be done on novel nanocarriers40,41.

In this work, we examined the benzimidazolone capsule’s drug delivery capabilities for the drugs gemcitabine and flutamide. Benzimidazolone cavitand-based nanocapsule have not been the subject of extensive studies in literature. Weak noncovalent interactions are essential for the synthesis of more selective and active ligands in medicinal chemistry42. Dimeric nanocapsules based on deep benzimidazolone cavitands can be great hosts for tiny medicinal molecules. Various appropriate guests can be bound by the deep cavity of the benzimidazolone nanocapsule43. It also facilitates the bridging of hydrogen bonds to other surfaces through its waterlogged interface. The surface presents a viable contender for adsorption applications due to the cavity’s ability to enhance drug adsorption44. Theoretical investigations, especially those involving density functional theory (DFT), have shed light on their molecular interactions and efficiency. Investigations into benzimidazolone derivatives have been used in encapsulation, with emphasis on their structural and electronic properties. For example, DFT analysis of 1-(cyclohex-1-enyl)-1,3-dihydro-2 H-benzimidazolone (CHBI) showed its adsorption characteristics on copper surfaces, exhibiting an 86.49% rate of corrosion inhibition45. Benzimidazole derivatives have also been explored as anticancer agents, where DFT studies have optimized their geometric structures and correlated theoretical results with experimental cytotoxicity data46. In addition, benzothiazole-imidazolone hybrids were investigated using DFT for insight into their binding interactions with bacterial DNA gyrase, with emphasis on their antimicrobial activity47.

Despite extensive theoretical investigations on benzimidazolone capsules as promising drug carriers, their potential for the targeted delivery of flutamide and gemcitabine remains unexplored in the literature. Therefore, the current work uses DFT calculations to examine the adsorption mechanism of flutamide and gemcitabine on the surface of benzimidazolone capsules. To investigate electrical structure, the frontier molecular orbital (FMO) analysis is employed. Additionally, non-covalent interaction (NCI) and quantum theory of atom in molecule (QTAIM) investigations are carried out to determine the nature and degree of interaction.

Computational insights

The Guassian 09 program is used for analyzing all the calculations. The M06-2X /6-31G(d) level of theory is selected for geometry optimization. The hybrid functional M06-2X, which has twice as much non-local exchange, is considered ideal for studying noncovalent interactions48. M06-2X gives results with reasonable accuracy for systems exhibiting dispersion forces39,40,41,42. In literature, there are various examples reported, where complex systems have been frequently evaluated with a similar level of theory49,50,51,52. GaussView 5.0 and Chemcraft software53 were utilized to visualize the optimized geometries. Several drug@capsule orientations were investigated in order to determine the most stable configuration with the lowest energy. The equation used to investigate the energy of complex is:

$${\text{DE}}\,=\,{{\text{E}}_{{\text{complex}}}} - ({{\text{E}}_{{\text{drug}}}}+{\text{ }}{{\text{E}}_{\text{C}}}_{{{\text{apsule}}}})$$
(1)

In Eq. (1): Ecomplex, Ecapsule and Edrug represent the electronic energies of drugs-capsule complexes, isolated capsules and drug, respectively. Quantum chemical simulations involving fragments (interacting) are usually prone to BSSE (basis set superposition error). Therefore, it is imperative to add corrections for such types of errors. In this regard, BSSE is an efficient approach to overcome the error. The Counter poise method corrects this energy as shown given below.

$${\text{D}}{{\text{E}}_{{\text{int}},{\text{ CP}}}}\,=\,{\text{D}}{{\text{E}}_{{\text{int}}}}--{{\text{E}}_{{\text{BSSE}}}}$$
(2)

where Eint.CP, Eint and EBSSE present the counterpoised interaction energy, raw complexation energy and energy after BSSE correction. To investigate the electronic changes Frontier molecular orbital (FMO) analysis is performed54. To find out charge transfer between drugs and capsule, natural bond orbital (NBO) and electron density differences (EDD) analyses was carried out55. EDD analysis provides a visual representation of the charge transfer between interacting atoms using colored surfaces, adding further to NBO results56. NBO charges are derived from DFT calculations by partitioning the electron density into localized “natural” orbitals in GaussView 5.0.

NCI analysis is used to visualize and determine the forces that interact between drugs and the capsule surface. To plot 2D RDG graphs and 3D-isosurfaces of drug@capsule complexes, Multiwfn 3.7 software is employed. In general, the non-covalent interaction index depends on two variables: electron density (ρ) and reduced density gradient (RDG), and the relationship between both of these variables is expressed in the following Eq. 

$$\:RDG=\frac{1}{{2\left(3\pi\:\right)}^{1/3}}\:\frac{\nabla\:\rho\:}{{\rho\:}^{3/4}}$$
(3)

Different colors on 3D iso surfaces correspond to different kinds of forces. Typically, three distinct color schemes are displayed, each of which stands for a particular form of interaction. For example, the green color symbolizes weak forces and London dispersion. Strong forces like hydrogen bonds are represented by the blue color, whereas steric repulsion between interacting species is represented by the red color. The strength of a weak nonbonding contact is represented by the thickness of iso surfaces. The strength of contact is strongly correlated with its thickness. The 2D NCI graph represents the relationship visually between sign (λ2) ρ (au.) on the x-axis and RDG (reduced density gradient) on the y-axis. On this graph, hydrogen bonding, weak van der Waals forces, and repulsive forces are represented, respectively, by the blue, green, and red spikes56,57,58.

The QTAIM analysis is mainly used for studying noncovalent interaction. The various topological parameters are used in QTAIM analysis to evaluate bond critical point (BCPs). These topological parameters are electron density, total density and laplacian.

$$\:\text{H}\left(\text{r}\right)=\text{V}\left(\text{r}\right)+\text{G}\left(\text{r}\right)$$
(4)

If the laplacian of electron density is greater than zero, it indicates weak intermolecular forces whereas, if the value of laplacian of electron density is less than zero it shows covalent bonding58,59,60,61. Multiwfn 3.7 is used for QTAIM analysis62.

Results and discussion

Geometric optimization

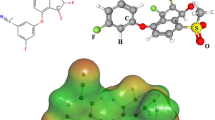
Two different drugs, gemcitabine and flutamide, have been selected for this investigation in order to examine their adsorption on benzimidazolone capsules as a drug delivery system. Chemical structure of both drugs is represented in Fig. 1. Figure 2 represents the optimized structure of the benzimidazolone capsule. Dimeric nanocapsules based on deep benzimidazolone cavitands are created from a resorcinarene core by covalent attachment of walls and adding additional characteristics like rigidified walls and intramolecular hydrogen bonding patterns in order to stabilize the malleable vase-like structures, are frequently used63. The dimeric nanocapsule based on benzimidazolone cavitands have symmetrical vase shape and hold C4v symmetry64.

Fig. 1
figure 1

Optimized geometries and simple 2D images of studies anticancer drugs.

Full size image
Fig. 2
figure 2

Optimized capsule geometry at the M06-2X/6-31G(d, p) level, highlighting key intermolecular interactions (dashed lines).

Full size image

The designed complexes are optimized to their most stable geometry using the M06-2X/6-31G(d, p) level of theory. In order to find the most suitable interaction site, all the possible orientations are studied whereas, the most stable geometries are selected for further analysis (see Fig. S1 of Supporting Information). Moreover, different possible conformations of drug molecules are also considered to get the most stable complex (see Fig. S2). The computed geometries of both GB and FLT complexes are presented in Fig. 3.

Two important factors for estimating interaction behavior are interaction distance and complexation energy (ΔE)65. As analyte approaches the surface (capsule) for complexation, bond distances decrease. Drug-capsule geometry interactions are determined by calculating complexation energies and the minimum interaction distances. In Table 1, we have presented the interaction distances and corresponding complexation energies for each complex (drugs@capsule).

Fig. 3
figure 3

The most stable geometries of drugs@Capsule surface at the M06-2X/6-31G(d, p) level of theory.

Full size image

The complexation energy (ΔE) values for both drugs@cap show that the drugs are physiosorbed on the capsule cavity; and the values are − 51.59 kcal/mol for GB@Cap and − 42.18 kcal/mol FLT@Cap complexes, respectively (see Table 1). With a complexation energy of -51.59 kcal/mol, the GB anticancer drug exhibits the strongest interaction then FLT@Cap complex.

Non-covalent interactions, such as hydrogen bonds and weak van der Waals forces, are indicated by the interaction distances (Angstrom). The shortest interaction distance in the case of GB@Cap complex is calculated for O7—H8 with interaction distance of 1.83Å. The interaction distances observed in GB@capsule are 2.03Å, 2.46Å, and 2.73Å for O1—H2, H4—O3, H5—O6, respectively (See Fig. 3). The F-atoms of GB and the O-atoms of Capsule exhibit strong hydrogen bonding in the stable optimized geometry of GB@capsule. Moreover, in the case of FLT@cap, the interaction distances of H1—F2, H—O4, N5—H6 are 2.65Ǻ, 2.37Ǻ and 2.64 Ǻ (Fig. 3) confirming the presence of strong hydrogen bonds between the atoms of drug and capsule.

The complexation energies are also calculated by using dispersion-corrected functional (e.g., ωB97XD). The inclusion of dispersion-corrected ωB97XD functional slightly affects the complexation energy of studied complexes. The complexation energy with dispersion correction ωB97XD functional is higher than those without correction. However, the trend of complexation energy is the same with and without dispersion correction. The complexation energies of GB@Capsule, and FLT@Capsule complexes are quite comparable for both M06-2X (ωB97XD) functionals. and complexation energy values are − 51.59 kcal/mol (-54.67 kcal/mol) and − 42.18 kcal/mol (-45.82 kcal/mol), respectively (see Table 1). The complexation energy of FLT is lower as compared to GB. The higher complexation energy values display the higher stability of drugs@Capsule. Overall, gemcitabine drug shows slightly higher stability as compared to flutamide. This might be due to the reason that gemcitabine fits better in the capsule cavity than flutamide.

Moreover, the Counterpoise approach is also considered to calculate the BSSE (basis set superposition error) for the studied complexes. The complexation energies of GB@Capsule, and FLT@Capsule complexes are quite comparable with one another, and complexation energy values are − 51.59 kcal/mol (BSSE=-48.21 kcal/mol) and − 42.18 kcal/mol (BSSE=-40.32 kcal/mol), respectively (see Table 1). The same order of BSSE corrected energy and complexation energy values is observed in both the studied drug@Capsule complexes. The calculated complexation energy results reveal the same trend and comparable values of Counterpoise corrected interaction energy for both studied anticancer drugs (see Table 1).

Table 1 Complexation energies ΔE (M06-2X), ΔE (ωB97XD), EBSSE in kcal/mol and bond lengths (Å) and of the drugs@capsule complexes at the M06-2X/ 6-31G(d, p) level of theory.
Full size table

Non-covalent interactions (NCI) analysis

NCI analysis is performed to obtain an in-depth understanding of the non-covalent interactions between the drugs@capsule complexes. 2D graphs and 3D iso surfaces are shown (Fig. 4) to examine the nature of attractive and repulsive forces between the drug and capsule complexes. It offers a clear description of non-covalent interactions using reduced density gradient (RDG) analysis, which is based on the second eigenvalue with electron density (ρ)66.

Fig. 4
figure 4

NCI 3D isosurfaces and 2D-RDG plots of stable GB@Cap and FLT@Cap complexes (iso value 0.004 a.u).

Full size image

The colored map in NCI analysis indicates the presence of weak van der Waals interactions between the drugs and the capsule surface, as seen by the appearance of a green and somewhat red isosurface. When looking at 3D iso-surfaces of GB@Cap, green patches between the drug molecule and the capsule surface indicate the presence of weak van der Waals interactions. The 2D map’s spikes, which are projected at the X-axis between 0.015 and − 0.015 a.u., also indicate weak van der Waals interactions. In the case of FLT@Cap, green spikes observed in 3D structures confirms the existence of non-covalent interactions between the drugs and molecules of the capsule. Furthermore, both complexes exhibit dispersed green spikes in 2D-RDG plots that range from − 0.015 a.u. to 0.005 a.u., validating weak van der Waals interactions. The steric repulsion that exists between some surface atoms is shown by the 3D red color patches (Fig. 4).

Similarly, strong electrostatic interactions are shown by the spikes on 2D NCI graphs at signλ2(ρ) > -0.01 (a.u.), whereas London dispersion forces exist below this negative value. Moreover, these results suggests that there are no covalent interactions between the drugs and the capsule, which facilitates the release of drug molecules at the targeted location.

Quantum theory of atoms in molecules (QTAIM) analysis

The strength and nature of interaction between drugs and capsule is characterized using QTAIM analysis. In QTAIM analysis, bond strength depends upon the (ρ) electronic density while the bond nature depends on the Laplacian of electronic density (∇2ρ) and sum of electron densities (H). In different molecular systems, Bader’s QTAIM analysis is often used to determine the non-covalent or nonbonding interactions67. According to topological evaluation, the bond critical points, which include electron density (ρ), Laplacian ∇2(ρ), and total electron density H(r), determine the type of nonbonding interactions. The sum of the local kinetic energy G(r) and potential energy V(r) determines the overall energy density H(r). The relationship can be shown as:

$${{\text{H}}_{({\text{r}})}}\,=\,{{\text{V}}_{({\text{r}})}}\,+\,{{\text{G}}_{({\text{r)}}}}$$
(5)

The topologies computed through the QTAIM analysis are given in Fig. 5, whereas the BCP parameters are presented in Table 2. The various topological parameters in QTAIM analysis are evaluated via BCPs (bond critical point), Laplacian of electronic density and total electronic values etc. .

The occurrence of weak intermolecular interactions is indicated by the Laplacian of the electron density (∇2ρ(r) > 0), whereas the existence of covalent bonding is indicated by the Laplacian of the electron density (∇2ρ(r) < 0)68. The link between the Laplacian of the electron density (∇2ρ(r)) and the density of kinetic energy (G(r)) and potential energy (V(r)) is demonstrated by equation;

$${\text{2G}}\left( {\text{r}} \right)\,+\,{\text{V}}\left( {\text{r}} \right){\text{ }}={\text{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\nabla ^{\text{2}}}r\left( {\text{r}} \right)$$
(6)

H(r) for non-covalent bonds must either be larger than or equal to 0, and covalent bonds will occur if it is less than 0. Values > 0 for the energy density H(r) and Laplacian ∆2ρ(r) often suggest the presence of non-covalent interactions, whereas values < 0 generally imply covalent interactions. Table 2 lists the topological characteristics for each complex, and Fig. 5 displays the molecular graph of these features, which includes the bond critical point (BCP) and bond path.

Fig. 5
figure 5

QTAIM analysis of studied drugs@capsule complexes with orange-colored dots on bond paths represents bond critical points (BCPs), whereas yellow lines between drug and capsule shows bond paths.

Full size image

The values of various parameters are evaluated through QTAIM analysis for drug@capsule complexes and are listed in Table 2, whereas 3D isosurfaces of drug@capsule are shown in Fig. 5. The values of Laplacian ∇2ρ and electron density (ρ) in Table 2 justified the noncovalent interactions in both studied drugs@capsule complexes. In QTAIM analysis, fifteen BCPs are found for FLT@cap (Table 2). The electronic density values of ρ(r) for these BCPs fall between 0.003 and 0.011 a.u. In contrast, H(r) and ∇2ρ(r) have values between 0.0004 and 0.0015 a.u. and 0.004 to0.05 a.u., respectively. The values of ∇2ρ, ρ(r), and H(r) indicate non-covalent contact that ranges from small to strong. The remaining two parameters, G(r) & −V(r)/G(r), exhibit non-covalent interactions.

Moreover, Table 2 shows fifteen BCPs according to the results obtained by the QTAIM analysis of GB@Cap complex. The ρ(r) electronic density values for these BCPs are determined to be in the range of 0.002–0.011a.u. The values of Laplacian electron density fall between 0.011 and 0.104 a.u. The values of topological parameters like G(r), H(r), V(r), and − V(r)/G(r) indicate non-covalent interactions. Overall, it can be evaluated that the strong non-covalent interactions are present.

Table 2 Topological parameters for studied drugs@capsule complexes obtained through QTAIM analysis.
Full size table

Electronic properties

Natural bond orbital (NBO) analysis

NBO analysis is carried out to understand the charge transfer between drugs and the capsule surface. When examining the type of interaction that exists between drugs and the capsule surface, electronic properties are crucial. Table 3 shows the NBO charges upon the interaction of drugs and capsule surface. Charge transfer from the drug towards the surface is shown by the positive value whereas negative value shows that the charge is transferred from surface to drugs69.

The observed NBO charge transfer values are − 0.017 and 0.007 for (FLT@Capsule) and (GB@Capsule). Positive NBO values show that charge is being transferred from the capsule to the FLT, whereas negative NBO values indicate that charge is being transferred from the GB to the capsule. This opposite trend could possibly because of the flutamide having a relatively simple structure than gemcitabine. Flutamide has a more electron-rich region or donating groups such as the nitrogen of the amide, it might donate electron density to the benzimidazolone capsule, resulting in a negative charge transfer, i.e., − 0.017 in the case of (FLT@Cap). While, gemcitabine contains fluorine atoms and a sugar moiety, which could make the molecule more electronegative compared to flutamide. The fluorine atoms are highly electronegative, which may pull electron density away from the benzimidazolone capsule, leading to a positive charge transfer i.e., 0.007 in the case of (GB@Cap).

The highest charge transfer is observed in the case of GB@Capsule. Furthermore, existence of weaker noncovalent interactions is revealed by the small NBO charge transfer values. The 3D iso-surfaces of the EDD study validate these quantitative results of the charge transfer.

Electron density differences (EDD)

To visualize the isosurfaces of the drug@capsule under study, EDD analysis is utilized. Figure 6 displays the drugs@capsule complex EDD graphs (Isovalue = 0.0004 a.u.). Multiwfn 3.7 software was used to obtain the EDD analysis results (isosurfaces). The interaction of the capsule and drug orbitals is represented by the purple and pink color isosurfaces that were produced using EDD analysis (Fig. 6). The purple color indicates the accumulation of electron density, whereas the pink color indicates the depletion of electrons.

Because of the electrostatic interactions between the H-atoms of the considered drugs and the N-atoms of the capsule surface, there is a greater accumulation of electron density between the drugs and the capsule surface, resulting in purple isosurfaces. Furthermore, in the case of the GB@capsule complex, these purple and pink surfaces confirm the transfer of charges toward dug from the capsule. For FLT@capsule complex, the charge transfer from drug to the capsules is validated through purple and pink isosurfaces. Figure 6 shows the pink isosurfaces, which indicate the depletion of electron density upon interaction. Electronic density distribution between the drugs and capsule surface is confirmed by EDD plots. The EDD results are further validated through NBO (charge transfer) analysis.

Fig. 6
figure 6

EDD plots of drugs@capsule with Iso value = 0.004 a.u. (Purple isosurfaces represent electron density accumulation, and pink isosurfaces shows electron density depletion)

Full size image

Frontier molecular orbital (FMO) analysis

FMO analysis is used to examine how the electrical properties of the capsule surface change when drug@capsule complex is formed. The FMO analysis is used to study the conductivity of selected system via H-L gap change. In general, as conductivity increases, the energy gap (HOMO-LUMO gap) decreases, but it decreases with a larger HOMO-LUMO gap70.

The energies of HOMO and LUMO, H-L gap and thier isosurfaces are presented in Table 3; Fig. 7, respectively. For the bare capsule surface, HOMO energy is − 6.88 eV and LUMO energy is − 0.22 eV, and the energy gap (EH−L) for bare capsule surface is − 6.66 eV. The calculated HOMO-LUMO (EH−L) energy gaps of FLT@Capsule complex is and GB@Capsule complexes are − 5.73 eV and − 6.54 eV, resepectively. For both studied drugs, upon adsorption of drugs on capsule surface appreciable reduction in energy gap (EH−L) is observed. Both drugs show almost similar behavior with minor variation in terms of variation HOMO-LUMO energy variation and their energy gap (EH−L). Upon FLT adsorption over capsule, energies of both HOMO and LUMO decrease which leads to reduction in EH−L gap of -5.73 eV, compared to -6.66 eV for isolated capsule. Whereas, the EH-L gap of GB@Complex is slightly decreased but is comparable to that of the bare capsule. This can be understood as, When gemcitabine binds to the capsule, the electron-withdrawing nature of gemcitabine may result in relatively weak electron donation to the capsule. This leads to a situation where the capsule’s electronic structure is not significantly altered, preserving the HOMO-LUMO gap in a range similar to the bare capsule.

In FLT@capsule complex, both HOMO and LUMO orbital density is present over drug, whereas in case of GB@capsule complex both HOMO and LUMO orbital density is located on the capsule surface. Overall, the FMO data clearly demonstrates that both drugs show a decrease in the EH−L gap as a result of complexation, indicating that the capsule surface exhibits greater sensitivity towards anticancer drugs.

Fig. 7
figure 7

HOMO-LUMO densities of the studied drugs@capsule surface.

Full size image
Table 3 FMO and NBO results of most stable drugs@capsule complexes.
Full size table

Density of states (DOS) analysis

The graphical representation of energy states is provided by DOS analysis. The density of states analysis can be used to deduce the electronic change of the capsule upon drug adsorption71. Figure 8 shows the DOS spectra of the drugs@capsule and bare capsule. The DOS spectra can be used to visualize the differences in peak intensities between a capsule that is relatively bare and one that is loaded with GB and FA. The variations in conductivity following drug adsorption over the capsule surface are revealed by these shifts and intensities in the peaks.

Fig. 8
figure 8

DOS spectra of drugs@capsule.

Full size image

Dipole moment (µ) analysis

The solubility of the drug molecule and its ease of release at the target site is determined by the change in dipole moment. Prior to drug adsorption, the bare capsule’s dipole moment (µ) is zero (0.004 D). Furthermore, isolated drug molecules have dipole moment values of 7.32 D for FLT and 5.44 D for GB. When the capsule interacts with the FLT and GB drugs, the dipole moment values in the resulting complexes shift to 5.79 D and 5.65 D, respectively. Strong interactions between the benzimidazolone capsule and the drugs, including hydrogen bonding, charge transfer, and electrostatic interactions, are responsible for the significant increase in dipole moment from 0.004 to 5.651 and 5.796 upon complexation of the capsule with gemcitabine and flutamide. Gemcitabine probably causes a large redistribution of electron density inside the capsule since it is a highly polar chemical with functional groups that can create strong interactions. As a result, the complex’s overall dipole moment is significantly higher than that of the bare capsule. The solubility of the complexes in aqueous media, which further aids in the mobility of drug molecules in a biological system, depends on their dipole moment. FLT’s dipole moment decreases slightly (from 7.32 D to 5.79 D), suggesting a weaker interaction, meaning FLT is likely to be released more easily. In contrast, GB’s dipole moment increases slightly (from 5.44 D to 5.65 D), indicating a stronger binding to the capsule, which would make GB harder to release. Thus, dipole moment analysis reveals that capsule can release FLT more effectively than GB on a target site.

pH effect

One of the most crucial steps is the release of the drug from the carrier surface to the target cell. The pH of a malignant cell environment is often lower than 6 than that of normal blood cells (7.35–7.45). We thus investigated the impact of pH on the GB@Capsule and FLT@Capsule complexes. In an acidic environment, we performed DFT simulations of drugs (gemcitabine and flutamide) loaded on benzimidazolone capsules (see Fig. 9). The flutamide and gemcitabine’s interacting sites (the N-atoms of the amide and amine groups) were protonated with H+ in an acidic medium, and the structure was then relaxed once again at the same theoretical level. When the GB@Capsule and FLT@Capsule complexes were compared in an acidic medium, the complexation energies of the two complexes drastically decreased, going from − 51.59 to -18.71 kcal/mole and from − 42.18 to -14.56 kcal/mole, respectively. In contrast, the GB@Capsule complex showed an increase in the interaction distances from 1.83 Å to 3.01 Å. This shows that, in contrast to GB, FLT can be easily offloaded from the carrier (benzimidazolone capsule) to the target location (Fig. 10). Numerous protons may also be affixed to the drug’s surface and other endpoints in an acidic environment. These protons might not have an impact on the drug’s release at the intended location, though.

Fig. 9
figure 9

Protonated geometries of bare capsule, GB@Capsule and FLT@Capsule complexes.

Full size image

Conclusion

Using DFT at M06-2X functional with 6-31G(d, p) basis set, the drug transport capability of porous material (capsule) is tested against anticancer drugs in the current investigation. Both of the investigated drugs exothermically adsorbed and the complexes are thermodynamically stable, according to the complexation energy (ΔE) values of most stable optimized geometries. The most stable complex, according to the results, is the GB@Capsule complex, which has the highest complexation energy at -51.59 kcal/mol. QTAIM analysis revealed that the strong electrostatic forces are responsible for the stability of the GB@capsule complex. Only noncovalent interactions between drugs and the capsule surface are found, according to the Laplacian and electron density values as well as the -V/G ratio of all complexes identified by QTAIM analysis. The presence of green spikes in noncovalent interaction (NCI) analyses indicated weak van der Waals contacts between interacting fragments. According to FMO analysis, the HOMO-LUMO energy gap (EH−L) decreased appreciably for all complexes under study. Given that malignant cells have an acidic pH in comparison to normal cells, the decrease in complexation energies obtained through DFT calculations suggest that anticancer drugs can be readily released at the targeted site. The key findings suggest that the capsule surface performs better when it comes to anticancer drug delivery.

Fig. 10
figure 10

Graphical abstract.

Full size image