Introduction

Rare diseases are complex, chronic, life-threatening (majority), and disabling conditions1,2,3. 50% to 75% of rare diseases target children, of whom 30% don’t live to celebrate their fifth birthday1,4. While 80% of rare diseases are genetic diseases, the rest are caused by external factors such as environment, infectious, or unknown1,5,6,7. Globally, the disease is categorized as a rare disease when it affects fewer than 1 in 2,000 in the European Union or less than 200,000 in the USA1,3,4,5. Recently, more than 7,000 rare diseases have been identified, affecting more than 350 to 400 million people worldwide1,4,5,8. Out of the 7,000 cases, only 5% have an approved treatment9. Rare diseases impose several unique challenges on the economy and healthcare system. In 2016, the USA Healthcare Cost and Utilization Project (HCUP) reported that the overall estimated cost related to rare diseases is $768 billion, comparable with $880 billion for common diseases3,6.

Patients living with RDs faced multiple challenges due to the lack of accurate and timely diagnosis; on average, physicians took approximately 7.6 years in the USA and 5.6 years in the U.K. to accurately diagnose the diseases, with multiple misdiagnoses throughout the way4,7,10. This delay in rare disease diagnosis can be explained by several aspects, such as limitations in disease perception, limited knowledge of the disease by the primary physician due to the small size of the affected population, and unavailable diagnostic tests and facilities.6,9,10. Unfortunately, the delay in finding the proper disease diagnosis can lead to the death of the patients after undergoing a painful journey of mistreatment and misdiagnosis10. Moreover, it is important to note that a lot of patients still live with the rare condition without being properly diagnosed11.

Those challenges motivated the launch of several initialize dedicated to early rare disease diagnosis and screening, such as the Korean Genetic Diagnosis Program for Rare Diseases (KGDP) Phase I and II6, International Rare Diseases Research Consortium (IRDiRC)7, and Alabama Genomic Health Initiative (AGHI)12. Most of those initialized focused on screening patients by targeting highly suspicious individuals, as recommended by their healthcare providers12. This is followed by confirming the case using conventional methods such as genome-based or exome-based gene panel/genomic sequencing6,11,12,13. In a similar vein and with the availability of electronic records, several works focused on utilizing the disease phenotype, image, and fluids to build disease diagnosis support systems14. Notably, one study proposed a phenotypic similarity algorithm based on calculating the one-to-all rank. The study focused on finding the patients’ disease phenotype and comparing it with existing and annotated diseases7. Medical records or electronic health records (EHRs) are equally important in disease diagnosis as the conventional methods. Those records provide an efficient and cost-effective way for early disease diagnosis to improve patient outcomes and disease management15. Unfortunately, to date, only a limited number of studies and efforts have been allocated to utilizing EHRs in rare disease landscapes.

Given the scarcity of rare diseases and the challenges associated with their diagnoses, recent research has turned towards leveraging artificial intelligence (AI) technologies to predict RD conditions. Brasil et al.4 explored the potential and challenges of using AI in various aspects of rare diseases. It looked into how AI could be used for diagnosing and understanding rare diseases, developing treatments, maintaining patient registries, and managing health records. The study highlighted the significant impact AI could have on people affected by rare diseases. Although various medical decision support systems exist to guide diagnosis and medical treatment, the majority utilized statistical approaches, not AI techniques16,17. AI technologies are not widely used in rare disease diagnosis due to the complexity of rare disease characteristics and the limited number of patients with similar phenotypes, disease severity, presentation, and progression18. Therefore, our study will be the first to fill the gap by training different AI models and comparing their performance using EHR data to diagnose patients with mucopolysaccharidosis (MPS), a rare metabolic disease.

Mucopolysaccharidoses (MPS) are a group of inherited inborn errors of metabolism disorders caused by different enzyme deficiencies involved in the breakdown of glycosaminoglycans. MPS is a progressive multisystem disorder with a heterogeneous spectrum of symptoms that varies based on the severity and the subcategory of MPS. The patients with MPS present with recurrent respiratory tract infections (upper respiratory tract infection, acute tonsilitis, pharyngitis, bronchiolitis, bronchitis, pneumonia) as well as recurrent otitis media. The other clinical presentations of these disorders are coarse facial features, macrocephaly, corneal clouding, inguinal or umbilical hernia, hepatosplenomegaly, valvular heart disease, dysostosis multiplex, limitation of joint movement, and gibbus deformity. In the severe form of the disease, they might present with hydrocephalus and developmental delay19,20,21.

In recent years, research efforts have been directed toward employing AI techniques in various healthcare applications such as: disease diagnosis, drug discovery and development, precision medicine, and clinical trials. Garavand et. al22 used machine learning to build a diagnostic model for coronary artery disease (CAD) based on clinical examination features. They compared different ML models for their effectiveness in diagnosing CAD cases, highlighting the potentials of SVM and RF ML models in detecting CAD patients from clinical examination data. Moreover, Ghaderzadeh et. al23 reviewed various studies that focus on the use of AI to address the antimicrobial resistance in the discovery and development of drugs, which showed the capabilities of AI models in recognizing new antimicrobial compounds, enhance existing drugs to takle the antimicrobial resistance, and forecasting drug resistance.

Concerning the utilization of AI techniques in precision medicine, Pudjihartono et al.24 discussed the strengths and weaknesses of different feature selection methods, namely filter, wrapper, and embedded methods, that could be used to overcome the curse of dimensionality challenge presented in the genotype data to build more accurate disease risk prediction models based on patients genetic data, contributing to the advances of AI tools in precision medicine. Additionally, a study by Carlier et al.25 applied ML approaches in designing an in silico clinical trial for a pediatric rare disease. They examined bone morphogenetic protein (BMP) treatment for congenital pseudarthrosis of the tibia (CPT) diseasee; by proposing an unsupervised ML model, namely ward hierarchical clustering, to cluster the virtual subject population into different groups based on their response to the BMP treatment along with the supervised Random Forest ML algorithm to identify the potential biomarkers in predicting the effectiveness of the therapy. Overall, AI-based methods have resolved many challenges in the field of healthcare.

Although AI has had noticeable and successful applications in healthcare, there is still a lack of research directed toward applying machine learning models—subfields of AI—for MPS early diagnosis in specific and rare diseases in general. In this study, we aim to fill the gap by implementing and comparing the performance of different machine learning models trained on de-identified and unstructured patients’ diagnosis data extracted from the Abu Dhabi Health Services Company (SEHA) healthcare system for early diagnosis of MPS diseases. Furthermore, we will explain and interpret the best model internal behavior and decision using SHapley Additive exPlanations (SHAP) and Local Interpretable Model-Agnostic Explanations (LIME) methods to understand and report the features that directed the model decision and its clinical validity. The key contributions of this work can be summarized as follows.

  1. 1.

    This is the first study to utilize AI and EHR data for MPS early diagnosis.

  2. 2.

    We trained and compared the performance of nine machine learning models across five feature selection methods: four automated feature selection methods and one feature selection based on domain experts’ knowledge.

  3. 3.

    We interpreted the best-performing model using SHAP and LIME, and clinically validated its outcomes using domain expert feedback.

  4. 4.

    Our work validates the applicability of machine learning for MPS diagnosis using only disease symptoms. This offers a non-invasive and cost-effective screening for MPS patients using EHR.

Results

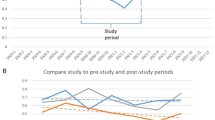
Our cohort includes registered patients aged 2 to 19 years old at SEHA from 2004 to 2022 (Fig. 1). A total of 106 patients (37 MPS patients and 69 control) were eligible to be included in the study. For those patients, we extracted 1186 historical medical diagnoses such as dental caries on smooth surface penetrating into dentin, acute pharyngitis due to other specified organisms, epistaxis, diarrheal, obesity, etc., to train the various machine learning models. Using nested cross-validation, we trained different combinations of the ML models and feature selection algorithms. Across the five cross-validation folds, the dataset had an average skewness of 2.53 (± 0.09) and kurtosis of 4.42 (± 0.46) before balancing. After applying SMOTE, the skewness increased to 2.98 (± 0.08) and kurtosis to 6.89 (± 0.48).

Fig. 1
figure 1

Study cohort selection flow diagram. Patient selection criteria and training and testing sets splitting of the dataset.

Full size image

Table 1 presents the average performance of the nine algorithms on the unseen / testing data as reported by the nested cross-validation. The Naive Bayes (NB) model trained on the domain experts’ features reported the overall best results, with Accuracy 0.93 (s.e. 0.08), Area Under the Receiver Operating Characteristics Curve (AUC): 0.96 (s.e. 0.04), Mathew’s Correlation Coefficient (MCC) 0.86 (s.e. 0.16), F1-score 0.91 (s.e. 0.1), Negative Predictive value (NPV) 0.98 (s.e. 0.03), Positive Predictive value (PPV) 0.86 (s.e. 0.15), Specificity (SP) 0.90 (s.e. 0.12), and Sensitivity (SE) 0.97 (s.e. 0.06). Figure 2 illustrates the ROC curve of NB for each of the five cross-validation folds. Moreover, Fig. 3 shows the best-case confusion matrix for NB for each of the five cross-validation folds. In each matrix, the model achieves a high count of true-positives and true-negatives showing that the classifier consistently distinguishes MPS versus control with few misclassification. For the AdaBoost model, the highest AUC reported is 0.95 by training the model using Chi-Square and expert features. For the decision tree, KNN, and MLP, mutual information features provided the best results over all the evaluation metrics (decision tree: Accuracy: 0.87, AUC: 0.9, F1-score: 0.75, and MCC: 0.84; KNN Accuracy: 0.84, AUC: 0.9, F1-score: 0.7, and MCC: 0.81 and MLP: Accuracy: 0.93, AUC: 0.95, F1-score: 0.84, and MCC: 0.9). While for Gradient Boosting and Random Forest, the best-reported results were based on the models trained on the Chi-square features; where Gradient Boosting reported Accuracy: 0.87, AUC: 0.92, F1-score: 0.74, and MCC: 0.84 and Random Forest reported Accuracy: 0.85, AUC: 0.91, F1-score: 0.72, and MCC: 0.83. Finally, for SVC, select from a model based on logistic regression features selection stated the highest performance reported for detecting MPS patients: Accuracy: 0.86, AUC: 0.92, F1-score: 0.75, and MCC: 0.84.

Table 1 The performance of different machine learning models for MPS prediction in the testing set.
Full size table
Fig. 2
figure 2

AUC curve of the best performing model across five folds.

Full size image
Fig. 3
figure 3

Confusion matrix of the best performing model across five folds.

Full size image

After finding the best model based on the best-reported performance in the evaluation metrics, which is NB trained on the domain expert, we conduct further analysis to understand and interpret the models’ decisions and explain why the model reached the reported conclusions using the SHAP and LIME summary plots. Figure 4 shows the importance of the features in order from highest to lowest reported by SHAP analysis. Following is the order of top 15 features from the most important to the least: acute gingivitis, plaque-induced, accretions on teeth, body mass index (BMI) pediatric, greater than or equal to 95th percentile for age, chronic gingivitis, plaque-induced, dental caries on smooth surface penetrating into dentin, acute pharyngitis, unspecified, acute tonsillitis due to other specified organisms, dental caries extending into dentine, acute tonsillitis due to other specified organisms, acute tonsillitis, unspecified, acute pharyngitis, acute bronchitis, nasal congestion, chronic rhinitis, and wheezing. Additionally, the feature importance of the best performing model is visualized using LIME method in Fig. 5. The top 15 features ordered by LIME from the most important to the least are: accretions on teeth, acute pharyngitis, unspecified, acute gingivitis, plaque-induced, acute pharyngitis, chronic gingivitis, plaque-induced, dental caries extending into dentine, dental caries on smooth surface penetrating into dentin, body mass index (BMI) pediatric, greater than or equal to 95th percentile for age, nasal congestion, acute tonsillitis due to other specified organisms, acute bronchitis, chronic rhinitis, acute tonsillitis due to other specified organisms, acute upper respiratory infection, and acute tonsillitis.

Fig. 4
figure 4

Variables Importance: Variable importance plot for Naive Bayes trained on the features extracted from a domain expert using SHAP analysis.

Full size image
Fig. 5
figure 5

Variables Importance: Variable importance plot for Naive Bayes trained on the features extracted from a domain expert using LIME Analysis.

Full size image

Discussion

Mucopolysaccharidosis (MPS) represents a group of rare inherited metabolic disorders characterized by the deficiency of lysosomal enzymes essential for the degradation of glycosaminoglycans (GAG), leading to their accumulation within cells and subsequent systemic symptoms26,27. MPS encompasses seven subtypes, each associated with distinct enzyme deficiencies and clinical manifestations28. The prevalence of MPS varies significantly across different populations, with certain ethnicities exhibiting higher incidences29. The infrequency of MPS poses significant challenges in diagnosis and management, further complicated by the wide spectrum of clinical presentations.

To the best of our knowledge, this is the first study that trained and compared the performance of different machine learning models to predict MPS cases. We trained nine machine learning models, namely, AdaBoost, Decision Tree, Gaussian Naive Bayes, Gradient Boosting Classifier, K-nearest Neighbors’ Algorithm, Logistic Regression, Multi-layer Perceptron Classifier, Random Forests, and Support Vector Classification in a combination of five features selection methods: Chi-square feature selection, domain experts feature set, select from the model (logistic Regression), Lasso 5-fold feature selection, Mutual information, Bat Algorithm, Genetic Algorithm using patients past medical history from SEHA medical records, UAE. The models were compared using various evaluation metrics such as accuracy, Area Under the Receiver Operating Characteristics Curve, F1-score, Matthews Correlation Coefficient, Negative Predictive Value, Positive Predictive Value, Specificity and Sensitivity on the unseen datasets.

Overall, NB trained using domain expert features reported the highest performance Accuracy 0.93 (s.e. 0.08), AUC 0.96 (s.e. 0.04), Mathew’s coefficient 0.86 (s.e. 0.16), F1-score 0.91 (s.e. 0.1), NPV 0.98 (s.e. 0.03), PPV 0.86 (s.e. 0.15), SP 0.90 (s.e. 0.12), and SE 0.97 (s.e. 0.06). Figures 4 and 5 represent the features selected by the NB model to detect MPS patients at early stages based on expert features. Both SHAP and LIME identified a highly consistent set of key features. The highest selected feature, interestingly, were the dental manifestations of the disease, mainly acute gingivitis, accretions on teeth, chronic gingivitis, and dental caries. It is well known that patients with MPS present with dental anomalies, deviations in eruption, malocclusions, TMJ pathology, macroglossia, gingival hyperplasia, and increased risk of caries and periodontal disease30. One of the studies reported 76% of patients with MPS IV had experienced dental caries and all patients with MPS showed evidence of a generalized unspecified enamel defect, and 43% of them exhibited marginal gingivitis31.

Patients with MPS have poor oral hygiene. These findings maybe as result of difficulties in maintaining oral hygiene since some of these patients have intellectual disabilities or restriction of joint movement which might affect their brushing techniques, poor follow up with dentist since they do have multiple significant co-morbidities. Some of the dental procedure require general anesthesia which is challenging in those patients because of airway involvement of the disease. Most of the time given the complexity of the disease, their follow up is also limited to tertiary centers31,32,33,34.

The other identified features of the disease were acute pharyngitis, acute tonsillitis, acute bronchitis, nasal congestion. Indeed, recurrent respiratory infection is the most common feature of these disorders. These features have been reported in most of the studies, it considered one of the early presentation of patients with MPS diseases in the first two year of life35,36,37.

Body mass index pediatric, greater or equal to the 95 percentiles, means that the cases are within the obese range of BMI. Patel et al studied the growth parameter of patients with MPS II and compared it with normal control. They have noted that 97% of studied patients had a BMI higher than the mean BMI of the normal control38. Another study investigated the natural history of growth parameter from untreated males followed prospectively in the Hunter Outcome Survey registry and found that BMI was above average throughout childhood until approximately 14–16 years of age39.

Most of these features are non-specific to MPS but the combination of these symptoms yields better prediction of MPS in our study. It also reflects the local practice of clinicians and their clinical documentation. Moreover, it highlights the significant burden of dental manifestations in our patients. In comparison, the data analysis of Hurler registry showed that umbilical and inguinal hernia as well as coarse facies and corneal clouding are among the early symptoms of patients with MPS I40.

On the other hand, based on the data from the registry of Hunter Outcome Survey the following symptoms were considered helpful in the diagnosis of the disease: facial dysmorphism, nasal obstruction or rhinorrhea, enlarged tongue, enlarged liver, enlarged spleen, joint stiffness which were given the weight of 2 while the other symptoms of hernia, hearing impairment, enlarged tonsils, airway obstruction or sleep apnea were given weight of 1. A mnemonic screening tool was developed based on these data with total score of 6 or greater with high risk of the MPS II41. Our model identified nasal congestion one of the high risk feature of the disease.

This research offers a cost-effective screening method for RD participants. It utilizes the current medical record system powered by AI models, eliminating the need for clinical experts to manually identify and flag suspicious undiagnosed cases. We validated the applicability of machine learning models for predicting MPS cases using patients’ past medical history from SEHA electronic health records, United Arab Emirates cohort. Our finding confirms the power of machine learning to detect rare disease cases, as reported by different evaluation metrics that are used to compare different ML models’ performance with unseen data.

Despite these strengths, our study has several limitations that could be improved upon in future studies. First, our study relies exclusively on diagnostic codes from a single healthcare system (SEHA) which is limited and may not capture relevant clinical differences. Additionally, because there are no prior studies on using machine learning to diagnose MPS using historical EHR data, we lacked an established benchmark for comparison and validation. Moreover, the study did not incorporate demographic information or any other data modalities which might improve the model’s performance and report more significant predictors for diagnosing MPS patients. The study also does not distinguish between MPS subtypes, which ultimately subtype-specific outcomes or predictive features. Furthermore, the study’s heavy reliance on EHR, which tends to naturally have noise, missing data, could have affected the feature selection and model accuracy. Finally, external validation on multi-center, ethnically diverse cohorts is necessary to confirm generalizability before using this framework in border clinical settings.

Conclusion

In conclusion, this study presented a machine learning framework for the early diagnosis of MPS relying on patients’ historical medical diagnoses extracted from EHR data. We evaluated multiple ML models in combination with different feature selection algorithms to efficiently diagnose patients. Our results demonstrate that incorporating domain expert-selected features with a Naïve Bayes model achieved the highest diagnostic accuracy in identifying MPS patients. Additionally, the feature importance of the best-performing model supported the common clinical manifestation presented in MPS disease, highlighting the model’s capabilities in capturing MPS disease pathology. The obtained results demonstrate the potential of utilizing ML models with historical diagnostic data in RD diagnosis, particularly MPS disease, enabling more efficient and cost-effective screening tools. Future research could involve integrating additional clinical data, such as laboratory results, imaging, and genetic information, with diagnostic features to further enhance predictive performance and contextual insight. Moreover, extending the framework to include larger, multi-center datasets could improve generalizability, while exploring MPS subtype classification could offer more precise and personalized diagnostic support.

Methods

Data source and study cohort

In this retrospective study, we extracted anonymized patients’ medical records from the Abu Dhabi Health Services Company (SEHA) healthcare system. The SEHA dataset is a high-dimensional UAE population healthcare data source that includes rich patients’ medical information such as demographics, comorbidity, symptoms upon admission, growth parameters, laboratory results, and medications. The final dataset included 106 patients, of which 37 were diagnosed with MPS and 69 were controls.

Study variables

The study outcome was the diagnosis of MPS; the variable was dichotomized (0 and 1), where one indicates MPS positive and zero otherwise. The covariates or independent variables included all patients’ medical history, which was also dichotomized to indicate the disease’s presence or absence. In total, we extracted 1186 covariates/comorbidities covering a wide range of medical conditions. Then after feature selection, the selected features were used to train the nine machine learning models. Table 2 presents the features identified by the domain expert.

Table 2 Clinical covariates selected based on domain expert knowledge.
Full size table

Machine learning framework

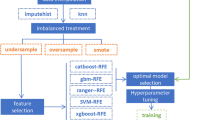
Figure 6 presents the study pipeline. We used Scikit-learn v1.3.0 of Python programming language v3.9.17 to implement the machine learning models along with Hyperopt v0.2.7 and Imbalanced-learn v0.11.0 python packages. We utilized nested-cross validation (double cross-validation) to stratify the dataset into training and testing sets, as well as to optimize feature selection algorithms and machine learning model parameters. The nested-cross validation consists of an outer loop and an inner loop. The outer loop is used to estimate the unbiased prediction accuracy of the machine learning models42; in this stage, we utilize stratified five-fold cross-validation to create training folds that the machine learning models use to learn the new representation that distinguishes MPS patients from the control patients. After training the models, we evaluated the trained models’ performance on the unseen testing fold. Based on the performance of different models in the testing set, we compared them to select the best model to tackle this challenge. Stratification sampling was selected for cross-validation to guarantee the training and testing are representative of the different groups’ distribution in our cohorts43. The inner loop of the nested-cross validation is responsible for hyperparameter optimization for both feature selection algorithm parameters and machine learning model parameters42 – hyperparameters (Table 3 Models’ hyperparameters). We applied Bayesian Optimization (BO)44 with five-fold cross-validation. The hyperparameter-tuning process supports us in automatically selecting the set of parameters that gives almost optimal results using the training set. During this process,100 sub-models were trained for each model and a feature selection-specific set of parameter values was selected during the optimization process. Since it is an optimization process, we set the objective function of the process to minimize the error on the validation set based on the Area Under the Receiver Operating Characteristic Curve (ROC AUC) score.

Fig. 6
figure 6

Machine learning workflow.

Full size image
Table 3 Models’ hyperparameters: machine learning models parameterized using a random search optimization algorithm of 100 different parameter settings with a 5-fold repeated stratified cross-validation to maximize the Area Under the Receiver Operating Characteristic Curve (AUC).
Full size table

Imbalaced data

MPS is a rare condition; therefore, our training set is expected to be severely imbalanced in the number of samples between the two groups (a minority of the samples are MPS patients’ records). It is well known that class imbalance affects machine learning techniques’ decisions and directs the decision to the majority class45. Therefore, several approaches were implemented to solve this problem, such as up-sampling the minority class or down-sampling the majority class. In this study, we applied the Synthetic Minority Oversampling Technique (SMOTE)46 to increase the number of samples in the minority class. SMOTE works by generating new synthetic data points by linear interpolation of MPS records and K-Nearest Neighbors; for this work, we fixed K to five neighborhoods of samples to be used for generating the new synthetic samples.

Fearure selection algorithms

Before training the model, we applied different supervised feature selection techniques to reduce the number of covariates for model training. The main objective of feature selection is to reduce the number of variables used to learn the new representation from the original dataset. This process helps to select the most informative features, exclude noisy or irrelevant features, prevent model overfitting, improve model performance, and minimize the computation power needed to run the code24,47,48. We employed four automated feature selection methods and one domain expert-reported feature set. The automated feature selection techniques are Chi-Square feature selection, Lasso (Least Absolute Shrinkage and Selection Operator), mutual information (MI), and select from the model (logistic Regression).

  • Chi-square feature selection is a univariate feature selection method that individually tests each feature and its relevance to output. A feature with a large Chi-Square value indicates a more important feature. The feature extracted is based on the hypothesis tests by selecting the statistically significant features where the significant level is set to p-value < 0.0524,48. The formula for Chi-Square is:

    $$\begin{aligned} \chi ^2 = \sum _{i} \frac{(O_i - E_i)^2}{E_i} \end{aligned}$$
    (1)

    Where: O is the observed frequency and E is the expected frequency.

  • Lasso with 5-fold cross-validation is an embedded-based method for feature selection. This method shrinks the regression coefficients to zero with respect to their contribution to the model output. Therefore, the algorithm selects the features based on their coefficient magnitude24,48, due to the L1 regularization. The lasso loss function is calculated as follows:

    $$\begin{aligned} \text {Minimize:} \sum _{i=1}^{n} \left( Y_i - \sum _{j=1}^{p} X_{ij} \beta _j \right) ^2 + \lambda \sum _{j=1}^{p} |\beta _j| \end{aligned}$$
    (2)

    Where n is the total number of samples, Y is the outcome, X is the independents/features, p is the total number of features, and \(\beta\) is the regression coefficient.

  • Mutual information is a multivariate features selection method based on selecting the subset of features based on their inter-dependencies and the outcome. The method chooses features with the highest entropy-based estimation with the target48. The MI represents as follows:

    $$\begin{aligned} \textit{I(X;Y)=H(X)-H(X|Y)} \end{aligned}$$
    (3)

    Where I(X; Y) is the MI for X, Y; H(X) represents the entropy for X, while H(X|Y) is the conditional entropy for X given Y.

  • Select from the model (logistic Regression) is a wrapper-based method for feature selection; the algorithm selects the features based on the magnitude of their coefficients reported by logistic Regression49. The logistic regression equation is:

    $$\begin{aligned} Y = \frac{e^{\beta _0 + \beta _1 X}}{1 + e^{\beta _0 + \beta _1 X}} \end{aligned}$$
    (4)

    Where y is the outcome, X is the independent/feature variable and \(\beta\) is the logistic regression coefficient.

  • Bat Algorithm (BA) is a metaheuristic inspired by bat echolocation. Each “bat” \(i\) has a position \(\textbf{x}_i\), a velocity \(\textbf{v}_i\), and a frequency \(f_i\)50. At iteration \(t\), the velocity and position update is:

    $$\begin{aligned} \begin{aligned} \textbf{v}_i^{\,t}&= \textbf{v}_i^{\,t-1} \;+\; \bigl (\textbf{x}_i^{\,t-1} - \textbf{x}_*^{\,t-1}\bigr )\,f_i^{\,t},\\ \textbf{x}_i^{\,t}&= \textbf{x}_i^{\,t-1} \;+\; \textbf{v}_i^{\,t}. \end{aligned} \end{aligned}$$
    (5)

    Where \(\textbf{x}_*^{\,t-1}\) is the best solution found up to iteration \(t-1\), and \(f_i^{\,t}\) is the bat’s frequency at iteration \(t\).

  • Generic Algorithm (GA) is an evolutionary method that evolves a population of solutions via selection, crossover, and mutation51. The probability of selecting individual \(i\) (with fitness \(F(\textbf{x}_i)\)) for reproduction is:

    $$\begin{aligned} p_i \;=\; \frac{F\bigl (\textbf{x}_i\bigr )}{\sum _{j=1}^{N} F\bigl (\textbf{x}_j\bigr )}. \end{aligned}$$
    (6)

    Where \(N\) is the population size, and \(p_i\) is the chance that \(\textbf{x}_i\) is chosen as a parent.

Machine learning algorithms

In this study, we developed and trained nine well-known machine learning models: the Adaptive Boost Classifier (AdaBoost), decision tree (DT), Naive Bayes (NB), gradient boosting classifier (XGBoost), k-nearest neighbors’ algorithm (KNN), logistic regression (LR), multi-layer Perceptron classifier (MLP), random forests (RF), and support vector classification (SVM). Following is a description of each method:

  • AdaBoost is an ensemble machine learning model based on training multiple classifiers to improve model performance by learning from their errors in sequential matter. The AdaBoost algorithm was first proposed by Yoav Freund and Robert Shapire in 1995 stemming from an example of optimizing decisions of a horse-race gambler52. It combines the power of weak learning (a decision tree with a single level as a base classifier) to build a powerful and robust classifier with the iterative approach53. AdaBoost has the power to adapt by improving the efficiency of classifiers such as decision trees but is very sensitive to noisy data and outliers. All weights start equally then on each round it increases the weights of misclassified samples, forcing the weak learner to focus on harder examples in subsequent iterations. The final model combines all weak learners aiming to minimize classification error52. The boosting algorithm is described as follows: Initialize the weight of distribution D on training example i on round \(t=1\):

    $$\begin{aligned} D_{t=1}(i) = \frac{1}{m}. \end{aligned}$$
    (7)

    For \(t = 1, \dots , T\):

    1. 1.

      Train weak learner using distribution \(D_t\).

    2. 2.

      Get weak hypothesis \(h_t: X \rightarrow \{-1, +1\}\) with error \(\varepsilon _t\):

      $$\begin{aligned} \varepsilon _t = \Pr _{x \sim D_t}[h_t(x) \ne y]. \end{aligned}$$
      (8)
    3. 3.

      Choose:

      $$\begin{aligned} \alpha _t = \frac{1}{2} \ln \left( \frac{1 - \varepsilon _t}{\varepsilon _t}\right) . \end{aligned}$$
      (9)

    Update:

    $$\begin{aligned} D_{t+1}(i) = \frac{D_t(i) e^{-\alpha _t y_i h_t(x_i)}}{Z_t}, \end{aligned}$$
    (10)

    where \(Z_t\) is a normalization factor.

    Output the final hypothesis:

    $$\begin{aligned} H(x) = \text {sign} \left( \sum _{t=1}^T \alpha _t h_t(x) \right) . \end{aligned}$$
    (11)

  • DT is a non-parametric flowchart-like tree structure consisting of nodes (features), leaf nodes (outcomes), and a set of decision rules. They were first introduced in the 1960s and have been used in various disciplines because they are robust, easy to use, and free of ambiguity. Several statistical algorithms are used to build decision trees such as CART (Classification and Regression Trees), C4.5, CHAID (Chi-Squared Automatic Interaction Detection) and QUEST (Quick, Unbiased, Efficient, Statistical Tree). Given their advantages decision trees can have some limitations such as overfitting and underfitting when using a small dataset, and using correlated input variables may lead to misleading model improvements54. The root node represents the top node in the tree; the tree is created in a recursive manner in which the rules are learned based on the values provided during the training time. Splitting refers to separating a single node (parent node) into many (child nodes) using input variables related to target variables by first identifying the most important input variables54. The popular splitting rules are Gini impurity (Gini) and information gain (entropy)49,53; which are expressed mathematically as follows:

    $$\begin{aligned} {\textit{Gini(E)}=} 1- \sum _{i=1}^{c} p_i^2 \end{aligned}$$
    (12)

    Where p is the probability that a sample belongs to a specific class (c).

    $$\begin{aligned} entropy: H(X) = - \sum _{i=1}^{n} p(x_i) \log _2 p(x_i) \end{aligned}$$
    (13)

    Where p is the probability of the entropy.

  • NB is a simple supervised statistical model based on the Bayes theorem. The model is built on the assumption that the features are independent, in which each feature’s effect is not related to/correlated with the other features49,53. It works by calculating prior probabilities of a given class label and its likelihood probability and returns the conditional probability of a given target. NB is one of the simplest algorithms and is much faster than other supervised algorithms as it only calculates probabilities. However, it has limitations, such as the assumption that all features are independent, which may not hold in real-world data. Additionally, it assigns zero probability to categorical variables not seen during training, leading to an inability to predict such cases55. The following is the mathematical formula for the NB model.

    $$\begin{aligned} P(c \mid x) = \frac{P(x \mid c) P(c)}{P(x)} \end{aligned}$$
    (14)

    Where P(c\(\mid\)x) is the posterior probability of class c given x, P(c) is the prior probability of class c, P(x\(\mid\)c) is the probability of the x given c (likelihood), and P(x) is the prior probability of the x.

  • XGBoost (eXtreme Gradient Boosting) is an ensemble machine learning model where the models are trained sequentially. It was first introduced by Tianqi Chen in 2014 as part of the Distributed (Deep) Machine Learning Community (DMLC) group56. XGBoost is particularly known for its high speed, performance and efficiency as it can utilize multiple CPU cores and it supports multiple loss functions making it adaptable. The prediction of XGBoost is based on the sum of outputs from multiple trees56. The main idea is that each subsequence model intends to improve the previous model’s performance by reducing errors using the gradient in a process known as boosting. The gradient minimizes the loss function by reducing the cumulative predicted errors by adding weak learners, typically DT53. XGBoost also has an objective function that balances model performance and the complexity of the model. This function consists of two key components: a loss term that measures prediction accuracy and a regularization term that prevents overfitting by controlling model complexity. The objective function is expressed as follows:

    $$\begin{aligned} \text {obj}(\theta ) = \sum _{i=1}^n l(y_i, \hat{y}_i) + \sum _{k=1}^K \Omega (f_k) \end{aligned}$$
    (15)

    where l is the loss function measuring the difference between prediction \(\hat{y}_i\) and target \(y_i\), and \(\Omega\) is the regularization term controlling model complexity.

  • KNN is an “instance-based learning”, one of the simplest non-parametric machine learning models. KNN classifier is widely used in multiple applications that include recognition and estimation and is the preferred classifier for its high simplicity and convergence22. During the inference phase, all the training values are used to assign a label to the new instance; typically, it’s a memory-based learning algorithm. The algorithm assigns a label to the new instance based on the majority vote for the nearest/closest k points in the training set using similarity measures functions such as Euclidean distance, Hamming distance, and Manhattan distance, etc49,53,57. In KNN, Euclidean distance is usually used for continuous variables while hamming distance is preferred for discrete variables22. For instance, the Euclidean distance is mathematically expressed as follows:

    $$\begin{aligned} d(\textbf{x}_i, \textbf{x}_j) = \sqrt{\sum _{n=1}^N (x_{i,n} - x_{j,n})^2} \end{aligned}$$
    (16)

    where \(\textbf{x}_i\) and \(\textbf{x}_j\) represent feature vectors, and N is the number of features.

  • LR is a probabilistic-based statistical model for binomial/binary outcomes and was introduced by COX in 195822. It uses a logistic probability distribution to model the relationship between the dependent (categorical) and independent variables. Logistic regression is easy to implement, interpretable, and provides probabilistic predictions, making it a preferred choice for binary classification. However, it assumes a linear relationship between predictors and log-odds, which can limit its effectiveness with complex or nonlinear data structures58. LR can suffer from overfitting, especially in the high-dimensional dataset; therefore, regularization techniques such as L1-penalty and L2-penalty are used49,53. The mathematical equation for LR is as follows:

    $$\begin{aligned} {\textit{g(z)}}= \frac{1}{1+ e {^{-z}}} \end{aligned}$$
    (17)

    Where z is a linear regression equation

  • MLP is a feed-forward artificial neural network model consisting of fully connected layers: an input layer (defined by the number of features), hidden layers (to learn the nonlinear representation of the input features), and an output layer (task-specific). Learning in MLP occurs by adjusting the connection weights in a back-propagation algorithm when the actual output deviates from the expected output. MLP is a commonly used supervised learning algorithm used in applications such as healthcare, finance, transportation, fitness and energy59. MLP is capable of learning both linear and non-linear functions making it universal, it has adaptive learning properties and is able to handle complex optimization problems. Its limitations include having too many parameters, which can result in redundancy, and has a weak generalization ability for neutral problems. The main building blocks of the MLP model are neurons, weights, activation functions, loss functions, and optimizers. Neurons are the computation units that take the weighted input values and produce the nonlinear output via the activation function; weights are parametric values that the model is trained to learn (similar to learning regression coefficients). The activation function is the transfer function that introduces the nonlinearity to learn complex decision boundaries in the model; the loss function is the cost function used to quantify the errors during the forward pass. Optimizer is the mechanism to adjust the network weights during back propagation49,53. Each node in the MLP incorporates a bias term, where the network processes n input variables X = \(\{x_1, x_2, ..., x_n\}\) through the input layer and produces m output variables Y = \(\{ y_1, y_2,..., y_n\}\) at the output layer60. The MLP’s total parameter count is calculated as follows:

    $$\begin{aligned} n_{h1} = \sum _{k=1}^{N_{h1}} h_k h_{k+1} + h_{N_h} n \end{aligned}$$
    (18)

    where the number of hidden nodes \(h_i\) in the ith layer is \(N_h\). Longer computational times are required to optimize an MLP when \(N_h\) and \(h_k\) are higher.

  • RF is an ensemble tree-based model introduced in 2001 that simultaneously trains collections of T trees (forest) independently. It uses two methods, random space approach and bagging DTs to create classification and Regression Trees (CART). These CART trees are binary decision trees built by continuously splitting data from a root node into child nodes, with each tree trained on bootstrap samples of the original data and searching randomly selected input variables for splits. This method handles challenges such as overfitting, underfitting, noise and outliers making it perfect for medical datasets22. Moreover, RF has key features that include effectively estimating missing data, managing unbalanced data accuracy by using Weighted Random Forest (WRF) and calculating variable importance in classification22. Each tree is built using a random sample or different sub-sample from the training set; the final prediction of the model denoted by \(\hat{y}\) is made based on the majority voting or average of generated tree decisions49,53 as provided by the following equation:

    $$\begin{aligned} \hat{y} = argmax_c \sum _{t=1}^T f(h_t(x) = c) \end{aligned}$$
    (19)

    where c is the label, T is the total number of trees in the forest, \(h_t(x)\) is the prediction output of the tth tree for input x.

  • SVC is a supervised machine learning algorithm that was introduced by Vladimir Vapnik as part of his work on statistical modelling theories and methods to minimize prediction errors22. It is a powerful parametric machine learning model that uses the kernel trick to deal with nonlinear representation in the input spaces; the kernel trick transfers the data points from lower to higher multidimensional space. The latter aims to find a good decision plane (hyperplane) that separates the different classes. SVC has been used for medical diagnosis classification and many more applications that require pattern recognition and regression estimation22. The model objective is to maximize the margin between the data points of different classes and the hyperplane- the closest points are the ones defined by the location of the hyperplane, and those points are named support vectors. The wider the margin range, the better the model. Allowing some misclassification can help to learn a wider range of margins and better hyperplane49,53,57. The SVM optimization problem can be expressed as:

    $$\begin{aligned} \min \frac{1}{2} \Vert \textbf{w}\Vert ^2 \end{aligned}$$
    (20)

    Here, \(y_i\) represents the class label (positive or negative) of a training sample i, and \(\textbf{x}_i\) is its feature vector representation. The optimal hyperplane is derived using the following equation:

    $$\begin{aligned} y_i (\textbf{w} \cdot \textbf{x}_i + b) \ge 1, \quad \forall i \end{aligned}$$
    (21)

    For all components of the training set, \(\textbf{w}\) and b must satisfy the constraints:

    $$\begin{aligned} y_i (\textbf{w} \cdot \textbf{x}_i + b) = 1 \end{aligned}$$
    (22)

    The data points \(\textbf{x}_i\) that satisfy \(|y_i| = 1\) are identified as support vectors.

    From a mathematical perspective, SVC aims to find the hyperparameter by:

    $$\begin{aligned} \text {minimizing } \frac{1}{m} + C \sum p_i \end{aligned}$$
    (23)

    where m is the margin width; p Points penalty, C is a regularization parameter (a trade-off between misclassification and margin width).

Benchmarking

We used logistic regression, which is the simplest classifier among all machine learning, as a benchmark model. We also trained the nine models using the original/all features and compared the results after applying different feature selection algorithms. In this study, we ended up training and testing 54 models (each model was trained 5 times for the outer loop, 5 times for the inner loop, and 100 times for hyperparameters optimization).

Performance evaluation metrics

We evaluated and compared the performance of different machine learning models on the testing set (unseen set) using various metrics, specifically, accuracy, Area Under the Receiver Operating Characteristics (ROC) Curve (AUC), F1-score, MCC, NPV, PPV, Specificity, and Sensitivity47. Metrics such as NPV, PPV, specificity, and sensitivity are particularly informative when evaluating models on imbalanced datasets, such as those commonly encountered in medical applications61.

Accuracy is measuring the percentage of the predicted samples the model got right; its values range between 0% (bad model) 0r 0 to 100 % (perfect model) or 1, which is defined as:

$$\begin{aligned} \text {Accuracy}= \frac{TP + TN}{TP + TN + FP + FN} \end{aligned}$$
(24)

Accuracy alone cannot be considered a good measure when working with an imbalanced dataset. Therefore, other evaluation metrics such as AUC, F1-score, and MCC must be considered. AUC is a well-known evaluation metric in the medical domain used to evaluate the discriminative capabilities of the model. AUC values range between 0 and 1; 0.5 indicates that the model made the decision based on random guessing, while 1 indicates a preferred model62. F1-score is a measure of accuracy; it is the harmonic mean of the precision and the recall; the measured value ranges between 0 (bad model) and 1 (perfect model). F1-measure mathematically defined as follows:

$$\begin{aligned} \text {F1 - score}= 2*\frac{precision X recall }{precision + recall} \end{aligned}$$
(25)

Where,

$$\begin{aligned} \text {Precision}= & \frac{TP}{TP + FP} \end{aligned}$$
(26)
$$\begin{aligned} \text {Recall}= & \frac{TP}{TP + FN} \end{aligned}$$
(27)

Where, TP, TN, FP, and FN refer to true positive, true negative, false positive, and false negative, respectively.

MCC is a statistical measure to quantify the model’s performance on all confusion matrix categories (TP, TN, FP, FN). It can be considered a Pearson correlation for discretization variables; MCC values range from -1 (bad model) to 1 (good model)63,64. The MCC computed as:

$$\begin{aligned} \text {MCC} = \frac{(TP X TN) - (FP X FN)}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} \end{aligned}$$
(28)

Where, TP, TN, FP, and FN refer to true positive, true negative, false positive, and false negative, respectively.

Positive Predictive Value (PPV), also called precision, measures the proportion of positive predictions that are actually positive65. The formula is given by:

$$\begin{aligned} \text {PPV} = \frac{TP}{TP + FP} \end{aligned}$$
(29)

Where TP, TN, and FP refer to true positive, true negative, and false positive, respectively.

Negative Predictive Value (NPV) measures the proportion of negative predictions that are actually negative65. The formula is given by:

$$\begin{aligned} \text {NPV} = \frac{TN}{TN + FN} \end{aligned}$$
(30)

Where TP, TN, and FN refer to true positive, true negative, and false negative, respectively.

Sensitivity (SE) (also known as True Positive Rate or recall) quantifies the proportion of actual positives that are correctly identified66. The formula is given by:

$$\begin{aligned} \text {Sensitivity} = \frac{TP}{TP + FN} \end{aligned}$$
(31)

Where TP, and FN refer to true positive, and false negative, respectively.

Specificity (SP) (also known as True Negative Rate) quantifies the proportion of actual negatives that are correctly identified66. The formula is given by:

$$\begin{aligned} \text {Specificity} = \frac{TN}{TN + FP} \end{aligned}$$
(32)

Where TN, and FP refer to true negative and false positive, respectively.

Model interpretation/explanation

Machine learning techniques provide a promising tool to tackle healthcare challenges; however, one of the main limitations of the wider use of ML in the healthcare system is the lack of model explainability and interpretability that signifies why the model made a specific decision about a particular patient62. For this study, we employed SHAP v0.43.0 and LIME v0.2.0.1 feature contribution analysis methods to understand and explain the output of the best predictive model. SHAP computed Shapley values which measure the contribution of each variable/feature to the final model output/prediction47,62. Using Shapley values, we compute a variable importance plot for overall model analysis45. It is important to remember that the SHAP value is interpreted as an accumulative effect of feature interaction; therefore, we can interpret it as a direct effect of a single feature47. On the other hand, LIME is a local explanation technique that generates simplified approximations of complex models around individual predictions67. This approach provides insight into how individual features contribute to specific predictions by perturbing the input data and observing changes in the model’s output.