A multi strategy bidirectional RRT* algorithm for efficient mobile robot path planning

Abstract

To address the issues of slow convergence speed and poor path quality of the traditional Rapidly-exploring Random Tree Star (RRT*) algorithm in complex environments, this paper proposes a Multi Strategy Bidirectional RRT* (MS-BI-RRT*) algorithm for efficient mobile robot path planning. In the new node generation phase, an expansion mode scheduling mechanism based on dynamic goal bias probability and expansion feedback is designed to enable adaptive switching among multiple expansion modes, thereby improving expansion efficiency. Meanwhile, a dynamic step size adjustment method based on local obstacle density is introduced to enhance expansion stability. During the parent node rewiring phase, a multi-factor path cost function is constructed to optimize parent node selection, thereby improving path quality. In the post-processing phase, a Bézier curve-based smoothing strategy is employed to improve trajectory continuity and dynamic controllability. Simulation results in five typical environments show that, compared with RRT*, BI-RRT*, APF-RRT*, BI-APF-RRT*, and GB-RRT*, MS-BI-RRT* algorithm reduces the average execution time by 77.50%, decreases the number of nodes by 76.41%, shortens the path length by 4.37%, and achieves a 100% success rate in all environments. These results demonstrate that the proposed method significantly improves convergence speed, path quality, and environmental adaptability, while exhibiting superior robustness.

Introduction

With the rapid advancement of artificial intelligence and automation, mobile robotic systems have seen widespread adoption in areas such as industrial manufacturing, warehouse logistics, and intelligent security^1,2. As a core technology enabling autonomous navigation and obstacle avoidance, path planning plays a crucial role in improving the operational efficiency and task execution quality of mobile robots³. Although various path planning algorithms have made remarkable progress in recent years, many still face significant challenges in real-world scenarios characterized by dense obstacles, complex layouts, or frequent environmental disturbances. These challenges, including slow convergence, poor path quality, and limited adaptability, limit the robustness and engineering applicability of existing planning algorithms^4,5.

Mainstream path planning algorithms are generally classified into three strategies: graph-based, sampling-based, and learning-based approaches⁶. Graph search algorithms, such as A* and Dijkstra, perform reliably in structured and low-dimensional environments. However, their search space grows exponentially, leading to substantial computational overhead and reduced efficiency⁷. Learning-based methods, including reinforcement learning and neural networks, can improve adaptability through offline training but often suffer from high training costs, limited generalization capability, and poor stability in dynamic conditions⁸. Sampling-based algorithms, particularly Rapidly-exploring Random Tree Star (RRT*) and its variants, have attracted significant attention due to their random sampling mechanism and low computational complexity. These methods provide better convergence and environmental adaptability in high-dimensional and unstructured scenarios⁹. RRT* improves upon the original RRT by introducing parent node selection and path rewiring mechanisms, which enable asymptotic optimality and enhance path quality. However, the algorithm still encounters several limitations in complex environments. Its expansion process lacks effective guidance, the rewiring phase requires high computational effort, and the resulting paths often exhibit excessive curvature variation and redundant nodes, which affect path smoothness and execution feasibility¹⁰.

To improve the convergence speed of the RRT* algorithm in complex environments, extensive research has focused on optimizing its structural design and sampling mechanisms, including nonuniform sampling strategies. BI-RRT* accelerates tree connection by simultaneously expanding from both the start and goal points, thereby improving overall search efficiency¹¹. Goal-Biased RRT* increases the sampling probability around the goal region to promote faster convergence¹². Informed-RRT* narrows the sampling space to a heuristic ellipsoidal region after obtaining an initial feasible solution, thereby reducing unnecessary exploration¹³. Smart-RRT* incorporates intelligent sampling and path pruning strategies to suppress redundant expansion and improve the efficiency of optimal path discovery¹⁴. DR-RRT* employs direction-aware nonuniform sampling to improve spatial adaptability in complex scenarios¹⁵. SOF-RRT* guides sampling toward low-cost areas to increase search efficiency¹⁶. FN-RRT* limits tree size and prunes invalid nodes to improve expansion efficiency and control memory usage¹⁷. VSR-RRT* dynamically adjusts the sampling radius based on obstacle distribution to enable adaptive exploration in densely populated environments¹⁸. Although these methods improve convergence speed, search efficiency, and local guidance, they mostly rely on fixed expansion mechanisms or single heuristic models. They often lack coordination among multiple expansion modes and fail to adapt to dynamic environmental characteristics, which limits the accuracy of path guidance and overall planning performance.

In terms of path quality optimization, various strategies have been developed to improve path structure and refine the parent node selection process. F-RRT* introduces auxiliary nodes during the path generation phase to effectively reduce redundancy and improve structural connectivity¹⁹. E-RRT* replaces traditional straight-line connections with elliptical curves to improve path smoothness and feasibility in narrow areas²⁰. LBT-RRT* introduces approximate cost factors and delayed graph evaluation to accelerate path generation and optimization while maintaining asymptotic optimality²¹. CCPF-RRT* applies multi-factor cost evaluation during the rewiring phase to enhance the rationality of parent node selection and improve overall path structure²². DOB-RRT* employs heuristic bidirectional pruning strategies to reduce redundant nodes and improve path continuity and execution performance²³. Although these methods offer improvements in path quality, their adaptability in complex environments remains limited.In scenarios with dense obstacles or frequent disturbances, many algorithms still exhibit instability, which restricts their suitability for high-reliability planning tasks.

To further improve trajectory smoothness and execution performance, path post-processing has become a key research direction. Common techniques include redundant node removal and curve interpolation using B-splines, Catmull-Rom splines, and Bézier curves²⁴. Compared with other interpolation methods, Bézier curves offer advantages such as structural simplicity, strong local controllability, and good derivative continuity.²⁵. These features allow Bézier-based smoothing to suppress curvature fluctuations while preserving the topological integrity of the original path, thereby improving trajectory controllability and dynamic stability.²⁶.

Despite notable progress in convergence speed and path structure optimization, existing path planning algorithms continue to face significant challenges in complex environments characterized by dense obstacles and spatial constraints. These challenges include insufficient path guidance, limited feasibility and robustness, and weak local search capabilities, all of which significantly hinder practical deployment. To overcome these limitations, this paper proposes a Multi Strategy Bidirectional RRT* (MS-BI-RRT*) path planning algorithm. The proposed method incorporates an expansion mode scheduling mechanism, a multi-factor path cost function, and a Bézier curve-based smoothing strategy across three critical phases: new node generation, parent node rewiring, and post-processing. Together, these components systematically enhance search efficiency, optimize the geometric structure of the path, and improve execution feasibility. The main contributions of this work are as follows:

• 1. (1) New node generation: An expansion mode scheduling mechanism is developed by integrating dynamic goal bias probability with expansion feedback. This enables adaptive switching among direct expansion, local translational expansion, and artificial potential field (APF) expansion, thereby enhancing search efficiency and adaptability in complex environments. In addition, a dynamic step-size adjustment strategy based on local obstacle density is introduced to enable adaptive control of expansion steps and improve expansion stability.

• 2. (2) Parent node rewiring optimization: A multi-factor path cost function is formulated by combining path length, turning angle, obstacle density, and clearance margin. This function guides the selection of parent nodes to optimize the geometric structure of the path, reduce redundant nodes and curvature fluctuations, and improve feasibility and local consistency.

• 3. (3) Path smoothing: A Bézier curve-based trajectory smoothing strategy is applied to reconstruct the continuity of the path formed by connecting the bidirectional trees. This approach mitigates sharp curvature changes and backtracking, improves trajectory continuity and dynamic control performance, and better supports the control requirements of mobile robots during path execution.

Related work

RRT*

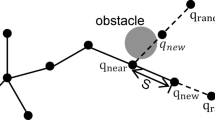
RRT* is an enhanced variant of the RRT algorithm. Its basic procedure is as follows: starting from the start point${p_{start}}$, a search tree T is initialized. In each iteration, a random sample point${p_{rand}}$is generated in the configuration space. The nearest node${p_{near}}$in the tree is identified, and the tree is extended from${p_{near}}$towards${p_{rand}}$with a fixed step size s to generate a new node${p_{new}}$. If the extension path does not collide with any obstacles, the${p_{new}}$is added to the tree. After the successful generating of the${p_{new}}$, the algorithm evaluates the path costs from neighboring nodes to the${p_{new}}$and selects the node with the lowest total cost as the parent node, so as to optimize the local tree structure. This process is repeated until the Euclidean distance between${p_{new}}$and the target point${p_{goal}}$is less than a predefined threshold f, and a collision-free connection is established, upon which a feasible path is finally constructed. At this point, a feasible path is eventually formed. Despite its asymptotic optimality, RRT* still suffers from unguided expansion and redundant path segments, which makes it difficult to reliably generate high-quality paths in complex environments. The basic principle is illustrated in Fig. 1, and the pseudocode is provided in Algorithm 1.

Algorithm 1 RRT* Algorithm.

Algorithm 2 ChooseParent.

Algorithm 3 Rewire.

Fig. 1

The schematic diagram of the RRT* principle. The small circles represent the nodes on the search tree, and the lines between the nodes represent the path. The dark blue areas represent obstacles, and the path cannot pass through these regions. This figure illustrates the principle of the RRT* algorithm.

BI-RRT*

BI-RRT* is a variant of the RRT*, whose core idea is to simultaneously construct two independent search trees from the start point${p_{start}}$and the goal point${p_{goal}}$, respectively expanding toward each other and attempting to connect. Specifically, during the expansion process, the two trees gradually approach each other. When a pair of nodes is found whose Euclidean distance is less than a predefined threshold f, and the connecting path between them is collision-free, the algorithm terminates expansion and backtracks from the connecting point to both the start and goal to form a feasible path. This bidirectional expansion mechanism significantly accelerates exploration and reduces path search time. Similar to RRT*, BI-RRT* is influenced by the randomness of sampling, which often results in the generation of redundant nodes. Furthermore, if the two trees fail to connect in a timely fashion, the resulting path may deviate significantly from the optimal solution, potentially increasing path length and degrading overall path quality. The basic principle is illustrated in Fig. 2, and the corresponding pseudocode is provided in Algorithm 4.

Algorithm 4 BI-RRT* Algorithm.

Fig. 2

The schematic diagram of the BI-RRT* principle. The small circles represent the nodes on the search tree, and the lines between the nodes represent the path. The dark blue areas represent obstacles, and the path cannot pass through these regions. This figure illustrates the principle of the BI-RRT* algorithm.

APF-RRT*

APF-RRT* is an enhanced variant of RRT*, which integrates the artificial potential field method²⁷. This method integrates attractive and repulsive potentials during path expansion, providing simultaneous goal-directed guidance and effective obstacle avoidance. It is particularly suitable for complex environments with dense or irregularly distributed obstacles. The algorithm begins by initializing a search tree T from the start point${p_{start}}$. In each iteration, a randomly samples point${p_{rand}}$is generated, and the then selects the nearest node${p_{near}}$in the tree. Then, the attractive force${F_{att}}$from the goal point${p_{goal}}$and ${p_{rand}}$, the repulsive force${F_{rep}}$ from nearby obstacles, resulting in a combined force${F_{total}}$applied to the node${p_{near}}$.The node${p_{near}}$is then extended in the direction of ${F_{total}}$with a fixed step size s to generate a new node${p_{new}}$.If the extension path is collision-free, it is added to the tree. The parent node of${p_{new}}$is selected based on the lowest cumulative path cost from its neighboring nodes, thereby optimizing the local path structure. This process is iteratively repeated until the path reaches near the target and a complete solution is formed. Compared with RRT, APF-RRT* enhances search efficiency and improves path quality, particularly in environments characterized by dense or complex obstacle distributions. However, in densely cluttered regions or near local minima, the force vector may become unstable, leading to path oscillation or expansion stagnation. When the goal is close to obstacles, repulsive forces may also weaken the attractive direction, adversely affecting path reachability and global convergence. The force analysis at node${p_{near}}$is illustrated in Fig. 3, and the pseudocode is provided in Algorithm 5.

Algorithm 5 APF-RRT* Algorithm.

Fig. 3

The force analytical graph of${p_{near}}$. The parallelogram law is used to combine two gravitational forces into a single resultant force. Similarly, the parallelogram law is used to combine the attractive and repulsive forces to form the final resultant force.

MS-BI-RRT* algorithm principle

This section introduces the principles of the MS-BI-RRT algorithm. Building upon the strengths of the BI-RRT algorithm, it improves path search efficiency and quality through the integration of multiple strategies. Algorithm 6 presents the pseudocode of the MS-BI-RRT* algorithm, illustrating its main process. The detailed content will be explained in the following sections.

Algorithm 6 MS-BI-RRT* Algorithm.

Algorithm 7 ExpandTree.

Algorithm 6 describes the overall framework of the algorithm, which is divided into three main phases:

New node generation phase (Steps 7–10 and 18–20, corresponding to Section 3.1): By employing a dynamic goal bias probability and expansion feedback mechanism, the algorithm enables adaptive switching among three expansion strategies. At the same time, a dynamic step-size adjustment is applied to enhance expansion efficiency and stability.

Parent node rewiring phase (Steps 11–12 and 21–22, corresponding to Section 3.2): A multi-factor path cost function is used to reconnect parent nodes, thereby optimizing the geometric quality of the path.

Bidirectional tree connection phase (Steps 28–29, corresponding to Section 3.3): Bidirectional tree search is performed to improve convergence efficiency.

Algorithm 7 further details the expansion logic of the new node generation phase, which includes the following core functions:

GetDynamicStep(): calculates the dynamic step size, as explained in Sect. 3.1.5.

steer(): performs direct expansion, with implementation described in Sect. 3.1.2.

LocalTranslationExpansion(): executes local translational expansion, as introduced in Sect. 3.1.3.

ImprovedAPFExpansion(): performs APF expansion, detailed in Sect. 3.1.4.

New node generation

Dynamic scheduling of expansion modes

Traditional RRT* algorithms typically adopt a direct expansion mode toward randomly sampled nodes, which lacks effective guidance toward the goal. In environments with dense obstacles or complex structures, expansion paths are frequently obstructed, leading to low search efficiency and failure to meet the requirements of efficient path generation for complex tasks. To enhance directional guidance, APF-RRT* introduces an artificial potential field (APF) during the expansion process. By constructing a resultant force field composed of attractive forces from the goal and repulsive forces from obstacles, the search tree can be guided more stably toward the goal region, thereby improving convergence speed and environmental adaptability. However, when the goal is close to obstacles, the repulsive force may dominate the resultant direction, causing the path to detour or even fail to reach the goal, ultimately degrading overall search performance.

In complex environments, static expansions modes often fail to balance search efficiency and adaptability. To address this, a dynamic scheduling mechanism for expansion mode is proposed. This mechanism adaptively switches among direct expansion, local translational expansion, and APF expansion based on the dynamic goal bias probability P and feedback from previous expansion results, thereby improving both path search efficiency and adaptability in complex environments. Specifically, during each expansion iteration, the algorithm first generates a random number$r \in [0,1]$,and compares it with the current dynamic bias probability P to determine the preferred expansion mode for this iteration. The specific cases are described as follows:

Case 1: When$r \leqslant P$, the algorithm prioritizes the goal-biased direct expansion mode. Specifically, the expansion begins from the node${p_{near}}$, which is closest to the goal point${p_{goal}}$, and extends along the direction toward the goal. If the expansion path encounters an obstacle, the algorithm attempts a local translational expansion to avoid it. If the translational expansion also fails, the mode switches to APF expansion, starting from the node nearest to a randomly sampled point${p_{rand}}$,with a new direction derived from the resultant force.

Case 2: When$r>P$, the algorithm directly employs APF expansion mode to enhance guidance capability and search efficiency in complex environments.

Parameter P is adaptively adjusted according to Eq. (1).

$$P=\left\{ {\begin{array}{*{20}{c}} 1&{if{\text{ }}f \leqslant {f_{th}}} \\ {{f_{th}}/f}&{else} \end{array}} \right.$$

(1)

where f represents the current cumulative failure count of biased expansions, and${f_{th}}$is the predefined failure threshold for goal-biased expansions. This threshold is determined through preliminary comparative experiments to balance goal-oriented guidance and environmental adaptability under different obstacle densities, ensuring an optimal trade-off between convergence speed and path quality. When the failure count does not exceed the threshold, the algorithm maintains$P=1$, prioritizing goal-biased expansion to accelerate path generation. Once the failure count surpasses the threshold, P gradually decreases, thereby weakening the preference for goal-biased expansion and increasing the usage frequency of APF expansion mode. This dynamic adjustment enhances guidance capability and random exploration efficiency in complex environments.

Direct expansion

In the path expansion process, the direct expansion mode generates new nodes by steering toward the target direction, allowing the path to more quickly approach the goal region. This approach exhibits strong directional guidance, especially in the early search phase or in open areas, which facilitates rapid convergence and reduces ineffective expansions, thereby improving path generation efficiency. The position of the new node ${p_{new}}$is calculated as shown in Eq. (2).

$${p_{new}}={p_{near}}+s \cdot \frac{{{p_{goal}} - {p_{near}}}}{{\left\| {{p_{goal}} - {p_{naer}}} \right\|}}$$

(2)

where${p_{near}}$denotes the node in the current tree that is closest to the target point${p_{goal}}$, and s is the dynamic step size. The adjustment method of s will be elaborated in Sect. 3.1.5. This parameter plays a crucial role in ensuring path adaptability in complex environments through dynamic adjustment.

Local translational expansion

To address failures in direct expansion, this paper introduces a local translational expansion mode. This expansion mode maintains the stability of the original expansion direction while slightly shifting the current path segment laterally in space. By doing so, the search tree is guided to generate feasible paths along obstacle boundaries, thereby improving the expansion success rate and adaptability to local environments. Specifically, when an expansion attempt fails due to collision, the algorithm constructs auxiliary search regions on both lateral sides of the original direction. It evaluates the feasibility of candidate paths generated through local translational shifting, based on the spatial distribution of nearby obstacles. This process ensures directional continuity while providing obstacle-avoidance capability, enhancing both the flexibility and robustness of the expansion process. The path construction principle of the local translational expansion mode is illustrated in Fig. 4. The detailed procedure is described as follows:

• 1. Auxiliary region construction: A collision point I is taken as the center, and a circle with a radius equal to the distance between the expansion node G and I is constructed to define the auxiliary region.

• 2. Translational direction selection: Using the line segment$GI$as the main axis, the auxiliary circle is divided into left and right candidate regions. Based on obstacle density, the region with lower collision risk is selected as the preferred local translational direction.

• 3. Local translational operation: In the selected translational direction, the original extension direction$GI$is laterally shifted as a whole to generate a new candidate path segment$G'I'$. The translational vector$\Delta \varvec{v}$is defined as shown in Eq. (3).

$$\Delta v=s \cdot \frac{{(1/2+\alpha )\varvec{n}+(1/2 - \alpha )h}}{{\parallel (1/2+\alpha )n+(1/2 - \alpha )h\parallel }}$$

(3)

where$\varvec{n}$denotes the unit normal vector$GI$, classified into left and right directions depending on the translational direction, $\varvec{h}$is the unit direction vector of$GI$, and$r=d/s$denotes the ratio between the expansion length and the adaptive step size. The updated positions of the endpoints after translation are given in Eq. (4):

$$\left\{ {\begin{array}{*{20}{c}} {G^{\prime}=G+\Delta \varvec{v}} \\ {I^{\prime}=I+\Delta \varvec{v}} \end{array}} \right.$$

(4)

4. Feasibility validation: The endpoint$I'$is first selected to form the candidate expansion path$GI'$,and its feasibility is checked. If a collision occurs, the algorithm then considers$G'$as the new node and attempts to construct an alternative path segment$GG'$. If both attempts fail, the local translational expansion is considered unsuccessful, and the APF expansion mode is adopted instead.

Fig. 4

Schematic of the local translational expansion. This figure shows the process of local translational expansion. By combining the unit normal vector of the original path with the same-direction unit vector, the translation direction is obtained.

Improved APF expansion

The traditional APF-RRT* algorithm incorporates the artificial potential field method, combining attractive and repulsive forces during path expansion. This approach effectively enhances directional guidance and search efficiency. Specifically, it defines the attractive potential field${U_{att}}({p_{near}})$, the repulsive potential field${U_{rep}}({p_{near}})$, and the total potential field${U_{total}}({p_{near}})$, as expressed in Eqs. (5)–(7).

$${U_{att}}({p_{near}})=\frac{1}{2}{k_a}{\rho ^2}({p_{near}},{p_{goal}})$$

(5)

$${U_{rep}}({p_{near}})=\left\{ {\begin{array}{*{20}{c}} {\frac{1}{2}{k_r}{{\left( {\frac{1}{{\rho ({p_{near}},{p_{obs}})}} - \frac{1}{{{\rho _0}}}} \right)}^2}}&{\rho ({p_{near}},{p_{obs}}) \leqslant {\rho _0}} \\ 0&{\rho ({p_{near}},{p_{obs}})>{\rho _0}} \end{array}} \right.$$

(6)

$${U_{total}}({p_{near}})=\sum {U_{rep}}({p_{near}})+\sum {U_{att}}({p_{near}})$$

(7)

where${p_{near}}$,${p_{goal}}$,and${p_{osb}}$represent the positions of the nearest point to the random point${p_{rand}}$, the goal, and the center of the obstacle, respectively.${k_a}$and${k_r}$are the weighting coefficients of the attractive and repulsive potential fields, respectively. ${\rho _0}$is the effective range of the repulsive potential field. The function$\rho ({p_{near}},{p_{goal}})$ represents the Euclidean distance between${p_{near}}$and${p_{goal}}$, while$\rho ({p_{near}},{p_{obs}})$ denotes the distance from${p_{near}}$to${p_{osb}}$. The attractive and repulsive forces are derived from the negative gradients of their corresponding potential functions, which guide the expansion node to approach the goal and avoid obstacles. Accordingly, the attractive force${F_{att}}({p_{near}})$, the repulsive force${F_{rep}}({p_{near}})$and the resultant guidance force${F_{total}}({p_{near}})$are defined as shown in Eqs. (8)–(10).

$${F_{att}}({p_{near}})={k_a}\rho ({p_{near}},{p_{goal}})$$

(8)

$${F_{rep}}({p_{near}})=\left\{ {\begin{array}{*{20}{c}} {{k_r}\left( {\frac{1}{{\rho ({p_{near}},{p_{obs}})}} - \frac{1}{{{\rho _0}}}} \right)}&{\rho ({p_{near}},{p_{obs}}) \leqslant {\rho _0}} \\ 0&{\rho ({p_{near}},{p_{obs}})>{\rho _0}} \end{array}} \right.$$

(9)

$${F_{total}}({p_{near}})=\sum {F_{rep}}({p_{near}})+\sum {F_{att}}({p_{near}})$$

(10)

The generation direction of the new node${p_{near}}$is determined by ${F_{total}}({p_{near}})$. Both ${p_{goal}}$and ${p_{rand}}$exert attractive forces on${p_{near}}$. When calculating the attractive force from${p_{rand}}$,the distance function$\rho ({p_{near}},{p_{goal}})$in Eq. (8) is replaced by$\rho ({p_{near}},{p_{rand}})$. Obstacles apply repulsive forces to${p_{near}}$,and the direction of${F_{total}}({p_{near}})$defines the generation direction of${p_{new}}$. Although APF-RRT* improves search efficiency by guiding toward the goal and away from obstacles, this approach may struggle when the repulsive force dominates the attraction near the goal, causing difficulty in reaching the target. To address this, an improved Artificial Potential Field (APF) method²⁸ is adopted in this study, which defines an attractive potential field${U_{att}}({p_{near}})$,a repulsive potential field ${U_{rep}}({p_{near}})$, whose detailed formulation is presented in Eqs. (11)–(13).

$${U_{att}}({p_{near}})=\frac{1}{2}{k_a}{\rho ^2}({p_{near}},{p_{goal}})$$

(11)

$${U_{rep}}({p_{near}})=\left\{ {\begin{array}{*{20}{c}} {\frac{1}{2}{k_r}{{\left( {\frac{1}{{\rho ({p_{near}},{p_{obs}})}} - \frac{1}{{{\rho _0}}}} \right)}^2}{\rho ^n}({p_{near}},{p_{goal}})}&{\rho ({p_{near}},{p_{obs}}) \leqslant {\rho _0}} \\ 0&{\rho ({p_{near}},{p_{obs}})>{\rho _0}} \end{array}} \right.$$

(12)

$${F_{total}}({p_{near}})=\sum {F_{rep}}({p_{near}})+\sum {F_{att}}({p_{near}})$$

(13)

where n is a positive integer. Unlike the traditional repulsive potential model, the improved formulation dynamically adjusts the repulsion magnitude based on the distance function$p({p_{near}},{p_{goal}})$. This approach is particularly effective when approaching the goal, mitigating the issue of excessively strong repulsion overwhelming attraction, which improves reachability and helps avoid entrapment in local minima. The modified expressions for the attractive and repulsive forces are given in Eqs. (14)–(17).

$${F_{att}}({p_{near}})={k_a}\rho ({p_{near}},{p_{goal}})$$

(14)

$${F_{rep}}({p_{near}})={F_{rep1}}({p_{near}}){\kern 1pt} {\varvec{n}_{ON}}+{F_{rep2}}({p_{near}}){\kern 1pt} {\varvec{n}_{NG}}$$

(15)

$${F_{{\text{rep}}1}}({p_{near}})={k_{\text{r}}}\left( {\frac{1}{{\rho ({p_{near}},{p_{obs}})}} - \frac{1}{{{\rho _0}}}} \right) \cdot \frac{{{\rho ^n}({p_{near}},{p_{goal}})}}{{{\rho ^2}({p_{near}},{p_{obs}})}}$$

(16)

$${F_{rep2}}(p)=\frac{n}{2}{k_r}{\left( {\frac{1}{{\rho ({p_{near}},{p_{obs}})}} - \frac{1}{{{\rho _0}}}} \right)^2} \cdot {\rho ^{n - 1}}({p_{near}},{p_{goal}})$$

(17)

In these,${\varvec{n}_{ON}}$is the unit vector pointing from the obstacle toward${p_{near}}$,${\varvec{n}_{OG}}$is the unit vector pointing from the goal point${p_{goal}}$to the node${p_{goal}}$. When${p_{near}}$is close to${p_{goal}}$,the repulsive force is attenuated to ensure that the node can reach${p_{goal}}$. ${F_{rep}}({p_{near}})$denotes the repulsive force, and the total force${F_{total}}({p_{near}})$is obtained by summing all attractive and repulsive components, as shown in Eq. (18).

$${F_{total}}({p_{near}})=\sum {F_{rep}}({p_{near}})+\sum {F_{att}}({p_{near}})$$

(18)

Dynamic step size

During the path expansion process, as the search tree extends from the current node toward a randomly sampled point to generate a new node, the probability of the expansion path intersecting with obstacles increases significantly with the rise in obstacle density within the local neighborhood. Using a large step size in regions with dense obstacles tends to result in collision detection failures; conversely, using an excessively small step size in sparse areas may lead to insufficient expansion distance, reducing search efficiency and compromising overall path quality²⁹. To address this, a dynamic step-size adjustment method based on local obstacle density is proposed in this paper to enhance the adaptability of path expansion under varying environmental conditions. The algorithm automatically reduces the step size in high-density obstacle regions to improve obstacle avoidance capability, while increasing the step size in sparse areas to accelerate search progress. The dynamic step-size s is computed as follows:

$$s={s_{\hbox{max} }}{e^{ - \lambda c}}$$

(19)

where${s_{\hbox{max} }}$represents the maximum step size, c denotes the obstacle density within the local neighborhood of the current node. A larger c indicates denser obstacles, resulting in a smaller step size to enhance obstacle avoidance capability; conversely, a smaller c represents a sparse region, allowing for a larger step size to improve path search efficiency.$\lambda$is the decay factor controlling the influence of obstacle density on step size. It should be noted that both excessively large and excessively small values of$\lambda$affect search efficiency: when$\lambda$is too large, the step size becomes overly sensitive to obstacle density, shrinking even in relatively sparse regions and leading to overly conservative expansion; when$\lambda$is too small, the step size adapts too slowly, preventing sufficient enlargement of the step size in open areas and similarly restricting expansion speed. In this work, a trade-off value of$\lambda$was determined through sensitivity analysis in multiple preliminary experiments to balance obstacle avoidance capability and search efficiency.

Parent node rewiring

In the traditional RRT* algorithm, parent node selection during the path rewiring phase is typically based on path length, which helps to shorten the path³¹. However, this approach often overlooks the structural characteristics of the path and its feasibility and safety in complex environments. To enhance the accuracy and robustness of path evaluation, this paper constructs a multi-factor path cost function that considers both geometric and environmental factors. By comprehensively evaluating path quality from multiple dimensions, the proposed method enhances adaptability in complex environments. Three key factors are designed as follows:

• 1. Path turning angle factor$\theta$, which quantifies the directional change between adjacent path segments. It helps suppress sharp turns and improves the smoothness of the generated path;

• 2. Obstacle density factor c, which represents the distribution density of obstacles along the path segment, thereby reflecting the local complexity and potential collision risk in the environment;

• 3. Obstacle clearance factor${d_{min}}$, defined as the minimum Euclidean distance between the path segment and the nearest obstacle, used to evaluate the safety margin of the path.

To visualize the geometric relationships and spatial meaning of these factors, Fig. 5 illustrates the structural interpretation of the path cost function. Specifically, $\theta$represents the turning angle formed by the path segments connecting the newly generated node, the candidate parent node, and its parent; c denotes the obstacle density within the circular region centered along the path segment between the new node and the candidate parent node; and${d_{min}}$is the minimum Euclidean distance between the path segment and the nearest obstacle.

Fig. 5

Schematic diagram of cost function principle. This figure illustrates the physical significance of the three path factors.

Based on the above three key path quality factors, a multi-factor path cost function is further formulated to quantify path quality, as shown in Eq. (20).

$$Cost=Cost({p_i})+\rho ({p_i},{p_{new}})+{\beta _1}c+{\beta _2}\theta +{\beta _3}{e^{ - {d_{min}}}}$$

(20)

where$Cost({p_i})$ is the accumulated path cost from the candidate parent node${p_i}$, and$\rho ({p_{i}},{p_{new}})$denotes the Euclidean distance between the new node${p_{new}}$and the candidate parent node${p_i}$. The weights${\beta _1}$,${\beta _2}$, and${\beta _3}$ control the influence of path turning angle, obstacle density, and obstacle clearance, respectively, on the overall cost. By appropriately tuning these weights, the algorithm can flexibly balance path smoothness, obstacle avoidance, and path length across different environments. Specifically, increasing${\beta _1}$promotes smoother paths by reducing sharp turns; increasing${\beta _2}$helps steer the path away from obstacles, which is particularly effective in cluttered environments; and increasing${\beta _3}$enhances safety by maintaining a sufficient clearance from obstacles, thereby reducing collision risks. The values of${\beta _1}$,${\beta _2}$,and${\beta _3}$are empirically determined through extensive simulations to achieve robust and adaptive performance across diverse scenarios.

Bidirectional tree connection and path generation

To alleviate convergence difficulties during the bidirectional tree search process, the algorithm assigns the global goal point as the expansion target for the start tree, while the newly generated node from the start tree serves as the expansion target for the goal tree³⁰。As the iterations progress, both trees expand within the environment. When a pair of nodes—one from each tree—are found such that their Euclidean distance falls below a predefined threshold and the direct connection between them is collision-free, the two trees are considered successfully connected, and the path search process is terminated. Subsequently, the algorithm traces back the path from the connection node to both the start and goal points, and merges the two partial paths into a continuous and feasible path. This path is then used in the subsequent trajectory smoothing and execution optimization stages.

Bézier curve-based smoothing

To enhance path feasibility and trajectory continuity, this paper introduces a smoothing strategy based on cubic Bézier curves after the initial path is generated. By locally re-interpolating the turning points along the path, the strategy improves the overall continuity of the trajectory. For each segment of the path, a cubic Bézier curve is constructed to effectively mitigate curvature discontinuities caused by non-smooth nodes, thereby better satisfying the control requirements of mobile robots in path tracking and task execution.

This smoothing method takes the discrete waypoints of the original path as the basis, denoted by$\{ {P_0},{P_{1}}, \ldots ,{P_n}\}$,where each point${P_i} \in {{\mathbb{R}}^2}$. To ensure natural transitions at the endpoints, two virtual endpoints${P_{ - 1}}$and${P_{n+1}}$are introduced and calculated using linear extrapolation, as shown in Eq. (21).

$$\left[ {\begin{array}{*{20}{c}} {{P_{ - 1}}} \\ {{P_{n+1}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 2&{ - 1}&0&0 \\ 0&0&{ - 1}&2 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{P_0}} \\ {{P_1}} \\ {{P_{n - 1}}} \\ {{P_n}} \end{array}} \right]$$

(21)

On this basis, a cubic Bézier curve is constructed for each path segment$[{P_i}_{},{P_{i+1}}]$, where the four control points are defined in Eq. (22):

$$\left[ {\begin{array}{*{20}{c}} {{B_0}} \\ {{B_1}} \\ {{B_2}} \\ {{B_3}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 0&1&0&0 \\ { - \frac{1}{6}}&1&{\frac{1}{6}}&0 \\ 0&{\frac{1}{6}}&1&{ - \frac{1}{6}} \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{P_{i - 1}}} \\ {{P_i}} \\ {{P_{i+1}}} \\ {{P_{i+2}}} \end{array}} \right]$$

(22)

where${B_0}$and${B_3}$ represent the start and end points of the current Bézier curve segment, respectively, while${B_1}$and${B_2}$are intermediate control points that regulate the curvature. This construction approach effectively smooths out sharp turns at the path’s corners while preserving the original geometric trend of the trajectory. Each segment of the curve is represented by the standard cubic Bézier formulation as shown in Eq. (23):

$$C(t)=\left[ {\begin{array}{*{20}{c}} 1&t&{{t^2}}&{{t^3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ { - 3}&3&0&0 \\ 3&{ - 6}&3&0 \\ { - 1}&3&{ - 3}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{B_0}} \\ {{B_1}} \\ {{B_2}} \\ {{B_3}} \end{array}} \right],\quad t \in [0,1]$$

(23)

All Bézier segments are concatenated in sequence to ultimately form a smooth and continuous trajectory.

Fig. 6

Five simulation environment. This figure shows five simulation environments, where the dark blue areas represent obstacles, and the path cannot pass through these regions.

Fig. 7

Simulation results of environment A. These figures show the simulation results, where green represents the start point, red represents the endpoint, blue and pink represent the expansion nodes, and the red curve represents the path found.

Fig. 8

Simulation results of environment B. These figures show the simulation results, where green represents the start point, red represents the endpoint, blue and pink represent the expansion nodes, and the red curve represents the path found.

Fig. 9

Simulation results of environment C. These figures show the simulation results, where green represents the start point, red represents the endpoint, blue and pink represent the expansion nodes, and the red curve represents the path found.

Fig. 10

Simulation results of environment D. These figures show the simulation results, where green represents the start point, red represents the endpoint, blue and pink represent the expansion nodes, and the red curve represents the path found.

Fig. 11

Simulation results of environment E. These figures show the simulation results, where green represents the start point, red represents the endpoint, blue and pink represent the expansion nodes, and the red curve represents the path found.

Table 1 Simulation data for environments A, B, and C.

Fig. 12

Comparison chart of simulation data. A comparison chart of the core indicators of three simulation results. The error bars represent the standard deviation, and the numbers at the top of the bars represent the coefficient of variation for each indicator.

Fig. 13

Simulation results under different step sizes. These figures show the simulation results, where green represents the start point, red represents the endpoint, blue and pink represent the expansion nodes, and the red curve represents the path found.

Table 2 Simulation data under different step sizes in Environment A.

Simulation results

Experimental setup

To evaluate the path planning performance of the proposed MS-BI-RRT* algorithm in complex environments, a series of systematic comparative simulation experiments was conducted using the MATLAB 2023b platform on a computer equipped with an Intel Core i5-12400 F processor. Five representative path planning algorithms were selected as baseline methods: RRT*, BI-RRT*, APF-RRT*, BI-APF-RRT*, and GB-RRT*.

The simulation environment was defined as a two-dimensional 100 × 100 space, with the start and goal points located at (0, 0) and (100, 100), respectively. To comprehensively evaluate the robustness and environmental adaptability of the proposed algorithm under different obstacle configurations, five test scenarios were designed, including three basic environments A, B, and C, and two robustness evaluation environments D and E. Environment A features densely and regularly distributed obstacles, environment B contains densely distributed obstacles in a random pattern, and environment C includes a narrow corridor structure. These scenarios are used to assess the overall performance of each algorithm in standard path planning tasks. Environments D and E introduce path symmetry interference and boundary perturbations, respectively, in order to test the algorithm’s stability and anti-interference capability under complex disturbance conditions. The layouts of the test scenarios are shown in Fig. 6. In each of the five scenarios, all six algorithms were executed independently 100 times to ensure statistical stability of the results and reduce random errors, while balancing computational cost and experimental efficiency. The maximum number of iterations was uniformly set to 2000, which was verified through preliminary experiments to guarantee a high success rate and convergence stability in complex environments, as well as to provide fair comparison conditions for different algorithms. All algorithms adopted the same termination criterion: if the sampling tree successfully connected to the goal or its ε-neighborhood (ε = 3.0) within the maximum iterations and the path was collision-free, it was considered a success; otherwise, failure was recorded. For feasible paths, the planning time directly reflects the convergence speed, where a shorter time indicates faster convergence.

Evaluation metrics include the mean and standard deviation of path length, execution time, and number of nodes, as well as the success rate. Summary results are presented in Table 1. The simulation results for each environment are shown in Figs. 7, 8, 9, 10 and 11, and the performance comparisons are illustrated in Fig. 12. In these figures, error bars represent the standard deviation, and the numbers above each bar indicate the coefficient of variation.

In addition, the Kruskal–Wallis non-parametric test was applied to evaluate the statistical significance of each performance metric. The results indicate that the proposed algorithm exhibits statistically significant differences compared to the baseline algorithms in terms of path length, execution time, and number of nodes (p < 0.01). Detailed statistical data for each test environment are provided in Supplementary Table S1.

Algorithm performance analysis

In the basic environments A, B, and C, the simulation results demonstrate that the proposed MS-BI-RRT* algorithm consistently outperforms the five comparison algorithms in all three key performance indicators: path length, execution time, and number of nodes. Specifically, the average path length was reduced by 5.59%, 5.70%, 4.55%, 1.02%, and 4.97%, respectively; the execution time was reduced by 90.23%, 61.64%, 93.00%, 73.18%, and 69.44%; and the number of nodes was reduced by 92.11%, 53.42%, 92.57%, 64.38%, and 79.57%. In addition, MS-BI-RRT* achieved lower standard deviations in all three metrics and significantly higher success rates than the other algorithms, indicating greater robustness and consistency of results. Among the comparison algorithms, RRT* lacks an effective path guidance mechanism and relies entirely on random sampling for expansion, leading to low search efficiency and poor path quality, particularly in dense obstacle areas. BI-RRT* improves tree connection speed through bidirectional expansion, but without structural optimization, it results in many redundant nodes, loose structure, and poor overall path geometry. APF-RRT* enhances guidance via artificial potential fields, but in complex environments, the dominant repulsive force may cause the path to fall into local minima, resulting in large fluctuations in success rate, increased execution time, and a sharp rise in node count. BI-APF-RRT* combines guidance with bidirectional expansion, which improves success rate and node count to some extent, but still suffers from slow convergence and insufficient search efficiency in complex scenarios. GB-RRT* incorporates gradient information to enhance goal bias and performs well in some settings, but in densely cluttered environments, it often produces highly oscillatory paths with poor continuity and controllability. Moreover, all the above algorithms employ fixed expansion step sizes and lack the ability to perceive and adapt to local environmental complexity, which further constrains the stability and quality of path generation. In contrast, MS-BI-RRT* demonstrates superior comprehensive performance in both the path generation and structural optimization stages. During the expansion phase, a scheduling mechanism based on dynamic goal bias probability and expansion feedback enables adaptive coordination among three expansion strategies, significantly improving search efficiency and environmental adaptability. Additionally, a dynamic step-size adjustment method based on local obstacle density allows flexible scaling of the expansion step, thereby improving success rate and path feasibility. In the parent node rewiring stage, a multi-factor path cost function is constructed to optimize the geometric structure, reduce redundant nodes and curvature fluctuation, and enhance the overall continuity and feasibility of the path.

In the robustness test scenarios D and E, MS-BI-RRT* again achieved the best performance across the key indicators of execution time, number of nodes, and success rate. Although BI-RRT*, BI-APF-RRT*, and GB-RRT* showed acceptable performance in success rate, they were still inferior to MS-BI-RRT*. RRT* and APF-RRT* exhibited significantly lower success rates and weaker stability. These results further confirm that MS-BI-RRT* can reliably generate high-quality paths even in structurally complex and disturbance-rich environments, demonstrating strong robustness and environmental adaptability.

Influence of step size adjustment on path performance

To evaluate the impact of the dynamic step-size strategy on the performance of the MS-BI-RRT* algorithm, a comparative experiment was conducted in Environment A. During the experiment, all parameters were kept consistent, except that the dynamic step size was replaced with a fixed step size for comparison. In this experiment, the dynamic step size$s \in [1,{s_{max}}]$, where${s_{max}}=2.4$. The path planning results are shown in Fig. 13, and the corresponding performance metrics are summarized in Table 2. The results indicate that shorter step sizes lead to smoother paths but lower expansion efficiency in open areas. Larger step sizes facilitate rapid traversal through open regions but may cause difficulties in dense obstacle clusters, increasing the likelihood of collisions and reducing expansion stability. The dynamic step-size mechanism adjusts the step size based on local obstacle density automatically increasing step size in open regions to improve expansion speed, and decreasing it in cluttered regions to enhance expansion success rate. The experimental results confirm that in environments with dense obstacles, the dynamic step-size strategy significantly enhances the algorithm’s environmental adaptability and expansion robustness.

Theoretical analysis

Probabilistic completeness

The MS-BI-RRT* algorithm introduces a dynamic goal bias strategy on top of RRT*, which improves convergence speed by preferentially sampling the goal point with a certain probability. When consecutive attempts to expand toward the goal fail beyond a certain threshold, the algorithm automatically decreases the goal bias probability and increases the random sampling probability, thereby maintaining the diversity of the sampling space. Although MS-BI-RRT* adopts a goal biasing mechanism, it ensures that at any time, any feasible region in the space still has a non-zero probability of being sampled. Therefore, the algorithm still satisfies probabilistic completeness. Theoretically, this property can be expressed as:

$$\mathop {\lim }\limits_{{n \to \infty }} P({T_1} \cap {T_2} \cap {p_{goal}} \ne 0)=1$$

(24)

where${T_1}$and${T_2}$represent the search trees rooted at the start and goal positions, respectively, and${p_{goal}}$denotes the goal node.

Asymptotic optimality analysis

Since the MS-BI-RRT* algorithm adopts a path optimization mechanism similar to that of RRT*, with the distinction that it employs a multi-factor path cost function, its asymptotic optimality is thus theoretically guaranteed. This property can be expressed as:

$$\mathop {\lim }\limits_{{n \to \infty }} Cost({T_n})=Cost(T*)$$

(25)

where$Cost({T_n})$denotes the cost of the path generated at the $n - th$iteration, and$Cost(T*)$denotes the cost of the globally optimal path.

Time complexity analysis

In the MS-BI-RRT* algorithm, the path tree is continuously expanded through iterations, where each iteration involves the generation of a new node, nearest neighbor search, neighborhood node retrieval, parent node selection, and path rewiring operations. Since linear scanning is used for nearest neighbor and neighborhood queries, the time complexity of a single iteration is$O( n)$, and the overall time complexity is$O( {n^2})$.

Conclusion

This paper presents MS-BI-RRT*, a multi strategy bidirectional path planning algorithm designed to address the limitations of traditional RRT* in complex static environments, such as slow convergence and low path quality. In the node expansion phase, an expansion mode scheduling mechanism based on dynamic goal bias probability and expansion feedback enables adaptive switching among direct expansion, local translational expansion and artificial potential field (APF) expansion. Additionally, a dynamic step size adjustment method based on local obstacle density is introduced to enhance expansion stability. In the parent node rewiring phase, a multi-factor path cost function that integrates path length, turning angles, obstacle density and clearance margin is employed to guide parent node selection, thereby improving the geometric quality of the path and enhancing local adaptability. In the post-processing phase, a Bézier curve-based smoothing strategy is applied to improve trajectory continuity and dynamic controllability, better satisfying the execution requirements of mobile robot systems. Simulation results demonstrate that MS-BI-RRT* outperforms five mainstream benchmark algorithms in terms of path length, execution time and node count, including RRT*, BI-RRT*, APF-RRT*, BI-APF-RRT* and GB-RRT*. Moreover, it maintains stable performance in environments with symmetric disturbances and narrow passages, exhibiting superior search efficiency, trajectory smoothness and planning robustness.

MS-BI-RRT* exhibits low computational overhead and minimal memory usage, with simulation results showing significantly shorter execution times than the comparison algorithms. Under the same iteration constraints, it converges to a feasible solution more quickly, demonstrating superior computational efficiency and decision responsiveness. Combined with its stability and high success rate, the algorithm shows strong potential for application in task scenarios requiring real-time performance, such as mobile robot path planning and industrial automation. Future work will involve testing on real hardware platforms and incorporating parallel optimization to further enhance its real-time applicability in dynamic environments.