Introduction

Multi-gene knockdown experiments have the potential to uncover differences in gene expression or cell phenotype, leading to a better understanding of gene function in biological processes. By perturbing gene combinations, it is possible to uncover epistatic and synergistic relationships that would not otherwise be observable in single-gene knockdown experiments. There are two fundamental challenges with this line of research. First, synergistic gene interactions in most studied contexts have been observed to be infrequent1. Second, while experimental budgets are often limited, the experimental design space is combinatorially large. For example, the total number of double-gene knockdown experiments using the entire human genome is on the order of \(10^8\). Even with modern high throughput screening technologies, it is typically not feasible to perform all experimental combinations. If an experimental budget affords performing between 100 and \(10^4\) experiments, then the design space is on the order of between \(10^{600}\) and \(10^{4\times 10^4}\) possible experimental configurations. Design spaces of this size are prohibitively large, making the extreme outliers of interest that much harder to find. The fundamental question we seek to address in this paper is: How do we efficiently search the prohibitively large design spaces in genetic interaction experiments while still discovering the infrequent interactions of interest?

When the cost of experimentation is high, sequential design of experiments (or active learning) has been proven to be more sample efficient than designing the entire sample space prior to performing experiments2. For gene knockdown experiments, active learning strategies have been investigated in several studies3,4,5,6,7,8. However, most of these works have been demonstrated in the context of single gene knockdowns on a particular phenotypic effect of interest. There has been very little work on active learning algorithms for pairwise knockdowns. This is primarily due to the quadratic increase in experimental costs and inherent complexity of predicting pairwise gene interactions. Two recent works have proposed active learning strategies for such tasks. In Jain et al.7 the authors proposed a novel gene-gene interaction test statistic that can be leveraged to guide sequential experimental designs. In Qin et al.9 the authors proposed a neural network model that leverages single-gene knockdown phenotypes to improve predictions of unseen double-gene knockdown phenotypes. There are, however, two fundamental limitations with these works: (1) a lack of integration of external data sources, such as knowledge graphs, and (2) the absence of computationally efficient batch diversification strategies. In this paper, we propose a Bayesian active learning framework for discovering pairwise host gene knockdowns that significantly reduce viral replication, while incorporating knowledge graphs and experimental batch diversification. We demonstrate our approach using the viral load endpoint of a \(356 \times 356\) gene-gene interaction dataset for HIV10, and we demonstrate the utility of knowledge graphs and batch diversification in the discovery process, as well as the general efficacy of our proposed framework. To the best of our knowledge, this is the first scalable probabilistic active learning framework for double-gene knockdowns which integrates knowledge graphs as side information and ensures batch diversification.

Despite the large experimental design space, we demonstrate that our proposed framework can rapidly identify the top pairwise gene knockdowns that produce the largest reduction in viral loads. We further demonstrate that side information in the form of knowledge graphs significantly improves performance during the initial rounds of the active learning process (in the low experimental data regime), whereas our proposed batch diversification scheme significantly improves performance during the later rounds (large experimental data regime). Thus, depending on the overall experimental budget, inclusion of knowledge graphs or batch diversification is critical to the discovery process. This framework is general and can be adapted to explore gene interactions in other contexts, such as synthetic lethality prediction and mapping epistatic effects across quantitative trait loci.

Methods

The experimental objective is the discovery of the top K strongest phenotypic outcomes resulting from all possible dual gene knockdowns given a fixed set of candidate genes. While such pairs can be identified by a brute force approach, depending on the organism, cell type, or phenotype of interest, it may not be feasible to perform an exhaustive search of all possible pairwise knockdowns because the number of experiments is too large. In practice we often have fixed experimental budgets, and our objective is to maximize the number of double-gene knockdown experiments performed that result in the strongest phenotypic response. In this paper we focus on double-gene knockdown experiments that measure the viral load as the phenotypic response of interest, and the objective is to find those experiments that result in minimal viral load.

Under a fixed experimental budget one option is to design the complete set of experiments in advance. However, in many situations sequentially designing the experiments can be superior to static designs11. In the sequential design of experiments, alternatively known as active learning, observations are made sequentially. At each step of the process one can leverage all data collected up to that point to guide future data collection, thereby minimizing the total number of observations needed. To measure the performance of active learning methods, we next define a metric which we call experimental coverage. If \(\mathcal {I}^*_K\) is the ground-truth set of the K gene pairs with the highest (or lowest) reaction measurements after perturbation, and \(\mathcal {I}_t\) is the list of all double-gene knock down experiments performed up until step t, then we define the experimental coverage as the fraction of elements in \(\mathcal {I}^*_K\) appearing in the set \(\mathcal {I}_t\):

$$\begin{aligned} \text {Coverage}(t,K)&= \frac{ \mathcal {I}_t \cap \mathcal {I}^*_K }{K}. \end{aligned}$$
(1)

Similar to other active learning objectives like cumulative regret minimization or top-arm identification, maximizing experimental coverage faces a fundamental tradeoff between exploitation and exploration. Exploration refers to choosing observations that are likely to be the most informative, while exploitation refers to choosing observations that are likely to be the most rewarding or least costly. One wishes to exploit the best perceived choices in order to maximize the overall objective, but due to the inherent uncertainty in the process one also needs to explore a range of choices to better learn which are likely to be the best. Though the experimental coverage has similarities to top-arm identification in the bandit literature and to recall-at-K in the recommender system literature, it is a fundamentally different performance measure, and one that is arguably the most relevant to experimentalists. To the best of our knowledge there are no known optimal learning algorithms to maximize experimental coverage. For this reason, we empirically investigate a range of well known acquisition functions that trade off exploration and exploitation to varying degrees. In this paper we consider pure greedy, maximum variance, Upper Confidence Bound, and Thompson sampling.

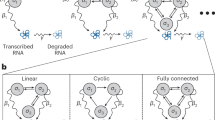
In this work we introduce a novel Bayesian active learning framework to maximize coverage under a fixed experimental budget. There are two fundamental components to this approach. The first is modeling the gene interaction data for predicting unknown interactions. The second is the sequential design of experimental batches. A diagram for this framework can be found in Fig. 1. We provide details on these components in the next two sections.

Fig. 1
figure 1

Schematic diagram showing Bayesian active learning framework with knowledge graph side information for genetic interaction discovery. Gene embeddings from the SPOKE knowledge graph are leveraged as prior information to inform the correlation between genes in a Bayesian matrix factorization model. An active learning framework with a novel and computationally efficient batch acquisition function sequentially chooses sets of experiments to perform. The method efficiently discovers gene pairs that result in phenotypic responses of interest.

Full size image

Bayesian matrix factorization for genetic interaction imputation

When confronted with a large sparsely observed matrix, it can be challenging to predict the unobserved entries. Problems of this sort are common in both online recommender systems12,13 as well as biological interaction data14,15. A standard method for dealing with this class of problems is matrix factorization12,13,16. The key idea behind matrix factorization for predicting interaction data is that the items that are interacting can be represented by low dimensional latent factors, such that the inner product of latent factors predicts the observable interaction value, such as a preference score in online recommender systems or a phenotypic response in a genetic interaction experiment. It is possible to learn these latent factors with incomplete observations of the interaction matrix. The assumption is that even for large matrices, much of the variation can be described by a much lower rank matrix (the matrices of latent factors), and by learning these low dimensional matrices one can predict unobserved entries in the large matrix. While these latent factors may not have direct biological interpretability, they enable prediction of unobserved gene-gene interactions, an essential component for advancing the active learning process.

Probabilistic variants of matrix factorization are particularly suitable for modeling noisy relational data16,17,18,19. Bayesian approaches that place prior distributions on the latent factors, known as Bayesian matrix factorization (BMF), have the advantage of principled uncertainty quantification through posterior inference of the latent factors, and hence the unobserved entries. In the remainder of this section we present the details of our BMF model that incorporates side information through a latent Gaussian process defined across the latent factors.

Consider a set of N genes which will be the candidate genes for double-gene knockdown experiments. We do not consider self-interactions and we assume the ordering of knockdowns does not matter to the experimental results. We assume only a small percentage of pairwise interactions can be observed. In this case the noise-free gene-gene interaction data can be modeled as a sparsely populated, symmetric \(N\times N\) matrix D, where the \(ij^{th}\) entry of this matrix contains a measurement from an experiment where genes i and j are knocked down. Due to experimental observation noise, repeated experiments are required, and we denote the \(n^{th}\) experimental observation of the \(ij^{th}\) gene pair by \(D^n_{ij}\). We let \(N_{ij}\) denote the total number of times the \(ij^{th}\) experiment is performed. We model the observed \(D^n_{ij}\)with the following Bayesian model.

$$\begin{aligned} {\sigma }^2&\sim \text {Inv-Gamma}(a,b) \\ {\sigma }^2_k&\sim \text {Inv-Gamma}(a_k,b_k) \ \ k=1,2,...,M \\ y_{jk}&\sim \mathcal {N}(0,\sigma ^2_k) \ \ j=1,2,...,N; \ k=1,2,...,M \\ D_{ij}^n&\sim \mathcal {N}(\varvec{y}_{i} \cdot \varvec{y}_{j}^T , \sigma ^2) \ \ i,j=1,2,...,N; \ n=1,2,...,N_{ij} \end{aligned}$$

The matrix \(Y \in \mathbb {R}^{N \times M}\) with \(i^{th}\) row \(\varvec{y}_i = (y_{i1}, y_{i2},..., y_{iM})\) has dimension \(N \times M\) where we assume \(M<< N\). Each of the N rows of Y represents an M-dimensional latent factor associated with the corresponding gene, and entries in the noise-free data matrix D can be approximated by the inner product of latent factors: \(\mathbb {E}[D] = Y Y^T\). If \(\Sigma\) is a matrix of zero-mean i.i.d. Gaussian noise, i.e., \(\Sigma _{ij} \sim \mathcal {N}(0,\sigma ^2)\), then the data matrix D can be written as \(D = Y Y^T + \Sigma\). Inv-Gamma denotes the inverse gamma distribution, a flexible prior distribution with support on the positive real line. The inverse gamma parameters a, b and \(a_k,b_k\) are fixed parameters chosen depending on the application.

One advantage of the BMF framework is the ability to incorporate side information via the choice of prior distributions on model parameters. Side information is any auxiliary information not directly observed as part of the data collection process. Typically side information comes in the form of feature vectors associated with each dimension of the observation matrix20,21,22,23,24,25,26,27. An alternative type of side information is graphical side information, consisting of known relations between dimensions of the observation matrix, which can be encoded as a graph, i.e., a set of nodes and vertices. In this study we leverage the Scalable Precision Medicine Oriented Knowledge Engine (SPOKE)28,29, a biological knowledge graph, as side information. SPOKE is a comprehensive graphical network of biomedical databases utilized for various applications, including drug repurposing30 and gene regulation31. The SPOKE knowledge graph features over 20,000 protein-coding human gene nodes sourced from Entrez Gene, as well as nodes corresponding to term annotations from the Gene Ontology database. Furthermore, the graph includes edges representing over 1 million genetic interaction relationships, indicating how the knockdown of one gene–achieved through techniques like short hairpin RNA or CRISPR–can lead to the upregulation or downregulation of another gene, as indicated by consensus transcriptional profiles.

Both probabilistic and Bayesian matrix factorization methods have been proposed that directly incorporate graph information in the form of an adjacency matrix or graph Laplacian25,27,32. Consider an undirected graph \(\mathcal {G} = (E, V)\) with edge set E and vertex (or node) set V of size \( N= |V|\). The adjacency matrix associated with graph \(\mathcal {G}\) is the \( N\times N\) matrix A such that the \(ij^{th}\) entry \(A_{ij}\) is equal to 1 if edge \(e_{ij} \in E\) and 0 otherwise. The degree matrix associated with \(\mathcal {G}\) is the \( N\times N\) diagonal matrix \(\tilde{D}\) with the \(i^{th}\) diagonal entry equal to the degree of node i, i.e., \(\tilde{D}_{ii} = \sum _{j=1}^{N} \mathbbm {1}\left\{ e_{ij} \in E \right\}\). The Laplacian of \(\mathcal {G}\) is defined as \(L = \tilde{D} - A\). The use of the graph Laplacian as a means of incorporating graphical side information in probabilistic matrix factorization was first proposed by Rao et al.32 and later extended to the Bayesian setting25,27.

Elyanow et al.33 used a model equivalent to that proposed in Rao et al.32 that leveraged gene-gene interaction data in a matrix factorization model for single-cell expression analysis. For methodological consistency we present the Bayesian version. Below we denote the \(k^{th}\) column of matrix Y by \(\varvec{y}_{:k}\) and the \(N \times N\) identity matrix by \(I_N\).

$$\begin{aligned} {\sigma }^2&\sim \text {Inv-Gamma}(a,b) \\ {\lambda }&\sim \text {Gamma}(a_0,b_0) \\ \varvec{y}_{:k}&\sim \mathcal {MVN}(0,(\lambda I_N + L)^{-1}) \ \ k=1,2,...,M \\ D_{ij}^n&\sim \mathcal {N}(\varvec{y}_{i} \cdot \varvec{y}_{j}^T , \sigma ^2) \ \ i,j=1,2,...,N; \ n=1,2,...,N_{ij} \end{aligned}$$

As shown by Strahl et al.25 the MAP estimator of this model can be found by minimizing the following objective function,

$$\begin{aligned} -||\mathcal {P}_{\Omega } (D - Y Y^T)||^2_F - \sigma^2 \text {tr}( Y^T (\lambda I_N + L) Y ), \end{aligned}$$

where \(\mathcal {P}_{\Omega }\) is an observation operator selecting out only the indices of D which have been observed, and \(\text {tr}(\cdot)\) is the matrix trace. This is equivalent to the original regularized probabilistic method proposed by Rao et al.32 In both models the effect of the graph Laplacian is to encourage the latent factors to be similar wherever genes are directly connected in the underlying graph \(\mathcal {G}\). More precisely, for the learned latent factor \(\varvec{y}_{:k}\) the introduction of the graph Laplacian encourages entries \(y_{ik}\) and \(y_{jk}\) to be similar whenever \(A_{ij}=1\), i.e., the nodes i and j are neighbors in the graph.

An alternative to directly using the graph Laplacian is to leverage node embeddings derived from the graph. Node embeddings encode graph information in real-valued feature vectors and can capture higher-order relationships in the graph that the graph Laplacian may miss. We utilized a scalable, memory-efficient graph embedding algorithm called Fast Random Projections (FastRP)34. This algorithm relies on random projections, which is a principled way of reducing dimensionality and removing noise (subspace filtering), critical for large heterogeneous knowledge graphs like SPOKE. The FastRP algorithm is able to capture higher-order structure in the graph by iteratively updating the embeddings using both a random projection matrix and the graph Laplacian. Alternative methods for graph embeddings include deep learning (DL) based approaches. While DL-based graph embedding methods also capture higher-order dependancies, they are computationally expensive and require extensive hyper-parameter tuning. Details of the FastRP algorithm are provided in the Supplementary Material.

To incorporate these SPOKE gene embeddings into our BMF model we utilized a latent Gaussian process (GP) defined across genes. This is known as kernelized probabilistic matrix factorization, and it extends probabilistic matrix factorization to include kernelized covariance matrices between the latent factors35,36. The Bayesian variant is known as kernelized Bayesian matrix factorization37,38. Let \(\varvec{x}_i\) be the SPOKE embedding associated with gene i. Let \(D\in \mathbb {R}^{N \times N}\) be a complete interaction matrix so that the \(ij^{th}\) entry, \(D_{ij}\), is one observation from a single experiment where genes i and j are both knocked down. Because multiple experiments can be made at each entry of D, we denote the \(n^{th}\) experimental observation as \(D^n_{ij}\). Because each entry can be observed a different number of times we let \(N_{ij}\) be the total number of times entry ij is observed. The latent GP matrix factorization model can then be written as follows.

$$\begin{aligned} {\sigma }^2&\sim \text {Inv-Gamma}(a,b) \\ \varvec{\phi }_{\varvec{k}}&\sim p(\varvec{\phi }) \ \ k=1,2,...,M \\ f_k | \varvec{\phi }_{\varvec{k}}&\sim \mathcal{G}\mathcal{P}(0, K_{\varvec{\phi }_{\varvec{k}}}(\cdot , \cdot )) \ \ k=1,2,...,M \\ y_{jk}&= f_k(\varvec{x}_j) \ \ j=1,2,...,N; \ k=1,2,...,M \\ D_{ij}^n&\sim \mathcal {N}(\varvec{y}_{i} \cdot \varvec{y}_{j}^T , \sigma ^2) \ \ i,j=1,2,...,N; \ n=1,2,...,N_{ij} \end{aligned}$$

The notation \(f \sim \mathcal{G}\mathcal{P}(0, K_{\phi })\) indicates that the function f is assumed to be drawn from a zero-mean Gaussian process with covariance function \(K_{\phi }\). Here \(\phi\) represents all parameters of the kernel function and \(p(\phi )\) is a suitable prior distribution over these parameters. There are many choices for the kernel function and hence for the parameters \(\phi\) and prior distribution \(p(\phi )\). In this work we use the radial basis function with white noise:

$$K_{\phi _k}(\varvec{x}_i, \varvec{x}_j) = \nu _k^2 \exp {\left\{ -\frac{|| \varvec{x}_i - \varvec{x}_j ||^2}{2\ell _k^2} \right\} } + \delta _{ij}\tau _k^2.$$

In this case we have \(\phi _k=( \nu_k^2, \ell_k^2, \tau_k^2)\). The value \(\nu _k^2\) is the output variance which controls how far on average the outputs of the GP (in this case the latent factors) are from its mean. The value \(\ell _k^2\) is the length scale parameter which governs how far you can reasonably extrapolate the function in input space (in this case the gene embedding space \(\mathbb {R}^M\)). The value \(\tau _k^2\) governs how much observation noise there is associated with the output of the GP. The function \(\delta _{ij}\) is the Kronecker delta function which is equal to 1 if \(i=j\) and 0 otherwise. Because all kernel parameters are positive we again place inverse gamma prior distributions on each. As in the standard BMF model, the parameters a and b are free parameters to be chosen depending on the application.

Finally, we note that because the latent factors \(\varvec{y}_{i}\) are not observed, this is a latent Gaussian process model. Typically in GP regression the output values \(\varvec{y}_{i}\) are observed along with their associated inputs \(\varvec{x}_{i}\). In our case, we only observe the interaction terms \(D_{ij}^n\) and must learn the latent GP outputs \(\varvec{y}_{i}\) and \(\varvec{y}_{j}\) as part of the inference process. The GP prior provides us with a likelihood function for each latent factor that models covariances across different genes as a multivariate normal distribution with covariance matrix determined by the gene embeddings and the chosen kernel function \(K_{\phi _k}\). More precisely, the random vector \((y_{1k}, y_{2k},..., y_{Nk})\) has a multivariate normal distribution where the covariance between \(y_{ik}\) and \(y_{jk}\) is given by \(K_{\phi _k}(\varvec{x}_i, \varvec{x}_j)\).

Batch active learning

In batch active learning multiple observations are made at each step of the data acquisition process. In this setting, in addition to exploration and exploitation, a third criteria–diversification–should be considered when determining which observations to make at each step. When making multiple observations in parallel it is desirable to avoid choosing observations that are highly correlated with one another, or more generally that have a high degree of total correlation39. More specifically, while it is desirable that all experimental points in the design space have high mutual information with the unknown parameters of interest, it is also important that the batch of observations have low mutual information amongst themselves. In the case of high-throughput double-gene knockdown experiments, a single batch of experiments can consist of hundreds of experimental observations. Ensuring low mutual information among hundreds of observation points at each step of the active learning process can be prohibitively expensive. To facilitate a computationally tractable approach to batch diversification, we propose a method that approximates low mutual information within batches by minimizing the aggregate pairwise correlation of the posterior predictive distributions of prospective batches. We next outline the details of this method.

We let the N genes be indexed by a set \([N] = \{ 1,2,...,N \}\) so that each gene pair is denoted by the tuple \((i,j) \in [N] \times [N]\). At step t of the active learning process, denote the current batch of gene-pair indices by \(\mathcal {I}_t\) and the current batch of observations by \(\mathcal {B}_t\). The cumulative set of observed double-gene knockdown experimental results is denoted by \(\mathcal {D}_t=\bigcup_{s \leq t} \mathcal{B}_{s}\). Let \(N^t_{ij} \le t\) be the number of times the experiment (i, j) has been performed up until and including at time step t. Then we have

$$\mathcal {D}_t = \{ D^n_{ij} | (i,j) \in [N ] \times [N ]; 0 \le n \le N^t_{ij} \}.$$

By convention the observation \(D^0_{ij}\) is a null observation for all i, j. The objective at step t is to choose a next batch of indices \(\mathcal {I}_t\) according to an acquisition function \(a_t: 2^{[N] \times [N]} \rightarrow \mathbb {R}\) which maps sets of gene pairs to a score on the real line. The acquisition function \(a_t\) should be chosen so that batches with high value indicate batches that are better for achieving the overall objective, i.e., maximal coverage. We will consider batches of a fixed size B, thus we will only consider subset \(\mathcal {I} \in 2^{[N] \times [N]}\) such that \(|\mathcal {I}|=B\). Defining \(\mathcal {I}_B = \{ \mathcal {I} \in 2^{[N] \times [N]}: |\mathcal {I}|=B \}\), batch selection can determined by

$$\begin{aligned} \mathcal {I}_{t+1} \in \mathop {\mathrm {arg\,max}}\limits _{ \mathcal {I} \in \mathcal {I}_B} a_t(\mathcal {I}). \end{aligned}$$

Note that the acquisition function is indexed by t since it will be a function of the data collected up until time t.

We consider several acquisition functions common in the sequential experimental design and multi-armed bandit literature. A fundamental tradeoff in active learning settings is exploration versus exploitation. An example of a pure exploitation strategy in a Bayesian setting is maximizing the reward’s posterior predictive mean value. We call this the mean acquisition function. An example of a pure exploration strategy is maximizing the reward’s posterior predictive variance. We call this the variance, or MaxVar, acquisition function. Optimal strategies from the multi-armed bandit literature strike a balance between these two extremes. In a frequentist setting, Upper Confidence Bound (UCB) methods are a class of acquisition functions that follow the principle of optimism in the face of uncertainty, and in their most basic form contain both a mean term and a variance term. We call this the UCB acquisition function and construct it using the posterior predictive mean and variance of the reward. A fully Bayesian strategy that strikes a balance between exploration and exploitation is Thompson sampling. This method involves sampling rewards from the posterior predictive distribution and choosing the optimal action based on these samples. This is a stochastic method that has shown good empirical performance in a wide range of bandit problems40.

Letting \(\mathcal {X} \subset [N] \times [N]\) be an arbitrary subset of the design space, and letting \(p(d_{ij}|\mathcal{D}_t)\) be the posterior predictive distribution for a future experimental observation at gene pair \((i,j) \in\mathcal{X}\), these acquisition functions are defined as follows.

$$\begin{aligned} \text {UCB}_t(\mathcal {X})&= -\sum _{(i,j)\in \mathcal {X}} \left( \mathbb {E}_{p(d_{ij}|\mathcal {D}_t)}[d_{ij}] - \lambda \mathbb {V}_{p(d_{ij}|\mathcal {D}_t)}[d_{ij}] \right) \end{aligned}$$
(2)
$$\begin{aligned} \text {mean}_t(\mathcal {X})&= -\sum _{(i,j)\in \mathcal {X}} \mathbb {E}_{p(d_{ij}|\mathcal {D}_t)}[d_{ij}] \end{aligned}$$
(3)
$$\begin{aligned} \text {variance}_t(\mathcal {X})&= \sum _{(i,j)\in \mathcal {X}} \mathbb {V}_{p(d_{ij}|\mathcal {D}_t)}[d_{ij}] \end{aligned}$$
(4)
$$\begin{aligned} \text {TS}_t(\mathcal {X})&= -\sum _{(i,j)\in \mathcal {X}} d_{ij}^* \ \ \text { where } \ \ d_{ij}^* \sim p(d_{ij}|\mathcal {D}_t). \end{aligned}$$
(5)

Because these acquisition functions are additive over single observations, they cannot account for similar or redundant information that may exist within a batch. To encourage batch diversity we add a diversity penalty term to the acquisition function.

$$\begin{aligned} a_t(\mathcal {I}_t) + \eta g_t(\mathcal {I}_t) \end{aligned}$$
(6)

The function \(g_t\) should be a measure of the diversity in the batch \(\mathcal {I}_t\) where larger values indicate greater diversity. The parameter \(\eta\) is a tunable parameter that determines how much diversity is desired in the batch. Possibilities for the function \(g_t\) could be the total pairwise mutual information within the batch, or a multivariate generalizations of mutual information, such as total correlation. While such functions would provide a measure of batch diversity, they are computationally expensive to approximate for large batch sizes. The direct optimization of (6) is a combinatorial optimization problem, and is in general NP-hard. Optimization may involve many evaluations of (6), and for this reason we need both \(a_t(\mathcal {I}_t)\) and \(g_t(\mathcal {I}_t)\) to be computationally tractable. To this end we propose the use of the aggregate pairwise correlation between all gene pairs in the batch, which measures the total amount of pairwise linear correlation within a batch. This can be measured using the posterior predictive samples, Pearson’s correlation coefficient and the Frobenius norm. We next provide the details of this function.

Let \(|| A ||_{F}\) be the Frobenius norm of a matrix A with ij entry \(a_{ij} \in \mathbb {R}\):

$$\begin{aligned} || A ||_{F} = \sqrt{ \sum _i \sum _j a^2_{ij} }. \end{aligned}$$
(7)

Consider a finite set of random variables \(\Omega = \{ \varvec{x}_1,..., \varvec{x}_n \}\) with the \(\varvec{x}_i\) taking values in \(\mathbb {R}^K\). For any \(S \subset \Omega\) let C(S) denote the \(|S| \times |S|\) Pearson correlation matrix of the random vectors in the set S. Without loss of generality assume \(S = \{\varvec{x}_1,..., \varvec{x}_m\}\) for some \(m \le n\). Then C(S) is the matrix with \(ij^{th}\) entry

$$\begin{aligned} C(S)_{ij} = C(\varvec{x}_i, \varvec{x}_j) \triangleq \frac{\sum _k^K (x_{ik} - \bar{x}_i)(y_{jk} - \bar{y}_j)}{ \sqrt{ \sum _k^K (x_{ik} - \bar{x}_i)^2} \sqrt{\sum _{k}^K (y_{jk} - \bar{y}_j)^2 }} \end{aligned}$$
(8)

where \(\varvec{x}_i = \frac{1}{K}\sum _{k}^{K}x_{ik}\) and \(x_{ik}\) is the \(k^{th}\) entry of vector \(\varvec{x}_i\).

In our case we consider \(\Omega\) to be the set of posterior predictive samples for all gene-pair interactions. More precisely, for gene pair \((i,j) \in [N] \times [N]\) we have samples \(( d_{ij}^1, d_{ij}^2,..., d_{ij}^T )\) which are samples drawn from \(p(d_{ij} | \mathcal {D}_t)\). If \(\mathcal {I} \in \mathcal {I}_B\), then \(C(\mathcal {I})\) is the \(B \times B\) Pearson correlation matrix of the posterior predictive samples of all gene pairs in the batch \(\mathcal {I}\). The acquisition function with batch diversification is then given by

$$\begin{aligned} \mathcal {I}_t \in \mathop {\mathrm {arg\,max}}\limits _{\mathcal {I} \in \mathcal {I}_B} \{ a_t(\mathcal {I}) - \eta ||C(\mathcal {I})||_F^2 \}. \end{aligned}$$
(9)

In addition to being computationally tractable relative to other methods like mutual information, the function (9) is also submodular. Submodularity is a property that generalizes the notion of diminishing returns to set-valued functions. This is an important property in combinatorial optimization problems, as there are theoretical guarantees that greedy solutions, i.e., solutions that construct the batch one element at a time, are guaranteed to come within a certain percentage of the optimal solution. Greedy solutions are a computationally efficient means for finding near-optimal solutions41. Details of the greedy algorithm can be found in the Supplementary Material.

Even with computationally efficient functions for \(a_t\) and \(g_t\), direct optimization of (9) is in general difficult and may not be computationally feasible for large design spaces. For this reason, we implement a heuristic random search algorithm that is computationally efficient and gives good empirical performance. Similar approaches have been proposed for computer vision tasks42,43. The idea is to generate a candidate pool of size \(B_{c}\) of potential gene pairs based solely on the acquisition function \(a_t\). The size \(B_{c}\) is a tunable parameter that correlates with the parameter \(\eta\). \(B_{c}\) should be equal to or larger than the batch size B, with larger values of \(B_{c}\) indicating a preference for more diversity. By restricting the search space to this candidate pool, we can dramatically reduce the search space when maximizing (9) while also ensuring that the batches have high aggregate acquisition scores, i.e., \(\sum _{(i,j) \in \mathcal {I}_t}a_t(i,j)\). Once the candidate pool has been reduced, we can construct the batches in a greedy manner due to the submodularity of (9). In particular we leverage a random greedy algorithm for maximizing non-monotonic, submodular functions with cardinality constraints41. We empirically studied the effects of the candidate pool size on algorithm performance.

Experimental results

To demonstrate our end-to-end batch Bayesian active learning framework with side information, we used cell-count-normalized luminescence intensity values from individual double-gene knockdown experiments with a luciferase reporter HIV virus10. The raw experimental data from Gordon et al.10 was obtained via personal communication with the lead author, David E. Gordon, on March 19, 2024. For each gene pair in the data, there were several experimental replicates, with a minimum of 8 and a maximum of 16. Figure 2 shows the averaged log HIV viral load data along with the empirical distribution of the values.

Fig. 2
figure 2

Log HIV viral load data from Gordon et al.10 (arbitrary units). The histogram in the lower pane shows the empirical frequency of log viral loads of off diagonal values, i.e., excluding single-gene knockdown results. The objective of our proposed method is to discover the lowest values in this matrix under a fixed experimental budget. We evaluated the performance of our method by determining how many of the lowest 400 gene pairs we uncover under a fixed number of experimental batches. The top 400 gene pairs are all associated with average log viral intensity values (arbitrary units, hereafter referred to simply as viral loads) below 8, which is in the extreme left tail of the distribution of log viral loads.

Full size image

At each step of the observation process, posterior inference on all model parameters was performed using Markov Chain Monte Carlo (MCMC) sampling. We used the Pyro44 implementation of the No-U-Turn sampler (NUTs)45. The Lawrence Livermore National Laboratory (LLNL) cluster Lassen was used to run multiple MCMC chains on a wide array of parameter values. For each configuration of parameters we ran 36 randomly initialized active learning experiments. For each experiment we ran 1000 warmup steps and 500 samples of NUTs. More than 1000 GPUs were used to run all the experiments. Note that the need for this level of resources was to run 36 independent realizations of a large number of parameter configurations in parallel. For a single configuration of parameters the full active learning process was run on a single GPU. For each run an initial batch of 400 gene pairs was uniformly chosen at random from all possible gene pairs. At each subsequent step, a BMF model was fit to the current aggregated data and a batch acquisition function was used to generate recommendations for the next batch. Recall that there is observation noise in the repeated HIV viral load measurements in the raw Gordon et al.10 data. To simulate observation noise in our active learning experiments, for each gene pair selected by the acquisition function, we sampled an HIV viral load measurement uniformly at random (with replacement) from the set of HIV viral loads in the Gordon et al.10 data. This way we were able to sample a given gene pair as many times as needed regardless of the number of observations in the dataset.

In addition to our kernelized BMF model, we also compared against several baseline methods. We used two baseline BMF models with no side information, and two BMF models with side information. The baseline models with no side information, which we refer to as baseline 1 and baseline 2, are based on the standard BMF model presented at the beginning of section 2.1. The two models with side information are extensions of baseline 1 and 2 leveraging the approach of Elyanow et al.33, which involves using the graph Laplacian of SPOKE as side information. All baseline models are then distinguished by the prior distribution on the BMF latent factors. Letting x be an indicator variable that is 0 when no side information is used and 1 when side information is used, the latent factor prior can be written as follows.

$$\begin{aligned} \varvec{y}_{:k}&\sim \mathcal {MVN}(0,(\lambda _k I_N + xL)^{-1}) \ \ k=1,2,...,M \end{aligned}$$

With this notation the baseline models with and without side information (SI) are as follows.

  • Baseline 1 with no SI: \(\lambda _k = \lambda\) for all k and \(x=0\)

  • Baseline 1 with Laplacian SI: \(\lambda _k = \lambda\) for all k and \(x=1\)

  • Baseline 2 with no SI: \(\lambda _k \ne \lambda _{\ell }\) for all \(k, \ell\) and \(x=0\)

  • Baseline 2 with Laplacian SI: \(\lambda _k \ne \lambda _{\ell }\) for all \(k, \ell\) and \(x=1\)

Note that Baseline 1 with Laplacian SI is equivalent to the model used by Elyanow et al.33 Baseline 2 with Laplacian SI is a more flexible generalization of this model that learns a separate regularization term \(\lambda _k\) for each factor k.

To further assess the performance of our proposed approach we also implemented uniform random sampling as a lower-bound on performance and an oracle algorithm as an upper-bound on performance. Uniform random sampling does not use any of the aggregated data to fit a model, nor does it leverage a data-driven acquisition function. It represents a worst-case, pure exploration method. The oracle algorithm involves fitting our kernelized BMF model to the entire dataset at the outset of the active learning process and computing the mean of the posterior predictive distribution on future observations. At each step the oracle selects the best batch of gene pairs according to the mean posterior predictive distribution from the remaining genes pairs that had not been previously chosen. By having access to a model trained on the entire dataset and selecting batches based on the mean acquisition function, the oracle algorithm represents a best-case, pure exploitation method.

We now present 15 unique parameter configurations which demonstrate the overall trends and effects of parameters on genetic interaction discovery. All results show the median and interquartile range of the cumulative experimental coverage (1) over the 36 randomly initialized experiments. Figure 3 shows experimental results for different acquisition functions with the kernelized Bayesian factor model (with SPOKE as side information) and batch diversification (candidate set size 800). As discussed in the next section, based on the empirical results UCB outperformed the other acquisition functions under most circumstances. Hence in Figs. 4, 5 and 6 we used UCB as the acquisition function and separately investigate the impact of SPOKE, candidate set size in batch diversification and the number of factors K, respectively.

Fig. 3
figure 3

Median and interquartile range of the cumulative experimental coverage (1) over 36 randomly initialized experimental runs on the Gordon et al. HIV viral load data (Fig. 2)10 using (a) the baseline 2 BMF model with no side information and no batch diversification, and (b) the kernelized BMF model with SPOKE side information and batch diversification. Pure random sampling is shown as a baseline and an oracle algorithm leveraging all available data is shown as an upper bound on performance. Different acquisition functions result in substantially different performance. UCB and a pure exploitation strategy (Mean) achieved the best short-term results (small experimental budget) while UCB and Thompson sampling achieved the best long-term results (larger experimental budget).

Full size image
Fig. 4
figure 4

Median and interquartile range of the cumulative experimental coverage (1) over 36 randomly initialized experimental runs on the Gordon et al. HIV viral load data (Fig. 2)10 for all baseline BMF models (with and without SPOKE side information) and the kernelized BMF model (with SPOKE side information). All BMF models used UCB with batch diversification (candidate set size 800). Pure random sampling is shown as a baseline and an oracle algorithm leveraging all available data is shown as an upper bound on performance. The SPOKE side information resulted in a clear improvement in performance early in the experimental process, suggesting that knowledge graph side information can significantly improve experimental coverage when experimental budgets are limited.

Full size image
Fig. 5
figure 5

Median and interquartile range of the cumulative experimental coverage (1) over 36 randomly initialized experimental runs on the Gordon et al. HIV viral load data (Fig. 2)10 for the kernelized BMF model (with SPOKE side information). All acquisition functions used UCB with batch diversification with varying candidate set size (CS), where larger candidate sets correspond to more batch diversification. All experimental steps are shown in Fig. 4a, while box-whisker plots for the results at steps 2 and 20 are shown in subfigures 5b and 5c, respectively. Early in the experimental process batch diversification degraded performance, while at later rounds batch diversification improved performance. The results in later rounds suggest there is an optimal amount of batch diversification near a candidate set size of 800.

Full size image
Fig. 6
figure 6

Median and interquartile range of the cumulative experimental coverage (1) over 36 randomly initialized experimental runs on the Gordon et al. HIV viral load data (Fig. 2)10 with the kernelized BMF model (with SPOKE side information) under a varying number of latent factors. The acquisition function for all results was UCB with batch diversification (candidate set size 800). There was a clear trend that increasing the complexity of the BMF model, i.e., increasing the number of latent factors, improved the performance of the active learning process. However, the performance appeared to saturate after around 20 latent factors.

Full size image
Fig. 7
figure 7

Information in the SPOKE knowledge graph suggests a significant amount of variation in the genes can be described by a single latent factor. This can be see by the singular values of the SPOKE gene embedding matrix in Fig. 7a, which clearly shows one dominant singular value. This suggests a BMF model with a single latent factor (\(K=1\)) should perform reasonably well. Interestingly, the learned latent factors in the \(K=1\) model correlate with the single-gene knockdown log viral load, which can be seen in Fig. 7b.

Full size image

Discussion

From Fig. 3 we see that UCB was the best acquisition function, with a pure greedy approach (minimizing the mean) a close second. The difference between UCB and pure greedy search was more accentuated without batch diversification, suggesting that batch diversification adds a degree of exploration to the pure greedy search. Note also that in the long run, Thompson sampling achieved similar coverage as UCB, but was more explorative, taking longer to reach the limiting coverage of UCB. The pure exploration approach of maximum variance was the worst performing acquisition function. In all, this result suggests an acquisition function that balances exploration, exploitation and batch diversification is the best at maximizing experimental coverage. Note that all methods significantly outperform the naive baseline of uniform random sampling.

From Fig. 4, which shows cumulative coverage results for UCB, we see that kernelized side information significantly improved the performance of the algorithm in early rounds (or when the experimental budget allows only a few rounds of active learning). Somewhat surprisingly, the addition of Laplacian side information in baseline models 1 and 2 degraded the performance in early rounds. There was a clear trend that suggests a more flexible prior distribution on the latent factors improved performance: Our kernelized model outperformed baseline 2, which in turn outperformed baseline 1. However, the fact that directly incorporating the Laplacian degraded the performance suggests how you incorporate graphical side information is critical for improving performance. Directly incorporating the Laplacian into the BMF model appeared to result in misspecified prior distributions, leading to the need for more data to compensate for this bias. Note that as more experimental data was collected, the performance of the baseline models caught up to that of the kernelized BMF model, which is intuitively pleasing as the effect of prior information should diminish as more data is collected. However, this advantage did not translate into higher coverage at later rounds. In this way, side information, when incorporated with a flexible modeling approach, can be extremely valuable when experimental budgets are low.

Figure 5 shows clear trends when considering different levels of diversification in the batch acquisition function. Recall that the larger the candidate pool is, the higher potential there is to diversify the batches. Thus large candidate pools correlate with more diversity. There was a clear tradeoff in performance when it came to the amount of diversity that was in each batch of observations. The larger the candidate pool was, the slower the increase in coverage. On the other hand, larger candidate pools eventually achieved better coverage. Note that if the batch sizes got too large, which corresponds to increasing the amount of batch diversity, the coverage results started to degrade. This suggests that batch diversity is less critical when experimental budgets are smaller, but batch diversity can yield better long-term performance when experimental budgets are larger. Note that it is possible to have too much diversity, as this tended to degrade performance in the long run.

The number of factors K that adequately capture the complexity of the underlying gene-gene interaction data is unknown a priori. While Bayesian nonparametric models such as the Indian Buffet process46 allow inference of K in a data driven manner, inference is typically hard due to slow mixing of MCMC samplers. Moreover, in an active learning context, we tend to have a small amount of data early in the process which increases the complexity of inferring K significantly. Instead of inferring K, we have leveraged the gene embeddings obtained from SPOKE to set K. More specifically, K was set to approximately capture the dominant singular values of the matrix of gene embeddings obtained from SPOKE. We approximated the rank by a simple visual inspection of the magnitudes of the singular values. Note that the largest singular value dominates all others, as can be seen in Fig. 7a, as it is an order of magnitude larger than all others. Looking at the remaining singular values we see that the magnitudes of the singular values rapidly decreases between the tenth and twentieth singular values. This suggests that a priori we should expect that a model with rank \(K=1\) should be able to explain a significant amount of variation in the data while models with a rank beyond \(K=20\) would show diminishing improvements with increasing complexity. We performed a sensitivity analysis of the coverage for different values of K, and this is, in fact, what we found. In general, as seen in Fig. 6, coverage improved with increasing K, and rapidly saturated around \(K=20\). Note that when \(K=1\) the inferred gene-specific latent factors are scalars, and these values correlate strongly with the single-gene knockdown values (see Fig. 7b). In this setting, the latent factors captured the effect of a single-gene knockdown on viral load. Because the predicted effect of a double-gene knockdown is obtained by multiplying the two corresponding latent scalars, the \(K=1\) BMF model was able to uncover interaction effects derivable from single-gene knockdown data, but not necessarily synergistic effects. This suggests that in this dataset single-gene knockdown results should be predictive of double-gene knockdown results to some extent. This general trend was recently reported by Ahlmann-Eltze and Huber and Anders47.

Table 1 Comparison of \(75^{th}\) percentile of gene pairs intersected with the top 400 gene pairs (ground truth).
Full size table

To discover double-gene knockdowns which are not explained fully by single-gene knockdowns, one would need to increase model complexity. Our results suggest that more complex BMF models, such as \(K =20\), can more consistently uncover additional gene pairs whose effects cannot be predicted solely from single-gene knockdowns. A list of these additional gene pairs is provided in Table 1. We identified gene pairs which were both in the ground truth top 400 gene pairs (in terms of minimum viral load) and were also chosen more than \(75\%\) of the time in our numerical experiments. There were no gene pairs chosen by the \(K=1\) model more than \(75\%\) of the time and less than \(75\%\) of the time by the \(K=20\) model. Table 1 shows those gene pairs that were chosen at least \(75\%\) of the time by the \(K=20\) model and were chosen less than \(75\%\) of the time by the \(K=1\) model. This list includes genes from the eukaryotic initiation factor 3 (EIF3) complex and members of the PAF complex (CTR9 and RTF1), each of which has previously been reported to have involvement with various steps in HIV gene expression48,49. Interestingly, in several cases, our algorithm identified pairs of genes whose knockdowns are believed to repress HIV replication by orthogonal mechanisms. For example, it is known that HIV reverse transcription depends on cellular biosynthesis of deoxyribonucleotides by RRM250. Our algorithm paired knockdowns of RRM2 with knockdowns of each of SUPT5H, believed to impede synthesis of HIV RNA transcripts by disruption of Tat transactivation51 and CNOT1, hypothesized to repress HIV replication via enhancement of innate immunity and upregulation of interferon-stimulated genes (ISGs)10.

Other authors52,53 have found evidence that certain host response pathways are conserved across diverse viral infections. This suggests that many of the epistatic relationships uncovered by our algorithm might also be relevant in other viral contexts. However, datasets systematically measuring the effect of dual host knockdowns in infection are very limited, and interaction effects cannot always be assumed to be conserved. For instance, EIF3–a translation initiation factor co-opted by a wide variety of viruses–frequently appears in anti-HIV knockdown pairs, suggesting a common role. By contrast, some genes paired with EIF3, such as those from the human PAF complex, may exhibit more virus-specific effects. For example, downregulation of PAF complex genes has a proviral effect in influenza A infection54, suggesting their role may be context dependent.

Finally, we note that because our framework is designed for a scalar objective function, it can be fit to any quantitative trait or other phenotypic endpoint that may be influenced by multiple genes. For this reason our model can be easily adapted for investigating more complex biological systems, such as the effect of dual gene knockdowns on polygenic traits such as cell proliferation rates, drug responses, or signaling pathway activity levels. The scalability of the proposed algorithm is primarily determined by the dimensions of the data matrix (gene-gene interaction matrix), with a lesser dependence on the structural complexity of the knowledge graph. The size of the data matrix directly affects the number of parameters in the factor model, thereby impacting the computational cost of MCMC inference. The number of parameters in the model is on the order O(KN) where K is the number of latent factors and N is the number of candidate genes. We assume the gene-gene interaction matrix is well approximated by a low rank matrix, which means that K is much smaller than N. Under this assumption the number of parameters grows linearly in both N and K, i.e., when the number of candidate genes increase or the structural complexity of the gene-gene interaction matrix increases. In contrast, the structural complexity of the knowledge graph influences the dimensionality of features generated via the random projection algorithm. However, since this feature extraction is performed only once as a preprocessing step, it does not significantly affect the overall scalability of the algorithm.