Creating nasal cycle simulations by processing MRI and CT scan data with image morphing algorithms

Abstract

The nasal cycle, characterized by alternating congestion and decongestion of the nasal passages, plays a vital role in nasal function. Predicting the nasal cycle using data from medical imaging modalities, such as magnetic resonance imaging (MRI) and computed tomography (CT), can help elucidate its impact on nasal physiology and inform surgical intervention strategies. This study introduces an image processing algorithm that predicts temporal variations in nasal airway morphology during the nasal cycle by utilizing a single MRI or CT scan from a patient. Our approach pipelines two algorithms: an active contour (snake) algorithm followed by a path planning algorithm. The active contour algorithm identifies corresponding sets of points between contours of the nasal wall and the desired turbinate geometry, while the path planning algorithm generates pathways connecting the corresponding point sets. This process enables the prediction of intermediate geometries between two different levels of nasal congestion observed at distinct time points during the nasal cycle. Prediction accuracy was assessed by comparing predicted and actual intermediate nasal turbinate geometries in scans taken from the same subject at different time points, using a total of six human patients. Two distinct path planning models, linear image morphing and A-star, were evaluated for their accuracy in predicting intermediate nasal geometries at various congestion levels. Cross-sectional area was used to characterize nasal airway geometry. Prediction accuracies for nasal geometries within respiratory regions, including middle and inferior turbinates, ranged from 72.51% − 92.17% for the linear image morphing method and from 70.73% − 90.8% for the A-star method. This algorithm-based tool offers a reliable means to estimate nasal geometries at different congestion levels throughout the nasal cycle using MRI and CT scan data. Coupling this technology with computational modeling could further aid in studying how the nasal cycle influences airflow dynamics under various breathing conditions or pathological states.

Introduction

The human nasal cavity is a complex structure that includes the nasal vestibule, three distinct turbinate regions (superior, middle, and inferior), and the nasopharynx³². Nasal geometry exhibits substantial variability among individuals due to differences in bone structure and temporal fluctuations, such as the nasal cycle^15,26. The study of nasal geometry and airflow dynamics provides insight into the complex functions of the nose, including olfactory sensation, filtration, humidification, and the warming of inhaled air^5,11,32. Additionally, such investigations can inform the analysis of nasal drug deposition under various physiological or pathological conditions, breathing states, and anatomical variations^18,20,27.

The periodic changes in nasal airway geometry are known as the nasal cycle^15,25,26,30. The nasal cycle has been observed in approximately 70–80% of the adult population^25,34. The periodicity of this ultradian cycle ranges from 30 min to 6 h¹⁵. During the nasal cycle, one nostril experiences airway constriction due to turbinate engorgement, while shrinkage of the turbinate on the contralateral side results in airway dilation²⁵. These cyclic changes in the congestive state are driven by asymmetric blood flow distribution between the two nasal passages. Increased blood flow causes expansion of the erectile tissue located on the inferior and middle turbinates, and the anterior nasal septum, creating a congested nasal airway (Fig. 1)^15,25. Literature suggests that nasal congestion and decongestion, which reflect vasodilation and vasoconstriction of the nasal mucosa respectively, are regulated by the autonomic nervous system¹⁵.

The underlying rationale for the existence of nasal cycles remains ambiguous. One hypothesis suggests that the low airflow velocities generated in the congested nostril help maintain nasal mucus hydration and support mucociliary clearance^4,8,30,35, which is used to remove harmful particles and substances from the airways^10,35. Consequently, nasal cycles may provide protection against respiratory infections and allergies^10,35. Alternatively, some researchers have proposed an olfaction-centered functional role for nasal cycles^21,28,31,39. According to this theory, nasal cycles can optimize each nostril for the detection of different odors by simultaneously transmitting two distinct sets of olfactory signals to the brain, thereby enhancing the overall olfactory range^21,28,31. Additionally, olfactory perception may be selectively tuned to certain odorants based on their sorption rates and the degree of stimulation of olfactory receptors, both of which are influenced by airflow properties, including rate and direction^21,28. Moreover, computational fluid dynamics (CFD) has been used to investigate how the nasal cycle influences temperature regulation inside the nasal cavity due to airflow velocity, pressure, and nasal resistance in a three-dimensional (3D) CT scan model with asymmetric nostril geometry, representing congested and decongested nostrils³⁴. Using CFD simulation in ANSYS Fluent, Wei et al. revealed that the congested side increases the heat of inhaled air effectively and rapidly due to greater wall contact and higher airflow velocity compared to the decongested side³⁴. Furthermore, the suspected influence of the nasal cycle on particle deposition within the nasal cavity may stem from fluctuations in air pressure caused by cyclic changes in nasal airflow patterns^21,28,31,34. Elucidating the underlying mechanisms of the nasal cycle through simulation of its behavior could potentially enhance the efficacy of systemic absorption via intranasal drug delivery systems and help uncover related factors that impact olfactory function²⁹.

Surgical procedures involving the nasal cavity typically include pre- and post-operative assessments using imaging modalities, such as magnetic resonance imaging (MRI) and computed tomography (CT). However, capturing the time-dependent morphological changes in nasal anatomy caused by the nasal cycle requires multiple scans over time. A method to simulate these changes without repeated imaging has yet to be developed. Such an approach would improve the evaluation of surgical outcomes by accounting for temporal variations like the nasal cycle.

To simulate the nasal cycle with scans of a single nasal cavity from only a few timepoints, it is necessary to generate intermediate geometries that represent different phases of the cycle. Predicting these intermediate geometries requires the implementation of morphing prediction techniques. Gaberino et al. developed a method to create intermediate states of the nasal cycle by offsetting the boundary of the airway in a nasal slice using the erosion/dilatation tool in Mimics™ (Materialise Inc.; Version 16.0; https://www.materialise.com/en/healthcare/mimics/mimics-core) and used them to estimate the nasal geometry at the midpoint of the nasal cycle⁶. However, they did not validate the accuracy of the predicted intermediate states. Nejati et al. proposed a deformable template method that creates an average nasal geometry using coronal CT slices taken at a single timepoint from multiple individuals²². This approach generates geometries representing nasal cycle transitions based on anatomical variation across patients at a single time point by using skeletonized representations of the nasal airway to reduce inter-individual variations. While this method avoids the need to artificially synthesize intermediate or transitional geometries characteristic of the nasal cycle, it requires acquiring CT scan data from numerous individuals²². In contrast, the present study introduces a technique to predict intermediate nasal geometries of the nasal cycle using a single MRI or CT dataset from an individual patient that captures approximate congestion and decongestion extremes in each nostril (Fig. 1).

Herein, we detail a computational method to simulate the morphology of the nasal cycle using two pipelined algorithms: an active contour algorithm and a path-planning algorithm. The morphological change we simulate is the expansion and contraction of the turbinate within the nasal passage. To achieve this, we consider two boundary contours, one representing the entire nasal cavity and one representing the turbinate. At full (100%) simulated expansion, the contour of the turbinate is anticipated to conform closely to the adjacent nasal cavity boundary. Building on this concept, we use the nasal cavity contour as an active contour that can conform to the shape of the turbinate, thereby simulating the morphological transitions of turbinate expansion and contraction within the nasal cavity wall at different phases of the nasal cycle.

The active contour algorithm, originally developed for identifying boundary edges and contours of objects in images¹⁶, is employed in our approach to identify corresponding sets of points on the boundaries of two distinct anatomical geometries, the fixed nasal cavity wall and the turbinates contained within it. The method allows a nasal contour to evolve and conform to anatomical features and offers increased accuracy and efficiency compared to manual point selection. Unlike other techniques, such as Procrustes analysis and the Iterative Closest Point (ICP) algorithm, the active contour method emphasizes local boundary features and provides non-rigid transformations^7,38. Feature-based algorithms, such as Scale-Invariant Feature Transform (SIFT) or Speeded-Up Robust Features (SURF), identify key points or local features within images instead of on object boundaries. The active contour method identifies corresponding points on the boundary contours of images as key features, which is more suitable for our approach^2,14.

To create a path between the corresponding sets of points identified by the active contour algorithm, we implemented two path planning models: linear image morphing and the A-star (A*) algorithm. Linear image morphing, originally introduced for smooth image transformation, was adapted for our purposes of creating linear pathways between points^9,36. Additionally, the A* algorithm, initially developed for efficient obstacle avoidance in autonomous robotic navigation⁹, was incorporated into our methodology to generate pathways, while treating anatomical boundaries as obstacles. Intermediate geometries of the nasal cavity at different phases of the nasal cycle can be generated using these pipelined algorithms to track paths. Reconstructing the nasal cycle using morphing algorithms to produce intermediate nasal geometries may prove useful for understanding the influence of the nasal cycle on nasal function, especially when supported by computational simulations^3,22, and for guiding surgical interventions for conditions impacted by the nasal cycle, such as septoplasty, turbinectomy, and functional rhinoplasty⁶.

Methods

Patient MRI and CT scan data

Deidentified CT imaging scan data from the head of a single healthy patient (Patient A) (female, 56 years old) were sourced from a data collection at the University of Chicago Medical Center to reconstruct nasal airway images for this study. The use of CT scan data in this study was approved by the University of Chicago Institutional Review Board. All CT scanning procedures conducted in this study adhered to the relevant IRB guidelines and regulations. Since the study analyzed pre-existing anonymized imaging data, the University of Chicago Institutional Review Board waived the requirement for patient informed consent (protocol number: IRB18-1247). During the CT scanning process, the patient was oriented in a supine position and remained awake. The CT scans were obtained with a planar resolution of 0.44 × 0.44 mm and an interslice spacing of 1 mm. Additional patient MRI or CT scan data sets (Patients B-F), taken at two time points and representing the approximate congestion and decongestion extremes in each nostril, were acquired from literature^1,13,24,33. The coronal sections from sequential scans were compared at approximately the same distance from the nares. Collectively, a total of 10 of these time-matched scans were supplied from patients (Patient A-F) and used to evaluate the accuracy of predicting nasal cycles with an algorithm. Nasal airway contours and corresponding data sources for all patients are summarized in Table 1.

Nasal cavity segmentation

Segmentation of the nasal cavity into airway, turbinate and mucosal portions was performed using a sequence of steps involving software-based image editing and drawing tools, along with custom segmentation algorithms. The entire flow process for segmentation of the nasal structures is visually summarized in Fig. 2(a) and was performed on coronal nasal slices with an end goal of obtaining an image with segmented turbinated regions and a segmented nasal cavity, with extracted turbinate regions. DICOM (Digital Imaging and Communications in Medicine) files containing the MRI or CT scan data were converted to JPEG (Joint Photographic Experts Group) format using MicroDicom DICOM Viewer (Version 2024.3; https://www.microdicom.com/) (Fig. 2(a1)).

Nasal airway regions were then segmented and isolated from the grayscale coronal MRI and CT images using ImageJ software (Version 1.54 g; https://imagej.net/ij/) through a series of image processing steps. First, a boxed region enclosing only the nasal passages was cropped from each image, and the cropped image was scaled by a factor of 5 to enhance visibility (Fig. 2(a2)). The nasal airway region appeared black, with pixel intensity value near 0 (black), while non-airway regions appeared gray. To segment the nasal airway region, a thresholding tool was used to set all gray appearing non-airway regions to 255 (white), while pixels in the airway region were set to 0 (black) (Fig. 2(a3)).

Next, turbinate regions were segmented using a series of steps outlined in Fig. 2(a). Initially, a skeletonized version of the nasal airway was generated in ImageJ (Fig. 2(a4)). A custom Python algorithm then segmented the nasal airway by its branches and assigned a unique color to each branch, following a three-step process. First, the algorithm segmented individual branches of the skeletonized airway at points of intersection (Fig. 2(a4)). Second, the skeletonized nasal airway image was superimposed on the original segmented nasal airway image. Third, the K nearest neighbor method was applied to mask different tiers of the segmented nasal airway with unique colors (Fig. 2(a5)), assigning colors based on the corresponding branch overlay. The resulting branch-based segmented airway image was imported into Microsoft PowerPoint (Version 2504; https://www.microsoft.com/en-us/microsoft-365/powerpoint), where drawing tools were used to create a line that delineates the boundary where each turbinate extends from the lateral nasal cavity wall (Fig. 2(a6)). The color of each line was matched to that of its corresponding branch.

Finally, the image with the demarcated turbinated regions (Fig. 2(a6)) was imported into ImageJ, to generate two separate images: (1) a segmented turbinate image (Fig. 2(a7)) and (2) a segmented nasal cavity with the turbinate regions extracted (Fig. 2(a8)). To create the segmented turbinate image, a multi-step process was implemented. First, the branch-based segmented airway image was converted to grayscale (if not already in grayscale), and the entire airway region was filled with a color that contrasted with the background. Next, a mask was created in which the turbinate regions appeared black against a white background (Fig. 2(a7)). To generate the segmented nasal cavity image, the turbinate regions in the branch-based segmented image (with demarcated wall boundaries) were filled with branch-specific colors (Fig. 2(a8)).

Since the custom Python algorithm changed the scale of the segmented image, the size scale of all the input images were also adjusted according to the original segmented nasal airway image using PowerPoint. The branch intersection points on the nasal airway image (Fig. 2(a4)) and the lowest point of the nasal airway boundary were considered for aligning the images (Fig. 2(a)). The outcomes of this image processing technique are illustrated in Fig. 2(b).

To make comparisons across images taken at different time points within a single patient dataset, the height of the airways segmented at corresponding locations was standardized in PowerPoint, ensuring consistent values across time points. The other dimensions were then scaled proportionally based on the adjusted height. Segmentation was subsequently performed using the previously described methodology.

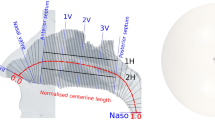
Variability in nasal geometry was observed within scan data acquired from the same patient at different time points. To align images of nasal slices at corresponding distances from the nares, a pair of bone-based anatomical landmarks was used as a reference: (1) the tip of the anterior maxillary spine, at the intersection of the nasal septum and maxilla bone, and (2) the beginning of the opening of choana, where the left and right airways merge (Fig. 3)²². This normalization process ensured that images captured at different time points corresponded to the same anatomical location prior to their input in the nasal cycle simulation algorithms.

Active morphing pipeline algorithm

Two inputs images were used for the proposed pipeline algorithm: 1) the segmented geometry of the turbinate in its decongested extreme and (2) the nasal cavity with the turbinate regions extracted (Fig. 2(b1)). A morphing pipeline algorithm comprising two distinct algorithms, an active contour (snake) algorithm¹⁶ and a path planning algorithm^9,36, was implemented (Fig. 4). The active contour algorithm is employed to identify corresponding sets of points between the contour of the decongested turbinate and the contour of the complementary nasal cavity. First, the contour of the nasal cavity (dotted red line in Fig. 2(b2)), serving as the active contour, was wrapped around the decongested turbinate to create a wrapped contour (solid cyan line in Fig. 2(b2)). The points along the contour remain consistent as the nasal cavity contour (dotted red) evolves into the turbinate contour (cyan). Subsequently, the corresponding point sets between the initial and final contours are input into the path planning algorithm, which generates paths between these corresponding points to create multiple intermediate turbinate geometries representing different phases of the nasal cycle (Fig. 2(b3)). These intermediate geometries serve as predicted turbinate contours that simulate the morphological transitions of the turbinate as it changes shape throughout the nasal cycle. While several intermediate turbinate geometries can be generated instantaneously using the pipeline algorithm, the maximum number of predicted geometries is limited by the computational power of the computer system.

Active contour algorithm

The active contour algorithm is capable of detecting object boundaries by iteratively evolving contours towards the boundary of the object of interest¹⁶. The following function (Eq. 1) is employed to drive this evolving process through the minimization of energy:

$$\:E=\:\int\:{E}_{internal}+{E}_{image}+\:{E}_{con}\:ds$$

(1)

where $\:{E}_{internal}$ represents the internal energy, $\:{E}_{image}$ represents the image forces, $\:{E}_{con}$ represents external constraint forces, and $\:d\text{s}$ represents the differential element along the evolving contour, corresponding to an infinitesimal segment of the contour.

$$\:{E}_{internal}=\:\alpha\:{\left(\frac{\partial\:v\left(s\right)}{\partial\:s}\right)}^{2}+\beta\:{\left(\frac{{\partial\:}^{2}v\left(s\right)}{\partial\:{s}^{2}}\right)}^{2}$$

(2)

In the internal energy equation (Eq. 2), α and β are weighting parameters, and $\:\text{v(s)}$ represents the contour, while $\:\text{s}$ denotes the coordinates of each point set along the contour. The internal energy term, $\:{E}_{internal}$, governs the smoothness and continuity of the contours by accounting for the elasticity and curvature of the contour. This smoothness and continuity were fine-tuned by adjusting the weighting parameters and the internal energy term (Eq. 2). The image forces, $\:{E}_{image}$, attract the contour towards the boundary of the region of interest, guided by the large image gradient, which represents the rate of change in pixel intensity or color in an image. Any additional user-defined constraint forces are incorporated through the external constraint forces term, $\:{E}_{con}$.

In our case, the outline of turbinate tissue segment is treated as the image object of interest, while the outline of nasal cavity segment is considered as the initial contour for the active contour algorithm. Utilizing the energy equation (Eq. 1), the boundary of the turbinate exerts forces that attract the initial contour toward it. As output, the algorithm provides the final attracted contour (wrapped contour), which conforms to the boundary of the image object, as shown in Fig. 2b. In other words, the contour of the nasal cavity segment wraps around the boundary of the turbinate. Notably, this final wrapped contour retains the same number of points as the initial unwrapped contour, enabling the identification of corresponding point sets between the initial and final contours. Transitional or intermediate states of the nasal cycle can then be created by generating a series of contours that evolve from the initial contour (entire nasal cavity) toward the final contour (turbinate tissue segment), or vice versa. These sequential intermediate contours can be defined by connecting the corresponding points between the initial and final contours with path planning algorithms, as explained in the subsequent section.

Path planning algorithms

In this study, path planning algorithms were employed in order to investigate an optimal trajectory between the two correspondent point sets associated with the boundary contour of the nasal airway and the wrapped contour for the turbinate created from the active contour algorithm. Considering the correspondent point sets as input, the path planning algorithm produced a set of plausible paths between such contours. Two pre-existing path planning algorithms are utilized in this study: the linear image morphing algorithm and A* algorithm.

Linear image morphing algorithm

The linear image morphing algorithm computes a path between two contours by performing linear interpolation between the corresponding point sets on these contours¹⁹ (See Fig. 4(a)). This algorithm only connects corresponding points by a straight continuous line and interpolates points along that line. The positions of the interpolated points along this linear path can be adjusted through the $\:\alpha\:$ parameter, as expressed in Eq. 3,

$$\:P\left(i\right)\:=\:(1-\alpha\:){P}_{1}\left(i\right)+\alpha\:{P}_{2}\left(i\right)\:$$

(3)

where $\:i$ denotes the corresponding point set, $\:P\left(i\right)$ represents the coordinates of the intermediate contour and $\:{P}_{1}\left(i\right)$ and $\:{P}_{2}\left(i\right)$ are the coordinates of the initial nasal airway contour and wrapped turbinate contour generated by the active contour algorithm, respectively. By initializing with corresponding point sets in two boundaries, this algorithm can gradually transform one set of points into the other as shown in Fig. 2(b).

A* path planning algorithm

The A* algorithm is a graph-based path planning method that finds the shortest path from a starting node to a goal node within a given map⁹. In the present study, the corresponding point sets between the wrapped turbinate boundaries and nasal airway, generated by the active contour algorithm, were respectively utilized as the start and goal nodes. The entire image segment of the nasal airway, bounded by the initial nasal cavity wall and the wrapped contour, was treated as the grid environment (Fig. 4(b)) in which the algorithm generates paths between corresponding points. The paths in between the turbinate and nasal wall are constructed by selecting the sequence of nodes between the corresponding points that minimizes the total cost as given in Eq. 4¹² (Fig. 4(b)). In Eq. 4,

$$\:f\left(n\right)=g\left(n\right)+h\left(n\right)$$

(4)

where $\:g\left(n\right)$ is the cost of reaching a particular node from the start node and $\:h\left(n\right)$ is the heuristic estimate of the cost to reach the goal node from $\:n$. In this context, $\:h(n$) is typically calculated using the Euclidean distance, allowing horizontal, vertical, and diagonal moves.

The algorithm initializes two lists: (1) an open list containing nodes to be evaluated (starting with the start node), and (2) a closed list for nodes that have been evaluated. At each step, the node in the open list with the lowest $\:f\left(n\right)$ is selected as the current node. If this node is the goal, the path is reconstructed by tracing back through its parent nodes. Otherwise, the current node is moved to the closed list, and each of its neighboring nodes are examined. If a neighboring node is in the closed list, it is skipped. If it is not in the open list, it is added with updated $\:g\left(n\right)$ and $\:h\left(n\right)$ values. If the neighboring node is already in the open list and the newly calculated $\:g\left(n\right)$ is lower than the previously recorded value, then its g(n) is updated and the current node is set as its parent node. This process repeats until the goal node is reached, ensuring that the most efficient path is found¹².

Validation of predicted intermediate geometries

To validate the path planning algorithms, we used the overlap metric to assess how accurately they predicted intermediate nasal geometries. Predicted contours of intermediate turbinate regions were compared with multiple actual intermediate turbinate contours from the same patient, captured at corresponding distances from the nares but at different timepoints. The overlap metric, defined as the ratio of the intersection to the union of two contours, was used to quantify the discrepancy between predicted and actual geometries. Each actual intermediate turbinate contour was matched to a predicted intermediate turbinate contour occurring at approximately the same phase of the nasal cycle though visual evaluation of intermediate geometries and the original scan data. The error in the overlap metric is expressed in Eq. 5,

$$\:Error\:in\:Overlap\:Metric\:\left(\%\right)=\left(1-\left|\frac{A\cap\:B}{A\cup\:B}\right|\right)\times\:100\%$$

(5)

where A represents the area of the actual intermediate turbinate region, B is the area of the predicted intermediate region, A ∩ B is the intersection of the two, and A ∪ B is their union.

Quantitative analysis of nasal cycles

The proposed methodology enables simulation and quantification of changes in the cross-sectional area (CSA) of either the entire nasal airway or turbinate- specific nasal airway regions under varying levels of congestion. Although our analysis focuses on the CSA of the entire nasal airway or airway regions surrounding specific turbinates, calculating the CSA of individual turbinates themselves is also possible and can serve as an indicator of congestion severity. The CSA is determined by counting black pixels representing the airway and converting this count to real-world dimensions by calibrating against the actual airway dimensions obtained from DICOM data. This pixel-based analysis allows for the independent evaluation of congestion severity within each turbinate region, offering improved insight into nasal airflow dynamics and particle deposition under different congestion conditions.

The percentage of congestion, defined in Eq. 6, quantifies the proportion of a path length that a point travels from the predicted intermediate contour to the nearest turbinate boundary, typically taken from the initial baseline turbinate geometry:

$$\:Congestion\:Percentage\:\left(\%\right)\:=\:\frac{{D}_{p}}{{D}_{Tot}}$$

(6)

where $\:{D}_{p}$ is the distance from a point on the predicted contour to the nearest turbinate boundary along its path, and $\:{D}_{Tot}$ is the total length of the path.

Results and discussion

The precise function of the nasal cycle remains unclear. Developing methods to identify and characterize associated structural changes could illuminate its role in olfaction and in conditioning inspired air through humidification, warming, and filtration. This study characterizes morphological changes in nasal structures during the nasal cycle by processing MRI/CT-derived images with a custom algorithm pipeline. Specifically, a pipeline integrating active contouring with two path planning strategies, linear image morphing or A*, was used to predict intermediate nasal geometries from a single MRI or CT scan. The pipelined algorithm generates transitional geometries by evolving an active contour, defined by the nasal cavity boundary, around the turbinate (or an erectile tissue region), using corresponding points shared between the initial and final contours to define paths for producing intermediate geometries.

Predicted intermediate turbinate geometries, generated by both path-planning algorithms for the same coronal section (including both inferior and middle turbinates) from Patient A, are shown in Fig. 5. Figure 6 shows the variations in predicted geometries at 50% congestion for three different coronal sections from the same patient, comparing results from both linear morphing and A* algorithms.

To evaluate the pipeline’s predictive accuracy, intermediate geometries were compared with actual intermediate turbinate contours from the same patient at matching locations and different time points. Patient A was the only subject with comprehensive nasal scans at two time points; corresponding locations were identified using anatomical landmarks (Fig. 3). For Patients B - F, imaging data from the literature provided corresponding coronal slices at two time points. Prediction accuracy was assessed using the percent error in the overlap metric, which quantifies the discrepancy between the predicted and actual contours.

Visual comparisons for Patient A demonstrated comparable performance between the two algorithms, with the linear morphing algorithm generating slightly lower prediction errors, overall (Fig. 7). Prediction errors across all patients, using MRI and CT data from both our dataset and previously published sources^1,13,24,33, are summarized in Table 2. Additionally, we assessed prediction errors by nasal region (Table 2). Overall, overlap metric errors ranged from 7.83 to 27.49% across all algorithms. When considering the airway region with expansion from a single turbinate, the linear morphing algorithm achieved the lowest errors: 9.56% for the middle turbinate and 7.83% for the inferior turbinate. However, the linear morphing algorithm sometimes failed to respect nasal airway boundaries (the nasal wall), whereas the A* algorithm consistently adhered to these boundaries (Fig. 4).

Further analysis revealed more pronounced shape variations in the posterior nasal cavity. As shown in Fig. 6, predicted turbinate contours in closer to the nasopharynx (Sect. 3) exhibited greater variability than those in the more anterior respiratory regions (Sects. 1 and 2). This may reflect more substantial expansion of posterior turbinates, which could increase geometric complexity and reduce prediction consistency. Prediction accuracy was also lower for simultaneous expansion of both middle and inferior turbinates compared to single-turbinate expansion (Table 2), possibly due to turbinate-specific variation in maximum expansion volumes. These findings suggest that future algorithm refinements should incorporate region-specific maximum tissue expansion profiles to improve accuracy.

The pipeline also quantified nasal cycle-induced congestion levels. CSA of the nasal airway was computed by counting the number of pixels representing the airway geometry and converting them to physical dimensions using a calibration based on each patient’s nasal cavity size. The CSA was calculated both for the entire airway (Fig. 8a) and for specific turbinate regions (Fig. 8b) as a function of congestion percentage. CSA of the nasal airway in Sects. 1 and 3 decreased nonlinearly with increasing congestion levels, whereas Sect. 2 exhibited a more linear reduction trend (Fig. 8a). In the turbinate-specific analysis, the CSA of the nasal airway around the inferior turbinate region also showed a nonlinear relationship with congestion levels. By contrast, CSA of the nasal airways around the middle turbinate exhibited a more linear relationship compared to the inferior turbinate (Fig. 8b). By quantifying reductions in CSA across congestion levels, our approach offers a metric for assessing the extent of airway obstruction.

Other research approaches, including those based on CSA, have been used to assess nasal obstruction and guide surgical treatment. For instance, Park et al. used acoustic rhinometry to measure the CSA at varying congestion levels to evaluate nasal obstruction and outcomes after septoplasty²³. Krzych-Fałta et al. applied optical rhinometry to monitor nasal mucosa edema, or congestion, by tracking changes in blood flow and infrared light transmission with nasal sensors¹⁷. This approach also enabled the measurement of nasal airflow pressure to assess the extent of nasal congestion¹⁵. While informative, these methods cannot estimate the CSA of turbinate-specific regions. By quantifying CSA variation for each turbinate, our approach can assess contributions of localized congestion to airflow resistance, offering insight into airflow behavior and the effects of decongestants³⁷. This level of anatomical detail may enhance diagnostic precision and support more targeted and effective treatment strategies.

A key advantage of our pipeline is that it requires only a single MRI or CT scan to generate intermediate nasal cycle geometries, making it particularly valuable for surgical preplanning in settings with limited resources. In contrast, Gaberino et al.⁶ relied on both pre- and post-surgical scans to capture the extremes of mucosal congestion and decongestion in each patient, then employed erosion and dilation tools to artificially construct mid-cycle geometries from each scan. However, their approach has not been validated against actual patient data, whereas our method was validated using patient scans acquired at different time points.

Nonetheless, our study has limitations specific to the richness of datasets that affect the robustness of prediction accuracy:

• 1. First, the limited availability of patient data restricted our ability to robustly validate the predicted geometries against actual scans of the congested and decongested extremes, acquired at multiple time points and anatomical locations across multiple patients.

• 2. Second, our dataset lacked transitional scans that captured intermediate nasal cycle states beyond the congested and decongested extremes. Incorporating additional reference intermediate contours from patient scans, captured at various levels of congestion at different time points, would allow the algorithm to simulate smoother and more gradual transitions, thereby improving prediction accuracy.

• 3. Third, the selected scans used to represent congestion and decongestion extremes may not fully capture the true physiological range for a given patient. In our simulations, we assumed that the most congested instance of a nasal slice represented full turbinate dilation across the entire nasal airway; however, actual extremes may differ depending on factors such as age and underlying health conditions¹⁵.

• 4. Fourth, the predicted geometries may not fully account for variations introduced by different breathing conditions, such as restful, shallow, heavy, sniffing, or rapid breathing (e.g., tachypnea).

Access to a larger and more diverse patient dataset, including detailed health and respiratory profiles, and the integration of a multi-stage path-planning approach using multiple initial contours would enable more accurate identification of nasal cycle extremes and enhance the pipelined algorithm’s performance across a broader range of physiological and clinical conditions.

The morphological metrics from our study could support computational analysis of nasal airflow patterns, aiding surgical planning for procedures such as septoplasty, turbinate reduction, and polypectomy by identifying target congested regions for geometric correction. Additionally, our algorithm enables the evaluation of congestion in patients with structural abnormalities.

Conclusion

This study presents a novel algorithm for simulating temporal variations in nasal cavity morphology using MRI and CT scan data. The algorithm successfully generates intermediate geometrical shapes at various congestion levels throughout the nasal cavity. Validation was performed by comparing algorithm-generated intermediate geometries with actual intermediate nasal shapes obtained from MRI and CT scans of the same patient at different time points. Additionally, we quantified variations in the cross-sectional areas of the entire nasal airway and specific turbinate regions under different congestion levels, providing insights into the dynamic nature of nasal airway geometry.

Our pipeline algorithm shows promise as a clinical tool to support surgical planning by identifying congested areas and quantifying the extent of tissue reduction required to alleviate obstruction. This capability could significantly enhance preoperative planning and improve surgical outcomes for nasal procedures. Future work will focus on refining the algorithm’s accuracy and expanding its clinical utility. Further validation studies involving larger and more diverse patient cohorts are necessary to establish the algorithm’s robustness and reliability across varying nasal anatomies and pathological conditions.

Fig. 1

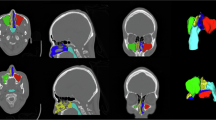
The nasal cycle refers to the periodic alternation of congestion and decongestion between the two nasal passages, a process that can be visualized with CT and MRI imaging. These coronal sections of the nasal cavity show dilation of the left nasal passage and constriction of the right, indicating left-side dominance and greater airflow through the left passage at the time of imaging.

Fig. 2

(a) MRI and CT scan data were preprocessed to segment turbinate regions and the entire nasal cavity (excluding the turbinates) using a combination of software-based image editing, manual drawing tools, and custom segmentation algorithms. MRI/CT scan data were converted into JPEG format using MicroDicom DICOM Viewer (1). Using ImageJ, scan images were then cropped and scaled (2), color-thresholded to segment the nasal airway (3) and transformed into a skeletonized nasal airway (4). Using a custom Python algorithm, the nasal airway skeleton was superimposed over the segmented airway image to generate a nasal airway image with subregions color-coded by branch level (5). A line (colored according to branch level) was drawn in Microsoft PowerPoint to demarcate the boundary where each turbinate region meets the nasal wall (6). Masking and filling tools from ImageJ were then used to create images with the turbinates appearing in black (7) and the nasal cavity segmented with subregions color-coded by branch level (8). (b) Process flow diagram illustrating the generation of intermediate or predicted turbinate contours that simulate structural morphing during the nasal cycle. (1) Segmented turbinate and nasal cavity (excluding turbinates) regions were prepared as inputs for the active contour algorithm. (2) The active contour (snake) algorithm wraps the nasal cavity contour around the decongested turbinate region, identifying corresponding point sets between the initial nasal cavity contour (dotted red) and the wrapped turbinate contour (cyan). (3) A path planning algorithm connects these corresponding point sets to create intermediate (transitional) turbinate contours. Gray-shaded boxes denote steps where algorithms (active contour and path planning) were applied.

Fig. 3

These CT scans include anatomical landmarks, the anterior maxillary spine (left) and the choana (right), used to compare data across different time points. The anterior maxillary spine is a bony projection situated at the base of the nasal aperture, at the midline where the two maxillae meet. The choana is the posterior opening of the nasal cavity where the nasal passages connect to the nasopharynx.

Fig. 4

Path planning algorithms. The path planning algorithms generate paths (blue lines) through the open airway space (outlined in red), which lies between the boundary of the original turbinate tissue region and the outer boundary of the nasal airway/cavity (excluding the turbinates). This outlined space also defines the navigable grid space for the algorithms. (A) The linear image morphing algorithm connects corresponding points using straight lines (blue), but it does not respect anatomical boundaries (red). The inset shows a pathway (blue) that crosses outside the open nasal airway boundary (red), highlighting this limitation. (B) The A* algorithm generates paths (blue) on a grid map from the start to goal nodes, while allowing for multiple directional turns and respecting the boundary constraints of the nasal airway contour (red). The algorithm calculates the heuristic cost to move from a particular node to the goal node, selecting the path with the lowest total cost as the best route. Inset grids are illustrative and not to scale.

Fig. 5

Sequence of predicted turbinate contours. Solid yellow lines show predicted turbinated contours generated by the linear image morphing and A* path planning algorithms for the same coronal nasal slice. These contours simulate the morphological changes in turbinate regions as the nasal cycle progresses.

Fig. 6

Nasal cycle simulation across three coronal views. Simulations using linear morphing and A* path planning algorithms are shown for three different coronal views of the nasal cavity. The initial turbinate geometry is indicated by the red hatched filling. The predicted turbinate contour at 50% congestion is outlined in cyan, and the corresponding expanded turbinate region filled with red and white hatch marks.

Fig. 7

Comparison of predicted and actual turbinate geometries. The percent error between predicted and actual intermediate turbinate geometry contours is shown across the nasal sections (Sects. 1–3, top to bottom) acquired at different timepoints for the same patient (patient A). Inset images display the nasal airway geometry with the lowest percent error (highlighted by a blue dotted line) between the predicted intermediate turbinate contour (solid yellow line) and the actual intermediate turbinate contour (red dashed line).

Fig. 8

Cross-sectional area (CSA) of the nasal airway for Patient A under varying congestion levels simulated by path planning algorithms. (a) Plot of the CSA for the indicated nasal airway versus congestion percentage for each algorithm. (b) CSA measurements of the nasal airway surrounding the middle and inferior turbinates plotted against congestion percentage for each algorithm. Note: bottom slice only contains the inferior turbinate region. LIM = Linear Imaging Morphing, A* = A-star, MT = Middle Turbinate, and IT = Inferior Turbinate.

Table 1 Nasal airway contours from medical imaging data acquired for this study and from previously published literature. Each section was obtained from a unique scan dataset corresponding to the indicated patient. Only the nasal sections shown were used to test the pipelined algorithm. CT scan data were used for four patients and MRI scan data for two patients. Nasal airway contours for patients B-F were adapted with permission from prior studies^1,13,24,33.

Table 2 Comparison of simulation error for full nasal airway expansion versus isolated expansion around turbinate regions during the nasal cycle. Coronal sections from various nasal cavity regions were analyzed to assess algorithm performance. Isolated expansion was evaluated only for the middle turbinate (MT) and inferior turbinate (IT) regions.