Convolutional autoencoder network lithology recognition based on scratch tests

Abstract

To address the characteristic of frequent lithological alternations in the continental shale of the Songliao Basin in China and meet the refined requirements of reservoir modeling, it is necessary to establish a higher-precision lithology identification method. This study conducted scratch tests on shale reservoir cores from the 2360m–2409m interval of the Qingshankou Formation in the Songliao Basin, Jilin, obtaining nine mechanical characteristic parameters, including hardness, compressive strength, and Poisson’s ratio. By integrating convolutional neural network (CNN) and auto-encode network (AE), a novel lithology identification method based on scratch data was proposed. The optimal lithology identification scale was selected, and the performance of this method was compared with that of other neural network approaches. The results demonstrate that when the identification scale is set at 20 × 9, the test dataset achieves an accuracy of 89.58%, with recall rates exceeding 84% across all lithology recognitions, outperforming other identification scales. The convolutional autoencoder network (CAE) exhibits superior accuracy and recall rates in lithology identification compared to other neural networks, enabling a more precise representation of the actual lithological characteristics. This study provides a novel methodological approach for reservoir lithology identification and lays a foundation for modeling fracture propagation in heterogeneous shale reservoirs.

Introduction

The continental shale oil in China’s Songliao Basin exhibits unique laminated and bedding-plane structures, characterized by frequent lithological alternations and complex reservoir spaces^1,2. Accurate lithology identification provides a robust analytical foundation for investigating complex fracture propagation in heterogeneous shale hydraulic fracturing^3,4. The conventional logging data with relatively coarse sampling intervals (decimeter- to meter-scale) exhibit limited capability in identifying thin-bed lithological variations. Furthermore, the primary surface characteristics of rocks may be altered due to outcrop weathering or drilling mud contamination, potentially leading to deviations in image-based lithological analysis from actual features. Consequently, there is an urgent need to develop a novel lithology identification methodology to achieve accurate reservoir lithology characterization, thereby facilitating efficient shale oil resource development.

Traditional lithology identification is based on expert experience and engineering data comparison, which is costly and relatively complex^5,6. Deep learning lithology identification methods in recent years establish relationships between lithology-sensitive attributes and lithology types from a large amount of observational data⁷, which brings the possibility of mining the correlation between features and lithology with reasonable accuracy. An Peng et al.⁸ trained deep neural networks and performed lithology identification using seven logging feature variables. Wang et al⁹ constructed a well logging Intelligent recognition model of lithology in work, which can achieve automatic recognition of rock images. Dong SQ et al.¹⁰ proposes the use of integrated learning strategies and principles in logging curves and lithologies, combined with ML methods as subclassifiers thereby reducing the variance error in the prediction process. Fu D¹¹ achieves cross-channel feature association in realising automatic prediction of core images, which significantly improves the model accuracy without increasing the model complexity. Sun et al.¹² analyzed three commonly used classifiers, one-versusrest SVM, one-versone SVM, and random forest, for lithology recognition of drill-following data, and found that random forest has fast training speed and high accuracy of recognition. Alzubaidi F¹³ developed a convolutional neural network-based method to classify images of drill core into three lithologies, and the model is based on the ResNeXt-50 architecture which outperforms the ResNeXt-v3 architecture in lithology identification. Gaochang Z¹⁴ aiming at the problem that the accuracy of image classification techniques is too low when classifying small-size rock images, a conditional residual deep convolutional adversarial network is proposed to effectively improve the rock classification accuracy. Manuel et al¹⁵ presents a new method for automatic lithological facies identification of log images using deep residual convolutional neural network, which is different from the previous processing of log data. As a representative of deep learning, convolutional neural network can automatically and intelligently learn the relationship between sample features with predictive robustness and superiority, with high accuracy in identifying lithology^16,17.

The aforementioned research findings demonstrate that deep learning represents an efficient approach for lithology identification. However, current methodologies relying on cuttings logging, well logging, and drilling data for lithological analysis are constrained by relatively large sampling scales and insufficient accuracy in characterizing rock properties^18,19. Scratch tests, as one of the primary methodologies for evaluating tribological and mechanical properties of materials, has been demonstrated to provide continuous characterization of rock mechanical properties^20,21. Zhang J et al.²² proposed a method to analyse the strain hardening index and plastic parameters such as interfacial coefficient of friction of metallic materials by scratch tests. Liu H et al.²³ The yield stress and interfacial coefficient of friction of materials were characterized by scratch tests using a Vickers indenter with high measurement accuracy. In the geotechnical field, scratch testing was initially used to measure rock hardness²⁴, other mechanical parameter calculations were successively validated as the theory developed. Thomas Richard et al.²⁵ demonstrated that compressive strength can be assessed from scratch tests and that smaller depths of cut maintain the rock in a ductile state. Akono A-T et al^26,27,28,29 correlated the results tested in scratch experiments with the fracture properties of the material, which can be quantitatively extracted at smaller length sizes. Lin J-S³⁰ gave the relationship between the angle of internal friction and the horizontal force as well as the vertical force by analyzing the Akono A-T experiment and the calculation process. Liu Hongtao et al³¹ analyzed the correlation between cohesion and uniaxial compressive strength and angle of internal friction of rocks obtained from scratch experiments and compared them with the results of triaxial compression experiments, and good agreement was obtained.

The aforementioned studies demonstrate that deep learning techniques can achieve efficient and accurate lithology identification. However, conventional approaches for acquiring lithological information exhibit inherent limitations, including coarse data sampling intervals and insufficient characterization precision of rock properties. In contrast, scratch test data enables continuous and precise characterization of rock mechanical parameters. This study develops an CAE architecture by integrating rock mechanical parameters obtained from core scratch tests with AE and CNN. The scratch test data are transformed into different sizes of two-dimensional feature matrices as model inputs. Through systematic optimization, the optimal feature representation dimension is determined, followed by comparative analysis with conventional models to validate the superior performance of the proposed method in terms of lithology identification accuracy and feature extraction capability. This study proposes an intelligent lithology identification method integrating deep learning algorithms with scratch test data, which is expected to overcome the limitations of conventional approaches and achieve precise discrimination of rock types, thereby establishing a foundation for investigating complex fracture propagation in heterogeneous shale hydraulic fracturing.

Result

The primary objective of this study is to identify the optimal scale for lithology identification using scratch test data and to validate the effectiveness of the proposed model by comparative analysis with backpropagation neural network (BP), random forest (RF), convolutional neural network (CNN), and residual neural network (ResNet). The evaluation incorporates confusion matrix analysis for each model, along with comprehensive assessments of overall accuracy and recall rates.

Identify size optimization

To optimize the lithology identification scale, Fig. 1 presents the accuracy and loss function curves of the test set obtained with different input dimensions. From the Fig. 1 it can be seen that the three sizes of the training model in the Mean Square Error (MSE) value of 0.003 when the model is relatively converged, and the fluctuation is relatively small, using the model of 20 × 9 in the iteration of about 50 times the model began to converge, and the convergence speed is faster compared with other sizes of the model.

Fig. 1

Accuracy and loss function of test set with different sizes: (a) accuracy (b) loss function.

Based on the comparison of the training results of the model with different sizes of inputs in (Table 1), the accuracy of the model can reach 89.95% on the training set and 89.58% on the test set using inputs of size 20 × 9, which is a better fit for the model. The accuracy of the test set is improved by 8.61 and 16.37 percentage points compared to the accuracy of the 10 × 9 and 30 × 9 inputs, respectively.

Table 1 Accuracy of training and test sets.

The stacked histograms for different recognized sizes are shown in (Fig. 2), and the recall for each rock type is shown in (Table 2). Using the recognition size of 10 × 9 makes the lithology recognition process unable to recognize all the features of the lithology, making the recognition accuracy of the mixed shale lower, and when the recognition size of 30 × 9 is used, the data of other lithologies are mixed with each type of lithology, which makes sandstone, dolomite, and mixed shale have lower accuracy. The recognition accuracy of each lithology is improved by 3.61, 10, 9.33, 14.81, 9.76%, and the recall is improved by 16.68, 8.83, 3.85, 1.23, and 9.36%, respectively, when the recognition size is 20 × 9, compared to the recognition size of 10 × 9. Compared to recognition size of 30 × 9 accuracy increased by 3.66, 5.32, 26.15, 43.08, 28.57% and recall increased by 18.46, 6.27, 32.63, 21.95, 2.74% respectively. The comparison yields that the recognition size of 20 × 9 predicted labels match the real labels to a greater extent and are able to identify the positive samples more accurately.

Fig. 2

The stacked histograms for different recognized sizes: (a) 10 × 9, (b) 20 × 9, (c) 30 × 9.

Table 2 Recall % for different recognition sizes.

Comparative experimental results

For rigorous verification of CAE’s lithology identification capability, four benchmark models—BP, RF, CNN and ResNet—were implemented for systematic comparison. From Fig. 3, it can be seen that the CAE model performs well in terms of the number of iterations and accuracy at convergence. The proposed model achieved an identification accuracy of 89.58%, representing improvements of 2.12, 9.62, 4.97, and 3.49% over the BP (87.72%), RF (81.72%), CNN (85.34%), and ResNet (86.56%) models, respectively. This comparative analysis demonstrates the superior lithology discrimination capability of the proposed approach.

Fig. 3

Comparison of model performance.

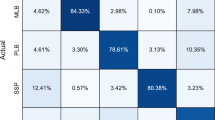
Figure 4 presents the confusion matrices obtained from different neural network recognition methods. The CAE improved the lithology identification accuracy by 6.25, 13.79, 5.12, 8.14, and 18.42%, respectively, compared with the RF; by 1.19, 5.32, 1.23, 1.09, and 4.65% compared with the BP; by 3.66, 7.61, 1.23, 6.90, and 5.88% compared with the CNN; and by 11.58, 3.13, 1.22, 1.94, and 2.22% compared with the NesNet.

Fig. 4

Confusion matrix of different methods of lithological discriminant analysis.

Table 3 displays the recall rates of the random forest and BP neural network. The convolutional autoencoder neural network achieved higher recall rates than the random forest by 13.94, 8.45, 10.09, 1.46, and 12.57%, and outperformed the BP neural network by 6.33, 0.52, 0.62, 1.46, and 5.02%. Compared with the convolutional neural network, the recall rates improved by 5.46, 4.23, 6.79, 0.08, and 10.17%, while the improvements over the NesNet neural network were 3.0, 3.0, 2.0, 2.0, and 11.43%, respectively.

Table 3 Recall table for different methods %.

The convolutional autoencoder neural network demonstrates a higher degree of alignment with the true labels in lithology identification, indicating its enhanced capability to accurately reflect the actual lithological conditions. This leads to improved reliability and precision in lithology recognition.

Discussion

The core of this study lies in the interdisciplinary integration of rock scratch testing technology with deep learning-based lithology identification algorithms to enhance the accuracy and efficiency of geological exploration and 3D geological modeling. Rock scratch technology provides a continuous and high-precision method for testing rock mechanical parameters, while the CAE network offers an advanced approach for rock classification analysis. This innovative methodological fusion effectively addresses the limitations of traditional well logging and image-based classification, such as excessive data sampling intervals, discontinuous core samples, and insufficient classification accuracy caused by variations in rock surface morphology.

Moreover, the CAE network demonstrates high recognition accuracy in processing fine textures and frequently alternating lithologies. Although challenges remain in algorithm optimization and the fusion of diverse data types, this interdisciplinary approach significantly enhances its practical application potential.

This study not only deepens the understanding of the mechanical behavior differences among various lithologies but, more importantly, provides an innovative technical solution for characterizing heterogeneous hydrocarbon reservoirs and supporting geological resource exploration and development. Future work will focus on further optimizing the applicability of this integrated method across different reservoir types and exploring more data-driven and deep learning-based geological research approaches to advance innovation and progress in geosciences.

Methods

In this section, we first present the geological and petrophysical background of the study area. Subsequently, we describe the methodology for data acquisition using scratch tests, followed by a detailed explanation of the network architecture construction and hyperparameter optimization of the algorithm. Finally, we specify the experimental environment and evaluation metrics. The overall workflow of this study is illustrated in the accompanying (Fig. 5).

Fig.5

The schematic diagram of the research workflow.

Geological background and data collection methods

Lithological characteristics of the Songliao basin

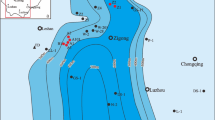
The rock specimens for the scratch tests were sourced from the Songliao Basin (Fig. 6), the largest Cenozoic continental sedimentary basin in eastern China. This basin currently holds proven recoverable shale oil reserves exceeding 7 billion tonnes, though existing extraction technologies can only access approximately 0.7 billion tonnes. This substantial gap underscores the critical need for enhanced lithological characterization of these shale reservoirs. The numbered zones 1–10 in Fig. 6 demarcate our study area within the Central Depression of the Songliao Basin, a region of particular stratigraphic interest for unconventional resource evaluation.

Fig. 6

Structural divisions map of Songliao Basin³².

The shale samples from the qingshankou formation in jilin oilfield, located within the central depression of songliao basin, represent typical lithological characteristics of the region. Through comprehensive expert analysis, these shales have been systematically classified into five distinct lithotypes: clayey shale, felsic shale, mixed shale, sandstone, and dolomite. The compressive strength properties of these lithological units, as determined by scratch testing, are presented in (Fig. 7).

Fig. 7

Compressive strength of different lithologies.

Figure 7 reveals distinct fluctuations in the compressive strength curves at lithological interfaces, with varying amplitude ranges observed among different lithotypes. These characteristic variations can be further elucidated through systematic data analysis.

Methodology for data acquisition via scratch test

Scratch tests technology is to control the axial load of diamond or carbide to make a precise trace on the surface of the specimen, using high-precision two-dimensional force sensors and high-precision displacement sensors to detect the axial force, tangential force, and the depth of indentation in the process of scribing, and at the same time, to observe the dynamic process of the mechanical behavior of the material such as the deformation and destruction of the material locally in the process of the experiment. Scratch test usually has a constant load and constant depth two test methods, in order to reduce the constant load test process of the cutter head up and down movement caused by experimental errors, this paper uses a constant depth loading.

Scratch tests process shown in Fig. 8, the specimen needs to be pre-cut to ensure that the test surface smooth, while the specimen two clamping end face also need to be cut smooth, to avoid the test process due to the unstable clamping led to the specimen’s rotation and deflection, thus affecting the results of the experiment. Clamp the processed specimen on the test bench, and adjust the specimen in the horizontal position through the observation of the level meter. Operate the control system to move the position of the cutterhead, in order to ensure that the depth of the scratch is a fixed value, first through the observation of the cutterhead will be placed under the specimen about 0.1mm to carry out a test scratch, and then the cutterhead down the depth of the experiment to start the experiment, the end of the experiment for the analysis of the data.

Fig. 8

Scratch test procedure.

The geometry of the scratch test is shown in (Fig. 9). A vertical force $F_{{\text{n}}}$ was applied so that the depth of the cutting head $d$ was always maintained 0.5mm, the width of the head $w$ was 2mm, and the inclination angle $\theta$ with the test piece was 30°. Horizontal force is applied to move the cutter head, and the scratch test data are collected every 0.4 mm during the horizontal movement. Due to the shearing effect, a part of the rock material was chipped off, and the origin of the coordinates was set at $d/2$ according to the fracture characteristics of the scratch.

Fig. 9

Schematic of the geometry of the scratch test.

Scratch testing as an experimental method for mechanical properties of materials was rationalized by Mohs hardness as early as 1812 as a quantitative indicator of scratch resistance for the classification of various minerals according to Kouqi L et al³³ The study of the rock hardness can be obtained from the projection of the cutter head on the moving plane:

$$H_{{\text{d}}} = \frac{{F_{{\text{n}}} }}{wd}$$

(1)

The choice is based on the interface between the blade and the material, the unstressed surface at $x > d/2\tan \theta$ and at ${\text{z}} = d/2$ the crack tip, and the closed material surface away from the crack tip, so that the only contribution to the J-integral comes from the interface of the blade.The J-integral provides the energy release rate $G$ as follows³⁴:

$$G = \frac{\kappa }{{E(w^{2} d)}}\left( {\frac{1}{2}F_{{\text{s}}}^{2} + \frac{3}{10}F_{n}^{2} } \right)$$

(2)

where, under the condition of plane stress $\kappa = 1$ and plane strain $\kappa = 1 - \upsilon^{2}$, $\upsilon$ is Poisson’s ratio and $E$ is elastic modulus.

The energy release rate is equal to the fracture energy during fracture extension of the crack, and the relationship between fracture toughness $K_{Ic}$ and energy release rate is:

$$G \equiv G_{f} = \kappa \frac{{K_{Ic}^{2} }}{E}$$

(3)

The fracture toughness of the rock is obtained by joining Eq. (2) and Eq. (3) as:

$$\sqrt {\left( {\frac{1}{2}F_{{\text{s}}}^{2} + \frac{3}{10}F_{n}^{2} } \right)} = K_{Ic} w\sqrt d$$

(4)

For each test, a fixed ratio is maintained between the vertical force $F_{{\text{n}}}$ and horizontal force $F_{s}$, which depends on the inclination of the rock and the friction of the tool, viz:

$$F_{{\text{n}}} = F_{s} \tan (\theta + \varphi )$$

(5)

where $\varphi$ is the angle of internal friction between the cutter head and the rock, from which the coefficient of friction between the cutter head and the rock specimen can be obtained $\mu = \tan \varphi$. The cohesive force C of the rock can be obtained according to the linear Moore Cullen criterion, as shown in Eq. 6:

$$C = \frac{UCS \cdot (1 - \sin \varphi )}{{2{\text{cos}}\varphi }}$$

(6)

where UCS is the uniaxial compressive strength of the rock, which is able to be output directly during the scratch tests $UCS = \frac{{F_{S} }}{wd}$.

Angle of internal friction in shear damage is linearly related to Poisson’s ratio³⁵, expressed as:

$$\nu = \frac{\arctan [\cos \varphi - (1 - \sin \varphi )\tan \varphi ]}{{90^{ \circ } }}$$

(7)

Figure 10 shows the line graphs of the scratch parameters of different lithologies, from which it can be seen that: the hardness of the clayey shale type shale is the smallest, the hardness of the sandstone is the largest, the cohesion of the long quartz grained shale is the largest, and the friction coefficient of the mixed grained shale is the smallest. The magnitude of the value of the same mechanical parameter varies from one lithology to another, and the lithology is determined by the different contents of minerals and their arrangement and depositional mode, the same mechanical parameter of each lithology has a certain inherent law, and the interrelationships that exist between each mechanical parameter will determine the category of the lithology, which provides a possibility of lithology identification through the scratch parameter.

Fig. 10

Line graph of scratch parameters for different lithologies.

The identification of lithology using scratch feature parameters requires accurate analysis of the variability and regularity within the same feature, as well as comprehensive consideration of the mutual influence and constraints between multiple features. The deep learning method can fully extract the correlation features between the data when predicting, and build a more accurate prediction model on this basis.

Data preprocessing

There was a horizontal displacement between the cutterhead and the rock specimen at the beginning of the scratch tests, and the mechanical parameters measured when the cutterhead just touched the specimen and when it left the specimen were unstable, and the number of such samples was small, so the abnormal data were excluded by using the normality test. For the data with missing lithology labels, they were clustered, and the one with the closest distance between the centre of the obtained clusters and the mean value of the known lithology data was given the same lithology labels to complete the data.

The feature extraction data in this paper is one-dimensional scratch data with 10,050 categorical data, including horizontal force $F_{{\text{s}}}$, vertical force $F_{{\text{n}}}$, uniaxial compressive strength UCS, hardness $H_{{\text{d}}}$, fracture toughness $K_{lc}$, angle of internal friction $\varphi$, coefficient of friction $\mu$, cohesion C, and Poisson’s ratio $\nu$ in each categorical data with 9 categories of feature data, which is a total of 90450 feature values. The training set and test set were randomly divided in the ratio of 8:2, as shown in (Table 4).

Table 4 Lithology recognition training and testing sets.

As illustrated in Fig. 10, the scratch characteristic data exhibit significant variations in magnitude. To eliminate the effects of unit and scale discrepancies among the scratch feature parameters, the z-score normalization method was applied in this experiment. The normalization formula is expressed as:

$$x^{\prime}_{i} = \frac{{x_{i} - \min (x_{i} )}}{{\max (x_{i} ) - \min (x_{i} )}}$$

(8)

where $\min (x_{i} )$ and $\max (x_{i} )$ represent the minimum and maximum values of feature parameters $x_{i}$, respectively, while $x^{\prime}$ denotes the normalized result of the feature value.

If a single scratch point or the corresponding eigenvalue at a smaller size is used for classification, it cannot reflect the structural distribution characteristics of different mineral components in different spatial combinations. If the selected division size is too large, it may contain different lithological information and thus reduce the accuracy of lithological identification. According to the actual lithology, the features in the consecutive n points are jointly used as input, i.e., the input is an n × 9 matrix, and each scratch data point corresponds to a lithological label value, which is transformed into a solo thermal code to obtain an n × 5 output matrix.

Algorithm description

The schematic diagram of CNN architecture is shown in Fig. 11, where feature information is extracted from the input data through the convolutional structure and the categories of the data are output through the fully connected layer. It utilizes multiple filters to build features and consists of three parts: convolutional layer, pooling layer and classification layer.

Fig. 11

Schematic diagram of CNN.

Scratch tests were systematically conducted on 107 rock specimens extracted from 33 core boxes spanning the depth interval of 2360–2409 m in the Qingshankou Formation within the Central Depression of the Songliao Basin. Each convolutional layer extracts local features of the image using locally connected and globally shared connections, and combines these features to form a feature mapping map, and then simplifies the output of the convolutional layer through pooling operations, using the principle of local correlation of the image to reduce the dimensionality of the features while retaining useful information; the output is the classification layer, which is a fully-connected network that combines the outputs of the previous layer through a serially connected The output is the classification layer, which is a fully connected network that expands the output of the previous layer through serial connections, and all the outputs of the expansion form a feature vector. The number of neurons in the output layer of the network is the number of types in the training image set, i.e. the number of type labels.

Autoencoder (AE) is an unsupervised deep learning algorithm that reconstructs the input data into outputs so as to learn different representations of the data, the goal is to maximise the information and minimise the reconstruction error while encoding to get the deeper regularities of the original data, the structure of the model is shown in (Fig. 12).

Fig. 12

Structure of the AE model.

CAE network is a more efficient unsupervised feature extractor by adding a convolutional structure on the basis of the traditional AE structure, adopting convolutional layers instead of fully connected layers, and preserving the local spatial structure of the data features in order to better mine the semantic information in the data. The network structure is divided into two stages, encoder and decoder, the encoder mainly consists of convolutional layers to achieve the extraction of high-level feature semantics of the input samples. The decoder consists of transposed convolutional layers, which is the inverse process of convolutional layers, and achieves the reconstruction of the input samples through the inverse convolution to minimise the difference between the input and output data and improve the recognition ability.

The convolutional layer is able to extract features from the data and its output can be expressed as:

$$A = x_{I}^{n} = R\left( {i\sum\limits_{{i \in K_{I} }} {x_{I}^{n - 1} } \times w_{ij}^{n} + b_{i}^{n} } \right)$$

(9)

where $x_{I}^{n}$ is the feature vector corresponding to the convolution kernel, $K_{I}$ is the convolution kernel, $w_{ij}^{n}$ denotes the jth weight coefficient of the ith convolution kernel in the nth layer, $b_{i}^{n}$ is the bias parameter, and $R$ is the activation function.

After the convolutional kernel operations, downsampling is required to be able to preserve useful information while reducing the dimensionality of the data, and the sampling layer uses a pooling technique to maintain the features and thus obtain scaling invariance. In CNN, the downsampling layer is usually followed by more convolutional layers for secondary feature extraction and these convolutional layers learn higher level features from the downsampled output. After multiple convolution and downsampling operations, the network is able to progressively abstract more representative features. The computational formula for downsampling is:

$$B = x_{j}^{i} = down(x_{j}^{i - 1} )$$

(10)

The transposed convolution is a forward convolution that increases the dimensionality of the input data and $\oplus$ represents the inverse convolution computation, with the output of the transposed convolution layer expressed as:

$$D = x_{I}^{\prime n} = R\left( {\sum\limits_{{j \in M_{l} }} {x_{i}^{\prime n - 1} } \oplus w_{ij}^{\prime n} + b_{i}^{\prime n} } \right)$$

(11)

The decoder reconstructs the features extracted from the individual convolutions, compares the input samples with the reconstructed samples, and evaluates the training effect of the model by using the MSE function as the loss function, which is a statistical parameter that predicts the mean of the sum of squares of the errors of the original data and the corresponding points, and $m$ is the number of samples denoted as:

$$loss = \frac{1}{m}\sum\limits_{i = 1}^{m} {(h(x_{i} ) - y_{i} )}$$

(12)

The network model structure of the convolutional self-coding neural network used in this paper is shown in Fig. 13, where the MaxPooling downsampling technique is introduced into the network structure to obtain the translational invariance of the features. The Relu function is used as the activation function to increase the linear relationship between each layer of the neural network to the maximum extent, which can achieve better mining and fitting training of data features. The last layer is the Sigmoid activation function, which maps the variables between [0,1] to achieve explicit prediction. For the whole network model, in order to prevent overfitting and improve the generalisation ability, it is processed by using the regularisation method, this paper adopts the Dropout regularisation method by directly modifying the number of parameters of the model mechanism, i.e., randomly dropping a certain proportion of neurons.

Fig. 13

CAE structure.

Hyperparameter optimization

In the field of deep learning, the choice of hyperparameters has a significant impact on model performance. In order to find the best combination of hyperparameters, this study employs the PSO algorithm, a search strategy based on group intelligence, for optimizing hyperparameters within a defined search space. The PSO algorithm is a meta-heuristic search algorithm that simulates the feeding behavior of a flock of birds, and its core lies in exploring the solution space and converging to the optimal solution through group cooperation and information exchange. In PSO, each particle searches for the optimal solution independently and records the best position found as an individual optimal solution. Particles collaborate with each other to determine the global optimal solution for the whole population by sharing their respective historical optimal positions. Subsequently, the particles advance the search process by dynamically adjusting their speed and position according to their individual optimum and the global optimum of the group.

Assuming that the position of the $i$ particle in the $d$ dimensional air is $x_{i} = (x_{i1} ,x_{i2} ,...,x_{id} )$, the flight speed is ${\mathcal{V}}_{i} = \left( {\begin{array}{*{20}c} {{\mathcal{V}}_{i1} ,{\mathcal{V}}_{i2} ,...,{\mathcal{V}}_{id} } \\ \end{array} } \right)$, the personal optimal solution is $P_{i} = (p_{i1} ,p_{i2} ,...,p_{id} )$, the current global optimal solution is $P_{{_{g} }} = (p_{{_{g1} }} ,p_{{_{g2} }} ,...,p_{{_{gd} }} )$, and the particle’s velocity and position update formula is as follows:

$$\left\{ {\begin{array}{*{20}c} {v_{id}^{t + 1} = w \cdot v_{id}^{t} + c_{{_{1} }} \cdot r_{{_{1} }} \cdot (p_{{_{id} }}^{t} - x_{{_{id} }}^{t} ) + c_{{_{2} }} \cdot r_{{_{2} }} \cdot (p_{{_{gd} }}^{t} - x_{{_{id} }}^{t} )} \\ {x_{{_{id} }}^{t + 1} = x_{{_{id} }}^{t} + v_{{_{id} }}^{t + 1} } \\ \end{array} } \right.$$

(13)

where $y$ is the velocity component of the $i$ particle in the $d$ dimension. $t$ is the number of iterations of the $i$ particle, $w$ is the inertia coefficient, $c_{1}$ and $c_{2}$ is the learning factor, $r_{1}$ and $r_{2}$ is a random number between (0,1). The schematic of the particle position update is shown in (Fig. 14):

Fig. 14

Schematic diagram of particle position update.

The flowchart of the particle swarm optimization algorithm is shown in (Fig. 15):

Fig. 15

Flow chart of particle swarm optimization algorithm.

In this study, PSO is used to optimize four key hyperparameters of the deep learning model: learning rate (LR), batch size (batch_size), weight_decay, dropout rate (dropout_rate), and number of iterations (epochs). The search range of hyperparameters is defined as: learning rate LR: [le-5,le-1], batch size batchsize: [3,128], weight decay weightaecay: [1e-5,1e-1], regularization ratio Dropout dropoutrate: [0.1,0.8], iteration number epochs:[20, 200].

The fitness_function assesses the hyper-parameter combination’s performance by calculating the model’s training loss, measured by the MSE. The Adam optimizer is used to optimize the loss function of the network so as to avoid gradient descent as well as non-convergence.The PSO algorithm is run in a population of 50 particles, each representing a hyper-parameter combination, over 100 iterations to find the optimal solution. The optimal learning rate of 0.0012, batch size of 8, decay weight of 0.032, regularization ratio of 0.301 and number of iterations of 150 are obtained.

Training and evaluation indicators

The experimental configuration and parameters of this experiment include: The computer processor is Intel(R) Core(TM) i5-10400F CPU @ 2.90GHz, the running memory is 16GB, the 64-bit operating system, and the editing language is python3.7.

In this paper, recall and accuracy are used to evaluate the performance of CAE networks for lithology classification.

1) The recall rate can be expressed as:

$$R = \frac{{N_{{{\text{TP}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{FN}}}} }}$$

(14)

where: $R$ is the recall rate; $N_{{{\text{TP}}}}$ and $N_{{{\text{FN}}}}$ are the number of true positive and false negative samples, respectively.

2) Accuracy:

$$P = \frac{{N_{{{\text{TP}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{FP}}}} }}$$

(15)

where: $P$ is the accuracy rate; $N_{{{\text{FP}}}}$ is the number of false positive samples.

Conclusion

In this study, we integrate rock scratch tests with CAE, yielding the following key findings:

• (1) Scratch experiments were conducted on core samples from a well in the Jilin Oilfield, located in the central depression of the Songliao Basin. Theoretical calculations derived mechanical parameters such as hardness and fracture toughness. Compared to conventional lithology identification data, this approach significantly enhances measurement continuity and resolution.

• (2) The proposed hybrid method provides a novel perspective and methodology for geological resource exploration and heterogeneous reservoir characterization.

• (3) Experimental results demonstrate that at a recognition scale of 20 × 9 pixels, the model achieves an accuracy of 89.58%, exhibiting superior fitting performance. The CAE outperforms other neural network approaches in both recall rate and accuracy.