Introduction

Motivation

To mitigate pollution, renewable energy sources (RESs), such as wind turbines and solar panels, are increasingly being integrated into power systems. These technologies utilize natural elements like sunlight and wind to produce electricity, but their output fluctuates due to the variability of these resources1. To address this challenge and ensure a steady energy supply, studies recommend pairing renewable units with storage systems2. This approach allows surplus energy from renewable sources to be stored during periods of high production and later utilized when energy demand exceeds renewable generation2. In addition to advancing sustainable energy solutions and curbing environmental pollution, integrating storage systems improves both the technical reliability and economic efficiency of power networks, especially within distribution systems. Electric vehicles (EVs) also play a pivotal role in reducing pollution. These vehicles typically charge by drawing energy from the power grid, representing a new category of consumers within the electricity network3. However, with strategic energy management, EVs can function as mobile storage units, offering added flexibility to the system. Future power networks, particularly distribution grids, are expected to see an increase in distributed generation along with the adoption of both stationary and mobile storage systems like EVs. Managing energy in such expansive and intricate networks poses significant challenges, but this complexity can be reduced by transitioning to smart microgrids (MGs). These localized systems integrate resources and storage devices within various consumption areas, enhancing technical and economic performance at multiple levels of the distribution network4. Research further suggests that combining renewable resources and storage units into hybrid systems yields greater technical and economic benefits than managing them separately5. For instance, integrating storage devices with renewable resources enhances system flexibility, which also positively impacts the upstream network’s adaptability. Implementing a hybrid system within a smart microgrid, supported by an advanced energy management framework, can foster improvements in operational efficiency, economic viability, network security, and overall system flexibility. As a result, this forward-looking approach is poised to drive optimal performance across modern power networks while simultaneously addressing environmental concerns.

Literature review

Numerous studies have been carried out in the domain of MG energy management. The authors of6 present a groundbreaking Active and Reactive Energy Management System designed for a MG that serves multiple consumer types while employing diverse pricing strategies. The study examines the effects of existing electricity pricing and regulations on energy distribution, billing, and the lifespan of storage units. Study in7 explores long-term energy scheduling in a MG that integrates hybrid hydrogen-battery storage system. The study devises an approximate semi-empirical model to effectively represent the power-dependent efficiency of hydrogen storage. Additionally, it presents a prediction-free, two-stagecoordinated optimization framework designed to produce an annual state-of-charge (SoC) reference for hydrogen storage offline. Work of8 introduces an effective one-to-one-based optimizer, offering an innovative energy management strategy for networked MGs to tackle environmental and economic challenges. This approach is notable for its strong exploratory capabilities, enabling it to find global solutions while avoiding local pitfalls, and for its ease of implementation. In9, it presents an innovative two-layer energy programming designed for MG clusters. This method leverages demand-side flexibility along with battery capabilities to reduce operational expenses and emissions, all while maintaining sufficient spinning reserves within each MG to avoid load-shedding. In the initial layer, it formulates optimal day-ahead operation plans. Meanwhile, the upper layer implements a collaborative strategy to enhance operational efficiency across the whole cluster. Research in10 introduces an energy scheduling platform utilizing an advanced probabilistic wavelet Petri neuro-fuzzy inference algorithm. This platform is designed to manage the Voltage/Frequency (V/F) index amidst the uncertainties presented by RESs and batteries. Work in11 offers a comprehensive techno-economic analysis focused on clean and efficient operation of two grid-connected low voltage MG systems. Meanwhile, the authors of12 develop a multi-objective optimization model for a MG energy programming. This model incorporates degradation costs and includes a carbon trading mechanism aimed at reducing greenhouse gas emissions. Additionally, it employs a demand response strategy to optimize energy load demand.

Various studies have proposed different models for the functioning of hybrid systems. One such model, referenced in13, addresses the optimal placement and sizing of a battery alongside a wind turbine. To tackle this allocation challenge, it utilizes a multi-objective function that optimizes techno-economic factors, including total active power losses, voltage deviation, and investment costs. Another study, detailed in14, introduces a coordinated optimization approach for trajectory planning and energy scheduling in hybrid electric unmanned aerial vehicles (UAVs). This method involves numerical simulations and experiments. It features an energy management layer and an optimal energy flight trajectory optimization layer, with the latter employing a fuzzy neural network and sequential convex optimization to enhance solar energy use. Reference15 delves into the design and optimization of a system combining wind turbines, photovoltaic panels, and a hybrid energy storage setup. This system integrates mechanical gravity energy storage with electrochemical batteries. An adaptive energy management strategy is proposed to optimize the integration of these components within the hybrid storage system. Moreover, the study in16 puts forward an intelligent Golden Jackal Optimization technique for managing distributed generation energy issues in battery storage systems and hybrid energy sources. The primary goals are minimizing operating costs and addressing MG energy management challenges. Ref17. investigates the techno-economic feasibility and optimal solution of a hybrid battery-photovoltaic-diesel unit intended to supply electricity to an academic center located in western Iran. In18, it proposes an analytic method to identify the best coalition among microgrids in multi-microgrid systems. In19, the effect of changes in the magnitude and angle of each line impedance, noncritical load, and critical load on the ability of voltage compensating of electric spring is investigated. Ref20. introduces a novel approach to improving voltage profiles in a 22-bus radial distribution network by integrating distributed generation with advanced optimization techniques. The summarized outcomes of these various studies are compiled in Table 1.

Table 1 The categorization of current works.
Full size table

Research gaps and contributions

The limitations in the field of optimal scheduling for microgrids and hybrid systems, as highlighted in Table 1 and the research background outlined in the previous section, are as follows:

  • In numerous studies concerning the optimal scheduling of MGs, operational and economic indicators are commonly addressed. However, systems also encompass various technical indicators, among which voltage security holds a critical role within distribution grids and MGs. This is particularly relevant as certain consumers are located at the far end of feeders, often at a considerable distance from the main power source, such as the upstream system. As a result, these consumers may experience low voltage magnitudes, where even minor changes in energy consumption could lead to voltage collapse. One of the advantages of MGs is their ability to incorporate diverse energy sources and storage devices, enabling the MG operator to exert effective control and optimally manage voltage security levels. Despite this potential, the specific issue of MG voltage security has received limited attention in existing research efforts. Additionally, enhancing one index does not necessarily improve others. For instance, boosting the economic performance might require sources and storage devices to inject significant active power into the MG, which could result in overvoltage issues within the network, subsequently weakening operational reliability. Therefore, it becomes essential for the MG operator to strike a balance in managing both technical and economic indicators simultaneously.

  • Energy management of resources and storage devices within a hybrid system yields more favorable outcomes compared to managing them individually, particularly in enhancing various economic and technical conditions of the power system. Despite this advantage, the application of hybrid systems comprising resources and storage devices in MGs has not garnered substantial attention. Furthermore, the integration of renewable energy sources into hybrid systems and MGs has shown significant growth due to their environmental benefits. However, the inherent uncertainty in the power generation of these units leads to discrepancies between real-time operations and day-ahead planning, which is described as a lack of flexibility. Energy storage systems play a key role in addressing these fluctuations by regulating the active power of renewable resources, thereby achieving higher flexibility levels for the network and hybrid system. Effective flexibility management entails the use of numerical indices, yet this approach has been explored in only a limited number of studies.

  • Bio-waste units (BUs) represent a type of renewable source capable of generating methane gas by processing environmental waste. This methane is then utilized in gas-fired energy systems, such as micro-turbines, to produce electrical energy at the turbine’s output. Despite their potential, limited research has explored the integration of BUs into MGs and hybrid systems. Nevertheless, projections suggest that incorporating BUs into power systems could yield promising outcomes in enhancing both the technical and economic performance of the grid. Additionally, the energy management of electric vehicles (EVs) offers a unique opportunity for these vehicles to function as mobile energy storage units. During charging or energy management processes, the active power control of EVs can be aligned with system operator demands, enabling them to mitigate power fluctuations caused by renewable sources. This flexibility allows EVs to act as adaptable resources within energy systems. However, this aspect has been addressed in relatively few studies thus far.

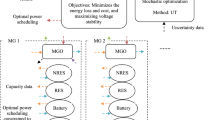
This article introduces a multi-objective scheduling framework for MG that addresses operational, economic, and voltage security objectives while integrating flexible renewable hybrid systems, including RESs and mobile storage systems, as depicted in Fig. 1. Key renewable resources contributing to the hybrid system include wind farms (WFs), which generate electricity, and bio-waste unit farms (BUFs) that utilize environmental waste to produce gas and subsequently electricity. The mobile storage component is represented by electric vehicle parking lots (EVPLs), playing a critical role in energy storage and management. Within this hybrid system, electricity is consumed and managed collaboratively by the MG, renewable resources, and EVPLs. Both renewable sources and electrical storage devices are typically equipped with power electronic converters that provide simultaneous control over their active and reactive power. As a result, hybrid systems serve dual functions in the MG: regulating reactive power and controlling active power flows. The proposed scheduling scheme features two primary objectives: minimizing the expected operational costs of the MG and maximizing voltage security. It operates within the constraints of an AC optimal operation model, incorporating voltage security limitations alongside operational and flexibility considerations for hybrid systems combining renewable units and EVPLs. In this context, EVPLs act as flexibility sources to balance power fluctuations arising from renewable energy variability across different scenarios, enhancing system stability and adaptability. Toaddress these objectives, the weighted function sum technique is employed to construct a single-objective model, followed by the application of a fuzzy decision-making approach to determine the optimal compromise solution. The scheme accommodates several uncertainties, including variations in wind speed, load demand, gas production from BUFs, energy prices, and EVPL parameters. A flexibility index is calculated to more accurately assess system performance under diverse conditions, requiring scenario-based evaluations of renewable resource generation power. To address uncertainties effectively, scenario-based stochastic optimization (SBSO) is utilized to model variable conditions, enabling precise evaluation of the system’s flexibility state. Compared to prior studies and methodologies, the proposed approach introduces several key innovations that significantly advance hybrid MG scheduling solutions:

  • Implementation of an energy management system in the microgrid based on simultaneous estimation of economic, operational, and voltage security objectives,

  • Optimal scheduling of renewable hybrid system with mobile (such as EVs) storage devices in the microgrid subject to flexibility constraints,

  • Implementation of a charging management system for electric vehicles to create the role of energy storage and a flexible source for EVs parking lot,

  • Using of the operation model for BUF in the hybrid system for production of electricity energy in order to improve energy efficiency, and.

  • Use of the hybrid system as a reactive power control source in the microgrid to improve operational, economic and voltage security indicators.

The upcoming sections of the paper are organized as follows: Sect. 2 introduces the multi-objective mathematical model for microgrid operation incorporating a hybrid system. Section 3 focuses on the single-objective model along with uncertainty modeling of the proposed framework. In Sect. 4, simulation results are provided for different cases to evaluate the system’s feasibility. Finally, Sect. 5 outlines the overall conclusions.

Fig. 1
figure 1

Power management strategy in the smart microgrid with flexi-renewable hybrid system.

Full size image

Multi-objective EMS of flexi-renewable EHs in MG

This section introduces a multi-objective approach to MG energy management, focusing on integrating a flexible renewable hybrid system. The formulation aims to minimize operating costs while maximizing the voltage security index. The model is subject to several constraints, including the MG scheduling framework, voltage security considerations, and the flexible operational dynamics of RESs and EVPLs within the hybrid system configuration.

MG objectives

This section introduces the mathematical model designed to address the operational, economic, and voltage security objectives for a MG. The formulation is detailed in the following subsections.

  1. (A)

    Microgrid Operation Cost (MOC): Eq. (1) focuses on minimizing the expected operational cost of the microgrid (MOC). This cost represents the expenditure associated with the energy acquired by the microgrid from the distribution system. The hourly cost is calculated as the product of the energy price and the active power flowing through the distribution substations2. Within this framework, the microgrid is interconnected with the distribution system via distribution posts, ensuring that all energy supplied by the upstream grid flows through these posts. Consequently, Eq. (1) incorporates the active power of these substations as a critical parameter.\

$$\hbox{min} \,\,\,\,\,\,\,MOC=\sum\limits_{{b,h,s}} {{\rho _S}{\lambda _{h,s}}{P_{DS\,b,h,s}}}$$
(1)
  1. (B)

    MG Security Index (MSI): The MSI, as defined in this paper through Eq. (2), incorporates the Worst Security Index (WSI). The WSI is determined by evaluating the weakest bus concerning its voltage magnitude21. Its value ranges from 0 to 1, where 0 signifies a voltage collapse within the microgrid, and a value of 1 corresponds to the microgrid operating under no-load conditions. To ensure adequate voltage safety margins for the network, it is essential to achieve the highest possible WSI for the microgrid. Equation (2) serves the purpose of maximizing the MSI, which is derived from the cumulative expected value of the WSI over time21.

$$\hbox{max} \,\,\,\,\,\,MSI=\sum\limits_{{h,s}} {{\rho _s}WS{I_{h,s}}}$$
(2)

Securable operation constraints of MG

This section addresses the constraints AC power flow, operational model, and voltage security within a MG. Equations (3)–(6) provide the foundation for the MG power flow model, as described in references21,22. Equation (3) defines the active power balance across MG buses, while Eq. (4) outlines the reactive power balance. Constraints (5) and (6) calculate the active and reactive power transmitted through distribution lines, respectively21,22. To solve the power flow equations, identifying the slack bus is essential. The slack bus serves as a reference point where both the voltage amplitude and phase angle are fixed, typically set to 1 p.u. and zero degrees, respectively18. In this study, the slack bus is specifically designated as a bus connected to the distribution grid via a distribution post. Operational limits within the microgrid are delineated by constraints (7)–(10)22. Constraint (7) formulates the voltage magnitude limits for all MG buses. These upper and lower limits are crucial for safeguarding network equipment from insulation damage due to overvoltage and preventing consumer outages caused by voltage drops. Additionally, constraints (8) and (9) specify distribution substation performance metrics, encompassing capacity and power factor restrictions. The capacity limitations of distribution lines are further detailed in Eq. (10)21. Voltage security formulations are introduced via constraints (11) and (12), based on the calculation of the WSI21. Equation (11) computes WSI for a weak bus (denoted as p), considering factors such as the voltage magnitude of its upstream bus (p − 1), and the active/reactive power flow between buses p and p − 121. Ensuring adequate voltage security necessitates maintaining WSI above a threshold value, typically set at 0.821, as modeled in Eq. (12). This criterion supports optimal voltage security conditions within the microgrid, as elaborated in Sect. 2.1.B.

$${P_{DS\,b,h,s}}+{P_{EH\,b,h,s}}+\sum\limits_{l} {{J_{l,b}}{P_{DL\,b,l,h,s}}} ={P_{C\,b,h,s}} - {P_{NS\,b,h,s}}\,\,\,\,\,\forall b,h,s$$
(3)
$${Q_{DS\,b,h,s}}+{Q_{EH\,b,h,s}}+\sum\limits_{l} {{J_{l,b}}{Q_{DL\,b,l,h,s}}} ={Q_{C\,b,h,s}}\,\,\,\,\forall b,h,s$$
(4)
$$\begin{gathered} {P_{DL\,b,l,h,s}}={g_{DL\,b,l}}{\left( {{V_{b,h,s}}} \right)^2} - {V_{b,h,s}}{V_{l,h,s}}\left( {{g_{DL\,b,l}}\cos \left( {{\alpha _{b,h,s}} -{\alpha _{l,h,s}}} \right)+{b_{DL\,b,l}}\sin \left( {{\alpha _{b,h,s}} - {\alpha _{l,h,s}}} \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall b,l,h,s \hfill \\ \end{gathered}$$
(5)
$$\begin{gathered} {Q_{DL\,b,l,h,s}}= - {b_{DL\,b,l}}{\left( {{V_{b,h,s}}} \right)^2}+{V_{b,h,s}}{V_{l,h,s}}\left( {{b_{DL\,b,l}}\cos \left( {{\alpha _{b,h,s}} - {\alpha _{l,h,s}}} \right) - {g_{DL\,b,l}}\sin \left( {{\alpha _{b,h,s}} - {\alpha _{l,h,s}}} \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\forall b,l,h,s \hfill \\ \end{gathered}$$
(6)
$$V_{b}^{{lo}} \leqslant {V_{b,h,s}} \leqslant V_{b}^{{up}}\,\,\,\,\,\forall b,h,s$$
(7)
$$\sqrt {{{\left( {{P_{DS\,b,h,s}}} \right)}^2}+{{\left( {{Q_{DS\,b,h,s}}} \right)}^2}} \leqslant S_{{DS\,b}}^{{up}}\,\,\,\,\,\forall b,h,s$$
(8)
$$\frac{{{P_{DS\,b,h,s}}}}{{\sqrt {{{\left( {{P_{DS\,b,h,s}}} \right)}^2}+{{\left( {{Q_{DS\,b,h,s}}} \right)}^2}} }} \geqslant 0.9\,\,\,\,\,\forall b,h,s$$
(9)
$$\sqrt {{{\left( {{P_{DL\,b,l,h,s}}} \right)}^2}+{{\left( {{Q_{DL\,b,l,h,s}}} \right)}^2}} \leqslant S_{{DL\,b,l}}^{{up}}\,\,\,\,\,\forall b,l,h,s$$
(10)
$$\begin{gathered} WS{I_{h,s}}={\left( {{V_{p - 1,h,s}}} \right)^4} - 4{\left( {{V_{p - 1,h,s}}} \right)^2}\left( {{R_{p,p - 1}}{P_{DL\,p,p - 1,h,s}}+{X_{p,p - 1}}{Q_{DL\,p,p - 1,h,s}}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, - 4{\left( {{X_{p,p - 1}}{P_{DL\,p,p - 1,h,s}} - {R_{p,p - 1}}{Q_{DL\,p,p - 1,h,s}}} \right)^2}\,\,\,\,\,\forall h,s \hfill \\ \end{gathered}$$
(11)
$$WS{I_{h,s}} \geqslant 0.8\,\,\,\,\,\forall h,s$$
(12)

Flexible operation of renewable hybrid system

This section outlines the flexible operational model of RESs and EVPL within the framework of a hybrid system. This system integrates renewable resources such as wind farms, bio-waste units, and mobile storage devices like EVPL. Storage devices not only serve as a key element for energy management in the hybrid system but also act as crucial sources of operational flexibility.

  1. (A)

    WF formulation: The WF model operates in accordance with constraints (13)–(15)1. Equation (13) calculates the WF’s generated active power, which is derived from the product of the WF’s capacity and the generation rate of this renewable source. The rate at which the WF generates power is driven by wind speed, as defined in Eq. (14)1. Specifically, if the wind speed falls within the range of cut-in and nominal speeds, the power generation rate increases linearly. When the wind speed exceeds the nominal speed but remains below the cut-out speed, the generation rate stabilizes at 1. In conditions where wind speeds are outside these defined ranges, the generation rate drops to zero. To integrate the WF with the network, an AC/AC converter is employed to regulate its output frequency1. This converter also provides simultaneous control over the reactive and active power in the grid. Consequently, Eq. (15) specifies the capacity limitations of this converter, establishing its operational threshold.

$$\,{P_{WF\,b,h,s}}={\phi _{WF\,b,h,s}}{\bar {S}_{WF\,b}}\,\,\,\,\forall b,h,s$$
(13)
$$\,{\phi _{WF\,b,h,s}}=\left\{ {\begin{array}{*{20}{c}} {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{v_{b,h,s}} \leqslant {v_{in}}} \\ {\frac{{{v_{b,h,s}} - {v_{in}}}}{{{v_r} - {v_{in}}}}\,\,\,\,{v_{in}} \leqslant {v_{b,h,s}} \leqslant {v_r}} \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{v_r} \leqslant {v_{b,h,s}} \leqslant {v_{out}}} \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{v_{b,h,s}} \geqslant {v_{out}}} \end{array}} \right.\,\,\,\,\,\,\,\,\,\forall b,h,s$$
(14)
$$\,\sqrt {{{\left( {{P_{WF\,b,h,s}}} \right)}^2}+{{\left( {{Q_{WF\,b,h,s}}} \right)}^2}} \leqslant {\bar {S}_{WF\,b}}\,\,\,\,\forall b,h,s$$
(15)
  1. (B)

    BUF model: BUF constraints revolve around the production of energy through the utilization of environmental waste. BUF begins its operation by generating gas from waste materials, with approximately 65% of this gas composed of methane. When equipped with a micro-turbine system, BUF leverages methane to generate electrical energy1. The efficiency and operation of this model are defined through constraints (16)–(18). In constraint (16), the active power output of BUF is determined using the product of BUF’s capacity and its power generation rate. This rate is calculated based on the ratio of gas produced by BUF to its maximum theoretical gas production, as specified in Eq. (17)1. Additionally, BUF is integrated into MG via an AC/AC converter, which ensures the adjustment of output frequency. Constraint (18) outlines the limitations on apparent power transitioning through this converter, serving to maintain system stability and operational integrity.

$$\,{P_{BUF\,b,h,s}}={\phi _{BUF\,b,h,s}}{\bar {S}_{BUF\,b}}\,\,\,\,\forall b,h,s$$
(16)
$$\,{\phi _{BUF\,b,h,s}}=\frac{{{G_{BU\,b,h,s}}}}{{{{\bar {G}}_{BU\,b}}}}\,\,\,\,\forall b,h,s$$
(17)
$$\,\sqrt {{{\left( {{P_{BUF\,b,h,s}}} \right)}^2}+{{\left( {{Q_{BUF\,b,h,s}}} \right)}^2}} \leqslant {\bar {S}_{BUF\,b}}\,\,\,\,\forall b,h,s$$
(18)
  1. (C)

    EVPL constraints: The EVPL model is a framework for managing the energy storage capabilities of EVs connected to a network through a charger equipped with a DC-AC inverter. This model allows EVPL to act as an effective energy storage system, with its functioning governed by constraints (19)–(24) as outlined in prior studies1,21,23. The charge and discharge rate of all EVs is restricted by constraints (19) and (20), ensuring uniformity. Moreover, EV batteries are designed to avoid simultaneous charging and discharging operations, as mathematically modeled in Eq. (21). Constraint (22) calculates the energy of all EVs during any given hour, factoring in the initial energy of the EVs, their energy status from the preceding hour, the energy received from the hybrid system during charging, and deducting the energy consumed by EVs along with that injected into the hybrid system via battery discharging. Constraint (23) sets limitations on the stored energy capacity within EV batteries, while constraint (24) dictates the upper limit of the charger capacity23. Importantly, the operating conditions in EVPL are dynamic; each scenario and moment presents a varying number and different types of EVs. Consequently, variables such as initial and final EV energy levels, charging and discharging rates, and charger capacities fluctuate based on time and scenario. For any given moment, parameters like CREV, DREV, and charger capacity, \({\bar {S}_{EV}}\), are determined by summing up the respective charging rate, discharging rate, and charger capacities of connected EVs. Additionally, at hour h, the EA (ED) reflects the aggregated initial (final) energy of EVs that are connected to (disconnected from) the grid at that specific hour23. This dynamic adaptability enhances the practicality and efficiency of the EVPL in managing energy flows within electric systems.

$$\,0 \leqslant {P_{CE\,b,h,s}} \leqslant C{R_{EV\,b,h,s}}\,\,\,\,\forall b,h,s$$
(19)
$$\,0 \leqslant {P_{DE\,b,h,s}} \leqslant D{R_{EV\,b,h,s}}\,\,\,\,\forall b,h,s$$
(20)
$$\,{P_{CE\,b,h,s}}{P_{DE\,b,h,s}}=0\,\,\,\,\forall b,h,s$$
(21)
$$\,{E_{EV\,b,h,s}}={E_{A\,b,h,s}} - {E_{D\,b,h,s}}+{E_{EV\,b,h - 1,s}}+{\eta _{CE}}{P_{CE\,b,h,s}} - \frac{1}{{{\eta _{DE}}}}{P_{DE\,b,h,s}}\,\,\,\,\forall b,h,s$$
(22)
$$\,{E_{EV\,b,h,s}} \geqslant 0\,\,\,\,\forall b,h,s$$
(23)
$$\,\sqrt {{{\left( {{P_{CE\,b,h,s}}+{P_{DE\,b,h,s}}} \right)}^2}+{{\left( {{Q_{EV\,b,h,s}}} \right)}^2}} \leqslant {\bar {S}_{EV\,b,h,s}}\,\,\,\,\forall b,h,s$$
(24)
  1. (D)

    Power balance formulation: This paper examines the active and reactive power demands of electrical consumers. The hybrid system fulfills these demands using renewable sources and EVPLs. When the active and reactive power produced by the system exceeds the load requirements, the surplus energy is directed to the microgrid. Conversely, if the load power surpasses the system’s generation capacity, the system draws the necessary active and reactive power from the MG. Equations (25) and (26) define the principles governing the active and reactive power balance within the hybrid system.

$${P_{HS\,b,h,s}}=\,{P_{WF\,b,h,s}}+{P_{BUF\,b,h,s}}+\left( {{P_{DE\,b,h,s}} - {P_{CE\,b,h,s}}} \right) - {P_{C\,b,h,s}}\,\,\,\,\forall b,h,s$$
(25)
$${Q_{HS\,b,h,s}}=\,{Q_{WF\,b,h,s}}+{Q_{BUF\,b,h,s}}+{Q_{EV\,b,h,s}} - {Q_{C\,b,h,s}}\,\,\,\,\forall b,h,s$$
(26)
  1. (E)

    Flexibility constraint: The generation of power from renewable sources is inherently unpredictable, leading to discrepancies between real-time and day-ahead scheduling outcomes in hybrid systems integrating renewable energy. Consequently, achieving a perfect balance between consumption and generation during real-time scheduling becomes challenging, resulting in what is commonly referred to as a flexibility deficit in hybrid systems5. To address this issue and enhance system flexibility, adjustable elements like EVPL, capable of managing active power, can be employed to mitigate fluctuations caused by renewable power sources. In pursuit of high flexibility in such systems, the discrepancy between the active power output across various scenarios and the expected scenario (referred to as scenario 1 with anticipated uncertainty data) should approach zero. This concept is mathematically represented in Eq. (27). Here, the parameter FT signifies the flexibility tolerance of the system; reducing FT to zero corresponds to achieving 100% flexibility within the electrical components of the hybrid system.

$$- FT \leqslant {P_{EH\,b,h,s}} - {P_{EH\,b,h,s=1}} \leqslant FT\,\,\,\,\,\,\forall b,h,s$$
(27)

Stochastic single-objective formulation

Determinate of the compromise point

The proposed scheme relies on two objective functions, as defined by Eqs. (1) and (2). To solves this multi-objective problem using traditional algorithms, it is necessary to transform the scheme into a single-objective representation. This paper employs the weighted function sum technique24 to establish an objective function, which is outlined in Eq. (28). The defined objective function focuses on minimizing the weighted sum of the normalized values of the functions MOC and MSI25. It is important to highlight that the objective functions in Eqs. (1) and (2) differ in their measurement units, i.e. MOC is quantified in $, whereas MSI is expressed in per unit (p.u). Consequently, their normalized values are applied in Eq. (28) to ensure comparability. Normalization involves calculating each function’s relative position within its range, expressed as the difference between the function’s value and its lower bound, divided by the range over which the function can vary. The range itself is derived from the difference between the maximum and minimum values of the respective function. To accurately determine these bounds, two distinct case studies are conducted, each aimed at solving the problem for one of the single-objective functions, either MOC or MSI. It is worth noting that MSI needs to be maximized according to Eq. (2); however, Eq. (28) specifies a “minimization” framework. To reconcile this discrepancy and effectively represent MSI within Eq. (28), its normalized value is adjusted. This requires calculating MSI’s deviation from its maximum value and dividing it symmetrically across its variability range, ensuring proper alignment with the minimization approach employed in the overall model.

$$\hbox{min} \,\,\,\,\,\,OF={\omega _{MOC}}\left( {\frac{{MOC - MO{C^{lo}}}}{{MO{C^{up}} - MO{C^{lo}}}}} \right)+{\omega _{MSI}}\left( {\frac{{MSI - MS{I^{up}}}}{{MS{I^{lo}} - MS{I^{up}}}}} \right)$$
(28)

In Eq. (28), ωMOC and ωMSI denote the weighting coefficients for the MOC and MSI functions within the objective model26. These parameters are constrained to values between zero and one, with the sum of ωMOC and ωMSI equaling one. The optimal solution varies for different weight combinations of these coefficients, leading to numerous possible optimal values27 for the MOC and MSI functions in the multi-objective model. The collection of all such optimal points is commonly referred to as the Pareto front24. To identify a single optimal solution, known as the compromise point, a balance is struck between the MOC and MSI functions. In this study, the fuzzy decision-making approach24 is employed to determine the compromise point. This method involves calculating the linear fuzzy membership function (fl) for each function based on varying values of ωMOC and ωMSI. Specifically, for any given set of weight coefficients, the values of the MOC and MSI functions are computed. If the value of a function (F) lies below its lower bound (Flo) or exceeds its upper bound (Fup), fl is assigned a value of one or zero, respectively. When F falls between Flo and Fup, fl is calculated as (F – Fup)/(Flo – Fup). Subsequently, theminimum value of fl across all Pareto front members is identified, denoted by χ. This process is repeated iteratively for each member of the Pareto front, with the compromise point ultimately based on the largest value of χ24. The steps involved in determining the compromise point are visually summarized in Fig. 2 via a flowchart.

Fig. 2
figure 2

Flowchart of calculation of compromise solution.

Full size image

Uncertainty model based on SBSO

The formulation outlined in Eqs. (1)–(27) incorporates several uncertain parameters28, including active and reactive power consumption (PC and QC), wind speed (v), gas production in BUF (GBU), energy price (λ), EVs charging and discharging rates (CREV and DREV), initial and final energy levels of EVs (EA and ED), as well as the size of EV chargers (\({\bar {S}_{EV}}\)). The primary aim of this analysis is to assess the flexibility of the hybrid system under varying conditions. To achieve this, different scenarios derived from renewable energy sources are explored to determine the flexibility index with precision. To address the uncertainties inherent in this case, the SBSO technique is employed. This approach leverages the roulette wheel (RW) mechanism alongside the simultaneous backward selection method (SBM). The RW mechanism is responsible for generating a high number of scenarios to account for uncertainties. For each scenario, values for uncertainty parameters are assigned based on their average and standard deviation29. Subsequently, the normal probability density function computes the probability of these assigned values. The overall probability for a scenario is derived by multiplying the probabilities of all individual uncertainties. The SBM step serves as a scenario reduction methodology. It involves selecting a subset of scenarios that are sufficiently distinct from each other to minimize redundancy. This ensures that only the most representative scenarios are applied to the scheme. Implementation details of this technique are elaborated in29. For the reduced set of scenarios, the probability of each new scenario is recalculated by dividing its original probability in RW by the sum of probabilities of all selected scenarios from RW. This approach thus streamlines the analysis while preserving key uncertainty characteristics for effective flexibility evaluation.

Discussion and simulation results

Scheme data

The described scheme is implemented on a 33-bus IEEE radial MG30, with Fig. 3 serving as its visual representation. Within this network, Bus 1 functions as the slack bus, maintaining a voltage of 1∠0. The system operates on a base power of 1 MVA and a base voltage rating of 12.66 kV. Voltage magnitudes across other buses adhere to permissible limits between 0.95 p.u. and 1.05 p.u., while further details about the posts and distribution lines can be referenced from source30. Peak load values at individual buses are determined based on data provided in30. Meanwhile, the expected daily load factor curve for electrical consumers is illustrated in Fig. 4, stemming from information in source1. For this MG, the consumer power factor stands at 0.85. Energy pricing varies across different time intervals: from 1:00–7:00 and 17:00–22:00, the price is 16$/MWh and 30$/MWh, respectively; during other hours, the price is 24$/MWh, according to reference21. The MG integrates seven hybrid systems, strategically positioned as depicted in Fig. 3. Details on source capacities, counts of EVs, as well as peak active and reactive load values can be found in Table 2. Figure 4 aggregates data depicting several key factors: daily electricity load factor curve1, relative wind speed values1, rate value of biogas production1, and EV penetration rates19. Wind turbines in this system operate within specific thresholds, cut-in, nominal, and cut-out wind speeds are defined as 2.5 m/s, 10 m/s, and 13 m/s, respectively27. Additionally, maximum wind speed reaches 10 m/s while biogas production caps at 13,800 m31. Information concerning EV including battery and charger capacity, discharge and charge rate, initial and final energy levels, and classifications of EV types are reported in1,21,23. Discharge and charge efficiencies are 92% and 93%, respectively, for EVs1. System flexibility within hybrid configurations is maintained by enforcing a tolerance boundary of 0.05 MW. Notably, uncertainty-related variables such as load demand, energy pricing, wind speed, biogas production, and EV specifications have an assumed standard deviation of 10% relative to expected values. To address uncertainties, RW algorithm generates 2,000 scenarios for the relevant parameters of the problem. Subsequently, the SBM selects 80 of these generated scenarios for practical application to the system.

Fig. 3
figure 3

IEEE 33-bus radial MG30 with hybrid system.

Full size image
Fig. 4
figure 4

Expected daily curve for load factor1, rate value for wind speed1 and BU gas1, and EVs penetration rate23.

Full size image
Table 2 Data of sources, storage systems and peak load in EHs.
Full size table

Results and discussion

The problem outlined in Sects. 2 and 3, combined with the data provided in Sect. 4.1, is modeled and simulated using the GAMS optimization software environment31. Subsequently, numerical results derived from a variety of case studies are presented.

  1. (A)

    Evaluation of the trade-off between economic and security objectives in MG: This section is crucial for optimizing economic and technical functions, as analyzed in this study. Figure 5 illustrates the Pareto front resulting from variations in the weighting coefficients, ωMOC and ωMSI, adjusted in steps of 0.033 while maintaining a flexibility tolerance of 0.05 MW. The horizontal axis starts with ωMOC = 1 on the far-left side and progresses to ωMSI = 1 on the far-right, with ωMOC decreasing and ωMSI increasing incrementally. At ωMOC = 1, the system achieves the minimum value of the MOC, equating to $1207.2. Conversely, at ωMSI = 1, the MSI peaks at 23.1 p.u., while the maximum MOC reaches $2307.5 under these conditions. Similarly, when ωMOC is set to 1, MSI hits its lowest point at 20.3 p.u. The difference between maximum and minimum values, referred to as the changing range, is calculated as $1100.3 for MOC and 2.8 p.u. for MSI. The direction of variation for these two functions is inversely related, as highlighted by Fig. 5. Optimizing MSI results in higher MOC, which occurs due to increased active and reactive power injection by the hybrid system, potentially inducing over-voltage issues within the network and consequently lowering MSI. Multiple optimal points emerge for this scheme based on these interactions. To identify a suitable compromise between MOC and MSI, fuzzy decision-making is employed as detailed in Sect. 3.1. Table 3 showcases solutions derived using different weight coefficient variations, incremented by steps of 0.01, along with results from various mathematical solvers available in GAMS optimization software, including IPOPT, CONOPT, DISOPT, MINOS, OQNLP, and BARON31. The outcomes show that DISOPT and OQNLP were unable to deliver feasible results due to the non-convex nature of the problem, attributed to integrating AC power flow equations, which limits solutions to local optima rather than global ones. Consequently, different solvers yield distinct local optimal points. Among these solvers, IPOPT emerges as the most effective, achieving the lowest MOC and highest MSI alongside superior convergence speed marked by fewer iterations and shorter runtime for extracting optimal solutions. Further comparison between Fig. 5; Table 3 reveals that the fuzzy decision-making process considering IPOPT solver successfully approximates near-optimal objective function values. For instance, under a compromise solution case, MOC amounts to $1465.1, i.e. approximately 23.4% away from its hypothetical minimum ($1207.2), calculated as ((1465.1–1207.2)/1100.3). Similarly, MSI values within the compromise solution fall about 17.9% short of their maximum potential (23.1 p.u.), solidifying its efficacy in balancing economic and security priorities within the proposed framework.

Fig. 5
figure 5

Pareto front for the proposed scheme at FT = 0.05 MW.

Full size image
Table 3 Compromise solution between MOC and MSI at FT = 0.05 MW for different solvers.
Full size table
  1. (B)

    Evaluating the Performance of Hybrid Systems in MG: Fig. 6 illustrates the expected daily variation in active and reactive power generation from sources, storage systems, and hybrid configurations, considering a flexibility tolerance of 0.05 MW. By comparing Figs. 4 and 6a, it is evident that the daily active power production curves of WFs and BUFs in Fig. 6a correlate with the relative values of wind speed and biogas availability, respectively. This relationship is supported by Eqs. (13) and (16), which demonstrate that the power generated by renewable resources is proportional to the product of their capacity and generation rate. This principle is reflected in Fig. 6a. During off-peak periods, EVs draw energy from hybrid systems, benefiting from lower energy prices at these times. Consequently, EVs execute their charging processes at minimal cost, optimizing the miinimization of MOC as defined by Eq. (1). Moreover, to enhance the efficiency of both MOC and MSI, EVs are set to charge between 12:00 and 16:00 to increase their stored energy. Later, between 17:00 and 22:00, they inject this energy back into the hybrid systems. Figure 6a also highlights the active power control by flexible resources such as EVPLs, which optimize their power usage throughout most operational hours. Since renewable sources continuously generate active power, managing flexibility becomes essential around the clock. The daily active power curve of hybrid systems, derived using Eq. (25), reveals that these systems primarily act as electricity generators for MG during most hours. Conversely, they become energy consumers during off-peak periods when EV power demand is high and renewable production is comparatively low. In contrast, Fig. 6b portrays the daily reactive power profiles of EVPLs, WFs, BUFs, and hybrid systems. These elements typically generate substantial reactive power during low-load hours when passive sources and EVPLs demand significant energy, as indicated in Fig. 6a. Producing higher reactive power mitigates potential voltage drop within MG during these periods. During peak hours, when passive load demand in MG is elevated, various sources and storage devices ramp up their reactive power production to ensure system stability. However, the reactive power output from these resources is minimal between 8:00–16:00 and 23:00–24:00. During these intervals, renewable resources generate substantial active power, which may risk overvoltage scenarios. To prevent such issues, reactive power production is deliberately reduced during these hours. Additionally, Fig. 6b showcases the hybrid systems’ reactive power generation pattern indicating that hybrid system predominantly function in reactive power generation mode throughout most operational hours. This operation ensures consistent system stability while addressing varying load demands in MG effectively.

Fig. 6
figure 6

Expected daily curve of, (a) active power, (b) reactive power for renewable sources, EVPLs and hybrid systems at FT = 0.05 MW.

Full size image
  1. (C)

    Evaluation of the technical and economic viability of the microgrid: This section focuses on assessing the feasibility of the proposed plan. This analysis is carried out through the examination of three distinct case studies: Case I involves conducting a load flow study within the microgrid, Case II builds upon Case I by incorporating renewable hybrid systems to evaluate their impact, and Case III expands on Case II by adding EVPL to understand their integrated effect.

In case II, it is assumed that renewable sources are the only producers of electrical energy. In the following, the status of economic (MOC), voltage security (MSI and poor bus), and operation indicators for the aforementioned case studies per flexibility tolerance of 0.05 MW are shown in Figs. 7, 8 and 9. The operation indicators include MG energy loss (MEL), maximum voltage drop (MVD), maximum overvoltage (MOV) and peak load carrying capability (PLCC). PLCC refers to how MG can feed the peak load with the specific daily load factor curve as shown in Fig. 4. Based on Figs. 7 and 8, and 9, it can be seen that the worst condition of the mentioned indicators is in case I. So this case includes the highest operating cost, energy loss, and voltage drop, and the lowest PLCC and MSI are established in this case. Because in this case, all electrical consumers in MG are fed by the distribution network. The presence of renewable sources in case II has improved the mentioned indicators. So that MOC, MEL and MVD in case II have decreased by 35.1%, 24.3% and 46.7% respectively with respect to the load flow study. PLCC and MSI are increased by 34.2% and 10.6%, respectively, compared to case (I) Of course, these conditions for increasing MOV about 0.031 p.u. But this value is less than its limit, i.e. 0.05 (1.05–1) p.u. In case III, the presence of EVPLs in renewable hybrid system has been investigated. In case III, the operating cost, energy losses and voltage drop are reduced by 40.9%, 33.5% and 53.3%, respectively, compared to case I, and PLCC and MSI has increased by 55.3% and 20.2%, respectively. MOV is also reduced by 64.5% compared to case (II) As another point, in all the studied cases, the weak bus in terms of voltage magnitude is equal to the bus 18. In other words, there is the highest voltage drop in this bus. But according to Fig. 9, the maximum voltage drop for cases II to III is less than 0.05 p.u. In other words, in cases II to III, there is a safe margin of voltage in all buses. Finally, in Table 4, the status of economic, operation, and voltage security indicators is reported for changes in flexibility tolerance (FT). Based on this table, mobile storage devices are able to obtain 100% flexibility conditions (FT = 0). But this situation is proportional to the increase in operating cost, energy loss and voltage drop, while overvoltage and PLCC are reduced. Also, MSI is slightly increased. By increasing the FT or freeing the flexibility constraint, the situation of economic and operation indicators improves, but the situation of voltage security has little changes. Because in this condition, the performance of storage devices and hybrid systems will be only for improving the state of operation, economy, and voltage security of MG.

Fig. 7
figure 7

Value of MOC, MEL and PLCC in the different cases at FT = 0.05 MW.

Full size image
Fig. 8
figure 8

Security state of MG based on MSI value in the different cases at FT = 0.05 MW.

Full size image
Fig. 9
figure 9

Voltage deviation in the different cases at FT = 0.05 MW.

Full size image
Table 4 Value of economic and technical indices of MG in case III for the different values of FT.
Full size table

Conclusions

In this article, the energy scheduling of microgrids with flexible renewable hybrid systems was presented in accordance with the estimation of operation, economic, and voltage security goals of network operator system. The proposed plan was responsible for minimizing the cost of operation, along with maximizing security of voltage. This design expressed the objective function as the minimization of the weighted sum of the aforementioned functions. The problem includes the model of optimal power flow, the limits of voltage security in the microgrid, the model of resources and storages operation in the form of a hybrid system, and the flexibility limitation of the hybrid system. Fuzzy decision-making method was used to extract the compromise solution. Scenario-based stochastic optimization was used to model uncertainties of load, renewable resources, mobile storage, and energy price. Based on the numerical results, it was observed that the IPOPT mathematical algorithm is able to obtain a more optimal point for the mentioned objective functions than other mathematical solvers, which is accompanied by a high convergence speed. Fuzzy decision-making method found a point as the compromise solution where the objective functions have the smallest distance from their optimal value. So that this distance for the economic, operation, and voltage security functions are around 23%, 39% and 18%, respectively. Based on the optimal performance of mobile storage devices or electric vehicles in hybrid systems, it has been able to achieve 100% flexibility conditions for systems. Also, the optimal performance of the systems in the proposed design has improved the economic, operation, and security situation of the microgrid about to 41%, 33%-65%, 20%, respectively, compared to the load flow studies.

In the proposed plan, modeling the risk arising from the uncertain parameters was not considered. However, risk modeling is needed to reduce economic and technical losses. This issue is included as future work in the proposed plan. Demand response is an energy management solution in the power system. Thus, it will have a favorable capability in improving the economic and technical conditions of the network. The use of demand response in the proposed project was considered as future work. In addition, photovoltaic systems are a renewable source that can be installed in many consumption areas. Although they do not produce energy during most operating hours (such as night hours), their presence in the power system has a favorable effect on improving the economic and technical conditions of the power system. The use of photovoltaics in the proposed project was considered as future work. In this paper, electric vehicles were used as energy storage, which in addition to the energy management capability, was also used as a source of flexibility. They are known as mobile storage. Their impact on the microgrid depends on the number of electric vehicles. However, stationary storage devices such as batteries and hydrogen storage systems are always present in the grid with a fixed capacity and can have a good ability to improve the economic and technical conditions of the microgrid. Hydrogen storage includes power to hydrogen and hydrogen to power technologies. The use of batteries and hydrogen storage systems in the proposed design is considered as future work. In the proposed design, it is assumed that the wind speed is the same for all wind turbines in the ideal case. However, in real conditions, this is not the case and the energy produced by the wind system is accompanied by a wake effect. This issue was considered in the proposed design as a future work. The hybrid system can include different sources and storage devices. It can manage multiple types of energy simultaneously. This increases the energy efficiency of the hybrid system. This is considered as future work in the proposed design.