Development of the generalized ridge estimator for the Poisson-Inverse Gaussian regression model with multicollinearity

Abstract

The Poisson-Inverse Gaussian regression model is a widely used method for analyzing count data, particularly in over-dispersion. However, the reliability of parameter estimates obtained through maximum likelihood estimation in this model can be compromised when multicollinearity exists among the explanatory variables. Multicollinearity means that high correlations between explanatory variables inflate the variance of the maximum likelihood estimates and increase the mean squared error. To handle this problem, the Poisson-Inverse Gaussian ridge regression estimator has been proposed as a viable alternative. This paper introduces a generalized ridge estimator to estimate regression coefficients in the Poisson-Inverse Gaussian regression model under multicollinearity. The performance of the proposed estimator is evaluated through a comprehensive simulation study, covering various scenarios and employing the mean squared error as the evaluation criterion. Furthermore, the practical applicability of the estimator is demonstrated using two real-life datasets, with its performance again assessed based on mean squared error. Theoretical analyses, supported by simulation and empirical findings, suggest that the proposed estimator outperforms existing methods, offering a more reliable solution in multicollinearity.

Introduction

Count data characterized by non-negative integer values frequently arises in various disciplines, necessitating the use of specialized regression models to explore relationships between the response variable and its predictors. These models facilitate the identification of significant explanatory variables and their impact on the response^1,2. Among the most commonly employed models is the Poisson regression model (PRM), which assumes that the mean and variance are equal (i.e., equi-dispersion). However, this assumption is often unrealistic in empirical datasets, where the variance either exceeds (over-dispersion) or is less than (under-dispersion) the mean. In such situations, applying the Poisson model may lead to biased estimates and unreliable conclusions³. To address the limitations of equi-dispersion, alternative count regression models, including the negative binomial (NBRM)⁴, Bell (BRM)⁵, quasi-Poisson (QPRM)⁶, generalized Poisson Lindley (GPLRM)⁷, Conway-Maxwell Poisson (CMPRM)⁸, and Poisson-Inverse Gaussian (PIGRM) models⁹, have been proposed. These models extend the Poisson framework to accommodate over-dispersed and under-dispersed data, thereby enhancing model accuracy and interpretability.

The PIGRM is highly effective for datasets with heavy tails, where a small number of extreme values differ significantly from most data near zero. This type of data is common in fields like actuarial science, biology, engineering, and medical research. The PIGRM is preferred over the NBRM for its ability to handle greater skewness and kurtosis, making it ideal for heavy-tailed count data⁹. Willmot³ highlighted the PIGRM as a better alternative to the NBRM for highly skewed and heterogeneous datasets. Putri et al.¹⁰ found PIGRM effective in managing overdispersion when compared to NBRM. Similarly, Saraiva et al.¹¹ used PIGRM for overdispersed dengue data, and Husna and Azizah¹² applied it to study dengue hemorrhagic fever in Central Java, showcasing its versatility for complex count data.

One of the fundamental assumptions of the generalized linear regression model is the absence of correlation among explanatory variables. However, in empirical settings, explanatory variables frequently exhibit strong or near-strong linear relationships, thereby violating this assumption and giving rise to the problem of multicollinearity¹³. This issue also manifests in the context of the PIGRM, where multicollinearity complicates parameter estimation, inflated variance, and increases mean squared error (MSE). The maximum likelihood estimator (MLE), commonly employed for estimating regression coefficients in the PIGRM, is particularly sensitive to multicollinearity, as it results in inflated variances and unreliable parameter estimates¹⁴. To tackle multicollinearity in regression models, ridge regression and the Liu estimator are two commonly studied techniques. Ridge regression, introduced by Hoerl and Kennard¹⁵, has been extensively explored, with notable studies focusing on optimal shrinkage parameters by Golub et al.¹⁶, and Alkhamisi et al.¹⁷. Segerstedt¹⁸ extended ridge regression to the generalized linear model (GLM), with further advancements by researchers like Månsson¹⁹, Saleh et al.²⁰, Amin et al.²¹, Sami et al.²², and Shahzad et al.²³. On anther hand Kejian²⁴ introduced the Liu estimator, which offers a linear shrinkage parameter $d$ and has been applied to different models. Kibria²⁵ and Alheety and Kibria²⁶ developed the Liu estimator for linear regression models (LRMs) and later Kurtoǧlu²⁷ defined the Liu estimator for GLMs. Then, inspiring further applications by Qasim et al.²⁸ and Bulut²⁹.

Several studies have focused on developing generalized versions of the ridge estimator to handle multicollinearity in different types of regression models. Rashad et al.³⁰ proposed a generalized ridge estimator for the NBRM, while Akram et al.³¹ extended this idea to both generalized ridge and generalized Liu estimators in the gamma regression. Fayose and Ayinde³² explored how to define an appropriate biasing parameter for the generalized ridge regression estimator, and Bhat and Raju³³ introduced a class of such estimators. Gómez et al.³⁴ discussed biased estimation using generalized ridge regression for multiple LRMs. Abdulazeez and Algamal³⁵ combined shrinkage estimation with particle swarm optimization to define a generalized ridge estimator. In addition, van Wieringen³⁶ applied the generalized ridge approach to estimate the inverse covariance matrix, and Mohammadi³⁷ suggested a test for detecting harmful multicollinearity based on this method. Bello and Ayinde³⁸ also proposed feasible generalized ridge estimators for models affected by both multicollinearity and autocorrelation. Recent works^30,35,39,40 have shown that the performance of biased estimators can be improved by allowing the biasing parameters to vary across observations (such as $k_j$) rather than using a fixed value (such as $k$). Based on this, the main goal of the present paper is to develop a more general form of the ridge estimator to better address multicollinearity in the PIGRM.

This paper discusses the advantages of the generalized ridge estimator in the PIGRM. We also present new methods for determining the optimal values of the shrinkage coefficients (kj), based on the methodologies of Rashad³⁰ and Dawood et al.³⁹ The careful selection of these coefficients is crucial to improving the performance of the biased generalized ridge estimation method. Monte Carlo simulations use the MSE to evaluate the performance of the proposed estimator compared to existing estimators. To validate the simulation results, we use two real-world data studies that confirm the effectiveness of the estimator, highlighting its improved accuracy and robustness in addressing problems related to multicollinearity.

The structure of this paper is as follows: Section 2 provides a summary of the PIGRM model and examines biased estimation approaches, including PIGRRE and the proposed estimator. It also discusses theoretical comparisons of the proposed estimator and methods for selecting biasing parameters. Section 3 describes the study and results of the Monte Carlo simulation used to evaluate the proposed estimator. Section 4 highlights the application of the estimator through two real-world datasets to confirm the simulation results. Finally, Section 5 summarizes the results and discusses their broader significance.

Methodology

The PIG distribution combines two probability distributions: the Poisson and the Inverse Gaussian. Let $Y$ represent a random variable following a Poisson distribution with a mean of $\mu \nu$, where $\nu$ itself follows an Inverse Gaussian distribution with mean 1 and dispersion parameter $\phi$. The probability mass function (PMF) of $Y$ is expressed as^1,41:

$$\begin{aligned} f(y|\mu , \nu ) = \frac{(\mu \nu )^y}{y!} \exp (-\mu \nu ), \end{aligned}$$

(1)

where $\nu \sim \text {IG}(1, \phi )$, and the probability density function of $\nu$ is given by⁴²:

$$\begin{aligned} g(\nu ) = \left( \frac{\phi }{2 \pi \nu ^3} \right) ^{1/2} \exp \left( -\frac{\phi (\nu - 1)^2}{2 \nu } \right) . \end{aligned}$$

(2)

The marginal PMF of $Y$, representing the PIG distribution, is derived by integrating over $\nu$. This results in the following expression:

$$\begin{aligned} P(Y = y|\mu ) =\sqrt{ \frac{2\phi }{\pi } }\frac{ \mu ^y \exp (\phi ) \textbf{R}_s(\alpha )}{y! \left( \frac{\alpha }{\phi } \right) ^s}, \quad \mu>0, \phi >0, y = 0, 1, 2, \dots , \end{aligned}$$

(3)

where $s = y - 0.5$, $\alpha ^2 = \phi ^2 \left( 1 + 2\frac{\mu }{\phi } \right)$, and $\textbf{R}_s(\alpha )$ denotes the modified Bessel function of the third kind⁴³. The mean and variance of the distribution are $E(Y) = \mu$ and $V(Y) = \mu + \frac{\mu ^3}{\phi }$, respectively.

In the context of PIGRM, the linear predictor $g(\mu ) = \eta _i$ is used, which is equivalent to $\mu = \exp {x_i^T \beta }$, where $\eta _i$ is the linear combination of the explanatory variables, defined as $\eta _i = x_i^T \beta$, where $\beta = (\beta _0, \beta _1, \dots , \beta _{p-1})^T$ is the vector of regression coefficients, and $x_i = (1, x_{i1}, \dots , x_{i(p-1)})^T$ is the vector of explanatory variables for the $i$-th observation^1,43.

To estimate the parameters of the PIGRM, the MLE method is employed. The log-likelihood function for the model is as follows:

$$\begin{aligned} \ell (\mu _i, \phi )& = \sum _{i=1}^{n} \left[ y_i \log (\mu _i) + \phi - \log (y_i!) - \frac{1}{2} \log \left( \frac{1}{\phi } \right)\right. \\&\quad \left.- \frac{2y_i - 1}{4} \log \left( 1 + 2 \frac{\mu _i}{\phi } \right) + \log \textbf{R}_{y-0.5} \left( \phi \sqrt{1 + 2 \frac{\mu _i}{\phi }} \right) \right] . \end{aligned}$$

(4)

The log-likelihood function with respect to the regression coefficients $\beta$ is given by:

$$\begin{aligned} \ell (\beta )& = \sum _{i=1}^{n} \left[ y_i x_i^T \beta + \phi - \log (y_i!) - \frac{1}{2} \log \left( \frac{1}{\phi } \right) - \frac{2y_i - 1}{4} \log \left( 1 + 2 \frac{\exp {(x_i^T \beta )}}{\phi } \right) \right.\\& \quad \left. + \log \textbf{R}_{y-0.5} \phi \left( 1 + 2 \frac{\exp {(x_i^T \beta )}}{\phi } \right) \right] . \end{aligned}$$

(5)

To obtain the MLE of the parameters, we differentiate the log-likelihood function concerning the parameters and set the derivatives equal to zero. The first derivative with respect to $\beta _j$ is¹⁰:

$$\begin{aligned} \frac{\partial \ell }{\partial \beta _j} = \sum _{i=1}^{n} \left[ x_i \left( y_i - \frac{\textbf{R}_{y_i - 0.5} (\alpha )}{\sqrt{1 + \frac{2}{\phi } \exp (x_i^T \beta )}} \exp (x_i^T \beta ) \right) \right] = 0. \end{aligned}$$

(6)

Similarly, thetove with respect to $\phi$ is:

$$\begin{aligned} \frac{\partial \ell }{\partial \phi } = \sum _{i=1}^{n} \left[ -\phi ^2 - y_i \phi + \frac{\phi ^2 \textbf{R}_{y_i - 0.5} (\alpha ) \left( 1 + \frac{\exp (x_i^T \beta )}{\phi } \right) }{\sqrt{1 + \frac{2}{\phi } \exp (x_i^T \beta )}} \right] = 0. \end{aligned}$$

(7)

To estimate the parameters $\beta$ and $\phi$ through MLE, numerical methods such as the Newton-Raphson algorithm or the iteratively reweighted least squares (IRLS) algorithm are utilized, given the non-linearity of the equations (Eqs. (6) and (7)). Upon completion of the iterative procedure, the MLE estimate for $\hat{\beta }$ is derived from the following expression¹⁴:

$$\begin{aligned} \hat{\beta }_{\text {MLE}} = (X^T \hat{W} X)^{-1} X^T \hat{W} \hat{u}, \end{aligned}$$

(8)

where $\hat{W} = \text {diag}(\mu _i + \alpha \mu _i^3)$ and $\hat{u}_i$, the adjusted response variable, is computed as $\hat{u}_i = \log (\mu ) + \frac{y_i - \mu _i}{\mu _i + \mu _i^3 / \phi }$. To evaluate the accuracy of the estimator, the mean squared error matrix (MSEM) and MSE of $\hat{\beta }_{\text {MLE}}$ are determined through spectral decomposition of the matrix $X^T\hat{W} X= \mathcal {Q} G \mathcal {Q}^T$. where $G = \text {diag}(g_1, g_2, \dots , g_p)$ is the diagonal matrix of the eigenvalues of $X^T \hat{W} X$, and $\mathcal {Q}$ is the orthogonal matrix with columns corresponding to the eigenvectors of $X^T \hat{W} X$.

The MSEM for the estimator is given by:

$$\begin{aligned} \text {MSEM}(\hat{\beta }_{\text {MLE}}) = \hat{\phi } \mathcal {Q} G^{-1} \mathcal {Q}^T. \end{aligned}$$

(9)

The MSE is calculated as:

$$\begin{aligned} \text {MSE}(\hat{\beta }_{\text {MLE}}) =\hat{\phi } \sum _{j=1}^p \frac{1}{g_j}, \end{aligned}$$

(10)

where $\hat{\phi }$ is the estimated value of $\phi$ and computed as $\hat{\phi } = \frac{\sum _{i=1}^n \frac{(y_i - \hat{\mu }_i)^2}{V(\hat{\mu }_i)}}{n - p}$.

Poisson-Inverse Gaussian ridge regression estimator

Segerstedt¹⁸ proposed a ridge regression estimator to handle multicollinearity in GLM as an alternative to the MLE. Accordingly, Månsson¹⁹, Månsson and Shukur⁴⁴, Kibria et al.⁴⁵, and Ashraf⁴⁶ apply it to many GLMs. Following this research, Batool et al.¹⁴ proposed a PIGRRE to address multicollinearity in PIGRM. The PIGRRE is given by:

$$\begin{aligned} \hat{\beta }_{k} = \left( X^{T} \hat{W} X + k I \right) ^{-1} X^{T} \hat{W} X \hat{\beta }_{\text {MLE}}, \end{aligned}$$

(11)

where $k~ (k>0)$ represents a PIGRRE parameter, and $I$ is the identity matrix of $p \times p$. In particular, when $k = 0$, the PIGRRE reduces to MLE. The bias and covariance matrix associated with the PIGRRE are as follows:

$$\begin{aligned} \text {Bias}(\hat{\beta }_k)= & E(\hat{\beta }_k) - \beta = -k G_k^{-1} \beta , \end{aligned}$$

(12)

$$\begin{aligned} \text {Cov}(\hat{\beta }_k)= & E\left[ \left( \hat{\beta }_k - E(\hat{\beta }_k)\right) \left( \hat{\beta }_k - E(\hat{\beta }_k)\right) ^T \right] = \hat{\phi } \left( \mathcal {Q} G_k^{-1} G G_k^{-1} \mathcal {Q}^T \right) , \end{aligned}$$

(13)

where $G_k = \text {diag}(g_1 + k, g_2 + k, \dots , g_p + k)$ is a diagonal matrix consisting of the eigenvalues of the covariance matrix, adjusted by the ridge parameter.

The MSEM of the PIGRRE estimator combines both the covariance and the squared bias:

$$\begin{aligned} \text {MSEM}(\hat{\beta }_k) = \text {Cov}(\hat{\beta }_k) + \text {Bias}(\hat{\beta }_k)\text {Bias}(\hat{\beta }_k)^T. \end{aligned}$$

(14)

Expanding the above expression:

$$\begin{aligned} \begin{aligned} \text {MSEM}(\hat{\beta }_k) = \hat{\phi } \left( \mathcal {Q} G_k^{-1} G G_k^{-1} \mathcal {Q}^T \right) + b_k b_k^T, \end{aligned} \end{aligned}$$

(15)

where $b_k = \text {Bias}(\hat{\beta }_k) = -k \mathcal {Q} G_k^{-1} \alpha$. The MSE is calculated as the trace of the MSEM:

$$\begin{aligned} \begin{aligned} \text {MSE}(\hat{\beta }_k) =\text {tr}\left( \text {MSEM}(\hat{\beta }_k)\right) = \hat{\phi } \sum _{j=1}^p \frac{g_j}{(g_j + k)^2} + \sum _{j=1}^p \frac{k^2 \alpha _j^2}{(g_j + k)^2}, \end{aligned} \end{aligned}$$

(16)

where $\alpha _j$ denotes the $j$-th component of the vector $\alpha = \mathcal {Q}^T \hat{\beta }_{\text {MLE}}$, representing the MLE-adjusted coefficient values.

Proposed estimator

Building on the work of Bhat and Raju³³ and extending the contributions of Rashad et al.³⁰ and Akram et al.³¹, we propose the generalized ridge estimator for the PIGRM. The Poisson-Inverse Gaussian generalized ridge estimator (PIGGRE) enhances standard ridge regression by assigning a unique shrinkage parameter to each regression coefficient, improving its ability to address multicollinearity.

In the PIGGRE method, the ridge parameter matrix is written as $K = \text {diag}(k_1, k_2, \ldots , k_p)$, where each $k_j$ controls how much shrinkage is applied to the $j$-th regression coefficient. This setup gives more flexibility and improves prediction accuracy and addresses multicollinearity than the standard PIGRRE approach.

Key scenarios in the PIGGRE framework include:

• 1. $k_j = 0$ for all $j$: the estimator reduces to the MLE.

• 2. $k_j = k$ (constant) for all $j$: the estimator corresponds to PIGRRE.

• 3. $k_j$ varying across coefficients: the estimator is referred to as PIGGRE

The PIGGRE is defined as:

$$\begin{aligned} \hat{\beta }_{K} = (X^T \hat{W} X + K)^{-1} X^T y= \left( X^T \hat{W} X + K \right) ^{-1} X^T \hat{W} X \hat{\beta }_{\text {MLE}}. \end{aligned}$$

(17)

The bias and covariance matrix associated with the PIGGRE are as follows:

$$\begin{aligned} \begin{aligned} \text {Bias}(\hat{\beta }_K) =&E(\hat{\beta }_K) - \beta \\ =&\left( X^T \hat{W} X + K \right) ^{-1} X^T \hat{W} X \hat{\beta }-\hat{\beta }\\ =&\left( I-K(X^T \hat{W} X + K)^{-1} \right) {\beta }-{\beta }\\ =&-K G_K^{-1} \beta , \end{aligned} \end{aligned}$$

(18)

$$\begin{aligned} \begin{aligned} \text {Cov}(\hat{\beta }_K) =&E\left[ \left( \hat{\beta }_K - E(\hat{\beta }_K)\right) \left( \hat{\beta }_K - E(\hat{\beta }_K)\right) ^T \right] \\ =&\left( X^T \hat{W} X + K \right) ^{-1} X^T \hat{W} X \text {Cov}(\hat{\beta }_{\text {MLE}}) \left( X^T \hat{W} X + K \right) ^{-1} X^T \hat{W} X \\ =&\hat{\phi } \left( \mathcal {Q} G_K^{-1} G G_K^{-1} \mathcal {Q}^T \right) . \end{aligned} \end{aligned}$$

(19)

The MSEM of the PIGGRE estimator is defined by:

$$\begin{aligned} \begin{aligned} \text {MSEM}(\hat{\beta }_K)&= \text {Cov}(\hat{\beta }_K) + \text {Bias}(\hat{\beta }_K)\text {Bias}(\hat{\beta }_K)^T\\&= \hat{\phi } \left( \mathcal {Q} G_K^{-1} G G_K^{-1} \mathcal {Q}^T \right) + b_K b_K^T, \end{aligned} \end{aligned}$$

(20)

where $G_K = \text {diag}(g_1 + k_1, g_2 + k_2, \dots , g_p + k_p)$ and $b_K = \text {Bias}(\hat{\beta }_K) = -K \mathcal {Q} G_K^{-1} \alpha$. The MSE is calculated as the trace of the MSEM:

$$\begin{aligned} \begin{aligned} \text {MSE}(\hat{\beta }_K) =\text {tr}\left( \text {MSEM}(\hat{\beta }_K)\right) = \hat{\phi } \sum _{j=1}^p \frac{g_j}{(g_j + k_j)^2} + \sum _{j=1}^p \frac{k_j^2 \alpha _j^2}{(g_j + k_j)^2}. \end{aligned} \end{aligned}$$

(21)

Superiority of PIGGRE

In this part, we compare the proposed PIGGRE method with other known estimators, such as MLE and PIGRRE. To support this comparison, we make use of the following lemma:

Lemma 1

Trenkler and Toutenburg⁴⁷. Consider two linear estimators of $\alpha$ , denoted by $\hat{\alpha }_i = U_i w$ for $i = 1, 2.$ Let $E = \text {Cov}(\hat{\alpha }_1) - \text {Cov}(\hat{\alpha }_2) ,$ where $\text {Cov}(\hat{\alpha }_i)$ is the covariance matrix of $\hat{\alpha }_i ,$ and assume $E > 0.$ Additionally, define the bias of $\hat{\alpha }_i$ as $b_i = (U_i X - I) \alpha .$ Then, the difference in MSEM between the two estimators can be expressed as:

$$\Delta (\hat{\alpha }_1-\hat{\alpha }_2)=\text {MSEM}(\hat{\alpha }_1) - \text {MSEM}(\hat{\alpha }_2) = \phi Q + b_1 b_1^T - b_2 b_2^T > 0,$$

where the MSEM of $\hat{\alpha }_i$ is given by:

$$\text {MSEM}(\hat{\alpha }_i) = \text {Cov}(\hat{\alpha }_i) + b_i b_i^T.$$

This inequality is satisfied if and only if:

$$b_2^T \left[ \phi E + b_1 b_1^T \right] ^{-1} b_2 < 1.$$

Theorem 2.1

The PIGGRE estimator, $\hat{\beta }_{K} ,$ is superior to an alternative estimator $\hat{\beta }_{\text {MLE}}$ if and only if:

$$\mathcal {Q}^T b_K^T \left[ \phi \left( G^{-1} - G_K^{-1} G G_K^{-1} \right) \right] b_K \mathcal {Q} < 1.$$

Proof

The difference (D) between the covariance matrices of the two estimators is given by:

$$\text {D} = \phi \left( G^{-1} - G_K^{-1} G G_K^{-1} \right) .$$

This can be expressed as:

$$\text {D} = \phi \, \text {diag} \left( \frac{1}{g_j} - \frac{g_j }{(g_j + k_j)^2} \right) _{i=1}^p.$$

The matrix $G^{-1} - G_K^{-1} G G_K^{-1}$ is positive definite if and only if $(g_j + k_j)^2 - g_j^2 > 0$ or $k_j^2 +2k_j g_j > 0$. It is evident that for $k_j > 0$ ($i = 1, 2, \ldots , p$), the term $k_j^2 +2k_j g_j^2 > 0$ is positive, ensuring that $G^{-1} - G_K^{-1} G G_K^{-1}$ is positive definite. Thus, by Lemma 3, the superiority condition of $\hat{\beta }_{K}$ over $\hat{\beta }_{\text {MLE}}$ is satisfied.$\square$

Theorem 2.2

The PIGGRE estimator, $\hat{\beta }_{K}$, is superior to an alternative estimator $\hat{\beta }_{k}$ if and only if:

$$\mathcal {Q}^T b_K^T \left[ \phi \left( G_k^{-1} G G_k^{-1} - G_K^{-1} G G_K^{-1} \right) + b_k\mathcal {Q} \mathcal {Q}^Tb_k^T\right] b_K \mathcal {Q} < 1.$$

Proof

The difference (D) between the covariance matrices of the two estimators is given by:

$$\text {D} = \phi \left( G_k^{-1} G G_k^{-1} - G_K^{-1} G G_K^{-1} \right) .$$

This can be expressed as:

$$\text {D} = \phi \, \text {diag} \left( \frac{g_j}{(g_j+k)^2} - \frac{g_j }{(g_j + k_j)^2} \right) _{i=1}^p.$$

The matrix $G_k^{-1} G G_k^{-1} - G_K^{-1} G G_K^{-1}$ is positive definite if and only if $(g_j + k_j)^2 -( g_j+k)^2 > 0$ or $k_j^2-k^2 +2 g_j(k_j-k) > 0$. It is evident that for $k_j > 0$ ($i = 1, 2, \ldots , p$), the term $k_j^2-k^2 +2 g_j(k_j-k) > 0$ is positive, ensuring that $G_k^{-1} G G_k^{-1} - G_K^{-1} G G_K^{-1}$ is positive definite. Thus, by Lemma 3, the superiority condition of $\hat{\beta }_{K}$ over $\hat{\beta }_{k}$ is satisfied.$\square$

The biasing parameters of the PIGGRE

To estimate the optimal values of $k_j$ for the proposed PIGRRE, the approach minimizes the MSE of the estimator, defined as:

$$T(k_1, k_2, \ldots , k_p) = \text {MSE}(\hat{\beta }_K) = \hat{\phi } \sum _{j=1}^p \frac{g_j}{(g_j + k_j)^2} + \sum _{j=1}^p \frac{k_j^2 \alpha _j^2}{(g_j + k_j)^2},$$

To find the optimal values of $k_j$, differentiate $T(k_1, k_2, \ldots , k_p)$ with respect to $k_j$ and set the derivative to zero $\frac{\partial T(k_1, k_2, \ldots , k_p)}{\partial k_j} = 0.$ Solving for $k_j$, we obtain:

$$\hat{k}_j = \frac{\hat{\phi }}{\hat{\alpha }_j^2},$$

where $\hat{\phi }$ and $\hat{\alpha }$ represent the estimated values of $\phi$ and $\alpha$, respectively.

Following Bhat and Raju³³ and Rashad et al.³⁰, we considered the following values of $K$:

$$\begin{aligned} \hat{K}_1= & \text {diag}\left( \frac{\hat{\phi }}{\hat{\alpha }_j^2}\right) , \end{aligned}$$

(22)

$$\begin{aligned} \hat{K}_2= & \text {diag}\left( \frac{1}{\hat{\alpha }_j^2}\right) , \end{aligned}$$

(23)

$$\begin{aligned} \hat{K}_3= & \text {diag}\left( \frac{1}{\hat{\phi }\hat{\alpha }_j^2}\right) , \end{aligned}$$

(24)

$$\begin{aligned} \hat{K}_4= & \text {diag}\left( \frac{p}{\hat{\phi }\hat{\alpha }_j^2}\right) , \end{aligned}$$

(25)

$$\begin{aligned} \hat{K}_5= & \text {diag}\left( p\sqrt{\frac{1}{\hat{\alpha }_j^2}}\right) . \end{aligned}$$

(26)

Monte Carlo simulation

Simulation design

The simulation procedure for evaluating the performance of the proposed estimator involves several steps, considering key factors such as sample size ($n$), the number of explanatory variables ($p$), levels of multicollinearity ($\rho ^2$), and dispersion parameters ($\phi$), as detailed in Table 1. The simulation process is outlined as follows:

• 1. Choose the regression coefficients $\beta = (\beta _1, \beta _2, \dots , \beta _{(p)})$ such that the sum of their squared values equals 1, i.e., $\sum _{j=1}^p \beta _j^2 = 1$. This normalization is a common assumption in regression modeling.

• 2. Use PIG($\mu , \phi$) distribution to generate the response variable $y_i$ for the PIGRM, where $\mu = \exp (x_i^T \beta )$. Here, $x_i^T$ represents the explanatory variables for observation $i$, and $\beta$ are the regression coefficients.

• 3. Simulate the correlated explanatory variables $x_{ij}$ using the formula:

  $$\begin{aligned} x_{ij} = \sqrt{1 - \rho ^2} \, F_{ij} + \rho \, F_{i(j+1)}, \end{aligned}$$

  where $F_{ij}$ are independent standard normal random variables. This ensures the correlation structure between the explanatory variables, with $\rho ^2$ controlling the degree of correlation. This step is repeated for $i = 1, \ldots , n$ and $j = 1, \ldots , p+1$.

• 4. Use the ‘gamlss‘ package in R to estimate the regression parameters based on the simulated data, selecting the PIG family for the model.

• 5. Repeat the generation of the entire data and estimation process for different combinations of $n$,$\rho$, $p$, and $\phi$ for 1000 replications to ensure the robustness of the results.

• 6. Evaluate the performance of the proposed estimator using the MSE criterion:

  $$\begin{aligned} \text {MSE}(\hat{\beta }) = \frac{\sum _{i=1}^R (\hat{\beta }_i - \beta )^T (\hat{\beta }_i - \beta )}{R}, \end{aligned}$$

  (27)

  where $\hat{\beta }_i$ represents the estimated parameters from the $i$-th replication, $\beta$ is the true parameter vector, and $R$ is the total number of replications (1000 in this case). This criterion quantifies the deviation between the true parameters and the estimated ones, helping to assess the accuracy of the estimator.

  Following Segerstedt¹⁸, Månsson and Shukur⁴⁴, and Batool et al.¹⁴, we use the following values of $k$ for PIGRRE:

  $$k_1 = \min \left( \frac{\hat{\phi }}{2 \hat{\alpha }_j^2 + \frac{\hat{\phi }}{g_j}}\right) , \quad \hat{k}_2 = \min \left( \frac{\hat{\phi }}{\hat{\alpha }_j^2}\right) , \quad \hat{k}_3 = \left( \frac{\hat{\phi }}{\sum _j^p \hat{\alpha }_j^2}\right) , \quad k_4 = \prod _{j=1}^p \left( \frac{\hat{\phi }}{2 \hat{\alpha }_j^2 + \frac{\hat{\phi }}{g_j}}\right) ^{\frac{1}{p}}, \quad k_5 = p\sum _{j=1}^p\left( \frac{\hat{\phi }}{2 \hat{\alpha }_j^2 + \frac{\hat{\phi }}{g_j}}\right) .$$

Table 1 Different factors considered in the simulation study.

Table 2 Estimated MSE for different estimators at p = 3 and $\phi =2$.

Table 3 Estimated MSE for different estimators at p = 3 and $\phi =4$.

Table 4 Estimated MSE for different estimators at p = 3 and $\phi =6$.

Table 5 Estimated MSE for different estimators at p = 6 and $\phi =2$.

Table 6 Estimated MSE for different estimators at p = 6 and $\phi =4$.

Table 7 Estimated MSE for different estimators at p = 6 and $\phi =6$.

Table 8 Estimated MSE for different estimators at p = 9 and $\phi =2$.

Table 9 Estimated MSE for different estimators at p = 9 and $\phi =4$.

Table 10 Estimated MSE for different estimators at p = 9 and $\phi =6$.

Fig. 1

MSE of different estimators under various factors in the simulation study.

Simulation results

Tables 2, 3, 4, 5, 6, 7, 8, 9 and 10 introduced the simulated MSE values for the MLE, PIGRRE, and PIGGRE, based on the results of the simulation analysis:

• 1. An increase in the degree of multicollinearity ($\rho$), the dispersion parameter ($\phi$), or the number of explanatory variables ($p$) results in higher MSE values for all estimators, indicating a degradation in performance under these conditions.

• 2. The MSE values decrease as the sample size ($n$) increases, emphasizing the role of larger sample sizes in improving estimator reliability and precision.

• 3. The PIGRRE demonstrates superior performance compared to the MLE across all scenarios, consistently yielding lower MSE values irrespective of variations in $\phi$, $\rho$, $p$, and $n$.

• 4. The PIGGRE outperforms the PIGRRE, achieving the lowest MSE values among the evaluated estimators across all parameters irrespective of variations in $\phi$, $\rho$, $p$, and $n$.

• 5. The results show that the proposed PIGGRE estimator works efficiently, especially when the dispersion parameter ($\phi$) is high and the explanatory variables are highly correlated. This indicates that the estimator is reliable even in complex situations where traditional methods may struggle.

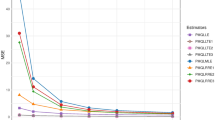
• 6. Figures 1a–d show the simulation results by presenting the mean squared errors (MSEs) for different estimators under various settings, such as different sample sizes ($n$), levels of multicollinearity ($\rho ^2$), numbers of predictors ($p$), and values of the dispersion parameter ($\phi$). The results clearly show that PIGGRE performs better than both PIGRRE and MLE by consistently achieving lower MSE values. This improvement is especially clear when using the ridge parameters $\hat{K}_1$ and $\hat{K}_4$, which help reduce estimation errors and improve the reliability of the method.

Applications

In this section, we compare our proposed estimator with existing estimators such as MLE and PIGRRE, using two real-world datasets to demonstrate the advantages and superiority of the proposed estimator and highlight its effectiveness in improving estimation accuracy, especially in the presence of multicollinearity.

Number of equations and citations

The performance of the proposed estimator is assessed using a real dataset from Fawcett and Higginson⁴⁸, which is available in R through the AER package under the name EquationCitations. This data investigates the relationship between the number of citations received by evolutionary biology publications and the number of equations per page in the cited papers. This dataset comprises 649 observations, with the response variable representing the total number of equations (y). The explanatory variables include the total number of citations received ($x_1$), the number of equations present in appendix ($x_2$), the number of equations present in the main text ($x_3$), the number of citations made by the authors of the paper ($x_4$), the number of citations from theoretical papers ($x_5$), and the number of citations from non-theoretical papers ($x_6$).

The response variable in this study is count data, which requires specialized models. We compared the PRM, NBRM, COMPRM, and PIGRM to identify the best fit for the relationship between the response variable and explanatory variables in the number of equations and citation data. The selection criteria were the log-likelihood (LL), the Akaike Information Criterion (AIC), and the Bayesian Information Criterion (BIC), where a lower AIC, BIC, and higher LL indicate a better model. Results in Table 11 show that the PIGRM outperforms the other models with the lowest AIC, BIC, and highest LL.

With six explanatory variables in the dataset, the eigenvalues of the matrix $X^T \hat{W} X$ are: 1754069.240, 76832.270, 59927.316, 17295.812, 4131.207, 129.039, and 63.036. Multicollinearity was assessed using the condition number (CN) and variance inflation factors (VIFs). The CN, defined as $\text {CN} = \sqrt{\frac{\lambda _{\max }}{\lambda _{\min }}},$ where $\lambda _{\max }$ and $\lambda _{\min }$ are the largest and smallest eigenvalues of $X^T\hat{W} X$, respectively, was calculated to be 166.81, indicating a high level of multicollinearity. In addition, the VIF for each explanatory variable, computed as: $\text {VIF}_j = \frac{1}{1 - R_j^2},$ where $R_j^2$ is the coefficient of determination from regressing the $j$-th variable on all other predictors, yielded values of 1201.15, 1.68, 1.57, 23.77, 255.37, and 463.52. These values confirm the presence of severe multicollinearity among several variables. This is further supported by the correlation matrix shown in Fig. 2, emphasizing the need for caution in interpreting parameter estimates and potentially adopting bias-reducing methods to improve model stability.

Fig. 2

Correlation matrix for explanatory variables in the number of equations and citations data.

Table 11 Comparison of model performance for the number of equations and citation data.

Table 12 Coefficients and MSEs of estimators in the number of equations and citation data.

The coefficients of the PIGRM are estimated using three methods: MLE, PIGRRE, and PIGGRE, as specified in Eqs. 8, 11, and 17, respectively. The corresponding MSEs for each estimator are computed using Eqs. 10, 16, and 21. The results indicate that MLE performs less favorably than PIGRRE across all ridge parameter estimators, as reflected by its higher MSE. Conversely, PIGGRE demonstrates improved performance compared to both MLE and PIGRRE, yielding lower MSE values. A comparison of the ridge parameter estimators used in PIGGRE, presented in Table 12, highlights that $\hat{K}_1$ through $\hat{K}_3$ outperform other existing estimators. These findings are consistent with the results observed in the simulation studies, supporting the efficacy of the proposed estimators.

Australian institute of sports

To empirically evaluate the proposed estimator’s performance, we utilize the Australian Institute of Sport dataset, as presented by Telford and Cunningham⁴⁹ and is available in the R software through the GLMsData package under the name AIS. This dataset encompasses physical and blood measurements of high-performance athletes from various sports, including basketball (BBall), field events, gymnastics (Gym), netball, rowing, swimming (Swim), track events over 400 meters (T400m), tennis, track sprints (TPSprnt), and water polo (WPolo). The dataset contains information for 202 athletes, comprising 102 males and 100 females. The response variable in this dataset is the plasma ferritin (in ng per decilitre) (y). In addition, the dataset includes 10 explanatory variables lean body mass (in kg) ($x_1$), height (in cm) ($x_2$), weight (in kg) ($x_3$), body mass index (in $\textrm{kg}/\textrm{m}^{2}$) ($x_4$), the sum of skin folds ($x_5$), percentage body fat ($x_6$), red blood cell count (in $10^{12}$ per liter) ($x_7$), white blood cell count (in $10^{12}$ per liter) ($x_8$), hematocrit (in percent) ($x_9$), and hemoglobin concentration (in grams per deciliter) ($x_{10}$)

The dependent variable in this analysis is count data, which necessitates appropriate models. To determine the best model for the relationship between the dependent variable and the explanatory variables in the context of the number of equations and citation data, we compared four models: the PRM, NBRM, COMPRM, and PIGRM. We evaluated the models based on three criteria: LL, AIC, and BIC. A lower AIC, BIC, and higher LL indicate a more suitable model. As shown in Table 13, the PIGRM provides the best fit, with the lowest AIC and BIC values and the highest LL.

The dataset includes ten explanatory variables, the eigenvalues of the matrix $X^T \hat{W} X$ are: 30689803.431, 702460.991, 114401.412, 8572.263, 1996.989, 1704.116, 1019.529, 123.657, 94.052, 19.553, and 0.037. Multicollinearity was assessed using the CN and VIFs. The observed CN value of 28699.25, alongside VIF values of 442.07, 56.21, 516.80, 79.96, 22.75, 7.27, 1.09, 15.95, 12.23, and 62.66, indicates substantial multicollinearity among the variables. These findings are further corroborated by the correlation matrix shown in Fig. 3. Such evidence highlights the necessity for careful interpretation and potential adjustments in subsequent analyses to mitigate the impact of multicollinearity.

Fig. 3

Correlation matrix for explanatory variables in the Australian Institute of Sports data.

Table 13 Comparison of model performance for the Australian Institute of Sports data.

Table 14 Coefficients and MSEs of Estimators for the Australian Institute of Sports Data.

The coefficients for the PIGRM were estimated using three methods: MLE, PIGRRE, and PIGGRE, as outlined in equations 8, 11, and 17. The corresponding MSEs were calculated based on equations 10, 16, and 21. The results indicate that MLE performs less effectively than PIGRRE, as reflected by its higher MSE values. In contrast, PIGGRE shows superior performance, with consistently lower MSEs compared to both MLE and PIGRRE. Additionally, a comparison of the ridge parameter estimators in PIGGRE, shown in Table 14, highlights that estimators $\hat{K}_1$ and $\hat{K}_4$ outperform $\hat{K}_2$, $\hat{K}_3$, and $\hat{K}_5$ in PIGGRE. This can be attributed to the nature of the data, including the degree of multicollinearity among the predictors, the level of dispersion, and the sample size. These factors collectively influence the performance of the estimators and the sensitivity of each to the choice of the biasing parameter K. Overall, the PIGGRE estimator demonstrates superior performance, which is consistent with both the simulation results and the findings of the first application.

Conclusion

The PIGRM is one of the most widely used models for analyzing overdispersed count data. In the PIGRM, MLE is used to estimate regression coefficients. However, when the explanatory variables are highly correlated, this leads to multicollinearity, a problem that reduces the reliability of the regression coefficients and inflates the variance. To address this, we introduced in this paper a new biased estimation method called the PIGGRE, which uses shrinkage parameter techniques to reduce the effect of multicollinearity. We evaluated the performance of the proposed PIGGRE through simulation studies with different scenarios, such as sample sizes, levels of dispersion, multicollinearity, and number of predictors. The results showed that PIGGRE outperformed both MLE and PIGRRE. In particular, using shrinkage parameters $K_1$ and $K_3$ resulted in the lowest MSE, demonstrating higher accuracy. To confirm the simulation study results, we also applied the proposed PIGGRE to two real datasets. The results of these applications provided significant support and confirmation of the simulation results, demonstrating the advantages of using PIGGRE. Therefore, we recommend using PIGGRE with values of $K_1$ and $K_3$ to address multicollinearity in PIGRM. This approach could be extended in future work to other models, such as the zero-inflated negative binomial model, the zero-inflated Poisson model, and the Conway-Maxwell-Poisson model. Although PIGGRE outperforms in the context of PIGRM under multicollinearity, there is one important limitation worth mentioning. The estimator’s performance depends mainly on the K values, which balance bias and variance, and suboptimal K values can affect the estimator’s performance, making the estimator sensitive to the choice of parameters. Further improvements could be achieved by incorporating accurate estimation techniques, such as those proposed by Omara⁵⁰ and Lukman et al.⁵¹.