Novel concept of linguistic fractional fuzzy information for effective water filtration decision-making problem based on WASPAS method

Abstract

The main purpose of water filtration techniques is to eliminate poisonous chemicals and microbes from sources of water in order to provide clear and safe water. Water purification is necessary for supplying the vital need for clean water to consume in a variety of areas, which involves the biological, medication, and health care industries. Despite the demands of manufacturing, its importance affects a country’s stability and success. Experts throughout the globe are thus investigating a number of promising methods to expand and preserve water supply. Finding the optimal water filtration technique for optimizing the health of humans requires the implementation of multi-criteria decision-making (MCDM) techniques. Therefore, the current manuscript addresses the task of identifying the best water filtration technique by introducing a novel method called the "LFF-WASPAS technique," relying on the implementation of linguistic fractional fuzzy set (LFFS). An LFFS serves as a generalization of all linguistic fuzzy sets. For this reason, at first, we address the linguistic fractional fuzzy sets along with their weighted averaging and weighted geometric aggregation operators (AoPs), in addition to various basic properties of all of these AoPs. Finding the weight data used in decision-making situations becomes more challenging whenever the experts’ weights are missing. To address this, we present an entropy measure and an Analytic Hieratical Process (AHP). Additionally, we successfully use the freshly described operators and the suggested strategy to choose the most efficient approach for water filtration on a commercial scale. Finally, we investigate the sensitive hypothesis over the suggested method in relation to water filtration techniques. Additionally, by contrasting the suggested decision-making method with those that already are available, we assess their effectiveness and reliability.

Introduction

Multi-criteria decision making (MCDM)^1,2,3 is a crucial task when dealing with modern decision-making circumstances. Due to the difficulty of daily-life circumstances, the unclear nature of the standards, and the personal nature of each person, experts usually need to contribute evaluation information concerning multiple types of requirements parameters.

A brief overview of fuzzy sets along with its extensions

After Zadeh initially presented the concept of fuzzy set (FS), many of academics have been investigating it⁴. All the FSs possess a truth grade (TG). By adding in the falsity grade (FG) upon the fundamental foundation of FS, Atanassov^5,6,7 created the intuitionistic fuzzy set (IFS). The IFS is acknowledged as a useful technique for handling ambiguity in circumstances requiring decision-making and is a magnificent expansion of FS. Consequently, Xu and Yager⁸ created several weighted geometric AoPs for IFS and extended these to selection complications, whereas Xu⁹ offered some weighted average AoPs. He et al.^10,11 used the geometric aggregated and average operations for IFS to solve decision-making challenges after conducting an extensive evaluation of these. Nevertheless, IFS is unable to address situations when experts indicate an attraction for items in which the total is larger than 1. In order to further develop the framework of IFS, Abdullah et al.¹² established a fractional fuzzy set (FFS) that includes two grades, TG and FG. FFS is a helpful instrument that acts as a generalization of all FSs and effectively solves difficulties, such as decision-making uncertainty. Subsequently, the FFS was expanded by Qiyas et al.¹³ to orthotriple fuzzy rough sets, which effectively manage uncertainty and unreliable information during decision-making situations. Although these investigations are closely related to the q-rung orthopair fuzzy set (q-ROFS)¹⁴, Abdullah et al.¹² additionally extended FFS to a rough set. FFS is a potent generalization that offers more adaptability in practical situations.

In decision-making problems, experts frequently wobble among multiple evaluation standards, which complicates the process. The information assessed during the FS and IFS, along with the FFS, is numerically and quantitatively expressed. In daily life, nevertheless, the majority of confusing or unclear knowledge that the experts evaluate includes descriptive qualities, such as "very good," "good," "normal," "bad," "very bad," and "extremely bad," along with many others. Such circumstances can be safely and effectively handled by using linguistic term sets (LTS). In consideration of the aforementioned, Zadeh¹⁵ created the idea of LTS and looked into a number of different kinds^16,17,18. Chen et al.¹⁹ created a decision-making method for resolving practical issues using an LTS. Under the format of a linguistic parameter, Zhang²⁰ suggested a linguistic intuitionistic fuzzy set (LIFS) made up of TG and FG and also covered how to apply it. In order to solve decision-making challenges, Kumar et al.²¹ created a few weighted average aggregation operations for LIFS. After introducing the linguistic Pythagorean fuzzy set (LPFS), Peng and Yang²² developed the weighted average and weighted geometric operators according to LPFS, both of which are capable of transmitting data that is more accurate compared to LIFS. The linguistic q-rung orthopair fuzzy set (Lq-ROFS) was proposed by Lin et al.²³. The total of the qth exponents of TG and FG in the Lq-ROFS does not exceed the qth exponent of the order of LTS. In order to choose the optimal hybrid electronic system, Abdullah et al.²⁴ created a double hierarchy linguistic neural network employing the Hamacher operational rules.

A brief overview of multi-criteria decision-making methods

A number of scientific techniques are implemented in the framework of MCDM^25,26. Information that consists of both quality and quantity may be addressed by these methods, as well as their functions, which are typically simple to employ. It is typically employed to resolve MCDM complications. Furthermore, widely recognized MCDM techniques like EDAS²⁷, GRA²⁸, TOPSIS²⁹, BMW³⁰, SWARA³¹, MOORA³², and numerous others may be employed for the purpose of handling information that consists of quantity and quality. Numerous academics have employed innovative approaches to significantly impact decision-making process. Zavadskas et al.³³ introduced an innovative effectiveness theoretical technique called weighted aggregated sum product assessment (WASPAS), which combines the weighted sum method (WSM) and weighted product method (WPM) to determine and evaluate the options with the highest level of accuracy. For example, Zavadskas et al.³⁴ broadened the WASPAS technique to feed MCDM challenges in interval-valued intuitionistic fuzzy data. Turskis et al.³⁵ provided a mixture of WASPAS along with AHP (Analytic Hierarchy Process) within fuzzy surroundings and employed it to choose the most effective purchasing products place constructing location. This technique has been successfully expanded for numerous decision-making challenges within various fuzzy concepts. The WASPAS approach for MCDM issues utilizing operations of interval type-2 fuzzy sets was created by Ghorabaee et al.³⁶. Sequentially Weight Assessment Ratio Analysis (SWARA) and the WASPAS and fuzzy expansions that have been addressed recently are two novel MCDM efficiency determination procedures. Mardani et al.³⁷ provided a comprehensive evaluation of methodology as well as implications with current fuzzy advancements. Three innovative approaches—the Multi-criterion Border Approximate area Comparisons (MABAC), WASPAS, and COPRAS methods—were put forth by Peng and Dai³⁸ to address the hesitant fuzzy soft decision-making. Mishra et al.³⁹ compared the effectiveness of telecommunication service companies in the Madhya Pradesh region of India using the intuitionistic fuzzy WASPAS approach. The precision of assessment outcomes in the MCDM procedure depends on the criteria weights calculation; as a consequence, multiple researchers have created a variety of weight-assessing techniques (Xu⁴⁰, Xu and Chen⁴¹). A variety of MCDM techniques, including ELECTRE⁴², TODIM⁴³, VIKOR⁴⁴, and PROMETHEE⁴⁵, along with numerous others, were developed and generalized according to an undetermined selection environment with various weight-assessment techniques. At the same time, FSs and their improvements have received greater interest in the domain of decision-making due to growing difficulty and duration constraints.

A brief overview of the water filtration techniques

The primary component within the hydrosphere of the globe and the essential fluids of all known organisms is water⁴⁶. But as technological developments and industry advanced, pesticides along with other hazardous materials attacked the water quality, raising the chance of several diseases including cancers. While certain chemicals might be dangerous to people, they may additionally have other bad impacts. On rare occasions, they can impact the water’s flavor by giving it something metallic or a similar undesirable flavor. Consuming water with chlorine may result in serious consequences for your health. By filtering the water, these impurities may be removed, decreasing the chance of getting sick following consumption^47,48,49. The majority of companies release garbage into neighboring streams, drainage systems, and rivers with no effective treatment, which pollutes the water since it includes hazardous chemicals⁵⁰. The development of crops can be negatively impacted by harmful substances and minerals that are absorbed by the earth and can accumulate in the roots⁵¹. In order to remove dangerous inorganic and organic matter as well as bacterial contaminants from water, particularly when the primary objective is to provide water for consumption, water filtration is an essential process. The requirement for safe, transferable water in a range of sectors, including chemicals, pharmaceuticals, and biomedical companies, is additionally fulfilled by water filtration. The quantity of impurities, including germs, viruses, fungus, suspended matter, worms, and algal growth, decreases considerably throughout the purifying procedure. Among the many positive health effects of drinking pure water are improved elimination, increased hydration, and quicker metabolism, reduced inflammation of the epidermis and forehead, stronger hair, and the loss of pollutants. Since there are several approaches of water filtration, therefore, it’s critical to describe a system for selecting the most effective one. For more detail regarding water filtration techniques, see Refs.^52,53.

Motivation of the study

As per the aforementioned overview, numerous structures that are helpful in solving problems related to decision-making have recently been created. As far as we are aware, there isn’t a concept or usage for the combined structures of FFS plus LTS for assessing decision-making difficulties. Additionally, all FSs are particular types of FFS. Motivated by these investigations, we are interested in expanding the LTS along with a FFS to create an enhanced structure known as linguistic fractional fuzzy set (LFFS) that can deal with challenges in decision-making environments.

The following is the main inspiration for this research.

• (a) To describe a novel notion of LFFS that offer more adaptability for using in real-world problems. It can cope with a lot of linguistic knowledge and give experts additional room in TG and FG. The idea of LFFS is an extension of the existing FFS as well as of various LTS. It can be seen graphically in Fig. 1.

• (b) To describe a series of AoPs for combining experts information in the context of LFFS, including linguistic fractional fuzzy weighted averaging (LFFWA), linguistic fractional fuzzy ordered weighted averaging (LFFOWA), linguistic fractional fuzzy weighted geometric (LFFWG), and linguistic fractional fuzzy ordered weighted geometric (LFFOWG). Additionally, several important characteristics of these AoPs are also established.

• (c) The framework of decision-making gets challenging whenever the weight data for the criteria as well as the expert are unknown. To handle this problem, we use entropy measure along with Analytic Hierarchy Process (AHP) to calculate the unknown weights of the experts and criteria, respectively.

• (d) This article focuses on creating a novel LFF-WASPAS decision-making approach for assessing alternatives within the LFFS environment because, as research concentrates on decision-making challenges, choosing a water filtration approach is a crucial field of study that may result in serious bad impacts on the wellness of humans.

Fig.1

Relation of LFFS with various linguistic fuzzy set extensions.

Contribution

In this manuscript, we integrated the ideas of FFS and LTS and employed the WASPAS method for selecting the best water filtration technique. The WASPAS method is a unique model for the visualization of linguistic amounts within the combined makeup of LTS and FFS, which helps in overcoming the shortcomings of the existing structures. It combines two distinct models: the weighted product model (WPM) and the weighted sum model (WSM). Because of this, the WASPAS approach can be extremely beneficial, and more significantly, its computational steps are very easy to understand.

The following summarizes the main development and contributions of this article:

• (a) The present research aims to develop a technique in the context of linguistic fractional fuzzy information, improving on the conventional WASPAS method. The LFF-WASPAS approach allows experts to communicate the high-grade selections in linguistic terms rather than quantitative numbers.

• (b) We also create a few AoPs that consist of weighted averaging along with weighted geometric operators and use these individuals for simulating LFFS decision-making challenges.

• (c) We use the suggested method to evaluate water filtration methods and determine the most productive water filtration technique.

• (d) To highlight the consistency of our proposed work, we perform a comparative study of the prescribed technique with the existing techniques in the literature and sensitive study to verify and illustrate the success of the provided technique.

Structure of the manuscript

This manuscript is organized in the following manner: Basic ideas about FS, IFS LTS, and FFS are presented in Section "Basic Concepts". The fresh idea of linguistic fractional fuzzy set (LFFS) is covered in Section "Construction of a Novel Linguistic Fractional Fuzzy Set", while Section "Operating rules of LFFVs" discusses operating rules that may assist in the decision-making procedure. In section "Linguistic Fractional Fuzzy aggregation operators", we discuss a series of AoPs that consist of linguistic fractional fuzzy weighted averaging (LFFWA), linguistic fractional fuzzy ordered weighted averaging (LFFOWA), linguistic fractional fuzzy weighted geometric (LFFWG), and linguistic fractional fuzzy ordered weighted geometric (LFFOWG) along with several of these important characteristics. A step-by-step explanation of the LFF-WASPAS approach within a linguistic fractional fuzzy environment is provided in Section "Improved WASPAS method under LFF information". The implementation of the suggested technique is explained in Section "Case study". The sensitivity analysis for our suggested approach based on various parameters is covered in Section "Sensitivity analysis based on the parameters and on decision-making". In order to demonstrate the effectiveness of our suggested approach, we contrast our technique with existing methods and explain the results and discussions in section "Result and discussion". Section "Conclusion" concludes the study and discusses future work directions. Acronyms and abbreviations are described in Table 1 and Table 2, respectively, with its meanings.

Table 1 The acronyms that are employed in this article.

Table 2 Symbols and its meanings.

Basic concepts

In this section, we discuss the basic concepts such as FS, IFS, FFS, and LTS that are going to be implemented afterwards.

Definition 1⁴

Assume that represents a fixed set. For every $\kappa \in \mathcal{U}$, a FS $A$ is represented as;

$$A=\left\{\langle \kappa , {\mu }_{A}\left(\kappa \right)\rangle | \kappa \in \mathcal{U}\right\};$$

in which ${\mu }_{A}\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ represents the TG which lies in the closed interval of $\left[0, 1\right]$.

Definition 2⁵

Assume that represents a fixed set. For every $\kappa \in \mathcal{U}$, the IFS $I$ is represented as;

$${\rm I}=\left\{\langle \kappa , {\mu }_{I}\left(\kappa \right) ,{\nu }_{\rm I}\left(\kappa \right)\rangle | \kappa \in \mathcal{U}\right\};$$

in which ${\mu }_{I}\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ represents the TG and ${\nu }_{\rm I}\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ represents the FG, satisfying the constraint $0\le {\mu }_{I}\left(\kappa \right)+{\nu }_{\rm I}\left(\kappa \right)\le 1$ for every $\kappa \in \mathcal{U}$.

Definition 3¹²

Assume that represents a fixed set. For every $\kappa \in \mathcal{U}$, the FFS $F$ is represented as;

$$F=\left\{\langle \kappa , {\mu }_{F}\left(\kappa \right) ,{\nu }_{F}\left(\kappa \right)\rangle | \kappa \in \mathcal{U}\right\};$$

in which ${\mu }_{F}\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ represents TG and ${\nu }_{F}\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ represents FG, satisfying the constraint $0\le {\mu }_{F}^{f}\left(\kappa \right)+{\nu }_{F}^{f}\left(\kappa \right)\le 1$ for every $\kappa \in \mathcal{U}$ and $f=p/q$ is any fractional element greater than or equal to 1.The grade of indeterminacy of FFS is mathematically described as follows;

$${\pi }_{F}={\left(1-{\left({\mu }_{F}\left(\kappa \right)\right)}^{f}-{\left({\nu }_{F}\left(\kappa \right)\right)}^{f}\right)}^{1/f}.$$

Definition 4¹⁵

Assume that $\mathcal{S}\ne \phi ,$ represents a fixed set with odd order, then LTS is mathematically represented as;

$$\mathcal{S}=\left\{{\mathcal{S}}_{a}|a=0, 1, 2, \dots ,\tau \right\};$$

where ${\mathcal{S}}_{a}$ represent probable linguistic term of the defined set. And assume that $\mathcal{S}$ be a non-void LTS of odd order, then the shape $\mathcal{S}=\left\{{\mathcal{S}}_{\beta }|{ \mathcal{S}}_{0}\le {\mathcal{S}}_{a}\le {\mathcal{S}}_{\tau } , a\in \left[0, \tau \right]\right\}$ is widened continuous linguistic term set in $\mathcal{S}$. ${\mathcal{S}}_{\text{a}}$ Implies to the fundamental linguistic if ${\mathcal{S}}_{a}\in \mathcal{S}$ in other case ${\mathcal{S}}_{a}$ implies to the virtual collection.

Construction of a novel linguistic fractional fuzzy set

In this section, we introduce a new idea that combines the concepts of LTS and FFS to effectively address inconsistencies in decision-making problems.

Definition 5

Assume that $\mathcal{S}=\left\{{\mathcal{S}}_{\beta }| \beta \in \left[0, \tau \right]\right\}$, and ${\mathcal{S}}^{\left[0, \tau \right]}=\left\{{\mathcal{S}}_{\beta }|{ \mathcal{S}}_{0}\le {\mathcal{S}}_{a}\le {\mathcal{S}}_{\tau } , a\in \left[0, \tau \right]\right\}$ represents the odd order LTS in $\mathcal{S}$. Then the LFFS is mathematically defined as follows;

$${\mathcal{L}}_{F}=\left\{\kappa , \left({\mathcal{S}}_{\mu }\left(\kappa \right),{\mathcal{S}}_{\nu }\left(\kappa \right)\right)|\kappa \in \mathcal{U}\right\};$$

in which ${\mathcal{S}}_{\mu }\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ and ${\mathcal{S}}_{\nu }\left(\kappa \right) : \mathcal{U}\to \left[0, 1\right]$ respectively, show TG and FG with the constraint that $0\le {\left(\frac{{\mathcal{S}}_{\mu }\left(\kappa \right)}{\tau }\right)}^{f}+{\left(\frac{{\mathcal{S}}_{\nu }\left(\kappa \right)}{\tau }\right)}^{f}\le 1$ or $0\le {\left(\mu \left(\kappa \right)\right)}^{f}+{\left(\nu \left(\kappa \right)\right)}^{f}\le \tau$ such with $\left(f=p/q\right)$ is any fractional element greater than or equal to 1. For various values of $\text{f}$ , we get different kinds of FSs.

• (a) For $f=p/q\ge 1$, and $p=q$, the LFFS shrinks to LIFS.

• (b) For $f=p/q\ge 1$, and $p=2q$, the LFFS shrinks to LPFS.

• (c) For $f=p/q\ge 1$, and $p=3q$, the LFFS shrinks to Lq-ROFS.

In simple manner, ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right)$ $\left(i=1, 2, \dots ,n\right)$ is called the linguistic fractional fuzzy value (LFFV).

Definition 6

Assume that ${\mathcal{L}}_{F}=\left({\mathcal{S}}_{\mu }, {\mathcal{S}}_{\nu }\right)$ is a LFFV. Then the grade of indeterminacy of LFFS can be described as follows;

$$\pi \left({\mathcal{L}}_{F}\right)={\mathcal{S}}_{\sqrt[ f]{\left({\tau }^{f}-{\mu }^{f}-{\nu }^{f}\right)}}.$$

(1)

We may also establish the rating function $\text{Sc}$ and the accuracy function $\text{Acc}$ as shown below.

Definition 7

Assume that ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right)$ $\left(i=1, 2, \dots ,n\right)$ is a collection of LFFVs, the score and accuracy functions are defined as follows:

$$Sc={\left(\frac{{\mu }_{i}}{\tau }\right)}^{f}-{\left(\frac{{\nu }_{i}}{\tau }\right)}^{f}\in \left[-1, 1\right];$$

(2)

$$Acc={\left(\frac{{\mu }_{i}}{\tau }\right)}^{f}+{\left(\frac{{\nu }_{i}}{\tau }\right)}^{f}\in \left[0, 1\right].$$

(3)

Based on these two equations, we can propose the following comparative technique for each pair of LFFVs.

Definition 8

Assume that ${\mathcal{L}}_{{F}_{1}}=\left({\mathcal{S}}_{{\mu }_{1}}, {\mathcal{S}}_{{\nu }_{1}}\right), {\mathcal{L}}_{{F}_{2}}=\left({\mathcal{S}}_{{\mu }_{2}}, {\mathcal{S}}_{{\nu }_{2}}\right)\in {\mathcal{S}}_{\left[0, \tau \right]}$ are two LFFVs, then.

• (1) From $Sc\left({\mathcal{L}}_{{F}_{1}}\right)\succ Sc\left({\mathcal{L}}_{{F}_{2}}\right)$, we mean that ${\mathcal{L}}_{{F}_{1}}\succ {\mathcal{L}}_{{F}_{2}}$.

• (2) From $Sc\left({\mathcal{L}}_{{F}_{1}}\right)\prec Sc\left({\mathcal{L}}_{{F}_{2}}\right)$, we mean that ${\mathcal{L}}_{{F}_{1}}\prec {\mathcal{L}}_{{F}_{2}}$.

• (3) When $Sc\left({\mathcal{L}}_{{F}_{1}}\right)=Sc\left({\mathcal{L}}_{{F}_{2}}\right)$, then

Whenever $Acc\left({\mathcal{L}}_{{F}_{1}}\right)\succ Acc\left({\mathcal{L}}_{{F}_{1}}\right)$, then ${\mathcal{L}}_{{F}_{1}}\succ {\mathcal{L}}_{{F}_{2}}$.

Whenever $Acc\left({\mathcal{L}}_{{F}_{1}}\right)=Acc\left({\mathcal{L}}_{{F}_{2}}\right)$, then ${\mathcal{L}}_{{F}_{1}}={\mathcal{L}}_{{F}_{2}}$ means they are same.

Definition 9

Assume that ${\mathcal{L}}_{{F}_{1}}=\left({\mathcal{S}}_{{\mu }_{1}}, {\mathcal{S}}_{{\nu }_{1}}\right), {\mathcal{L}}_{{F}_{2}}=\left({\mathcal{S}}_{{\mu }_{2}}, {\mathcal{S}}_{{\nu }_{2}}\right)\in {\mathcal{S}}_{\left[0, \tau \right]}$ are two LFFVs, then we have.

• (1) ${\mathcal{L}}_{{F}_{1}}={\mathcal{L}}_{{F}_{2}}$ if and only if ${\mathcal{S}}_{{\mu }_{1}}={\mathcal{S}}_{{\mu }_{2}}$ and ${\mathcal{S}}_{{\nu }_{1}}={\mathcal{S}}_{{\nu }_{2}}$;

• (2) ${\mathcal{L}}_{{F}_{1}}^{C}=\left({\mathcal{S}}_{{\nu }_{1}}, {\mathcal{S}}_{{\mu }_{1}}\right)$;

• (3) Union; ${\mathcal{L}}_{{F}_{1}}\cup {\mathcal{L}}_{{F}_{2}}=\left\{max\left({\mathcal{S}}_{{\mu }_{1}}, {\mathcal{S}}_{{\mu }_{2}}\right), min\left({\mathcal{S}}_{{\nu }_{1}}, {\mathcal{S}}_{{\nu }_{2}}\right)\right\}$;

• (4) Intersection; ${\mathcal{L}}_{{F}_{1}}\cap {\mathcal{L}}_{{F}_{2}}=\left\{min\left({\mathcal{S}}_{{\mu }_{1}}, {\mathcal{S}}_{{\mu }_{2}}\right), max\left({\mathcal{S}}_{{\nu }_{1}}, {\mathcal{S}}_{{\nu }_{2}}\right)\right\}$;

• (5) ${\mathcal{L}}_{{F}_{1}}<{\mathcal{L}}_{{F}_{2}}$ if and only if ${\mathcal{S}}_{{\mu }_{1}}<{\mathcal{S}}_{{\mu }_{2}}$ and ${\mathcal{S}}_{{\nu }_{1}}>{\mathcal{S}}_{{\nu }_{2}}$.

Definition 10

Assume that ${\mathcal{L}}_{{F}_{1}}=\left({\mathcal{S}}_{{\mu }_{1}}, {\mathcal{S}}_{{\nu }_{1}}\right), {\mathcal{L}}_{{F}_{2}}=\left({\mathcal{S}}_{{\mu }_{2}}, {\mathcal{S}}_{{\nu }_{2}}\right)\in {\mathcal{S}}_{\left[0, \tau \right]}$ are two LFFVs with $f\ge 1$. The standardized Hamming distance ${\mathcal{d}}_{\mathcal{H}\mathcal{d}}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}\right)$ for ${\mathcal{L}}_{{F}_{1}}$ and ${\mathcal{L}}_{{F}_{2}}$ can be described as follows;

$${\mathcal{d}}_{\mathcal{H}\mathcal{d}}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}\right)=\frac{\left|{\mu }_{1}^{f}-{\mu }_{2}^{f}\right|+\left|{\nu }_{1}^{f}-{\nu }_{2}^{f}\right|+\left|{\pi }_{1}^{f}-{\pi }_{2}^{f}\right|}{2{\tau }^{f}};$$

(4)

Operating rules of LFFVs

We may suggest some operating laws for LFFVs centered on existing LIFVs and LPFVs.

Definition 11

Assume that ${\mathcal{L}}_{{F}_{1}}=\left({\mathcal{S}}_{{\mu }_{1}}, {\mathcal{S}}_{{\nu }_{1}}\right), {\mathcal{L}}_{{\text{F}}_{2}}=\left({\mathcal{S}}_{{\upmu }_{2}}, {\mathcal{S}}_{{\upnu }_{2}}\right)\in {\mathcal{S}}_{\left[0,\uptau \right]}$ are two LFFVs with $f\ge 1, \aleph >0$. Then the operating laws for LFFVs can be described as follows;

$${\mathcal{L}}_{{F}_{1}}\oplus {\mathcal{L}}_{{F}_{2}}=\left({\mathcal{S}}_{\tau {\left({\left(\frac{{\mu }_{1}}{\tau }\right)}^{f}+{\left(\frac{{\mu }_{2}}{\tau }\right)}^{f}-{\left(\frac{{\mu }_{1}}{\tau }\right)}^{f}\cdot {\left(\frac{{\mu }_{2}}{\tau }\right)}^{f}\right)}^{1/f}} , {\mathcal{S}}_{\tau \left(\frac{{\nu }_{1}{\nu }_{2}}{{\tau }^{2}}\right)}\right).$$

(5)

$${\mathcal{L}}_{{F}_{1}}\otimes {\mathcal{L}}_{{F}_{2}}=\left({\mathcal{S}}_{\tau \left(\frac{{\mu }_{1}{\mu }_{2}}{{\tau }^{2}}\right)} , {\mathcal{S}}_{\tau {\left({\left(\frac{{\nu }_{1}}{\tau }\right)}^{f}+{\left(\frac{{\nu }_{2}}{\tau }\right)}^{f}-{\left(\frac{{\nu }_{1}}{\tau }\right)}^{f}\cdot {\left(\frac{{\nu }_{2}}{\tau }\right)}^{f}\right)}^{1/f}}\right)$$

(6)

$$\aleph \cdot {\mathcal{L}}_{{F}_{1}}=\left({\mathcal{S}}_{\tau {\left(1-{\left(1-{\left(\frac{{\mu }_{1}}{\tau }\right)}^{f}\right)}^{\aleph }\right)}^{1/f}} , {\mathcal{S}}_{\tau {\left(\frac{{\nu }_{1}}{\tau }\right)}^{\aleph }}\right)$$

(7)

$${\mathcal{L}}_{{F}_{1}}^{\aleph }=\left({\mathcal{S}}_{\tau {\left(\frac{{\mu }_{1}}{\tau }\right)}^{\aleph }} , {\mathcal{S}}_{\tau {\left(1-{\left(1-{\left(\frac{{\nu }_{1}}{\tau }\right)}^{f}\right)}^{\aleph }\right)}^{1/f}}\right)$$

(8)

Linguistic fractional fuzzy aggregation operators

In this part, we constructed a series of linguistic fractional fuzzy AoPs for various LFFVs. Let Ϻ represent the entire set of all LFFVs.

Linguistic fractional fuzzy weighted averaging operators

Definition 12

Assume that ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ is a collection of LFFVs. The LFFWA operator is a function of dimension n $\text{LFFWA }: {\text{M}}^{n}\to \text{M},$ such that

$$\text{LFFWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\omega }_{1}{\mathcal{L}}_{{F}_{1}}\oplus {\omega }_{2}{\mathcal{L}}_{{F}_{2}}\oplus \dots {\omega }_{n}{\mathcal{L}}_{{F}_{n}}$$

(9)

where $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ denotes the weight vector of ${\mathcal{L}}_{{F}_{i}}\left(i=1, 2, \dots ,n\right)$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$.

Theorem 1

For a combination of LFFVs ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$, the fused value achieved by utilizing LFFWA operator, as described in Eq. (9) is also a LFFV and is described as follows;

$$\text{LFFWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)=\left({\mathcal{S}}_{\tau {\left(1-\prod_{i=1}^{n}{\left(1-{\left(\frac{{\mu }_{i}}{\tau }\right)}^{f}\right)}^{{\omega }_{i}}\right)}^{1/f}} , {\mathcal{S}}_{\tau {\prod_{i=1}^{n}\left(\frac{{\nu }_{i}}{\tau }\right)}^{{\omega }_{i}}}\right)$$

(10)

Proof

By using mathematical induction principle, we can prove it easily.

By using Eq. (10), we achieve certain important characteristics of the LFFWA operator.

Theorem 2

Assume that ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ be a combination of LFFVs along with its weight vector $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$. The LFFWA operator fulfills the below characteristics as;

(1) (Characteristic of Idempotency). Assume that all ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ are same that is, ${\mathcal{L}}_{{F}_{i}}={\mathcal{L}}_{F}$, then we have

$$\text{LFFWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\mathcal{L}}_{F}.$$

(11)

(2) (Characteristic of Boundedness). Assume that ${\mathcal{L}}_{{F}_{i}}^{+}=\underset{1\le i\le n}{\mathit{max}}\left\{{\mathcal{L}}_{{F}_{i}}\right\}$ and ${\mathcal{L}}_{{F}_{i}}^{-}=\underset{1\le i\le n}{\mathit{min}}\left\{{\mathcal{L}}_{{F}_{i}}\right\}$ where $\left(i=1, 2, \dots ,n\right)$. So we have

$${\mathcal{L}}_{{F}_{i}}^{-}\le \text{LFFWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)\le {\mathcal{L}}_{{F}_{i}}^{+}.$$

(12)

(3) (Characteristic of Monotonicity). Assume that ${\mathcal{L}}_{{F}_{i}}$ and ${\mathcal{L}}_{{F}_{i}^{*}},$ where $\left(i=1, 2, \dots ,n\right)$ be two different LFFSs such that ${\mathcal{L}}_{{F}_{i}}\le {\mathcal{L}}_{{F}_{i}^{*}}$. Then we have

$$\text{LFFWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)\le \text{LFFWA}\left({\mathcal{L}}_{{F}_{1}^{*}}, {\mathcal{L}}_{{F}_{2}^{*}}, \dots ,{\mathcal{L}}_{{F}_{n}^{*}}\right).$$

(13)

Proof

Straightforward.

Next, we propose LFFOWA operator for LFFVs.

Definition 13

Assume that ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ is a combination of LFFVs. The LFFOWA operator is a function of dimension n $\text{LFFOWA }: {\text{M}}^{n}\to \text{M},$ such that

$$\text{LFFOWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\omega }_{1}{\mathcal{L}}_{{F}_{\sigma \left(1\right)}}\oplus {\omega }_{2}{\mathcal{L}}_{{F}_{\sigma \left(2\right)}}\oplus \dots \oplus {\omega }_{n}{\mathcal{L}}_{{F}_{\sigma \left(n\right)}}$$

$$=\left({\mathcal{S}}_{\uptau {\left(1-\prod_{\text{i}=1}^{\text{n}}{\left(1-{\left(\frac{{\upmu }_{\upsigma \left(\text{i}\right)}}{\uptau }\right)}^{\text{f}}\right)}^{{\omega }_{\text{i}}}\right)}^{1/\text{f}}} , {\mathcal{S}}_{\uptau {\prod_{\text{i}=1}^{\text{n}}\left(\frac{{\upnu }_{\upsigma \left(\text{i}\right)}}{\uptau }\right)}^{{\omega }_{\text{i}}}}\right)$$

(14)

In which ${\mathcal{L}}_{{F}_{\sigma \left(i\right)}}=\left({\mathcal{S}}_{{\mu }_{\sigma \left(i\right)}}, {\mathcal{S}}_{{\nu }_{\sigma \left(i\right)}}\right)$ represents the $\text{ith}$ biggest of ${\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots , {\mathcal{L}}_{{F}_{n}}$ and $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$ is the related weight vector.

On the same fashion to theorem 6, we also have certain characteristics of LFFOWA operator.

Theorem 3

Assume that ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ be a combination of LFFVs along with its weight vector $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$. The LFFWA operator fulfills the below characteristics as;

(1) (Characteristic of Idempotency). Assume that all ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ are same that is, ${\mathcal{L}}_{{F}_{i}}={\mathcal{L}}_{F}$, then we have

$$\text{LFFOWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\mathcal{L}}_{F}.$$

(15)

(2) (Characteristic of Boundedness). Assume that ${\mathcal{L}}_{{F}_{i}}^{+}=\underset{1\le i\le n}{\mathit{max}}\left\{{\mathcal{L}}_{{F}_{i}}\right\}$ and ${\mathcal{L}}_{{F}_{i}}^{-}=\underset{1\le i\le n}{\mathit{min}}\left\{{\mathcal{L}}_{{F}_{i}}\right\}$ where $\left(i=1, 2, \dots ,n\right)$. So we have

$${\mathcal{L}}_{{F}_{i}}^{-}\le \text{LFFOWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)\le {\mathcal{L}}_{{F}_{i}}^{+}.$$

(16)

(3) (Characteristic of Monotonicity). Assume that ${\mathcal{L}}_{{F}_{i}}$ and ${\mathcal{L}}_{{F}_{i}^{*}},$ where $\left(i=1, 2, \dots ,n\right)$ be two different LFFSs such that ${\mathcal{L}}_{{F}_{i}}\le {\mathcal{L}}_{{F}_{i}^{*}}$ . Then we have

$$\text{LFFOWA}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)\le \text{LFFOWA}\left({\mathcal{L}}_{{F}_{1}^{*}}, {\mathcal{L}}_{{F}_{2}^{*}}, \dots ,{\mathcal{L}}_{{F}_{n}^{*}}\right).$$

(17)

Proof

Straightforward.

Linguistic fractional fuzzy weighted geometric operators

In this section, we presented a few linguistic fractional fuzzy weighted geometric AoPs, such as LFFWG and LFFOWG operators, in the context of LFFS.

Definition 14

A LFFWG operator, described as a combination of LFFVs ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$, is a function of dimension n $\text{LFFWG }: {\text{M}}^{n}\to \text{M},$ such that

$$\text{LFFWG}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\otimes }_{i=1}^{n}{\left({\mathcal{L}}_{{F}_{i}}\right)}^{{\omega }_{i}}$$

$$=\left({\mathcal{S}}_{\tau {\prod_{i=1}^{n}\left(\frac{{\mu }_{i}}{\tau }\right)}^{{\omega }_{i}}}, {\mathcal{S}}_{\tau {\left(1-\prod_{i=1}^{n}{\left(1-{\left(\frac{{\nu }_{i}}{\tau }\right)}^{f}\right)}^{{\omega }_{i}}\right)}^{1/f}}\right)$$

(18)

Such that $\text{M}$ is a combination of each LFFVs, $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$ is the corresponding weight vector.

Corresponding to the LFFWA operator, the LFFWG operator also holds the subsequent characteristics:

Theorem 4

Assume that ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ be a combination of LFFVs along with its weight vector $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$. The LFFWG operator fulfills the below characteristics as;

(1) (Characteristic of Idempotency). Assume that all ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$ are same that is, ${\mathcal{L}}_{{F}_{i}}={\mathcal{L}}_{F}$, then we have

$$\text{LFFWG}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\mathcal{L}}_{F}.$$

(19)

(2) (Characteristic of Boundedness). Assume that ${\mathcal{L}}_{{F}_{i}}^{+}=\underset{1\le i\le n}{\mathit{max}}\left\{{\mathcal{L}}_{{F}_{i}}\right\}$ and ${\mathcal{L}}_{{F}_{i}}^{-}=\underset{1\le i\le n}{\mathit{min}}\left\{{\mathcal{L}}_{{F}_{i}}\right\}$ where $\left(i=1, 2, \dots ,n\right)$. So we have

$${\mathcal{L}}_{{F}_{i}}^{-}\le \text{LFFWG}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)\le {\mathcal{L}}_{{F}_{i}}^{+}.$$

(20)

(3) (Characteristic of Monotonicity). Assume that ${\mathcal{L}}_{{F}_{i}}$ and ${\mathcal{L}}_{{F}_{i}^{*}},$ where $\left(i=1, 2, \dots ,n\right)$ be two different LFFSs such that ${\mathcal{L}}_{{F}_{i}}\le {\mathcal{L}}_{{F}_{i}^{*}}$. Then we have

$$\text{LFFWG}\left({\mathcal{L}}_{{\text{F}}_{1}}, {\mathcal{L}}_{{\text{F}}_{2}}, \dots ,{\mathcal{L}}_{{\text{F}}_{\text{n}}}\right)\le \text{LFFWG}\left({\mathcal{L}}_{{\text{F}}_{1}^{*}}, {\mathcal{L}}_{{\text{F}}_{2}^{*}}, \dots ,{\mathcal{L}}_{{\text{F}}_{\text{n}}^{*}}\right).$$

(21)

Proof

Straightforward.

Definition 15

A LFFOWG operator, described as a combination of LFFVs ${\mathcal{L}}_{{F}_{i}}=\left({\mathcal{S}}_{{\mu }_{i}}, {\mathcal{S}}_{{\nu }_{i}}\right) \left(i=1, 2, \dots ,n\right)$, is a function such that

$$\text{LFFOWG}\left({\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots ,{\mathcal{L}}_{{F}_{n}}\right)={\left({\mathcal{L}}_{{F}_{\sigma \left(1\right)}}\right)}^{{\omega }_{1}}\otimes {\left({\mathcal{L}}_{{F}_{\sigma \left(2\right)}}\right)}^{{\omega }_{2}}\otimes \dots \otimes {\left({\mathcal{L}}_{{F}_{\sigma \left(n\right)}}\right)}^{{\omega }_{n}}$$

$$=\left({\mathcal{S}}_{\tau {\prod_{i=1}^{n}\left(\frac{{\mu }_{\sigma \left(i\right)}}{\tau }\right)}^{{\omega }_{i}}}, {\mathcal{S}}_{\tau {\left(1-\prod_{i=1}^{n}{\left(1-{\left(\frac{{\nu }_{\sigma \left(i\right)}}{\tau }\right)}^{f}\right)}^{{\omega }_{i}}\right)}^{1/f}}\right)$$

(22)

In which ${\mathcal{L}}_{{F}_{\sigma \left(i\right)}}=\left({\mathcal{S}}_{{\mu }_{\sigma \left(i\right)}}, {\mathcal{S}}_{{\nu }_{\sigma \left(i\right)}}\right)$ represents the $\text{ith}$ greatest of ${\mathcal{L}}_{{F}_{1}}, {\mathcal{L}}_{{F}_{2}}, \dots , {\mathcal{L}}_{{F}_{n}}$ and $\omega ={\left({\omega }_{1}, {\omega }_{2}, \dots , {\omega }_{n}\right)}^{T}$ such that ${\omega }_{i}>0$ and $\sum_{i=1}^{n}{\omega }_{i}=1$ is the related weight vector.

The LFFOWG operator likewise has the characteristics specified in Theorem 7.

Improved WASPAS method under LFF information

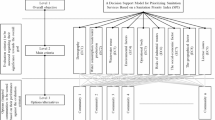
The WASPAS method serves as a popular and simple MCDM technique for a variety of decision-making problems. The weighted sum method (WSM) plus the weighted product method (WPM), two well-known MCDM techniques, are combined in this technique. In the ongoing portion, we will construct the LFF-WASPAS approach to address MCDM challenges in the context of linguistic fractional fuzzy information. Figure 2 shows the stepwise algorithm required to use the LFF-WASPAS approach.

Fig.2

The structure of proposed LFF-WASPAS method.

Suppose that $\mathcal{A}=\left\{{\mathcal{A}}_{1}, {\mathcal{A}}_{1}, \dots , {\mathcal{A}}_{m}\right\}$ represents a collection of $\text{m}$ alternatives and $\mathcal{B}=\left\{{\mathcal{B}}_{1}, {\mathcal{B}}_{2}, \dots ,{\mathcal{B}}_{n}\right\}$ is the collection of $\text{n}$ criteria along with an unknown weight vector $\omega >0$ such that $\sum_{\text{j}=1}^{\text{n}}{\omega }_{\text{j}}=1$. Using LFFS details, consider $\text{l}$ experts having unknown weight vectors $\Phi >0$ and $\sum_{\text{j}=1}^{\text{n}}{\Phi }_{\text{j}}=1$ being asked to allocate weights to every alternative based on all criteria. The following steps classify the LFF-WASPAS technique, which we use to choose the best option from various options that satisfy certain criteria.

Step 1 (Creation of linguistic fractional fuzzy assessment matrix (LFFAM)): Every expert assesses the parameters for picking the best options. Experts evaluate options based on certain criteria and assign them within the shape of LFFV. The LFF expert matrix for $k$ experts appears as follows.

$${\mathcal{B}}_{1} {\mathcal{B}}_{2} \dots {\mathcal{B}}_{n}$$

$$\mathfrak{Q}={\left[{\mathfrak{Q}}_{ij}^{l}\right]}_{m\times n}=\begin{array}{c}{\mathcal{A}}_{1}\\ \begin{array}{c}{\mathcal{A}}_{2}\\ \vdots \end{array}\\ {\mathcal{A}}_{m}\end{array}\left(\begin{array}{ccc}\begin{array}{cc}{\mathfrak{Q}}_{11}^{l}& {\mathfrak{Q}}_{12}^{l}\end{array}& \cdots & {\mathfrak{Q}}_{1n}^{l}\\ \begin{array}{cc}{\mathfrak{Q}}_{21}^{l}& {\mathfrak{Q}}_{22}^{l}\end{array}& \cdots & {\mathfrak{Q}}_{2n}^{l}\\ \begin{array}{cc}\vdots & \vdots \\ {\mathfrak{Q}}_{m1}^{l}& {\mathfrak{Q}}_{m2}^{l}\end{array}& \begin{array}{c}\ddots \\ \dots \end{array}& \begin{array}{c}\vdots \\ {\mathfrak{Q}}_{mn}^{l}\end{array}\end{array}\right);$$

(23)

where ${\mathfrak{Q}}_{ij}^{l}=\left({\mathcal{S}}_{{ \mu }_{ij}}^{l}, {\mathcal{S}}_{{ \nu }_{ij}}^{l}\right), \left(i=1, 2, \dots ,m\right), \left(j=1, 2, \dots ,n\right)$ and $\left(l=1, 2, \dots ,k\right).$

Step 2 (Standardization of LFFAM): It is necessary for the normalization of any non-beneficial criteria present in decision-making challenges. Non-beneficial criterions are transformed into beneficial criterion using the next formula.

$${\mathcal{N}}^{c}=\left\{\begin{array}{c}\left({\mathcal{S}}_{{ \mu }_{ij}}^{l}, { \mathcal{S}}_{{ \nu }_{ij}}^{l}\right);for benefit criterion\\ {\left({\mathcal{S}}_{{ \mu }_{ij}}^{l}, { \mathcal{S}}_{{ \nu }_{ij}}^{l}\right)}^{c}; for cost criterion\end{array}\right.$$

(24)

Step 3 (Analyzing the expert weights): Sometimes experts find it difficult to determine an accurate amount for alternative ${\mathcal{A}}_{i}$ in associated with criteria ${\mathcal{B}}_{j}$ because of imperfect understanding by humans and data that is not clear Due to its capacity to manage ambiguity, experts convey their thoughts in the context of LFFV. Thus, it is essential to first assess the experts’ weight in the manner described below. (a) Use the following entropy measure in order to calculate the expert’s weights.

$${\rm E}\left({R}_{i}^{l}\right)=\frac{1}{m}\sum_{i=1}^{m}\left[\frac{1}{n}\sum_{j=1}^{n}\left[\left\{\left(\sqrt{2}cos\pi \left|\frac{\frac{{ \mu }_{ij}}{\tau }-\frac{{ \nu }_{ij}}{\tau }}{4}\right|\right)-1\right\}\times \frac{1}{\sqrt{2}-1}\right]\right];$$

(25)

Hence, these experts’ weights are then calculated using Eq. (26) in the manner that follows:

$${\Phi }^{l}={\rm E}\left({R}_{i}^{l}\right)/ \sum_{l=1}^{k}{\rm E}\left({R}_{i}^{l}\right) , l=1, 2, \dots ,k.$$

(26)

Step 4 (Establishing linguistic fractional fuzzy aggregated assessment matrix (LFFAEM)): For establishing the group evaluation matrix throughout the decision-making procedure, the LFF aggregated assessment matrix is developed by combining the expert opinions of everyone involved. Using the suggested LFFWA, the LFF aggregated assessment matrix is created utilizing Eq. (10), which is shown as follows:

$${\mathcal{B}}_{1} {\mathcal{B}}_{2} \dots {\mathcal{B}}_{n}$$

$$\mathfrak{Q}={\left[{\mathfrak{Q}}_{ij}\right]}_{m\times n}=\begin{array}{c}{\mathcal{A}}_{1}\\ \begin{array}{c}{\mathcal{A}}_{2}\\ \vdots \end{array}\\ {\mathcal{A}}_{m}\end{array} \left(\begin{array}{ccc}\begin{array}{cc}{\mathfrak{Q}}_{11}& {\mathfrak{Q}}_{12}\end{array}& \cdots & {\mathfrak{Q}}_{1n}\\ \begin{array}{cc}{\mathfrak{Q}}_{21}& {\mathfrak{Q}}_{22}\end{array}& \cdots & {\mathfrak{Q}}_{2n}\\ \begin{array}{cc}\vdots & \vdots \\ {\mathfrak{Q}}_{m1}& {\mathfrak{Q}}_{m2}\end{array}& \begin{array}{c}\ddots \\ \dots \end{array}& \begin{array}{c}\vdots \\ {\mathfrak{Q}}_{mn}\end{array}\end{array}\right);$$

(27)

Step 5 (Calculation of criterion weights): We constructed the subsequent analytic hierarchy process (AHP)⁵⁴ for the purpose to identify the corresponding significance of every criterion:

$${\mathfrak{F}}_{i}=\frac{\sum_{i=1}^{m}\left(Sc\left({\mathfrak{Q}}_{ij}\right)\right)+n/2-1}{n(n-1)};$$

(28)

$${\omega }_{j}=\frac{{\mathfrak{F}}_{i}}{\sum_{i=1}^{n}{\mathfrak{F}}_{i}} .$$

(29)

Step 6 (Calculation of weighted sum model): Use the following equation to compute the measures of the weighted sum model (WSM) ${\mathcal{S}}_{i}^{\left(a\right)}$ of all options.

$${\mathcal{S}}_{i}^{\left(a\right)}=\sum_{j=1}^{n}{\omega }_{j}{\mathfrak{Q}}_{ij}.$$

(30)

Step 7 (Calculation of weighted product model): Use the following equation to compute the measures of the weighted product model (WPM) ${\mathcal{S}}_{i}^{\left(b\right)}$ of all options.

$${\mathcal{S}}_{i}^{\left(b\right)}=\prod_{j=1}^{n}{\left({\mathfrak{Q}}_{ij}\right)}^{{\omega }_{j}}.$$

(31)

Step 8 (Calculation of combined measures): For each choice, determine the combined measures of the WASPAS technique using the following formula:

$${\mathcal{S}}_{i}=\mathcal{t}{\mathcal{S}}_{i}^{\left(a\right)}+\left(1-\mathcal{t}\right){\mathcal{S}}_{i}^{\left(b\right)} ,$$

(32)

where $\mathcal{t}\in [0, 1]$ is the sensitivity combining factor. It is designed to determine WASPAS correctness based on the accuracy of the starting criterion.

Step 9 (Final Ranking): Sort the options in sequence of reducing ${\mathcal{S}}_{i}$ amounts (also known as classic scoring amounts).

Step 10 The end.

Case study

In this section, we implemented our proposed LFF-WASPAS technique to choose the best water filtration system in an environment with a LFFS framework. Water, a clear, unflavored, and tasteless liquid, is essential for the existence of nature. It refers to an organic component. The chemical structure for H₂O is a pair of hydrogen atoms with a single oxygen atom. Water may be present in the form of solids (frozen), liquids (water), or gases (vapor). Water is the only material that, under typical temperature and pressure situations, is capable of existing permanently in all three forms. Numerous facets of our lives, such as water retention, cultivation, manufacturing, transportation, and recreation, depend heavily on water. Nonetheless, as corporations have grown, many people around the world are becoming increasingly worried regarding their ability to access clean and safe drinking water, as water contamination can cause a variety of health problems, some of which are life-threatening. Water is the fundamental requirement for a living organism to survive, but as corporations expand in diameter the quantity of drinking water is becoming a major worry. Moreover, providing pure drinking water to household locations is the most important duty of the governing bodies. Water pollution may lead to a variety of health issues, especially those that are dangerous. The subsequent techniques (alternatives) are employed to prepare clear water on a commercial level:

${\mathcal{A}}_{1}:$(1) Reverse osmosis (RO): The reverse osmosis (RO) technique uses a membrane that is semi-permeable to remove dispersed elements, pollutants, and nutrients from water. This extremely efficient system for water filtration is widely utilized in residences and industry. The RO system can be seen in Fig. 3.

Fig. 3

Reverse Osmosis process.

${\mathcal{A}}_{2}:$(2) Deionization: Deionization describes the procedure of eliminating elements that are charged through water. It is widely utilized in order to eliminate pollutants from water, particularly in situations requiring extreme purity, including tests in labs, manufacturing operations, and certain housing water filtering technologies. The Deionization system can be seen in Fig. 4.

Fig. 4

Deionization process.

${\mathcal{A}}_{3}:$(3) Distillation: Distillation for purifying water is a procedure that eliminates contaminants by heating water to produce vapor followed by compressing the resulting heat into pure liquid. The technique starts by boiling polluted water until it vaporizes; leaving contaminants such as salts, nutrients, and bacteria in the container that originally contained it. The Distillation process can be seen in Fig. 5.

Fig. 5

Distillation process.

${\mathcal{A}}_{4}:$(4) Electrodialysis (ED): Electrodialysis (ED) is a procedure that separates ions from water, usually for distillation or purification to remove sodium chloride, nutrients, and other electrically charged pollutants. It is an electrolytic procedure in which an electric field drives ions through ion-selective barriers, distinguishing it from water. The ED system can be seen in Fig. 6.

Fig. 6

Electrodialysis process.

${\mathcal{A}}_{5}:$(5) Chlorination: Chlorination is the procedure of disinfecting water with chlorine. Chlorine is injected into the water, killing any dangerous germs or viruses that may be involved. This approach effectively kills the majority of the bacteria that cause diseases. The Chlorination system can be seen in Fig. 7.

Fig. 7

Chlorination process.

In order to assess each of these approaches, the following parameters (criteria) must be taken into consideration:

${\mathcal{B}}_{1}:$(1) (Environmental Factor): The filtration of water can be impacted by a wide range of variables in the environment, such as temperature, contaminants, transparency, and global warming. All things considered, surroundings can significantly affect the filtering of water and need to be considered while planning and putting into place water filtration systems.

${\mathcal{B}}_{2}:$(2) (Economical Factor): Water filtration is a costly procedure requiring large expenditures on technological developments, infrastructure, and worker resources. The expenditure of products like chemical substances, energy, and material used in water filtration can significantly impact its effectiveness.

${\mathcal{B}}_{3}:$(3) (Water Quality Factor): The filtration procedure depends on the desired degree of pureness for the product that is produced. The purity of water requirements vary by industry and implementation, affecting the cleaning procedure and necessary filtration levels.

${\mathcal{B}}_{4}:$(4) (Socio-political Factor): The socio-political factor may have a large influence on water filtration. Authorities must ensure their citizens in order to access to clean water for drinking. Accessibility to safe water is an essential right for humans. Several socio-political issues, including socioeconomic dynamics, public wellness, and political turbulence, might impact the availability of pure water.

Here is a step-by-step assessment approach for identifying the efficient water filtration technique employing the suggested LFF-WASPAS technique within the LFFS environment.

Step 1 (Creation of linguistic fractional fuzzy assessment matrix (LFFAM)): We collected expert information from three water filtering experts. Each expert shared helpful information through their skills and work in the sector. Information was acquired using structured interviews with assessment surveys. Their particular evaluations were thoroughly reviewed and archived. Experts assign the LFF to choices that match particular criteria using an LS amount according to $\mathcal{S}=\{{\mathcal{S}}_{0}=\text{normal}, {\mathcal{S}}_{1}=\text{low }{\mathcal{S}}_{2}=\text{slightly low}, {\mathcal{S}}_{3}=\text{very low}, {\mathcal{S}}_{4}=\text{high}, {\mathcal{S}}_{5}=\text{slightly high}, {\mathcal{S}}_{6}=\text{very high}\}.$ The expert’s matrices have been founded on the collection of data shown in Tables 3, 4, and 5.

Table 3 Expert matrix 1.

Table 4 Expert matrix 2.

Table 5 Expert matrix 3.

Step 2 (Standardization of LFFAM): For this particular circumstance, every single requirement is beneficial, which allows us to omit the standardization stage.

Step 3 (Analyzing the expert weights): The entropy measure associated with every expert’s weight may be calculated utilizing Eq. (25) as follows:

$$\text{\rm E}{\text{R}}^{1}=0.896617,\text{\rm E}{\text{R}}^{2}=0.912418,\text{\rm E}{\text{R}}^{3}=0.912219,$$

Then the expert’s weights are computed using Eq. (26) as follows:

$${\Phi }_{1}=0.329487, {\Phi }_{2}=0.335293, {\Phi }_{3}=0.335220.$$

Step 4 (Establishing linguistic fractional fuzzy aggregated assessment matrix (LFFAEM)): Table 6 shows the LFFAEM calculated using the LFFWA operator defined in Eq. (10) with expert weight knowledge.

Table 6 Combined matrix (using LFFWA operator).

Step 5 (Calculation of criterion weights): Using the AHP approach given in Eq. (28), the criterion weights are computed as follows:

$${\upomega }_{1}=0.247187, {\upomega }_{2}=0.262328, {\upomega }_{4}=0.236421, {\upomega }_{5}=0.254004.$$

Step 6 (Calculation of weighted sum model): Eq. (30) calculates the weighted sum model (WSM) ${\mathcal{S}}_{i}^{\left(a\right)}$ for every choice.

$${\mathcal{S}}_{1}^{\left(a\right)}=0.2667, {\mathcal{S}}_{2}^{\left(a\right)}=0.1976, {\mathcal{S}}_{3}^{\left(a\right)}=0.2804, {\mathcal{S}}_{4}^{\left(a\right)}=0.2341, {\mathcal{S}}_{5}^{\left(a\right)}=0.2502.$$

Step 7 (Calculation of weighted product model): Eq. (31) calculates the weighted product model (WPM) ${\mathcal{S}}_{i}^{\left(b\right)}$ for every choice.

$${\mathcal{S}}_{1}^{\left(b\right)}=0.2421, {\mathcal{S}}_{2}^{\left(b\right)}=0.1790, {\mathcal{S}}_{3}^{\left(b\right)}=0.2716, {\mathcal{S}}_{4}^{\left(b\right)}=0.2225, {\mathcal{S}}_{5}^{\left(b\right)}=0.2300.$$

Step 8 (Calculation of combined measures): The combined measure of the LFF-WASPAS approach for every choice is calculated utilizing Eq. (32) using $\mathcal{t}= 0.5$.

$${\mathcal{S}}_{1}=0.2544, {\mathcal{S}}_{2}=0.1883, {\mathcal{S}}_{3}=0.2760, {\mathcal{S}}_{4}=0.2283, {\mathcal{S}}_{5}=0.2401.$$

Step 9 (Final Ranking): The final ranking of each alternative which is obtained by using LFF-WASPAS method is shown in Table 7.

Table 7 Final ranking of the proposed method.

Based on Table 7, we concluded that distillation (${\mathcal{A}}_{3}$) is the best technique for water filtration. The graphical visualization of the suggested LFF-WASPAS technique is depicted in Fig. 8.

Fig. 8

Graphical visualization of alternatives based on proposed LFF-WASPAS method.

Sensitivity analysis based on the parameters $\mathcal{t}$ and ${\varvec{f}}$ on decision-making

Sensitivity analysis is an established technique for checking the stability and accuracy of various approaches and operators. This is accomplished through noticing shifts in ordering and modifying the parameters of the methods or AoPs. In this portion, we will discuss how the parameters $\mathcal{t}$ and $f$ affect the outcomes of the decision-making procedure, which is obtained from the proposed LFF-WASPAS method. Firstly, we modify the parameter $\mathcal{t}$ inside the interval [0, 1]. The investigation indicates that modifications in parameter $\mathcal{t}$ values inside the mentioned interval have no impact on overall decision-making ranking. The outcomes and its final ranking for different parameter $\mathcal{t}$ values obtained from the proposed LFF-WASPAS method are shown in Table 8. We discover that modifying the parameter quantity produces no impact on the whole ranking but raises the alternatives’ ratings in numbers. An excellent illustration of this study is Fig. 9, which presents a full picture of the sensitivity analysis and illustrates where the rating is sensitive to modifications in the amounts of each parameter. This shows the flexibility and accuracy of our proposed LFF-WASPAS method.

Table 8 Sensitivity analysis.

Fig. 9

Sensitivity analysis.

Next, we talk about how factor $f$ affects the ranking outcomes alternatives. To start, we modified the factor $f$ employing the suggested approach to generate an integrated data representation that is more precise. The calculated outcomes of various amounts for $f$ ∈ [3/2, 21/2] are illustrated in Table 9 to examine the impact on overall ranking. Table 9 makes it clear that the alternative ordering for different $f$ values employing the suggested LFF-WASPAS approach is exactly the same, which confirms that the selection process is appropriate for different $f$ inputs. The amounts of $f$ represent an extra assessment space of information for experts. Whenever the value of $f$ improves, experts can provide additional evaluation information as required.

Table 9 Sensitivity Analysis.

Additionally, we may clearly explain that the alternative scores determined by the suggested technique drop as the value of $f$ increases, and there is a slightly change in the position of ${\mathcal{A}}_{1}$ and ${\mathcal{A}}_{5}$ but the optimal alternative stays the same. In a comparable way, we changed the previously stated value $f$ and used the suggested approach to get the identical outcome. The overall effect of parameter $f$ on the decision-making process is graphically discussed in Fig. 10.

Fig. 10

Sensitivity Analysis.

Result and discussion

In this section, we have compared our suggested decision-making model to various existing operators and approaches for the purpose of determining the success and dependability of the method we propose. Doing this, we use the identical expert as well as weight knowledge that are described in Tables 3, 4, and 5. The suggested approach uses LFFS and employs averaging operators. Following that, Table 10 presents the final outcomes for the water filtration strategies depending on the MCDM techniques, which include EDAS, GRA, MOORA, and CoCoSo techniques, employing the combined expert data regarding the water filtration strategies provided in Table 6 and the corresponding criterion weights (0.247187, 0.262328, 0.236421, and 0.254004).

Table 10 Ranking outcomes via exciting and proposed models.

The overall ranking outcome is displayed in Table 11. The final outcomes of the recommended decision-making technique, together with those derived from various MCDM techniques; show a significant amount of stability in the final ranking. Contrasting with various existing MCDM methods, the suggested decision-making method is stable and consistent because, despite the possibility of various techniques for assessing the requirements, the final ordering of the alternatives is largely the same throughout all methodologies. Therefore, the suggested approach yields similar outcomes, demonstrating its suitability for use in actual MCDM issues.

Table 11 The ranking of expert’s outcomes.

Hence, distillation is the most efficient technique for water filtration, allowing ever one to get clean water, as seen in Fig. 11 and Table 8, depending on the MCDM techniques and the suggested decision-making framework utilizing the details that were provided. When comparing to existing MCDM techniques, the outcomes of the suggested approach demonstrate an impressive quality of stability in the evaluation of options. The overall pattern of rankings is consistent across the different methods every approach uses to assess requirements, indicating the suggested strategy’s consistency and stability. This stability throughout several assessment approaches demonstrates that the approach yields trustworthy outcomes, validating its efficacy in daily-life decision-making situations, like identifying a water filtration selection.

Fig. 11

Ranking outcomes through various existing and proposed approaches.

In the final analysis, the suggested decision-making framework reliably produces trustworthy evaluations using a variety of MCDM techniques and operates with precision. Although the effectiveness of computation may differ based on the technique employed, the outcomes demonstrate that this approach is quite feasible.

Conclusion

This paper concentrated on a novel notion of linguistic fractional fuzzy sets (LFFSs). The two concepts of fractional fuzzy set (FFS) along with linguistic term set (LTS) are combined to form the LFFS, providing an improved and adaptable approach to expressing vagueness and unpredictability. We started by going over the fundamental idea of LFFS, along with several properties and the AoPs for LFFS. In this paper, we also demonstrated a number of characteristics of the mentioned AoPs using linguistic fractional fuzzy inputs. Following that, we proposed the LFF-WASPAS technique, an innovative decision-making framework that utilizes linguistic fractional fuzzy information. Next, we used the suggested methodology to determine the most effective water filtering strategy. For the purpose do this, we used linguistic fractional fuzzy context to gather information from experts regarding the water filtering techniques. The procedure of the suggested method works well for LFFSs, while the LFF-WASPAS methodology considers two strategies, the WSM and WPM, before reaching a conclusion. The diagram displays the recommended method’s stepwise procedure. Numerous MCDM methodologies have validated the ranking findings, and the established methodology is explained mathematically. It has been determined that distillation is the best strategy for water filtration in order to improve water clarity based on the findings from the suggested model. A sensitivity study was carried out for the suggested method according to their parameters in order to assess how successful the suggested strategy is. For the purpose to confirm the reliability and strength of our recommended technique, we also tested it with several MCDM techniques. The findings of the comparison and sensitivity investigations show that the suggested method is a trustworthy as well as reliable assessment method.

Drawbacks and future directions

The suggested operators in the LFFS are important structures for decision-making models; however, they only work with one-dimensional information. This research is unable to address numerous scenarios using two-dimensional data. In order to remove these drawbacks, in further research, we will work to construct these AoPs for CLFFVs. To handle more complicated and ambiguous information as well as improve the model’s capacity to handle more complicated decision-making contexts. Additionally, we will attempt to use TODIM, MARCOS, MABAC CODAS, MULTI-MOORA, and several other approaches to decision-making to address more complicated problems related to everyday life.

The importance of this research

The LFFS provide a lot of linguistic information’s and more versatility in real-world problems. It is a combination of the FFS and LTS that are already in use. In a variety of situations in which complicated, ambiguous, or imperfect details are needed, LFFS broaden the scope of decision-making problems and enable researchers to convey data more precisely. Following are few of the importance of LFFS:

• (a) Linguistic Expression and Modelling for Compound Structures: Using linguistic concepts in FS improves human connection, making it simpler for people with no expertise to understand and deal with information and systems. Using ambiguous or incomplete information’s when decision-making can lead to better, updated, correct, and complicated outcomes. Such a device can be beneficial for systems of regulation, decision-making, and optimization.

• (b) Upgraded description of unpredictability: Numerous real-life events do not easily adjust into traditional mathematical frameworks. The LFFS offer improved ability to properly convey the complexity and further information of these events. These methods offer greater flexibility in representing TG and FG and may be adjusted to specific issue domains. This freedom allows for the description of various unclear and confusing data.

• (c) Adaptable Management Frameworks with Aggregation Operators: Linguistic fractional fuzzy sets may develop dynamic systems of control. Improve system efficiency and resilience by managing circumstances and unpredictability. The LFFS operators enable aggregation of LFFVs, opposing the IFS and PFS approaches.

• (d) Risk assessment and planning: LFFS is useful for risk assessment and planning. This approach may effectively handle complicated risks, particularly those with several unknown components. This technique results in better efficiency computations and decision-making procedures. This minimizes complications and speeds up calculations. Nevertheless, current solutions are insufficient to handle this type of situation. LFFVs supply data to the experts. The proposed approach can handle information collected by traditional techniques but possesses an opportunity for significant enhancements.