Introduction

Critical infrastructure networks are an integral part of any city, as they serve as lifelines that provide various essential of services across communities1. Each infrastructure network is often dependent on other networks to function properly, and a disruption in one network can result in a loss of performance in all connected networks2,3,4. Proper operation of these dependent infrastructure networks is crucial for a functioning society, particularly from the perspectives of economic productivity, public health, and national security, among others5,6. For instance, the first 100 hours of blackout duration have a significantly pronounced impact, reducing output by 73%, which is a substantial economic impact of blackouts on GDP7. In addition, blackouts can lead to increases in mortality and morbidity, as well as inadequate health care and treatment due to the limited operation of health care facilities8. Blackouts can disrupt water distribution, leading to acute infectious diarrheal diseases, recurrent or chronic diarrheal episodes, and non-diarrheal diseases9. At the same time, the absence of electricity and water could reduce the provision of health services.

Therefore, it is imperative to investigate ways to enhance the resilience of critical infrastructure networks, enabling them to withstand disruptions and recover faster after disruptive events10. The increasing complexity of infrastructure networks with modernization leads to the growth of dependencies between infrastructure networks1,11, making the task of improving infrastructure resilience even more challenging. This raises significant concerns regarding the use of reliability alone as a classical risk assessment metric for infrastructure12. Given the limited resources available to any community, the focus must be on identifying the most critical components within networks13 so that they can be leveraged to improve the overall resilience of interconnected networks and the community as a whole.

Several studies have been conducted on developing frameworks for capturing the behavior of dependent infrastructure networks, whether it be understanding the impact of various hazards on damage14,15 or the dynamics of recovery after a disruptive event16. Methods for modeling dependent infrastructure networks broadly include empirical frameworks17, fault trees18, agent-based modeling19, system of system approaches20, economic-theory21,22,23, complex systems24,25,26 and network-based models27. While all methods have their respective advantages, network-based models have gained popularity specifically over the last decade or so28,29. The network-based approach allows flexibility in capturing the global and local behavior exclusive to different infrastructure networks. With significant growth in computational technology, network-based approaches have garnered considerable attention in recent years27,30,31.

Any infrastructure system can be represented as a graph network, where nodes represent components and edges represent the links within a system. For instance, in a power network, the power stations can be represented as nodes and the transmission lines can be represented by the edges. By extending the concept of graph networks to multiple infrastructure systems, the dependent relationships between the functionalities of different networks can also be modeled. The dependent relationship between interconnected networks can be modeled using network theory, such that a change in the functionality of a network can be translated into an impact on others. Network-oriented approaches allow for intuitive representations of critical infrastructures by incorporating detailed mechanisms32, such that individual component failures under a disruption can be modeled, and the functionality of different components of an infrastructure system can be evaluated. Network-based approaches can be broadly categorized into—(1) flow-based and (2) topology-based frameworks17. Detailed flow-based models have been developed in recent years for different types of infrastructure systems, including power33, water34, healthcare18, and transportation networks35, to model the impact of extreme events, like earthquakes36, hurricanes37, on their individual performance. Taking network-based models one step further, holistic models capable of incorporating more than one lifeline and their respective dependencies have also been developed to investigate the dynamics of complex multi-level networks38,39,40,41,42. While these and other studies have focused on capturing high-resolution dynamics of dependent infrastructure networks, the widespread application of such models is still limited by their complexity, both in terms of implementation and computation. In addition, such high-fidelity models require extensive data, which are not always readily available. In contrast, topology-based frameworks provide a more generalized approach to assessing network behavior by modeling the dependent infrastructure systems based on their topology, with discrete states for each node or edge component43. While they do not capture the intricate mechanisms of each infrastructure system, topology-based approaches can be utilized in conjunction with other graph theory concepts to study the vulnerabilities of the systems.

In graph theory, centrality measures44 are indicators of importance for determining the influence of nodes and edges within a network based on specific criteria. Over the years, research in identifying influential nodes within different types of networks has led to significant developments of different forms of centrality and influence metrics45,46,47,48,49. One of the most researched challenges in network science is determining the ability to identify and prioritize the most important nodes. Thus, this prioritization could help streamline investments to maintain the functioning of power plants. The process of identifying and ranking the most influential nodes is critical for gaining a deep insight into a system’s structure and dynamics50. The concept of capturing influential nodes to better understand and regulate a system’s performance has been observed in different fields of science51,52,53,54. Although centrality measures have found specific benefits in modeling infrastructure systems as well10,55, such studies are limited in their application to specific infrastructure networks or by their requirement of extensive data for modeling. Due to the increasing complexity of infrastructure networks, it is crucial to identify the influence of individual assets in determining their impact on the overall stability of a community. While most studies on network resilience have utilized graph theory concepts in detail to capture the dynamics of dependent infrastructure systems, there is a need for generalized metrics to determine the importance of nodes under computational and data constraints56.

This study proposes a framework for determining the influence of both node and edge assets in infrastructure networks, taking into account their interdependence with other networks. Critical infrastructure systems in the city of Lima (Peru) are considered for analysis. Each network is modeled as a graph network, where assets are represented as nodes and their connectivity is established through links/edges between assets. Connectivity is established between different networks to capture the connectivity between them. The proposed influence metrics are tested by calculating the influence factor of individual assets (node and edge) and comparing the results with those of degree centrality. To measure the performance of each metric, the percentage of the population affected by the removal of individual nodes is evaluated. The proposed influence metrics correlate more with the population affected than the traditional centrality measure.

Interdependent infrastructure graph formulation

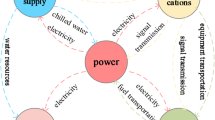
Infrastructure systems form the foundation of any city and are dependent on each other for proper functioning. Several critical infrastructure systems are considered in studies regarding community resilience17, ranging from physical to social and cyber systems. In this study, four critical infrastructure systems (CIS) are considered within the metropolitan area of Lima—(1) Power, (2) Water, (3) Healthcare, and (4) Transportation networks. Each network comprises important assets that provide services to other networks and population areas, such as power stations in the power network and water treatment plants in the water network, as shown in Fig. 1. Furthermore, each network comprises edges connecting these assets to other networks and population areas. To model each CIS, an individual network is established by first identifying critical assets, followed by linking the assets within each network to their respective service areas, which entail assets for other dependent infrastructure systems and population areas. The infrastructure networks are modeled as a graph network comprising nodes, that represent the assets and edges that represent the transmission or distribution lines. Each asset within an infrastructure network is linked to its corresponding service area, which includes (1) assets of the same network, (2) other dependent infrastructure networks, and (3) population areas. The population areas in this study are considered as parcel data, such that each parcel covers an area of 1\(Km^2\). Even though certain data on power and water networks were available, in this study, we focused on testing a computationally friendly framework that can be easily scaled. To circumvent extensive processing related to the different infrastructure networks considered, we utilized the topology of the transportation network as a surrogate for the power transmission and water distribution networks. Figure 1a shows the connectivity between the different networks within the selected area of Lima and Callao for this study.

Graph details

In the Lima Metropolitan Area, a total of 75 power stations are identified. The list of power substations is classified into two subcategories––(1) Major and (2) Minor power stations, based on their respective capacity. All stations with capacity \(>200\) kW are considered major stations, and all below the threshold are considered minor stations. Based on this classification, 17 major stations and 58 minor stations were identified. The transmission lines for the power network are characterized by (1) a primary network that connects major power substations with minor power substations and (2) a secondary network that connects the minor substations with population areas and other service areas. Due to the lack of explicit details on the transmission line networks (both primary and secondary), it is assumed in this study that the power transmission lines follow along the road lines57 and the topology of the transportation network is utilized to find connectivity between power stations and other service areas. The connectivity is established based on proximity by evaluating the shortest distance on the power network between power assets and other infrastructure assets and population areas. A detailed explanation of connectivity is provided in the following section. The capacity of each link in the transmission network is assumed to be equal; hence, no constraints associated with the capacity of transmission lines are considered in this study. Accurate modeling of a power network requires accounting for its internal redundancy. The main focus of this study was to provide a computationally friendly modeling alternative with minimal data requirements; hence, certain details were sacrificed during implementation. If \(G_p = (V_p, E_p)\) represents the graph for the power network, \(V_p\) represents the assets, and \(E_p\) represents the transmission lines. The node assets are considered as set \(V_p = v_p^M \cup v_p^m\), such that \(v_p^M\) represents the major power stations, and \(v_p^m\) represents the minor power stations. Similarly, the power transmission lines are defined by set \(E_p = e_p^M \cup e_p^m\), such that the edge set \(e_p^M\) represents the primary transmission network between major and minor power stations and the edge set \(e_p^m\) represents the secondary transmission network connecting minor stations to different service areas. Specific details on the assets for the power network were provided by the National Center for Disaster Risk Assessment, Prevention and Reduction (CENEPRED) and are discussed in Supplementary Information S1.

In the selected analysis area, a total of 46 water assets were identified, comprising 11 water treatment plants and 35 water reservoirs. The water treatment plants are assumed to provide water to the water reservoirs, which in turn provide water to other areas. All water reservoirs are assumed to be steel elevated tanks. Similar to the power network, the water pipelines are assumed to have a similar topology to the road network due to the limitation of existing data for the water transmission system. Significant spatial overlapping was observed for the list of water reservoirs; hence, reservoirs sharing the exact location were clustered together to reduce the total number of reservoirs to 35. The water distribution network comprises two components—(1) Primary distribution lines that connect water treatment plants with water reservoirs and (2) Secondary distribution lines that connect water reservoirs with population areas. If \(G_w = (V_w, E_w)\) represents the water network graph, \(V_w\) and \(E_w\) represent the water assets and distribution lines. The node assets are defined by the set \(V_w = v_w^T \cup v_p^r\), where \(v_p^T\) represents the water treatment plants, and \(v_p^r\) represents the water reservoirs. The distribution lines are defined by the set \(E_w = e_w^T \cup e_w^r\), such that \(e_w^T\) represents the distribution network connecting water treatment plants to water reservoirs and the edge set \(e_w^r\) represents the secondary distribution network connecting water reservoirs to different service areas. Some details on the water network are discussed in Supplementary Information S2 of the SI text.

A total of 147 hospitals were identified in the Lima and Callao regions. Each hospital is assumed to be connected to different population areas through the transportation network. The population areas are considered parcel areas of size 1\(Km^2\). A total of 3,592 population areas are identified, and the detailed description of the healthcare network and population data are described in Supplementary Information S3. The transportation network is formulated as an undirected graph, assuming the travel time in either direction of each edge to be the same. A total of 174,887 nodes are identified that comprise street intersections, and a total of 438,468 edges are identified that entail different types of roads, ranging from primary to tertiary. A detailed description of transportation network formulation is discussed in Supplementary Information S4.

Fig. 1
figure 1

(a) Dependencies considered between different infrastructure networks. The direction of the arrows shows the flow of services from one system to another. (b) The topology of the multi-layered infrastructure graph comprises power, water, healthcare, and population networks. (c) Method for establishing connectivity between the node assets of different dependent networks. The connectivity is evaluated based on the shortest path calculated on a transmission network. All maps were developed in QGIS 3.22.3 (https://www.qgis.org)58 and MATLAB R2022b (https://www.mathworks.com)59.

Full size image

Connectivity between infrastructure networks

Due to data limitations, certain assumptions were considered during the formulation of each infrastructure network. It is assumed that the service area for any asset is most likely to be closer than far away, and no redundancy is considered for any networks, as shown in Fig. 1. In other words, any service area, whether an asset or population area, is served by only one asset from other networks. For example, if a particular power or water network asset fails, it will result in a loss of service to all areas connected to it, as there is no alternative service source for those areas/assets. Using the discussed assumption of proximity, connections are established between population parcels and infrastructure systems, particularly power, water, and healthcare networks. Figure 1a shows the dependencies between the different infrastructure systems in Lima within this study. Not all possible dependencies were considered. For instance, even though water reservoirs sometimes require power to function, in this study, no correlation is assumed. Similarly, the water network also provides service to other infrastructure networks, like power networks, but the water network is assumed not to have a direct impact on the functionality of power or other networks; as a result, the correlation or dependency of the power network on the water network for maintaining functionality is weak. Only strong dependent relationships are considered in determining critical components, as they are expected to be the driving factor.

For each network, the assets are assumed to be connected to a single transmission line i.e., each asset has only one point of contact with its respective transmission network. The point of contact for each asset is determined based on the assumption that the asset is connected to the closest geographical point on the transmission network. For each asset, the Euclidean distance to every node in the network is calculated, and the node with the minimum distance determines the point of connectivity on the network for the asset. The shortest Euclidean distance cannot be used to establish connectivity between assets of different networks. It gives an inaccurate representation since it is not necessary that the path corresponding to the shortest Euclidean distance would be geographically present in the transmission network. The connectivity between any two assets i and j belonging to networks \(G_i\) and \(G_j\) is established based on Eq. (1), where \(\Omega ^{G_i}(i,j)\) is the shortest path between nodes i and j on network \(G_i\) (Fig. 1c). Therefore, the provided network \(G_j\) depends on network \(G_i\) for proper functionality. Dijkstra’s shortest path algorithm60 is utilized to evaluate the shortest paths on any graph network.

$$\begin{aligned} \min _{i \in G_i, j \in G_j} \Omega ^{G_i}(i,j) \end{aligned}$$
(1)

The connectivity can be described by the adjacency matrix \(A_{(G_i,G_j)}\), such that \(a(i,j) \in A_{(G_i,G_j)}\) describes the connectivity between node i of the network \(G_i\) and node j of the network \(G_j\). The Adjacency matrix is calculated as shown in Eq. (2), where \(d_{G_i}(i,j)\) is the distance calculated between nodes i and j on network \(G_i\),

$$\begin{aligned} a(i,j) = {\left\{ \begin{array}{ll} 1 & \text { if } d_{v}(i,j) = \Omega ^{G_i}(i,j) \\ 0 & \text { if } d_{v}(i,j) < \Omega _{G_i}(i,j) \end{array}\right. } \end{aligned}$$
(2)

Identifying important assets

It is widely acknowledged that the proper functioning of critical infrastructure systems necessitates collaboration among individual infrastructure systems. For instance, water, transportation, and healthcare networks depend on power networks for proper functionality. Similarly, there exists a different degree of dependency between individual infrastructure systems, and it is essential to capture these dependencies to better understand the role of each asset in evaluating recovery. Connections are established between assets of different infrastructure networks to establish relationships among them. Depending on the role of each infrastructure, some tend to have a substantial degree of dependence, while others have weak dependence. Weak dependent relationships are considered within the modeling framework. For instance, the functionalities of healthcare and water networks strongly correlate with power network functionality, whereas the opposite is not true. The functionality of the power network can be affected by a drop in the functionality of power and healthcare networks; however, the correlation is not nearly as strong. The shortest distance assumption is used to establish connectivity between assets of different networks, as considered in the formulation of power and water networks.

Node influence factor

A definition for the node influence factor is proposed to evaluate the importance of individual nodes within a network. The proposed definition of the influence factor is derived based on the concept of PageRank centrality. The PageRank algorithm assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, to measure its relative importance within that set61. In other words, a web page is considered important if it connects to other important web pages. Using this definition, an influence factor is proposed, as shown in Eq. (3), where \(I_{(p)}\) is the influence factor of node p and \(N^{(k)}\) is the set of nodes connected to node k. The influence factor provides a relative score of importance, which can be utilized to rank nodes based on their importance in the overall functionality of the network. To obtain the relative influence of a node k such that k belongs to network \(G_k\), the influence factor obtained from Eq. (3) is normalized by the maximum value observed amongst all nodes of network \(G_k\), as given by Eq. (4).

$$\begin{aligned} I_{(k)} = \sum _{p \in N^{(k)}} \frac{I_{p}}{N_{N^{(k)}}} \end{aligned}$$
(3)
$$\begin{aligned} I_{(k)}^n = \frac{I_{(k)}}{\max _{k \in G_k}I_{(k)}} \end{aligned}$$
(4)

The fundamental concept behind the influence factor is that an asset can be considered important if it provides service to other assets. The importance can be further quantified by the extent to which the failure of an asset would impact all infrastructure systems. While the impact of an asset can be defined in several ways, we define the influence of an asset by the extent to which population areas are impacted. The effect of each facility on the population is derived in multiple steps. In the first step, the connectivity of the selected facility is determined. For instance, a Major power station provides supply to minor power stations, which in turn further supply to hospitals, water treatment plants, and population areas. In the next step, the number of population nodes linked directly or indirectly to each facility is calculated. In the mentioned example, the minor power stations are directly linked to population areas, allowing for the calculation of how many population areas are served by each station. Since the major power stations are serving the population areas indirectly through the minor power stations, the population areas connected to the minor power stations are utilized to serve the population areas connected to the major power stations. As an example, a particular power station would be considered important if its failure would result in the loss of power to a high percentage of the population.

Fig. 2
figure 2

(a) Topology of a Multi-layered graph comprising different infrastructure networks shown, (b) Connectivity path shown for a node based on the flow of services from the node to different parts of the interconnected graph. (c) The concept outline for calculating the node influence metric by considering the connectivity of a node asset to others. (d) The concept outline for calculating the edge influence metric by considering the connectivity path to node assets.

Full size image

As shown in Fig. 2, in order to calculate the influence factor for any asset k in network G the influence factors of all nodes serviced by the node have to be calculated in the reverse order of connectivity. For instance, if the connectivity path of node k is given by \(k \xrightarrow {G}{k_1} \xrightarrow {G_1}{k_2}... \xrightarrow {G_{n-1}}{k_n}\) then to calculate the influence factor of node k, the influence factors of all connected nodes have to be calculated in the reverse order of connectivity. A sample case is discussed in Methods and Materials section of the SI to illustrate the calculation of node influence factors for the minor power station, considering its dependencies with other networks. One important point to note is that the final destination of all connectivity paths originating from any infrastructure network ends with the population network \(G_{pop} \in (V_{pop},E_{pop})\). The normalized influence factor (\(I_{(p)}^n\)) of individual population parcel \(p \in V_{pop}\) is calculated as given by Eq. (5), where \(N^{pop}_{p}\) is the population in parcel p. The system of equations shown in this study is applicable for unidirectional dependencies. To apply the discussed framework to cases involving bidirectional dependencies between different infrastructure systems, specific modifications would be required. For instance, if the water network provides service to the power network, the influence factor of water reservoirs would have to be expanded to include influence factors of major and minor power stations, and the updated set of equations would have to be solved using an iterative algorithm.

$$\begin{aligned} I_{(p)}^n = \frac{N^{pop}_{p}}{\sum _{p \in V_{pop}}} N^{pop}_{p} \end{aligned}$$
(5)

Edge influence factor

In addition to identifying influential assets, identifying important transmission lines can prove to be significantly beneficial in optimal resource allocation. In the case of a transmission network, any link is considered important if it plays a vital role in the transfer of resources between assets. Based on the concept of Betweenness centrality62, a modified formulation for the influence factor of transmission lines is proposed, as shown in Eq. (6), where g is the selected transmission line in network \(G_m\), m is a node asset in network \(G_m\) such that it provides service to the node asset n in network \(G_n\). The term \(\sigma _{m,n}\) is the total number of transmission paths connecting the node assets of network \(G_m\) with that of network \(G_n\) and \(I_{(n)}\) is the importance of node asset n. The term \(\gamma _{(m,n)}(g)\) is defined as shown in Eq. (7), where \(\Omega (m,n)\) is the shortest path connecting node assets m and n.

$$\begin{aligned} I_{g \in G_m} = \frac{1}{\sigma (m,n)} \sum _{m \in G_m} I_{(n)}\gamma _{(m,n)}(g) \end{aligned}$$
(6)
$$\begin{aligned} \gamma _{(m,n)}(g) = {\left\{ \begin{array}{ll} 1 & \text { if } g \in \Omega (m,n) \\ 0 & \text { otherwise } \end{array}\right. } \end{aligned}$$
(7)

In the case of betweenness centrality, the higher the number of occurrences of a particular transmission line, the higher its importance. However, this is not always true for the proposed influence metric for edge assets. Based on the proposed metric definition, all transmission paths are not similar in terms of importance, as they are weighted by the importance of the node asset to which they are connected. For instance, an edge will have higher importance if it provides service to an asset of high importance than to one of low importance. This way, the connectivity of the service node is also considered while evaluating the importance of the transmission edge. That is to say, the influence factor for an edge asset in the power network, when considering its connectivity to the water treatment plant, will take into account the degree of connectivity of the water treatment plant to other service areas it is connected to. This definition makes the edge assets’ influence factor dependent on the node assets’ influence factor. Therefore, the node influence factors must be calculated before the edge influence factors can be calculated. A sample case is discussed in the Methods and Materials section for minor power stations, considering its interdependencies with other networks. The definition of influence factors proposed in this study is just one possibility. Alternate definitions based on the same concept can also be utilized. One approach is to modify the influence factor of edge assets to account for the node’s importance from where the service originates. A recent study56, utilized the concept of graph theory to analyze risk in complex systems. The study explored the application of two centrality measures – Hubs and Authority- in determining the most important nodes within a dependent infrastructure system. The influence metric discussed in this study is quite similar in concept to Hubs centrality, except the Hub and Authority values are interlinked with each other, i.e., nodes with high Authority are the nodes that have connections to nodes with high Hub values and vice versa. In case of the influence metric, we remove the dependency on authority and simplify by only considering the impact on population areas.

Results

The analysis is conducted for the city of Lima to identify important assets within each critical infrastructure network separately while considering their respective dependencies based on the proposed formulations. The analysis calculates influence factors for individual nodes and edge assets within each infrastructure system considered while considering their dependencies. The performance of the proposed influence metrics is compared with that of degree centrality for each infrastructure system to highlight the ability of the proposed metrics to better identify critical assets. While an in-depth comparison would involve other centrality and importance measures from graph theory, the scope of this study is limited to the application of the proposed framework.

Infrastructure node assets

A performance metric is first determined to evaluate the efficacy of the proposed influence measure for node assets. The impact on any asset of critical infrastructure can cause disruption of service not only to the networks directly connected but also to the networks that are further provided with service by the directly connected networks. Since all networks, directly or indirectly, provide services to population areas, quantifying the extent of their effect on the population indicates an asset’s influence. To measure the effectiveness of the proposed metric, a graph-based centrality is also tested to gauge the extent of influence of individual assets. Degree centrality is a measure that accounts for the connections of a node with its neighbors62. By definition, degree centrality can be further classified into—(1) indegree, (2) outdegree, and (3) total degree. The Indegree of a node is calculated as the sum of all incoming weights from neighboring nodes, and the outdegree is the opposite, as it is the sum of all outgoing weights from a node to its neighbors. At the same time, the Total Degree is the combination of the two. Based on the three definitions, the outdegree models the outward connectivity of a node asset, which strongly correlates with nodes the provide services to other assets. Therefore, it is considered a suitable measure for comparison with the proposed influence metric.

Fig. 3
figure 3

Results comparison shown between the proposed influence metric calculated and degree centrality for node assets of (a) Major power stations, (b) Minor power stations, (c) Water treatment plants, (d) Water reservoirs, and (e) Hospitals. The spatial distribution of node assets for each network is also shown. All maps were developed in QGIS 3.22.3 (https://www.qgis.org)58 and MATLAB R2022b (https://www.mathworks.com)59.

Full size image

Figure 3 shows the calculated influence factors, outdegree, and percentage of population affected by the failure of a particular asset in different networks while considering all the dependencies between the networks (as shown in Fig. 1a). The population affected shown for each case is calculated by removing the corresponding node asset from the interconnected network and determining the percentage population affected by lack of service. In other words, we traced the dependency linkages from each infrastructure asset node to the population nodes, and that includes direct and indirect linkages. In some cases, like minor power stations and water reservoirs, the assets serve multiple networks. As a result, the influence factor is evaluated by combining the results of individual cases. The results of these intermediary cases are shown in Supplementary Information S1. Based on the results, it can be observed that assets in high-density population areas that are close to other assets show similar importance due to the availability of alternate options. However, assets that are further away from other assets demonstrate higher importance since there are no alternative options. Comparing the results between the two metrics (Influence and Degree), as shown in Fig. 3, it can be observed for each network that most node assets with high population impact also demonstrate a high influence factor but not a high degree centrality value. This suggests that the calculated influence metrics correlate more with the population affected than the degree centrality. Furthermore, the population affected calculated for different networks also demonstrates the relative sensitivity of different networks and individual assets within each network in terms of their impact on the community. Selective assets within major power stations and water treatment plant networks are observed to have a much higher impact on the population than other networks. For instance, asset Id 1 in the major power station and asset Id 9 in the water treatment plant networks are observed to influence \(25\%\) and \(27\%\) of the population, while in the case of minor power stations, water reservoirs, and hospitals the maximum impact on population is observed to be \(14\%\), \(10\%\) and \(6\%\). This can be attributed to the fact that for networks with a smaller number of assets, the lower redundancy places a higher burden on the assets. Since this study does not consider redundancy for any facility, each population area receives utility from only one facility. Due to this factor, the geographic location and density of facilities govern the importance of each facility.

Fig. 4
figure 4

Pearson correlation of the affected population with respect to (a) proposed the node influence factor and Degree centrality, and (b) the proposed edge influence factor and Betweenness centrality.

Full size image

The Pearson correlation coefficient between each network influence factor and population affected is also calculated and compared with the correlation between outdegree centrality and the same in Fig. 4a to demonstrate the effectiveness of the proposed metrics over degree centrality. For all cases, the correlation value of the proposed influence metric is observed to be close to 1 and significantly higher than that for degree centrality. This is to be expected since the influence metric considers the impact of a node asset on not only the assets/service areas directly linked but also on those not linked directly. While the degree centrality only considers the impact of a node on its immediate neighbors, which are at one degree of separation. This is also the reason why the degree centrality shows a high correlation, similar to the influence metric, for the healthcare network, since the healthcare network is directly linked to the population areas.

Infrastructure edge assets

The influence factors are also calculated for edge assets in the power, water, and healthcare networks, based on the formulation proposed in Eq. (5), to identify the most important edges in each network. Figure 5 shows the results for networks with edges of influence factor higher than 0.10. The results for intermediary cases of minor power stations and water reservoirs are presented in Supplementary Information S6. Similar to node assets, the effectiveness of the edge influence metric was measured by comparing the performance of the calculated influence metric for edge assets with the performance of a traditional centrality metric. In this case, Betweenness Centrality is utilized for comparison purposes because it evaluates how central an edge is within a network by considering the shortest paths the cross through the edge62. The most influential edge assets identified based on betweenness centrality for each infrastructure network are also shown in Fig. 5 for comparison. The influence factors are also calculated for edge assets in the power, water, and healthcare networks, based on the formulation proposed in Eq. 5, to identify the most important edges in each network. Fig. 5 shows the results for networks with edges of influence factor higher than 0.10. We selected the threshold of 0.10 just to highlight the best edges in the figures since more than \(95\%\) of the edges are observed to have an influence factor value of less than 0.10. Due to this reason, if the influence factor values of all edges are displayed in the figures, it is quite impossible to identify the edges with higher importance value edges \((> 0.10)\).

Fig. 5
figure 5

Results comparison shown between the proposed influence metric calculated and degree centrality for edge assets connecting, (a) Major power stations, (b) Minor power stations, (c) Water treatment plants, (d) Water reservoirs, and (e) Hospitals. The edge assets with values less than 0.10 are shown in gray, and edge assets with values higher are shown by the colormap. All maps were developed in QGIS 3.22.3 (https://www.qgis.org)58 and MATLAB R2022b (https://www.mathworks.com)59.

Full size image

Based on the results, a clear distinction can be observed between the two metrics. In some cases, like major and minor power stations, the most influential edges identified can be considered a subset of the edges identified by the influence metric. This is understandable since the edge influence metric considers the impact of the node influence metric, which introduces a higher degree of correlation. On the other hand, the betweenness centrality assumes equal weight of each shortest path through an edge, ignoring the impact of a higher degree of connectivity. For example, when evaluating the most important edges connecting the major and minor power stations using the influence metric, each path considered through an edge is weighted by the node influence factor of the connecting minor power station. As a result, an edge that considers the importance of minor stations as a weight factor can assess the impact of the edge on not just the minor power stations but also other assets that are serviced by the connected minor power station. To quantify the effectiveness of the proposed edge influence metric, correlation values with the affected population are calculated for the two edge metrics considered, following the same approach as the influence metric analysis for nodes. Figure 4b illustrates the correlation values between the edge influence metric and betweenness centrality for various networks. As expected, the proposed metric shows a significantly higher correlation for all infrastructure networks.

Discussion

In this study, a set of influence metrics is proposed based on the concepts of traditional centrality measures to identify important node and edge assets in a multi-layered interdependent infrastructure environment. The city of Lima in Peru is chosen as a testbed for evaluating the effectiveness of the proposed influence metrics. The performance of the node influence metric is compared with degree centrality, and the performance of the edge influence metric is compared with the betweenness centrality. To measure the performance of each metric, the calculated values for a node are compared with the percentage of the population affected when the particular node is removed from the system. For a metric to be effective, the calculated metric value must strongly correlate with the population affected. Both of the proposed metrics outperformed the traditional centrality measures by a significant margin. In this study, a population parcel size of \(1 km^2\) is utilized for the Lima testbed. A common question to be asked is whether the influence factors can be affected by the size of the population parcel utilized. While the value of influence factors may change when altering the parcel size, the relative ranking in importance between the asset nodes is not expected to change drastically, as the population areas are linked to infrastructure assets based on the shortest distance.

While several frameworks exist for identifying influential nodes in complex networks, the metrics proposed in this study are explicitly designed for interdependent infrastructure systems. The simplicity of implementation and their minimal data requirement make them an appealing option for the research problem in question. However, certain limitations are associated with the proposed metrics that must be considered. This study shows the application of proposed metrics on a topological network-based approach for modeling interconnected infrastructure systems. However, the metrics can also be applied to a detailed flow-based network approach, but this may significantly increase the computational time in that case. In flow-based models, evaluating all node influence metrics would require significant computational resources. Another limitation of the proposed metric is the assumption that no redundancy was considered when establishing connectivity between the different networks. For instance, each hospital and population area is connected to only one power station. If the networks are established to consider redundancies, the proposed metrics would not be suitable for determining influential nodes, as they could not account for the parallel paths generated due to redundancy.

Due to the limited scope of this study, not all aspects of the proposed framework have been discussed in this study. The proposed framework can be scaled to more complex interdependent systems, but certain modifications will be required in specific cases. In the case of Lima, all dependencies considered between the different infrastructure systems were unidirectional. Additional unidirectional dependencies can be easily added to the framework by updating the connectivity paths for each infrastructure node. However, if systems with bidirectional dependencies are considered, then the importance factors would have to be calculated using an iterative procedure, similar to the Hyperlink Induced Topic Search (HITS) algorithm utilized in graph theory.

While the proposed metrics may not directly apply to other network systems due to the difference in infrastructure architecture, they provide a computationally friendly framework to identify critical assets within infrastructure systems. By identifying these critical assets, the communities can be better prepared for disruptive events and aid in the optimal allocation of resources post-hazard to accelerate the recovery. Disaster response planning can be a complex affair as it requires substantial knowledge of the role of different infrastructure systems. Since the majority of infrastructure systems are interdependent, a detailed analysis is required to ascertain the importance of different infrastructure assets. The proposed methodology offers a simplistic approach to identifying the relative importance of each asset within the context of all infrastructure systems. By identifying important assets, targeted investment in the most influential assets can improve the overall resilience of the infrastructure systems to disruption events, like natural hazards.

Material and methods

Degree centrality

Degree centrality is a type of graph centrality that determines how central a node is considering the node’s connectivity with its immediate neighbors. For a graph \(G \in (V,E)\), such that V is the set of nodes and E is the set of edges, the degree centrality of a node i can be defined by 3 definitions—(1) Indegree (2) Outdegree and (3) Total Degree. Indegree refers to the centrality value of a node when considering the incoming edge weights from its neighbors, as given by Eq. (8), where \(N_b(i)\) is the set containing neighboring nodes for node i and a(j, i) is the edge weight from node j to node i. Similarly, Outdegree is the centrality of a node considering the outgoing edge weights from node i to its neighbors, as shown in Eq. (9). The Total Degree, as the definition suggests, is the combination of Indegree and Outdegree (Eq. 10).

$$\begin{aligned} C_i^d(i) = \sum _{j \in N_b(i)} a(j,i) \end{aligned}$$
(8)
$$\begin{aligned} C_o^d(i) = \sum _{j \in N_b(i)} a(i,j) \end{aligned}$$
(9)
$$\begin{aligned} C_t^d(i) = C_i^d(i) + C_o^d(i) \end{aligned}$$
(10)

Betweenness centrality

Betweenness centrality determines how central a node or an edge is, considering the shortest paths between all possible node pairs. For a graph \(G \in (V,E)\) with node set V and edge set E, the betweenness centrality for any edge \(e \in E\) is given by Eq. 11, where \(\sigma (v_1,v_2)(e)\) is the number of shortest paths between all node combinations \((v_1, v_2)\) that include the edge e and \(\sigma (v_1,v_2)\) are the total number of shortest paths between all node pairs.

$$\begin{aligned} C^b(e) = \sum _{(v_1,v2) \in V} \frac{\sigma _{(v_1,v_2)}(e)}{\sigma _{(v_1,v_2)}} \end{aligned}$$
(11)

Influence factor calculation

A sample case is shown here to demonstrate the step-by-step procedure for evaluating the influence metric of node and edge assets of a particular infrastructure network. The steps for Influence factor calculation of minor power stations (Fig. 6) are shown below.

Fig. 6
figure 6

Connectivity between infrastructure assets shown when evaluating the influence factor of minor power stations assets.

Full size image

Node influence factor

  1. 1.

    If the influence factors for network \(G_i\) is to be evaluated all connections from \(G_i\) to other networks \(G_j\) are identified first, followed by connections between the identified networks \(G_j\). The connectivity for minor power stations are shown in Fig. 6.

  2. 2.

    The influence factor for minor stations depends on three other infrastructure systems—(1) water treatment plants, (2) hospitals, and (3) population areas. To evaluate the influence factor of minor stations, their influence on each of the individual connected infrastructure systems has to be calculated.

  3. 3.

    If \(I^{(m,pop)}_{(k)}\) is the influence of minor power station node \(k \in V_{m}\) when considering connectivity only with the population areas and \(N^{(pop)}_{(k)}\) is the set of population areas connected to node k, the influence factor is given by Eq. (12), where \(I^{(pop)}_{p}\) is the influence factor of individual population areas p.

    $$\begin{aligned} I^{(m,pop)}_{(k)} = \sum _{p \in N^{(pop)}_{(k)}} I^{(pop)}_{p} \end{aligned}$$
    (12)
  4. 4.

    Similarly, the influence factor of minor power stations when considering connectivity with only the healthcare network is given by Eq. (13), where \(I^{(h)}_{p}\) is the influence factor of individual hospitals given by Eq. (14) such that \(k \in V_{h}\) represent the hospital nodes.

    $$\begin{aligned} I^{(m,h)}_{(k)} = \sum _{p \in N^{(h)}_{(k)}} I^{(h)}_{p} \end{aligned}$$
    (13)
    $$\begin{aligned} I^{(h,pop)}_{(k)} = \sum _{p \in N^{(pop)}_{(k)}} I^{(pop)}_{p} \end{aligned}$$
    (14)
  5. 5.

    The influence factor for minor power station nodes considering connectivity only with Water Treatment Plants can be calculated similar to the previous two cases. However, in this case, there are higher degrees of connectivity that need to be considered. The influence factor of node minor power station k is given by Eq. (15), where the influence factor for water treatment plant nodes \(I^{(T)}_{p}\) is further calculated by considering its connectivity with the water reservoir network, as shown in Eq. (16), where \(k \in V_{T}\) represent the water treatment plants.

    $$\begin{aligned} I^{(m,T)}_{(k)} = \sum _{p \in N^{(T)}_{(k)}} I^{(T)}_{p} \end{aligned}$$
    (15)
    $$\begin{aligned} I^{(T,r)}_{(k)} = \sum _{p \in N^{(r)}_{(k)}} I^{(r)}_{p} \end{aligned}$$
    (16)

    The water reservoir network provides direct service to the healthcare and population areas. Therefore, the influence of water reservoirs is dependent on the two networks. To evaluate the influence factor \(I^{(r)}_{p}\), the individual influence of water reservoirs on hospitals and population areas would have to be evaluated first, similar to Step 2. For the sake of avoiding repetition, the steps for evaluating individual influence factors of water reservoirs for hospitals \(I^{(r,h)}_{k}\) and population areas \(I^{(r,pop)}_{k}\) are not shown here. The effective influence factor for water reservoirs is then calculated by Eq. (17), where \(\beta _{j = 1,2}\) are the weight factors considered for connected networks j. In this study, all infrastructure systems are given the same importance; hence, \(\beta _{1} = \beta _{2} = 1/2\) in this case.

    $$\begin{aligned} I^{(r)}_{(k)} = \beta _{j=1}.I^{(r,h)}_{k} + \beta _{j=2}.I^{(r,pop)}_{k} \end{aligned}$$
    (17)
  6. 6.

    Once all individual influence factors have been calculated between the power station and the three connected networks, the effective influence of minor power station \(I^{(m)}_{(k)}\) is given by Eq. (18), where \(\beta _{1} = \beta _{2} = \beta _{3} = 1/3.\)

    $$\begin{aligned} I^{(m)}_{(k)} = \beta _{j=1}.I^{(m,T)}_{k} + \beta _{j=2}.I^{(m,h)}_{k} + \beta _{j=3}.I^{(m,pop)}_{k} \end{aligned}$$
    (18)

Edge influence factor

  1. 1.

    To evaluate the influence factor of edge assets, it is necessary to first evaluate the node influence factors of all networks.

  2. 2.

    To calculate the influence factor of minor power station edges that provide service to other networks, the influence factor of edges corresponding to each connected asset has to be calculated, which in this case are (1) water treatment plants (2) hospitals and (3) population areas.

  3. 3.

    The influence factor of edges connecting minor power stations with water treatment plants is given by Eq. (19), where \(\gamma _{(m,n)}(g)\) is 1 if the edge g is a part of the shortest path connecting nodes m and n and 0 if not. \(I_{(n)}\) is the influence factor of the water treatment plant node n calculated previously.

    $$\begin{aligned} I_{g \in E_{m,T}} = \frac{1}{\sigma (m,n)} \sum _{m \in V_{m}, n \in V_{T}} I_{(n)}\gamma _{(m,n)}(g) \end{aligned}$$
    (19)
  4. 4.

    Similarly, the influence factor of edges connecting minor power stations with hospitals and population areas is given by Eqs. (20) and (21), where \(I_{(n)}\) in the equations are the influence factor of hospital and population nodes.

    $$\begin{aligned} I_{g \in E_{m,h}} = \frac{1}{\sigma (m,n)} \sum _{m \in V_{m}, n \in V_{h}} I_{(n)}\gamma _{(m,n)}(g) \end{aligned}$$
    (20)
    $$\begin{aligned} I_{g \in E_{m,pop}} = \frac{1}{\sigma (m,n)} \sum _{m \in V_{m}, n \in V_{pop}} I_{(n)}\gamma _{(m,n)}(g) \end{aligned}$$
    (21)
  5. 5.

    The effective influence of each edge connecting the minor power station is then calculated as given by Eq. (22), where \(\beta _{1} = \beta _{2} = \beta _{3} = 1/3\)

    $$\begin{aligned} I_{g} = \beta _{1}.I_{g \in E_{m,T}} + \beta _{2}.I_{g \in E_{m,h}} + \beta _{3}.I_{g \in E_{m,pop}} \end{aligned}$$
    (22)