Bidirectional decision analysis of online Ride-hailing enterprises based on fuzzy theory and cloud model

Abstract

At present, quantitative data is mainly used as the basis for service-oriented enterprise decision-making. However, a single dimension and type of analysis cannot accurately reflect the uncertainty of enterprise operations. To solve this problem, a hybrid decision method based on fuzzy analytic hierarchy process (F-AHP) and two-dimensional cloud model is constructed, aiming to help service-oriented enterprises represented by online ride-hailing (ORH) optimize their strategies to adapt to the changing market. Firstly, a multi-layer index system is constructed from the two key dimensions of enterprise management and user service, and F-AHP is introduced to calculate the weight of each index, which weakens the fuzziness of human subjective judgment based on comprehensive analysis from the inside out. Secondly, four ORH enterprises are taken as examples; survey data and standard score intervals are qualitatively expressed through the two-dimensional backward cloud generator. Finally, the two-dimensional forward cloud generator is used to quantitatively evaluate the comprehensive situation of each ORH enterprise. The proposed method realizes effective conversion between quantitative description and qualitative concepts, and its effectiveness is verified by comparing it with existing methods. The results show that gaps among ORH enterprises are mainly concentrated in management rather than in service. Market performance largely determines an enterprise’s basic operation scale, while user service quality determines its future development space.

Introduction

Online ride-hailing (ORH), with its strong resource allocation ability and high mobile Internet technology, has become a key development industry in the era of the sharing economy¹. ORH refers to an enterprise that connects drivers and users with symmetrical demand information in real-time through mobile software or Internet platforms². ORH businesses include tailored car services, online car rentals, and carpooling services³. There are three main reasons why ORH has gained a foothold in the travel market. Firstly, the accuracy and transparency of information under high-tech Internet technology enhance trust between drivers and users. Secondly, the sharing model maximizes benefits for owners with spare vehicles and time⁴. Thirdly, the emergence of ORH not only facilitates people’s daily travel but also reduces the number of vehicles on the road, thus effectively easing urban traffic congestion and greenhouse gas emissions⁵.

Although both ORH and taxis aim to provide passenger services, their service characteristics and modes are different⁶. In terms of service characteristics, ORH follows the law of free competition in the market, with pricing based on the supply and demand relationship between users and drivers. Instead of competing in a completely free market, taxis have a public product character. In terms of service mode, ORH does not use a traditional cruise service model like taxis; rather, it connects the needs of drivers and users based on big data, GPS, and other new technologies⁷.

Since 2010, ORH enterprises have mushroomed in the Chinese market, reaching more than 30 enterprises during a period of great prosperity. In the initial stage, due to the similarity of models and lack of distinct characteristics, all enterprises could only attract users through subsidy strategies. The ORH market was once trapped in a “price war” because each enterprise kept increasing its maximum discount⁸. This vicious competition resulted in the rapid marginalization of many underfunded enterprises.

The two characteristics of the ORH industry are the main reasons for intensifying this virulent price competition³. One is product homogeneity. Although the service types and operating vehicles of each ORH enterprise are slightly different, they essentially aim to meet users’ travel needs. Another is price transparency. Each ORH enterprise’s pricing rules are transparent, allowing users to easily compare prices and choose services. Due to these characteristics, it is difficult for each ORH enterprise to accurately evaluate its core competitiveness in the same market environment. As a result, each enterprise cannot develop correct and effective development strategies and can only compete for user resources through price subsidies.

Therefore, designing an accurate and comprehensive decision-making method to analyze users’ feelings and operational data can help each ORH enterprise assess its advantages and disadvantages, and provide targeted optimization suggestions. Through decision analysis, ORH enterprises can overcome competition misunderstandings and focus on improving service quality and expanding business types, thereby realizing the benign development of the entire industry.

At present, research on ORH mainly focuses on the supervision of policy and legislation^6,9,10, the analysis of participants’ behaviors^11,12,13, and strategies for enterprise operation^14,15,16. Only a few studies have evaluated ORH. For example, Wu et al.¹⁷ evaluated the impact of ORH services on environmental protection, and the results showed that ORH services replaced other travel methods such as busing, walking, and cycling, thus leading to an increase in fuel use. Guo et al.¹⁸ evaluated the impact of ORH on the new car sales market. By analyzing data from new car license plates, it was shown that although the entry of a single ORH platform would lead to a decline in the purchase of new cars, competition between platforms would promote an increase in the sales of car brands commonly adopted by ORH drivers.

In enterprise analysis, the commonly used research methods include factor analysis, regression analysis, and so on^19,20. However, these methods often yield purely quantitative or qualitative results, which have disadvantages such as low accuracy and credibility. Even when qualitative and quantitative methods are combined, the qualitative analysis part is often summarized into an abstract mathematical framework²¹, ignoring the randomness and fuzziness of natural language.

Randomness refers to the fact that information has been clearly defined but may not be apparent, and fuzziness refers to the fact that information is difficult to define accurately but already exists²². These two factors constitute the uncertainty in the decision-making process. Although many theoretical models, including probability theory and rough sets, have been used in the study of uncertainty, these models can cause partial information loss due to their rigorous constraints²³.

Based on the existing research, it can be found that the current analysis of service-oriented enterprises is mainly from a single dimension, ignoring the analysis of the factors affecting development from the inside out. At the same time, most analyses are primarily based on language scales, which do not fit the actual situation where most user analyses are conducted in natural language. In addition, few studies consider the large differences in the types and numbers of initial analysis samples. This study helps to fill this research gap.

To reflect the uncertainty of qualitative concepts and quantitative data, this paper constructs a decision-making method based on the fuzzy analytic hierarchy process (F-AHP) and two-dimensional cloud model. There are three main contributions. First, the proposed method can effectively address the differences in understanding the importance of various indexes, avoiding overly broad fuzzy intervals while fully considering the uncertainties in decision-making scenarios. In the ORH industry, there exists a significant amount of vague information, such as “the service is not bad”. At the same time, enterprises, users, and regulatory authorities attach different degrees of importance to core industry indexes such as security, convenience, and price rationality. The proposed method can help enterprises accurately identify competitive focuses and avoid resource misallocation.

Second, on the basis of eliminating the unfairness and incompleteness of a single dimension, the cloud generator is utilized to transform quantitative data and qualitative concepts from multiple perspectives, addressing the ambiguity of the initial samples and analysis results. In the ORH industry, if the analysis is only conducted from the perspective of user service or internal management, it cannot truly reflect an enterprise’s competitiveness in a complex market. Meanwhile, the proposed method can effectively handle the conversion between qualitative concepts such as user evaluations and quantitative data such as daily active users, ensuring that evaluation results are not distorted and preventing enterprises from misjudging their own strengths and weaknesses.

Third, considering that there is currently less research on service-oriented enterprises and that the ORH industry is still in its development stage, the proposed method comprehensively reflects the competitive situation of enterprises under the interaction between management operations and service demands, avoiding inaccurate results due to the one-sidedness of the evaluation perspective. It helps enterprises clearly grasp the impact of internal and external linkages on the market pattern, prompting them to adjust their development strategies in a timely manner, enhance user stickiness, and respond to competitors’ impacts.

The remainder of this paper is organized as follows: “Literature review” introduces the theory and literature of the analytical methods and the cloud models, respectively. “Methods” presents the calculation steps of F-AHP and the two-dimensional cloud model, and then constructs the implementation structure of the proposed method. “Analysis procedure” first designs a comprehensive index system for ORH, and then constructs standard comment sets from both enterprise and user dimensions. Finally, based on obtaining the formulas for cloud numerical characteristics and membership degrees, the calculation steps of the proposed method are summarized. “Material” introduces the analysis objects and processes initial data. “Results” calculates the cloud number characteristics of each enterprise, verifies, and analyzes the results. “Conclusions” summarizes the main conclusions of this paper and introduces future research directions.

Literature review

Literature of analytical methods

The weight determination of the index is an important step in evaluating the rationality and accuracy of the entire decision-making method. According to the different sources of the original data, existing weight calculation methods can be classified into subjective weighting methods and objective weighting methods²⁴. Subjective weighting methods determine weights based on the subjective opinions of experts, mainly including the analytic hierarchy process (AHP) and F-AHP²⁵. Objective weighting methods determine weights based on the relationships among the original data, mainly including entropy-based methods²⁶.

Although objective weighting methods are more rigorous than subjective weighting methods, entropy-based methods have difficulty effectively dealing with ambiguity in qualitative indexes and expert decision-making²⁷. The analysis of ORH enterprises includes multiple qualitative indexes, which are difficult to quantify through objective data. Meanwhile, entropy-based methods are mainly used to measure the uncertainty of information but cannot describe the randomness in the analysis. In addition, although entropy-based methods can be used for multi-level weight calculation, they are not as effective as subjective weighting methods such as F-AHP in complex hierarchical analysis problems.

Decision analysis based on machine learning methods is a research hotspot. Machine learning encompasses deep learning and reinforcement learning. The neural networks in deep learning can handle multi-variable inputs and capture complex high-dimensional nonlinear relationships²⁸. Reinforcement learning methods combined with optimization solvers can effectively generate decision-making schemes that blend data-driven and knowledge-driven approaches²⁹. However, actual decision-making often involves multiple static factors and dynamic changes, while most of the research in machine learning is conducted in simplified scenarios³⁰. For instance, in machine learning research on urban traffic decision-making, some studies have ignored factors such as driver income fairness and order allocation distance to reduce computational load, which impact vehicle scheduling^31,32. Therefore, machine learning methods face challenges related to high computational costs and limited applicability. At the same time, some machine learning methods struggle to explain the internal logic of their results³³, making it difficult to effectively deal with fuzziness and uncertainty in the analysis process. In addition, the analysis of ORH enterprises involves qualitative indexes and expert decision-making, which makes it difficult to meet the large amount of numerical data required by machine learning. Therefore, this paper adopts a subjective weighting method to determine index weights.

The AHP invented by Saaty³⁴, which combines quantitative and qualitative analysis, can effectively study the non-sequential relationships among the levels of the target criterion system and comprehensively measure the judgment differences of decision makers. Therefore, AHP is widely used in determining weights for multi-criteria decision problems. However, AHP may generate some issues, including differences between judgment consistency and matrix consistency when there are many indexes³⁵.

By applying fuzzy logic, it can flexibly adapt to a variety of input data while reducing the influence of differences, thereby better describing the uncertainty in complex practical situations³⁶. Van and Pedrycz³⁷ first proposed the judgment method of using triangular fuzzy numbers to represent fuzzy comparisons based on the fuzzy set theory introduced by Zadeh³⁸. After that, different scholars proposed many F-AHP methods. For example, Buckley³⁹ identified the fuzzy priority comparison ratio with a trapezoidal membership function, and Chang⁴⁰ proposed an improved F-AHP method for paired comparison using triangular fuzzy numbers.

Fuzzy theory deals with uncertainty mainly through fuzzy sets and membership functions⁴¹; it is widely used in decision analysis. For example, Nasution et al.⁴² proposed a decision criterion method based on F-AHP to determine the best route between the departure and destination points according to the driver’s driving preferences and the conditions of each road section. Compared with other methods, the proposed method had better recommendation effects and flexibility. However, this study did not take into account driving preferences such as road closures and waiting times at traffic lights, making it difficult to conform to the actual real-time dynamic changes of the road. Mudahishu et al.⁴³ utilized F-AHP to assess the influence of factors such as drainage density, land use, slope, and rainfall on flood hazard maps, thereby conducting an accurate geographical evaluation of flood characteristics. The experiment demonstrated that F-AHP had good compatibility with historical flood records, providing effective support for urban safety management decisions. However, when the number of flood influencing factors exceeded two groups, the accuracy of this assessment decreased. Ratnayake et al.⁴¹ proposed a novel algorithm called Cascade Adaptive Neuro-Fuzzy Inference System. This algorithm adopted a reasoning mechanism based on fuzzy rules; thus, it was capable of adapting to various complex decision-making scenarios. However, due to generating a large number of variables by this algorithm, it required sufficient storage space in the microcontroller. Bello et al.⁴⁴ employed F-AHP to select 21 criteria from environmental, economic, and social dimensions to evaluate sustainable rice cultivation practices in Nigeria. The survey results indicated that enhancing stakeholders’ performance in the rice value chain could boost productivity and food security in the region. However, this study only analyzed specific stakeholder groups’ viewpoints, resulting in poor generalizability of its conclusions.

Due to the continuous changes in digital platforms and service industries, enterprise analysis methods are gradually improving to adapt to new business models and development needs. Ye et al.⁴⁵ proposed an analytical method based on the extended belief rule base model, which analyzed enterprise performance from a predictive perspective and addressed the issue that data envelopment analysis (DEA) could not handle negative data. However, their research only evaluated the annual performance of enterprises and did not focus on important short-term factors such as monthly performance. Zhang et al.⁴⁶ incorporated the time dimension into the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) and constructed a credit system for business-to-business platforms. They pointed out that high-quality service platforms were conducive to enterprises’ supply chain financing. To address the issue of inconsistent results caused by applying different indicators and DEA models, this study introduced the time dimension but did not explicitly state the data frequency. The insufficiency of data frequency can easily lead to insufficient sensitivity in dynamic evaluation. Yang et al.⁴⁷ employed the evidence reasoning approach to integrate homogeneous efficiency, heterogeneous efficiency, and mixed efficiency, effectively distinguishing between different enterprises’ performances and resolving inconsistencies due to varying indexes and DEA models used in different scenarios; however, this study did not clearly define their applicable boundaries. Gao et al.⁴⁸ proposed a collaborative asset valuation model based on big data to address value assessment issues for Internet platforms, emphasizing that a platform’s investment value should exceed its cost of capital. However, they did not take into account external influences such as market fluctuations, thus limiting the accuracy of their model. Jia et al.⁴⁹ combined F-AHP with particle swarm optimization algorithms to effectively evaluate application levels and performance of industrial Internet platforms in power generation equipment industries; however, the application scenarios of industrial Internet platforms are highly dependent on industry characteristics, making it difficult for evaluation indexes constructed based on this industry to be directly extended to other industrial fields.

Overall, the research on the determination of index weights can be divided into subjective weighting methods and objective weighting methods. Subjective weighting methods can handle qualitative indexes and fuzzy decision-making scenarios. However, AHP has the problem of consistency differences, while F-AHP can effectively reduce deviations through fuzzy logic. Objective weighting methods determine weights based on data relationships; although they are more rigorous, they find it difficult to handle qualitative indexes and fuzziness, and their effectiveness in complex hierarchical analysis is inferior to that of subjective methods. Although machine learning methods are a research hotspot, they are limited by computational costs and scene simplification, making it difficult to deal with uncertainties. Therefore, their applicability in ORH enterprise analysis is limited. In subjective weighting methods, F-AHP handles uncertainty through fuzzy sets and membership functions and is suitable for multi-criteria complex decision-making. It has been applied in fields such as transportation, disaster assessment, and agriculture. Other analytical methods, such as the extended belief rule base model and time dimension TOPSIS, are mainly applied in areas like enterprise performance prediction and credit system construction; however, they have limitations such as ignoring dynamic factors and external risks.

Literature of cloud models

At present, research on the cloud model mainly focuses on four aspects. In terms of bidirectional cognitive computing^50,51, forward cloud transform (FCT) and backward cloud transform (BCT) are important tools for realizing bidirectional cognitive transformation. There are more studies on BCT algorithms than on FCT algorithms because BCT can realize the transformation from concept extension to connotation, and the stability of different BCT algorithms varies.

In terms of similarity measurement⁵², the cloud model provides a qualitative analysis method that is more consistent with human cognition for the representation of the knowledge mining process. For example, the cloud similarity measurement can be used to accurately measure whether the concept generates public sentiment in the detection of online public opinions.

In terms of granular computing⁵³, granularity in the cloud model refers to the measurement of the information contained in concepts, analyzing the data in the theoretical domain space from different conceptual hierarchies. The Gaussian cloud transform can realize changes in multi-granularity and adaptively generate concepts, thereby solving the problem of variable granularity in the cloud model. Jiang et al.⁵⁴ proposed a rough integrated asymmetric cloud model, aiming to address large-scale group decision-making problems in multi-granularity linguistic environments. This model combined rough numbers with the asymmetric cloud model and presented a new method for calculating distance and similarity, taking into account individual preferences’ subjectivity and expressing unbalanced preference trends asymmetrically. However, this study did not clearly define the boundaries of the multi-granularity linguistic environment it was applicable to, thereby limiting its universality.

In terms of the two-dimensional cloud model⁵⁵, due to the limitations of the rule generator, the one-dimensional cloud model can only represent a single input or output. The two-dimensional cloud model is more consistent with the actual reasoning situation determined by a variety of factors. However, because of the coupling relationship between dimensions, it is more difficult to divide the high-dimensional data space. Therefore, there is relatively little research on the two-dimensional cloud model.

In addition, the decision-making research based on the cloud model mainly applies the one-dimensional cloud model. Based on the cloud model, Yu et al.⁵⁶ selected 11 indexes from three dimensions, namely inducing environment, influencing factors, and inducing factors, to analyze the risk of heavy rain in Changzhou City, China. The research results showed that the cloud model could adapt to the randomness and fuzziness of urban heavy rain risk assessment. However, there was a conceptual overlap between inducing environment and inducing factors, which might lead to an unreasonable distribution of index weights and affect the rigor of the assessment. Peng et al.⁵⁷ proposed an evaluation cloud model to address the issue of large-scale water gushing during tunnel construction and verified the reliability of this proposed model based on actual risk levels of water gushing in tunnels. However, determining weights through AHP in this study was prone to subjective bias, which might lead to index weights being inconsistent with their actual influence. Jiang et al.⁵⁸ proposed a probabilistic hesitant fuzzy integrated cloud model for large-scale group emergency decision-making. In this model, the probabilistic hesitant fuzzy set expressed subjective information from decision-makers while comprehensively considering uncertainty and randomness in information using a cloud model. This method did not require additional information during calculation processes effectively avoiding information distortion; however, it did not take into account the interrelationships among the evaluation attributes, which was not conducive to mining deep-level information.

Overall, the cloud model provides a method that conforms to human cognitive characteristics for qualitative and quantitative analysis in knowledge mining. Its core value lies in the matching judgment between concepts and data through similarity measurement. Bidirectional cognitive computing is the core field for the cloud model in achieving bidirectional conversion between qualitative concepts and quantitative data, with its key tools being FCT and BCT. Granular computing focuses on the multi-level analysis of concept information measurement in the cloud model, aiming to achieve transformation and adaptive generation of concepts at different granularities. Although the two-dimensional cloud model is more suitable for multi-factor decision-making research, related studies are relatively scarce due to dimensional coupling. Decision-making based on the cloud model is mostly applied to one-dimensional models. Existing research has proven the value of the cloud model through practical cases such as risk assessment and emergency response.

Research gaps

The similarities between this paper and existing research on index analysis are mainly two points. First, it is explained that scientific weight setting is of great significance in obtaining accurate results. Second, it is pointed out that the optimization of the decision method is mainly achieved through the fusion of methods with strong correlation. Compared with existing studies, the differences in this paper are mainly reflected in the following three aspects.

First, the analysis results of most studies rank alternatives based on ratings, which makes it difficult to accurately reflect the relationship between quantitative data and qualitative information. The proposed method can convert the qualitative judgment of the decision maker into quantitative weights based on F-AHP and effectively transform the analysis results into both quantitative and qualitative forms through the two-dimensional cloud generator, allowing the decision maker not only to clearly know the ranking of each alternative but also to intuitively understand the gaps among them. In contrast, some traditional uncertainty methods may focus on quantitative analysis, making it difficult to fully consider qualitative factors or lacking effective quantitative means when dealing with qualitative information.

Second, the existing research on service-oriented enterprises mainly analyzes from the external perspective of users, while less consideration is given to the internal perspective of management. However, business operation is a complex systematic project that requires the integration of internal and external factors to enhance market competitiveness. The proposed method can decompose complex problems into multi-dimensional indexes with a clear hierarchy based on F-AHP. By comprehensively reflecting external service demands and internal management elements, it effectively resolves differences in evaluators’ understanding of the importance of different indexes and the subjectivity of their judgments. Meanwhile, by relying on mutual conversion between qualitative concepts and quantitative data in the two-dimensional cloud model, the connection between enterprise dimensions and user dimensions is presented intuitively, clearly depicting their roles in an uncertain environment to ensure that evaluation results are not distorted. In contrast, some uncertainty analysis methods find it difficult to comprehensively consider multiple factors in the operation of service-oriented enterprises due to a lack of structured hierarchical decomposition and correlation display capabilities. Therefore, this study effectively resolves issues related to separating internal and external perspectives as well as neglecting uncertainty in analyzing service-oriented enterprises, providing a research method with practical value for optimizing enterprise decision-making.

Third, most of the current evaluations are in natural language, rather than using language scales or rating scales as in traditional analysis studies. Considering that there are many types of evaluation, the proposed method can intuitively reflect the fuzziness of qualitative concepts and the randomness of quantitative data through images of a comprehensive evaluation cloud, thereby obtaining reasonable results. In contrast, some traditional uncertainty methods can only deal with a single type of uncertainty and lack visual expressions.

Methods

Fuzzy analytic hierarchy process

In this paper, F-AHP is used to determine the weights of the comprehensive indexes of the ORH enterprise. Since 1983, many different F-AHP methods have been proposed. This paper adopts the method proposed by Buckley³⁹, and its calculation steps are shown as follows.

For the indexes of the same layer, evaluators compare two indexes (i and j) each time using the triangular fuzzy preference scale⁵⁹, as shown in Table 1. The triangular fuzzy number is composed of three real values, which represent the lower bound, modal value, and upper bound of the fuzzy number respectively. For example, if evaluators use the triangular fuzzy number (2, 3, 4) to represent their judgments, it means that the degree of importance of i over j is between 2 and 4, most likely 3.

Table 1 Triangular fuzzy preference scale.

Let $\:{\stackrel{\sim}{d}}_{ij}^{k}$ represent a set of the k_th evaluator’s preference of one index (i) over another (j). The pairwise comparison matrices are constructed as shown in (1).

$$\:{\stackrel{\sim}{A}}^{k}=\left[\begin{array}{ccc}{\stackrel{\sim}{d}}_{11}^{k}&\:{\stackrel{\sim}{d}}_{12}^{k}&\:\dots\:\\\:{\stackrel{\sim}{d}}_{21}^{k}&\:\dots\:&\:\dots\:\\\:{\stackrel{\sim}{d}}_{n1}^{k}&\:{\stackrel{\sim}{d}}_{n2}^{k}&\:\dots\:\end{array}\begin{array}{c}{\stackrel{\sim}{d}}_{1n}^{k}\\\:{\stackrel{\sim}{d}}_{2n}^{k}\\\:{\stackrel{\sim}{d}}_{nn}^{k}\end{array}\right]$$

(1)

The arithmetic average $\:{\stackrel{\sim}{d}}_{ij}$ of the k_th evaluator’s judgment values is found as shown in (2). Thus, the triangular fuzzy judgment matrix for each layer index can be obtained.

$$\:{\stackrel{\sim}{d}}_{ij}=\frac{{\sum\:}_{k=1}^{K}{\stackrel{\sim}{d}}_{ij}^{k}}{K}$$

(2)

The fuzzy weight of each index is obtained by the geometric mean method³⁹.

The geometric mean of the fuzzy comparison value of index i to other indexes is calculated respectively as shown in (3).

$$\:{\stackrel{\sim}{r}}_{i}={\left({\prod\:}_{j=1}^{n}{\stackrel{\sim}{d}}_{ij}\right)}^{1/n},i=\text{1,2},\dots\:n$$

(3)

Then, the fuzzy weight of the i_th index, represented by a triangular fuzzy number is computed as stated in (4).

$$\:{\stackrel{\sim}{w}}_{i}={{\stackrel{\sim}{r}}_{i}({\stackrel{\sim}{r}}_{1}{\stackrel{\sim}{r}}_{2}\dots\:{\stackrel{\sim}{r}}_{n})}^{-1}=({lw}_{i},{mw}_{i},{\mu\:w}_{i})$$

(4)

The centre of area method is used as the defuzzification method⁶⁰.

The non-fuzzy value $\:{M}_{i}$ of the fuzzy number $\:{\stackrel{\sim}{w}}_{i}$ can be obtained by (5).

$$\:{M}_{i}=\frac{{lw}_{i}+{mw}_{i}+{\mu\:w}_{i}}{3}$$

(5)

The normalized weight $\:{N}_{i}$ is obtained via (6).

$$\:{N}_{i}=\frac{{M}_{i}}{{\sum\:}_{1}^{n}{M}_{i}}\:,\:i=\text{1,2},..n$$

(6)

Two-dimensional cloud model

Definition of cloud model

Li⁶¹ proposed a certification model: a cloud model for the two-way conversion of qualitative concepts and quantitative data based on probability measure space. The definition of the one-dimensional cloud model is shown below:

Given a qualitative concept A defined over a universe of discourse $\:X=\left\{x\right\}$, let $\:x\in\:U$ be a random instantiation of the concept A and $\:{\mu\:}_{A}\left(x\right)\in\:\left[\text{0,1}\right]$ be the certainty degree of x belonging to A. Then, the distribution of x in X can be called a cloud, and x can be defined as a cloud drop. The membership degree $\:{\mu\:}_{A}\left(x\right)$ is in the sense of fuzzy set theory. Therefore, the certainty degree of x belonging to the concept A is a probability distribution rather than a fixed number.

In this way, the one-dimensional cloud model can effectively integrate the randomness and fuzziness of concepts through the three numerical characteristics as follows:

Expectation Ex is the mathematical expectation of the cloud drops belonging to a concept in the universe of discourse. It can be regarded as the most representative and typical sample of the qualitative concept.

Entropy En represents the uncertainty measurement of a qualitative concept. It is determined by both the randomness and the fuzziness of the concept. On the one hand, as a measure of randomness, En reflects the dispersing extent of the cloud drops. On the other hand, it is also a measure of fuzziness, representing the acceptable scope of the universe of discourse.

Hyper-entropy He is the degree of uncertainty associated with entropy En.

The one-dimensional cloud diagram and its three numerical characteristics are shown in Fig. 1. Each point in the cloud map represents a cloud droplet, which is the basic building block of a cloud. The expectation represents the central location of the cloud droplet distribution. Entropy is used to express the degree of uncertainty of the cloud. The greater the hyper-entropy, the more dispersed the cloud droplets.

Fig. 1

One-dimensional cloud diagram and its numerical characteristics.

According to the definition of the one-dimensional cloud model, the three numerical characteristics of the two-dimensional cloud⁶² can be further obtained as expectation $\:({Ex}_{1},{Ex}_{2})$, entropy $\:({En}_{1},{En}_{2})$, and hyper-entropy $\:({H}_{1},{H}_{2})$. A two-dimensional cloud diagram is shown in Fig. 2. In a two-dimensional cloud model, the expectation represents the center of a cluster of cloud droplets. Entropy directly reflects the range of elements that can be conceptually accepted in the two-dimensional number field space. Hyper-entropy represents the cohesion of the cloud droplets.

Fig. 2

Two-dimensional cloud diagram.

Although the one-dimensional cloud model can effectively deal with the uncertainty of a single dimension, in the complex market competition under the joint effect of internal operation and external analysis, analysis from only one perspective may lead to deviations in the results. Therefore, this study uses the two-dimensional cloud model to effectively combine the enterprise dimension and the user dimension, evaluate the ORH industry intuitively and accurately, and provide valuable insights for managers in strategic optimization. The generation process of a two-dimensional cloud model includes a two-dimensional forward cloud generator and a two-dimensional backward cloud generator⁶³. By using these two generators, the two-way conversion of qualitative concepts and quantitative data in the analysis process can be realized.

Two-dimensional forward cloud generator

The numerical characteristics of a pair of one-dimensional cloud models can be used to represent the fuzziness and uncertainty under the joint action of the two dimensions. The two-dimensional forward cloud generator is shown in Fig. 3.

Fig. 3

Two-dimensional forward cloud generator.

Algorithm 1: Implementation of the two-dimensional forward cloud generator.

Two-dimensional backward cloud generator

The characteristics of the visual cloud image can be reflected by the numerical characteristics of the cloud. The expected value, entropy, and hyper-entropy synthetically describe the properties of the two-dimensional backward cloud generator. The two-dimensional backward cloud generator is shown in Fig. 4.

Fig. 4

Two-dimensional backward cloud generator.

Algorithm 2: Implementation of two-dimensional backward cloud generator.

Hybrid decision method

The implementation structure of the hybrid decision method is shown in Fig. 5, which is mainly divided into three stages. The first stage is to determine the experts and the objects to be evaluated, design the indexes for two-dimensional analysis, and standardize the collected initial data. In the evaluation of ORH enterprises, it is recommended that the invited experts have a thorough understanding of the overall development trend of the ORH industry, including the industry’s development history, market size, growth trend, and competitive landscape. Meanwhile, experts should possess professional data analysis and processing capabilities and be able to make decisions based on fuzzy information. In addition, experts with management experience in service enterprises or transportation enterprises will be given priority consideration.

The second stage is to calculate the index weights based on F-AHP. Firstly, the experts compare all indexes pairwise to obtain the triangular fuzzy judgment matrix reflecting the importance of each index in each dimension. Secondly, the fuzzy weight of each index is obtained. Finally, the non-fuzzy values and standard weights of each index are derived.

The third stage is mainly based on the cloud model. Experts first design the standard review set by combining the two dimensions and use the forward cloud generator to obtain the standard review cloud figure. Secondly, based on the index weights calculated by F-AHP, the normalized data are transformed into cloud numerical characteristics by using the backward cloud generator. Thus, the connection between F-AHP and the two-dimensional cloud model is achieved through the index weights. Finally, the forward cloud generator is used to obtain the evaluation cloud figure of each object, and the result is obtained by comparing it with the standard comment cloud figure. Please see Sect. 4.4 for specific solution steps of the proposed method.

Fig. 5

Implementation structure of the hybrid decision method.

Although there are excellent research achievements, the proposed method has two advantages. On the one hand, the proposed method can reduce the influence of uncertainty on the results. In F-AHP, a fuzzy number is used to express the fuzziness of analysis. On this basis, the fuzzy range is further quantified by combining the entropy of a two-dimensional cloud model, which avoids the problem that the fuzzy number interval is too broad. At the same time, the hyper-entropy of the two-dimensional cloud model can describe random fluctuations to make up for F-AHP’s shortcomings in reflecting randomness and describe uncertainty in analyzing ORH enterprises more comprehensively. In addition, F-AHP can better reflect experts’ tendencies at each level of index, and the two-dimensional cloud model can balance subjectivity and objectivity in analysis by randomly generating many cloud drops and providing an accurate decision-making basis.

On the other hand, this method can not only rank the analysis objects and show their differences, but also directly reflect the advantages and disadvantages of each object. Specifically, the proposed method can evaluate and sort through the expected value in the comprehensive characteristics and intuitively show the differences of each ORH enterprise through the cloud diagram. Based on calculating multiple index weights by F-AHP, the performance of each ORH enterprise in different dimensions is dynamically analyzed using the cloud drop distribution generated by the two-dimensional forward cloud generator.

At present, many studies focus on a certain aspect of the enterprise but do not analyze the enterprise from a global perspective. However, multi-dimensional analysis is an important way to adapt to the development of multiple markets. At the same time, most studies ignore the uncertainty of concepts in natural language. To get the most authentic feedback, enterprises do not ask users to rate according to a specific language scale. Most enterprises allow users to leave comments or suggestions for improvement based on their experience. For example, users’ comments include “relatively satisfied and not bad.” How to obtain effective information from similar language is the key factor that determines analysis accuracy.

Analysis procedure

Index system

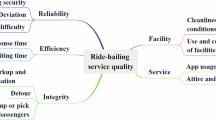
This paper constructs an index system from the two dimensions of enterprises and users to evaluate the situations of ORH enterprises, as shown in Fig. 6. At present, most analyses of service-oriented enterprises are mainly conducted from the user perspective because the core of such enterprises is to improve user satisfaction and thus enhance user needs. Therefore, according to the service nature of ORH services, two first-level indexes, ride satisfaction index (C) and app (application program) satisfaction index (D), are set in the user dimension.

Based on this, the enterprise dimension is added. It is not comprehensive to evaluate an enterprise only from external feedback; by combining internal situations and external feedback, accurate results can be reflected from a global perspective. Due to the strict regulations governing ORH data, it is challenging to access comprehensive information beyond market penetration, monthly active users, and daily active users. Nevertheless, awareness, loyalty, and recommendation are critical indexes that reflect an enterprise’s operational performance. Therefore, the data for these operational indexes were obtained through expert evaluation.

In Fig. 6, four first-level indexes are designed in different dimensions: management index (A) and operation index (B) in the enterprise dimension; ride satisfaction index (C) and app satisfaction index (D) in the user dimension. The design of these four first-level indexes is based on the relevant regulations for ORH enterprises and their business operations as stipulated in the “Interim Measures for the Administration of Online Taxi Booking Business Operations and Services” issued by the Ministry of Transport of China⁶⁴. The four first-level indexes correspond to different second-level indexes; the meanings of the 13 s-level indexes are explained below.

Fig. 6

Comprehensive index system of ORH.

For the design of indexes in the enterprise dimension, we analyze the market expansion logic and management effect evaluation of service-oriented enterprises in theories such as customer relationship management and brand management^65,66. On this basis, we refer to the analysis of management and operation from the reports of Chinese ORH enterprises such as DiDi and UCAR. Market penetration (A1) refers to the ratio between the number of users of a certain enterprise and the total number of users that the entire market may have at that time. Monthly active users (A2) and daily active users (A3) refer to the number of users (excluding those who repeatedly log in) who use the services of a certain enterprise within a statistical period (one day/one month). A2 and A3 respectively weigh user stickiness and recession cycles of ORH services from macro and micro perspectives. Through market penetration and user activity, the management level of the enterprise can be well reflected.

Enterprise awareness (B1) refers to people’s understanding of the name, logo, and service type of a certain enterprise. User loyalty (B2) refers to the degree of users’ favorable impression of a certain enterprise, which determines whether users are willing to repeatedly use the services of the enterprise. Enterprise recommendation (B3) measures the likelihood that a certain user will recommend a certain enterprise to others. Due to the fierce competition in the ORH market, enterprise awareness is the basis for operation, and user loyalty is key to sustainable operation. Enterprise recommendations can enhance both enterprise awareness and user loyalty. Therefore, these three indexes are selected to evaluate the operational effect of ORH enterprises.

For the design of indexes related to the user dimension, customer satisfaction theory indicates that the quality of user experience is the core of the competitiveness of service-oriented enterprises⁶⁷. Based on this theoretical support, the establishment of these indexes refers to the calculation methods for “reputation value” from DiDi, driver service standards from CaoCao, and driver performance assessment standards from UCAR. Ride safety (C1) refers to users’ trust in personal and property safety when using ORH services. Vehicle comfort (C2) refers to users’ comfort with the vehicle. Driver satisfaction (C3) refers to users’ satisfaction with the driver.

Customer service satisfaction (D1) refers to the user’s satisfaction with the service attitude and efficiency of customer service personnel. Software operability (D2) refers to the degree of convenience and rapidity for users when using enterprise software. Because users’ demand for ORH is sent anytime and anywhere, this puts a high requirement on the response speed of the software. Car-hailing success rate (D3) refers to users’ satisfaction with waiting time and frequency of successfully matched vehicles. Because demand for ORH is dynamic and can be affected by user cancellations, it is necessary to evaluate the probability of successful matching of demand. Price rationality (D4) refers to users’ acceptance of prices in different scenarios.

The design of the four first-level indexes and thirteen second-level indexes, based on relevant literature and industry standards, has been reviewed by enterprise experts and university scholars, ensuring the scientific validity and rationality of the ORH index system. The indexes in the enterprise dimension have achieved full coverage from management to operation, ensuring that decisions can control the development direction of the enterprise. The indexes in the user dimension focus on core experiences of offline travel and online services, ensuring that decisions can accurately capture user needs. In addition, indexes such as market penetration and enterprise awareness are related to an enterprise’s competitive position in the market. Indexes such as price rationality and user loyalty are related to corporate profitability and long-term development. Indexes such as ride safety and driver satisfaction correspond to industry regulatory requirements, ensuring that decisions take into account both short-term competition and long-term survival. Overall, user-oriented indexes provide external feedback on the operational effectiveness of enterprises, while enterprise-oriented indexes serve as internal drivers of user satisfaction. The designed index system covers all dimensions including market conditions, users, operations, and sustainability, providing a comprehensive and accurate assessment basis for competition decisions and strategy optimization for ORH enterprises.

Standard comment sets

The comment grades and score intervals of the enterprise dimension and the user dimension are shown in Table 2. Each dimension is divided into five comment grades by experts, with the third grade “Mediocre” as the neutral value, gradually increasing to the left grade and gradually decreasing to the right grade. The score intervals $\:\left(\text{0,1}\right]$ of each dimension are divided into five segments by experts. The closer a score is to 1, the higher it is; conversely, the closer a score is to 0, the lower it is. The comment grade corresponding to the i_th score interval $\:({\lambda\:}_{i}^{min},{\lambda\:}_{i}^{max}]$ is converted to numerical characteristics $\:SC({{E}_{x}}_{i},{{E}_{n}}_{i},{{H}_{e}}_{i})(i=\text{1,2},\dots\:,5)$ of the standard comment cloud model using (12)-(14). The numerical characteristics are calculated based on the upper and lower limits of each interval, and boundary parameters are described by half-normal clouds.

$$\:{E}_{xi}=\left\{\begin{array}{c}{\lambda\:}_{i}^{min}\:\:\:\:\:\:i=1\\\:\frac{{\lambda\:}_{i}^{min}+{\lambda\:}_{i}^{max}}{2}\:\:\:\:\:\:\:1<i<5\\\:{\lambda\:}_{i}^{max}\:\:\:\:\:\:i=5\end{array}\right.$$

(7)

$$\:{{E}_{n}}_{i}=\left\{\begin{array}{c}\frac{{\lambda\:}_{i}^{max}-{\lambda\:}_{i}^{min}}{6}\:\:\:\:\:\:\:\:\:\:1<i<5\\\:\frac{{\lambda\:}_{i}^{max}-{\lambda\:}_{i}^{min}}{3}\:\:\:\:\:\:\:\:\:\:\:i=1or5\end{array}\right.$$

(8)

$$\:{{H}_{e}}_{i}=k$$

(9)

In (14), k is a constant that can be adjusted according to the fuzzy degree of the comment set. For instance, if the fuzziness of the concept is weak, k can be set to a small value, such as 0.02–0.05 as defined in this study. If the fuzziness of the concept is stronger, the hyper-entropy can be appropriately increased. Meanwhile, some studies adopt empirical proportional relationships; for instance, setting the hyper-entropy as one-third of the entropy ensures the correlation between hyper-entropy and entropy^56,57,58. In different application situations, the hyper-entropy of the standard comment cloud can be adjusted to adapt to different criteria and maintain flexibility and adaptability in the model.

Take calculating the numerical characteristics of the comment grade “High” as an example. Because it is known that $\:i=4$ and its score interval is $\:(0.55,0.75]$, according to (12), $\:{E}_{x3}=\frac{0.55+0.75}{2}=0.65$. According to (13), $\:{{E}_{n}}_{3}=\frac{0.75-0.55}{6}\approx\:0.033$. The value of k is determined by the expert based on the fuzzy degree of the comment set; therefore, $\:{{H}_{e}}_{3}=0.03$. Similarly, the numerical characteristics of each comment grade in different dimensions can be obtained.

Table 2 Standard comment sets.

It is necessary to establish a comprehensive standard comment for ORH enterprises to accurately evaluate different dimensions. According to the comment grades of the enterprise dimension and the user dimension, the comprehensive standard comment is divided into “very good,” “good,” “mediocre,” “bad,” and “very bad.” These five comprehensive standard comments correspond to the numerical characteristics of the two dimensions. The two-dimensional forward cloud generator can be used to convert comprehensive standard comments into a standard comment cloud, as shown in Fig. 7. Because “very good” and “very bad” are represented by ascending and descending half-normal clouds, some cloud drops in Fig. 7 exceed the boundary of [0,1]. Only cloud drops within the boundary [0,1] are considered in the analysis of objects.

Fig. 7

Standard comment cloud.

Cloud numerical characteristic and membership degree

The cloud of each second-level index is called the base cloud of its first-level index, and the first-level index can be obtained by the combination of its base cloud. Equation (10) can be used to combine the cloud numerical characteristic $\:{C}_{i}({{E}_{x}}_{i},{{E}_{n}}_{i},{{H}_{e}}_{i})$ of the second-level index to get the first-level index cloud numerical characteristic $\:{C}_{i}{\prime\:}({{E}_{x}}_{i}^{{\prime\:}},{{E}_{n}}_{i}^{{\prime\:}},{{H}_{e}}_{i}^{{\prime\:}})$. $\:{w}_{i}$ is the weight of each second-level index.

$$\:\left\{\begin{array}{c}{{E}_{x}}_{i}^{\prime\:}={\sum\:}_{i=1}^{n}{{E}_{x}}_{i}{w}_{i}\\\:{{E}_{n}}_{i}^{\prime\:}=\frac{{\sum\:}_{i=1}^{n}{{E}_{n}}_{i}{w}_{i}^{2}}{{\sum\:}_{i=1}^{n}{w}_{i}^{2}}\\\:{{H}_{e}}_{i}^{\prime\:}=\frac{{\sum\:}_{i=1}^{n}{{H}_{e}}_{i}{w}_{i}^{2}}{{\sum\:}_{i=1}^{n}{w}_{i}^{2}}\end{array}\right.$$

(10)

Equation (11) can be used to combine the cloud numerical characteristic $\:{C}_{i}{\prime\:}({{E}_{x}}_{i}^{{\prime\:}},{{E}_{n}}_{i}^{{\prime\:}},{{H}_{e}}_{i}^{{\prime\:}})$ of the first-level index to get the comprehensive cloud numerical characteristic $\:C({E}_{x},{E}_{n},{H}_{e})$ of each enterprise.$\:\:{w}_{i}{\prime\:}$ is the weight of each first-level index.

$$\:\left\{\begin{array}{c}{E}_{x}=\frac{{\sum\:}_{i=1}^{n}{{E}_{x}}_{i}^{\prime\:}{{E}_{n}}_{i}^{\prime\:}{w}_{i}^{\prime\:}}{{\sum\:}_{i=1}^{n}{{E}_{n}}_{i}^{\prime\:}{{w}_{i}}^{{\prime\:}}}\\\:{E}_{n}={\sum\:}_{i=1}^{n}{{E}_{n}}_{i}^{\prime\:}{w}_{i}^{\prime\:}\\\:{H}_{e}=\frac{{\sum\:}_{i=1}^{n}{{H}_{e}}_{i}^{\prime\:}{{E}_{n}}_{i}^{\prime\:}{w}_{i}^{\prime\:}}{{\sum\:}_{i=1}^{n}{{E}_{n}}_{i}^{\prime\:}{{w}_{i}}^{{\prime\:}}}\end{array}\right.$$

(11)

After obtaining the comprehensive cloud numerical characteristics of each enterprise, the comprehensive membership degree $\:{\xi\:}_{j}$ of each enterprise and each standard comment cloud is calculated according to (17). According to the principle of maximum membership, the final comprehensive result for each enterprise is the corresponding interval of the standard comment cloud with the maximum membership degree.

$$\:{\xi\:}_{j}={exp}\left(-\left(\frac{{\left({x}_{i}-{{E}_{x}}_{1j}\right)}^{2}}{2{\left({{E}_{n}}_{1j}\right)}^{2}}+\frac{{\left({y}_{i}-{Ex}_{2j}\right)}^{2}}{2{\left({{E}_{n}}_{2j}\right)}^{2}}\right)\right)\:\:i=1,j=1,..,5$$

(12)

In (17), $\:{x}_{i}$ and $\:{y}_{i}$ refer to the two-dimensional normal random numbers generated by each enterprise in the two-dimensional forward cloud generator. $\:({{E}_{x}}_{1j},\:{{E}_{n}}_{1j})$ and $\:({Ex}_{2j},\:{{E}_{n}}_{2j})$ respectively refer to the expectation and entropy of the standard evaluation in the two dimensions.

Meanwhile, (18) can be used to calculate the membership degree of each enterprise in each dimension.

$$\:{\xi\:}_{j}=exp\left(-\frac{{\left({x}_{i}-{{E}_{x}}_{j}\right)}^{2}}{2{\left({{E}_{n}}_{j}\right)}^{2}}\right)$$

(13)

In (18),$\:\:{x}_{i}$ refers to the normal random number generated by each enterprise in the one-dimensional forward cloud generator. $\:{{E}_{x}}_{j}$ and $\:{{E}_{n}}_{j}$ refer to the expectation and entropy of the standard evaluation in single dimension, respectively.

In the cloud drop $\:({x}_{i},{y}_{i},{\mu\:}_{i})$ generated by the forward cloud generator, $\:{\mu\:}_{i}$ represents the membership degree of $\:{(x}_{i},{y}_{i})$ belonging to this linguistic value. Therefore, according to the definition of the cloud model, (17) and (18) denote the formulas used to calculate $\:{\mu\:}_{i}$ in cloud drops⁶⁸. Meanwhile, previous studies have indicated that normal membership functions are more appropriate for characterizing various fuzzy concepts compared to other classical membership functions⁶³.

Solution steps of the hybrid decision method

In the analysis scenario with natural language comments and multiple dimensions, the solution steps of the hybrid decision method based on F-AHP and the two-dimensional cloud model are as follows:

Step1: Determine the experts involved in this analysis and the objects to be evaluated, design two-dimensional indexes, and collect sample data.

Step2: Ask the experts to score all the indexes in combination with Table 1 and compare them in pairs. Assuming that all experts have the same authority, the triangular fuzzy judgment matrix reflecting the importance of each index in each dimension is obtained by using (1) and (2).

Step3: Use (3) and (4) to find the geometric mean $\:{\stackrel{\sim}{r}}_{i}$ and the fuzzy weight $\:{\stackrel{\sim}{w}}_{i}$ of each index, respectively.

Step4: Use (5) and (6) to get the non-fuzzy value $\:{M}_{i}$ of each index and the normalized weight $\:{N}_{i}$; then, the normalized weight $\:{N}_{i}$ is the weight of each index.

Step5: Experts design the score interval by combining the two dimensions. The score interval is divided into (0,1); the closer to 1, the higher the score, and the closer to 0, the lower the score.

Step6: Use (12)-(14) to convert the comment grade corresponding to the i_th score interval $\:[{\lambda\:}_{i}^{min},{\lambda\:}_{i}^{max}]$ into the numerical characteristics $\:SC({{E}_{x}}_{i},{{E}_{n}}_{i},{{H}_{e}}_{i})(i=\text{1,2},\dots\:,5)$ of the standard comment sets. Then the two-dimensional forward cloud generator is used to obtain the standard comment cloud image.

Step7: After standardized processing of sample data, the corresponding cloud numerical characteristics are obtained through the one-dimensional backward cloud generator.

Step8: The comprehensive cloud numerical characteristics of each object can be obtained through the index weights obtained in Step 4 and (15)-(16). Two-dimensional forward cloud generator is used to obtain the evaluation cloud image of each object, and compare it with the standard comment cloud image.

Step9: Calculate the comprehensive membership degree of the object and the standard comments according to (17), and use (18) to calculate the membership degree under a single dimension, so as to obtain the final result.

Through these solution steps, the proposed method can be widely applied to common analysis studies such as tourism, e-commerce, and the catering industry.

Material

Analysis objects

DiDi, UCAR, CaoCao, and ShouQi, four ORH enterprises that occupy a mainstream position in the Chinese market, are selected as the analysis objects and shown in Fig. 8.

Fig. 8

Four analysis objects.

DiDi established its dominant position in the ORH market through a price subsidy strategy. Nine business systems are designed for different user groups, among which the fast ride and tailored car services are its strongest core businesses.

UCAR is an Internet travel enterprise launched jointly with a third-party enterprise, featuring tailored car services and car rental services. This enterprise is mainly aimed at middle- to high-end user groups, providing customized services for commuting, chartered cars, and airport pickups.

ShouQi is an ORH enterprise owned by the Shou Qi group. This enterprise is independently operated by the group and signs labor contracts with drivers holding employment licenses. ShouQi has a variety of business models, such as tailored car services, taxis, substitute driving, and international transport.

Caocao is China’s first new-energy vehicle-based shared mobility service platform to obtain an ORH license. It attaches great importance to the environmental performance of vehicles and the driving experience, and has outstanding performance in energy conservation and emission reduction. Caocao adopts an intelligent dispatching system and sets up a security customer service team, providing a variety of services for different scenarios such as real-time ride-hailing and pre-ordered rides.

Sample data

The questionnaire survey and data collection were conducted for ORH enterprises. To avoid any deviation, the questionnaire survey of this study adopted stratified sampling to ensure that the sample covered all subgroups of ORH users, such as low-frequency users and the elderly group. The data collection period was from May 2023 to May 2024, and the questionnaire survey period was in May 2024; a total of 432 valid questionnaires were collected. The above data came from a research project. Among the respondents of the questionnaire, 52.1% were male and 47.9% were female. The gender ratio was basically balanced with a slight bias towards males, which is in line with the characteristic that male users of ORH services tend to travel for business purposes slightly more frequently. The proportion of people aged 18–25 is 23.7%, those aged 26–35 account for 44.1%, those aged 36–45 make up 22.3%, and those aged 46 and above constitute 9.9%. This survey covers all age groups, which is in line with the actual situation that the core users of ORH services are mainly young and middle-aged people. In terms of usage frequency distribution, 24.3% of the respondents use ORH services once a week or less; 40.8% use it two to three times a week; 21.6% use it four to six times a week; and 13.3% use it seven times or more per week. This distribution indicates that ORH has become an important mode of daily transportation for people overall; thus, the demographic distribution of the respondents aligns with common characteristics of ORH users, providing a reasonable data basis for subsequent analysis.

In the user dimension, the initial data of the indexes were obtained through online questionnaires randomly distributed to users of ORH enterprises. In the enterprise dimension, the initial data of the operation indexes were obtained from the scores of four experts based on the questionnaire survey results and relevant news reports. The initial data of the management indexes were obtained through reports from each enterprise (data from DiDi, UCAR, CaoCao, and ShouQi were selected for comparison, excluding data from other ORH enterprises). In enterprise reports, there are a few cases where the data on monthly active users and daily active users are missing. In response to situations where the monthly active user data for a certain enterprise in a specific month was missing, we estimated it by combining data from three months before and after that month with the industry’s growth rate during that same period. For situations where daily active user data for a certain enterprise was missing, we calculated the average ratio of daily active users to monthly active users for this enterprise and then estimated daily active users based on this month’s monthly active users and the average ratio.

In the management index of the enterprise dimension, because the units of its initial data are different and the differences among the values are large, standardized processing is carried out using (19). The processed data are shown in Table A1 in Appendix A due to the large number of these data. Table A1 shows the market penetration (A1), monthly active users (A2), and daily active users (A3) of the four enterprises over one year.

$$\:Y=\frac{{log}_{10}\left({x}_{i}\right)}{{{log}_{10}\left({x}_{i}\right)}^{max}+{e}^{-1}}\:\:\:\:\:(0<i\le\:12)$$

(14)

In (19), $\:{log}_{10}\left(x\right)$ is a common preprocessing method used to narrow the large gap between the initial data. For example, two initial data with a large gap in daily active users(A3) are $\:1.5044\times\:{10}^{7}$ and $\:9.5\times\:{10}^{4}$. $\:{{log}_{10}\left({x}_{i}\right)}^{max}$ is the maximum value in the initial data of an enterprise in a certain index after standardization, and $\:{e}^{-1}$ ensures the accuracy of data standardization while making the maximum value of $\:Y$ not be 1⁶⁹.

The initial data of the operation index in the enterprise dimension are scored by four experts. The scoring interval is 0–1, where 1 is the highest score and 0 is the lowest score, with two decimal places kept. The experts’ scoring results are shown in Table 3. This table shows the scores of the four enterprises in enterprise awareness (B1), user loyalty (B2), and enterprise recommendation (B3).

Table 3 Experts scoring results.

The initial data of all second-level indexes in the user dimension are the average scores of the corresponding questions. In the questionnaire, relative questions are scale questions with a score range of 0–5, with 0 as the lowest score and 5 as the highest score. All the average scores are divided by 5 to obtain standardized data, as shown in Table 4. This table shows the average scores obtained by the four enterprises in seven aspects: ride safety (C1), vehicle comfort (C2), driver satisfaction (C3), customer service satisfaction (D1), software operability (D2), car-hailing success rate (D3), and price rationality (D4).

Table 4 Standardized data of survey questionnaires.

Results

Index weights

Triangular fuzzy judgment matrix

The three experts pairwise compared and rated all the indexes in order to objectively evaluate the weight of each index. Combined with the triangular fuzzy preference scale shown in Table 1, the experts’ judgments on the importance of the indexes are obtained. Assuming that the authority of each expert is consistent, (1) and (2) are used to obtain the triangular fuzzy judgment matrices reflecting the importance of the first-level and second-level indexes in each dimension. This method can effectively test the consistency of judgment before and after establishing the partial order relation among experts, as shown in Tables 5 and 6.

Table 5 Judgment matrices of the enterprise dimension.

Table 6 Judgment matrices of the user dimension.

Weight calculation

For the enterprise dimension and user dimension, the geometric mean $\:{\stackrel{\sim}{r}}_{i}$ and the fuzzy weight $\:{\stackrel{\sim}{w}}_{i}$ of each index are obtained, as shown in Table 7. $\:{\stackrel{\sim}{r}}_{i}$ is calculated by (3), and then $\:{\stackrel{\sim}{w}}_{i}$ is calculated by (4).

Table 7 Geometric mean and fuzzy weights.

The non-fuzzy value $\:{M}_{i}$ and the normalized weight $\:{N}_{i}$ of each index in the enterprise dimension and the user dimension are obtained, as shown in Table 8. $\:{M}_{i}$ of the fuzzy weight $\:{\stackrel{\sim}{w}}_{i}$ can be obtained by (5). The normalized weight $\:{N}_{i}$ is obtained by normalization of (6).

The normalized weights in Table 8 are summarized to obtain the comprehensive index weights of the ORH enterprises, as shown in Table 9. Among all the second-level indexes, ride safety (C1) has the highest weight. This is because incidents that damage personal and property safety will not only cause irreparable serious harm to users but also affect the harmonious order of society, making the public lose confidence in ORH enterprises and even in the whole industry.

Table 8 Non-fuzzy values and normalized weights.

Table 9 Comprehensive index weights.

Results analysis

Comprehensive cloud numerical characteristics

The data of each enterprise in Table A1 and Table 3 are converted by the one-dimensional backward cloud generator⁵⁰ to obtain the corresponding cloud numerical characteristics. Because the data in Table 4 are average values, they directly correspond to the standard comment sets of the user dimension in Table 2 to obtain the cloud numerical characteristics.

For example, the C1 value of DiDi in Table 4 is 0.75, which belongs to the score interval of U3 in Table 2. By replacing the expectation in the U3 numerical characteristic with 0.75, the numerical characteristic of DiDi in C1 can be obtained as (0.75, 0.025, 0.025). The cloud numerical characteristics of each enterprise are shown in Table 10. This table respectively shows the cloud numerical characteristics of four enterprises on 13 s-level indexes, where the first cloud digital feature is expectation, the second is entropy, and the third is hyper-entropy.

Table 10 Cloud numerical characteristics of each enterprise.

The comprehensive cloud numerical characteristics of each enterprise are obtained by combining the index weights shown in Table 9 and (15)-(16), as shown in Table 11. This represents the numerical characteristics of the cloud for each enterprise at each level and in each dimension.

Expectations in numerical characteristics can be used as an important reference for enterprises to evaluate their own strengths and weaknesses. By comparing the expectations of each enterprise in Table 11, it can be found that DiDi performs best in the enterprise dimension, while CaoCao performs best in the user dimension. The expectation gap between enterprises in the user dimension is small, indicating that the ORH industry is currently focusing on user service experience. In contrast, the difference between the maximum expectation and the minimum expectation in the enterprise dimension is 0.481, indicating that an imbalance phenomenon is obvious in terms of enterprise scale and market expansion.

Entropy in numerical characteristics can help enterprises understand fluctuations in their own performance. According to Table 11, it can be found that the entropy value of the user dimension for ShouQi is the largest, indicating that ShouQi has a large degree of dispersion in user experience. Some users may have a good experience, while others have a bad experience. Therefore, ShouQi needs to focus on analyzing the reasons for this difference and improve overall user evaluation.

Hyper-entropy can help enterprises judge whether their performance in different dimensions is easily affected by the external environment. It can be found from Table 11 that, except for DiDi’s hyper-entropy in the enterprise dimension, the other hyper-entropy values are small; that is, the stability of the remaining three enterprises is high. DiDi needs to pay attention to changes in the market in a timely manner and take measures in advance for possible emergencies.

Table 11 Comprehensive cloud numerical characteristics of enterprises.

Comparative analysis of methods

In order to verify the feasibility of the proposed method in evaluating ORH enterprises, TOPSIS, weighted aggregated sum product assessment (WASPAS), multi-attributive border approximation area comparison (MABAC), and Monte Carlo simulation (MC) are used as result comparison methods. These methods are widely used in the field of multi-objective decision-making, and the detailed solution process can be referred to in^70,71,72,73.

Among these models, TOPSIS sorts the ORH enterprises by calculating the relative proximity of each enterprise to the positive ideal solution and the negative ideal solution, where the positive ideal solution is the combination of the optimal values of each index, and the negative ideal solution is the combination of the worst values of each index. WASPAS combines the weighted sum model and the weighted product model to prioritize ORH enterprises based on comprehensive optimality criteria. MABAC combines AHP to determine rankings by calculating the distance between each firm and the boundary approximate region. MC defines a probability distribution for each index to quantify uncertainty and ranks ORH enterprises by analyzing the mean, standard deviation, and confidence interval of simulated composite scores. The calculation results of all models and rankings of ORH enterprises are shown in Fig. 9. It can be seen from Fig. 9 that the development gap among ORH enterprises is mainly concentrated in enterprise management rather than user service.

Fig. 9

Comparison of method results.

The ranking of the enterprise dimension for the four comparison models is DiDi > UCAR > CaoCao > ShouQi. The ranking of the user dimension for the four comparison models is CaoCao > UCAR > ShouQi > DiDi. These results are consistent with the rankings obtained from the expectations of the comprehensive cloud numerical characteristics, which proves the accuracy and feasibility of the hybrid decision method.

Although the four models used for comparison can accurately obtain the analysis ranking of a single dimension, TOPSIS, WASPAS, and MABAC have difficulty reflecting the fuzziness and randomness in multi-dimensional analysis architectures. In the calculation process of TOPSIS, each index is treated as an independent factor. However, there is a correlation between the indexes of each dimension in the analysis of ORH enterprises, which affects the accuracy of TOPSIS’s analysis results. WASPAS combines two weighting methods in its calculation process, which leads to large differences in the analysis results due to small changes in weights. MABAC is suitable for analyzing numerical data; however, it introduces additional errors when quantifying qualitative information and increases subjectivity in determining attribute boundary values. Although MC is a classical method for dealing with uncertainty, its resulting instability is enhanced with an increase in data size. At the same time, MC results are affected by the accuracy of the probability distribution of variables. Compared with other methods, the proposed method can reduce uncertainty and intuitively analyze ORH enterprises’ performance under different dimensions through cloud images, helping decision makers accurately judge differences from competitors.

Results discussion

Let the number of cloud drops be N = 3000. According to the two-dimensional forward cloud generator, the comprehensive evaluation cloud drops and cloud figures for four enterprises can be generated.

Results discussion of DiDi

It can be seen from Fig. 10 that the comprehensive evaluation cloud of DiDi is mainly located between the “very good” and the “good” standard comment clouds. Most cloud drops in the enterprise dimension are in the “very good” range. Some cloud drops in the user dimension fall into the “good” range, while others fall into the “mediocre” range.

Fig. 10

Evaluation cloud of DiDi. a Front view; b Top view.

It is necessary to further verify the analysis results by calculating the membership degree because the result error may be caused by judging directly from the figures. According to (17), the membership degree of DiDi for each standard comment is calculated as shown below. $\:\:{{{\upxi\:}}_{\text{L}1}=6.761\times\:{10}^{-3},\:\:{\upxi\:}}_{\text{L}2}=9.546\times\:{10}^{-24},\:\:{{\upxi\:}}_{\text{L}3}=2.113\times\:{10}^{-66},\:\:{{\upxi\:}}_{\text{L}4}=2.929\times\:{10}^{-120},\:\:{{\upxi\:}}_{\text{L}5}=1.701\times\:{10}^{-99}$. According to the principle of maximum membership degree, the value of $\:{{\upxi\:}}_{L1}$ is the largest, so the comprehensive evaluation of DiDi is “very good”.

Meanwhile, (18) is used to calculate the membership degree under each dimension. In the enterprise dimension, $\:{{\upxi\:}}_{E1}=0.461$ is the maximum membership degree, so DiDi in this dimension is evaluated as “very high”. In the user dimension, $\:{{\upxi\:}}_{U3}=0.410$ is the maximum membership degree, so DiDi in this dimension is evaluated as “mediocre”.

The main reason for the above results is that the types and quantities of businesses launched by DiDi basically cover all market segments of the ORH industry, making it superior to other enterprises in management and operational aspects such as market penetration and enterprise popularity. This also means that the user base for DiDi is far larger than that of other enterprises. Therefore, DiDi would face more personalized demands and higher expectations, which may make it more difficult to guarantee user satisfaction compared to other enterprises.

Based on the above analysis, three recommendations are proposed for DiDi. First, leveraging its corporate strengths such as resource integration and industry influence, DiDi should integrate brand promotion with user engagement more closely. For instance, in response to the social call for carbon neutrality, DiDi could design a public welfare activity where users can receive a green travel discount coupon after completing a certain number of carpooling trips. This not only utilizes corporate resources to reinforce the brand’s commitment to social responsibility but also fosters stronger user identification through active participation. Second, given that the evaluation of the user dimension is “mediocre,” DiDi should establish a comprehensive system that spans from feedback collection to the implementation of improvements. Specifically, the company should expand user feedback entry points through the app homepage, social media platforms, and other channels. Additionally, it should enhance its feedback processing capabilities in terms of response time and resolution effectiveness, thereby enabling users to clearly perceive the impact and value of their feedback. Third, it is recommended that DiDi establish a user demand-driven strategic adjustment mechanism; regularly conduct comprehensive evaluations from both enterprise and user perspectives; clarify the alignment between enterprise management and user needs, and thereby achieve a dynamic balance between internal operations and external development.

Results discussion of UCAR

It can be seen from Fig. 11 that the comprehensive evaluation cloud of UCAR is mainly located between the “good” and the “mediocre” standard comment clouds. Most cloud drops in both the enterprise dimension and the user dimension are located in the “good” range, and only a small part of cloud drops falls in the “mediocre” range.

Fig. 11

Evaluation cloud of UCAR. a Front view; b Top view.

According to (17), the membership degree of UCAR for each standard comment is calculated as shown below.${\xi _{L1}} = 6.725 \times \:{10^{ - 10}},$${\xi _{{\text{L}}2}} = 1.640 \times \:{10^{ - 1}},$${\xi _{{\text{L}}3}} = 2.234 \times \:{10^{ - 9}},$$\xi {\:_{{\text{L}}4}} = 5.716 \times \:{10^{ - 36}},$$\xi {\:_{{\text{L}}5}} = 2.921 \times \:{10^{ - 46}}$. According to the principle of maximum membership degree, the value of $\:{{\upxi\:}}_{\text{L}2}$ is the largest, so the comprehensive evaluation of UCAR is “good”.

In the enterprise dimension, $\:{{\upxi\:}}_{\text{E}2}=0.388$ is the maximum membership degree, so UCAR in this dimension is evaluated as “high”. In the user dimension, $\:{{\upxi\:}}_{\text{U}2}=0.834$ is the maximum membership degree, so UCAR in this dimension is evaluated as “satisfactory”.

The main reason for the above results is that the main business of UCAR is the tailored car service, which has relatively small user demand compared with the businesses of carpooling service and fast ride service. Therefore, the market penetration and user activity of UCAR are relatively low compared with DiDi. However, UCAR guarantees user experience through strict examination of drivers and vehicles, resulting in a higher net recommendation value from users than that of the other three enterprises and promoting the improvement of its comprehensive evaluation. Thus, by focusing on a particular segment of the market to create brand characteristics, UCAR has won the loyalty of users who have these demands.

Based on the above analysis, three recommendations are proposed for UCAR. First, it is recommended that UCAR leverage its strong foundation in service customization and vehicle management to avoid engaging in homogenized competition during business expansion and instead focus on addressing the specific needs of core user segments. For example, the enterprise could optimize its transportation capacity allocation algorithms for specific scenarios such as airports and business districts, thereby establishing a positive feedback loop between business growth and user satisfaction. Second, based on achieving “satisfactory” in the user dimension, UCAR should shift from meeting basic needs to creating unexpected experiences. For instance, it can invite high-frequency users to become “experience officers” and offer corresponding benefits. After collecting service suggestions in real time, UCAR should quickly improve by combining the resource allocation capabilities of the enterprise dimension. Thirdly, before expanding into new businesses, it is recommended that UCAR first verify the authenticity of demand through user dimension assessment data to ensure that the enterprise’s capabilities are in sync with user demands so as to continuously consolidate and enhance user satisfaction in the development process.

Results discussion of CaoCao

It can be seen from Fig. 12 that the comprehensive evaluation cloud of CaoCao is mainly located between the “good” and the “mediocre” standard comment clouds. The cloud drops in the enterprise dimension are mostly located in the “mediocre” range, while the cloud drops in the user dimension mainly fall into the “good” range.

Fig. 12

Evaluation cloud of CaoCao. a Front view; b Top view.

According to (17), the membership degree of CaoCao for each standard comment is calculated as shown below.${\xi _{{\text{L}}1}} = 1.570 \times \:{10^{ - 12}},$$\xi {\:_{{\text{L}}2}} = 4.270 \times \:{10^{ - 6}},$$\:\xi {\:_{{\text{L}}3}} = 2.048 \times \:{10^{ - 6}},$$\xi {\:_{{\text{L}}4}} = 1.825 \times \:{10^{ - 22}},$$\xi {\:_{{\text{L}}5}} = 3.927 \times \:{10^{ - 35}}$. According to the principle of maximum membership degree, the value of $\:{{\upxi\:}}_{\text{L}2}$ and $\:{{\upxi\:}}_{\text{L}3}$ are largest, and the gap between them is very small. Therefore, it can be considered that the comprehensive evaluation of CaoCao is between “good” and “mediocre”.

In the enterprise dimension, $\:{{\upxi\:}}_{\text{E}3}=0.089$ is the maximum membership degree, so CaoCao in this dimension is evaluated as “mediocre”. In the user dimension, $\:{{\upxi\:}}_{\text{U}2}=0.053$ is the maximum membership degree, so CaoCao in this dimension is evaluated as “satisfactory”.

As an enterprise in China that took the lead in applying new energy technologies to the shared mobility sector, CaoCao has built a reputation for being low-carbon. Because CaoCao is in the process of exploring environmental protection operations, the evaluation of the enterprise dimension is mediocre. Given that the service model of ORH is relatively fixed, it is difficult to derive new market segments. Therefore, in the initial stage of its establishment, the regular business carried out by CaoCao struggled to obtain a large number of orders in the highly competitive ORH market. In recent years, taking energy conservation, emission reduction, and safety guarantees as breakthrough points, CaoCao has continuously expanded its business scope, aiming to provide users with a one-stop healthy lifestyle; thus ensuring that the evaluation of the user dimension is satisfactory.

Based on the above analysis, three recommendations are proposed for CaoCao. First, CaoCao’s performance in operation management is “mediocre”, but the “satisfaction” from the user dimension indicates that its service quality has been recognized. Therefore, CaoCao should rely on user travel data to optimize its cost structure, ensuring that the efficiency of the enterprise is improved without compromising the user experience. Second, low-carbon and environmental protection are core features of CaoCao. It is suggested to create a low-carbon brand promotion campaign with high user participation, such as allowing users to accumulate “low-carbon points” to exchange for gifts. This will help the enterprise’s positioning spread through word-of-mouth among users, making up for CaoCao’s shortcomings in terms of popularity and promotion at the enterprise dimension. Third, it is necessary to deepen user engagement through innovative incentive mechanisms and convert user feedback into improvement directions at the enterprise dimension. For instance, when users complete their feedback, in addition to “low-carbon points”, they can also be given “low-carbon medals” to enjoy privileges such as priority car-hailing and free rides on their birthdays.

6.3.4. Results discussion of ShouQi

It can be seen from Fig. 13 that the comprehensive evaluation cloud of ShouQi is mainly located between the “good” and the “mediocre” standard comment clouds, and mostly nears the “mediocre” range. The cloud drops in the enterprise dimension are mostly located in the “mediocre” range. In the user dimension, the cloud drops mainly fall in the “good” range, while some cloud drops are in the “mediocre” range.

Fig. 13

Evaluation cloud of ShouQi. a Front view; b Top view.

According to (14), the membership degree of ShouQi for each standard comment is calculated as shown below. $\:{{{\upxi\:}}_{\text{L}1}=1.157\times\:{10}^{-15},\:\:{\upxi\:}}_{\text{L}2}=2.472\times\:{10}^{-10},\:\:{{\upxi\:}}_{\text{L}3}=3.783\times\:{10}^{-2},\:\:{{\upxi\:}}_{\text{L}4}=2.730\times\:{10}^{-17},{\:\:{\upxi\:}}_{\text{L}5}=1.794\times\:{10}^{-31}$. According to the principle of maximum membership degree, the value of $\:{{\upxi\:}}_{\text{L}3}$ is the largest, so the comprehensive evaluation of ShouQi is “mediocre”.

In the enterprise dimension, $\:{{\upxi\:}}_{\text{E}3}=0.405$ is the maximum membership degree, so ShouQi in this dimension is evaluated as “mediocre”. In the user dimension, $\:{{\upxi\:}}_{\text{U}2}=0.570$ is the maximum membership degree, so ShouQi in this dimension is evaluated as “satisfactory”.

The main reason for the above results is that ShouQi lacks strong market recognition. Similar to UCAR, ShouQi mainly provides private car services to middle and high-end users, and it is relatively weak in terms of management, operation, and user satisfaction; therefore, ShouQi cannot be the first choice for users with such demands. In addition, ShouQi is operated independently by the ShouQi group, and all the vehicles are approved by the government and owned by the group, resulting in poor management flexibility and a small total supply.

Based on the above analysis, three recommendations are proposed for ShouQi. First, it is recommended that ShouQi conduct an in-depth analysis of core user satisfaction scenarios across the user dimension, such as punctuality for business travel and vehicle cleanliness for family trips, in order to establish a distinctive brand positioning. ShouQi needs to be upgraded from the ordinary “safe and comfortable” to a specific positioning bound to user experience. Second, blind business expansion should be avoided. ShouQi should focus on extending the service chain in areas that satisfy users and upgrade the user service system simultaneously. For instance, a “full-service solution for business travel” can be developed based on the high satisfaction of business travel users. Third, in contrast to the highly competitive ORH market in major cities, it is recommended that ShouQi evaluate the untapped market potential in smaller cities and develop tailored market entry strategies. Rather than directly replicating urban business models, the enterprise should implement localized adaptations based on user satisfaction service standards that are empirically validated.

Comparative discussion

By comparing the results of the four ORH enterprises, it can be concluded that DiDi has compensated for its mediocre performance in the user dimension through its significant advantages in the enterprise dimension, thus achieving the best comprehensive evaluation. This is because the comprehensive weight reflects the characteristics of the ORH industry that emphasizes operational efficiency, avoiding the one-sidedness of a single-dimensional ranking. Although CaoCao performed well in terms of users, its comprehensive evaluation is between “good” and “mediocre”. This is because cloud digital features quantified the uncertain impact of CaoCao’s shortcomings, making the comprehensive evaluation more in line with the actual logic of coordinated development of management effectiveness and service experience. The good performance of UCAR in each single-dimensional evaluation is visually presented through the two-dimensional cloud figure, placing it second in the comprehensive evaluation, which reflects the impact of balance on the overall competitiveness. The evaluation grades of ShouQi and CaoCao in both user and enterprise dimensions are the same, but due to the relatively low quantitative evaluation value, ShouQi ranks last in the qualitative comprehensive evaluation, demonstrating the effectiveness of the proposed method in the conversion between qualitative concepts and quantitative values.

The proposed method, by leveraging F-AHP, not only quantifies the relative importance of different dimension indexes but also reflects the fuzziness of expert judgments. Through the two-dimensional cloud generator, it further combines quantitative values and qualitative evaluations, accurately presenting the analysis of different dimensions of ORH enterprises, thus avoiding “either-or” arbitrary conclusions in traditional evaluations. Meanwhile, the proposed method visually presents the uncertainty of the evaluation results. For instance, the cloud droplets of CaoCao are distributed between “good” and “mediocre”, thus being closer to reality than the traditional evaluation method that ranks based on numerical results. Furthermore, the proposed method not only retains structured logic in the analytic hierarchy process but also links qualitative and quantitative indexes through fuzzy theory, making the analysis results both rigorous and easy for enterprises to understand and apply.

In practical applications, the proposed method converts management capabilities and user experience into intuitive qualitative conclusions, facilitating users to make choices based on their own needs. For instance, users who prioritize travel efficiency can choose DiDi first, while those who value service experience may consider CaoCao. Meanwhile, the proposed method can help enterprises accurately identify the direction for improvement and promote healthy competition. The government can also implement differentiated supervision based on the comprehensive evaluation results. For instance, it can strengthen compliance checks for enterprises with poor evaluations in the enterprise dimension and invite those with good evaluations in the user dimension to share their successful experiences, thereby promoting the transformation of the ORH industry from a single-scale competition to a coordinated development of enterprises and users.

Conclusions

As a new travel mode under the background of the sharing economy, ORH has made outstanding contributions to alleviating urban traffic congestion and improving the allocation of surplus resources since its emergence. However, due to the characteristics of product homogeneity and price openness in the ORH industry, it is difficult for most enterprises to determine their core competitiveness and expand their market share. Therefore, it is of great significance to design a scientific and comprehensive decision-making method to analyze the market segment of the ORH industry and the actual situation of each enterprise.

This paper takes the four ORH enterprises that occupy a major share of the Chinese market as examples and constructs multi-level indexes from the two dimensions of enterprise management and user service. The proposed method first calculates the weight of the first and second level indexes based on F-AHP, then quantitatively describes the initial samples and the standard comment set through the two-dimensional backward cloud generator, and finally uses the two-dimensional forward cloud generator to qualitatively evaluate the comprehensive situation of each ORH enterprise.

There are four main research results. First, in the comprehensive analysis of the four enterprises, DiDi is the best and ShouQi is the worst. This shows that DiDi is in a leading position in the market, while ShouQi still needs improvement in overall operation. Second, in the single-dimensional analysis, the gap between enterprises in the user dimension is small, indicating that the overall level of services provided by each enterprise is relatively close, and subtle differences may affect users’ choices. The gap among the evaluated objects in the enterprise dimension is large, which indicates that performance of enterprises in strategic management and resource integration is uneven. Third, by comparing the single-dimensional analyses of DiDi and UCAR, it can be found that advantages in management and operation can make up for disadvantages in user services and ensure a high level of comprehensive evaluation. This highlights the important supporting role of management and operation for overall performance of enterprises. Fourth, by comparing the single-dimensional evaluations of CaoCao and ShouQi, it can be found that better user service can help enterprises improve their comprehensive evaluation when management and operation levels are similar. This shows that on the premise of ensuring basic operational scale, improving user service quality is key to achieving long-term development.

Based on the results, this paper puts forward the following two suggestions for ORH enterprises. On the one hand, the core business and main users of the enterprise should be accurately positioned. Other businesses should be derived from fully establishing brand characteristics, rather than blindly following trends and losing market value. On the other hand, enterprises should focus on the service experience of users. The expansion of market share should be based on improving user loyalty and recommendation levels, rather than through vicious competition that puts users in a state of passive choice.

The analysis of service-oriented enterprises generally faces the problem of large differences in the types and quantities of initial samples. The proposed method combines the advantages of F-AHP and the two-dimensional cloud model, which can reduce the influence of fuzziness and randomness in the decision-making process, and realize effective conversion between qualitative concepts and quantitative data. At the same time, this analysis framework realizes multi-level visual analysis, reduces the subjective impact of analysis by randomly generating cloud drops, and helps decision makers accurately analyze results from different dimensions in complex scenarios.

Policymakers can use the framework to conduct a comprehensive analysis of ORH enterprises, determine their compliance and operations, and provide a basis for industry regulation. The competition focuses and user demands of the ORH market can be analyzed by policymakers, and corresponding optimization policies can be formulated according to the indexes with poor performance in the results to continuously enhance the vitality of the industry. ORH enterprises can effectively identify competitive strengths and weaknesses with the help of the proposed method to support their strategic decision-making. Based on the analysis of operational performance in each region, resource allocation is optimized through vehicle scheduling and other methods to effectively improve user engagement.

In addition to the analysis of service-oriented enterprises, the proposed method can also be used in risk analysis to reduce the subjectivity and fuzziness of risk indexes and evaluation levels. At the same time, due to numerous uncertainties in the production process, it is often difficult to make an accurate quality assessment. Through the application of the proposed method, quality supervision of the production process can be optimized.

This study has some limitations that provide opportunities for future research. The proposed method is suitable for static data analysis, and has poor adaptability to dynamic data such as time series data. For example, when analyzing the time-varying data such as the market shares of service-oriented enterprises, the proposed method lacks a processing mechanism for the dynamic changes of the data, which affects the timeliness of the results. In future research, the dynamic parameter adjustment mechanism will be introduced, so that the decision method can automatically adjust the parameters according to the changing characteristics of dynamic data in real time, thereby improving the adaptability to dynamic situation. Meanwhile, the proposed method is limited to data processing in two-dimensional space. Considering that with the continuous advancements of high technology and the diversification of user needs, the factors affecting the development of service-oriented enterprises in the future will be more diverse, and two-dimensional analysis cannot fully cover all important factors. When dealing with high-dimensional data, the proposed method not only consumes a lot of computing resources, but also may lead to poor interpretability of the results. Therefore, the decision method based on three-dimensional cloud model will be the direction of our future research. An optimization algorithm is designed to map the cloud drops into the three-dimensional space, and the locations of the cloud drops are determined according to the membership function to provide a more comprehensive analysis for enterprises.