An adaptive coverage method for dynamic wireless sensor network deployment using deep reinforcement learning

Abstract

Coverage optimization stands as a foundational challenge in Wireless Sensor Networks (WSNs), exerting a critical influence on monitoring fidelity and holistic network efficacy. Constrained by the limited energy budgets of sensor nodes, the imperative to maximize network longevity while sustaining sufficient coverage has ascended to the forefront of research priorities. Traditional deployment methodologies frequently falter in complex topographies and dynamic operational environments, encountering difficulties in striking an optimal equilibrium between coverage quality and energy efficiency. To mitigate these inherent limitations, this paper introduces ACDRL (Adaptive Coverage-Aware Deployment based on Deep Reinforcement Learning)—a novel strategy that enables intelligent, self-optimizing node placement in WSNs through deep reinforcement learning paradigms. Our proposed framework establishes a sophisticated deep reinforcement learning architecture integrating a multi-objective reward mechanism and hierarchical state representation, which innovatively resolves the dual predicaments of coverage optimization and energy balancing in intricate scenarios. Extensive simulation results validate that ACDRL consistently outperforms state-of-the-art approaches by maintaining superior coverage ratios, significantly extending network operational lifespan, and demonstrating enhanced adaptability in high-density deployment scenarios.

Introduction

Wireless Sensor Networks (WSNs), as the core component of intelligent sensing systems, have become a critical link connecting the physical and virtual worlds amid the digital transformation wave. With their distributed sensing, autonomous networking, and low-power characteristics, WSNs are reshaping the paradigm of data collection and environmental monitoring^1,2,3,4. Composed of numerous miniature intelligent nodes, WSNs capture environmental data through built-in sensors and work collaboratively via wireless communication to form an integrated system. From precision irrigation in agriculture to predictive maintenance of industrial equipment, from wildlife habitat monitoring to smart building energy consumption management, the applications of WSNs have permeated all aspects of the socio-economic landscape^5,6,7. However, beneath this extensive applicability lies a persistent challenge: the coverage issue in practical deployments remains a fundamental bottleneck constraining WSN technology’s full potential. Traditional static deployment methods often fail to balance the trade-off between coverage quality and system resource consumption, especially in scenarios with complex terrain or dynamically changing demands^8,9. For example, in earthquake early warning systems, improper sensor placement may result in a lack of monitoring in key areas, while in border surveillance applications, overly dense node distribution could lead to rapid energy depletion^10,11,12.

Against this backdrop, traditional wireless sensor network deployment paradigms primarily include deterministic layout schemes and random dispersion strategies^13,14. These methods have achieved certain successes in controlled environments and large-scale rapid deployment scenarios, respectively. Geometric programming constructs the theoretically optimal coverage using triangular or hexagonal grids, while probabilistic distribution models predict the coverage effects of a large number of nodes based on statistical principles^15,16. However, these classical methods face numerous challenges in practical applications. The geometric layout assumes flat terrain with no obstacles; once the environment becomes complex or contains barriers, its theoretical optimality is difficult to maintain¹⁷. While random distribution is easy to implement, it cannot ensure the sensing quality of critical areas and often leads to uneven node distribution and energy waste^18,19,20. More critically, as the demands for sensing tasks dynamically change and the spatial-temporal heterogeneity of environmental conditions increases, static deployment schemes fail to adapt to such variations, causing coverage efficiency to degrade rapidly over time²¹. Furthermore, existing deployment strategies generally lack a comprehensive consideration of real-world factors, such as node energy heterogeneity, communication interference, and sensing capability degradation, resulting in a significant gap between theoretical models and practical outcomes²². In multi-objective optimization, traditional methods typically employ simplified treatments, such as weighted summation, which makes it difficult to effectively balance multi-dimensional objectives, such as coverage, energy consumption, and cost.

To address these limitations, artificial intelligence technologies^23,24 have sparked a wave of transformation in the wireless network field in recent years, injecting unprecedented intelligent power into traditional communication systems. Deep learning, with its outstanding feature extraction capabilities, has shown significant advantages in applications such as IoT traffic prediction and intelligent traffic control²⁵. Meanwhile, reinforcement learning (RL), as a learning paradigm based on the “interaction-reward” mechanism, is particularly suitable for sequential decision-making problems in wireless networks. Traditional Q-learning has been successfully applied in channel allocation and heterogeneous network interference management in mobile communication systems. Notably, reinforcement learning demonstrates unique potential in the optimization of WSN deployment²⁶. Unlike static deployment methods, RL-based WSN deployment strategies continuously optimize node positions through environmental interactions, achieving a dynamic balance between coverage and energy efficiency^27,28. Especially in scenarios with dynamically changing environmental conditions, RL agents can adaptively adjust sensor density distribution according to spatiotemporal variations in coverage demands, effectively avoiding monitoring blind spots²⁹. The multi-agent reinforcement learning (MARL) framework further provides a theoretical foundation for distributed collaborative deployment in WSNs, enabling the network to achieve global coverage optimization while minimizing communication overhead³⁰. Deep reinforcement learning (DRL), by combining the representational power of deep neural networks with the decision-making mechanism of reinforcement learning, further enhances the strategy learning efficiency in complex WSN deployment scenarios, offering an effective approach to solving coverage optimization problems in high-dimensional state spaces³¹.

Building on these advancements, this study tackles the coverage sensing deployment problem in WSNs using a Reinforcement Learning (RL) framework. Traditional WSN deployments often face complex terrains and dynamic environmental changes, which pose significant challenges to conventional heuristic algorithms. These traditional methods are particularly ill-equipped to handle heterogeneous sensing requirements and energy constraints, making it difficult to achieve multi-objective optimization. In response to these challenges, we propose an ACDRL deployment strategy framework. By incorporating deep neural networks, ACDRL effectively approximates high-dimensional state-action value functions, thereby addressing the complex environmental state representations inherent in WSN deployments. The key innovation of ACDRL lies in its dual reward mechanism and adaptive learning rate adjustment strategy, which dynamically balance the maximization of coverage with the efficient management of energy consumption.

The main contributions of this paper are as follows:

• 1. A deep reinforcement learning framework specifically designed for WSN deployment problems is proposed. This framework effectively handles high-dimensional state spaces using deep neural networks, enabling adaptive modeling for complex environments and heterogeneous sensing requirements, overcoming the limitations of traditional deployment methods in dynamic environments.

• 2. An innovative reward function system is designed, considering both coverage maximization and energy consumption balancing as two objectives. Through an adaptive learning rate adjustment strategy, the algorithm convergence is accelerated, achieving an approximately optimal deployment strategy under multi-objective optimization.

• 3. A hierarchical state representation method is developed to reduce learning complexity, effectively addressing the dimensionality disaster problem in large-scale sensor network deployments. This improves the scalability and practicality of the algorithm, allowing ACDRL to be applied to larger-scale and more complex real-world WSN deployment scenarios while maintaining performance advantages.

The remainder of the paper is organized as follows: Section 2 briefly reviews related work in the field of target coverage and the fundamentals of reinforcement learning; Section 3 introduces the basic concepts related to WSN coverage; Section 4 outlines the basic principles of ACDRL; Section 5 presents the experimental results; and finally, Section 6 summarizes the research and discusses future research directions.

Related work

Literature review

Coverage optimization, as one of the core issues in WSNs, has a decisive impact on network quality of service and system performance³². Essentially, the coverage problem involves how to effectively deploy and schedule limited sensor resources to meet specific sensing requirements. Depending on the monitoring targets, researchers classify the coverage problem into three typical paradigms: point coverage, barrier coverage, and area coverage. Point coverage focuses on continuous monitoring of discrete target points; barrier coverage aims to minimize the probability of unmonitored penetrations; while area coverage emphasizes comprehensive sensing within a specific spatial range³³. To address these problems, various algorithmic strategies have been proposed in the literature, such as location-based coverage methods, techniques that estimate distances using signal strength, and dynamic coverage control mechanisms that combine mobile nodes. In recent years, some innovative studies have explored coverage algorithms that do not require location, distance, or angle information, providing feasible solutions for resource-constrained environments³⁴.

From an architectural perspective, coverage control algorithms can be divided into centralized and distributed categories. In large-scale sensor networks, distributed scheduling protocols have gained widespread attention due to their good scalability. Typical distributed coverage control usually adopts a time-slot division mechanism, where sensor nodes wake up at the start of each round and make activity decisions through local communication³⁵. However, this message-exchange-based decision-making mode may lead to significant energy consumption as the network scale increases, which contradicts the energy-saving goals of WSNs. To overcome this challenge, various optimization strategies have been proposed, including adaptive wake-up mechanisms, learning-based activity prediction, and hierarchical coverage scheduling frameworks³⁶. Particularly, recent studies show that reinforcement learning techniques can reduce redundant message exchanges and optimize node activity decisions, significantly reducing protocol overhead while ensuring coverage quality. This provides a new approach for next-generation intelligent WSN coverage control³⁷.

Table 1 Comparative analysis of WSN coverage optimization methodologies.

Reinforcement learning (RL), as a key technology in the field of artificial intelligence, establishes a real-time interaction mechanism between the agent and the environment, thereby enabling a new paradigm for sequential decision optimization⁴⁵. Within the framework of Markov decision processes (MDP), RL demonstrates significant potential in solving complex decision-making problems.⁴⁶ Traditional Q-learning, due to its simplicity and efficiency, has been widely applied in the field of network optimization. La et al.³⁸ optimized the balance between the number of monitoring targets and charging time using Q-learning, while Wei et al.³⁹ and Soni et al.⁴⁰ applied it to charging path planning, effectively improving system efficiency and network lifespan. As problem complexity increases, deep reinforcement learning (DRL) overcomes the limitations of traditional tabular Q-learning in handling high-dimensional continuous state spaces by integrating the representational power of deep neural networks with the decision-making mechanism of RL⁴⁷. Deep Q-Networks (DQN), as a representative algorithm of DRL, approximates the state-action value function using neural networks, showing outstanding performance in fields such as video games, robotics, and WSNs⁴⁸. The charging optimization algorithm based on DRL proposed by Cao et al.⁴¹ successfully maximized system revenue under MC capacity constraints, while the actor-critic framework developed by Jiang et al.⁴² and Yang et al.⁴³ effectively reduced the number of non-working nodes while extending the network lifetime. Mohajer et al.⁴⁴propose a novel dynamic offloading framework that addresses the challenges of traffic fluctuations and resource diversity in mobile edge networks. Their approach integrates a sparse multi-head graph attention mechanism for accurate traffic prediction and an adaptive offloading strategy based on the twin delayed deep deterministic policy gradient algorithm, achieving enhanced performance and adaptability in various operational scenarios. Despite the clear advantages of DRL in handling complex environmental decisions, challenges such as data dependency, computational overhead, and algorithm instability still need to be addressed through innovative framework designs and optimization techniques^49,50. The comparison and limitations of existing methods are detailed in Table 1.

Work motivation

The deployment of wireless sensor networks faces three fundamental challenges: (1) the dimensionality curse in large-scale networks where traditional methods fail to scale, (2) the dynamic adaptation gap where static strategies cannot respond to spatiotemporal variations, and (3) the multi-objective conflict between coverage quality, energy efficiency, and network longevity. While deep reinforcement learning (DRL) offers promising solutions, standard architectures lack hierarchical state representations for network structures, conventional reward designs oversimplify coverage-energy trade-offs, and fixed learning-rate mechanisms cannot adapt to dynamic WSN environments. Our work addresses these limitations through three key innovations: a hierarchical state abstraction capturing global-local patterns, a time-variant reward architecture dynamically reweighting objectives, and gradient-aware learning rate adaptation for non-stationary optimization landscapes.

Coverage models in wireless sensor networks

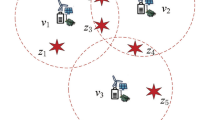
This section first defines the research boundaries and core assumptions, laying the theoretical foundation for the subsequent discussion. It then delves into the coverage sensing model in WSNs and its mathematical representation. By systematically reviewing the evolutionary trajectory and applicable scenarios of existing coverage models in the WSN field, key parameters and technical indicators are extracted, and a formalized description framework for the coverage sensing deployment problem is established. This formalization not only facilitates the precise formulation of the problem but also provides the necessary theoretical support for the subsequent reinforcement learning-based solutions. Coverage models in wireless sensor network are shown in Fig. 1.

Fig. 1

Schematic diagram of wireless sensor network coverage sensing deployment.

Assumptions

The research framework adopts a discrete-time model, dividing the system evolution process into continuous time periods. To accurately describe the coverage sensing deployment problem, the following formalized model assumptions are established:

• 1. The sensor node distribution function $P(x,y) \sim U(A)$, where $A$ represents the target coverage area, and the node positions follow a uniform distribution over the area, reflecting the randomness of the deployment. However, in real-world scenarios, non-homogeneous terrains are common. To address this, we introduce a non-uniform distribution function $P'(x,y)$ that accounts for terrain variations and obstacles. This distribution can be adapted based on prior knowledge of the environment, allowing the model to better reflect real-world conditions.

• 2. The location sensing capability $L_i = (x_i, y_i)$ holds for each node $i \in {1, 2, ..., N}$, and the communication connectivity graph ( G(V, E) ) satisfies full connectivity, i.e., $\forall i, j \in V, (i, j) \in E$. In practical deployments, maintaining full connectivity may not always be feasible, especially in dynamic environments. We relax this assumption by allowing partial connectivity and incorporating a connectivity maintenance mechanism in the deployment strategy to ensure robust communication.

• 3. The assumption of homogeneous sensing capability is defined, with the sensing radius of all nodes being a constant $R_s$, and the sensing model adopts a binary disk model:

  $$\begin{aligned} C_i(p) = {\left\{ \begin{array}{ll} 1, & \text {if } d(L_i, p) \le R_s \\ 0, & \text {otherwise} \end{array}\right. } \end{aligned}$$

  (1)

  where, $d(\cdot , \cdot )$ represents the Euclidean distance. To enhance the model’s applicability to heterogeneous sensor networks, we extend the sensing model to include both binary and probabilistic components. The binary model is used for deterministic coverage, while the probabilistic model accounts for sensing uncertainties and varying capabilities across different nodes. During training, the model dynamically switches between these two components based on the node’s specific sensing characteristics and environmental conditions.

• 4. The global node count $N$ is known to all nodes in the network, constituting the deployment density parameter, which influences the formulation of the coverage strategy. In dynamic environments, the node count may vary due to node failures or additions. We address this by incorporating a dynamic node count estimation mechanism, allowing nodes to adapt their strategies based on real-time network information.

Actual application environment

In real-world deployment environments, the sensing capabilities of sensor nodes are influenced by various environmental factors, which make the traditional binary disk model inadequate for accurately describing coverage characteristics. Environmental noise, signal attenuation, terrain obstruction, and atmospheric conditions, among other factors, contribute to the probabilistic nature of the sensing capabilities. Therefore, this study introduces a probabilistic sensing model to more precisely characterize the coverage characteristics of nodes.

Given a sensor node $s_i$ and a target point $p$, the probabilistic sensing function $P_{det}(s_i, p)$ is defined as follows:

$$\begin{aligned} P_{det}(s_i, p) = {\left\{ \begin{array}{ll} 1 & \text {if } d(s_i, p) \le d_1 \\ e^{-\alpha (d(s_i, p) - d_1)^\beta } & \text {if } d_1 < d(s_i, p) \le d_2 \\ 0 & \text {if } d(s_i, p) > d_2 \end{array}\right. } \end{aligned}$$

(2)

Here, $d(s_i, p)$ represents the Euclidean distance between the node $s_i$ and the target point $p$; $d_1$ denotes the reliable sensing radius, within which the probability of detecting the target is 1; $d_2$ represents the maximum sensing radius, beyond which the node cannot detect the target. The parameters $\alpha$ and $\beta$ control the decay rate and the shape of the sensing probability curve, respectively, and are closely related to the sensor type and environmental characteristics.

Based on the above probabilistic sensing model for a single node, the probability $P_{cov}(p)$ of a target point $p$ being successfully sensed by at least one node in the network is derived as follows:

$$\begin{aligned} P_{cov}(p) = 1 - \prod _{i=1}^{N} (1 - P_{det}(s_i, p)) \end{aligned}$$

(3)

Assume that area $A$ is discretized into $M$ points of interest (PoIs), where each point $p_j$ can have a different coverage demand weight $w_j$. The overall coverage quality of area $A$ is defined as follows:

$$\begin{aligned} Q_{cov} = \frac{1}{M} \sum _{j=1}^{M} w_j \cdot (1 - \prod _{i=1}^{N} (1 - P_{cov}(p_j, s_i) \cdot \delta _i)) \end{aligned}$$

(4)

where, $\delta _i \in \{0, 1\}$ represents the operational state of sensor $s_i$ (1 for active, 0 for sleep).

Furthermore, considering the dynamic changes in node energy status, an energy-aware factor $\lambda _i(t)$ is introduced to reflect the impact of the remaining energy of node $s_i$ at time $t$ on its sensing capability:

$$\begin{aligned} \lambda _i(t) = \min {1, \frac{E_i(t)}{E_{th}}} \end{aligned}$$

(5)

where, $E_i(t)$ represents the remaining energy of node $s_i$ at time $t$, and $E_{th}$ is the energy threshold required for normal sensing.

Incorporating the energy factor, the corrected sensing probability function is expressed as follows:

$$\begin{aligned} P'{det}(s_i, p, t) = \lambda _i(t) \cdot P{det}(s_i, p) \end{aligned}$$

(6)

This probabilistic sensing model not only more accurately reflects the sensing characteristics in real-world environments but also naturally integrates energy constraints into the coverage calculation process. This provides a more realistic environmental model for the adaptive deployment strategy based on reinforcement learning, helping the algorithm learn more robust deployment strategies during the training process.

ACDRL for WSN coverage optimization

Hierarchical state representation

To address the challenge of high-dimensional state spaces in wireless sensor network (WSN) coverage and sensing deployment, a novel hierarchical state representation method is proposed. This approach not only reduces computational complexity but also adaptively captures the dynamic characteristics of the network:

$$\begin{aligned} \textbf{s} = [\textbf{s}_{global}, \textbf{s}_{local}, \textbf{s}_{neighbor}] \end{aligned}$$

(7)

where: $\textbf{s}_{global}$ represents the global network coverage state, with a dimension of $d_g<< M$, $\textbf{s}_{local}$ represents the local sensor state, including energy levels, current sensing radius, $\textbf{s}_{neighbor}$ represents the aggregated features of neighboring node states.

The global state is reduced in dimension through region segmentation and feature aggregation:

$$\begin{aligned} \textbf{s}_{global} = \Phi (A, \{P'{det}(s_i, p, t)\}_{j=1,i=1}^{M,N}) \end{aligned}$$

(8)

where $\Phi$ is a dimensionality reduction function, which can be based on region partitioning feature aggregation or principal component analysis. This representation method enables efficient fusion of multi-scale state information, allowing the sensor network to achieve adaptive region priority adjustment and dynamic balance between energy consumption and coverage quality under limited computational resources. Additionally, it facilitates real-time optimization of the network topology.

To ensure robustness under partial observability and node failures, the hierarchical state representation incorporates mechanisms for synchronization and fault tolerance. Specifically, the local and neighbor states are periodically updated to reflect the current operational status of each node and its surroundings. In the event of node failures, the global state representation is designed to accommodate dynamic changes in network topology, allowing the system to adaptively adjust its strategy based on the remaining active nodes.

Action space

In wireless sensor network (WSN) coverage sensing deployment, the actions that each sensor node can perform at a specific time step constitute its action space:

$$\begin{aligned} \textbf{a}_i = [\delta _i, r_i] \end{aligned}$$

(9)

where: $\delta _i \in \{0, 1\}$ represents the active/sleep decision, enabling dynamic control of the network’s activity level. $r_i \in [0, r_i^{max}]$ represents the adjustment of the sensing radius, which can be discretized into K levels, supporting fine-grained control of sensing capability.

The reward function is designed to balance the trade-offs between activating more nodes and expanding individual node coverage. Specifically, the energy efficiency reward component $R_{ene}$ penalizes excessive use of sensing radius, encouraging nodes to optimize their energy consumption while maintaining adequate coverage. This ensures that the network can adaptively adjust its strategy based on the current energy levels and coverage requirements, achieving a dynamic balance between coverage quality and energy conservation.

Multi-objective cooperative reward function

To address the dual challenges of coverage efficiency and energy constraints in wireless sensor networks, a multi-objective reward function is designed, which simultaneously considers the maximization of coverage and the balance of energy consumption:

$$\begin{aligned} R(s, a) = \alpha \cdot R_{cov}(s, a) + \beta \cdot R_{ene}(s, a) + \gamma \cdot R_{bal}(s, a) \end{aligned}$$

(10)

where: The coverage reward is given by:

$$\begin{aligned} R_{cov}(s, a) = Q_{cov} \end{aligned}$$

(11)

The optimization aims to achieve effective coverage of the target area, focusing on high-value regions and the elimination of coverage blind spots. The energy efficiency reward is:

$$\begin{aligned} R_{ene}(s, a) = -\frac{1}{N} \sum _{i=1}^{N} \frac{E(r_i)}{e_i} \end{aligned}$$

(12)

The reward for energy efficiency encourages nodes to adjust their sensing strength based on their remaining energy, maximizing energy usage efficiency. The reward for load balancing is:

$$\begin{aligned} R_{bal}(s, a) = -\sigma (\{\frac{e_i^{init} - e_i}{e_i^{init}}\}_{i=1}^{N}) \end{aligned}$$

(13)

where $\sigma$ represents the standard deviation, which is used to measure the imbalance in energy consumption. By minimizing the standard deviation of energy consumption $\sigma$, the network load balancing is promoted, thereby extending the overall network lifetime.

It should be noted that while the standard deviation is a common metric for measuring energy consumption imbalance, it may not be robust under skewed distributions. Alternative metrics such as the Gini coefficient could also be considered for more accurately capturing the energy imbalance in certain scenarios. The Gini coefficient, which is often used in economics to measure inequality, can provide a different perspective on the distribution of energy consumption across nodes. However, in our current model, the standard deviation is chosen due to its simplicity and computational efficiency. Future work could explore the integration of other metrics to enhance the robustness of the load balancing reward.

The coefficients $\alpha$, $\beta$, and $\gamma$ can be dynamically adjusted over time to balance the optimization objectives at different stages.

$$\begin{aligned} \alpha (t)= & \alpha _0 \cdot (1 - e^{-\lambda _{\alpha } \cdot t}) \end{aligned}$$

(14)

$$\begin{aligned} \beta (t)= & \beta _0 \cdot e^{-\lambda _{\beta } \cdot t} \end{aligned}$$

(15)

$$\begin{aligned} \gamma (t)= & \gamma _0 \cdot (1 - e^{-\lambda _{\gamma } \cdot t}) \end{aligned}$$

(16)

The reward function is designed with a time-varying weighting system, where energy efficiency is prioritized at the beginning of the network deployment (with a larger $\beta$), and as time progresses, the focus gradually shifts towards coverage quality and load balancing (with increasing $\alpha$ and $\gamma$), enabling dynamic strategy adjustment throughout the WSN lifecycle.

Hierarchical actor-critic network structure

To address the challenge of high-dimensional decision space in wireless sensor network deployment, a deep reinforcement learning model based on the Actor-Critic architecture is employed:

Actor Network: $\pi _{\theta }(a|s)$, outputs the probability distribution of taking actions in a given state. By introducing a hierarchical decision process, it first determines the node’s working state ($\delta$), and then optimizes the sensing radius (r). Additionally, this network integrates an attention mechanism, which dynamically focuses on key areas and energy-constrained nodes.

Critic Network: $V_{\phi }(s)$, estimates the state value function. By using a dual time-scale evaluation, it simultaneously considers immediate coverage rewards and long-term network lifetime, while also incorporating graph convolution layers to effectively capture the spatial correlations among nodes.

Both networks share the underlying feature extraction layers to accelerate knowledge sharing and improve learning efficiency. A graph feature extraction module, specifically designed to adapt to the dynamic changes in the wireless sensor network topology, is also integrated.

Gradient-aware adaptive learning rate adjustment

To accelerate the algorithm’s convergence and adapt to the dynamic environments in WSN deployment, an adaptive learning rate adjustment strategy is designed:

$$\begin{aligned} \eta (t) = \frac{\eta _0}{1 + \kappa \cdot t^{\omega }} \cdot \exp (\xi \cdot |\nabla J(\theta )|) \end{aligned}$$

(17)

where $\eta _0$ is the initial learning rate, and $\kappa$ and $\omega$ control the rate of learning decay, while $\xi$ is the gradient-based adaptive factor. This learning rate adjustment scheme combines time decay and gradient-adaptive mechanisms, providing a higher learning rate in regions with large gradients to quickly escape local optima, while ensuring stable convergence over time.

The choice of the gradient-aware learning rate adjustment mechanism is motivated by the need to balance exploration and exploitation in the dynamic WSN environment. The parameter $\xi$ plays a crucial role in determining the sensitivity of the learning rate to the gradient magnitude. A careful selection of $\xi$ is necessary to ensure that the learning rate adaptation does not lead to instability, especially in the presence of noise which is common in WSN deployments. Experimental analysis and parameter tuning are required to determine the optimal values for $\xi$, $\kappa$, and $\omega$, taking into account the specific characteristics of the WSN application and the level of environmental noise. Future work could investigate more sophisticated adaptive learning rate strategies that incorporate additional information about the environment’s dynamics and the agent’s performance over time.

ACDRL algorithm pseudocode

Algorithm 1

ACDRL for WSN Coverage Optimization

Convergence analysis

Theorem 1

Under following conditions, ACDRL converges to optimal policy with probability 1:

• 1. State space $\mathcal {S}$ and action space $\mathcal {A}$ are compact

• 2. Learning rates satisfy Robbins-Monro conditions: $\sum _{t=1}^{\infty } \eta (t) = \infty$, $\sum _{t=1}^{\infty } \eta ^2(t) < \infty$

• 3. Value estimator $V_{\phi }$ is Lipschitz continuous in compact parameter space

Proof Sketch

Using stochastic approximation framework:

• 1. Define joint parameter space $\Theta = \{\theta , \phi \}$: $\Theta _{t+1} = \Theta _t + \eta (t)[h(\Theta _t) + \xi _t]$ where $h(\cdot )$ is update direction vector, $\xi _t$ martingale noise

• 2. Construct Lyapunov function: $L(\Theta ) = \mathbb {E}_{\pi _{\theta }}[V_{\phi }(s) - V^*(s)]^2 + D_{KL}(\pi _{\theta }||\pi ^*)$

• 3. Prove under adaptive learning rate: $\lim _{t\rightarrow \infty } \nabla _{\Theta } L(\Theta _t) = 0$ a.s.

• 4. Analyze ODE system: $\dot{\Theta } = h(\Theta )$ showing equilibrium corresponds to Nash solution

• 5. Bound approximation error using GCN properties

$\square$

Remark

The adaptive learning rate (Eq.17) satisfies:

$$\begin{aligned} \sum _{t=1}^{\infty } \frac{\eta _0 \exp (\xi g_t)}{1+\kappa t^{\omega }} = \infty ,\quad \sum _{t=1}^{\infty } \left( \frac{\eta _0 \exp (\xi g_t)}{1+\kappa t^{\omega }}\right) ^2 < \infty \end{aligned}$$

(18)

where $g_t = |\nabla J(\theta _t)|$. Exponential term temporarily boosts learning rate during large gradients, while denominator ensures ultimate convergence.

Simulation results and analysis

Analysis of factors influencing coverage

Table 2 Simulation parameters.

Extensive simulation experiments are conducted on the ns-2 platform to comprehensively evaluate the performance of the ACDRL model⁵¹. In the experimental design, a 300$\times$300 meter simulation environment is constructed, where 2,500 sensor nodes are randomly and uniformly distributed, each with a 30-meter effective sensing radius. The specific parameters of the experiment are shown in Table 2. To provide a complete picture of the experimental setup, we have included the DRL-specific training parameters in Table 3, such as the initial learning rate, batch size, and discount factor $\gamma$.

Table 3 DRL training parameters.

Table 4 Coverage rate versus time.

To enhance the clarity and reproducibility of our experimental setup, we have introduced Table 3, which details key DRL training parameters such as the initial learning rate, batch size, and discount factor $\gamma$. These parameters are essential for understanding the training process and replicating our results. Utilizing the parameter settings from equation 2, with $\alpha = 0.6$ and $\beta = 0.4$, the coverage performance of the wireless sensor network after deployment is presented in Table 4.

To provide a more comprehensive evaluation of the robustness of our ACDRL model, we have incorporated variance values for each data point in Table 4. These variance values, denoted as ± in the table, offer insights into the stability and reliability of the coverage performance across multiple simulation runs. These statistical measures are crucial for assessing the robustness of the ACDRL model in various scenarios.

In practical deployment scenarios, wireless sensor networks are often challenged by factors such as hardware defects, adverse weather conditions, electromagnetic interference, energy depletion, and signal attenuation. These factors can lead to node performance degradation or complete failure, which in turn affects network topology and overall service quality. To evaluate the robustness of the ACDRL algorithm under such challenging conditions, we have designed a series of targeted experiments to simulate node failures and assess the model’s performance.

Fig. 2

Effect of node’s failure on coverage ratio.

Random node failures with a proportion of 0.05 are introduced into the simulation environment, and the network coverage performance changes at different time points are tracked and recorded^52,53. Figure 2 presents the key results of this analysis. From Fig. 2(a), it can be observed that when the total number of nodes is 1,500, even with 5% of the nodes failing, the ACDRL algorithm is able to maintain approximately 87% coverage, demonstrating significant fault tolerance. More notably, as shown in Fig. 2b, when the node density is increased to 2,500, the impact of the same proportion of node failures on system performance is further reduced, with the coverage rate decreasing by only about 4.3%.

This excellent fault tolerance is attributed to the adaptive learning mechanism of ACDRL. The algorithm not only optimizes node distribution during the initial deployment phase but also dynamically adjusts the coverage strategy during operation, effectively responding to changes in network topology. When certain areas experience coverage gaps due to node failures, neighboring nodes can autonomously adjust their coverage range and operational cycle through the reinforcement learning framework, thereby filling these gaps. This distributed self-healing feature enables ACDRL to perform exceptionally well in high-density deployment scenarios, providing reliable support for large-scale practical applications.

Fig. 3

Network lifetime versus node density.

As shown in Fig. 2, although increasing the sensor node density enhances network robustness, its effect on the initial coverage improvement exhibits diminishing returns. When 1,500 nodes are deployed in the network, even with a certain proportion of nodes failing, ACDRL is still able to maintain a high coverage rate through its intelligent learning mechanism. More notably, when the number of nodes increases to 2,500, the impact of the same proportion of node failures on the system coverage rate is significantly reduced, which demonstrates that ACDRL has stronger fault tolerance in high-density deployment scenarios. Figure 3 presents the relationship between node density and network lifetime, and the data indicates that the ACDRL algorithm effectively balances the relationship between coverage rate and energy consumption. This advantage stems from the core design concept of the algorithm–maintaining the minimum necessary active node set while ensuring that coverage requirements are met. Notably, ACDRL can dynamically adjust node wake-up patterns based on environmental changes and energy consumption, achieving load balancing and preventing energy depletion in specific areas, which would otherwise cause coverage holes. This adaptive energy management mechanism enables ACDRL to demonstrate significant advantages in large-scale deployment scenarios with resource constraints.

Comparison of reinforcement learning methods

Table 5 Comparative experiment parameters.

Table 6 Comparison of key features among different methods in the literature.

Fig. 4

Coverage rate versus node density.

To comprehensively evaluate the comparative performance of ACDRL against existing mainstream coverage optimization algorithms, a standardized testing environment is constructed where up to 1,000 sensor nodes are randomly distributed within a 60$\times$60 meter area, and each node has a sensing radius of 12 meters, the specific parameters of the experiment are shown in Table 5. Table 6 provides a comparison of key features among different methods in the literature. Each column represents a specific feature: Online scheduling indicates whether the method supports dynamic online scheduling; Sensing coverage indicates whether the method optimizes sensor coverage; and Survival of nodes indicates whether the method considers node survival, such as through energy-saving strategies to extend node lifetime.

Figure 4 presents the coverage rate comparison results based on the probabilistic attenuation sensing model under different node density conditions. The data clearly shows that, while the performance of various algorithms is similar in the low-density deployment stage (node count < 300), ACDRL gradually exhibits significant advantages as the number of nodes increases. Especially when the node density reaches a moderate level, the coverage rate of ACDRL is, on average, about 2.5% higher than that of competing algorithms such as OPFS⁵⁴, DDPG⁵⁵, and DQN⁵⁶. This performance advantage mainly arises from ACDRL’s adaptive learning ability–by continuously interacting with the environment, the algorithm can identify coverage holes and optimize node wake-up strategies to form a more efficient coverage pattern. More importantly, ACDRL is able to maintain a continuously growing coverage rate in high-density areas (node count > 700), while other algorithms tend to reach saturation, which fully demonstrates the adaptability and scalability of the deep reinforcement learning-based coverage optimization method in complex network environments.

Conclusion and future work

This study presents ACDRL, a novel deep reinforcement learning-based deployment strategy for wireless sensor networks that simultaneously optimizes coverage and energy efficiency. The key innovation of ACDRL is its adaptive learning mechanism that combines spatial feature extraction with dual-stream value estimation, enabling sensor nodes to dynamically adjust their operational parameters through environmental interactions while considering network topology, energy states, and coverage requirements. The framework incorporates a novel reward shaping technique that balances immediate coverage gains with long-term energy conservation, along with a dynamic exploration-exploitation strategy that automatically adapts to network conditions. Extensive simulations demonstrate ACDRL’s superior performance compared to conventional methods (OPFS, DDPG, DQN), particularly in challenging scenarios involving high-density deployments and node failures. These results highlight the framework’s robustness and practical applicability. Future work will investigate ACDRL’s extension to heterogeneous networks, mobile sensor scenarios, and multi-objective optimization problems to further improve network performance in complex environments.

Future work will investigate ACDRL’s extension to heterogeneous networks, mobile sensor scenarios, and multi-objective optimization problems to further improve network performance in complex environments. Specifically, we aim to integrate heterogeneous node capabilities (e.g., varying sensing ranges and energy capacities) into the state representation and develop a multi-agent communication protocol to handle cooperative deployment of mobile sensors, while expanding the reward function to incorporate latency and communication overhead metrics for more comprehensive optimization.