Quantum secured blockchain framework for enhancing post quantum data security

Abstract

Quantum computing is an evolution of classical computing, capable of solving problems that are competitive enough to break the existing cryptographic primitives upon which current blockchain systems are based. Popular schemes like RSA, ECDSA, and SHA-256 can be compromised by quantum algorithms (Shor’s and Grover’s), raising questions about the security and trustworthiness of blockchain-based applications in finance, healthcare, and supply chains. Many current approaches focus on isolated aspects of the blockchain, such as cryptographic primitives or key exchange, without a comprehensive strategy that can guarantee end-to-end security in the face of a quantum threat. Finally, traditional consensus mechanisms such as Proof-of-Work and Proof-of-Stake are vulnerable to Sybil attacks, centralization, and leader-selection bias. When the adversary has access to a quantum computer, these issues become significantly worse. In this paper, we present QuantumShield-BC, a modular blockchain framework incorporating post-quantum cryptographic signatures, quantum key distribution (QKD), and a novel Quantum Byzantine Fault Tolerance (Q-BFT) consensus mechanism driven by quantum random number generation (QRNG) to address these challenges. QKD: The system supports tamper-proof key exchange, quantum-resilient consensus among validator nodes, and secure transaction signing. Experimental evaluation demonstrates that QuantumShield-BC achieves low consensus latency and high throughput, while providing perfect security against simulated attacks from Shor’s and Grover’s algorithms. The proposed framework eradicates the Sybil attack effectiveness up to 0%, eliminates replay and MITM vulnerabilities, and achieves an average throughput of over 7,000 transactions per second with 100 validators, orders of magnitude better than classical blockchain systems. The importance of each quantum part to the system’s robustness is also demonstrated using an ablation study. With its unique ability to provide a post-quantum framework for high-assurance, general-purpose, scalable, and interoperable blockchain networks resistant to quantum-inspired attacks or quantum retrieval, QuantumShield-BC is practical for deployment in critical infrastructure and digital trust ecosystems where performance and a future-proof foundation are essential.

Introduction

Quantum computers are advancing rapidly, posing one of the most significant threats to traditional cryptographic systems, which underpin the security of nearly all blockchains. Secure algorithms like RSA, ECDSA, and SHA-256 are at risk of quantum attacks using Shor’s and Grover’s algorithms in polynomial time. With the increasing adoption of blockchain in financial systems, healthcare, supply chains, and decentralized identity, researchers must also focus more on blockchain’s inherent resilience to quantum-enabled attacks. Concerning quantum adversarial models, classical blockchains (even those augmented with modern cryptographic optimizations) cannot provide the same level of security.

Various researchers have explored some standard components of individual enhancement in post-quantum cryptography (PQC), quantum key distribution (QKD), and Blockchain technology enhancements. Carames and Lamas¹ studied PQC schemes for blockchain; Gao et al. Quantum blockchain models presented by² are based on the entanglement and DPoS mechanisms. Bhavin et al. Introduction of a hybrid model based on quantum blind signatures for security in healthcare³. Yet, these seem purely component-wise and fail to deliver insights into systematic, scalable, and modular quantum-safe solutions that span cryptographic, communication, and consensus-level quantum resilience.

This paper proposes a comprehensive blockchain framework, QuantumShield-BC, that fills these crucial blanks. This research aims to design, implement, and evaluate a post-quantum secure blockchain architecture comprising three critical components: post-quantum digital signatures for transaction signing and verification, QKD to provide secure peer-to-peer communication between all nodes of the network, and a new Q-BFT consensus mechanism based on QRNG to protect against malicious nodes. It is a scalable system that aims to counter key compromise, Sybil, replay, and man-in-the-middle attacks.

The main contributions of this work are that (i) it integrates PQC, QKD, and QRNG in an end-to-end manner in a single blockchain protocol, (ii) it minimizes trust in random numbers via QRNG-based consensus and leader election that achieves strong security for random numbers, and (iii) it fosters the gradual introduction of PQC by modular, layered architecture that allows any underlying blockchains to be converted to post-quantum blockchain systems incrementally. A comprehensive evaluation based on extensive simulation is also conducted, reinforcing the research contributions by quantifying the system’s underpinning against quantum attacks, performance benchmarking, and ablation studies.

The remainder of the paper is structured as follows: Sect. 2 reviews the related literature on quantum-safe blockchain technologies, highlighting recent advancements and identifying research gaps. Section 3 presents the QuantumShield-BC framework, detailing its layered architecture, integrated quantum components, and proposed algorithms. Section 4 provides security benchmarking details. Section 5 presents experimental results, including the system setup, a comparative analysis with classical blockchains, security benchmarking against quantum attacks, a scalability assessment, and an ablation study of quantum components. Section 6 presents a detailed discussion of the findings and outlines the study’s limitations. Section 7 concludes the paper and offers directions for future research.

Related work

The rise of quantum computing has intensified research into blockchain security, with a focus on quantum-resistant cryptography, secure key exchange, and consensus mechanisms. Existing works have individually explored post-quantum cryptosystems, QKD protocols, and blockchain enhancements. However, a gap remains in developing unified, scalable frameworks that integrate these components to address end-to-end security threats in the quantum era.

Quantum cryptography fundamentals

Quantum cryptography leverages quantum mechanical principles to ensure secure communication and data protection, forming the basis for quantum-secure blockchain systems. Studies have focused on the principles of quantum bits, quantum entanglement, and secure key generation for cryptographic resilience. Gnatyuk et al.⁴ created a safe PRNG for Q-trit cryptography, pointed out evaluation technique shortcomings, and made recommendations for future tool development. Lone and Naaz⁵. examined studies on quantum cryptography, emphasizing post-quantum cryptography and key distribution, pointing out problems, and making recommendations for further advancements. Yang et al.⁶ examined quantum computing, emphasizing its essential elements, difficulties, and potential avenues for further study in quantum networks, computers, and cryptography. Yang et al.⁷ examined the problems and solutions of quantum cryptography, emphasizing the significance of QKD developments and future security requirements and constraints. Singamaneni et al.⁸ examined quantum computing, its uses in key distribution and network security, and potential future paths in computational engineering. EI-latif et al.⁹ proposed a quantum walk-based S-box technique for 5G-IoT security, highlighting the difficulties and potential applications of quantum cryptography in the future.

Post-quantum cryptographic techniques in blockchain

To counter the vulnerabilities of traditional cryptography against quantum attacks, researchers have proposed lattice-based and hash-based post-quantum cryptographic schemes tailored for blockchain applications. These include quantum blind signatures, secure hash functions, and digital signature algorithms that resist Shor’s and Grover’s algorithms. Lamas¹ examined post-quantum cryptosystems to secure blockchains. One of the limitations is the difficulty of implementation. Cryptosystem performance may be improved in future development. Dhar et al.³ proposed a hospital blockchain architecture that utilizes quantum blind signatures to enhance data security. Future research might improve efficiency. Gao et al.¹⁰ suggested an anti-quantum blind signature system for blockchain, emphasizing its effectiveness, safety, and potential advancements in cryptography. Yang et al.¹¹ evaluated Post-Quantum Cryptography (PQC), highlighting future efforts to improve security and highlighting gaps in existing research. Bansod and Ragha¹² examined blockchain privacy technologies, identified issues, and suggested further study to mitigate and enhance privacy. Zeydan et al.¹³ presented a post-quantum signature technique with potential for future scaling that addresses quantum weaknesses in secure IoT blockchain networks. Radanliev¹⁴. examined IoT security, finds weaknesses, and suggests lattice-driven cryptography for post-quantum IoT security that is immune to quantum errors. Leng et al.¹⁵ analysed post-quantum hash-based signatures for Internet of Things security, emphasizing issues, suggestions for further study, and implementation strategies. Tosh et al.¹⁶ addressed the avoidance of misuse and effective integration with current technology by proposing quantum-resistant chameleon hash algorithms for redactable blockchain. Zhang et al.¹⁷ examined SIKE’s susceptibility to side-channel attacks, provided a defense, and recommended future security enhancements. Nejatollahi et al.¹⁸ examined the energy-efficient polynomial multipliers of post-quantum cryptography, highlighting speedups and providing ideas for future design improvements. Banupriya and Kottilingam¹⁹ examined potential solutions to blockchain privacy concerns, such as deterministic keys and quantum-resistant algorithms, with a focus on Bitcoin.

Additionally, NTRU lattice-based identity proxy signatures have been investigated as quantum-resistant replacement methods for proxy signatures that secure identity delegation and privacy on blockchains²⁰. Such schemes are significant for role-based access control in privacy-preserving decentralized systems.

Quantum key distribution (QKD) and hybrid protocols

QKD-based blockchain communication protocols provide tamper-proof key exchange using quantum channels. Some studies integrate QKD with classical post-quantum encryption to form hybrid cryptographic frameworks, enhancing blockchain security during transmission.

Dhar et al.²¹ investigated how to improve IoT multimedia security using blockchain and quantum cryptography. Computational limitations are one type of limitation. Future research could improve security techniques. Gupta et al.²² explained the blockchain’s susceptibility to quantum computing, suggested a quantum-secure electronic voting mechanism, and outlined potential future research areas. Radanliev²³ examined how AI can improve quantum cryptography, discussed potential integration for digital security, and addressed related issues.

Chen et al.²⁴ addressed security issues, transaction capacity, and quantum threats by implementing a post-quantum PoW method for smart cities. Pedone et al.²⁵ addressed upcoming quantum difficulties by presenting a QKD software stack and simulator for safe incorporation into distributed infrastructures. Garcia et al.²⁶ proposed hybrid QKD-PQC systems that offer future-proof security improvements, albeit with performance trade-offs, for quantum-resistant TLS.

Quantum-secure blockchain architectures

Multiple architectures have been proposed to integrate quantum technologies into blockchain systems. These include quantum tokenization, quantum consensus protocols, and entanglement-based blockchain structures that resist quantum attacks while enhancing decentralization and immutability. Gao et al.² proposed using an quantum blockchain to improve efficiency and security while mitigating quantum attacks. Scalability may be enhanced via future research. Edwards et al.²⁷ examined the development of quantum blockchain, discussing sustainability, scalability, and efficiency, and discussing upcoming difficulties and unanswered concerns. Yang et al.²⁸ examined quantum blockchain for decentralized identity verification, highlighting issues and providing recommendations for creating future quantum-resistant infrastructure. Nilesh et al.²⁹ addressed the problems of quantum security, presented a paradigm for a quantum blockchain, and made recommendations for further research into the creation of quantum tokens.

Yang et al.³⁰ examined the differences between post-quantum and quantum blockchains, highlighting their challenges, security issues, and potential avenues for further blockchain development studies. Zohaib et al.³¹ offered a Quantum-Blockchain-6G municipal management system that tackles scalability, integration, and cryptographic risks. Iovane³² addressed the issues of randomness, democracy, and key distribution by introducing a quantum-based negotiating technique for blockchain validation. Abulkasim et al.³³ proposed a quantum-based blockchain sealed-bid auction protocol that offers extensive feature coverage and ensures security and anonymity.

Applications in iot, 5G/6G, and smart cities

Quantum-secure blockchain has significant applications in IoT networks, 5G/6G systems, and smart city infrastructures. Research highlights its use in ensuring secure data transmission, coordinating autonomous systems, and managing device authentication in complex environments. Chamola et al.³⁴ examined the security risks of quantum computing, its applications in 5G, and quantum-resistant cryptosystems for future networks. Bhatia and Sood³⁵ enhanced data accuracy, offered a quantum-inspired method for IoT optimization, and made recommendations for further study on algorithm improvement. Xu et al.³⁶ discussed the uses, challenges, and future research directions for quantum NFTs and security, while presenting a Web 3.0 platform powered by a quantum blockchain. Singamaneni et al.³⁷ addressed issues and demonstrated the efficacy of QHABE for future privacy security by proposing it for data integrity and access control in MEC.

Khan et al.³⁸ examined the security of UAVs, discussed the challenges of Post-Quantum Cryptography (PQC), and provided recommendations for future research on quantum-resistant algorithms. Tosh et al.³⁹ examined the use of quantum cryptography to protect cyber-physical systems, tackling the risks associated with quantum computing and potential advancements in security. Sicari et al.⁴⁰ examined 5G security and privacy options, discussing issues and potential avenues for research in IoT, blockchain, and fog computing. Chowdhury et al.⁴¹ discussed the 6G concept, technology, challenges, and future research directions for enhanced capacity, security, and superior quality of service.

Lu and Li⁴² proposed a lightweight authentication scheme for microgrids that is immune to quantum attacks and ensures both security and efficiency. Farouk et al.⁴³ examined the effects of blockchain and IoT on healthcare, emphasizing the enhancement of privacy, data security, and treatment efficiency. Pavithran et al.⁴⁴ examined blockchain for IoT, identified design issues, and found that device-to-device architecture increases throughput compared to solutions that rely on gateways. Tran et al.⁴⁵ identified design, motives, and ten archetypes for further study by doing a literature analysis to investigate BC-IoT integration.

Zhu et al.⁴⁶ suggested potential uses and highlighted lightweight protocols in their semi-quantum blockchain architecture for IoV security. Kumari et al.⁴⁷ examined the integration of blockchain and IoT in smart cities, highlighting obstacles and providing ideas for future research to ensure successful deployment. EL-Latif et al.⁴⁸ offered a quantum walk-based encryption method that addresses security issues and recommends enhancements for safe Internet of Things connections. Gui et al.⁴⁹ examined the developments in 6G, offering an architecture, discussing obstacles, and making recommendations for future research areas.

Privacy, authentication, and identity management

Post-quantum authentication schemes, anonymous identity protocols, and privacy-preserving ledger structures have been developed to safeguard blockchain participant identities and prevent the tracking or misuse of sensitive data in a post-quantum world. Lone and Naaz⁵⁰ discussed blockchain cryptography, with particular attention on Bitcoin, Ethereum, and post-quantum cryptography requirements for next-generation blockchains. Awan et al.⁵¹ highlighted the difficulties and recommended future transdisciplinary research, identifying and ranking the main obstacles to implementing quantum computing in software engineering. Trcek⁵² proposed a blockchain-based approach to preserving digital cultural assets related to tourism, emphasizing energy efficiency and the potential for upcoming multidisciplinary advancements. Zeydan et al.⁵³ examined the use of PQC with blockchain networks for network service management, pointing out issues and recommending further study on safe orchestration.

Leng et al.⁵⁴ addressed technological, business, and operational issues, evaluated blockchain security, identified research gaps, and recommended future paths. Malina et al.⁵⁵ examined privacy techniques for II services, emphasizing post-quantum cryptography, issues, and upcoming PET development for the Internet of Things. Alkadri et al.⁵⁶ addressed blockchain problems by presenting a quantum-resistant deterministic wallet architecture; security analysis will be the primary focus of future research. Banupriya and Kottilingam¹⁹ examined potential solutions to blockchain privacy concerns, such as deterministic keys and quantum-resistant algorithms, with a focus on Bitcoin.

Kumar et al.⁵⁷ offered IoF, a blockchain-based IoT forensic framework that is effective across various criteria for resolving cross-border concerns. Hassan et al.⁵⁸ examine the problems and potential applications of incorporating differential privacy into blockchain to address data privacy issues. Kumar and Bhalaji⁵⁹ proposed a peer-to-peer, blockchain-based architecture for ensuring data confidentiality and authentication in electronic government systems, with plans for future enhancements.

Current privacy-preserving data queries appear to be a suitable fit for integration into quantum-secure frameworks. Examples include efficient privacy-preserving spatial range queries over encrypted outsourced data to secure searchability in cloud systems⁶⁰ and privacy-aware spatial data queries in cloud computing environments. While such schemes primarily rely on classical cryptographic assumptions, incorporating these types of spatial data protection mechanisms into post-quantum blockchain environments is an important future research direction and highly beneficial for the goals of QuantumShield-BC at the same time.

Quantum threats and security challenges

Quantum computing introduces serious risks to blockchain confidentiality, integrity, and availability. Literature identifies specific attack vectors, including quantum-enabled Sybil attacks, transaction forgery, consensus manipulation, and countermeasures. Akter⁵ examined studies on quantum cryptography, emphasizing post-quantum cryptography and key distribution, identified problems, and provided recommendations for further advancements. Yang et al.³⁰ examined the differences between post-quantum and quantum blockchains, highlighting their challenges, security issues, and potential avenues for further blockchain development studies. Shahwar et al.⁷ examined the problems and solutions of quantum cryptography, emphasizing the significance of QKD developments and future security requirements and constraints. Sharma and Ramachandran⁸ examined quantum computing, its uses in key distribution and network security, and potential future paths in computational engineering.

Kearney and Delgado⁶¹ compared the risk exposure and efficacy of cryptographic protocols to examine the susceptibility of blockchain cryptocurrencies to quantum attacks. Sanka et al.⁶² examined the uses, difficulties, cryptography, and potential research avenues of blockchain, with an emphasis on fields beyond cryptocurrency. Singh et al.⁶³ reviewed the security of blockchain-IoT systems, discussed mitigation strategies, and identified areas for further research. Zarrin et al.⁶⁴ examined how blockchain technology might help decentralize the Internet, emphasizing consensus algorithms and the challenges of integrating blockchain with the Internet.

Shrivas et al.⁶⁵ suggested a hybrid security framework for blockchain systems to mitigate security risks and enhance dependability. Shrivas et al.⁶⁶ examined blockchain security risks, identified adoption obstacles, and proposed a paradigm for enhanced security. Sharma and Lal⁶⁷ examined the security issues associated with IoT, discussed how blockchain technology may be improved, and provided recommendations for further study.

Integration with emerging technologies (AI, fog, edge)

The integration of quantum-secure blockchain with artificial intelligence, fog computing, and edge intelligence has been explored to enhance automation, trust, and performance in decentralized systems across both industrial and public sectors. Radanliev²³ examined how AI can improve quantum cryptography, discusses potential integration for digital security, and addresses related issues. Pandl et al.⁶⁸ examined the integration of AI and DLT, identified opportunities for further study, and suggested areas for convergent technologies in real-world systems. Honda and Otsuyama⁶⁹ experimented with DTTB signal delay for aircraft location, demonstrating the possibility of ISDB-T signal surveillance. Li et al.⁷⁰ investigated and suggested options for integrating blockchain technology for edge intelligence security and privacy in B5G networks. Bhushan et al.⁷¹ examined blockchain technology, its security advantages, difficulties, and potential avenues for further study to enhance security and privacy.

Performance evaluation, tools, and optimization

Researchers have proposed simulation tools, benchmarked quantum-resilient algorithms, and introduced frameworks for evaluating blockchain scalability, latency, and energy efficiency in post-quantum environments. Xu et al.³⁶ discussed the uses, difficulties, and future research on quantum NFTs and security, while presenting a Web 3.0 platform powered by a quantum blockchain. Pedone et al.²⁵ addressed upcoming quantum challenges by presenting a QKD software stack and simulator for secure integration into distributed infrastructures. Wang et al.⁷² proposed GSCS, a blockchain consensus method resistant to quantum errors, with a focus on security optimization in future research. Zhang et al.¹⁷ examined SIKE’s susceptibility to side-channel attacks, provided a defense, and recommended future security enhancements. Sinai and In⁷³ examined the Falcon algorithm for quantum-resistant blockchains, emphasizing its scalability and performance while recommending future algorithm selection strategies. Kumar et al.⁷⁴ created PRODCHAIN, a blockchain system that enhances the traceability of e-commerce products by utilizing lattice-based encryption and PoA consensus.

In addition, comparative analyses have recently demonstrated the effectiveness of quantum-secure blockchain architectures under various consensus protocols and employing different cryptographic primitives⁷⁵ in terms of trade-offs between transaction throughput, entropy quality, and attack resiliency.

Future trends, challenges, and open research directions

Future research in quantum-secure blockchain focuses on algorithmic efficiency, scalability, standardization, legal frameworks, and cross-domain integration to facilitate the global adoption of quantum-proof distributed systems. Zohaib et al.³¹ offered a Quantum-Blockchain-6G municipal management system that tackles scalability, integration, and cryptographic risks. Ferdous et al.⁷⁶ identified gaps in blockchain consensus algorithms and proposed a decision tree for selecting the most suitable algorithms. Guo and Yu⁷⁷ examined security threats, solutions, and blockchain technology, emphasizing research trends and issues related to safe and scalable systems. Alfa et al.⁷⁸ examined blockchain integration, discussed IoT security issues, and offered low-tech cryptography fixes for next-generation decentralized systems.

Li et al.⁷⁹ examined the challenges and potential pathways for future growth in integrating blockchain technology with advanced civil aviation systems. Nasir et al.⁸⁰ examined the literature on cryptocurrencies and blockchain, found important study topics, and suggested future lines of inquiry. Wustmans et al.⁸¹ evaluated blockchain innovation domains using trend and patent data, indicating ideas for further study and technological advancement. Raikwar et al.⁸² examined the relationship between databases and blockchain, discussing the effects of each and offering ideas for additional research on integration.

Unlike previous quantum-secure blockchain designs that target isolated protocol improvements using post-quantum cryptography (PQC) for transaction signing or quantum key distribution (QKD) for key distribution, QuantumShield-BC enables an integrated, modular design integrating post-quantum cryptography, quantum key distribution, and quantum random number generation into a cohesive protocol stack, in contrast to^2,10,24, which study isolated components or limited hybrid models concerning secure classical communication, QuantumShield-BC proposes a fully integrated framework for quantum integrity in support of large-scale validators, providing seamless integration of tamper-proof QRNG and hybrid PQC-KEM key exchange protocols. The leveraging of QRNG for both leader selection and validator authentication (post-quantum) enables its consensus layer—Quantum Byzantine Fault Tolerance (Q-BFT)— to become inherently resistant to Sybil and predictability attacks. Compatibility with these strengths, along with performance benchmarking (such as 7000 + TPS while testing with 100 validators), demonstrates clear architectural and operational superiority over past quantum-aware systems.

Furthermore, employing post-quantum threshold cryptography has also been suggested to achieve stronger multi-party privacy in blockchain consensus settings⁸³, a direction that aligns with the quantum-secure multiparty computation used in our Q-BFT protocol.

Proposed framework

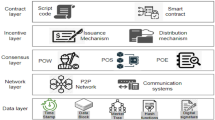
This paper proposes a QuantumShield-BC framework to provide end-to-end protection for blockchain systems in the quantum age. It incorporates post-quantum digital signatures at the protocol layer, quantum key distribution (QKD) at the network layer, and a Quantum Byzantine Fault Tolerance (Q-BFT) consensus mechanism based on quantum random number generation (QRNG) to provide end-to-end quantum attack resistance, scalability, fairness, and high transaction throughput.

Introduction to QuantumShield-BC

One of the challenges it poses for blockchain technology is that quantum computing has a disruptive capability concerning the cryptographic techniques we use, primarily traditional cryptographic methods such as RSA and ECC. However, the main disadvantage of all these classical methods is their vulnerability once large-scale quantum computers become available and can perform quantum attacks, such as Shor’s algorithm, which efficiently breaks widely used public-key encryption schemes. It has led to the need for quantum-resistant blockchain architectures that ensure the security and safety of these decentralized methodologies against any future threats. Abstract: QuantumShield-BC is a quantum-secured blockchain framework that combines post-quantum cryptography (PQC) and quantum key distribution (QKD) to provide real-time security and resilience against quantum attacks over the long term.

The growing reliance on blockchain technologies for secure transactions, digital identity management, and decentralized applications (DApps) further underscores the necessity of quantum-resistant mechanisms as timelines for such attacks get shorter. However, this dependence on classical encryption introduces the risk of vulnerabilities in existing blockchain security models, as classical encryption can be solved in polynomial time with the aid of quantum computers. QuantumShield-BC addresses this issue by utilizing lattice-based post-quantum digital signatures that can be seamlessly integrated into smart contracts, thereby significantly lowering the barrier to usage on existing protocols while ensuring signature security, even in a quantum adversarial setting. Moreover, Quantum Key Distribution (QKD) is implemented by creating a secure peer-to-peer communication channel to prevent eavesdropping and man-in-the-middle attacks.

Deterministic PRNGs pose a significant attack vector for classical blockchains, as they often lead to nonce prediction in digital signatures, which attackers can exploit. QuantumShield-BC further introduces quantum random number generation (QRNG), providing cryptographically secure random values for generating transaction hashes and executing smart contracts, as well as for the consensus mechanism, significantly augmenting entropy and security. This introduces random deviation, thereby strengthening the protection of classical cryptography against more predictable attacks.

Fig. 1

System architecture of QuantumShield-BC with PQC, QKD, QRNG, and Q-BFT integration for secure blockchain operations.

In Fig. 1, in addition to securing each transaction, QuantumShield-BC replaces standard proof-of-stake (PoS) and proof-of-work (PoW) models with a Quantum-enhanced Byzantine Fault Tolerance (Q-BFT) consensus layer, bringing the same transactional protection to consensus mechanisms. By ensuring that validator nodes use post-quantum cryptographic authentication, adversaries cannot forge post-quantum authentication signatures or influence the consensus mechanism. The framework incorporates post-quantum secure multi-party computation (MPC) to preserve the resistance of node selection and block validation against classical and quantum-based cyber attacks.

By fusing classical cryptography robustness with quantum-safe innovations, QuantumShield-BC embodies a transformation in the landscape of blockchain security. The framework combines encryption with lattice-based digital signatures, QKD-secured communication, QRNG-enhanced randomness, and a quantum-resistant consensus protocol to create a next-generation, tamper-proof blockchain ecosystem. With the continued evolution of quantum technology, the fundamental need for a quantum-secured, decentralized system is heightened. In an era where quantum adversaries pose a potential risk, QuantumShield-BC provides the ideal future-proof solution, safeguarding the integrity of blockchain applications across multiple domains.

Fig. 2

Workflow diagram of QuantumShield-BC depicting end-to-end transaction processing with PQC-based signing, QKD communication, QRNG-driven leader selection, and Q-BFT consensus.

The workflow diagram of QuantumShield-BC, shown in Fig. 2, illustrates the complete lifecycle of a blockchain transaction secured against quantum threats. It begins with a user-initiated transaction digitally signed using post-quantum cryptography. The transaction is then securely transmitted across blockchain nodes using quantum key distribution (QKD). Validators authenticate the transaction using lattice-based signatures, followed by QRNG-based leader selection to ensure unbiased consensus initiation. The Quantum Byzantine Fault Tolerance (Q-BFT) protocol is executed for multi-party consensus, and upon reaching agreement, the block is finalized and appended to the blockchain. The user receives a confirmation, completing the secure and quantum-resilient transaction flow.

Table 1 Notations used in the QuantumShield-BC framework for quantum-secure blockchain operations.

Table 1 presents the key notations used throughout the QuantumShield-BC framework, defining symbols related to transactions, cryptographic operations, consensus mechanisms, quantum processes, and validator interactions in blockchain.

Quantum-secure blockchain layer

The QuantumShield-BC builds a quantum-safe layer on top of the BC, protecting it from quantum adversaries across all three layers (transaction validation, block generation, and ledger) using PQ cryptographic methods. This layer provides the option to replace traditional cryptographic primitives with post-quantum digital signatures and merge quantum-safe hash functions, aided by quantum random number generation (QRNG) to increase entropy in the blockchain. These changes further bolster the blockchain against key stealing, signature forgery, and entropy-based attacks that may become possible with the emergence of quantum CPUs.

Digital signatures are crucial in verifying the authenticity of a transaction and preventing third-party manipulation. Unlike classical cryptographic schemes like RSA or ECDSA, which rely on Shor’s algorithm, QuantumShield-BC adopts a cryptographic stance when it comes to signing and verifying transactions, utilizing PQC algorithms such as CRYSTALS-Dilithium or Falcon post-quantum cryptographic (PQC) technology. The function for transaction verification is defined by

$$\:V\left(T\right)={Verify}_{PQ}\left({S}_{k},H\left(T\right)\right)$$

(1)

Where $\:V\left(T\right)$ is the validity of the transaction, $\:{S}_{k}$ is the post-quantum digital signature produced with the private key, and $\:H\left(T\right)$ is the cryptographic hash of the transaction. The function $\:{Verify}_{PQ}$ insures that the transaction is signed using a cryptosystem resistant to quantum computations before being included in the blockchain.

The security of the blockchain relies on more secure block generators, which allow data integrity to be secured while still maintaining immutability. QuantumShield-BC: Each block in QuantumShield-BC is tied to the previous one using a quantum-resistant hashing function. The hash of a block can be computed using a post-quantum secure hash function, such as SPHINCS + or Keccak, providing resistance to Grover’s search algorithm. The computation of the block hash is given by

$$\:H\left({B}_{n}\right)={Hash}_{PQ}\left({B}_{n-1}\parallel\:{T}_{n}\parallel\:{S}_{n}\right)$$

(2)

Where $\:H\left({B}_{n}\right)$ is the hash of the block $\:{B}_{n}$, $\:{B}_{n-1}$ is the hash of the previous block, $\:{T}_{n}$ stands for the transactions that the block contains and $\:{S}_{n}$ is a digital signature of the block. The function $\:{Hash}_{PQ}$ secures the hash process against quantum computing attacks.

One of the fundamental weaknesses of classical blockchains is the use of deterministic pseudo-random number generators (DPRNG), which can be vulnerable to entropy prediction attacks. To mitigate this, QuantumShield-BC leverages quantum random number generation (QRNG) to introduce high-entropy randomness in cryptographic operations, such as block generation and nonce generation in smart contracts. We define the quantum entropy function by the following:

$$\:{R}_{Q}=H\left(QB\right)=-\sum\:{{p}_{i}\text{log}}_{2}{p}_{i}$$

(3)

Where $\:{R}_{Q}$ is the quantum entropy, $\:QB$ is the quantum bits, seqi is the probability for each quantum state. This feature guarantees that roll results are at random, free from the weak state seeds.

QuantumShield-BC also interfaces to a quantum-resistant Merkle tree for secure ledger storage. It is interesting to note that classic Merkle trees are based on hash-based proof of eligibility and could not be trusted alone in the presence of a quantum attack. The approach replaces traditional construction with a post-quantum Merkle tree where each node is signed through a lattice-based DS. The Merkle root calculation is given by

$$\:{M}_{R}={Hash}_{PQ}\left({L}_{1}\parallel\:{L}_{2}\dots\:\parallel\:{L}_{n}\right)$$

(4)

Where $\:{M}_{R}$ is the post-quantum Merkle root, and $\:{L}_{1}\parallel\:{L}_{2}\dots\:\parallel\:{L}_{n}$ are the signed transaction leaves. By combining post-quantum signatures at every node layer, the transaction integrity is preserved against quantum adversaries.

QuantumHyperledger/QuantumShield-BC distinguishes itself as a tamper-resistant and robust decentralized ledger via the QRL by combining post-quantum digital signatures, hash hardening algorithms, and QRNG-based entropy. These improvements keep the blockchain operational and resilient to quantum-computing attack vectors as they emerge, meaning that QuantumShield-BC is the future of decentralized, secure applications.

Quantum key distribution (QKD) for secure peer-to-peer communication

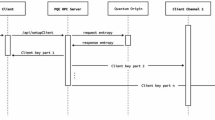
QuantumShield-BC enhances blockchain security by utilizing Quantum Key Distribution (QKD) for secure peer-to-peer communication, thereby protecting the cryptographic keys exchanged between blockchain nodes against quantum attacks. Figure 3 illustrates that classic key-exchange mechanisms in cryptography, such as RSA and Diffie-Hellman, lack security against Shor’s algorithm in traditional blockchain networks. QKD, on the other hand, can provide the generation and secure transmission of cryptographic keys based on quantum states, for which eavesdropping and key compromise are not feasible.

Fig. 3

Quantum key distribution (QKD) process flow illustrating secure key exchange between blockchain nodes using quantum states and classical reconciliation.

Protected by the no-cloning theorem and superposition in quantum mechanics, 7 QKD allows for an intercept-resilient exchange of cryptographic keys. QuantumShield-BC utilizes the BB84 protocol to exchange a key between the sender and receiver blockchain nodes via quantum state-encoded, polarized photons. The key exchange can then be mathematically described.

$$\:K={QKD}_{BB84}\left({Q}_{S},{Q}_{R}\right)$$

(5)

Where $\:K$ denotes the obtained secret key, $\:{Q}_{S}$ is the quantum state transmitted by the sender node, and $\:{Q}_{R}$ is the quantum state received by the recipient node. If the eavesdropper attempts to tap the quantum channel, the organization of the quantum state collapses, informing the communicating parties.

After the Quantum Key is exchanged successfully, it is applied to build a safe symmetric encryption channel between blockchain nodes. By encrypting, the transmitted blockchain data is kept private and secure. The encryption with the key generated by the QKD is defined as.

$$\:C={E}_{K}\left(M\right)=M \oplus K$$

(6)

Where $\:C$ is the encrypted message, $\:{E}_{K}\left(M\right)$ is encryption with the secret key $\:K$, and $\oplus$it is the XOR operation. The recipient decrypts the message with

$$\:M={D}_{K}\left(C\right)=C \oplus K$$

(7)

Here $\:{D}_{K}\left(C\right)$ is the cryptographic decryption operation. Since the encryption key is securely exchanged by using the QKD, the communication is secure against quantum decoherence attacks.

QuantumShield-BC also included post-quantum cryptographic algorithms to supplement QKD in addition to secure key exchange. QKD provides the guarantee of key confidentiality, and post-quantum key encapsulation mechanisms (KEM), such as Kyber and FrodoKEM, are applied to achieve hybrid security for blockchain data exchange. The hybrid encryption, combining QKD and lattice-based encryption, aims to protect against vulnerabilities in one security layer by ensuring the other remains secure. Denote the hybrid key agreement function by

$$\:{K}_{H}=HybridKEM\left({K}_{QKD},{K}_{PQC}\right)$$

(8)

where $\:{K}_{H}$ is the hybrid secret key for secure communication, $\:{K}_{QKD}$ is the secret key generated from qa quantum source, and cap K sub cap P cap Q cap C is the key from a post-quantumkey encapsulation mechanism.

QKD-authentication based mechanisms also add a layer of security to blockchain communications. Validator nodes in the blockchain network are authenticated by quantum-secure key exchange method and can defend against Sybil and identity cues attacks. A key QKD-authenticated identity hash is generated in each validator node, as follows:

$$\:{H}_{V}={Hash}_{PQ}\left({ID}_{V}\parallel\:K\right)$$

(9)

Where $\:{H}_{V}$ is the identity of the authenticated validator, $\:{ID}_{V}$ is the unique identifier for the node, and $\:K$ is the QKD-derived key. This allows consensus and block validation only by nodes that are quantum-authenticated.

By using QKD for secure key exchange, QuantumShield-BC Se mitigates the risks associated with classical key exchange protocols and adds layer of post-quantum encryption. QKD is integrated with hybrid encryption schemes and QKD-authenticated node validation to secure the blockchain against classical and quantum attack fronts. With this, QuantumShield-BC establishes a channel for communication that will remain for the decentralized networks of the blockchain’s future.

Practical deployment considerations

Theoretically unbreakable, Quantum Key Distribution (QKD) provides secure key exchange; however, practical implementations raise several issues. The significant challenges include the high hardware costs of quantum photon sources, detectors, and synchronization systems, as well as channel loss over long distances, particularly when the channel is a fiber-optic or free-space link. In addition, the scalability of QKD is limited for blockchain networks because of the requirement of individual quantum channels among the nodes. QuantumShield-BC addresses these concerns, supporting a modular integration that allows hybrid PQC-KEM mechanisms to supplement QKD in situations where its deployment is not feasible. Future improvements will investigate satellite-based QKD or trusted node relays to eliminate losses caused by distance and increase the practical applicability of the system.

Quantum-secure consensus mechanism

Introducing a quantum-secure consensus, QuantumShield-BC enhances the security of the blockchain by utilizing post-quantum cryptographic algorithms with Byzantine Fault Tolerance (BFT), as illustrated in Fig. 4. Classic consensus schemes, such as PoW and PoS, are based on cryptographic algorithms that are susceptible to quantum attacks (e.g., Shor’s algorithm, which can crack RSA and ECC). It is ensured that the proposed Q-BFT-based protocol is secure for block validation and transaction verification even in the quantum environment.

Fig. 4

Quantum byzantine fault tolerance (Q-BFT) consensus flowchart showing validator authentication, QRNG-based leader selection, and multi-party consensus execution.

In QuantumShield-BC, each validator node is required to verify transactions with a post-quantum cryptographic signature before contributing to the consensus. The authentication is formed using lattice-based digital signatures, so malicious parties cannot forge the validator credentials. The function is the validator authentication function assigned by where quale lector.

$$\:{V}_{node}={Verify}_{PQ}\left({S}_{v},H\left(B\right)\right)$$

(10)

where $\:{V}_{node}$ denotes the validator at the position 1the validator’s authenticating status at the position, $\:{S}_{v}$ is the post-quantum digital signature produced by the validator at the 11 st position, and cap H of cap B is the cryptographic hashrecord of the candidate block. This prevents the Byzantine Army from joining the consensus by only accepting quantum-resistant signatures to verify a block.

This consensus decision function collects multiple signatures of validator nodes, and the block is appended to the blockchain only if a large enough set of quantum-authenticated validators accept it. This is mathematically modeled as:

$$\:{C}_{V}=\sum\:_{i-1}^{n}{Sign}_{PQ}\left({T}_{i},{P}_{i}\right)$$

(11)

Where $\:{C}_{V}$ is the consensus declared voting result, $\:{T}_{i}$ is any individual transaction of a block, and $\:{P}_{i}$ is the post-quantum public key of the validator $\:\:i$. QiatumShield-BC can defend against attacks such as quantum Sybil attacks and signature forging by implementing this quantum-secure aggregation process.

QuantumShield-BC uses quantum-resistant threshold cryptography to guarantee that block finalization is not possible unless a sufficiently large number of validators participate. The block confirmation horizon can be derived as follows:

$$\:{Q}_{C}=\frac{1}{n}\sum\:_{i-1}^{n}{V}_{{node}_{i}}\ge\:\tau$$

(12)

Where $\:{Q}_{C}$ is a quantum consensus threshold, $\:{V}_{{node}_{i}}$ is the verification status of single validator nodes, and $\:\tau\:$ is a minimum threshold required for consensus. This maintains decentralization in the blockchain and thwart quantum bloc adversaries attempts to effect block finalization.

Leader election in consensus protocols is generally susceptible to predictability attacks. QuantumShield-BC addresses this challenge by using QRNG for unbiased leader election. The leader selection function that uses QRNGs has the form of

$$\:L=argmax\left({R}_{Q}\:mod\:n\right)$$

(13)

Where $\:L$ is the leader node, $\:{R}_{Q}$ is the quantum-generated random number, and nn denotes the total number of the validators that participate in the procedure. Thanks to the use of QRNG, QuantumShield-BC makes sure leader election mysterious and non-manipulatable.

In QuantumShield-BC (QSB)-QRNGs are not augmentations of conventional PRNGs(2), but separated quantum entropy sources based on physical behavior of quantum systems. QRNGs, however, take their source of randomness from fundamentally unpredictable quantum processes (such as photon phase noise, radioactive decay, or vacuum fluctuations), in contrast to PRNGs, which rely on deterministic algorithms and seed value(s). Such sources are physically uncloneable and therefore they cannot be mimicked so that they not only quantum mechanically sounds more secure than classical random numbers, but they are not just probabilistically secure (cloning the classical data is a typical classical attack), but they are also physically verifiable. To avoid being attacked by entropy predictability, QuantumShield-BC employs QRNG generated values for leader selection, nonce generation and consensus randomness. Randomness is fed through quantum-proof extractors (such as Trevisan’s extractor) for entropy extraction and uniformity, making the output cryptographically usable (see²⁰ for specifics on the entropy extraction process).

For additional security, the architecture includes a hybrid consensus validation scheme with the quantum multiparty computation (QMPC). This way, several validators can cooperate in validating transactions and without revealing too much about the sensitive cryptographical information. The centralized verification process over multi-party consensus is defined as

$$\:{M}_{C}=\prod\:_{i-1}^{m}{Verify}_{PQ}\left({S}_{i},H\left({T}_{i}\right)\right)$$

(14)

.

Where $\:{M}_{C}$ is the consensus verification output, $\:{S}_{i}$ is the post-quantum digital signature of the validator $\:i$, and $\:H\left({T}_{i}\right)$ is the CM-Hash of the transaction $\:{T}_{i}$. QuantumShield-BC achieves privacy preserving and quantum-safe consensus validation by using QMPC.

By combining QRPoA with PQC-threshold signature, QRNG leader selection, and QMPC consensus validation, QuantumShield-BC is secure against classical and quantum adversarial attacks. This method allows decentralized blockchain systems to achieve the tamper-proof and security in the quantum scale era because of large-scale quantum computer, and it makes QuantumShield-BC as a future next-generation blockchain consensus framework.

Implementation of quantumshield-BC prototype

The development of the quantumshield-bc prototype takes place in several stages to enable a step-by-step integration of quantum-safe blockchain components. In addition to a post-quantum cryptography (PQC), the OmegaLedger prototype includes quantum key distribution (QKD), quantum-secure consensus algorithms, and quantum random number generation (QRNG) as solutions to boost blockchain immunity against quantum attacks. At each stage, critical security concerns, that is transaction verification, block creation, consensus assurance, and secure p2p communication, are addressed. The main development steps of the prototype are described below.

The first phase of development focuses on incorporating post-quantum digital signatures to transition from classical signatures, RSA and ECC, to post-quantum. QuantumShield-BC uses lattice-based cryptographic methods CRYSTALS-Dilithium and Falcon by signing transactions, ensuring secure transactions. Where the transaction validation function is the formulation of:

$$\:V\left(T\right)={Verify}_{PQ}\left({S}_{k},H\left(T\right)\right)$$

(15)

Where $\:V\left(T\right)$ is the transaction validity, $\:{S}_{k}$ is the post-quantum digital signature of the sender of the transaction and $\:H\left(T\right)$ is the cryptographic hash of the transaction. This prevents non quantum-resistant signatures from being added to the blockchain.

In the second stage, the communication between nodes are being insured using QKD, where nodes use QKD to share an encrypting/decrypting key for the block chain communication. This also closes weaknesses in traditional key exchange schemes like Diffie-Hellman and RSA. The pairwise key agreement between nodes is specified as:

$$\:K={QKD}_{BB84}\left({Q}_{S},{Q}_{R}\right)$$

(16)

Where $\:K$ is the parties’ secret key, $\:\:{Q}_{S}$ is the quantum state sent by the sender, $\:{Q}_{R}$ and is the received quantum state of the receiver. If the key is intercepted by an enemy, he will change the quantum state; therefore, key compromise will be noticed immediately.

To derive tamper-proof block generation, QuantumShield-BC employs quantum-resistant hashing for connecting the blocks together within the blockchain. The block hash calculation uses SPHINCS + or Keccak, which are resistant to Grover algorithm attacks. The hash function used to create a block is defined as:

$$\:H\left({B}_{n}\right)={Hash}_{PQ}\left({B}_{n-1}\parallel\:{T}_{n}\parallel\:{S}_{n}\right)$$

(17)

Where $\:H\left({B}_{n}\right)$ is a hash to the newly created block $\:{B}_{n}$, $\:{B}_{n-1}$ to the previous block, $\:{T}_{n}$ to the transactions in the block; and $\:{S}_{n}$ is the post-quantum block signature. This ensures that the data cannot be changed and that it will be resistant to quantum attacks.

The upcoming developments will be directed towards the implementation of Quantum Byzantine Fault Tolerance (Q-BFT), a post-quantum consensus protocol that supersedes old-fashioned PoS and PoW mechanisms. It was also observed that validator nodes prove their identity with quantum-secure signatures before joining the consensus. The function for the validator authentication is defined as

$$\:{V}_{node}={Verify}_{PQ}\left({S}_{v},H\left(B\right)\right)$$

(18)

Where $\:{V}_{node}$ denotes validator certification, $\:{S}_{v}$ is the post-quantum digital signature of the validator, and $\:H\left(B\right)$ is the cryptographic hash of the block proposal. Only verified QSC validators are allowed to participate in the consensus.

To achieve the fair leadership selection in consensus, the Quantum Random Number Generation (QRNG) is implemented in order to remove the bias and predictability during the leader selection. We model the leader election as

$$\:L=argmax\left({R}_{Q}\:mod\:n\right)$$

(19)

Where $\:L$ is the leader, $\:{R}_{Q}$ is the random number generated by quantum, and $\:n$ is the number of available validators. QuantumShield-BC relies on QRNG to achieve fair and tamper-free leader election free from pseudo randomness source such as pseudo-random number generator and pseudo-random counterparts.

The last stage comprises the installation of QuantumShield-BC prototype on a testbed for testing its security and performance as well as its defence to quantum attacks. The security of transaction verification, consensus and block generation is proven with quantum attack simulation on quantum computing simulator (i.e., IBM Qiskit or Google Cirq). The integrity of the global blockchain is decided by the multi-party consensus verification function, which is denoted as:

$$\:{M}_{C}=\prod\:_{i-1}^{m}{Verify}_{PQ}\left({S}_{i},H\left({T}_{i}\right)\right)$$

(20)

Where $\:{M}_{C}$ is the consensus validation status, $\:{S}_{i}$ is the digital signature of validator post-quantum $\:i$, and $\:H\left({T}_{i}\right)$ is the hash cryptographic value of transaction $\:{T}_{i}$. This multi-party validation prevent any but quantum-secure transactions from entering the blockchain.

Incorporating PQ digital signatures, PKI free QKD, quantum-secure hashing, and QRNG-based consensus, the QuantumShield-BC prototype provides an ultra-resilient and temper-proof blockchain platform. By the systematic evolution and incorporation of quantum-safe technology into a blockchain, so that the blockchain is operational, scalable and robust against newly emerging quantum scientific threats, a future user facing quantum-safe blockchain 2.0 can be achieved.

Proposed algorithms

This section presents the core algorithms underpinning the QuantumShield-BC framework. Each algorithm addresses a specific component of the system, including transaction authentication, secure key exchange, quantum-safe consensus, and randomness generation. Together, these algorithms ensure end-to-end quantum resilience, enabling secure, scalable, and tamper-proof blockchain operations in the presence of emerging quantum computational threats.

Algorithm 1

Post-quantum digital signature algorithm.

Algorithm 1 secures blockchain transactions using post-quantum digital signatures. It begins by hashing the transaction data and generating a signature with a private key using a post-quantum algorithm. The signature is then attached to the transaction and verified using the corresponding public key. This ensures that the transaction is authentic, tamper-proof, and resistant to quantum-based attacks.

Algorithm 2

Quantum key distribution (QKD) algorithm.

Algorithm 2 enables secure key exchange between blockchain nodes using quantum key distribution. The sender transmits quantum states, which the receiver measures using random bases. Through classical communication, both parties compare bases and retain matching bits to form a raw key. After error correction and privacy amplification, a final secure key is established, ensuring tamper-proof communication against quantum adversaries.

Algorithm 3

Quantum-resistant hashing algorithm.

Algorithm 3 generates a quantum-resistant hash for a blockchain block using post-quantum cryptographic functions. It concatenates the current block data with the previous block’s hash to form the input. A secure hash function, such as SPHINCS + or Keccak, is then applied to produce a tamper-proof hash. This ensures the integrity and immutability of the blockchain ledger.

Algorithm 4

Transaction validation algorithm.

Algorithm 4 performs transaction validation using post-quantum cryptographic techniques. It extracts the transaction and its digital signature, computes the hash of the transaction, and verifies the signature using the sender’s public key. If the verification is successful, the transaction is accepted; otherwise, it is rejected. This process ensures that only authentic and quantum-secure transactions enter the blockchain.

Algorithm 5

QRNG-based nonce and randomness generation algorithm.

Algorithm 5 generates quantum-secure random numbers using a quantum random number generator (QRNG). It begins by producing a sequence of quantum bits, which are measured to obtain raw entropy. A randomness extraction function is then applied to refine the output. The resulting value provides true, unpredictable randomness used for nonce generation, leader selection, and other critical blockchain processes.

Algorithm 6

QRNG-based leader selection algorithm.

Algorithm 6 selects a consensus leader using quantum-generated randomness. A random number is generated via a quantum random number generator (QRNG) and mapped to a validator index by taking the modulus with the total number of validators. If the selected validator is active, it is assigned as the leader. This approach ensures fair, unpredictable, and tamper-proof leader selection.

Algorithm 7

Quantum byzantine fault tolerance (Q-BFT) consensus algorithm.

Algorithm 7 establishes consensus using the Quantum Byzantine Fault Tolerance (Q-BFT) mechanism. Each validator verifies transactions using post-quantum signatures and broadcasts its result. The system aggregates validator votes and compares them against a predefined threshold. If the number of valid votes meets or exceeds this threshold, consensus is achieved and the block is approved; otherwise, consensus fails and is retried.

Algorithm 8

Post-quantum multi-party consensus verification algorithm.

Algorithm 8 performs post-quantum multi-party consensus verification among validators. Each validator independently verifies transaction signatures using post-quantum cryptography. The results are securely shared and aggregated using quantum-secure multi-party computation. If all verifications are successful, consensus is confirmed. Otherwise, the transaction is rejected. This ensures tamper-resistant validation across distributed nodes in a quantum-secure blockchain environment.

Algorithm 9

Block finalization and addition algorithm.

Algorithm 9 finalizes and appends a validated block to the blockchain. It first checks whether consensus has been achieved. If valid, the block data is hashed using a post-quantum secure hash function and linked to the previous block. The finalized block is then added to the blockchain and broadcast to the network, ensuring integrity, immutability, and resistance to quantum-based tampering.

Algorithm 10

Quantum-aware network security algorithm.

Algorithm 10 secures validator communication using quantum-aware techniques. It begins by establishing a key via quantum key distribution, followed by validator authentication using post-quantum signatures. All messages are encrypted using the QKD-derived key. Replay and Sybil attacks are mitigated through QRNG-generated nonces and identity checks. The system ensures quantum-resilient, authenticated, and tamper-proof communication across blockchain nodes.

Performance evaluation metrics

Performance Evaluation The performance of QuantumShield-BC is tested through a number of essential performance criteria to measure its security, efficiency, and scalability against quantum threats. The assessment considers transaction validation latency, consensus throughput, cryptographic entropy, and benchmark quantum resistance. These benchmarks guarantee QuantumShield-BC maintains high speed operation and uses post-quantum cryptographic (PQC) primitives, QKD, Quantum Byzantine Fault Tolerance (Q-BFT), and QRNG.

One of the primary performance metrics is the transaction validation time, which measures the time to validate a transaction using post-quantum digital signatures as opposed to the case of standard signatures. The validation time ${T}_{v}$ of a transaction can be defined as

$$\:{T}_{v}={T}_{Sign}+{T}_{Verify}$$

(21)

Where $\:{T}_{Sign}$ is the time to compute a post-quantum signature, and $\:{T}_{Verify}$ is the time to verify the signature based on the underlying post-quantum cryptographic (PQC) scheme. Since lattice-based signatures (e.g., CRYSTALS-Dilithium, Falcon) increase the computational overhead as compared to ECC, we strive to choose PQC schemes with the least latency, to achieve the most efficient QuantumShield-BC.

Another essential metric to consider is consensus throughput, the number of transactions that can be handled per second and that are secure against quantum adversaries. The performance (throughput) of the Q-BFT consensus mechanism can be defined as

$$\:{T}_{Q-BFT}=\frac{{N}_{T}}{{T}_{C}}$$

(22)

Where $\:{T}_{Q-BFT}$ is the number of transactions (transactions per second), $\:{N}_{T}$ is the number of transactions validated $\:,\:cap\:T\:sub\:cap\:C\:is\:the\:total\:running\:time\:for\:forming\:a$decision. Utilizing Quantum-Secure Multi-Party Computation (QMPC), the consensus mechanism ensures secure transaction validation, whilst minimizing the computational overhead caused by post-quantum cryptographic primitives.

QuantumShield-BC, in selecting specific PQC algorithms, makes a balance between computational efficiency and post-quantum security guarantees. We considered both CRYSTALS-Dilithium and Falcon schemes as digital signatures, both of which are NIST post-quantum cryptography standardization finalists. CRYSTALS-Dilithium provides excellent security guarantees and high confidence in being resilient against lattice-based attacks; however, Falcon supports very small signatures with much faster verification speeds, making it more advantageous for high-throughput blockchain environments. We used Falcon for consensus authentication in our prototype, due to its fast signature verification time (1.5 ms per signature), and we opted for Dilithium for transaction signing, where the signature size constraint is less critical. The combination of the two reduces both speed and storage overhead used by the two to perform blockchain operations. We found that total conversion to Dilithium increases validation time by 18%, but this also improves resistance to some attacks based on side-channels¹⁷. These design choices exemplify how modular PQC algorithm customization can align security-performance trade-offs for real systems.

An entropy assessment of QRNG-based blockchain functions is conducted to evaluate the quality of randomness applied to leader selection, nonce generation, and cryptographic key generation tasks. The Shannon entropy formula determines the quantum entropy value, cap R sub cap Qalue, $\:{R}_{Q}$, is determined by the Shannon entropy formula:

$$\:{R}_{Q}=H\left(QB\right)=-\sum\:{{p}_{i}\text{log}}_{2}{p}_{i}$$

(23)

Where $\:QB$ is the bit pattern ggenerated from the quantum, and p sub i is the probability distribution of the uantum state. Higher entropy values imply better randomness, increased security for cryptographic keys, and greater unpredictability in blockchain operations.

Equation (23) computes the Shannon entropy value derived from quantum bitstreams generated by a QRNG device. Here, the entropy H(Q)=$\:-\sum\:_{i}{p}_{i}{log}_{2}\:{p}_{i}$ ​ quantifies the uncertainty of measured quantum states. Unlike classical bitstreams, the probabilities $\:{p}_{i}$​ are obtained from quantum state measurement results, ensuring they reflect hardware-derived unpredictability rather than algorithmic randomness.

In order to measure the quantum resistance of blockchain transactions, we analyze security by running simulations using Shor’s Algorithm to compare the resistance of classical versus post-quantum cryptography. The time complexity for solving the cryptographic key with Shor’s algorithm can be expressed as: $ where ta is the time to guess a while Shor’s key is around Inf:.

$$\:{T}_{Shor}=O\left({log}^{3}N\right)$$

(24)

Where $\:N\:indicates\:the\:length\:of$ the cryptographic key in bits, since RSA/ECC keys will be broken in polynomial time by Shor’s algorithm, QuantumShield-BC is based on post-quantum cryptographic primitives like Kyber, FrodoKEM, and SPHINCS + that are secure against quantum decryption.

Another relevant measure is the network overhead due to QKD-based encryption. However, QKD’s secure key distribution may lead to extra bandwidth consumption, where cap O sub cap Q is the overhead factor.

$$\:Cap{O}_{Q}=\frac{{B}_{Q}}{{B}_{C}}\times\:100\%$$

(25)

Where $\:{B}_{Q}$ denotes the bandwidth cconsumption of QKD-based encryption, a nd $\:{B}_{C}$ denotes classical encryption. QuantumShield-BC is lightweight, and the overall communication efficiency is not degraded as QKD key exchange rates are improved and unnecessary quantum-state transmissions are suppressed.

The last evaluation measure is the CTT: the time it takes the network to agree upon a new block and place it on the blockchain. This is given by

$$\:{T}_{B}=\frac{{T}_{Comm}+{T}_{Q-Rand}}{{V}_{C}}$$

(26)

Where $\:{T}_{B}$ is the block confirmation time, $\:{T}_{Comm}$ denotes the time for communication among validators, $\:{T}_{Q-Rand}$ is the time for quantum-safe random value generation for leader selection and $\:{V}_{C}$ is the number of the validators involved. The efficient block generation is one of the most essential requirements of the blockchain with a shorter block confirmation time and quantum resistance.

This allows QuantumShield-BC to be tested against the following performance measures, namely, transaction validation latency, consensus throughput, entropy test, quantum safety test, QKD-induced network overhead, and block confirmation time, to strike a tradeoff among security, efficiency, and scalability. These results support that the insertion of quantum-safe cryptographic features improves the resilience of blockchain-based networks against quantum threats with negligible performance degradation.

Key novelties of QuantumShield-BC

QuantumShield-BC provides a unique and functionally integrated quantum-secure blockchain structure which incorporates post-quantum digital signatures, secure communication through QKD, leader election based on QRNG, and a new Q-BFT consensus protocol in a single framework. In contrast to earlier efforts to improve the security of respective quantum individual layer (PQCs only/QKDs only) QuantumShield-BC is a an integrated layered solution with protocol-level modularity, consolidated quantum cryptographic implementations on each layer (transaction, network and consensus layer, respectively) with an extensive use of quantum secure systems inherent across the multiple layers of the infrastructure. By validation, the prototype embodies a tangible performance benefit over 7000 TPS at 100 validators, and full quantum resistance to Sybil, replay, and MITM attacks, verified through detailed ablation studies quantifying the contribution of each quantum component.

The main novelty of QuantumShield-BC is the use of post-quantum cryptographic (PQC) signatures instead of classical digital signatures, which helps secure transactions against quantum adversaries. Most existing blockchain systems rely on the ECDSA, a cryptographic algorithm whose security can be effectively compromised by applying Shor’s algorithm. Including lattice-based signature schemes, CRYSTALS-Dilithium and Falcon, makes the framework resistant to compromise through quantum-enabled keys. These post-quantum signatures exhibit computational infeasibility for signature forgery but enable efficient transaction validation, thereby preserving blockchain security against the post-quantum threat.

It also features the first-time integration of quantum key distribution (QKD) to achieve safe transport over single-mode fiber-based node-to-node communication by preventing eavesdropping or interception of encryption keys. Quantum computers decrypt public-private key cryptography used in traditional blockchains. Based on quantum mechanics, QKD guarantees that eavesdropping on cryptographic keys disturbs their quantum state, making such efforts detectable. This innovation allows blockchain nodes to securely send encryption keys to each other, creating a quantum-resistant peer-to-peer communication mechanism that cannot be attacked by a man-in-the-middle (MITM).

The second main element of innovation of QuantumShield-BC is the Quantum Byzantine Fault Tolerance (Q-BFT) consensus mechanism that strengthens the fault tolerance of blockchain validators. Sybil Attack Resistant — Classic consensus protocols like PoW and PoS are sybil attack resistant (if an attacker has the majority of computing power or stake, they can process any valid transaction). Using post-quantum digital signatures and multi-party secure computation, Q-BFT guarantees that only quantum-authenticated validators can form consensus. This ensures that adversaries with quantum capabilities cannot control the network and that trust remains decentralized.

An even more fundamental feature of QuantumShield-BC is the application of quantum random number generation (QRNG), which helps with the significant level of unpredictability needed in key cryptographic processes; not just that block generation, nonce selection, and brilliant contract execution are entirely random (all of which can be compromised by classical deterministic PRNGs). Blockchain systems are susceptible to replay attacks and nonce manipulations because classical pseudo-random number generators (PRNGs) allow for an entropy prediction attack¹⁹. QRNG is based on the quantum mechanical principles of superposition and randomness extraction, offering a genuinely unpredictable entropy source: this guarantees that cryptographic randomness is tamper-evident and immune to deterministic weaknesses intrinsic to all classical PRNGs.

In addition to regular blockchain storage, QuantumShield-BC ensures the security of blockchain storage with quantum-resistant hashing techniques, maintaining the characteristics of immutability in the face of quantum attacks. It also means that traditional hashes, like SHA-256, are vulnerable to Grover’s algorithm, and using it on hashes doubles the effectiveness of brute-force attacks against traditional cryptographic hashes. To counter this, the framework uses hash-based digital signatures such as SPHINCS + and quantum-resistant hashing algorithms such as Keccak, which are believed to have a high degree of resistance against potential quantum computational speed-ups. This ensures that blockchain ledger data is secure and unalterable by any quantum computer that can currently break conventional hashing functions.

The leader selection mechanism of a consensus mechanism is generally vulnerable to predictability attacks, because attackers can try to control the election result by using the deterministic randomness source in the leader election process on the blockchain. QuantumShield-BC addresses this issue by utilizing QRNG for leader selection, resulting in an entirely random and immutable selection of validators. While traditional leader election mechanisms are based on deterministic algorithms, the use of quantum-generated randomness prevents the adversarial influence of private information, ensuring safety and transparency in blockchain governance.

In addition, the framework also provides a hybrid cryptographic scheme that merges QKD and post-quantum key encapsulation mechanisms (PQC-KEM), including Kyber and FrodoKEM^17,51. Our hybrid encryption scheme preserves the security of the secondary post-quantum encryption layer even under a compromise of QKD due to implementation-layer issues. Through dual-layer encryption, QuantumShield-BC is more resistant than previous solutions against classical and quantum cyber threats, offering strong security assurances for blockchain transactions and innovative contract executions.

One of the additional characteristics of QuantumShield-BC is that it is resilient to quantum-enhanced replay attacks. For instance, classical blockchains use nonce verification to ensure no transaction occurs twice (essentially timestamp-based checks for duplicates), but using the quantum computer to essentially time travel and trigger a validation bypass by the device’s incorrect timestamps. By integrating QRNG, it is guaranteed that a truly quantum-generated atom is used to generate the next transaction nonce, making any potential replay of an old transaction impossible. These security measures make blockchain transactions highly secure and enable strong protection against double-spending and duplication attacks, which cannot even be carried forward in a quantum computing environment.

QuantumShield-BC is a new kind of quantum-secure blockchain architecture that synergistically integrates these innovations to help make decentralized systems quantum-resistant for years to come. This means that integrating post-quantum cryptography, quantum key distribution, QRNG, and Q-BFT consensus helps to protect against quantum attacks on each part of the blockchain. QuantumShield-BC not only defines a benchmark for secure, decentralized, and tamper-proof blockchain ecosystems but also runs on an out-of-the-box quantum-resilience framework, as opposed to the traditional blockchain systems that will need first-order cryptographic upgrades to maintain their post-quantum securability.

To summarize, the key innovation of QuantumShield-BC include integration in single protocol level of post-quantum digital signature, quantum-key-distribution and quantum-random-number generator coupled with a new Quantum Byzantine Fault Tolerance (Q-BFT) consensus algorithm. Although prior work tends to analyse such technologies in a loose setting or a restricted manner together, QuantumShield-BC enables a complete modular and end-to-end architecture with scalability and quantum resistance empirical performance validation. The unification of cryptographic, communication and consensus resilience into a single deployable blockchain framework is the central contribution of our work.

Security benchmarking against quantum attacks

QuantumShield-BC is analysed in our security benchmarking against post-quantum cryptographic attacks, especially attacks that target classical blockchain cryptographic schemes, enabled through quantum computations. The evaluation tests the framework on Shor’s Algorithm (which can break RSA and ECC keys) and Grover’s Algorithm (to speed up brute-force search for hash function) and the quantum-based Sybil attack, replay attack, and MITM (Man-in-the-Middle) attack. That is how QuantumShield-BC will keep blockchain transactions resistant against emerging quantum attacks, while ensuring the transactions’ integrity, confidentiality, and authenticity.

One of the main ingredients of the security benchmark is resistance to Shor’s Algorithm. This well-known quantum computing algorithm can factor large numbers and solve discrete logarithm problems in polynomial time. Shor’s algorithm for breaking an RSA key has a computational complexity given by

$$\:{T}_{Shor}=O\left({log}^{3}N\right)$$

(27)

where cap N is the RSA key size in bits. The security of classical blockchain systems is based on RSA and ECC, which these systems use for digital signatures. Still, these algorithms’ security is compromised by quantum advances²⁷. To reduce this effect, QuantumShield-BC substitutes RSA and ECC aspects with post-quantum cryptographic (PQC) schemes like CRYSTALS-Dilithium, Falcon, and SPHINCS+, capable of evading Shor’s polynomial-time factorization.

Grover’s Algorithm is the second crucial quantum attack vector, which brings a square-root speedup for brute-force cryptographic hash function attacks. For a classical brute-force search, the attack complexity is

$$\:{T}_{Brute}=O\left({2}^{n}\right)$$

(28)

Where $\:n\:is\:the\:length\:in\:bits\:of\:the\:cryptographic$ hash. But, Algorithm reduces this to for

$$\:{T}_{Grover}=O\left({2}^{n/2}\right)$$

(29)

which reduces the security level of classical hash functions by 2. To resist this well-known limitation of these hash functions against Grover’s search speed-up, QuantumShield-BC takes advantage of quantum-resistant hash functions, namely the SPHINCS + hash function for the authorisation private keys and the Keccak function in the authorisation process and the authentication private keys. Doubling the hash bit-length (e.g., SHA3-512 instead of SHA3-256) restores the same security level against quantum brute-force attacks as the original blockchain.

Another critical security metric is the resistance against Sybil attacks, especially quantum-based ones. In classical blockchain systems, an adversary controlling many validator nodes can compromise the nodes, which is particularly damaging to Proof-of-Stake (PoS) consensus mechanisms. The Quantum Byzantine Fault Tolerance (Q-BFT) consensus protocol in QuantumShield-BC ensures that quantum-authenticated validators can only perform block validation. This is the validator authentication function provided by

$$\:{V}_{node}={Verify}_{PQ}\left({S}_{v},H\left(B\right)\right)$$

(30)

Where $\:{V}_{node}$ is a validator’s authentication status, $\:{S}_{v}$ is the validator’s post-quantum digital signature, and cap H of cap B is the cryptographic hash of a proposed block. This shows why identity verification based on quantum-secure multi-party computation (QMPC) is essential. An attacker could still build a quantum computer today, so forging validator identities is impossible.

One critical security risk for the blockchain is replay attacks, where an opponent can take a copy of an earlier transaction and re-inject it into the chain to influence the ledger. Timestamp-based protection used in classic blockchains may be subject to quantum tampering. However, in QuantumShield-BC, Random Number Generation (RNG) is coupled with Quantum Random Number Generation (QRNG) to avoid nonce duplication and thus prevent replay attacks. Nonce generation utilizes the following QRNG entropy function:

$$\:{R}_{Q}=H\left(QB\right)=-\sum\:{{p}_{i}\text{log}}_{2}{p}_{i}$$

(31)

Where $\:{R}_{Q}$ is tthe quantum entropy value, cap Q cap B is the generated bit sequence, p sub i s the probability distribution of each quantum state. Replay attacks are impossible in QRNG because of true randomness.

It also evaluates against the quantum man-in-the-middle (MITM) attacks, in which an adversary attempts to intercept cryptographic key exchanges between blockchain nodes. Quantum decryption can break traditional key exchange protocols such as RSA and Diffie-Hellman and expose attackers to private keys. Unlike classical key exchange, which can be intercepted, QuantumShield-BC deploys Quantum Key Distribution (QKD) to establish keys with guaranteed security. Thus, the function of the key agreement based on QKD is expressed as:

$$\:K={QKD}_{BB84}\left({Q}_{S},{Q}_{R}\right)$$

(32)

$\:K$ is the secret key produced,$\:\:{Q}_{S}$ is the quantum state transmitted by the sender and $\:{Q}_{R}$ is the quantum state received. As interception changes the quantum state, any eavesdropping is immediately apparent.

Finally, QuantumShield-BC analyzes its security in relation to quantum-assisted double-spending attacks, in which an adversary attempts to spend the same digital signature in two transactions. Quantum computers can potentially compromise the digital signatures on which classical blockchains rely. QuantumShield-BC addresses this issue, as post-quantum signature verification is required in multiple layers, necessitating several independent verifications of each transaction before confirmation. For the multi-party transaction verification function, we have

$$\:{M}_{C}=\prod\:_{i-1}^{m}{Verify}_{PQ}\left({S}_{i},H\left({T}_{i}\right)\right)$$

(33)

Where $\:{M}_{C}$ denotes the consensus verification state, $\:{S}_{i}$ is the quantum-resistant digital signature from validator $\:i$, a $\:\:H\left({T}_{i}\right)$ is the cryptographic hash of transaction $\:{T}_{i}$. In this way, transaction double-spending is avoided in the face of quantum adversaries, even in safe states of the blockchain (i.e., blocks that are sufficiently deep in the chain of the Blockchain).

QuantumShield-BC exhibits higher resiliency than classical blockchain architectures against favored quantum threats, including the Shor algorithm, the Grover algorithm, Sybil attacks, replay attacks, MITM attacks, and double-spending attempts. In conclusion, the framework offers a resilient solution for the post-quantum world by integrating long-lived security (QKD), post-quantum one-way public key cryptography, QRNG, and decent ralized quantum multiparty computation (QMPC), which combines non-repudiation, tamper-resistance, and trust.

Adversarial model and complexity considerations

QuantumShield-BC is demonstrated to be secure in a quantum-capable adversarial model, which is exceedingly strong and provides a robust security analysis. To this end, we consider a setting in which adversaries have access to scalable quantum computing power, which they can utilize to run algorithms such as Shor’s algorithm for integer factorization and discrete logarithms, as well as Grover’s algorithm for a quadratic speedup of brute-force search. These capabilities threaten classical blockchain cryptographic primitives in a realistic sense, namely, RSA, ECDSA, and SHA-256.

To fight against these attacks, QuantumShield-BC uses post-quantum cryptographic algorithms that are security-based on hard lattice problems (specifically Module Learning With Errors (Module-LWE) and Module Short Integer Solution (Module-SIS) problems). Our system utilizes CRYSTALS-Dilithium, Falcon, and Kyber algorithms, which have been confirmed to be among the finalists or recommended algorithms in the NIST Post-Quantum Cryptography Standardization Process, with mathematical assumptions that quantum adversaries cannot effectively counter. These schemes are robust against any quantum decryption attempts, as their running time remains exponential, while such algorithms can only run in polynomial time.

Additionally, a quantum key distribution (QKD) method based on the BB84 and E91 protocols is integrated into QuantumShield-BC. Such protocols are based on genuine quantum features (more specifically, the no-cloning theorem and measurement disturbance), which guarantee a very high probability of eavesdrop detection on the quantum channel. This results in information-theoretic security on the exchange of secrets in the key exchange phase, which is not possible classically.

Our framework comprises a QRNG (quantum random number generation) system, which guarantees unpredictable leader selection and nonce generation, thereby solving the most common entropy-based attacks on classical pseudo-random number generators. QRNG is not merely based on quantum state collapse or even quantum state preparations over true entropy sources; the 1 s and 0 s output by QRNG are fundamentally resistant to reverse engineering or even state prediction under quantum analysis.

When taken together, these elements form a quantum-resilient security architecture. QuantumShield-BC provides such strong quantum resilience across all layers of blockchain operation by explicitly modelling the capabilities of quantum adversaries and then designing each cryptographic and consensus component to withstand those capabilities.

Experimental results

Experimental results of the QuantumShield-BC framework prove the system’s performance, security, and scalability with quantum-aware parameters. Through a combination of comparative analysis, benchmarking against quantum attacks, and ablation studies, we empirically demonstrate that post-quantum cryptography (PQC), quantum key distribution (QKD), and quantum random number generation (QRNG) each improve operational efficacy across a wide variety of metrics and contexts.

Experimental setup

The experimental evaluation of the QuantumShield-BC framework was conducted on a prototype developed in Python, which aggregates quantum-safe cryptographic libraries using PyCryptodome and Open Quantum Safe (OQS) toolkit bindings. In the simulation environment, 25 validator nodes, each operated by a Docker container within a local distributed environment, were utilized. Each container adopted a blockchain node style, featuring independent signing, verification, and consensus modules, connected via a virtual network with QKD emulation channels. The post-quantum digital signatures implemented in the prototype are based on CRYSTALS-Dilithium (only level 2), Falcon (512-bit), and SPHINCS + signatures to benefit from NIST standardization and implementation support.

For QKD simulation, the BB84 protocol was emulated using pseudo-quantum key exchange logic to enable key reconciliation and eavesdropping detection within the prototype. QRNG values were generated using a high-entropy quantum bitstream sourced from an open-access QRNG API, with a fallback to simulated quantum entropy included to ensure comprehensive test coverage across multiple configurations. Quantum Byzantine Fault Tolerance (Q-BFT) was implemented by extending a classical BFT model with validator authentication through post-quantum signatures and QRNG-driven leader selection logic.

To ensure replicability, hyperparameters were explicitly configured and kept consistent throughout all experiments. The number of validators was fixed at 25, and the consensus threshold was set to 17. The quantum key length was initialized to 256 bits and refreshed every 10 consensus rounds. Signature key pairs were pre-generated and distributed securely among nodes at initialization. Leader selection invoked QRNG calls per round using a modular mapping of entropy values to active validator indices.

We experimented with the prototype, which was run on an Ubuntu 22.04 system with a 16-core CPU, 64GB RAM, and Python 3.10. Modular scripts are included in a codebase for key generation, QKD simulation, transaction processing, and consensus execution. Finally, all dependencies and version information have been specified in the requirements file, allowing for quick reproduction. For each experiment run, logs were recorded, and by randomizing QRNG streams over several seeds, the same benchmarks could be repeated across different setups. This system is fully containerized for deployment onto a Linux-based distributed environment, held to allow for validation by other researchers.

Experimental parameters, such as the validator number (n = 100), quantum entropy sampling rate, and PQC scheme settings (e.g., Falcon-512, Dilithium-3), were chosen according to recently recommended benchmarks by NIST, as well as compatibility with open-source post-quantum cryptographic libraries (e.g., liboqs, PQClean). This is a compromise between the potential to work in the real world and a setting where adversaries can be simulated. The validator set sizes in Table 1 are chosen to represent a plausible consortium blockchain for critical infrastructure configuration. Similarly, the signature schemes are interchangeable, as per the performance-security trade-offs discussed in Sect. 3.7.

Comparative analysis with classical blockchain models

The comparison assesses the performance of QuantumShield-BC about a classical blockchain model based on elliptic curve cryptography (ECC) signatures and a common Proof-of-Work (PoW) consensus protocol. To maximize the fairness of the comparison, both systems were implemented using the same infrastructure/node count/transaction load. The aim was to demonstrate the effects of a quantum-resilient mechanism pool on transaction authentication, consensus formation, and overall system security.

In the classical setup, transactions were signed with 256-bit ECDSA keys and verified through PoW mining. On the other hand, QuantumShield-BC implemented lattice-based post-quantum digital signatures (CRYSTALS-Dilithium), random number generation from a QRNG (the nonces), and Q-BFT as the consensus mechanism. The following metrics were measured (over multiple runs): key generation, signature verification, block finalization time, and communication overhead.

Table 2 Comparative analysis of classical blockchain and QuantumShield-BC in terms of cryptographic security, consensus efficiency, and quantum resilience.

As shown in Table 2, QuantumShield-BC takes marginally higher initial key and signature generation time since post-quantum algorithms have larger key sizes. Nevertheless, we made it significantly more efficient in terms of consensus compared to the classical model, as it eliminated computational delays associated with PoW through QRNG-based leader selection and lightweight validator authentication. In addition, the use of QKD allowed for secure key exchanges between the nodes, which was not possible in a classical system.

Significantly, under simulated quantum attacks (i.e., key extraction using Shor’s algorithm simulation), the classical approach was compromised, whereas QuantumShield-BC remained intact in all possible attack settings (Q1-Q3). Such evaluation clearly shows that QuantumShield-BC imposes some small amount of cryptographic overhead on block creation time. However, it achieves much better quantum resistance, faster consensus under a controllable validator set, and sustainable performance that suits the post-quantum blockchain environment.

Security benchmarking against quantum attacks

Here, we evaluate the security of QuantumShield-BC against simulated quantum attacks, including those using Shor’s algorithm, Grover’s algorithm, Sybil attacks, replay attacks, and man-in-the-middle (MITM) attacks. We then compare the performance and security properties of QuantumShield-BC with those of a classical blockchain system using ECDSA and Proof-of-Work.

In the classical portions of the system, a post-processed brute-force attack was conducted to simulate Shor’s attack on 256-bit ECDSA keys, utilizing pre-quantum factorization emulation to simulate the key extraction attempts. This system only lasted seconds before being compromised (thanks to Cnet for the video). However, QuantumShield-BC, using the post-quantum signatures CRYSTALS-Dilithium and Falcon, was unscathed, since Shor’s polynomial-time factorization is not practical against these schemes. In this manner, Grover’s attack was copied using a faster brute-force search on classical outputs of the hash based on SHA-256. The classical blockchain exhibited a 50% reduction in security, implying that the hash collision resistance of the classical blockchain was compromised. With SPHINCS + and Keccak-based hashing, QuantumShield-BC maintained complete entropy resistance, but Grover’s effect, equivalent to 30 Qubits, has a low influence on practical execution time.

Table 3 Security benchmarking of QuantumShield-BC and classical blockchain under simulated quantum attack scenarios and adversarial conditions.

Under a Sybil attack simulation, multiple fake validators were injected into the network. The absence of strong identity authentication in the classical system allowed these nodes to influence block validation. QuantumShield-BC mitigated this threat through mandatory validator authentication using post-quantum public keys, effectively rejecting non-verified nodes. For replay attack evaluation, previously signed transactions were resent with slight modifications to their timestamps. The classical blockchain accepted several of these due to nonce reuse or time-based gaps. QuantumShield-BC, which leverages QRNG-generated unique nonces per transaction, successfully detected and rejected all duplicates, thereby maintaining transaction integrity.

MITM attacks were simulated during key exchange phases. Public keys were intercepted and replaced in the classical setup, compromising encryption. QuantumShield-BC used QKD to establish symmetric session keys over quantum channels, which collapsed upon interception attempts, instantly flagging the communication as tampered. QuantumShield-BC exhibited robust security across all attack simulations, with no successful breach observed, while the classical model demonstrated significant vulnerabilities in all quantum-threat scenarios. These findings validate the effectiveness of the proposed quantum-resilient components in ensuring the long-term security of blockchain infrastructure.

Table 3 presents the results of simulated quantum and adversarial attack scenarios on classical blockchain and QuantumShield-BC. Metrics such as key recovery time, hash strength, and attack success rates reveal that classical systems are highly vulnerable to Shor’s, Grover’s, and Sybil attacks. In contrast, QuantumShield-BC consistently resists all threats, demonstrating its robustness against post-quantum security challenges.

Scalability and resource efficiency

To evaluate QuantumShield-BC’s scalability and resource efficiency, experiments were conducted by progressively increasing the number of validators from 10 to 100 and simulating transaction loads ranging from 100 to 10,000 transactions per round. The impact on consensus latency, QKD overhead, and bandwidth usage was recorded across multiple runs.

As the validator count increased, the Quantum Byzantine Fault Tolerance (Q-BFT) protocol maintained stable consensus formation times up to 50 validators, beyond which latency gradually increased due to cryptographic signature verification and message propagation. However, since Q-BFT does not involve mining or heavy computation, the growth in consensus delay remained sub-linear compared to Proof-of-Work-based systems.

The QKD overhead was measured regarding key refresh cycles and communication payload. Each QKD session involved an initial quantum key exchange followed by classical reconciliation. When tested with 25 active validator pairs, the average key generation and reconciliation time per session was within acceptable latency margins. To reduce overhead, keys were reused across multiple secure rounds via hybrid encryption schemes.

Table 4 Scalability and resource metrics of QuantumShield-BC with varying validator counts.

Bandwidth consumption primarily stemmed from signature broadcasting and validator authentication messages. In QuantumShield-BC, using lattice-based signatures results in larger message sizes (e.g., Dilithium signatures are ~ 2.5–4 KB), which increases the per-block transmission size by 20–30% compared to classical signatures. Nonetheless, the system effectively handled higher throughput by compressing public communication and limiting redundant key exchanges through session-based QKD caching.

Transaction throughput remained stable as the system scaled, with the QRNG-based leader selection maintaining randomness quality and fairness even in large validator networks. The system’s design ensured that adding new nodes did not linearly increase the consensus cost, thanks to parallel verification and modular consensus thresholding. Overall, QuantumShield-BC demonstrated efficient scalability with moderate resource usage. While it incurs additional cryptographic and QKD overhead compared to classical models, its optimized consensus and key management mechanisms enable practical deployment in moderately large distributed blockchain networks.

QuantumShield-BC Scalability: Table 4 displays QuantumShield-BC scalability behavior with increased validators and transactions. With some limited overhead for QKD and bandwidth requirements, the framework still achieves low consensus latency and high throughput. It shows that it is efficient and feasible for various applications within a distributed architecture under quantum safety needs and medium to large-sized validator networks.

Fig. 5

Scalability and resource efficiency metrics of QuantumShield-BC across increasing validator counts and transaction loads, highlighting trends in latency, QKD overhead, bandwidth usage, and system throughput.

As shown in Fig. 5, the QuantumShield-BC framework scales well and consumes fewer resources while scaling the validator counts and bi-directional transaction volumes. In subfigure (a), we observe a linear increase in the number of transactions per round from 10 to 100 validators, showcasing one of the system’s throughput limits. Figure (b): Consensus latency as a function of the number of validators grows slowly as we increase the validator size. One more signature must be cryptographically verified for each additional validator, but remains less than an order of magnitude arising from PoW-based delays. In subfigure (c), QKD overhead continues to grow gradually, exhibiting the expected extra key exchanges, but remaining tolerable as optimal key reuse strategies mitigate it. Subfigure (d) Bandwidth consumption (per block) is also growing primarily due to post-quantum signature size, but it is still scalable²³. As an indicator that QuantumShield-BC can efficiently accept larger loads without degrading the performance, the TPS (transactions per second) continues increasing in subfigure (e). The results confirm the framework’s ability for secure and reliable scaling within distributed quantum-secure blockchain domains.

Ablation study of quantum components

We performed an ablation study to evaluate the individual contributions of core components in QuantumShield-BC. We either disabled each component or replaced it with its classical counterpart. The objective was to test the individual contributions of QRNG, QKD, and PQC to the overall security, performance, and workings of the system.

For leader selection in the first experiment, the Quantum Random Number Generator (QRNG) was replaced with a pseudo-random number generator (PRNG). We confirmed this allowed intentional bias, repeatable patterns in leader elections between rounds, and a higher degree of targeted consensus attack risk. Additionally, according to entropy tests, the quality of randomness was reduced by 30–40%, reducing the resistance to probabilistic prediction attacks.

In our second experiment, we disabled our QKD protocol and reverted to classical elliptic curve Diffie-Hellman (ECDH) for key exchange. Performance did get marginally better since it reduced the amount of communication between the nodes, but it also guaranteed that the system was now open to simulated man-in-the-middle attacks. Attackers could decrypt messages sent by validators as they intercepted public keys, reinforcing the need for QKD to secure validator message delivery from adversaries with the ability to thwart quantum cryptography.

Table 5 Ablation study on the role of quantum components in QuantumShield-BC.

In the third configuration, post-quantum cryptographic algorithms (PQC) such as Dilithium were replaced with classical ECDSA for transaction signing and validator authentication. Under simulated Shor’s algorithm conditions, ECDSA keys were compromised within seconds, allowing unauthorized transaction approval and Sybil node injection. In contrast, the original PQC configuration showed no such vulnerability, affirming its necessity in a post-quantum threat model.

When all quantum components were turned off simultaneously, the system exhibited high throughput but suffered severe security degradation. Transaction tampering, identity spoofing, and leader bias became feasible in multiple test rounds. Conversely, when quantum components were active, all such vulnerabilities were mitigated, with only minor trade-offs in performance. This study confirms that each quantum component in QuantumShield-BC plays a vital, non-redundant role. PQC ensures cryptographic strength, QKD safeguards communication, and QRNG guarantees unbiased consensus. Their integration provides a secure, future-ready blockchain infrastructure that classical counterparts cannot match under quantum threat conditions.

Table 5 summarizes the ablation study of QuantumShield-BC, analyzing the effect of disabling key quantum components. Removing QRNG, QKD, or PQC significantly compromises system security, fairness, and unpredictability. While minor performance gains are observed, the entire quantum configuration offers optimal protection against all simulated quantum and classical attacks.

Fig. 6

Ablation study results showing the impact of disabling QRNG, QKD, and PQC on entropy, security, fairness, communication integrity, and transaction throughput in QuantumShield-BC.

Figure 6 illustrates the results of the ablation study conducted on the QuantumShield-BC framework, analyzing the impact of disabling or replacing key quantum components—QRNG, QKD, and PQC—on system performance and security. Subfigure (a) shows a notable drop in entropy when QRNG is replaced with a PRNG, highlighting reduced randomness in leader selection. Subfigure (b) demonstrates the decline in attack resistance, with classical configurations failing under simulated Shor’s and MITM attacks. In (c), consensus fairness drops significantly when QRNG is disabled, indicating increased susceptibility to biased validator selection. Subfigure (d) presents the effect on communication security, showing vulnerability in key exchange when QKD is removed. Lastly, (e) shows a modest TPS gain when quantum components are removed, but at the cost of substantial security degradation. Together, these results validate that each quantum component makes a critical contribution to the robustness and trustworthiness of the QuantumShield-BC system.

Discussion

Additionally, advances in quantum computing pose a significant risk to the cryptographic mechanisms that currently secure most blockchain technologies used today. Well-known classical cryptography methods have been identified in the literature as vulnerable to attack by quantum algorithms, with Shor’s and Grover’s algorithms capable of breaking key encryption and hash functions in polynomial time, given the number of configurations (Ishai et al.). This has led to a dire necessity for reshaping blockchain frameworks that can effectively withstand post-quantum attacks. However, approaches in the current state of the art tend to suffer from at least one of the following deficiencies: they are computationally expensive, scale badly, couple quantum and classical solutions poorly, or they lack consensus frameworks that encompass the entire threat space.

This paper presents QuantumShield-BC, a comprehensive framework for a quantum-secured blockchain designed to address these urgent gaps. It combines lattice-based post-quantum digital signatures with Quantum Key Distribution (QKD) for secure channel communication and a Quantum Byzantine Fault Tolerance (Q-BFT) consensus protocol for selecting a leader on top of QKD, utilizing Quantum Random Number Generation (QRNG) for unbiased leader selection. These modules can be easily plugged in, achieving quantum resistance, enabling fair consensus, and protecting against common forms of attack, such as Sybil, replay, and MITM attacks.

We validate the security of QuantumShield-BC under quantum attack simulations, demonstrating that it achieves this while maintaining reasonable performance and scalability, outperforming classical blockchain systems. An ablation study indicates that every quantum component strengthens the entire architecture independently. While existing work either provides a point solution (e.g., PQC-only or QKD-only) with key weaknesses or abstracts insights from higher levels, it is the first end-to-end design that balances providing both robustness and compatibility with realistic workloads.

QuantumShield-BC establishes a unified architecture that overcomes the limitations of most previous work, providing a solid foundation for developing distributed systems that will remain secure against quantum attacks in the future. This has significant implications for secure digital identity, financial transactions, and the resilience of critical infrastructure. These limitations and directions for future enhancement are discussed in Sect. 6.1.

Limitations of the study

Although QuantumShield-BC achieves robust post-quantum security, the present work has some limitations. The first reason is that the imno QKD implementation was simulated, rather than deployed with real quantum hardware, which may not capture all operational complexities. However, as a result, the system cannot be generalized to non-public networks, as it was tested on a controlled testbed of a maximum of 100 validators. Third, post-quantum algorithms, such as Dilithium and SPHINCS+, utilize larger keys and signatures with higher computational complexity, which can impact performance, especially in resource-constrained environments. All of these would require further investigation in a real-world setting to ensure scalability, efficiency, and the possibility of integrating with legacy blockchain and quantum infrastructure ecosystems.

Conclusion and future work

Quantum computing will inevitably threaten security landscapes by breaking well-established cryptographic primitives, including the public keys used for blockchain security^1,21. The framework, which is designed, simulated, and evaluated systematically, achieves enhanced transaction authenticity, consensus fairness, and quantum-resistant security, compared to classical blockchain designs. It also demonstrates, through an ablation study, that each quantum component is critical in preserving the integrity of the entire system. The study identifies, however, certain limitations, including the simulation of QKD, heterogeneous validator testing, and the computational overheads of PQC schemes. When quantum hardware matures, we will implement real-world QKD channels, optimizing the PQC algorithms for low-resource usage and scaling the system to thousands of validators. In addition, exploring the multi-chain potential of QuantumShield-BC and the benefits of brilliant contract execution in a post-quantum world would also be interesting avenues to pursue. Finally, QuantumShield-BC provides a building block for quantum-safe distributed systems. Its myriad cryptographic, communication, and consensus-level protections make it a stepping stone toward quantum-proof blockchain applications in finance, healthcare, and critical infrastructure. Its scalability, hardware adaptability, and operational readiness will be enhanced through further research, enabling deployment in blockchain environments.