Introduction

Steels and their alloys are the primary materials that are extensively used in infrastructure development, fabrication of machine components, building of commercial vehicles, and the production of countless consumer goods1. The role of steel and its alloys is significant in these sectors and necessitates the continuous exploration of innovative welding technologies to enhance the correlation between structure and properties. In this context, FSW has emerged as a transformative technique, offering distinct advantages that address some of the longstanding challenges associated with traditional fusion welding processes.

Steel’s strength, machinability, and versatility make it ideal for industrial applications. However, traditional welding approaches that utilize material fusion through extreme temperatures tend to have a multitude of problems, particularly when working with thick regions of steel. The collection of problems, such as heat-affected zone, residual stresses, and the potential to have defects within the welded joints, has driven the exploration of alternative approaches to welding2.

FSW has advanced infrastructure development by offering improved mechanical performance, environmental safety, and operational reliability over conventional welding3. FSW is a solid-state process that uses a rotating tool to generate heat and join materials without melting. This different approach leads to welds with finer microstructures, improved mechanical attributes, minimal distortion, and reduced alterations in shape compared to traditional methods, addressing some of the key limitations of older processes. Input parameter optimization of FSW is the driving force toward achieving the best structure-property correlations and mechanical strength. It must be optimized for welding AISI 1018 steel since these parameters sensitize very strongly to heat generation and distribution. This steel grade offers a good equilibrium between strength and machinability, thus making it a suitable choice for investigating FSW parameter optimization intricacies. Key parameters include welding speed, tool rotational speed, and shoulder diameter. The output responses, such as microstructures and mechanical properties, are greatly influenced by their interconnected dynamics.

Extensive research has been conducted on FSW of aluminum alloys, particularly AA6xxx and AA2xxx series alloys and lightweight materials4,5,6,7. In contrast to aluminum, which achieves UTS in the range of 250–320 MPa post-FSW, carbon steels like AISI 1018 demand optimized thermal and mechanical conditions to preserve higher UTS levels (435 MPa) and achieve improved ductility. Recent studies indicate the investigation of the effect of process parameters on microstructure and mechanical properties, but the effect of welding speed, tool rotational speed, and shoulder diameter on weld integrity is not fully explored8,9,10. Moreover, while multi-response optimization techniques like GRA and PCA have been used in other materials11,12,13, their use in optimizing the FSW process for carbon steel is still underdeveloped.

Recent studies have demonstrated the influence of reinforcement and parameter optimization in FSW of aluminum alloys. Sabry14 incorporated Al-SiC matrix reinforcement in dissimilar FSW of AA6061 and AA6082 and reported a significant increment in strength, ductility, and corrosion resistance. Extensive studies by the same author demonstrated that TiB₂ and Al₂O₃ reinforcements in Al6061–Al6082 alloy joints led to superior structural integrity and improved tribological performance15. The effect of tool parameters on the strength of AA2024 and A356-T6 was also studied extensively, showing notable sensitivity of tensile and impact strengths to tool rotation and traverse speed16. Additionally, GRA-based Taguchi methods have been used for multi-weld quality optimization in aluminum flange joints17,18 and for evaluating friction stir welded 6061-T6 flanges19. Comparative analysis of FSW and TIG welding techniques in AA6082 also indicated differences in joint performance and microhardness profiles20. Other statistical studies have examined how clamping torque, pitch, and rotation speed influence weld quality and defect minimization21. These studies provide important benchmarks for mechanical properties in aluminum FSW, where UTS values typically range between 250 and 320 MPa and elongation from 10 to 18%, depending on alloy and processing conditions.

While several studies have reported microstructural evolution in different FSW zones, limited work has focused on correlating these structural changes with optimized mechanical performance in AISI 1018 carbon steel using integrated multi-response decision-making techniques. In addition, tensile strength, ductility, and impact resistance trade-offs have not been addressed systematically, which complicates finding universally ideal welding conditions.

This research addresses these gaps by systematically investigating the effects of key FSW parameters through an orthogonal array design, experimental evaluation, and both single and multi-response optimization. The novelty of this study lies in the integrated use of GRA and PCA for multi-objective optimization, enabling a comprehensive correlation between mechanical properties and microstructural evolution. This approach is largely unexplored in the context of AISI 1018 carbon steel, where most previous studies focus on aluminum alloys or single-response methods.

Experimentation

Selection of machine tool for experimentation

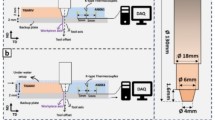
A custom-built Friction Stir Welding (FSW) machine was employed for the present study. The machine (Model: FSW-4T-HYD) has been developed using modular industrial components such as a high-torque STARK spindle system, hydraulic actuators, and programmable control for feed and thrust. The machine tool setup used in the present study is shown in Fig. 1, and its technical specifications are presented in Table 1.

Fig. 1
figure 1

The FSW setup used in the current investigation.

Full size image
Table 1 Specification of the FSW machine employed in the present study.
Full size table

Workpiece material

A 3 mm-thick carbon steel plate was used in the study. Table 2 shows the chemical composition and mechanical properties of the AISI 1018 steel grade obtained through Optical Emission Spectroscopy (OES) analysis.

Table 2 Chemical composition (wt%) and mechanical properties of the base metal.
Full size table

Rectangular plates of 200 × 40 × 3 mm were cut from a standard 6′ × 4′ AISI 1018 carbon steel plate supplied by SAIL. A butt joint was prepared by keeping the two plates of the same dimensions together using a fixture.

Tool selected for experimentation

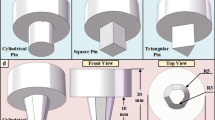
Figure 2 represents the profile for the tungsten carbide tool used in the current investigation. The tool used in the present study was made of tungsten carbide (WC) with 7% cobalt (Co) binder, a composition selected for its excellent wear resistance, high hardness, and thermal stability. These properties make it ideal for friction stir welding of carbon steels, as the tool maintains structural integrity under high loads and temperatures, enabling consistent heat generation and long tool life without premature wear. The tool pin is designed as a truncated cone, with a pin length of 2.8 mm and a pin diameter of 6 mm. A 3° tool tilt (θ) was applied to enhance material flow and weld quality. A truncated cone pin profile was selected because it can yield effective material flow, consistent heat distribution, and enhanced mechanical properties in FSW of carbon steel. In comparison with other pin profiles, the truncated cone profile maximizes stirring action and minimizes defects like voids and tunnelling. It also promotes grain refinement through effective heat generation and plastic deformation22.

Fig. 2
figure 2

Tool profile used for FSW of steel.

Full size image

Implementation of optimization techniques for FSW parameters

The optimization of FSW parameters is implemented in this study to enhance the mechanical properties of AISI 1018 steel joints by systematically determining the most effective welding conditions. Traditional welding processes often result in inconsistent mechanical performance due to uncontrolled heat input and material flow.

The use of GRA is particularly beneficial in this case as it converts multiple performance metrics into a single relational grade, facilitating an efficient decision-making process. PCA further refines the analysis by identifying the most influential parameters, reducing dimensionality, and improving the reliability of the results. This optimization approach minimizes experimental iterations while maximizing weld quality, ensuring that the selected process parameters lead to structurally sound and high-performance welded joints. The process of optimization is further illustrated in detail by the following sequential steps. This methodology is illustrated in Fig. 3.

Step 1: Defining the output responses. The optimization procedure was initiated by establishing the desired performance goals for a given process. The output responses examined in this study are UTS, PE, RA, and IE. UTS and IE were prioritized for their relevance to strength and toughness, while PE and RA provided insights into ductility and plastic deformation, enabling a comprehensive mechanical assessment. This initially involves optimizing each of the four individual responses as mentioned above using a single-response optimization approach, followed by multi-response optimization of the combined output responses.

Step 2: Selecting the input parameters along with their levels: Three parameters, namely welding speed (N), tool rotational speed (N), and shoulder diameter (D), are considered in the study. The values of V, N, and D can be varied within a range, where V ranges between 60 and 210 mm/min, N ranges between 430 and 750 rpm, and D ranges between 15 and 20 mm. The selection of these parameter ranges was based on the authors’ previously published study23, 26, 32 and practical feasibility in FSW of carbon steel. The selected levels are intentionally non-uniform to reflect real-world process limitations and allow finer optimization around expected critical points. The ranges are validated based on earlier trials and industrial feasibility. Lower welding speeds ensure sufficient material mixing, and the low rotational speed prevents excessive heat generation, which can cause grain coarsening, material softening, and defects like voids. The chosen tool rotational speed range balances heat input to prevent excessive softening, grain coarsening, and defects such as voids or tunnel formation. The shoulder diameter was selected to optimize heat distribution and material flow, ensuring adequate stirring action for defect-free welds. Each of these factors is categorized into three levels as indicated in Table 3. After conducting optimization, the output responses were obtained using the optimized set of factors, which were compared to those obtained using the initial set of factors.

Fig. 3
figure 3

Flowchart showing the methodology of single/multi-response optimization of process parameters.

Full size image
Table 3 Selected input parameters and levels.
Full size table

Step 3: Finalising the orthogonal array (OA): In this study, three parameters, each having three levels, are examined. Therefore, L9 OA is utilized, as illustrated in Table 4. L9 OA is preferred over L27 because it effectively captures the main effects with minimal experimental runs. L27 would have 27 trials, adding workload without much added understanding. L9 accomplishes statistical efficiency with fewer trials while still ensuring data dependability through three replications per experiment.

Table 4 Design matrix used for the experimentation.
Full size table

Step 4: Conducting the experiments: The assessment of the UTS, PE, RA, and IE is conducted by performing a total of nine experiments, with three trials each. The data is displayed in Table 5.

Table 5 Outcomes of the experiment conducted.
Full size table

Step 5: Data analysis for determining the effect of input parameters: The larger-the-better (LTB) loss function was used to calculate the S/N ratio32, as shown in Eq. (1), to maximize the output response33.

$$S/Ni=-10log=\:\frac{\text{1}}{{\text{n}}_{\text{tr,i}}}\sum\:_{\text{u=1}}^{{\text{n}}_{\text{tr,i}}}\frac{\text{1}}{{{\text{y}}_{\text{u}}}^{\text{2}}}\text{)}$$
(1)

Here, ‘ntr, i’ represents the number of trials for the ith experiment, ‘u’ indicates the trial order, ‘i’ represents the experiment number, and ‘yu’ indicates the performance characteristic. The study sets ntr, i’ to 3, and i takes a value of 9. For single-response optimization, Eq. (1) is employed to compute the S/N ratio. However, for multi-response optimization, aiming to simultaneously maximize UTS, PE, RA, and IE. Initially, GRA standardizes the observed response data, aligning their values within a scale from zero to one. The following steps were followed to implement the multi-response optimization.

  1. 1.

    Normalization of Experimental Data.

To normalize the experimental data, Eq. (2) is applied for LTB response24.

$$\:{\text{y'}}_{\text{i}}\left(\text{k}\right)\text{=}\frac{{\text{y}}_{\text{i}}\left(\text{k}\right)\text{-min[}{\text{y}}_{\text{i}}\left(\text{k}\right)\text{]}}{\text{max}\left[{\text{y}}_{\text{i}}\left(\text{k}\right)\right]\text{-min[}{\text{y}}_{\text{i}}\left(\text{k}\right)\text{]}}$$
(2)

yi’(k) represents the normalized data obtained through GRA for the kth response of the ith experiment. Simultaneously, yi(k) represents the average of the kth response in the ith experiment, with the minimum and maximum values denoted as min[yi(k)] and max[yi(k)].

  1. 2.

    Calculation of Grey Relational Coefficients (GRCs).

Subsequently, in the calculation of the GRC, the normalized values are employed to assess the connection between the target information and the observed experimental results. This analytical process is crucial for assessing the relationship between the normalized and average data, thereby offering valuable insights into experimental correlations. GRC ξi (k) is presented by Eq. (3).

$$\xi\:\text{i}\left(\text{k}\right)\text{=}\frac{{\Delta}_{\text{min}}+\Psi\Delta_{\text{max}}}{\Delta_{\text{0i}}\left(\text{k}\right)+\Psi\Delta_{\text{max}}}$$
(3)

Δ0i(k) = | y0i(k) − yi (k) | shows discrepancy of desired data. The distinguishing coefficient Ψ is a number in the interval [0, 1]. Δmin and Δmax are the minimum and maximum values of yi(k). It should be noted that it is not possible to directly compare the originally measured responses, since they have different units of evaluation, and must be translated to GRCs to be compared to each other. Nevertheless, these responses represent different aspects.

  1. 3.

    Determination of Grey Relational Grades (GRGs).

For the LTB approach, GRCs were converted into an overall value GRG once it has been weighted. GRG is calculated by Eq. (4).

$$\gamma_{\text{i}}\text{=}\sum\:_{\text{k=1}}^{\text{r}}\omega\left(\text{k}\right)\xi\text{i(k)}$$
(4)

Where γi represents the GRG for all responses in the ith experiment. ω(k) denotes the weighting factor of the kth response with \(\:\sum\:_{\text{k=1}}^{\text{r}}\omega\left(\text{k}\right)\text{=1}\). Optimizing welding processes is crucial for ensuring good quality, and this depends on handling multiple aspects simultaneously. To achieve this, researchers often use a combination of two methods: GRA and PCA. This is quite different from the traditional way of optimizing based on a single factor. The GRA and PCA are powerful statistical tools that have successfully identified optimal parameter combinations across various aspects.

  1. 4.

    Formation of GRC Matrix.

PCA is a statistical tool for multiple-objective optimization. It deals with complex, critically important, and highly interrelated information by simplifying and consolidating it- the system retains the major portions of the information in easily manageable forms through linear arrangements. PCA presents multi-factor optimizations as easy to handle under single response optimization because different sets of information are combined into a few simpler sets. This work initiates variable relationships determination initially, and then, GRCs are calculated that are required to form a matrix by Eq. (5)

$$\:\text{y=}\left[\begin{array}{cccc}{\text{y}}_{\text{1}}\text{(1)}&\:{\text{y}}_{\text{1}}\text{(2)}&\:\ldots&\:{\text{y}}_{\text{1}}\text{(k)}\\\:{\text{y}}_{\text{2}}\text{(1)}&\:{\text{y}}_{\text{2}}\text{(2)}&\:\text{..}&\:{\text{y}}_{\text{2}}\text{(k)}\\\:\vdots&\:\vdots&\:\ldots&\:\vdots\\\:{\text{y}}_{\text{j}}\text{(1)}&\:{\text{y}}_{\text{j}}\text{(2)}&\:\ldots&\:{\text{y}}_{\text{j}}\text{(k)}\end{array}\right]$$
(5)

Here, yp(q) represents the GRC for each response, with p ranging from 1 to j experiments and q from 1 to k quality responses. For this study, j is set to 9, and k is set to 3. Following this, Eq. (6) can be applied to generate the coefficient correlation matrix.

$$\:{\text{R}}_{\text{jl}}\text{=}\left(\frac{\text{Cov(}{\text{y}}_{\text{p}}\left(\text{q}\right)\text{,}{\text{y}}_{\text{p}}\text{(l)}}{\sigma_{\text{yp}}\left(\text{q}\right)\text{*}\sigma_{\text{yp}}\left(\text{l}\right)}\right)$$
(6)
  1. 5.

    Application of PCA to determine the optimal parameters.

The calculation of eigenvalues and eigenvectors is carried out using the Rji array according to Eq. (7).

$$\left( {R - {\lambda _k}{I_j}} \right){V_{pk}} = 0$$
(7)

Principal components (PCs) are determined by using Eq. (8).

$$\:{\text{Z}}_{\text{jk}}\text{=}\sum\:_{\text{i=1}}^{\text{n}}{\text{Y}}_{\text{j}}\left(\text{p}\right)\text{*}{\text{V}}_{\text{pk}}$$
(8)

Where Zjk represents the kth PC. The way eigenvalues and PC are organized is like arranging them from the most important to the least. This order helps to highlight and prioritize the components based on their contributions to understanding the variation in the data. Hence, the first eigenvalue linked with the first principal component represents the most significant contribution to variance.

After obtaining the S/Ni for both single-response and multi-response problems, an average S/Ni of each factor f is denoted by \(\:\stackrel{\text{-}}{{\text{S/N}}_{\text{i,f,l}}\text{}\text{}}\)and expressed by Eq. (9).

$$\:\stackrel{\text{-}}{{\text{S/N}}_{\text{i,f,l}}\text{}}\text{=}\frac{\text{1}}{\text{m}}\sum\:{\text{S/N}}_{\text{i,f,l}}$$
(9)

Here, m represents the total observations for the lth level of factor f, and S/Ni, f,l is the S/Ni value associated with factor f for the 1 st level. The delta (Δ) values are calculated by Eq. (10).

$$Delta{\text{ }}\Delta = max{\text{ }}\left( {S/{N_{i,f,l}}} \right) - min{\text{ }}\left( {S/{N_{i,f,l}}} \right)$$
(10)

The ranking obtained by Δ is structured in a descending order, aligning with the significance of factors’ impact on process performance.

Step 6: Variance analysis (ANOVA): The application of ANOVA on S/Ns is employed to obtain the influence of control factors on responses. Additionally, ANOVA is utilized to estimate the variance associated with the effects and the prediction error.

Step 7: Confirmatory test: Applying the optimal levels is essential to predict and validate improvements in responses. This involves using the identified optimal factor settings to anticipate and confirm enhancements in the desired outcomes.

Results and discussions

Optimization of FSW process parameters for single response

To optimize individual responses, the consideration of S/N values is essential. The primary goal of this investigation is to maximize specific responses, including UTS, PE, RA, and IE. Determining optimal levels involves calculating the average S/N values for outcomes, as illustrated by Fig. 4. Higher S/N values indicate superior quality characteristics. Table 6 outlines the elevated S/N ratios for UTS, PE, RA, and IE, which are 55.03, 28.14, 36.31, and 30.68, respectively.

Table 6 S/N values for different response parameters.
Full size table

In the case of UTS, the experimental run 9, characterized by a welding speed at level-3, tool rotational speed at level-3, and shoulder diameter at level-1, produced the highest S/N. Regarding PE, the peak S/N is achieved in experimental run 7, where welding speed is at level-3, tool rotational speed is at level-2, and shoulder diameter is at level-1. Similarly, for RA, the maximum S/N is observed in experimental run 9, where welding speed is at level-3, tool rotational speed is at level-1, and shoulder diameter is at level-2. Lastly, for IE, the highest S/N is identified in experiment 7, with welding speed at level-3, tool rotational speed at level-3, and shoulder diameter at level-1.

The optimal levels for UTS and IE are depicted in Fig. 4 (a, d). This corresponds to a welding speed set at 210 mm/min (level 3), a tool rotational speed of 750 rpm (level 3), and a shoulder diameter of 15 mm (level 1). Figure 4 (b) shows optimal levels for PE, which corresponds to a welding speed set at 210 mm/min (level 3), a tool rotational speed of 550 rpm (level 2), and a shoulder diameter of 15 mm (level 1). Figure 4 (c) depicts the optimal levels for RA, which corresponds to a welding speed set at 210 mm/min (level 3), a tool rotational speed of 430 rpm (level 1), and a shoulder diameter of 18 mm (level 2).

Fig. 4
figure 4

Plots depicting the main effects of S/N for (a) UTS, (b) PE, (c) RA, (d) IE.

Full size image

Probability plots

Figure 5 provides a visual representation of the relationship between the experimental data and the fitted line. The alignment of data points along the 45-degree reference line in the probability plots indicates that the residuals are approximately normally distributed. This satisfies the normality assumption required for the validity of the ANOVA. This visual evidence supports the subsequent statistical analysis conducted using the Anderson-Darling Test (ADT).

To quantitatively validate the normality assumption, ADT computes specific statistics and derives a p-value. The ADT statistics, in the present study, demonstrate relatively low values. This indicates that the observed data does not deviate significantly from the expected values under a normal distribution. The p-values obtained for UTS, PE, RA, and IE were 0.052, 0.532, 0.331, and 0.244, respectively, all exceeding the 0.05 threshold. Hence, based on the chosen level of significance, there is insufficient evidence to reject the assumption of normality for the data. These findings provide reassurance regarding the validity of assuming a normal distribution for the dataset under consideration.

Fig. 5
figure 5

Normal probability plots of the response parameters.

Full size image

ANOVA and main effect plots

The ANOVA results for output responses, i.e., UTS, PE, RA, and IE, were compiled and presented in Tables 7, 8 and 9, and 10, respectively. The plots of means are presented in Fig. 6.

Based on the information presented in Table 7 concerning UTS, tool rotational speed exhibits the highest statistical significance with a contribution of 46.96%. Following closely is the welding speed with a contribution of 35.06%, signifying its noteworthy influence on the UTS as well. Conversely, shoulder diameter is observed to have a relatively insignificant impact, contributing a mere 8.65% to the UTS. Tool rotational speed and welding speed have a strong influence on UTS, while shoulder diameter does not exhibit a significant effect. These findings shed light on the varying degrees of importance among the input parameters, emphasizing the crucial role of N and V in determining UTS. Figure 6 (a) exhibits the main effect plots depicting the characteristics of UTS. The plot indicates that an increase in welding speed corresponds to an increase in UTS. Higher welding speeds form finer microstructures, improving strength27,28.

On the contrary, the main effect plot shows a negative correlation between UTS and tool rotational speed. An increase in the value of N corresponds to a decrease in UTS. This phenomenon can be explained by the adverse effects of high rotational speeds on the weld joint. Increased tool rotational speed generates frictional heat, which will lead to excessive plastic deformation and the formation of defects, thereby compromising joint strength28.

Fig. 6
figure 6

Plot (Main effects) of means for (a) UTS, (b) PE, (c) RA, (d) IE.

Full size image
Table 7 ANOVA table for UTS of welds.
Full size table

Additionally, the plot indicates that UTS decreases by increasing the shoulder diameter. The correlation between UTS and shoulder diameter is linked to the heat produced during welding. A greater shoulder diameter leads to a larger contact area, causing higher heat generation. Excessive heat can lead to thermal degradation and adversely affect the mechanical properties of joints, resulting in a reduction in UTS28. Upon examining the PE, it becomes apparent that welding speed holds the utmost influence, exhibiting a significant contribution of 87.19%. This implies that the welding speed has a substantial impact on PE. In contrast, both the tool rpm and shoulder diameter have negligible contributions to the PE, with meager percentages of 1.06% and 1.55%, respectively. These findings suggest that variations in the tool rotational speed and shoulder diameter have minimal impact on PE. To provide a visual representation and facilitate a comprehensive understanding, the ANOVA table corresponding to these findings is presented in Table 8. The results confirm that welding speed significantly influences elongation, whereas tool rotational speed and shoulder diameter have minimal impact. The 87.19% contribution highlights the welding speed’s dominant role.

Table 8 ANOVA table for PE.
Full size table

Figure 6 (b) illustrates the main effect plots concerning PE. The plots indicate important trends regarding the relationship between PE and various factors in the welding process. Primarily, the findings reveal that PE rises alongside an increase in welding speed. This can be attributed to the notion that elevated welding speeds often yield a finer microstructure, thereby enhancing the joint’s ductility and capacity for deformation19,20. Moreover, the plot illustrates a more complex association between the PE and tool rpm. As the tool’s rotational speed increases, there is a corresponding increase in PE. This can be explained by the heightened heat input at higher rpm, which enhances the material’s ductility. However, beyond a certain point, a further increase in tool rpm led to a decrease in PE. This decrease can be attributed to excessive heat input, which can induce grain growth and reduce ductility19.

While examining the ANOVA results for RA, an insight is presented in Table 9. Notably, the factor that exerts the most substantial influence is welding speed, contributing significantly with a percentage contribution of 87.26%. This finding underscores the significant impact of variations in welding speed on the RA. Conversely, both the tool rpm and shoulder diameter are observed to have relatively insignificant contributions. Tool rotational speed contributes a mere 1.99%, while shoulder diameter contributes 6.81%. The findings indicate that variations in the tool rpm and shoulder diameter have minimal impact on RA.

Table 9 ANOVA table for RA.
Full size table

The main effect plots of RA are presented in Fig. 6 (c). This plot reveals that increasing the welding speed correlates with a higher RA. This correlation can be explained by the greater energy input and plastic deformation experienced by the material during higher welding speeds. Consequently, the material exhibits greater deformation and reduction in cross-sectional area19,20. The plot further illustrates that PE initially rises as the tool’s rotational speed increases, but eventually reaches a peak and subsequently decreases. At lower rotational speeds, the increased tool rotational speed contributes to enhanced plastic deformation and subsequent reduction in area. However, beyond a certain point, further increases in rotational speed led to excessive heat input and material softening, resulting in reduced plastic deformation and a decrease in the percentage reduction in area19. Lastly, RA exhibits an upward trend with an increase in shoulder diameter up to a certain threshold, beyond which it begins to decline. Initially, the larger shoulder diameter provides increased contact area and improved heat generation, resulting in enhanced plastic deformation and a higher RA. However, beyond a certain shoulder diameter, factors such as increased heat dissipation and potential defects begin to limit the plastic deformation, leading to a decrease in the percentage reduction in area28.

Table 10 illustrates the ANOVA results for impact energy, providing valuable insights into the influential factors. Welding speed is the most influential factor, contributing 63.29% to the impact strength (p < 0.05). This finding underscores the crucial role of welding speed in determining the Impact strength. Following welding speed, shoulder diameter exhibits a noteworthy contribution of 17.37%, indicating its considerable impact on the measured variable. Conversely, tool rotational speed is observed to have an insignificant effect on Impact strength, contributing a mere 1.43%.

Table 10 ANOVA table for IE of welds.
Full size table

The error percentage exceeding 10% in Tables 8 and 10 may be due to experimental variations and external uncertainties beyond control. FSW is a sophisticated process wherein microstructure evolution and mechanical properties are extremely sensitive to minimal changes in heat input, tool wear, and material heterogeneities. Also, metallurgical changes, plastic deformation characteristics, and grain refinement mechanisms yield inherent variability, leading to variation in the results of the experiments. Though every effort was taken to reduce these uncertainties, phenomena like thermal dissipation, distribution of localized strain, and slight deviation in the tool penetration depth may introduce an error above the tolerable level. However, despite this variability, the statistical significance of key parameters remains evident, as reflected in the percentage contributions calculated through ANOVA.

Figure 6 (d) shows the plots for IE, indicating that increasing welding speed corresponds to a higher impact energy. As the welding speed increases, the material undergoes more intense deformation, resulting in higher impact energy29. Likewise, as the tool’s rotational speed increases, there is a corresponding rise in the impact energy. This increased rotational speed generates more heat and plastic deformation, thereby improving impact energy. The higher rotational speed facilitates enhanced material flow and deformation, leading to improved impact energy29. Additionally, impact energy decreases with an increase in shoulder diameter up to a certain level, after which it starts to increase. Initially, the smaller shoulder diameter allows for better heat generation and material flow, resulting in higher impact energy, but beyond a certain threshold, an increase in shoulder diameter leads to reduced heat input and limited plastic deformation, resulting in reduced impact energy. A further increase in shoulder diameter expands the contact area that facilitates better material flow and heightened plastic deformation, resulting in a subsequent increment in the impact energy30,31.

Multi-Response optimization

GRA-PCA is used in this study as it provides a structured and efficient method for multi-response optimization. While GRA simplifies complex decision-making by converting multiple performance measures into a single relational grade, PCA reduces dimensionality by transforming correlated mechanical properties into a set of uncorrelated principal components. This allows objective determination of response weights, enhancing the robustness of the optimization. Their combination leverages the strengths of both—GRA’s ranking and PCA’s dimensional reduction—to deliver a robust multi-response optimization. Unlike TOPSIS, which depends on predetermined weights and requires additional decision-making steps, or hybrid GRA-TOPSIS, which involves higher computational effort without yielding significant advantages for correlated responses, GRA-PCA offers a more practical and reliable alternative. It was selected in this study for its objectivity in weight assignment, reduced subjectivity in decision-making, and computational efficiency—features particularly beneficial when analyzing highly correlated responses such as UTS, PE, RA, and IE2425,.

Table 11 Table showing normalized values of GRC and GRG for the response parameters.
Full size table

The objective is to compare the effectiveness of multi-objective optimization using GRA alone versus GRA combined with PCA. To quantify the relationship between variables, GRC for individual responses is obtained using Eq. (3). Additionally, the unweighted grey relational grade (GRG), determined using Eq. (4), is employed as an indicator of the performance. The results of the same are presented in Table 11. In PCA, Eq. (7) is utilized to calculate the eigenvalues along with their corresponding variance contributions and eigenvectors. The results are presented in Table 12.

As shown in Table 12, the first principal component (PC) makes a substantial contribution, explaining as much as 70.3% of the variance in the four quality characteristics. Figure 7 shows a scree plot illustrating variance distribution across components. PCA assigns weights like ‘importance scores’, where responses with greater variance influence are given higher weight in the optimization.

Table 12 Calculations of Eigen values and Eigen vectors for PCs.
Full size table
Fig. 7
figure 7

Scree Plot based on PCA Eigenvalues.

Full size image

The squares of the eigenvectors linked to the primary PC, chosen as weights, are presented in Table 13. These weights are specifically determined to be 0.145, 0.2777, 0.2560, and 0.3214 for UTS, PE, RA, and IE, respectively.

Table 13 Contribution of variance in response variables for the initial PC.
Full size table

Using the weights established via PCA and GRCs, W-GRGs are calculated for each experiment using Eq. (4). Subsequently, these W-GRGs are arranged in a ranking and presented in Table 14. Significantly, Experiment No. 7 is recognized as the sample with the highest values for both GRG and W-GRG. Table 15 presents the average GRG and W-GRG values, which consistently indicate that the predicted optimal combination of input parameters for achieving superior mechanical properties is V3N3D1. This combination, corresponding to a welding speed of 210 mm/min (level 3), tool rotational speed of 750 rpm (level 3), and shoulder diameter of 15 mm (level 1), was identified through optimization analysis and subsequently validated through confirmatory testing.

Table 14 Table showing normalized values of GRC, GRG, and W-GRG for the response parameters.
Full size table

Contribution of input parameters that affect the weld integrity

GRA is employed to find out the relative contribution of FSW input parameters (V, N, D) on the mechanical properties of AISI 1018 steel weldments. The objective of GRA is to determine the contribution of every parameter towards output responses, i.e., UTS, PE, RA, and IE.

The input parameter contribution is obtained from GRCs, which are calculated for every response after normalizing the experimental data. The GRG is then obtained by averaging the GRCs, giving a single numerical value that reflects the overall performance of every experiment. The greater the GRG, the more effective the combination of process parameters concerning weld quality.

To enhance the accuracy of the analysis, Principal Component Analysis (PCA) is coupled with GRA to provide proper weighting to every response parameter. This ensures that responses with greater influence on the mechanical properties (like UTS and PE) are assigned more weight in the final optimization process. The findings of the GRA-PCA technique indicate that the greatest contribution to the mechanical properties is welding speed, followed by tool rpm, and the least contribution is observed for shoulder diameter. Such a trend is consistent with the basic knowledge of FSW, in which welding speed is known to dominate heat input and material flow, and hence the final microstructure and mechanical performance of the welded joint.

Table 15 Summary of average GRG and W-GRG for responses.
Full size table

Confirmatory tests

The experimental results demonstrate notable improvements in mechanical properties after single response optimization. UTS increased from 549.76 MPa to 570.27 MPa, reflecting a 3.73% enhancement. This improvement can be credited to the careful adjustment of input parameters, which helps to create stronger weld bonds and improve overall joint strength.

In terms of ductility, PE showed a modest increase of 1.97%, rising from 23.82 to 24.29%. More significantly, RA, which indicates the material’s ability to undergo deformation before fracture, increased substantially by 36.46%, going from 47.93 to 65.41%. This rise in RA suggests that the optimized conditions encourage better material flow and reduce defects during the friction stir welding process, resulting in a more flexible and durable joint.

IE also improved from 33.91 J to 34.71 J, a 2.35% increase. This gain is likely due to finer-grain structures formed under optimized welding conditions, which reduce brittleness and enhance toughness.

When considering multiple response optimization to find the best combination of input parameters, the experimental data confirmed enhancements across all measures: UTS improved by 3.73%, PE by 7.30%, RA by 23.13%, and IE by 2.35%. The predicted values closely matched the experimental findings, validating the optimization approach and confirming that the selected parameters effectively improve the quality and mechanical performance of the welded joints. These improved values are in close alignment with those reported in earlier works on similar steels28,29,30.

Trade-off analysis in multi-response optimization

The multi-response optimization findings indicate a clear enhancement in mechanical properties, but understanding trade-offs between output responses is important in understanding the optimization process. A noteworthy finding indicates that an increase in UTS improves joint strength but results in a lesser elongation from the inverse relationship between strength and ductility. Higher UTS values typically exhibit a finer grain structure, which, while increasing load-bearing capabilities, reduces deformability and elongation.

The same trade-off exists when optimizing for RA and IE. Higher impact energy values imply better toughness, but if there is too much softening from excessive heat input, there will be a decline in strength. The input parameters selected for the experiments (welding speed and tool rotational speed) attempted to balance UTS, PE, and IE.

Microstructural analysis

The microstructural characterization was done on a cross-sectional geometry extracted from the welded joint prepared using the optimal machine setting. The removed cross-section underwent polishing with silicon carbide emery paper. Following the polishing, the samples were etched in 3% nital solution. Various magnifications of the SEM were used to view the microstructures. Microstructural evaluation revealed the following features:

In Fig. 8(a), there is a distinct boundary visible, delineating the transition between the stirred zone and the unaffected base metal. To better understand the welding process, the image is magnified, revealing multiple zones formed during welding. These regions, notably the heat-affected zone (HAZ), stir zone (SZ), and thermomechanical affected zone (TMAZ), are identifiable, as illustrated in Fig. 8(b). Moreover, in Fig. 8(c), there is a detailed focus on the last two zones, showcasing the enhancement of grain structure and the dynamic recrystallization process unfolding within the TMAZ region. Such a detailed analysis reveals nuanced microstructural alterations occurring throughout the welding procedure. The pin’s deformation and the heat generated by the shoulder’s friction collectively impact both the nugget zone and TMAZ. The pin rotation within the stir zone causes a distinct change in the orientation of crystallographic planes. Furthermore, the influence of the shoulder surface is more evident on the upper part of the weld in contrast to the lower part, ascribed to the increased centrifugal force in material flow. Lakshminarayanan et al.34 and Tiwari et al.35 presented similar findings. Unlike the original metal, grain dimensions in the stirred zone refine due to higher temperature and deformation (Fig. 9). The boundary between the nugget zone and TMAZ is distinctly illustrated in Fig. 9(c). SEM analysis revealed that the average grain size in the SZ was approximately 4–6 μm, significantly finer than the 10–12 μm grains in the TMAZ, confirming the effect of dynamic recrystallization.

The microstructural evolution observed is significantly impacted by the refinement mechanisms of dynamic recrystallization (DRX) and controlled thermal input during FSW. DRX primarily takes place in the stirred region because of heavy plastic deformation and localized thermal cycling, resulting in the development of fine, equiaxed grains that improve the strength and toughness of the joint. The nugget zone, in which maximum plastic deformation is realized, shows the finest microstructure because of continuous dynamic recrystallization. The high dislocation density and grain boundary migration also aid grain refinement and lower the occurrence of weld defects, along with an increase in mechanical integrity.

The heat input determines the microstructural properties of the weld. Too much heat input, normally generated due to the high rotational speed of the tools, can result in grain coarsening that adversely impacts strength and toughness. Simultaneously, too little heat generation at low rotational speeds can create incomplete material flow, resulting in defects like voids or insufficient fusion. This investigation identifies an optimal combination of tool rotational speed and welding speed that controls heat input, allowing sufficient material softening for proper mixing while avoiding excessive grain growth. The fine microstructure with evenly distributed grains resulting from this technique led to better mechanical properties.

To further validate these results, the microstructural findings were compared with prior literature for FSW of carbon steel. Studies conducted by Sundar Raju et al.36 and Wang et al.37 have concluded that smaller grain sizes and dynamic recrystallization occur in the stirred zone because of shear-controlled heat input and mechanical mixing. Additionally, a study by Wang et al.38 highlights that grain refinement in the TMAZ significantly impacts the mechanical properties of welded joints, which agrees with the findings in the present study.

Fig. 8
figure 8

Microstructural transition from base metal to stirred zone, highlighting grain refinement.

Full size image
Fig. 9
figure 9

The microstructure of the welded joint from the base metal to the Stirred zone-TMAZ transition.

Full size image

Microhardness testing

The microhardness test was conducted to examine local variations in mechanical strength across different weld regions. It provides an effective means to evaluate how thermal cycles and material flow during FSW influence the properties of the stir zone, TMAZ, and HAZ. This measurement supports the microstructural observations and tensile test results by confirming improvements in hardness distribution under optimized processing conditions.

The test was conducted using a FISCHERSCOPE HM2000S microhardness tester. A load of 100 g was applied with an increment of 1 mm on the weld surface. Figures 10 and 11 show the transverse and top-section microhardness profiles, respectively. Higher microhardness is observed in the nugget zone, while the TMAZ and HAZ show values almost similar to the base metal. Wang et al.39 and Tamjidi et al.40 reported similar results.

The hardness variation between the weld zones is due to the metallurgical changes involved in the FSW process. The nugget zone (NZ) is subject to dynamic recrystallization (DRX) and severe plastic deformation, and develops a fine-grained microstructure, resulting in increased hardness. The TMAZ, however, partially deforms and is subjected to heat, giving rise to elongated grains but no full-scale recrystallization, thus resulting in moderate hardness. HAZ, having been exposed solely to thermal conditions, experiences grain coarsening, which results in decreased hardness relative to the NZ.

In addition, the tool rotation-induced asymmetric material flow impacts the hardness distribution. The material transported by the shoulder is transferred from the retreating side of the weld, around the tool, and deposited on the advancing side, resulting in greater microhardness on the advancing side than on the retreating side. This is because there is more strain hardening and finer grain structures on the advancing side.

Fig. 10
figure 10

Weld microhardness profile (transverse section).

Full size image
Fig. 11
figure 11

Weld microhardness profile (top portion).

Full size image

Practical implications of the study for industrial applications

The results of the present study are of great practical importance for the industries that use AISI 1018 carbon steel extensively, including the automobile, construction, and manufacturing industries. The optimal FSW parameters revealed in this study can improve the structural integrity, mechanical strength, and durability of welded joints and address common challenges in industrial applications.

In the automobile industry, the application of the FSW process with appropriate parameters could also improve the performance of the parts, such as chassis components, drive shafts, and structural reinforcements. The improvement of UTS and IE endows it with stronger load-carrying ability and crash resistance, which shows the potential to replace traditional welding methods. Reduction of defects such as porosity and residual stress further enhances the fatigue life of welded joints, and hence, longer vehicle structures.

In the construction sector, where AISI 1018 steel is applied extensively in structural frames, bridges, and tall buildings, the use of optimized FSW parameters yields stronger and more dependable joints. Increased percentage elongation and reduction in area lead to higher ductility to resist failure under dynamic loadings. Its ability to join high-strength defect-free welds without additional filler material while providing reduced environmental impact makes FSW an attractive option for sustainable and cost-effective infrastructure construction.

In manufacturing and heavy industry, the adoption of optimized FSW methods has the potential to enhance the production processes. Parts undergoing cyclic loading, like hydraulic systems, pipes, and pressure vessels, can reap the rewards of the superior mechanical properties provided through the optimized weld process. Elimination of residual stresses and refinement of microstructures guarantees a longer life.

Conclusions

Based on experimental and optimization results of FSW process parameters, the following significant conclusions can be inferred:

  • FSW of AISI 1018 carbon steel with a tungsten carbide insert containing a 7% cobalt binder yielded welds with superior mechanical and metallurgical properties than the base metal.

  • Single and multi-response optimization techniques identified welding speed as the most significant factor, followed by tool rotational speed and shoulder diameter, which influence UTS, PE, RA, and IE.

  • The optimal parameters for achieving maximum mechanical properties were determined to be V3N3D1 (210 mm/min welding speed, 750 rpm of the tool, and 15 mm shoulder diameter), resulting in appreciable weld performance improvement.

  • Single-response optimization improved the mechanical properties by 3.73% for UTS, 1.95% for PE, 36.46% for RA, and 2.35% for IE, while multi-response optimization achieved improvements of 3.73%, 7.30%, 23.13%, and 2.35%, respectively. Although single-response optimization yielded the highest individual improvement in RA, the multi-response approach provided more balanced and consistent enhancements across all mechanical properties, making it more effective for overall weld quality optimization.

  • Mechanical property trade-offs were noted, with UTS and impact energy enhancements being uniform in both optimizations, whereas PE had a higher increase in multi-response optimization, and RA improvement was less than in single-response optimization.

  • Microstructural examination identified clear weld zones, such as the stirred zone, TMAZ, and HAZ, with fine-grain refinement in the stirred zone, resulting in enhanced mechanical properties.

  • The combination of GRA-PCA with the Taguchi method gave a structured and effective method for optimizing process parameters, reducing experimental iterations, but with balanced improvements in both strength and ductility.

  • The optimized process parameters are highly industrially relevant, enhancing weld quality in automotive, construction, and manufacturing sectors where improved mechanical performance is of primary importance.