Introduction

Wheat is one of the primary food crops in China, covering an area of 244 million hectares1,2. The wheat seeder plays a crucial role in seed utilization and yield3, with the seed metering device being a key component of the wheat seeder. Most existing seed metering devices are of the outer grooved wheel type, characterized by a simple structure, compact size, and smooth transposition4,5. The outer grooved wheel can be categorized into two structures: straight groove type and oblique groove type. The operation of the straight groove type results in a pulsating seed flow; specifically, when the groove wheel turns to the tooth groove, the seed quantity increases, whereas it decreases when the wheel turns to the tooth ridge6. Wang et al.7 improved the design of the outer grooved wheel by substituting the straight grooved wheel with a spiral grooved wheel. This modification, due to the inclined tooth groove structure, facilitates a continuous seeding state, significantly reducing the occurrence of seeding fluctuations and promoting uniform and stable seeding. Extensive research has been conducted both domestically and internationally, focusing on optimizing the structure and examining the influence of various parameters on seeding performance. Yu et al.8 enhanced the structure of the straight grooved wheel by incorporating an elastic seed scraping tongue, resulting in a nearly closed groove state that eliminates the driving layer and ensures mandatory seed drainage. Zhang et al.9 employed simulation methods to optimize the dimensions of the straight groove structure. Singh et al.10 designed and optimized a cotton seed seeder based on the mechanism’s characteristics. Liu et al.11 conducted a comprehensive comparative analysis of the impact of the working length of the spiral wheel seeding device on seeding uniformity, revealing that a longer working length improves seeding performance under consistent seeding amounts and forward machine speeds.

The advanced statistical methods such as response surface methodology (RSM), analysis of variance (ANOVA), Taguchi methods, and genetic algorithms (GA) are carried out on the optimization of machining processes and machinability. These methodologies are pivotal in optimizing manufacturing processes and predictive modeling. GA is methods inspired by biological evolutionary processes that provide solutions to complex optimization and search problems, which are widely used in technology-focused countries such as the United States, Japan, Germany, and the United Kingdom, particularly in fields like engineering, artificial intelligence, and bioinformatics12. RSM is a statistical technique used in experimental design and optimization processes. It was first developed in the 1950s by George E. P. Box and K. B. Wilson. This method aims to model and analyze results obtained from experimental data to understand and optimize the relationships between dependent and independent variables13. ANOVA is a method developed to compare whether there are statistically significant differences among group means. ANOVA evaluates the effects of one or more levels of independent variables on a dependent variable. Important results such as the F-statistic and p-value are obtained from the analysis14. Taguchi method is an approach that aims to improve product or process quality by optimizing control variables. Taguchi developed a special design with an orthogonal arrangement that can be used to study the entire parameter space with only a small umber of experiments, and often involves an iterative process to achieve better results15. For instance, Chen et al.16 employed the Taguchi method, RSM, and a hybrid GA-PSO approach to systematically optimize plastic injection process parameters, the results showed that the proposed model not only enhances the stability in the injection molding process, but also reduces the costs of and time spent in the process. Romelin et al.17 offered a comparative analysis using RSM and Taguchi method in optimizing the performance of a hydraulic ram pump, and reveals distinct experimental designs and optimization outcomes. Guo et al.18 presented a systematic multi-objective optimization method for product quality characteristics in fiber-reinforced composite manufacturing, demonstrating the application of advanced optimization techniques in complex manufacturing processes.

Currently, the majority of seeders in our country utilize the outer grooved wheel type seed metering device. Therefore, studying seed performance and enhancing the structure of this mechanism holds significant practical value. Traditional test methods are difficult to capture fast-moving particles, and have the disadvantages of low accuracy and long time. In recent years, the discrete element method (DEM) has been widely used to study motions of particles. The DEM is a numerical method that takes into account the interactions of discrete particles in contact and allows the evaluation of mutual force interactions. Especially, DEM is used for the design, optimisation, and performance testing of agricultural machines, such as seed drills19,20,21. This paper employs EDEM software to conduct a seed discharge simulation test on the outer grooved wheel seed metering device, aiming to optimize the structure and working parameters that primarily influence seed discharge performance. Additionally, field experiments are performed to validate the optimization results.

Mechanism parameters and working principle of spiral outer grooved wheel seed metering device

Structure composition

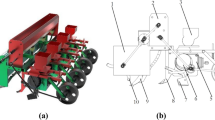
The spiral outer grooved wheel seed metering device primarily consists of the outer grooved wheel, seed inlet, seed outlet, blocking sleeve, inner tooth-shaped retaining ring, and driving shaft, as illustrated in Fig. 1.

Fig. 1
figure 1

Structure diagram of the spiral outer grooved wheel seed metering device. (1) Cleaning brush. (2) Grooved wheel fixed end cover. (3) Drive shaft. (4) Outer grooved wheel. (5) Seed inlet. (6) Seed shell. (7) Seed outlet. (8) Blocking sleeve. (9) Inner tooth type stop ring.

Full size image

The design of the spiral outer grooved wheel presented in this paper is depicted in Fig. 2. By varying the number of grooves (n), the groove depth (b), and the groove radius (r), the volume of a single groove can be altered. Additionally, the uniformity of the seed metering device is influenced by adjustments to the lead angle of the chute and the rotation speed of the grooved wheel. The designed groove radius (r) is set at 30 mm, while other parameters are primarily determined by the number of grooves (n). Four size parameters are detailed in Table 1. Due to the interaction force between the tooth groove surface and the inner tooth-shaped retaining ring, an excessively large lead angle of the outer grooved wheel can lead to increased force and potential damage to the component. In this study, the lead angle of the groove wheel is varied from 0 to 15°, specifically at 0°, 5°, 10°, and 15°. The suitable rotation speed range of the grooved wheel during wheat sowing is found to be n = 9–60 r/min22, with specific speeds of 30 r/min, 40 r/min, and 50 r/min discussed in this paper. The working length (L) is taken to be 30 mm.

Fig. 2
figure 2

The structure of spiral outer grooved wheel.

Full size image
Table 1 Structure parameters of spiral outer grooved wheel.
Full size table

Curve equation of the outer groove wheel

The tooth groove structure of the outer grooved wheel exhibits a specific inclination, primarily influenced by parameters such as the length and lead angle of the grooved wheel. The outer grooved wheel was vertically expanded to create a two-dimensional plane (Fig. 3), and the equation of the tilt curve was derived using formula (1).

Fig. 3
figure 3

Despite structure of outer grooved wheel.

Full size image
$$\left\{ \begin{gathered} x=R \times \cos \left[ {360t \cdot L/\left( {2\pi R} \right)} \right] \hfill \\ y=R \times \sin \left[ {360t \cdot L/\left( {2\pi R} \right)} \right] \hfill \\ z=Ht \hfill \\ \end{gathered} \right.$$
(1)

Where R is the radius of the outer groove wheel, mm; β is the spiral lead Angle, °; L is the length corresponding to the ascending Angle β, mm; H is the length of the outer groove wheel, mm.

Working principle and parameter analysis

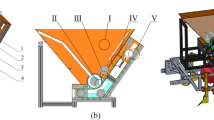
When the outer groove wheel rotates, wheat seeds in the seed box flow into the seed metering device by gravity, filling the groove before rotating and discharging through the seed brush and seed outlet under the force exerted by the outer groove wheel of the seed discharge device. Additionally, a layer of seeds at the outer edge of the groove wheel is ejected at a lower speed due to the intermittent impact of the convex tips of the groove teeth, referred to as the driving layer seeds. The movement of these seeds gradually transitions from the circumference of the groove wheel to the stationary layer23. The seeds released by the groove wheel, along with the driving layer, fall into the seed pipe from the seed outlet and subsequently descend into the seed ditch through the trencher.

Wheat seeds undergo three distinct stages within the outer grooved wheel seed metering device24: seed filling, seed clearing, and seed protection. A force analysis was conducted, with the simplified model illustrated in Fig. 4. During the seed filling stage, as seeds descend from the seed box into the tooth groove of the outer grooved wheel, they experience the force of their own gravity as well as the forces exerted by other seeds. At this point, the seeds are in a state of equilibrium, and the resultant force Q in the vertical direction is calculated using formula (2).

Fig. 4
figure 4

Schematic diagram of wheat seed stress during the working process of the outer grooved wheel. (a) Seed filling. (b) Seed clearing. (c) Seed protection.

Full size image
$$Q\,=\,F{\text{cos}}a\,+\,G$$
(2)

Where F is the force of the seed on other seeds, N; G is the seed gravity, N; α is the Angle between gravity and the force.

In the seed clearing state, when the groove was filled with wheat seeds, the available space became saturated, necessitating the removal of excess seeds using a seed cleaning brush. Through the combined action of the groove (Fm) and the seed cleaning brush (Fn), the surplus seeds were effectively swept away from the outer groove wheel.

During the seed protection stage, the seeds primarily move in a circular motion with the outer groove wheel. Due to spatial constraints, the seeds remain stationary in relation to the groove, exhibiting the same motion mode and speed as the groove itself. The seeds are predominantly influenced by gravity and the action of the groove (N), with the resultant force (Fn) calculated using formula (3).

$$\left\{ \begin{gathered} {F_m}=G+N \hfill \\ {F_h}=mr{\omega ^2} \hfill \\ {F_m} \geqslant {F_h} \hfill \\ \end{gathered} \right.$$
(3)

Where N is the force of the groove of the outer groove wheel on the seed, N; r is the distance from the center of the seed to the center of the outer groove wheel, m; ω is the angular speed of the outer groove wheel rotation, rad/s; m is the seed mass, kg.

Discrete element method simulation experiments and verification

Multi-factor experiments design

Based on the outer grooved wheel structure and its operational principles, the factors influencing its structural parameters and operational effectiveness primarily include the lead angle (0° to 15°), the number of grooves (10 to 16), and the groove rotation speed (30 to 50 r/min). To ensure the selected data is more reasonable, the change amplitude for the lead angle was set at 5°, while the change amplitude for the number of grooves was set at 2. Consequently, in accordance with the Box-Behnken test design principles, the groove rotation speed (x1), lead angle (x2), and number of grooves (x3) were designated as independent variables and simulated using EDEM software to derive the coefficient of variation (Y) as the response variable. Two sets of three-factor and three-level tests were conducted, with the factor level codes presented in Tables 2 and 3, respectively. In total, two sets of response analysis tests were performed, as illustrated in Tables 5 and 7. The values of X1, X2, and X3 in the tables represent the factor-coded values.

Table 2 Coding of factors and levels for the first group.
Full size table
Table 3 Coding of factors and levels for the second group.
Full size table

Experimental material

Geometric model of wheat and seed metering device

The operation of the seed metering device was simulated and analyzed using EDEM software under various parameters of the outer groove wheel. The wheat grains were treated as discrete units, with their shape and size identified as factors influencing the pulsatility of the outer grooved wheel. This paper presents a statistical analysis of the dimensions of five wheat varieties commonly used in China: Yinchun 9, Jiuchun 6, Linmai 35, Longchun 30, and Lantian 30. The observed lengths ranged from 6.02 to 7.10 mm, widths from 2.53 to 3.89 mm, and thicknesses from 2.67 to 3.43 mm. Given the relatively close dimensions of width and thickness, the structure of the grains was determined to be approximately ellipsoid, with an average major axis of 6.50 mm, a short axis of 3.20 mm. Additionally, wheat particles were simplified as uniform linear elastic materials with homogeneous properties25and the ellipsoid model of the wheat particles was constructed from spherical particles (Fig. 5a). To facilitate simulation and reduce computational load, the non-contact components of the seed feeder structure were omitted. The 3D model was created using Pro/E software and subsequently imported into EDEM software in .IGS format (Fig. 5b).

Fig. 5
figure 5

Model of wheat and seed metering device were drawn using EDEM 2022.2.0 (1) Seed metering device. (2) Wheat particles. (3) Square counter. (a) Wheat model. (b) Initial assembly model.

Full size image

Verification experiment materials

To accurately compare with the simulated test, the bench seeding experiment platform was selected for verification. The test bench primarily consisted of a conveyor belt, seed metering device, seed box, motor, and frequency converter, as illustrated in Fig. 6. Notably, the outer grooved wheel was fabricated using 3D printing technology, and its rotational speed was regulated by the E1000-0007T3 inverter. The wheat seed utilized was Jiuchun No.6, which had a 1000-grain weight of 46.8 g and a moisture content of 15.8%.

Fig. 6
figure 6

The bench seeding experiment platform.

Full size image

Experimental method

Parameter settings

Due to the negligible normal and tangential damping forces generated between the surfaces of wheat grains under the driving force of the outer groove wheel and the influence of gravity, these forces can be ignored. Consequently, the Hertz-Mindlin non-sliding contact model was employed to analyze the motion dynamics of wheat within the seed metering device26. The shell of the seed feeder and the seed cleaning brush were constructed from plastic. A hopper is placed directly above the seed feeder to fill the wheat seed, seed mass flows continuously from this hopper to the metering device. The hopper is a rectangular structure with dimensions of 180 mm in length, 120 mm in width, and 100 mm in height. The physical and contact parameters25,27 of each material utilized in the simulation model are presented in Table 4.

Table 4 Input parameters used for simulation in DEM modelling.
Full size table

Data extraction in EDEM

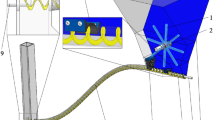
Wheat particles flow out through the seed outlet, propelled by the driving force of the outer grooved wheel. To ensure the integrity of the extracted data and prevent the repeated counting of wheat particles, a square counter of appropriate dimensions was installed at the seed outlet (Fig. 5b). The height of the square counter from the center of the grooved wheel is 34 mm.

Verification experiment methods

In this study, the operational performance test of the seed planter was conducted in accordance with the standards28,29 of GB/T 9478 − 2005 “Test Method for Grain Drill” and JBT 9783 − 1999 “Seed Planter with Outer Groove Wheel”. The test focused on the coefficient of variation. To prevent seed bullets from falling during the test, a paper catheter was attached to the seed outlet. Once the working conditions stabilized, a length of 120 cm was captured on the conveyor belt and photographed. The images were then divided into 20 segments for counting and statistical analysis, and the test was repeated nine times. Formulas (4) to (6) were employed to determine the coefficient of variation30.

$$\overline {x} =\frac{1}{n}\sum\limits_{{i=1}}^{n} {{x_i}}$$
(4)
$$\sigma =\sqrt {\frac{1}{n}\sum\limits_{{i=1}}^{n} ( {x_i} - \overline {x} {)^2}}$$
(5)
$$CI=\frac{\sigma }{{\overline {x} }} \times 100\%$$
(6)

Where \({\text{x}}(\_\_)\) is the mean of seeding quantity; n is the number of samples; xi is the amount of seeding quantity within each sample; σ is the standard deviation of seeding quantity; CI is the coefficient of variation.

The flow rate is a crucial indicator for assessing the operational efficiency of the seed metering device. Once the device operates steadily, the seeds that fall within a 5-second interval are collected and evaluated for their quality. The flow rate is then calculated using formula (7).

$$f=\frac{{{m_s}}}{t}$$
(7)

Where f is the flow rates, g/s; ms is the seed mass discharged by the seed metering device within time t, g; t is the seeding time, s.

Data processing and analysis

In this study, three-dimensional modeling of components was performed using Pro/E Version 5.0 software. Additionally, EDEM 2022 Version 8.3.0 was employed to create discrete element method (DEM) simulation models. The obtained data were converted into relevant curves and equations using the Design Expert Version 12.0.3.0 software.

Results and analysis

Analysis of seeding process

Figure 7 illustrates the normal seeding simulation process of the outer grooved wheel metering device. At a simulation time of 1 s (Fig. 7a), the groove wheel begins to rotate, allowing seeds to enter the groove and complete the seed filling process. By 1.5 s (Fig. 7b), the seed clearing process is finalized, with seeds fully occupying the groove and entering the seed protection phase, characterized by uniform and constant quantity and speed. As time progresses, at 1.75 s (Fig. 7c), the combined effects of gravity, centrifugal force, and other seed pressures facilitate the movement of seeds within the groove into the metering zone, preparing for entry into the square counter. At 1.76 s (Fig. 7d), the first wheat seed enters the square counter and begins to be counted. By 1.81 s (Fig. 7e), the first seed reaches the seed discharge port and, under the influence of gravity, falls into the seed discharge tube. At this point, the first seed completes the entire process of seed filling, clearing, protection, and discharge. To ensure the continuity of the seeding process, this study commenced counting at 1.9 s, with a counting duration of 5 s and a time interval of 0.05 s.

Fig. 7
figure 7

Simulation process of seed metering was drawn using EDEM 2022.2.0 (a) 1 s. (b) 1.5 s. (c) 1.75 s. (d) 1.76 s. (e) 1.81 s.

Full size image

Analysis of the results of the first group tests

Experimental design and results

The design and results of the first group experiments are presented in Table 5. Utilizing Design-Expert software to analyze the obtained test results, a quadratic regression model of the coefficient of variation Y, represented by the coded values of each factor, was derived, as illustrated in formula (8).

$$\begin{aligned} Y\,=\, & {\text{11}}.{\text{41}} - {\text{1}}.{\text{34}}{X_{\text{1}}} - 0.{\text{79}}{X_{\text{2}}}\,+\,0.{\text{43}}{X_{\text{3}}}\,+\,0.{\text{52}}{X_{\text{1}}}{X_{\text{2}}}\,+\,0.{\text{74}}{X_{\text{1}}}{X_{\text{3}}} \\ & - 0.{\text{21}}{X_{\text{2}}}{X_{\text{3}}}\,+\,0.0{\text{1}}{X_{\text{1}}}^{{\text{2}}} - 0.{\text{17}}{X_{\text{2}}}^{{\text{2}}} - {\text{1}}.{\text{51}}{X_{\text{3}}}^{{\text{2}}} \\ \end{aligned}$$
(8)
Table 5 Response surface test design and results of first group.
Full size table

The variance analysis of the regression equation is presented in Table 6. The F value and P value serve as indicators for this analysis. A larger F value and a smaller P value suggest a higher reliability of the analysis results. In Table 6, the F value for the coefficient of variation regression model is 12.36, with a P value of less than 0.0001 (P < 0.01), indicating a high degree of fit for the coefficient of variation within the regression model. The primary terms, X1 (rotational speed) and X2 (lead angle), exhibit significant effects on the coefficient of variation. The second term, X32, also has a significant influence, while the other terms do not. In Eq. (8), the absolute values of the factors X1, X2, and X3 are 1.34, 0.79, and 0.43, respectively. Thus, the influence of various factors on the coefficient of variation (Y1) is ranked from largest to smallest as follows: X1 (groove rotation speed), X2 (lead angle), and X3 (groove number).

Table 6 Variance analysis of regression equation.
Full size table

Using Design Expert optimization toolbox, the regression equation model was optimized and solved, and the optimal parameters were obtained 49.6 r/min of groove rotation speed, 9.59° of lead Angle, and 10 of groove number. Under these conditions, the coefficient of variation was 8.75%.

Analysis of model interaction terms

The response surface diagram illustrating the relationship between various factors was generated based on Eq. (8). One of the test factors was set to zero, allowing for a more detailed discussion of the effects of the remaining factors on the test indicator. The strength of interaction among the factors was assessed based on the shape of the response surface, an ellipse indicated a significant interaction between two factors, whereas a circle suggested the absence of such interaction31,32.

Figure 8a illustrates that when the groove number was at level 0 (12), the coefficient of variation decreased as the groove rotational speed and lead angle increased. This decrease can primarily be attributed to the reduction in distance between adjacent wheat particles with increasing groove rotational speed. Furthermore, as the lead angle increased, the distance between the wheat in the upper part of one alveolus and the wheat in the lower part of the adjacent alveolus decreased, resulting in a lower coefficient of variation. Figure 8b indicates that when the lead angle was at level 0 (5°) and the groove rotational speed remained constant, the coefficient of variation initially increased and then decreased with an increase in the groove number. When the groove number was held constant, a decrease in the groove rotational speed led to a reduction in the coefficient of variation, suggesting that the seeding effect diminishes with increasing groove rotational speed. Figure 8c shows that when the groove rotational speed was at level 0 (40 r/min) and the lead angle was constant, the coefficient of variation initially increased and then decreased with a larger groove number. Conversely, when the groove number was held constant, the coefficient of variation decreased as the lead angle increased.

Fig. 8
figure 8

Response surface of interaction factors to the coefficient of variation (Y) for first group. (a) Response surface under factors X1 and X2. (b) Response surface under factors X1 and X3. (c) Response surface under factors X2 and X3.

Full size image

Analysis of the results of the second group tests

Experimental design and results

The design and results of the second group of experiments are presented in Table 7. The obtained test results were analyzed using Design-Expert software, leading to the development of a quadratic regression model for the coefficient of variation Y, represented by the coded values of each factor, as illustrated in formula (9).

$$\begin{aligned} Y\,=\, & {\text{9}}.{\text{45}} - 0.{\text{68}}{X_{\text{1}}}\,+\,0.0{\text{3}}{X_{\text{2}}} - {\text{1}}.{\text{27}}{X_{\text{3}}}\,+\,0.{\text{19}}{X_{\text{1}}}{X_{\text{2}}}\,+\,0.{\text{64}}{X_{\text{1}}}{X_{\text{3}}} \\ & - 0.0{\text{1}}{X_{\text{2}}}{X_{\text{3}}}\,+\,0.{\text{18}}{X_{\text{1}}}^{{\text{2}}} - {\text{1}}.{\text{21}}{X_{\text{2}}}^{{\text{2}}} - 0.{\text{19}}{X_{\text{3}}}^{{\text{2}}} \\ \end{aligned}$$
(9)
Table 7 Test design and results of response surface of second group.
Full size table

The variance analysis of the regression equation is presented in Table 8. The F value of the coefficient of variation regression model was 14.67, and the P value was less than 0.0001 (P < 0.01), indicating a high degree of fit for the coefficient of variation within the regression model. The primary terms, X1 (rotational speed) and X3 (groove number), exhibited significant effects on the coefficient of variation. Additionally, the interaction term X1 × 3 and the quadratic term X22 also demonstrated significant effects, while the other terms did not significantly impact the coefficient of variation and can therefore be disregarded. In Eq. (9), the absolute values of factors X1, X2, and X3 are 0.68, 0.03, and 1.27, respectively. Consequently, the influence of the various factors on the coefficient of variation (Y), ranked from largest to smallest, was X3, X1, and X2, corresponding to groove number, groove rotation speed, and lead angle, respectively.

Table 8 Variance analysis of regression equation.
Full size table

Using Design Expert optimization toolbox, the regression equation model was optimized and solved, and the optimal parameters were obtained 43.15 r/min of groove rotation speed, 9.81° of lead Angle, and 16 of groove number. Under these conditions, the coefficient of variation was 6.98%.

Analysis of model interaction terms

The response surface diagram illustrating the relationship between various factors was generated based on Eq. (9). One of the test factors was set to zero, allowing for a detailed discussion of the effects of the remaining factors on the test indicator. Figure 9a demonstrates that when the groove number was at level 0 (14) and the lead angle remained constant, the coefficient of variation decreased as the groove rotation speed increased. Conversely, when the groove rotation speed was held constant, the coefficient of variation initially decreased before increasing as the lead angle rose. This behavior can be attributed to the fact that a small lead angle tends to cause pulsation, while excessively large lead angles and groove rotation speeds can lead to issues such as filling unsaturation or accumulation, which ultimately destabilizes seeding. Figure 9b indicates that when the lead angle was at level 0 (10°) and the groove rotational speed was constant, the coefficient of variation first increased and then decreased with an increase in the groove number. Additionally, when the groove number remained constant, the coefficient of variation decreased with a reduction in groove rotational speed. Figure 9c illustrates that when the groove rotational speed was set to level 0 (40 r/min) and the lead angle was constant, the coefficient of variation decreased with an increase in groove number. Furthermore, when the groove number was held constant, the coefficient of variation initially decreased and then increased as the lead angle increased.

Fig. 9
figure 9

Response surface of interaction factors to the coefficient of variation Y for second group. (a) Response surface under factors X1 and X2. (b) Response surface under factors X1 and X3. (c) Response surface under factors X2 and X3.

Full size image

Test verification results

To verify the reliability of the simulation results, the optimization parameters were evaluated. The optimal parameters identified were a groove rotation speed of 43 r/min, a lead angle of 9.8°, and a groove number of 16. The test was repeated nine times. The errors between the test results and the simulated values are presented in Table 9, while the seeding effect is illustrated in Fig. 10.

Table 9 Testing results and error.
Full size table
Fig. 10
figure 10

Verification test of metering performance.

Full size image

According to the calculations presented in Table 9, the average flow rate and coefficient of variation from nine repeated seeding tests were 6.20 g/s and 7.20%, respectively. In comparison to the simulated value, the mean relative errors for the flow rate and coefficient of variation were 7.31% and 4.97%, respectively. The uniform model size of wheat in the simulation test and the differing shapes and sizes of the seeds on the test platform resulted in a test value for the seed distribution uniformity index that was higher than the simulated value. However, the overall relative error remained small, indicating that the simulation test of the outer groove wheel seed metering device is a feasible method for optimizing the performance parameters of seed distribution. Furthermore, the regression model demonstrates a certain degree of reliability.

Discussion

The seed metering device is a fundamental component of seeder. The outer grooved wheel seed metering device is characterized by its simple structure and strong versatility, making it widely applicable in various seed planting equipment. To mitigate the pulsatility effect during seeding and enhance seeding uniformity, researchers have investigated the structure and operational parameters of the outer grooved wheel seed metering device. By optimizing parameters such as the spiral lift angle, working length, and Rotation speed of sheave, the performance of the wheel seeding device has been significantly improved4,33. However, due to the diversity of seeding objects, this study conducts a thorough analysis of the seeding process associated with the outer grooved wheel seed metering device for wheat, optimizing critical parameters such as lead angle, groove number, and groove rotation speed.

The DEM is a numerical method that takes into account the interactions of discrete particles in contact and allows the evaluation of mutual force interactions. With this method, simulation is performed by using translational and rotational motion equations for each particle34. So, numerical simulation methods can demonstrate good advantages. This study can capture detailed changes in seed particles during the process of seeding from a simulation perspective, making up for the shortcomings of existing experimental methods. The research conclusion can deepen the understanding of the interaction between the seed metering device and the seed, and provide useful references for the design and optimization of machinery. The best performance of the seed metering device was found to have a coefficient of variation of 4.97%. Values of coefficient of variation around 9.5% and 4.37% were reported by Huang and Boydas et al.19,21 and they were considered to be good enough for seeder. Similarly, the researchers employed the discrete element method to optimize and validate the spiral groove wheel fertilizer apparatus. The coefficient of variation between the simulation and experimental results ranges from 5.60 to 10.89%, while the relative error in fertilization amount varies from 9.96–12.73%35,36. These findings further demonstrate that the optimization of the structural parameters of the seed metering device using the discrete element method is highly reliable.

Predictive modeling in manufacturing can identify key influencing factors, establish the mapping relationship between controllable parameters and quality indicators, and quickly locate the optimal parameter combination, significantly reducing material and time costs. To improve the accuracy of prediction, the combination of multiple technologies can significantly enhance the accuracy of prediction. For instance, in the hybrid modeling of RSM and ANN, RSM is first used to preliminarily screen variables, and then ANN is employed for fine modeling. Optimize the ANN hyperparameters by using the genetic algorithm to improve the convergence speed. This approach significantly raises fabrication standards by minimizing errors and improving product quality. By comparing and combining methods such as Taguchi, ANOVA, and RSM, a more robust optimization strategy can be provided. Öztürk et al.12,37,38 has conducted in-depth research in this aspect. Using GA and RSM, the energy consumption and machinability of cast iron was optimized, the optimal parameter values under different methods were obtained, and the contribution rates of different factors to the response index were given in combination with the ANOVA method. In order to optimize the cutting parameters in the slot milling process of AISI 316 stainless steel on CNC milling machine, experimental data were modeled using machine learning methods of regression analysis and artificial neural networks. Response surface methodology and Analysis of Variance were employed to determine optimal thrust values, which provided a comprehensive understanding of how design and operational factors influence UAV engine performance. RSM analysis commonly utilizes second-degree polynomial functions. These functions are created based on data obtained through experimental design and aim to understand the relationships between dependent and independent variables, facilitating the optimization of complex processes. The Taguchi method focuses on creating robust design that are resistant to variations in control factors, and often involves an iterative process to achieve better results. The RSM method shows a complex mathematical equation involving interactions between variables, while the Taguchi method provides a simpler equation.

Conclusion

Through the response surface test, the parameters of the spiral outer grooved wheel seed metering device were analyzed using the coefficient of variation, resulting in two sets of experimental data. Subsequently, we employed the parameter optimization module in Design-Expert software to refine the parameters. Ultimately, the optimal parameters were established as 43 r/min for the curtain groove rotation speed, 9.8° for the curtain lead angle, and 16 for the curtain groove numbe. Under these optimal parameters, the predicted value of the coefficient of variation was 6.98%.

To verify the reliability of the entire design process, we conducted experimental validation. The final results indicated that the coefficient of variation ranged from 6.48 to 7.61%, with an average value of 7.20%. The relative error of the coefficient of variation between the test value and the calculated value was 4.97%, demonstrating that it is feasible to optimize the performance parameters of the outer groove wheel seed metering device using the discrete element method.